Abstract
The article emphasises both the advantages and disadvantages of photovoltaic power plant deployment, assessing the current stage of development as well as the deficient characteristic criteria, such as the occupied specific surface area or the associated unpredictability. The authors consider that current technologies related to photovoltaic plants provide a maximum efficiency of approximately 28%. Consequently, management methods must be applied in order to improve efficiency and eliminate the reported deficiencies. When assessing a medium- to high-power PV plant, the initial investment, projected efficiency, and parameters of the desired plant are correlated, and sometimes, a cheaper and less efficient power plant can be recommended. Although solar trackers may represent a viable solution in certain scenarios, their effectiveness is strongly influenced by various factors, including panel orientation, climatic conditions, installed capacity, and the specific technologies. These variables can significantly affect such systems’ overall efficiency and suitability. The present study proposes a statistical approach to assessing the economic efficiency of photovoltaic systems equipped with solar trackers, aiming to enhance energy production performance. The results are correlated and validated using field data obtained from existing literature studies to ensure the reliability and accuracy of the analysis. For a better analysis, the paper presents two methods, ANOVA and STEM, which are derived from quality control. The novelty aspect of this proposal consists of the combination of specific data obtained from the PVGIS platform with a new approach for optimisation of energy production in photovoltaic systems based on geographical coordinates. The STEM statistical method provides a high degree of novelty because, although it is a well-known method, it has not yet been applied to analyse the technical and economic efficiency of photovoltaic systems. One of the main advantages of this method is its ability to incorporate a wide range of technical and economic performance parameters. A case study is provided to evaluate the benefits of implementing the STEM method.
1. Introduction
When considering applications such as PV power plants, substantial increases in technical and economic performance can be achieved by improving safety in operation, location, and mounting systems, as well as optimising specific management parameters. This involves the application of statistical methods.
The first theme addressed in the article is selecting the tilt angle of the PV panels used on a PV plant to optimise the efficiency of photovoltaic systems using statistical analysis based on the ANOVA method. There are several nonparametric methods of statistical analysis, the most common being the description of the Kruskal–Wallis test in Excel [1], using the Taguchi and ANOVA Analysis for PV plants [2], a multi-objective design optimisation strategy for hybrid PV plants [3], one-way ANOVA analysis of variance [4], operating parameters and degradation of PV [5], and statistical methods and artificial neural network approaches for PV plant decisions [6].
The second approach involves a managerial and statistical analysis based on a STEM-type method. Economic efficiency analysis should be conducted during the initial phase of developing a new photovoltaic (PV) plant. This analysis must consider technical and financial factors relevant to the specific location of the proposed facility. Quality management systems began to be developed in the early 20th century as statistical sampling techniques were introduced into the quality control methodology. In the following years, there was an increasing demand for increased productivity. It became apparent that a more robust, structured, and logical approach to quality control was needed. There are numerous statistical methods for product quality control, including the impact of product quality on sales, as demonstrated by the Sales Training Evaluation Model (STEM) [7,8]. Thus, the technical level method can be used to evaluate the quality of products based on the von Neumann–Morgenstern utility principle and the Cobb–Douglas production functions [9]. A relation of the form defines the absolute technical level (Hai) [10,11].
The STEM method currently used in the education system, where STEM stands for science, technology, engineering, and mathematics, although it shares the same acronym, is distinct from the sales method STEM discussed in this context.
2. Literature Review
2.1. Review of High-Performance Technologies for PV Cells and Modules
Due to the exponential growth of industrial production, with significant implications for the development of energy sources and all types of transportation, there is an urgent need to reduce the carbon footprint. Therefore, most countries worldwide are interested in developing and optimising renewable energy sources: solar, wind, geothermal, hydropower, ocean energy, and bioenergy. The photovoltaic (PV) conversion provides the most outstanding development dynamics. According to the Clean Energy Technology Observatory [12], in 2022, the cumulative global installed photovoltaic capacity exceeded one terawatt (TW), while cumulative electricity generation from photovoltaic sources was approximately 158 terawatt-hours (TWh). Considering this dynamic, various equipment and processes use PV systems for an efficient power supply [13]. Despite certain shortcomings in solar energy conversion efficiency, it remains one of the most reliable and affordable energy sources, especially in remote areas. Its conversion can provide electricity to supply isolated households by ensuring the end-users’ energy consumption and management of other potential various generation sources [14] or different equipment for monitoring environmental parameters or biodiversity protection, such as behavioural barriers associated with river water intakes [15].
In theory, the maximum efficiency of a single junction p-n solar cell is 30% at 1.1 eV, but the maximum laboratory efficiency for a single junction is about 27%. At the same time, the efficiency of photovoltaic modules is lower than that of a PV cell due to resistive losses in the solar cells, as well as variations in individual solar cell efficiencies [16]. Although the conversion efficiency of hydroelectric power plants is around 90% and that of power plants is about 40%, both have a very low carbon footprint. Yet, a series of arguments plead for the priority of photovoltaic conversion [17,18,19]. First of all, solar energy is practically available everywhere, unlike hydroelectric power, and, relative to nuclear power plants, there are no radioactive residues. However, although PV systems have an almost zero carbon footprint, this can be significant if the manufacturing processes are taken into account [20,21]. Additionally, extending the lifespan of PV modules and addressing waste management at the end of their lifespan have recently become significant concerns in the context of the circular economy. This concern becomes more pressing as the prospect of equipping photovoltaic power plants with lithium-based batteries becomes a requirement for efficiency. Therefore, recycling these devices will involve more significant challenges than recycling PV modules.
The history of photovoltaic conversion will soon complete two centuries of existence, with its beginnings marked by the French experimental physicist Alexandre-Edmond Becquerel in 1839. The progress in this field has been modest given that over the last half-century, we have witnessed an exponential increase in efficiency [16,22]. Thus, nowadays, apart from technologies of the first-generation a-Si, c-Si mono and polycrystalline, there are envisaged superior efficiencies characterising the new technologies, even in the commercial field, as presented in Table 1:

Table 1.
Efficiency of various PV panels [16,23,24].
The table above should also include thin-layer cadmium telluride (CdTe) solar cells, which are the second most common photovoltaic PV technology after crystalline silicon, representing 21% of the U.S. market and 4% of the global market in 2022, with an efficiency of approximately 24%, and GaAs module technology with concentrators (Fresnel lenses), which can reach an efficiency of 28% [25,26].
2.2. Analysis of the PV Market in Romania
The cumulative global PV installed capacity increased from 483.1 GW in 2018 to 580.2 GW in 2019, representing a 21% relative growth [27]. It further increased from 866.02 GW in 2021 to 1055.03 GW in 2022, representing a 22% relative growth [28]. The highest contribution of currently installed PV systems is identified in Asia. Relevant examples come from China (175 GW in 2018 and 392.46 GW in 2022), Japan (55.5 GW in 2018 and 83.1 GW in 2022), and India (26.8 GW in 2018 and 62.85 GW in 2022). Europe comes in second regarding PV installed capacity, with considerable shares in Germany (45.9 GW in 2018 and 66.66 GW in 2022), while the UK has an insignificant increase (13.4 GW in 2018 and 14.66 GW in 2022).
Specific prices for PV panels decreased approximately linearly starting in 2008, by about 35% on the American market and by about 80% on the European market, likely due to cheaper imports from China [29,30]. For instance, in the USA, the mean price of PV panels varied from USD 2.51 to USD 3.31 per watt in 2020, while the average costs were USD 0.40–USD 0.60 per watt for polycrystalline panels and USD 0.60–USD 0.90 per watt for monocrystalline panels as of January 2020. Chinese production became the market leader relatively quickly, starting in 2007. Since China is the world’s largest manufacturer and consumer of PV cells and modules, Chinese production has driven down prices from USD 4.73 per watt in 2007 to USD 0.19 per watt in 2020 [29].
Considering the significant variability of the statistical data available in the literature, Table 2 includes several relevant commercial offers of photovoltaic modules available on the Romanian market in February 2024 based on various technologies: Si-mono and poly-crystalline, PERC and TOPCon technologies, bifacial variant, and GaAs technology with concentrators (Fresnel lenses), all with an efficiency between 17% and 28%. Table 2 is based on the prices provided by retailers’ online shops in Romania.

Table 2.
Commercial analysis of the PV market in Romania for 2024.
The efficiency shown in Column 4 is calculated by dividing the PV module’s peak power output from Column 3 by the maximum irradiation in the region (1000 W/m2) for the panel area from Column 2.
2.3. Assessment of PV Power Plants’ Operating Conditions
The final product of a power plant is the electric power supplied to the grid at 50 Hz and various voltage levels, depending on the power plant’s structure. For photovoltaic plants, the voltage level varies depending on the injection points in the system, which include 11 kV, 33 kV, 110 kV, and 400 kV. Electricity is a product; like any product, it must meet its quality requirements. They are specified in the IEC 61000-4-30:2015+A1:2021 and EN 50160 standards [31,32]. A PV system that does not comply with these standards will generate problems for the transmission and distribution grids, potentially risking disconnection from the power system. These interruptions can affect the efficiency of photovoltaic plants, decreasing the installed power/electricity produced ratio.
2.4. Using Statistical Methods for the Assessment of PV Power Plants
Parametric statistical techniques begin with a series of conditions regarding the normality and homogeneity of the subjects’ results distribution. Nonparametric techniques are also referred to as statistical techniques that are independent of data distribution when these conditions are not met. Nonparametric tests can be used when there are doubts about the normality of statistical data. The advantage of nonparametric tests is that they are more robust, meaning they use fewer assumptions than parametric tests. Nonparametric tests do not need a known a priori distribution of observed data or a large volume of data.
2.5. Prediction of PV System Performance Using PVGIS Platform
A geographic information system (GIS) is a computer system used to create, store, analyse, and process global information. GIS technology can be applied in various scientific fields, including resource management, environmental impact studies, mapping, and route planning. For photovoltaic system applications, the most used are the web applications from the National Renewable Energy Laboratory (NREL) and PVGIS.
NREL is led by the U.S. Department of Energy’s Office of Energy Efficiency and Renewable Energy and the Alliance for Sustainable Energy, LLC, a partnership between Battelle and MRIGlobal. NREL’s geospatial data science research utilises geographic information systems to produce maps, analyses, models, applications, and visualisations that inform energy planning and production, including the PVWatts Calculator. The analogue of this application for Europe is the PVGIS Platform.
PVGIS is a web application that provides users with data on solar radiation and energy production generated by photovoltaic systems in most parts of the world. It is entirely free to use, with no restrictions on how the results can be used, and no registration is required. The application utilises terrestrial and satellite databases that have been statistically processed over extended periods [33].
The necessary input data consider the following:
- The location on the displayed map or the analytical entry of the geographical position (latitude and longitude);
- Choosing the database for solar irradiation;
- Photovoltaic cells/panels technology (Si-mono/polycrystalline);
- Installed power of the photovoltaic power plant [kWp];
- System power losses (typical 14%);
- Orientation of the panels according to azimuth (−90° East, 0° South, and 90° West, respectively);
- Orientation of the panels according to the angle of inclination to the horizontal—in the case of the mount without tracking;
- Characteristic of the tracking system (one or two axes);
- Economic data:
- ▪
- Cost of investment (in the currency of the respective country);
- ▪
- Interest rate [%/an];
- ▪
- Estimated service life [years].
The output data include the following:
- Global horizontal irradiation (GHI)—This value is the monthly sum of the energy of solar radiation hitting one square meter from a horizontal plane, measured in kWh/m2;
- Direct average irradiation (DNI)—This value is the monthly sum of the solar radiation energy hitting one square meter always oriented in the direction of the sun, measured in kWh/m2, including only the radiation coming directly from the sun;
- Global irradiation, optimal angle—This value is the monthly sum of the solar radiation energy hitting one square meter oriented toward the equator at the angle of inclination that gives the highest annual irradiation, measured in kWh/m2;
- Global irradiation, selected angle (GTI)—This value is the monthly sum of the solar radiation energy hitting one square meter from a plane oriented toward the equator at the angle of inclination chosen by the user, measured in kWh/m2;
- Ratio of diffuse radiation to global radiation—Much of the radiation that reaches the ground does not come directly from the sun but from scattering clouds and water vapour from the air (blue sky). This is known as diffuse radiation. This number represents the fraction of the total radiation that reaches the ground due to diffuse radiation.
- Electricity production per month (January–December). According to input data for photovoltaic systems, PVGIS can also calculate the cost of electricity generated by the photovoltaic system. The calculation is based on a “Levelized Cost of Energy” (LCOE) method, similar to how a fixed-rate mortgage is calculated.
- The total cost of purchasing and installing the photovoltaic system in the currency of the respective country;
- The interest rate, in % per annum, is assumed to be constant throughout the lifetime of the photovoltaic system;
- Estimated lifespan of the photovoltaic system in years.
The data provided by PVGIS are used as a precursor to investigate the possibility of increasing efficiency through statistical methods, either by optimising the structure of photovoltaic systems (ANOVA method) or by optimising specific economic parameters (STEM method). Higher-efficiency photovoltaic plants will help reduce the cost of an installed photovoltaic system, decrease the occupied area, and implicitly substantially improve the technical and economic parameters related to circular economy principles.
3. Methodology
Statistical methods can be applied to achieve the efficient operation of PV systems. Therefore, the methodology for each approach is described below.
The following outlines the theory and methodology utilised for applying statistical methods to analyse the efficiency of the photovoltaic (PV) system: ANOVA for optimising the PV module’s structure and STEM for optimising specific economic parameters.
3.1. ANOVA Method Regarding Operational and Structural Analysis
The parametric statistical techniques begin with a series of conditions regarding the normality and homogeneity of the subjects’ results distribution. Nonparametric techniques are also referred to as statistical techniques that are independent of data distribution when these assumptions are not met. The advantages of this technique lie in its ability to process a diverse range of data, both qualitatively and quantitatively. Nonparametric tests can be used when there are doubts about the normality of statistical data. The advantage of nonparametric tests is that they are more robust and use fewer assumptions than parametric tests. Nonparametric tests do not need a known a priori distribution of observed data or a large volume of data. The main disadvantage is the lower power to detect the falsity of a null hypothesis. There are several nonparametric methods, the most common being:
- Fisher’s test technique—(χ2);
- Mann–Whitney U test (equivalent to the independent parametric t-test);
- Wilcoxon test of paired ranks (ANOVA equivalent of repeated measurements or t-dependent);
- Kruskal–Wallis ANOVA test of ranks, equivalent to simple ANOVA (data are converted to ranks).
- Analysis of variance (ANOVA) is a statistical formula that compares variances across different groups’ means (or averages). In this paper, we propose using the Kruskal–Wallis ANOVA test of ranks to determine the tilt angle of the panels based on geographical coordinates and season.
The primary phenomenon that generates the application of statistical methods is data variability. The general notion of variability refers to the measurable deviations of individual values from a central value, known as the mean (μ). By analysing statistical collectivity with the help of central tendency indicators, the manifestation of a particular phenomenon can be predicted. A collectivity has a specific internal organisation defined by how individual values are distributed around the central value. Thus, one central value may be credible, and another may not. For this reason, the central tendency analysis must be supplemented with indicators of variation and the form of distribution.
In probability theory and statistics, variance is the mean of the squared deviations of a random variable from its mean. Informally speaking, it measures the distance of individual (random) values in a crowd from their average. Variance is a crucial concept in statistics, used in both descriptive and inferential statistics, as well as in hypothesis testing and Monte Carlo methods. Statistical methods are widely used throughout science.
Analysis of variance (ANOVA) is a statistical method used to compare the means of three or more groups. Its purpose is to determine whether there are significant differences between groups and to identify which groups have these differences. ANOVA compares the variability between groups (intergroup variability) with the variability within groups (intragroup variability). If the intergroup variability is significantly greater than the intragroup variability, then we can conclude that there are significant differences between the groups.
In the article, the Kruskal–Wallis H test will be applied using Relationship (1):
- N = the size of the sample analysed (total number of observations across all groups);
- k = number of groups;
- R = the sum of the ranks of a group; ni = the number of elements in a group.
3.2. Application of STEM Method Focused on Economic Efficiency
The managerial approach based on a STEM-type statistical analysis is currently applied to product competitiveness analysis. As mentioned, this method is used for the first time in photovoltaic power plants, which are considered market-promoted products. The process was applied to five existing PV plants with six known characteristics, three of which represent the subset of characteristics whose value is directly proportional to the quality of the product, and the other three represent the subset of characteristics whose value is inversely proportional to the quality of the product, as described in the next section.
The technical level method can evaluate product quality based on the von Neuman–Morgenstern utility principle and the Cobb–Douglas production functions [9]. A form relation defines the absolute technical level Hai [10,11].
where
- S1 represents the subset of characteristics whose value is directly proportional to the quality of the product;
- S2 represents the subset of characteristics whose value is inversely proportional to the quality of the product;
- i represents the product for which the technical level is calculated;
- 1 represents the reference product (any of the analysed products can be considered a reference);
- a is a constant that defines the technical level of the reference product (usually a = 1000, to differentiate the products sufficiently);
- j is the characteristic of the product;
- Kij is the value of the characteristic j for product i;
- γj represents the weight of the characteristic j.
The relative technical level can also be calculated with the relation:
The product with the highest technical level has a value of 100, while the others have values below this.
The primary challenge is determining the weights of the characteristics, γj, to apply the above relations. Two methods are primarily known for this: the MISENIT and STEM methods [10,11]. The MISENIT method is based on the elasticity of the operating expense function, which is the property of a function that changes when its argument changes. The STEM method is less finesse than the previous one. Still, it allows, on the other hand, a faster calculation of the weights, given that the analyst must be a specialist in exploiting the respective products. To accomplish this, the characteristics are compared two by two, defining a matrix with the elements aj1j2 established as follows:
where Kj are the quality characteristics.
The signs that intervene have the following meanings:
(≫)—much more important;
(>)—more important;
(≈)—equivalent;
(<)—less important.
Under these conditions, the weights of the characteristics are calculated with Relation (5):
The STEM method algorithm flowchart shows the computing steps for the relative technical level evaluation:
According to Figure 1, the first step of the presented algorithm involves selecting parameters from sets S1 and S2, respectively. For PV power plants, the three parameters whose value is directly proportional to the electricity supplied are the panel’s efficiency, expressed in percentages, the installed power of the panel, described in Wp, and the presence of a tracking-type orientation system. The parameters whose value is inversely proportional to the efficiency of the electricity supplied are the surface area of the panel (m2), the specific cost of the panel (EUR/Wp), and the total losses of the photovoltaic system relative to inverters, transformers, and cables (typically 14%). The second step involves selecting several PV power plants for product quality analysis, whose parameters, as mentioned above, are well defined. The third step is crucial because it consists of assigning scores to the mutual influences between the six parameters of sets S1 and S2, respectively, according to Relationship (4). These influence scores are presented in a table or matrix with terms aj, as illustrated in the next chapter for a specific case. Based on this table, the range γj, the exponent from Equation (2), is calculated according to Relation (5).
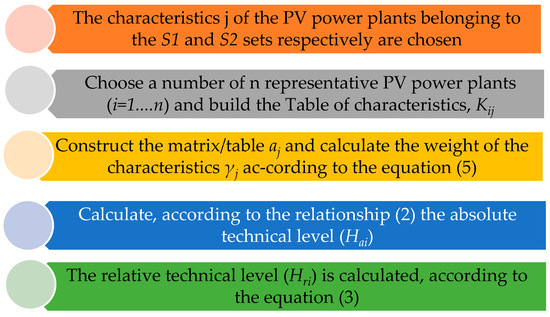
Figure 1.
The STEM method algorithm flowchart.
Finally, steps four and five only apply Relations (2) and (3) to calculate the absolute and relative technical level.
4. Results
When assessing a medium-to-high-power photovoltaic plant, the initial investment, projected efficiency, and parameters of the desired plant are correlated. In some cases, a cheaper and less efficient plant may be recommended. This paper presents two methods for enhanced analysis: ANOVA and STEM, which are derived from quality control principles.
4.1. Analysis of the ANOVA Method Results
Regarding the statistical methods, a presentation of the PVGIS platform [30] with input and output data was provided to predict electricity production for a photovoltaic plant based on geographical and meteorological parameters, as well as the technical data of the used PV panels. Based on the data provided by the PVGIS platform, an analysis is conducted to examine the impact of a panel inclination angle on electricity production. The literature shows that orientation tracking systems can increase efficiency by up to 30% (depending on latitude), as shown in Figure 2, generated by the PVGIS platform.
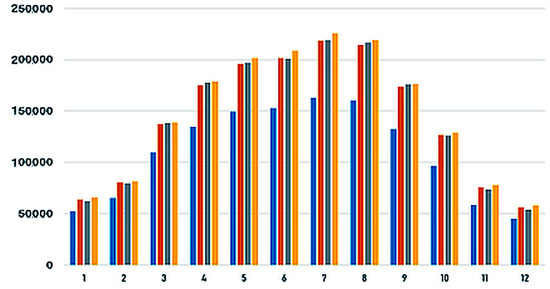
Figure 2.
Tracking influence on monthly electricity production for latitude 45° for fixed (blue) and adjustable tilt angle: vertical (red), horizontal (grey), and two-axle (orange).
Series 1 (blue) represents the monthly electricity production for the photovoltaic system of 1.19 MWp in the case of fixed panels inclined at an angle of 30°, series 2 (red) and 3 (grey) for the case of single-axis tracking system—azimuth and tilt (inclination), respectively—and series 4 (orange) for the case of two-axis tracking systems. It is observed that there is no significant difference between the three tracking systems (with one axis and with two axes, respectively).
Although the increase in electricity production is significant in the case of tracking systems, they are more complex, require maintenance, and may not be cost-effective for all applications. This analysis is fundamental to deciding to what extent the investment is economically justified, depending on geographical coordinates.
In this respect, the statistical analysis carried out by the ANOVA method, corroborated by the data obtained through the PVGIS platform, shows the following: on the one hand, between three consecutive months, there is no statistically significant difference between the groups in terms of the angle of inclination; on the other hand, the panels can be segmented according to the angle of inclination.
Keeping the criterion of three consecutive months, obtained by applying the ANOVA method, as an example for the case of latitude 45°, an optimal arrangement would be the following:
- For June, July, and August, an optimum tilt angle of 30° is obtained;
- For September, October, and November, an optimal tilt angle of 50° is obtained;
- For December, January, and February, an optimal tilt angle of 70° is obtained;
- For March, April, and May, an optimal tilt angle of 40° is obtained.
The methodology remains valid for other geographical coordinates, provided the data are available from the PVGIS platform.
- Case analysis—Fixed tilt angle
The statistical analysis begins with the specific case of a photovoltaic power plant with a capacity of 1.19 MWp [34], which generates a declared amount of renewable energy of approximately 1428 MWh/year. The envisaged PV system is 26°55′ east longitude and 46°35′ north latitude in Romania. Table 3 summarises these data, obtained through the PVGIS platform (PVGIS—re.jrc.europa.eu—European Union [33]) for each month of the year, with the values provided in MWh.

Table 3.
PVGIS predicts the annual energy production (MWh) of PV plants at seven different tilt angles.
The influence of the panels’ inclination on annual electricity production will be analysed statistically, applying the Kruskal–Wallis test to sets of cases with three distributions.
We propose analysing two sets of cases, each with three distributions, using July as a reference, as shown in Table 4.

Table 4.
Distributions per month for the data analysed.
The selected cases were chosen so that we have two sets of data with different ranges of variation (5 months and 3 months, respectively) to apply the presented statistical method. Table 5 shows the characteristic values that express the amount of electrical energy obtained depending on the inclination angle.

Table 5.
Case A: Monthly energy production and ranks related to the panel’s angle (in MWh).
These values were selected from Table 3 above. Column 37° means the optimum value of the tilt angle of the panel for which the maximum annual electric energy is obtained according to the PVGIS platform for the geographical and climatological coordinates considered.
Next, Table 6 was built with 24 columns corresponding to the 24 values from Table 5, representing the ranks under Relation (2). The values are placed in ascending order. Where we have identical values, the corresponding rank is the arithmetic mean of the ranks corresponding to similar values. Ranks are relative numbers to 100, which represents the minimum value.

Table 6.
Case A: Table of values with explanation of ranks.
Next, the table of ranks was built for the three analysed months: May, July, and September (Table 7).

Table 7.
Case A: The analysis (table of ranks) for May, July, and September.
The last two rows in Table 7 represent the sum of the ranks and the square of the sum of the ranks for the analysed cases, respectively. Next, the equation characteristic of the HSTAT (Kruskal–Wallis test) was applied:
Relationship (6) represents the value of the test applied in the present case, called the H statistic (HSTAT).
The value thus obtained is compared with χ2 obtained from the Chi-Square Distribution Table for 2 degrees of freedom (df = 2) and alpha = 0.05 (statistical confidence interval of 95%), and the value obtained is
According to the theory, hypothesis H0, for which the three distribution probabilities are equivalent, is denoted by HSTAT > χ2, meaning that hypothesis H0 is rejected due to a significant difference between the groups.
As a conclusion, for case A, the H0 hypothesis is rejected because the value of HSTAT is greater than the χ2. There is a significant difference between the analysed groups.
Next, the same algorithm was applied for case B, as presented in Table 8.

Table 8.
Case B: Monthly energy production (in MWh) and ranks related to the panel’s angle for June, July, and August.
Table 8 is similar to the above-presented Table 5, with the May, July, and September triad replaced by June, July, and August.
Table 9 presents the table of values for Case B, similar to Table 6. Table 10 presents the table of ranks for Case B, which is identical to Table 7.

Table 9.
Case B: A table of values with explanation of ranks.

Table 10.
Case B: The analysis (table of ranks) for June, July, and August.
For case B, the H0 hypothesis cannot be rejected because the value of HSTAT is smaller than the χ2, as presented in Equation (8). In this case, with the analysed months having similar energy production values, there is no significant difference between the analysed groups, as indicated by the Kruskal–Wallis H test.
4.2. Applying the STEM Method Results
According to the flowchart in Figure 1, the following steps were considered:
- Step 1
The characteristics j of the PV power plants belonging to the sets S1 and S2, respectively, are chosen:
- Efficiency of photovoltaic panels (E), the greater, the better;
- Nominal power of a panel (P), the greater, the better;
- Tracking systems (T), the greater, the better;
- Panel surface (S), the smaller, the better;
- The specific cost of a panel (C), the smaller, the better;
- Overall losses (L), the smaller, the better.
- Step 2
It chose five representative PV power plants (i = 1 … 5), with the respective general characteristics:
- PV power plant Borzesti (Romania), 1.19 MWp—considered the reference [34], using monocrystalline PV panels;
- PV power plant Stupini–Brasov (Romania), 20 MWp, Ref. [35] monocrystalline panels;
- PV power plant, Ouarzazate (Morocco), 20 kW, Refs. [36,37,38] using HCPV technology, including tracking;
- PV power plant Elazig (Turkey), 1 MWp, Ref. [30], using polycrystalline panels;
- PV power plant Bisha (Saudi Arabia), 10 MWp, Ref. [39] using monocrystalline panels and a single-axis tracking system.
Furthermore, the characteristics table identified in Step 1 was constructed using data extracted from the bibliography for the proposed PV plants (Table 11). Since PV Power Plant 1 was considered the reference, the following notations were assigned: 2 ≡ A, 3 ≡ B, 4 ≡ C, and 5 ≡ D.

Table 11.
Characteristics of the chosen PV power plants.
The PV builders provide the values for efficiency (E), the rated power of the used PV panel (P), panel surface (S), and the specific cost of a PV panel (C) in Table 11 [27,31,32,33,34,35,36].
In the above table for the tracking systems (T) parameter, a coefficient of 1.10 (+10%) was assigned for photovoltaic systems without tracking and 1.30 (+30%) for those with tracking because systems oriented according to the sun improve yield by approximately 30%. At the same time, a tracking system increases costs by about 10% compared to the specific cost (C), as specified in the fifth row of the table above.
For the overall losses (L) parameter from Table 11, it is currently considered that these losses represent approximately 14% of the electricity produced by a PV power plant, which is equal to all the PV plants analysed. In the future, if a plant diminishes its own losses, this parameter can be adjusted accordingly.

Table 12.
Table of characteristics, Kij.
- Step 3
The coefficients aij (0, 1, 2, 4) from Table 13 have been assigned, according to Relationship (6), from the weight we attribute to the influence of the quality characteristics Kij on the product compared two by two, as presented in Table 12.

Table 13.
The weight of the characteristics γj.
In Table 13, the matrix/table aj was built. The weight of the characteristics γj was calculated according to Relation (7):
- Step 4
In the end, the absolute technical level, Hai, was calculated according to Relationships (2,3), considering the HREF = 1000:
HaA ≈ 1045
HaB ≈ 549
HaC ≈ 865
HaD ≈ 904
- Step 5
The relative technical level, Hri, shall be calculated in [%] from HREF = 1000, using Relation (4):
HrA = 104.5%
HrB = 54.9%
HrC = 86.5%
HrD = 90.4%
Result: HrA > HREF > HrD > HrC > HrB.
Following this analysis, the best-performing PV power plant is Stupini–Brasov (Id 2), followed by Id 1 (reference), Id 5, Id 4, and Id 3, respectively.
5. Discussion
When assessing a medium-to-high-power PV plant, the initial investment, projected efficiency, and parameters of the desired plant are correlated, and sometimes, a cheaper and less efficient power plant can be recommended. For a more comprehensive analysis, the paper presents two methods, ANOVA and STEM, which are derived from quality control.
Regarding statistical methods, the PVGIS platform, which contains input and output data, was presented to predict electricity generation for a PV power plant based on geographical and meteorological parameters, as well as the technical data of the panels used. Based on the data provided by the PVGIS platform, an analysis is conducted to examine the impact of panel tilt angle on electricity production.
Cases A and B prove that using a fixed-tilt panel for generating maximum annual energy amount (as provided through PVGIS) is about 37°, but this is not the best solution because there are substantial variations in the monthly production.
By looking for the criterion of three consecutive months, for the case of latitude 45°, an optimal seasonal tilt angle would be the following:
- 30° for June, July, and August;
- 50° for September, October, and November;
- 70° for December, January, and February;
- 40° for March, April, and May.
From Table 3, the annual energy production for the optimum tilt angle of 37° is 1327 MWh, while the sum of energy with seasonal tilt angle is 1354 MWh. Seasonal activities to modify the tilt angle are not economically justified unless they can be incorporated into periodic maintenance procedures.
Solar tracking systems, such as single-axis or dual-axis trackers, can increase energy production by 28% or 31% compared to fixed panels. However, they are more complex, require maintenance, and may not be cost-effective for all applications.
Next, the economic efficiency of five different PV power plants was analysed using the STEM statistical method, based on the data presented in the bibliography. The technical and economic parameters considered in this analysis are the declared efficiency of the photovoltaic panels, the power and panel surface according to the catalogue data, the specific cost of a panel (EUR/Wp), the estimated losses, and the presence or absence of a tracking system. The data analysis showed that the most efficient are those with panels with monocrystalline Si technology without a tracking system. Although from a technical point of view, the PV power plant with HCPV technology (utilising a concentrator and tracking system) is the most efficient, from an economic perspective, it is surpassed by the other four systems. Thus, as a perspective for applying the STEM statistical method, an additional parameter should be introduced regarding the effective cost of the land rented or purchased for a PV power plant to highlight the adequate savings obtained by applying HCPV technology.
Monocrystalline silicon panels have been considered the most economically efficient solution, especially for medium-to-small-scale projects, due to their high efficiency, long lifespan (25–30 years), and high performance per square meter.
Although tracking systems can enhance energy output, various studies have identified key factors that may limit their overall financial viability. These include the significantly higher initial investment costs (estimated to increase total system expenditures by 25–40% due to the addition of motors, gears, sensors, and control software), as well as increased risk of mechanical failure, particularly in environments with ice, sand, or heavy precipitation that can impair tracking functionality. Furthermore, the system’s energy consumption, while relatively low, also contributes to operational costs.
In addition, tracking the sun is minimally beneficial in high-latitude regions or areas with frequent cloud cover. For example, during Romania’s cold and cloudy months, photovoltaic energy production can drop below 10%, even when using tracking systems, as only diffuse light is available.
Trackers require more space between rows to avoid shadowing as they move, reducing land-use efficiency.
Considering all the mentioned factors, the conclusion was that adding extra production capacity to a photovoltaic system (more panels) was more cost-effective than increasing efficiency with trackers.
The value of the STEM method lies in its flexibility to incorporate various technical and economic parameters. For instance, S1 represents a value directly proportional to the quality of the product, while S2 denotes a value inversely proportional to the product’s quality.
6. Conclusions
The statistical analysis, presented using the ANOVA method and the Kruskal–Wallis test, aims to determine the influence of an optimal tilt angle on the season. From the study of the data presented in Table 5, it was found that for May, July, and September (as examples), there is a significant difference in the influence of the tilt angle of the panels. If the time parameter analysed is restricted to the summer months of June, July, and August (Table 8), it was found that there is no significant difference regarding the tilt angle of the panels. Thus, it can be concluded that an alternative method could be to abandon tracking systems and build PV power plants with groups of panels oriented from the beginning under the optimal angle corresponding to each season for systems in temperate areas with four seasons.
The novel aspect of this proposal is the combination of specific data obtained from the PVGIS platform with a new approach to optimising electricity production in photovoltaic systems based on geographical coordinates. Instead of using costly tracking orientation systems that require elaborate maintenance, the proposed method suggests dividing the photovoltaic modules into groups. Each group would have a different tilt angle optimised for a specific season.
The STEM statistical method presents a high degree of novelty because, although it is a well-known method, it has not yet been applied to analyse photovoltaic systems’ technical and economic efficiency. One of the main advantages of this method is its ability to incorporate a wide range of technical and economic performance parameters from both the S1 and S2 categories, as illustrated. By applying this method, we can significantly expand the scope for statistical analysis of the investment efficiency of photovoltaic systems.
The statistical analysis leads to a conclusion consistent with the known situation worldwide. Data analysis indicated that, under the conditions considered in this study, the most economically efficient PV power plants use monocrystalline silicon modules and do not employ tracking systems. By correlating data from the PVGIS platform with findings from existing literature, this study aims to provide a clearer perspective to support investment decision-making, particularly by minimising uncertainties related to the strong dependency on various external factors. The analysis revealed that, in most cases, increasing the installed capacity of a photovoltaic system (by sizing a larger array) is more cost-effective than improving efficiency through the use of tracking systems. Nevertheless, solar trackers remain a viable option in specific contexts. This article also discusses the limitations encountered, particularly those associated with the availability and reliability of validation data.
Author Contributions
Conceptualization, D.-A.S. and E.T.; methodology, D.-A.S. and E.T.; software, D.-A.S.; validation, M.-G.M.; formal analysis, D.-A.S.; investigation, E.T.; resources, L.-A.E.-L.; data curation, L.-A.E.-L.; writing—original draft preparation, D.-A.S.; writing—review and editing, L.-A.E.-L. and E.T.; visualization, M.-G.M. and G.C.; supervision, G.C.; project administration, D.-A.S.; funding acquisition, L.-A.E.-L. and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Research, Innovation and Digitization, CCCDI–UEFISCDI, project no. 61/2024 INFUSE (Information Fusion of Multi-Vector Real-Time Data Streams for Energy Management in Emerging Power Grids), project no. PN-IV-P7-7.1-PTE-2024-0249 (Automated Behavioural Barrier for Biodiversity Conservation by Avoiding Fish Capture in River Water Intakes), and Nucleu contract no. 42N/2023, project no. PN 23140101/2023 (Superior Exploitation of Renewable Energy Sources through Highly Energy-Efficient Equipment Development for Electricity Production and the Intelligent Control of its Distribution and Use).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We are grateful to Sorin-Cristian Ionescu from the Faculty of Entrepreneurship, Business Engineering, and Management at the National University of Science and Technology POLITEHNICA, Bucharest, for supervising the experiments.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study, the collection, analysis, or interpretation of data, the writing of the manuscript, or the decision to publish the results.
References
- Bobbitt, Z. How to Perform a Kruskal-Wallis Test in Excel. 2020. Available online: https://www.statology.org/kruskal-wallis-test-excel/ (accessed on 18 June 2024).
- Oğuz Kaan Çinci, O.K.; Adem Acir, A. Optimization of Array Design in Photovoltaic Power Plants Using the Taguchi and ANOVA Analysis. Gazi Univ. J. Sci. Part C Des. Technol. 2023, 11, 1195–1208. [Google Scholar] [CrossRef]
- Fan, W.; Kokogiannakis, G.; Ma, Z. A multi-objective design optimisation strategy for hybrid photovoltaic thermal collector (PVT)-solar air heater (SAH) systems with fins. Sol. Energy 2018, 163, 315–328. [Google Scholar] [CrossRef]
- Trambitas, R. Analysis of Variance (ANOVA) Compare Several Means, University Babes-Bolyai Cluj-Napoca, Romania. Available online: https://math.ubbcluj.ro/~tradu/applstat/anovaart.pdf (accessed on 8 April 2025).
- Kudelas, D.; Taušová, M.; Tauš, P.; Gabániová, L.; Koščo, J. Investigation of Operating Parameters and Degradation of Photovoltaic Panels in a Photovoltaic Power Plant. Energies 2019, 12, 3631. [Google Scholar] [CrossRef]
- Samy, M.M.; Almamlook, R.E.; Elkhouly, H.I.; Barakat, S. Decision-making and optimal design of green energy system based on statistical methods and artificial neural network approaches. Sustain. Cities Soc. 2022, 84, 104015. [Google Scholar] [CrossRef]
- Pietro De Giovanni, P.; Zaccour, G. A survey of dynamic models of product quality. Eur. J. Oper. Res. 2023, 307, 991–1007. [Google Scholar] [CrossRef]
- Lupton, R.A.; Weiss, J.E.; Peterson, R.T. Sales Training Evaluation Model (STEM): A Conceptual Framework. Ind. Mark. Manag. 1999, 28, 73–86. [Google Scholar] [CrossRef]
- Grabinski, M.; Klinkova, G. Explaining Cobb-Douglas with the New Mathematics of Inteduct. Theor. Econ. Lett. 2023, 13, 136077. [Google Scholar] [CrossRef]
- Ionescu, S.C. Arhitectura Calitatii (Quality Architecture); Politehnica Press: Bucharest, Romania, 2013; pp. 49–59. ISBN 978-606-515-441-4. [Google Scholar]
- Ionescu, S.; Grecu, I. Optimizări în Management: Culegere de Probleme (Optimizations in Management: Collection of Problems); Politehnica Press: Bucharest, Romania, 2015; pp. 101–110. ISBN 978-606-515-635-7. [Google Scholar]
- Clean Energy Technology Observatory: Photovoltaics in the European Union—2022 Status Report on Technology Development, Trends, Value Chains and Markets. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC130720 (accessed on 10 May 2024).
- Circiumaru, G.; Chihaia, R.-A.; El-Leathey, L.-A.; Voina, A. Experimental Study of a Fish Behavioral Barrier Based on Bubble Curtains for a River Water Intake; Environmental Sciences; IntechOpen: London, UK, 2024; Available online: http://dx.doi.org/10.5772/intechopen.1003997 (accessed on 4 May 2025). [CrossRef]
- Information Fusion of Multi-Vector Real-Time Data Streams for Energy Management in Emerging Power Grids, INFUSE, Project No. 61/2024, Ministry of Research, Innovation and Digitization, CCCDI–UEFISCDI. Available online: http://infuse-project.eu/ (accessed on 8 April 2025).
- El-Leathey, L.-A.; Anghelita, P.; Constantin, A.-I.; Circiumaru, G.; Chihaia, R.-A. System for Indoor Comfort and Health Monitoring Tested in Office Building Environment. Appl. Sci. 2023, 13, 11360. [Google Scholar] [CrossRef]
- Vodapally, S.N.; Ali, M.H.A. Comprehensive Review of Solar Photovoltaic (PV) Technologies, Architecture, and Its Applications to Improved Efficiency. Energies 2023, 16, 319. [Google Scholar] [CrossRef]
- Ijagbemi, K. Skills Development for Sustainable Manufacturing. Chapter 2: Sustainable Power Technology: A Viable Sustainable Energy; BoD–Books on Demand: Norderstedt, Germany, 2017; ISBN 978-953-51-4602-5. [Google Scholar] [CrossRef][Green Version]
- EIA U.S. Energy Information Administration. What Is the Efficiency of Different Types of Power Plants? 2024. Available online: https://www.eia.gov/tools/faqs/faq.php?id=107&t=3 (accessed on 14 May 2024).
- Graus, W.; Worrell, E. Trend in efficiency and capacity of fossil power generation in the EU. Energy Policy 2009, 37, 2147–2160. [Google Scholar] [CrossRef]
- European Union. Greenhouse Gas Emissions from Fossil Fuel Fired Power Generation System. 2023. Available online: https://op.europa.eu/en/publication-detail/-/publication/221658dd-9556-4591-86ea-51544346a8f7 (accessed on 15 May 2024).
- Gatti, M.; Martelli, E.; Di Bona, D.; Gabba, M.; Scaccabarozzi, R.; Spinelli, M.; Vigano, F.; Consonni, S. Preliminary Performance and Cost Evaluation of Four Alternative Technologies for Post-Combustion CO2 Capture in Natural Gas-Fired Power Plants. Energies 2020, 13, 543. [Google Scholar] [CrossRef]
- Green, M.A. Photovoltaics: Coming of age. In Proceedings of the 21st IEEE Photovoltaic Specialists Conference, Orlando, FL, USA, 21–25 May 1990. [Google Scholar] [CrossRef]
- Blakers, A.; Wang, A.; Milne, A.-M.; Zhao, J.; Green, M.-A. 22.8% efficient silicon solar cell. Appl. Phys. Lett. 1989, 55, 1363–1365. [Google Scholar] [CrossRef]
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Hinken, D.; Rauer, M.; Hao, X. Solar cell efficiency tables (Version 60). Prog. Photovolt. 2022, 30, 687–701. [Google Scholar] [CrossRef]
- U.S. Department of Energy, Solar Energy Technologies Office. Cadmium Telluride. 2024. Available online: https://www.energy.gov/eere/solar/cadmium-telluride#:~:text=CdTe%20solar%20cells%20are%20the,more%20than%20doubled%20in%20efficiency (accessed on 18 May 2024).
- Macsun Solar, “HCPV”. Available online: http://www.macsunsolar.com/en/showpro.php?id=89 (accessed on 28 May 2024).
- IRENA International Renewable Energy Agency. Renewable Capacity Statistics. 2020. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2020/Mar/IRENA_RE_Capacity_Statistics_2020.pdf (accessed on 28 May 2024).
- IRENA International Renewable Energy Agency. Renewable Capacity Statistics. 2023. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2023/Jul/IRENA_Renewable_energy_statistics_2023.pdf (accessed on 29 May 2024).
- Amine Allouhi, A.; Rehman, S.; Buker, M.S.; Said, Z. Up-to-date literature review on Solar PV systems: Technology progress. market status and R&D. J. Clean. Prod. 2022, 362, 132339. [Google Scholar] [CrossRef]
- Gürtürk, M. Economic feasibility of solar power plants based on PV module with levelized cost analysis. Energy 2019, 171, 866–878. [Google Scholar] [CrossRef]
- Legarreta, A.E.; Figueroa, J.H.; Bortolin, J.A. An IEC 61000-4-30 class a—Power quality monitor: Development and performance analysis. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Masetti, C. Revision of European Standard EN 50160 on power quality: Reasons and solutions. In Proceedings of the 14th International Conference on Harmonics and Quality of Power—ICHQP, Bergamo, Italy, 26–29 September 2010; pp. 1–7. [Google Scholar] [CrossRef]
- European Commission; EU Science Hub. “PVGIS User Manual” (PVGIS-SARAH, PVGIS-NSRDB, PVGIS-ERA5). Available online: https://joint-research-centre.ec.europa.eu/photovoltaic-geographical-information-system-pvgis/getting-started-pvgis/pvgis-user-manual_en (accessed on 18 June 2024).
- Agentia Nationala pentru Protectia Mediului (National Agency for Environmental Protection). Centrala Electrica Fotovoltaica (Photovoltaic Power Plant) 1,19 MWp, Borzesti, Bacau, Romania. 2022. Available online: http://www.anpm.ro/documents/14011/73035009/Memoriu+de+prezentare+acord+mediu+292+final+CEF+04.2022.pdf (accessed on 24 June 2024).
- Institutul de Tehnica de Calcul. Cluj (Institute of Computer Technology) PV Power Plant “Braşov Stupini Merilor FN, Studiu de fezabilitate (Feasibility Study). 2012. Available online: http://www.itc-cluj.ro/negoiu/negoiu-StudiiFezabilitate.htm (accessed on 24 June 2024).
- Kingdom of Morocco “Collaboration Program with the Private Sector for Disseminating Japanese Technology fot Promotion of Concentrator Photovoltaic Power Generation System (“CPV”) at Ouarzazate in Morocco” Final Report (Public Version) Japan International Cooperation Agency (JICA)Sumitomo Electric Industries, Lt4. 2017. Available online: https://openjicareport.jica.go.jp/pdf/12285060.pdf (accessed on 4 May 2025).
- Horowitz, K.A.W.; Woodhouse, M.; Lee, H.; Smestad, G.P.; NREL. A Bottom-Up Cost Analysis of a High Concentration PV Module. 2015. Available online: https://www.nrel.gov/docs/fy15osti/63947.pdf (accessed on 4 May 2025).
- Sumitomo Electric. Osaka, Japan “Concentrator Photovoltaic System”. Available online: https://sumitomoelectric.com/products/cpv (accessed on 26 June 2024).
- Rehman, S.; Ahmed, M.A.; Mohamed, M.H.; Al-Sulaiman, F.A. Feasibility study of the grid connected 10 MW installed capacity PV power plants in Saudi Arabia. Renew. Sustain. Energy Rev. 2017, 80, 319–329. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).