River Surface Space–Time Image Velocimetry Based on Dual-Channel Residual Network
Abstract
:1. Introduction
2. Materials and Methods
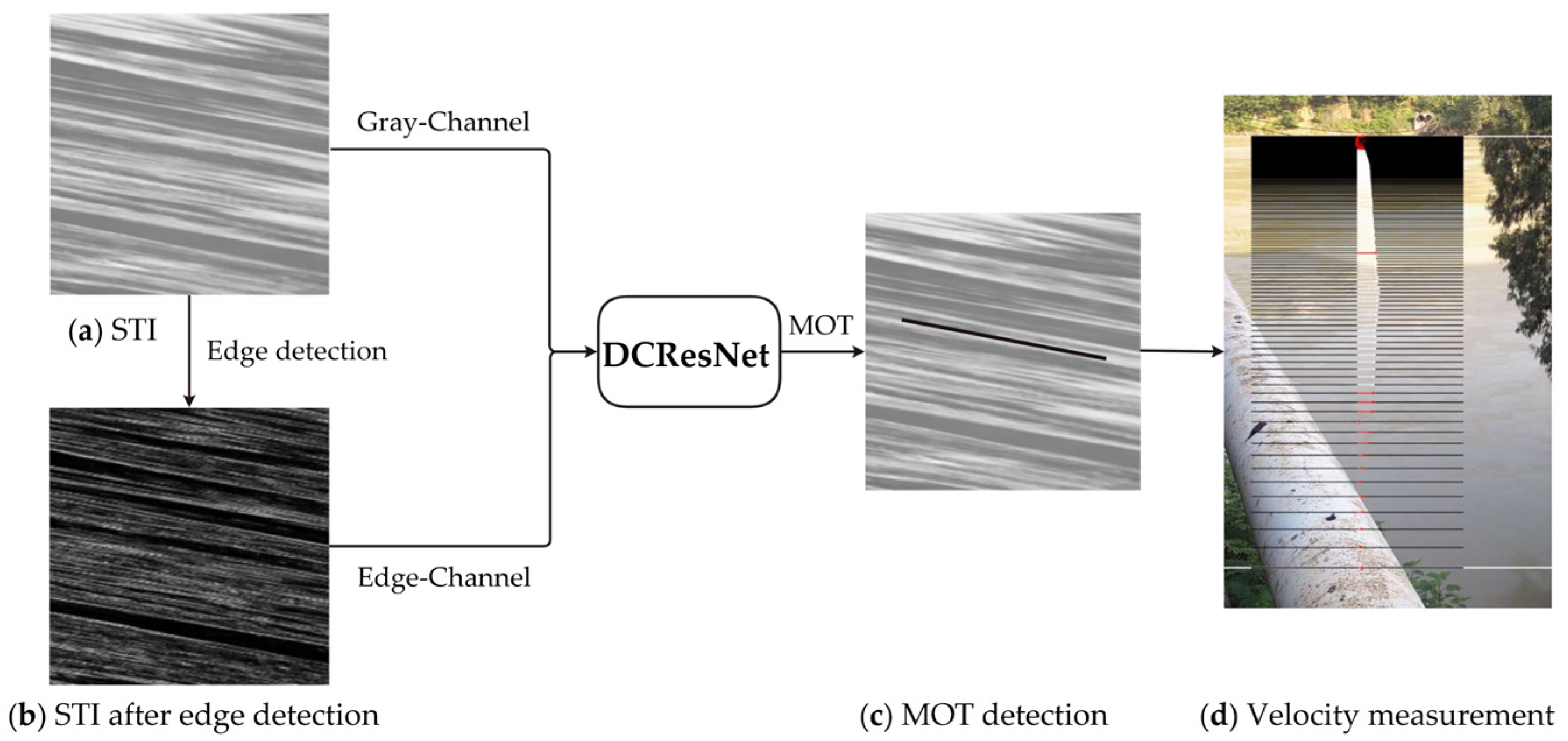
2.1. Basic Principle of STIV
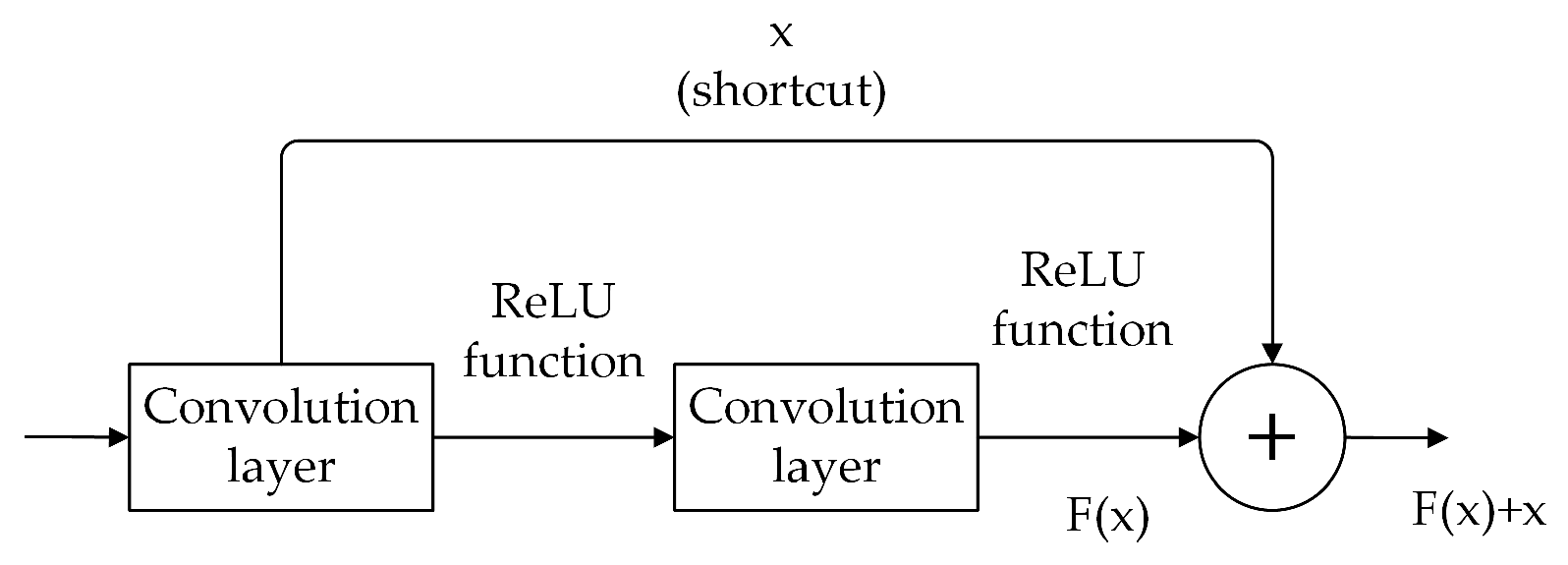
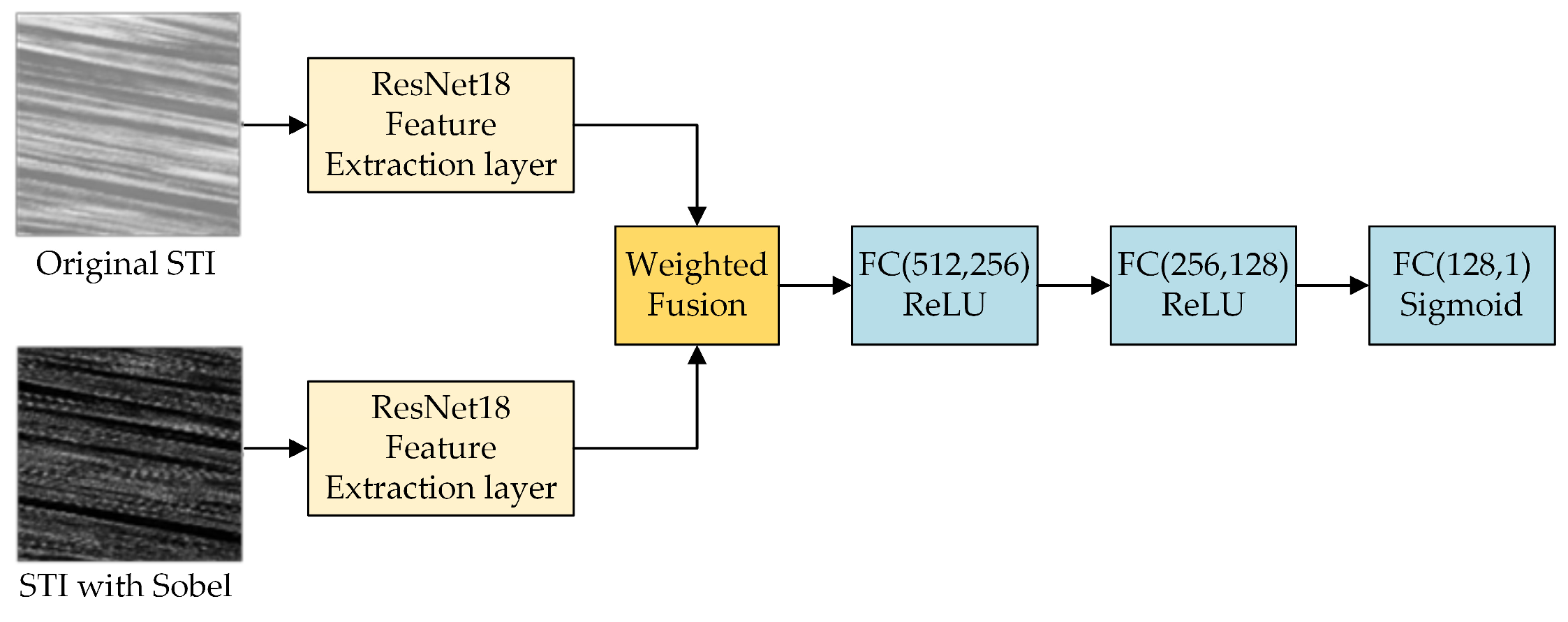
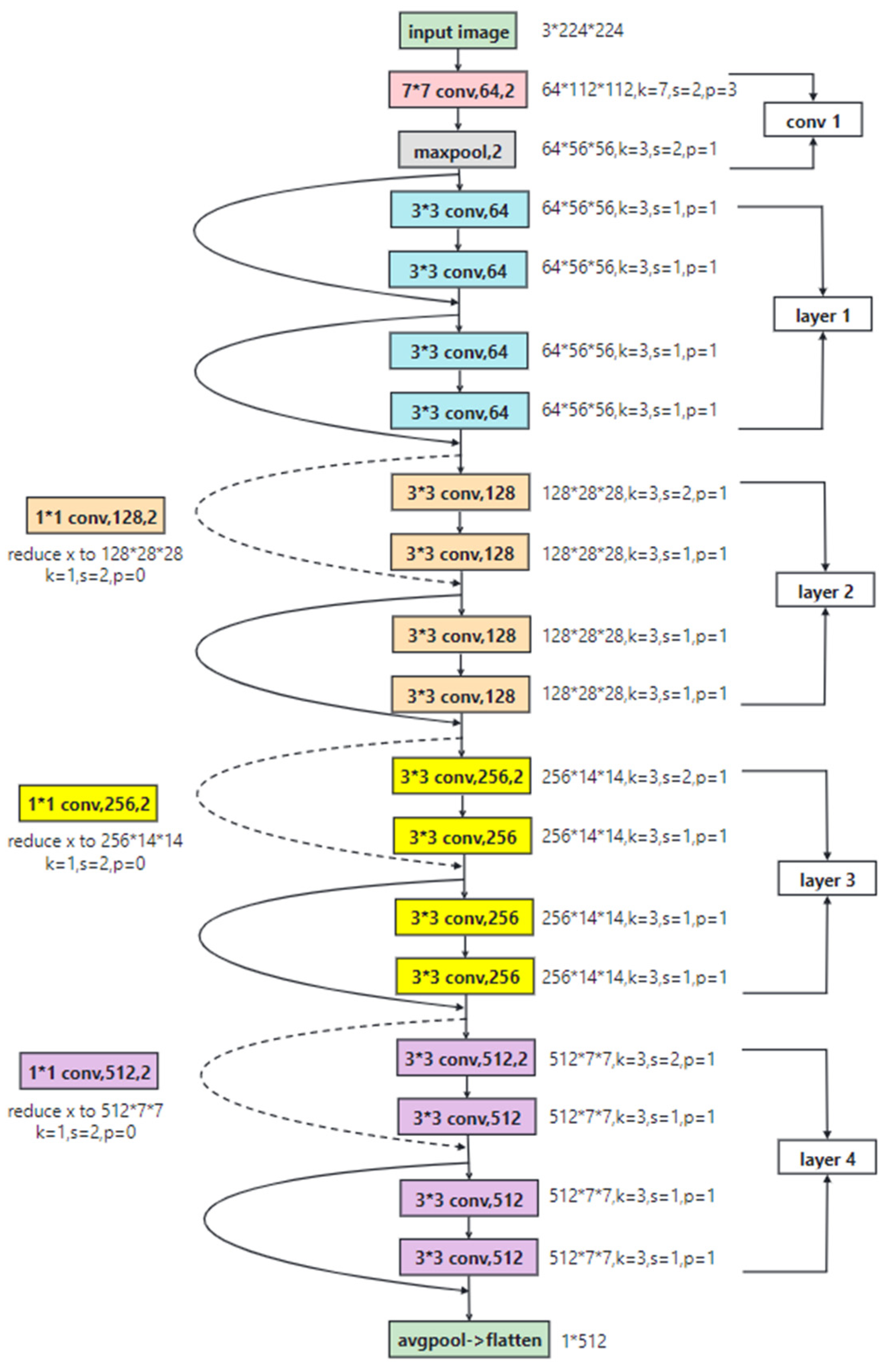
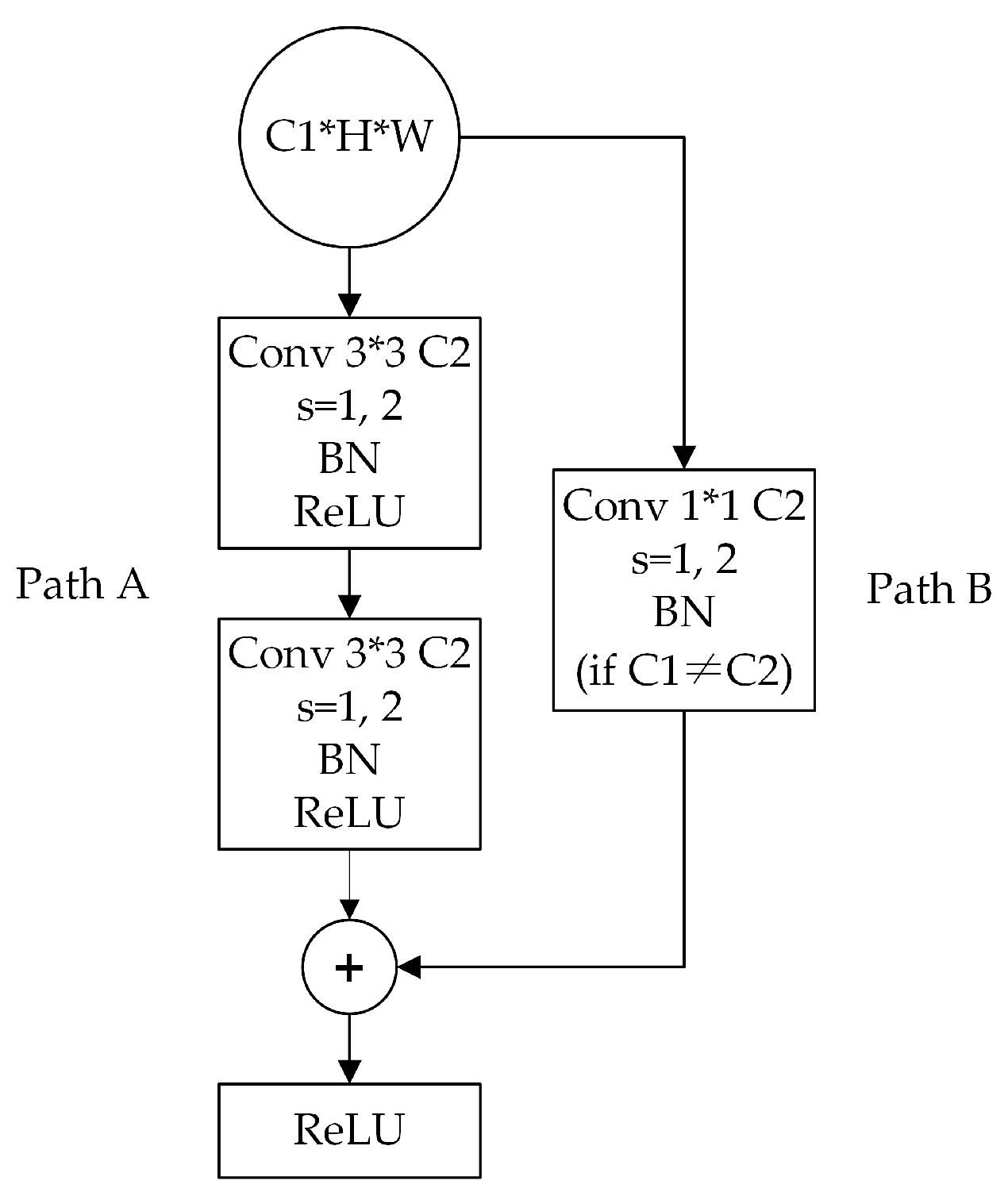
2.2. Dual-Channel Residual Network Model
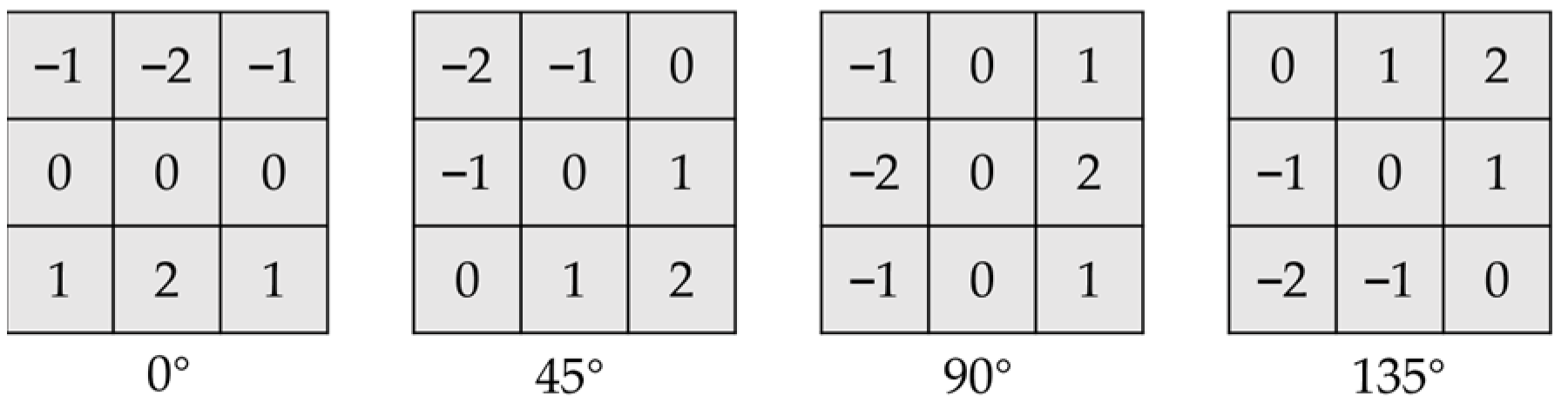
2.3. Adaptive Threshold Sobel Operator
3. Model Training and Fusion Coefficient Determination
3.1. Dataset Construction
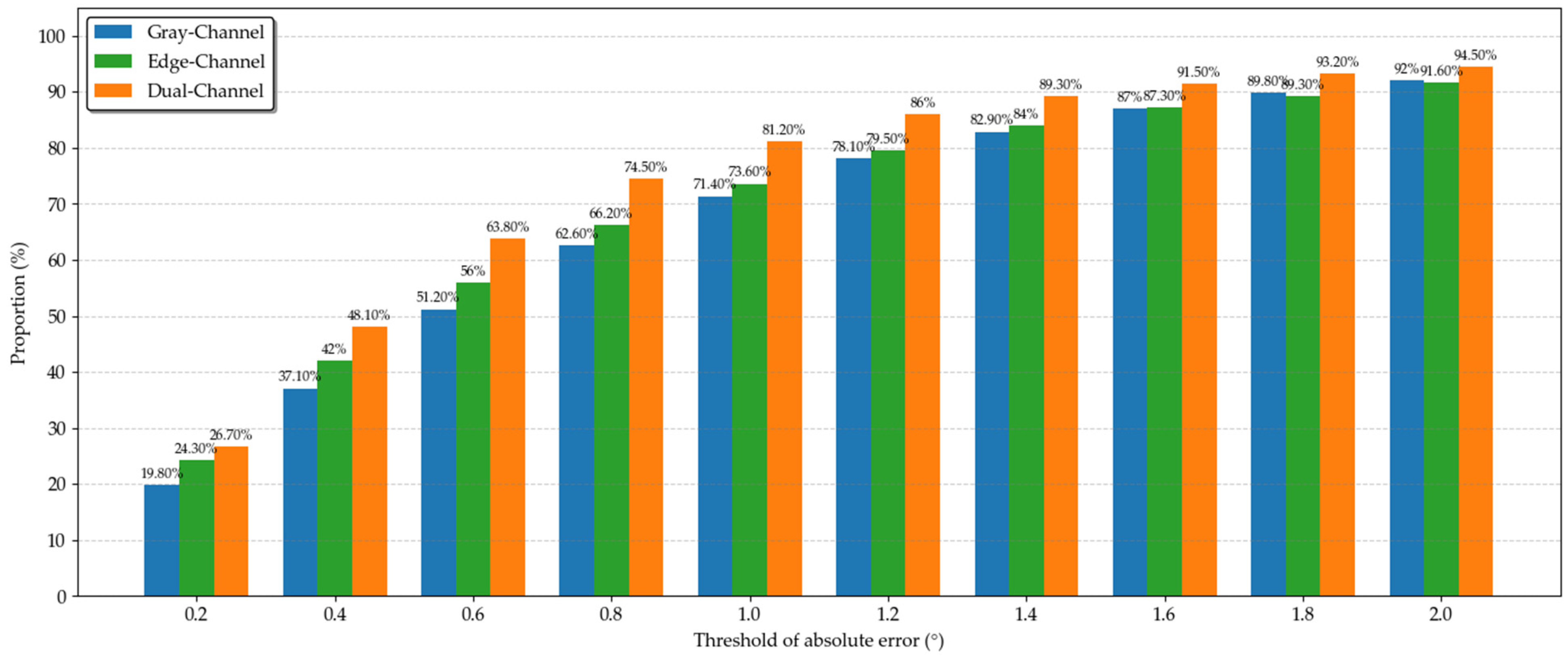
3.2. Determination of Fusion Coefficient
4. Experiments and Discussions
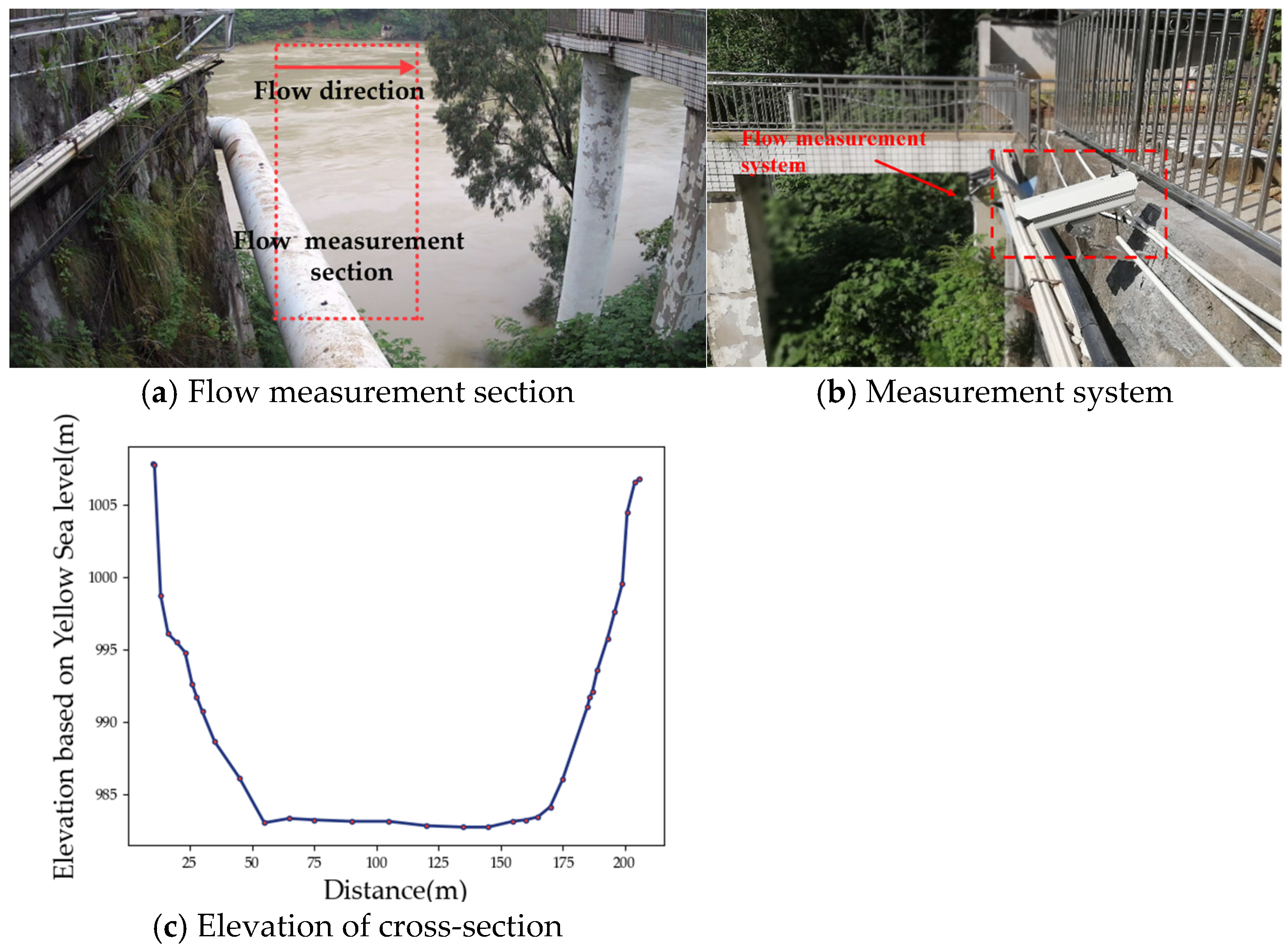
4.1. Experimental Platform and Evaluation Method
4.2. MOT Detection Comparison Experiments
4.3. Surface Velocity Comparison Experiments
4.3.1. Experimental Settings of Surface Velocity Measurement
4.3.2. Test 1: Sunny Day at Panzhihua Station
4.3.3. Test 2: Rainy Day at Panzhihua Station
4.3.4. Test 3: Cloudy Day at Hebian Station
4.4. Vertical Average Velocity Comparison Experiment
4.4.1. Experimental Settings of Vertical Average Velocity Measurement
4.4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, G.; Li, J.; Feng, P.; Liu, J.; Wang, Y. Impacts of climate and land-use change on flood events with different return periods in a mountainous watershed of North China. J. Hydrol. Reg. Stud. 2024, 55, 101943. [Google Scholar] [CrossRef]
- Perks, M.T.; Sasso, S.F.D.; Hauet, A.; Jamieson, E.; Le Coz, J.; Pearce, S.; Peña-Haro, S.; Pizarro, A.; Strelnikova, D.; Tauro, F.; et al. Towards harmonisation of image velocimetry techniques for river surface velocity observations. Earth Syst. Sci. Data 2020, 12, 1545–1559. [Google Scholar] [CrossRef]
- Dobriyal, P.; Badola, R.; Tuboi, C.; Hussain, S.A. A review of methods for monitoring streamflow for sustainable water resource management. Appl. Water Sci. 2017, 7, 2617–2628. [Google Scholar] [CrossRef]
- Jodeau, M.; Hauet, A.; Paquier, A.; Coz, J.L.; Dramais, G. Application and evaluation of LS-PIV technique for the monitoring of river surface velocities in high flow conditions. Flow Meas. Instrum. 2008, 19, 117–127. [Google Scholar] [CrossRef]
- Coz, J.L.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef]
- Tsubaki, R.; Fujita, I.; Tsutsumi, S. Measurement of the flood discharge of a small-sized river using an existing digital video recording system. J. Hydro-Environ. Res. 2011, 5, 313–321. [Google Scholar] [CrossRef]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 2008, 44, W00D19. [Google Scholar] [CrossRef]
- Thumser, P.; Haas, C.; Tuhtan, J.A.; Fuentes-Pérez, J.F.; Toming, G. RAPTOR-UAV: Real-time particle tracking in rivers using an unmanned aerial vehicle. Earth Surf. Process. Landf. 2017, 42, 2439–2446. [Google Scholar] [CrossRef]
- Tauro, F.; Tosi, F.; Mattoccia, S.; Toth, E.; Piscopia, R.; Grimaldi, S. Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations. Remote Sens. 2018, 10, 2010. [Google Scholar] [CrossRef]
- Fujita, I.; Watanabe, H.; Tsubaki, R. Development of a non-intrusive and efficient flow monitoring technique: The space-time image velocimetry (STIV). Int. J. River Basin Manag. 2007, 5, 105–114. [Google Scholar] [CrossRef]
- Tsubaki, R. On the Texture Angle Detection Used in Space-Time Image Velocimetry (STIV). Water Resour. Res. 2017, 53, 10908–10914. [Google Scholar] [CrossRef]
- Fujita, I.; Kobayashi, K.; Logah, F.Y.; Oblim, F.T.; Alfa, B.; Tateguchi, S.; Kankam-Yeboah, K.; Appiah, G.; Asante-Sasu, C.K.; Kawasaki, R.; et al. Accuracy of Ku-stiv for Discharge Measurement in Ghana, Africa. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2017, 73, I_499–I_504. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Li, H.; Liu, L. Development and application of an image-based flow measurement system. Water Resour. Inf. 2018, 3, 7–13. [Google Scholar] [CrossRef]
- Zhen, W.; Chen, H.; Chen, D.; Cai, F.; Fang, W.; Chen, D.; Wang, R.; He, X.; Wang, B.; Guo, L. The Ecological Flow Intelligent Supervision Platform Based on Wuhan University’s AiFlow Visual Flow Measurement Technology and Its Application. J. Water Resour. Res. 2024, 13, 347–354. [Google Scholar] [CrossRef]
- Hydro-STIV. Available online: https://hydrosoken.co.jp/service/hydrostiv.php (accessed on 25 June 2024).
- Fujita, I.; Notoya, Y.; Tani, K.; Tateguchi, S. Efficient and accurate estimation of water surface velocity in STIV. Environ. Fluid Mech. 2019, 19, 1363–1378. [Google Scholar] [CrossRef]
- Zhen, Z.; Huabao, L.; Yang, Z.; Jian, H. Design and evaluation of an FFT-based space-time image velocimetry (STIV) for time-averaged velocity measurement. In Proceedings of the 2019 14th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Changsha, China, 1–3 November 2019. [Google Scholar]
- Zhao, H.; Chen, H.; Liu, B.; Liu, W.; Xu, C.-Y.; Guo, S.; Wang, J. An improvement of the Space-Time Image Velocimetry combined with a new denoising method for estimating river discharge. Flow Meas. Instrum. 2021, 77, 101864. [Google Scholar] [CrossRef]
- Tani, K.; Fujita, I. Wavenumber-frequency analysis of river surface texture to improve accuracy of image-based velocimetry. E3S Web Conf. 2018, 40, 8. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Yuan, Z.; Dong, R.; Wang, J. Sensitivity analysis of image filter for space-time image velocimetry in frequency domain. Chin. J. Sci. Instrum. 2022, 43, 43–53. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Kan, M.; Zhang, J.; Chen, X. AgeNet: Deeply Learned Regressor and Classifier for Robust Apparent Age Estimation. In Proceedings of the IEEE International Conference on Computer Vision Workshop, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Luo, P.; Tian, Y.; Wang, X.; Tang, X. Switchable Deep Network for Pedestrian Detection. In Proceedings of the Computer Vision & Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 899–906. [Google Scholar]
- Zhang, J.; Shan, S.; Kan, M.; Chen, X. Coarse-to-Fine Auto-Encoder Networks (CFAN) for Real-Time Face Alignment. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Watanabe, K.; Fujita, I.; Iguchi, M.; Hasegawa, M. Improving Accuracy and Robustness of Space-Time Image Velocimetry (STIV) with Deep Learning. Water 2021, 13, 2079. [Google Scholar] [CrossRef]
- Hu, Q.; Wang, J.; Zhang, G.; Jin, J. Space-time image velocimetry based on improved MobileNetV2. Electronics 2023, 12, 399. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, H.; Huang, K.; Chen, M.; Wang, J.; Liu, B. Optimization of Space-Time image velocimetry based on deep residual learning. Measurement 2024, 232, 114688. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Chen, L.; Meng, J.; Sun, Y. Surface space-time image velocimetry of river based on residual network. J. Hohai Univ. (Nat. Sci.) 2023, 51, 118–128. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, W.; Liu, Q.; Wang, Y. Survey of residual network. Appl. Res. Comput. 2020, 37, 1292–1297. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Li, W.; Du, Q.; Zhai, L. Dual-Channel Residual Network for Hyperspectral Image Classification With Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5502511. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition; IEEE: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Israni, S.; Jain, S. Edge detection of license plate using Sobel operator. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 3561–3563. [Google Scholar]
- Zhai, Q.; Liu, Q.; Zhang, J.; Huang, Y.; Gao, Y. Research and Implementation of Sobel Edge Detection System Based on Smooth Adaptive. In Proceedings of the 17th China Aviation Measurement and Control Technology Annual Conference, Xi’an, China, 5 November 2020. [Google Scholar]
- Kuo, P.-H.; Huang, C.-J. A High Precision Artificial Neural Networks Model for Short-Term Energy Load Forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.; Yuan, Z.; Gao, L. Validity Identification and Rectification of Water Surface Fast Fourier Transform-Based Space-Time Image Velocimetry (FFT-STIV) Results. Sensors 2025, 25, 257. [Google Scholar] [CrossRef]















| Scenario | Training Set (Piece) | Test Set (Piece) |
|---|---|---|
| normal | 16,800 | 8400 |
| vortex | 8400 | 3360 |
| flare | 8400 | 3360 |
| obstacle | 8400 | 3360 |
| rain | 8400 | 3360 |
| Regression Model | Dual-Channel | Edge-Channel | Gray-Channel |
|---|---|---|---|
| MAE | 0.64 | 0.87 | 0.82 |
| SD | 0.71 | 1.01 | 1.43 |
| Scenario | Dual-Channel | Edge-Channel | Gray-Channel |
|---|---|---|---|
| normal | 0.41 | 0.61 | 0.65 |
| vortex | 1.10 | 1.14 | 1.15 |
| flare | 0.57 | 0.81 | 0.82 |
| obstacle | 0.33 | 0.34 | 0.44 |
| rain | 1.17 | 1.50 | 1.36 |
| Number | Starting Distance (m) | FFT (°) | DCResNet (°) | Label Value (°) | AE (°) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 45 | 81.45 | 80.30 | 80.89 | 0.56 | 0.59 |
| 2 | 65 | 81.97 | 82.22 | 82.20 | 0.23 | 0.02 |
| 3 | 75 | 80.57 | 80.63 | 80.80 | 0.23 | 0.17 |
| 4 | 85 | 80.01 | 80.35 | 80.48 | 0.47 | 0.13 |
| 5 | 95 | 78.95 | 78.62 | 78.80 | 0.15 | 0.18 |
| 6 | 115 | 77.39 | 77.48 | 77.52 | 0.13 | 0.04 |
| 7 | 130 | 75.43 | 74.56 | 74.45 | 0.98 | 0.11 |
| 8 | 145 | 68.10 | 66.30 | 66.10 | 2.00 | 0.20 |
| 9 | 160 | 18.55 | 41.50 | 43.39 | 24.84 | 1.89 |
| Number | Starting Distance (m) | FFT (m/s) | DCResNet (m/s) | Label Value (m/s) | RE (%) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 45 | 2.48 | 2.18 | 2.33 | 6.44 | 6.44 |
| 2 | 65 | 3.91 | 4.05 | 4.03 | 2.98 | 0.50 |
| 3 | 75 | 3.92 | 3.94 | 4.01 | 2.24 | 1.75 |
| 4 | 85 | 4.15 | 4.30 | 4.36 | 4.82 | 1.38 |
| 5 | 95 | 4.16 | 4.04 | 4.11 | 1.22 | 1.70 |
| 6 | 115 | 4.29 | 4.32 | 4.34 | 1.15 | 0.46 |
| 7 | 130 | 4.20 | 3.95 | 3.92 | 7.14 | 0.77 |
| 8 | 145 | 3.08 | 2.96 | 2.79 | 10.39 | 6.09 |
| 9 | 160 | 0.44 | 1.15 | 1.25 | 64.8 | 8.00 |
| Number | Starting Distance (m) | FFT (°) | DCResNet (°) | Label Value (°) | AE (°) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 50 | 23.95 | 77.11 | 78.02 | 54.07 | 0.91 |
| 2 | 60 | 80.44 | 79.69 | 80. 01 | 0.43 | 0.32 |
| 3 | 75 | 80.42 | 80.62 | 80.78 | 0.36 | 0.16 |
| 4 | 85 | 79.31 | 78.60 | 78.31 | 1.00 | 0.29 |
| 5 | 95 | 78.50 | 79.03 | 78.75 | 0.25 | 0.28 |
| 6 | 105 | 77.02 | 77.39 | 77.21 | 0.19 | 0.18 |
| 7 | 120 | 74.55 | 75.02 | 74.68 | 0.13 | 0.34 |
| 8 | 140 | 76.12 | 67.59 | 65.34 | 10.78 | 2.25 |
| 9 | 160 | 23.30 | 39.12 | 37.25 | 13.95 | 1.87 |
| Number | Starting Distance (m) | FFT (m/s) | DCResNet (m/s) | Label Value (m/s) | RE (%) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 50 | 0.20 | 2.06 | 2.21 | 90.95 | 6.79 |
| 2 | 60 | 3.28 | 3.04 | 3.16 | 3.80 | 3.80 |
| 3 | 75 | 3.66 | 3.75 | 3.81 | 3.94 | 1.57 |
| 4 | 85 | 3.69 | 3.47 | 3.37 | 9.50 | 2.97 |
| 5 | 95 | 3.92 | 4.12 | 4.01 | 2.24 | 2.74 |
| 6 | 105 | 3.80 | 3.93 | 3.87 | 1.81 | 1.55 |
| 7 | 120 | 3.71 | 3.84 | 3.74 | 0.80 | 2.67 |
| 8 | 140 | 4.75 | 2.85 | 2.56 | 85.55 | 11.33 |
| 9 | 160 | 0.56 | 1.06 | 0.99 | 43.43 | 7.07 |
| Number | Starting Distance (m) | FFT (°) | DCResNet (°) | Label Value (°) | AE (°) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 2 | 81.30 | 84.87 | 85.24 | 3.94 | 0.37 |
| 2 | 4 | 85.49 | 86.24 | 86.56 | 1.07 | 0.32 |
| 3 | 6 | 86.66 | 86.65 | 86.47 | 0.19 | 0.18 |
| 4 | 8 | 86.11 | 86.15 | 85.9 | 0.21 | 0.25 |
| 5 | 10 | 85.69 | 86.02 | 86.05 | 0.36 | 0.03 |
| 6 | 12 | 85.07 | 85.61 | 85.31 | 0.24 | 0.30 |
| 7 | 14 | 84.66 | 85.10 | 84.91 | 0.25 | 0.19 |
| 8 | 16 | 81.75 | 81.65 | 84.32 | 2.57 | 2.67 |
| 9 | 18 | 83.67 | 83.56 | 83.88 | 0.21 | 0.32 |
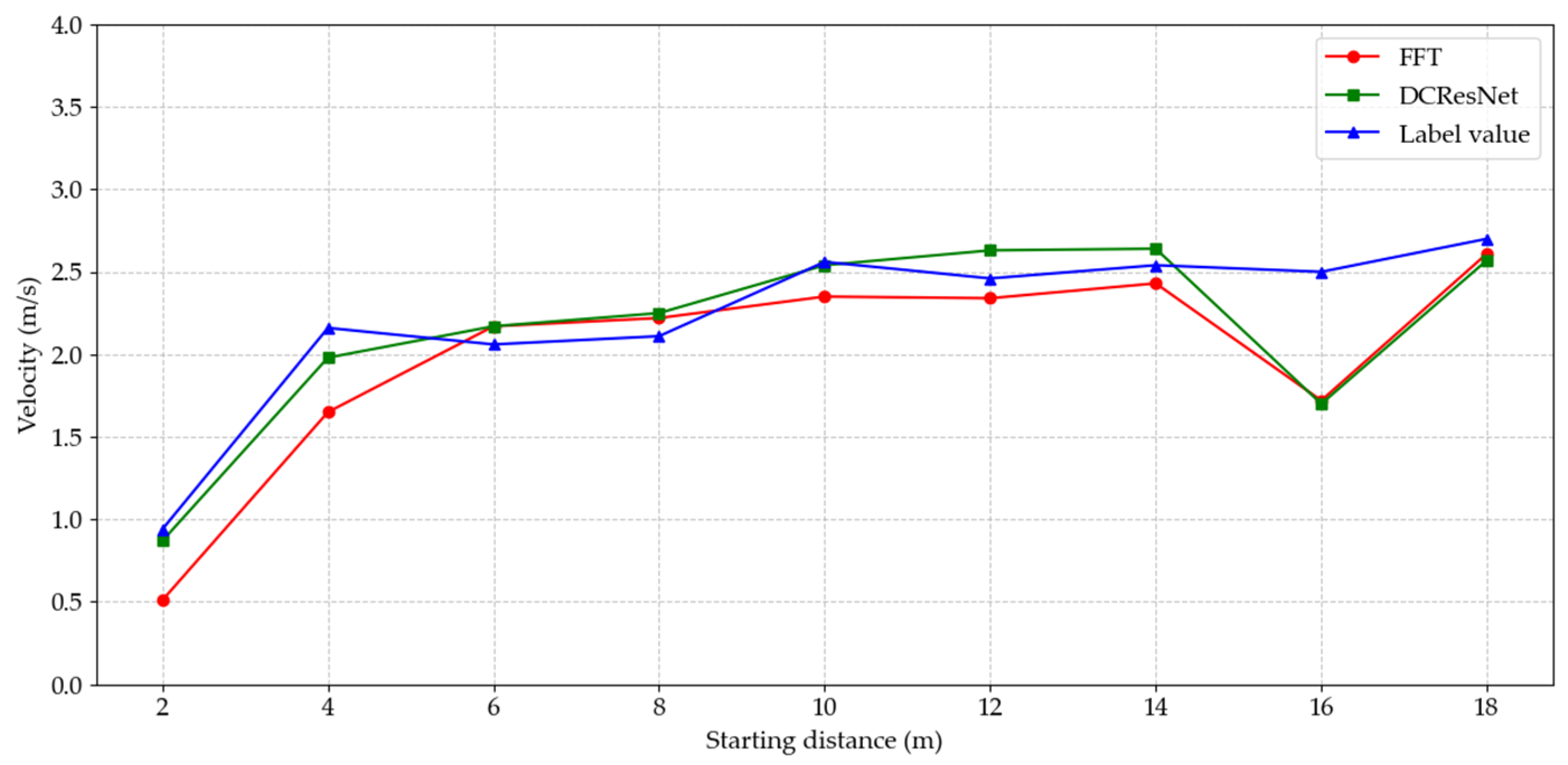
| Number | Starting Distance (m) | FFT (m/s) | DCResNet (m/s) | Label Value (m/s) | RE (%) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 2 | 0.51 | 0.87 | 0.94 | 45.74 | 7.45 |
| 2 | 4 | 1.65 | 1.98 | 2.16 | 23.61 | 8.33 |
| 3 | 6 | 2.17 | 2.17 | 2.06 | 5.34 | 5.34 |
| 4 | 8 | 2.22 | 2.25 | 2.11 | 5.21 | 6.64 |
| 5 | 10 | 2.35 | 2.54 | 2.56 | 8.20 | 0.78 |
| 6 | 12 | 2.34 | 2.63 | 2.46 | 4.88 | 6.91 |
| 7 | 14 | 2.43 | 2.64 | 2.54 | 4.33 | 3.94 |
| 8 | 16 | 1.72 | 1.7 | 2.50 | 31.20 | 32.00 |
| 9 | 18 | 2.61 | 2.57 | 2.70 | 3.33 | 4.81 |
| Number | Starting Distance (m) | FFT (°) | DCResNet (°) | Label Value (°) | AE (°) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 55 | 82.71 | 82.91 | 82.60 | 0.11 | 0.31 |
| 2 | 65 | 81.66 | 81.72 | 81.54 | 0.12 | 0.18 |
| 3 | 90 | 80.61 | 80.83 | 80.69 | 0.08 | 0.14 |
| 4 | 105 | 79.32 | 79.53 | 79.40 | 0.08 | 0.13 |
| 5 | 120 | 78.18 | 78.52 | 78.38 | 0.20 | 0.14 |
| 6 | 135 | 77.55 | 77.32 | 77.41 | 0.14 | 0.09 |
| 7 | 155 | 73.10 | 70.21 | 69.81 | 3.29 | 0.40 |
| 8 | 165 | 70.52 | 58.45 | 56.80 | 13.72 | 1.65 |
| 9 | 175 | 72.02 | 37.69 | 38.20 | 33.82 | 0.51 |
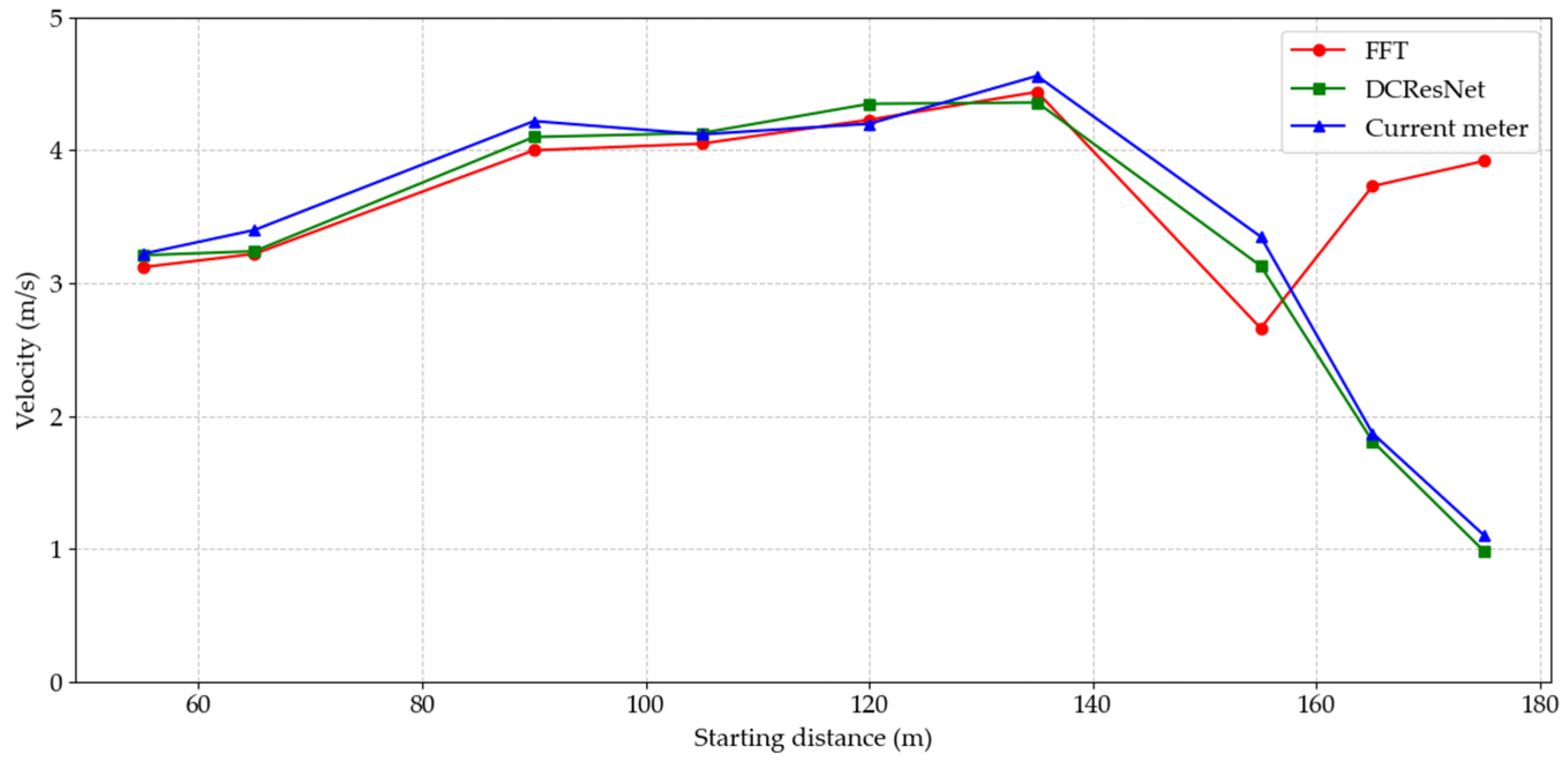
| Number | Starting Distance (m) | FFT (m/s) | DCResNet (m/s) | Current Meter (m/s) | RE (%) | |
|---|---|---|---|---|---|---|
| FFT | DCResNet | |||||
| 1 | 55 | 3.12 | 3.21 | 3.22 | 3.11 | 0.31 |
| 2 | 65 | 3.22 | 3.24 | 3.40 | 5.29 | 4.71 |
| 3 | 90 | 4.00 | 4.10 | 4.22 | 5.21 | 2.84 |
| 4 | 105 | 4.05 | 4.13 | 4.12 | 1.70 | 0.24 |
| 5 | 120 | 4.23 | 4.35 | 4.20 | 0.71 | 3.57 |
| 6 | 135 | 4.44 | 4.36 | 4.56 | 2.63 | 4.39 |
| 7 | 155 | 2.66 | 3.13 | 3.35 | 20.60 | 6.57 |
| 8 | 165 | 3.73 | 1.81 | 1.87 | 99.47 | 3.21 |
| 9 | 175 | 3.92 | 0.98 | 1.10 | 256.36 | 10.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Zhang, Z.; Chen, L.; Li, H. River Surface Space–Time Image Velocimetry Based on Dual-Channel Residual Network. Appl. Sci. 2025, 15, 5284. https://doi.org/10.3390/app15105284
Gao L, Zhang Z, Chen L, Li H. River Surface Space–Time Image Velocimetry Based on Dual-Channel Residual Network. Applied Sciences. 2025; 15(10):5284. https://doi.org/10.3390/app15105284
Chicago/Turabian StyleGao, Ling, Zhen Zhang, Lin Chen, and Huabao Li. 2025. "River Surface Space–Time Image Velocimetry Based on Dual-Channel Residual Network" Applied Sciences 15, no. 10: 5284. https://doi.org/10.3390/app15105284
APA StyleGao, L., Zhang, Z., Chen, L., & Li, H. (2025). River Surface Space–Time Image Velocimetry Based on Dual-Channel Residual Network. Applied Sciences, 15(10), 5284. https://doi.org/10.3390/app15105284





