Interpretability Study of Gradient Information in Individual Travel Prediction
Abstract
1. Introduction
2. Related Work
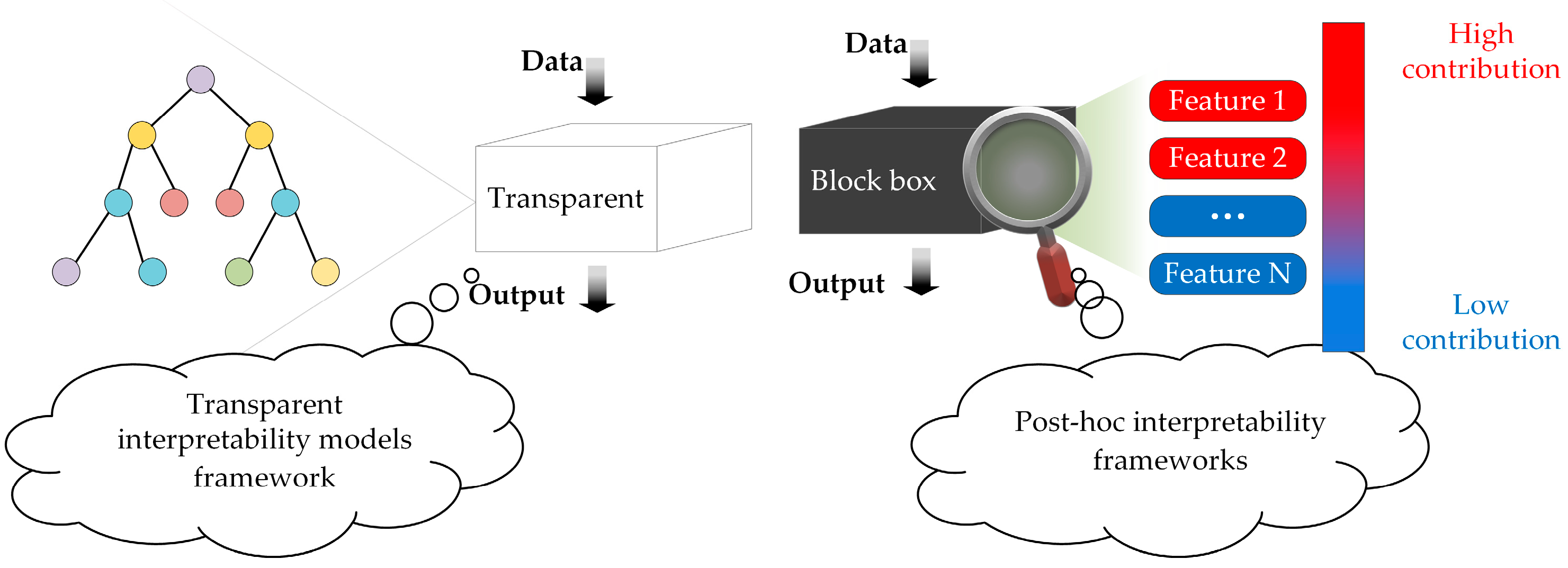
2.1. Transparent Interpretability Models Framework
2.2. Post Hoc Interpretability Framework
3. Methods
3.1. Individual Travel Prediction and the Concept of Interpretability
3.2. Analogy Between an Image Recognition Task and an Individual Travel Prediction Task
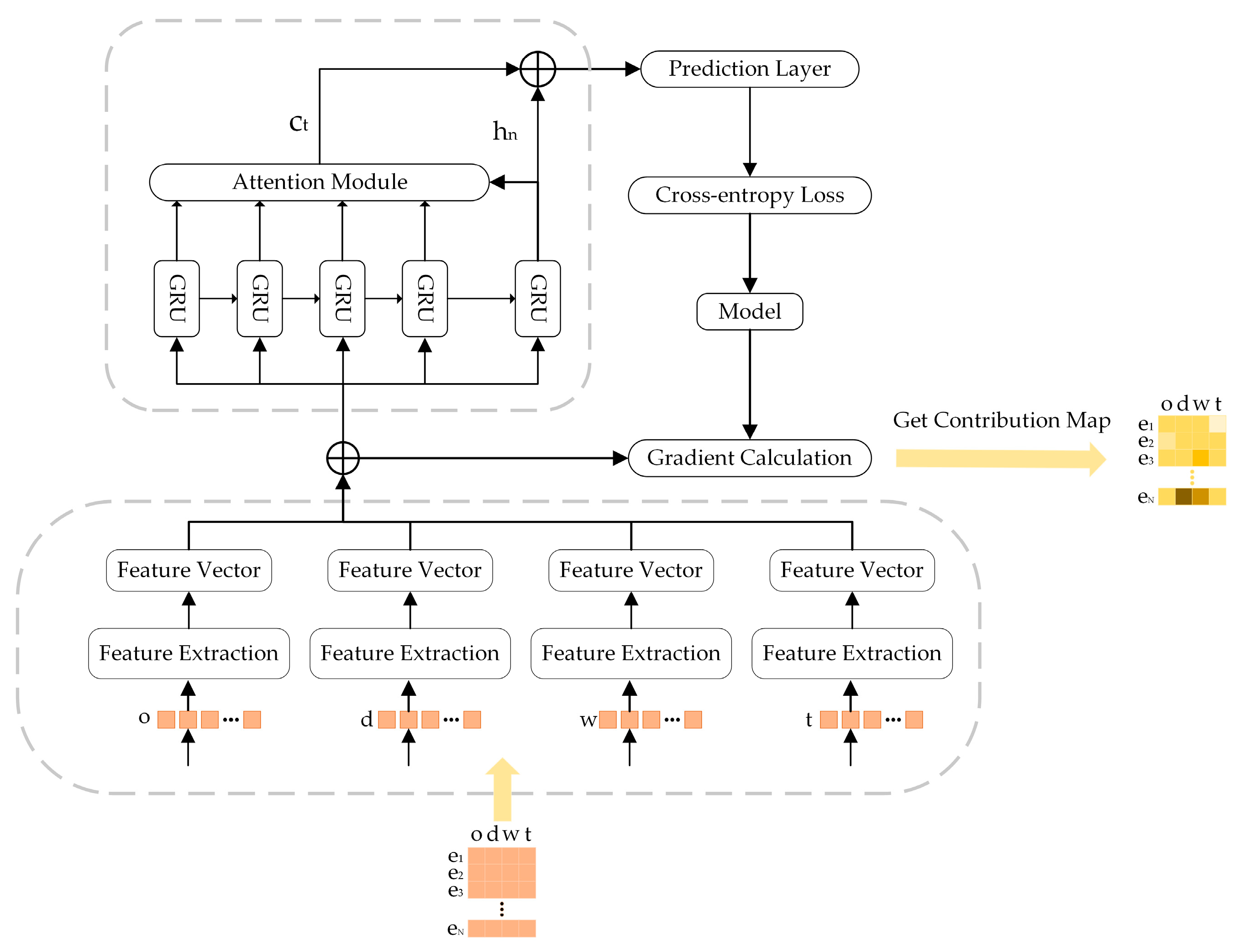
3.3. Saliency Methods Based on Gradient Information
4. Experiment
4.1. Model Training
4.2. Mask Matrix
4.3. Benchmarking
- Jensen–Shannon Divergence (JS): The Jensen–Shannon divergence is a metric for assessing the difference between two probability distributions. The formula for calculating the Jensen–Shannon divergence of the model’s output distribution is as follows:
- 2.
- Predictive Accuracy Difference Ratio (PA): PA is a metric that measures the decline in prediction accuracy when the model faces masked data. The formula for calculating PA is as follows:
4.4. Feature Impact Analysis
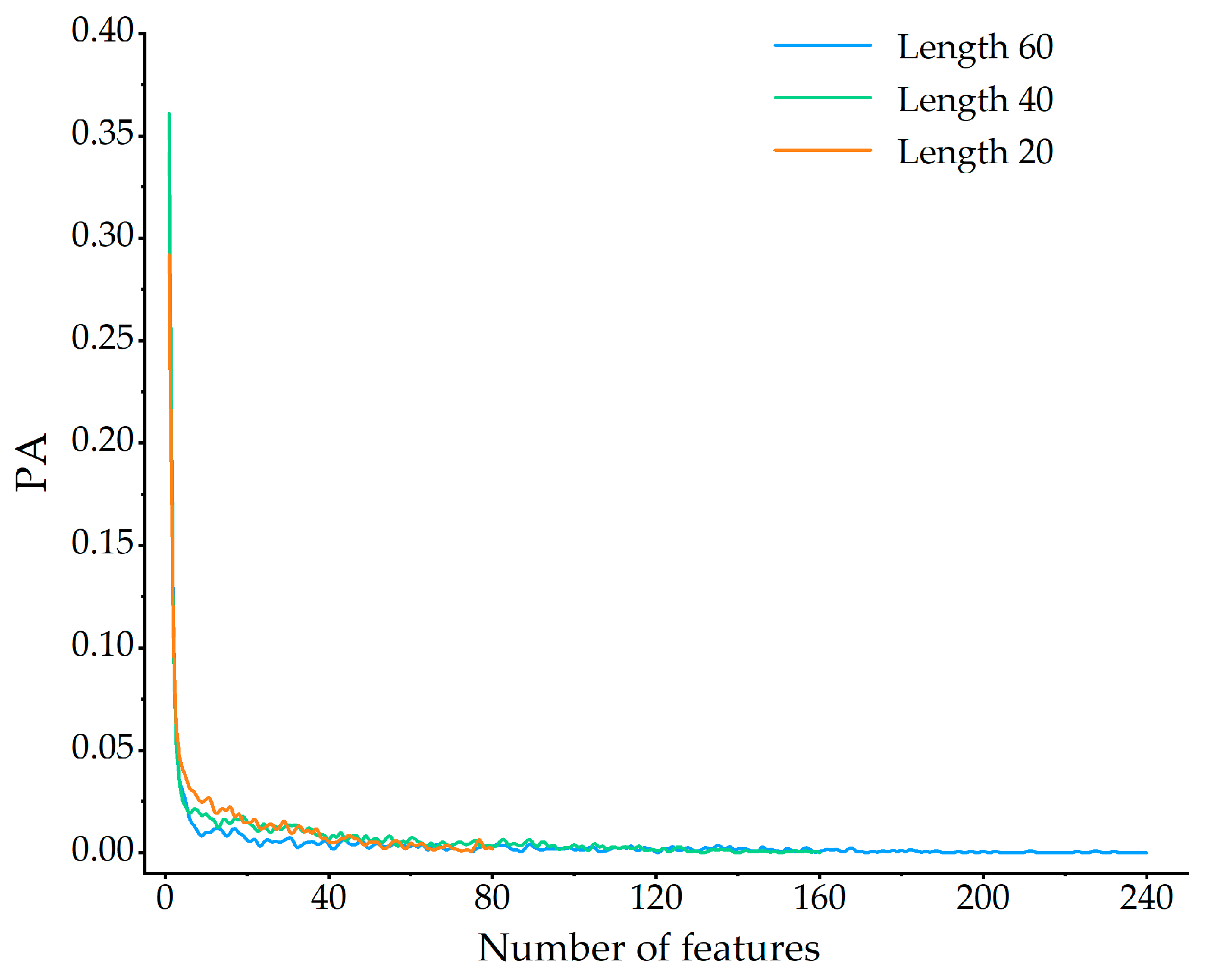
4.4.1. Analysis of Single-Feature Mask Results
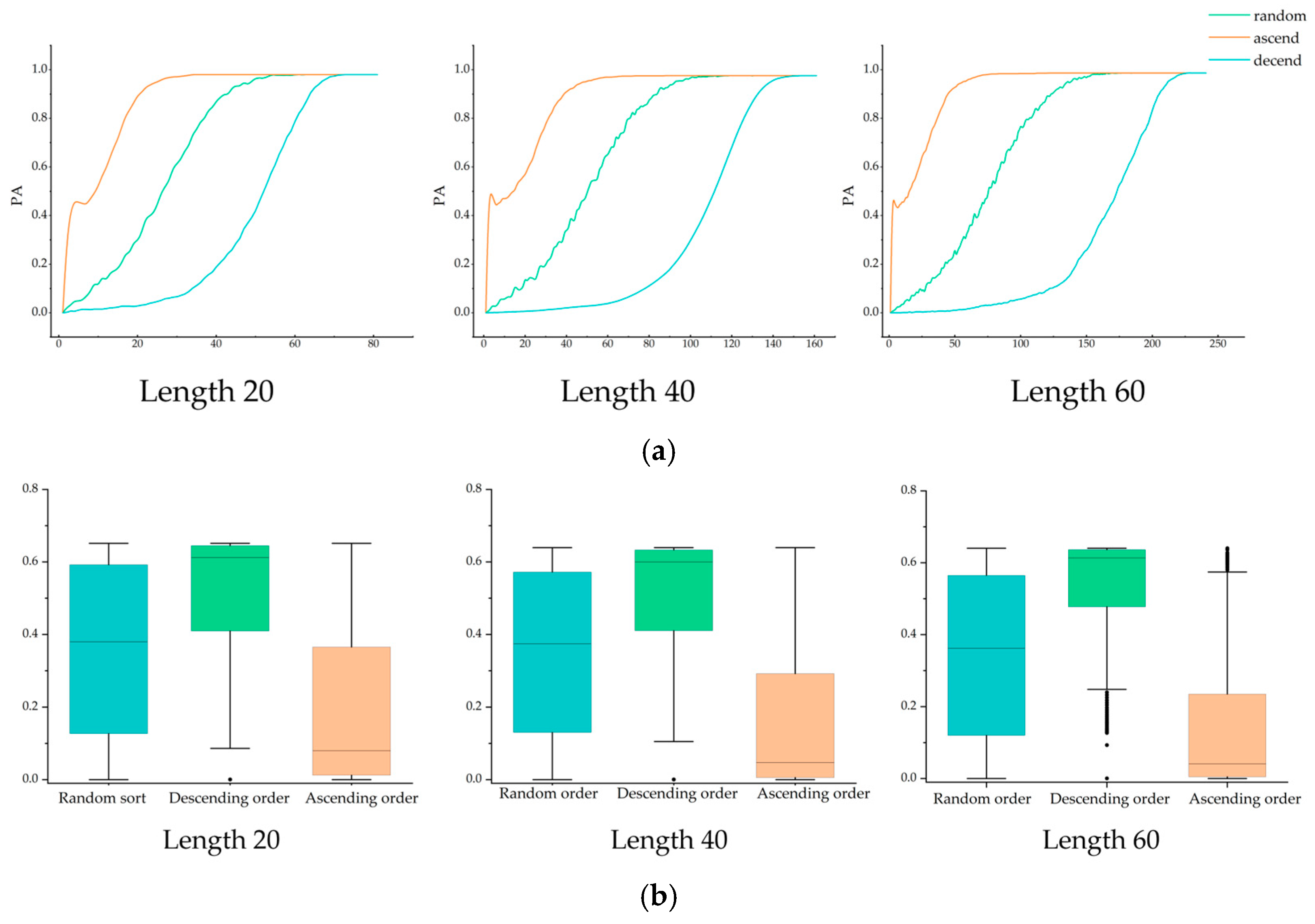
4.4.2. Comparison of Multi-Feature Masking Policies
5. Interpreting Predictions Using Contribution Maps
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Q.; Lu, Q.; Liu, Z.; Yang, Z. Expressway toll station management and control decision-making system based on event feature machine learning. Highway 2025, 2, 312–318. [Google Scholar]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, Z.; Gu, J.; Zhou, M.; Li, Y.; Zhang, L. Analyzing high speed rail passengers’ train choices based on new online booking data in China. Transp. Res. Part C Emerg. Technol. 2018, 97, 96–113. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, P. Individual mobility prediction review: Data, problem, method and application. Multimodal Transp. 2022, 1, 100002. [Google Scholar] [CrossRef]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Turin, Italy, 1–4 October 2018; pp. 80–89. [Google Scholar]
- Huang, L.; Zheng, W.; Deng, Z. Tourism Demand Forecasting: An Interpretable Deep Learning Model. Tour. Anal. 2024, 29, 465–479. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–16 August 2016; pp. 1135–1144. [Google Scholar]
- Wang, S.; Ding, S.; Xiong, L. A new system for surveillance and digital contact tracing for COVID-19: Spatiotemporal reporting over network and GPS. JMIR mHealth uHealth 2020, 8, e19457. [Google Scholar] [CrossRef]
- Theissler, A.; Spinnato, F.; Schlegel, U.; Guidotti, R. Explainable AI for time series classification: A review, taxonomy and research directions. IEEE Access 2022, 10, 100700–100724. [Google Scholar] [CrossRef]
- Hu, L.; Wang, K. Computing SHAP Efficiently Using Model Structure Information. arXiv 2023, arXiv:2309.02417. [Google Scholar]
- Sushil. Interpreting the interpretive structural model. Glob. J. Flex. Syst. Manag. 2012, 13, 87–106. [Google Scholar] [CrossRef]
- Navada, A.; Ansari, A.N.; Patil, S.; Sonkamble, B.A. Overview of use of decision tree algorithms in machine learning. In Proceedings of the 2011 IEEE Control and System Graduate Research Colloquium, Shah Alam, Malaysia, 27–28 June 2011; pp. 37–42. [Google Scholar]
- Tang, L.; Xiong, C.; Zhang, L. Decision tree method for modeling travel mode switching in a dynamic behavioral process. Transp. Plan. Technol. 2015, 38, 833–850. [Google Scholar] [CrossRef]
- Jia, S.; Lin, P.; Li, Z.; Zhang, J.; Liu, S. Visualizing surrogate decision trees of convolutional neural networks. J. Vis. 2020, 23, 141–156. [Google Scholar] [CrossRef]
- Guo, M.; Ye, P.; Liu, X.; Xiong, G.; Zhang, L. An Interpretability Analysis of Travel Decision Learning in Cyber-Physical-Social-Systems. In Proceedings of the 2021 IEEE 1st International Conference on Digital Twins and Parallel Intelligence (DTPI), Beijing, China, 15 July–15 August 2021; pp. 340–343. [Google Scholar]
- Saputra, R.; Sihabuddin, A. Mobility Prediction Using Markov Models: A Survey. In Proceedings of the 2024 7th International Conference on Informatics and Computational Sciences (ICICoS), Semarang, Indonesia, 17–18 July 2024; pp. 508–513. [Google Scholar]
- Kumar, M.R.; Kamisetty, S.S.S.; Reddy, N. A robust approach for road traffic prediction using Markov chain model. In Proceedings of the 2023 Seventh International Conference on Image Information Processing (ICIIP), Solan, India, 22–24 November 2023; pp. 663–669. [Google Scholar]
- Chen, Y.; Jin, Z.; Li, C. Trip purpose prediction based on hidden Markov model with GPS and land use data. In Proceedings of the 2020 IEEE 5th International Conference on Intelligent Transportation Engineering (ICITE), Beijing, China, 11–13 September 2020; pp. 55–59. [Google Scholar]
- Jin, Z.; Chen, Y.; Li, C.; Jin, Z. Trip destination prediction based on hidden Markov model for multi-day global positioning system travel surveys. Transp. Res. Rec. 2023, 2677, 577–587. [Google Scholar] [CrossRef]
- Madsen, A.; Reddy, S.; Chandar, S. Post-hoc interpretability for neural NLP: A survey. ACM Comput. Surv. 2022, 55, 155. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Yin, G.; Huang, Z.; Fu, C.; Ren, S.; Bao, Y.; Ma, X. Examining active travel behavior through explainable machine learning: Insights from Beijing, China. Transp. Res. Part D Transp. Environ. 2024, 127, 104038. [Google Scholar] [CrossRef]
- Yang, Z.; Tianyuan, S.; Caiyun, Q. The impact of the built environment in the surrounding areas of Nanjing urban rail transit stations on residents’ activities—Analysis based on gradient boosting decision tree and SHAP interpretation model. Sci. Technol. Eng. 2023, 23, 7509–7519. [Google Scholar]
- Li, W.; Deng, A.; Zheng, Y.; Yin, Z.; Wang, B. Analysis of Residents’ Travel Mode Choice in Medium-sized City Based on Machine Learning. J. Transp. Syst. Eng. Inf. Technol. 2024, 24, 13–23. [Google Scholar]
- Slik, J.; Bhulai, S. Transaction-Driven Mobility Analysis for Travel Mode Choices. Procedia Comput. Sci. 2020, 170, 169–176. [Google Scholar] [CrossRef]
- Covert, I.; Lee, S.I. Improving kernelshap: Practical shapley value estimation using linear regression. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; PMLR: New York, NY, USA; pp. 3457–3465. [Google Scholar]
- Bento, J.; Saleiro, P.; André, F.C.; Figueiredo, M.A.T.; Bizarro, P. TimeSHAP: Explaining Recurrent Models through Sequence Perturbations. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining (KDD’21), Virtual, 14–18 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 2565–2573. [Google Scholar]
- Balouji, E.; Sjöblom, J.; Murgovski, N.; Chehreghani, M.H. Prediction of Time and Distance of Trips Using Explainable Attention-based LSTMs. arXiv 2023, arXiv:2303.15087. [Google Scholar]
- Masampally, V.S.; Verma, R.; Mitra, K. Application of TimeSHAP, an explainable AI Tool, for Interpreting. In Optimization, Uncertainty and Machine Learning in Wind Energy Conversion Systems; Springer: Singapore, 2025; pp. 243–266. [Google Scholar]
- Jin, C.; Tao, T.; Luo, X.; Liu, Z.; Wu, M. S2N2: An Interpretive Semantic Structure Attention Neural Network for Trajectory Classification. IEEE Access 2020, 8, 58763–58773. [Google Scholar] [CrossRef]
- Ahmed, I.; Kumara, I.; Reshadat, V.; Kayes, A.S.M.; Heuvel, W.-J.v.D.; Tamburri, D.A. Travel time prediction and explanation with spatio-temporal features: A comparative study. Electronics 2021, 11, 106. [Google Scholar] [CrossRef]
- Vijaya, A.; Bhattarai, S.; Angreani, L.S.; Wicaksono, H. Enhancing Transparency in Public Transportation Delay Predictions with SHAP and LIME. In Proceedings of the 2024 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 15–18 December 2024; pp. 1285–1289. [Google Scholar]
- Srivastava, N.; Gohil, B.N. Ridership Trend Analysis and Explainable Taxi Travel Time Prediction for Bangalore Using e-Hailing. In Proceedings of the 7th International Conference of Transportation Research Group of India (CTRG 2023); Springer Nature: Berlin/Heidelberg, Germany, 2025; Volume 2, pp. 383–400. [Google Scholar]
- Zhang, P.; Koutsopoulos, H.N.; Ma, Z. DeepTrip: A deep learning model for the individual next trip prediction with arbitrary prediction times. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5842–5855. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Zhang, C.; Sun, F.; Meng, F.; Guo, A.; Jin, D. Deepmove: Predicting human mobility with attentional recurrent networks. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 1459–1468. [Google Scholar]
- Hosain, M.T.; Jim, J.R.; Mridha, M.F.; Kabir, M. Explainable AI approaches in deep learning: Advancements, applications and challenges. Comput. Electr. Eng. 2024, 117, 109246. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: New York, NY, USA; pp. 3319–3328. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: New York, NY, USA; pp. 3145–3153. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]







| Dimension | Interpretation Granularity | Computational Efficiency |
|---|---|---|
| Decision tree | Static | O(N) |
| KernelSHAP | Static | O(2N) |
| TimeSHAP | Static and Temporal | O(2N-i) |
| LIME | Static | O(N) |
| Gradient (ours) | Static and Temporal | O(N) |
| Image Recognition Tasks | Travel Prediction Task |
|---|---|
| Pixel | Feature |
| Intensity Size | Value Size |
| Label Category | Option/Forecast Target |
| Label Set | Option Set |
| Sequence Length | 20 | 40 | 60 |
|---|---|---|---|
| Training Set Accuracy | 59.04% | 60.10% | 59.16% |
| Test Set Accuracy | 57.82% | 58.51% | 57.50% |
| Sequence Length | JS | PA |
|---|---|---|
| 20 | 0.0863 | 0.292 |
| 40 | 0.1050 | 0.361 |
| 60 | 0.0929 | 0.342 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Zhang, P.; Song, X.; Li, Y. Interpretability Study of Gradient Information in Individual Travel Prediction. Appl. Sci. 2025, 15, 5269. https://doi.org/10.3390/app15105269
Su Z, Zhang P, Song X, Li Y. Interpretability Study of Gradient Information in Individual Travel Prediction. Applied Sciences. 2025; 15(10):5269. https://doi.org/10.3390/app15105269
Chicago/Turabian StyleSu, Ziheng, Pengfei Zhang, Xiaohui Song, and Yifan Li. 2025. "Interpretability Study of Gradient Information in Individual Travel Prediction" Applied Sciences 15, no. 10: 5269. https://doi.org/10.3390/app15105269
APA StyleSu, Z., Zhang, P., Song, X., & Li, Y. (2025). Interpretability Study of Gradient Information in Individual Travel Prediction. Applied Sciences, 15(10), 5269. https://doi.org/10.3390/app15105269





