Analysis of Buffeting Response and Stay Cable Fatigue Damage in Super-Long-Span Carbon Fiber-Reinforced Polymer (CFRP) Cable-Stayed Bridges
Abstract
1. Introduction
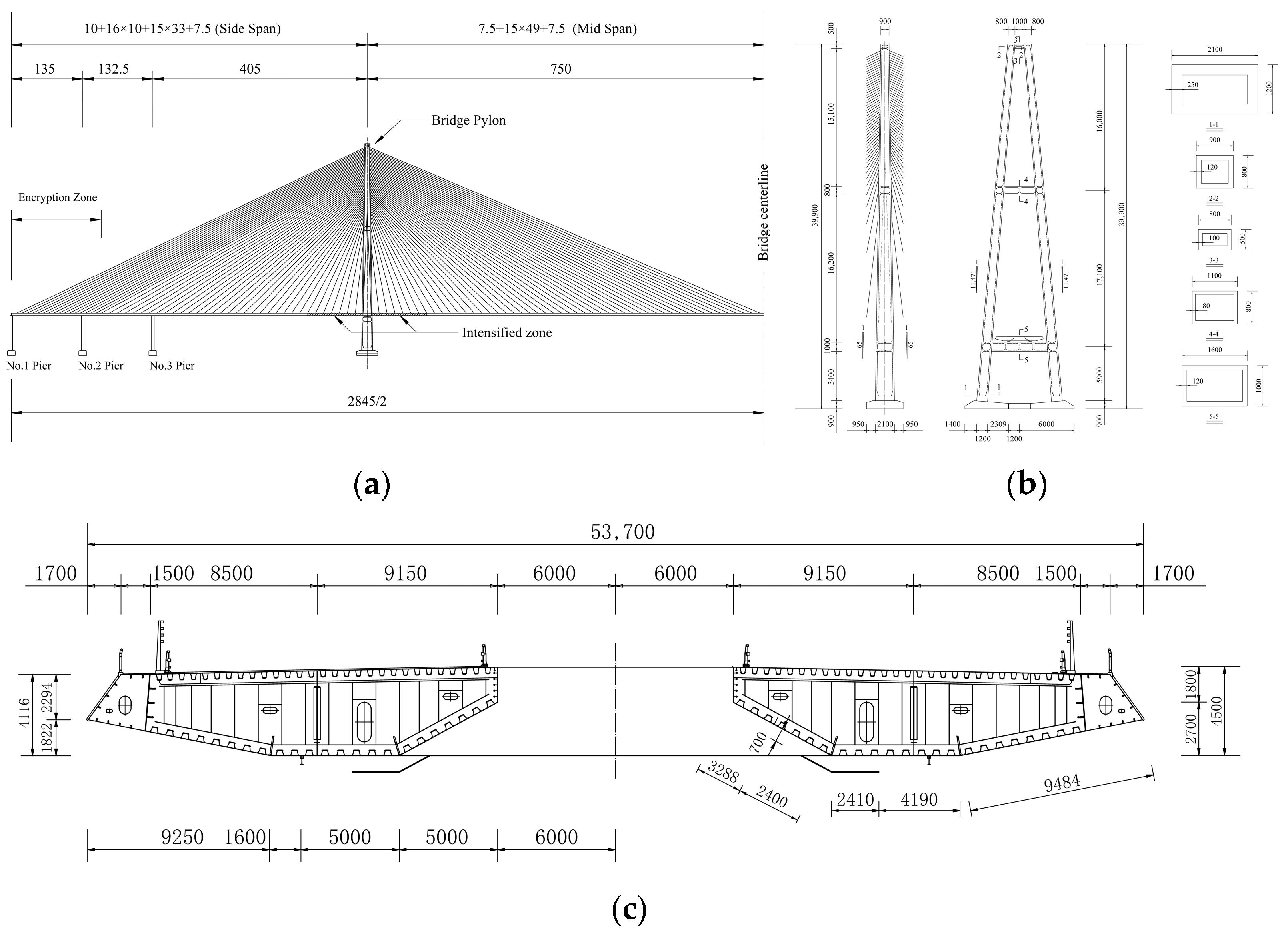
2. Structure Description
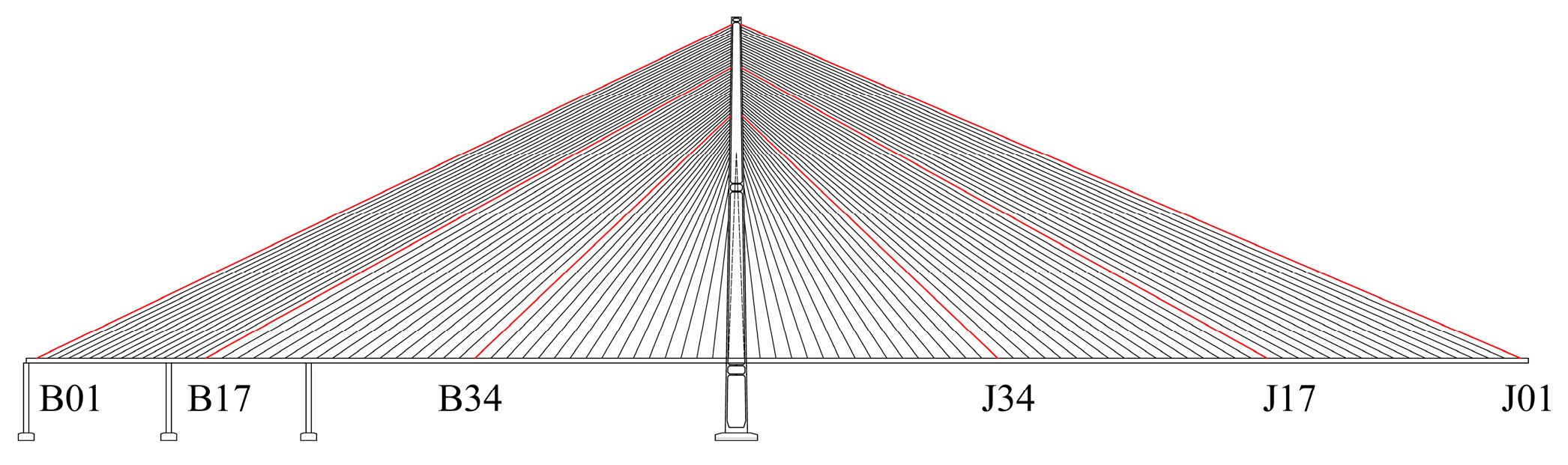
2.1. General Information of the Bridge Scheme with Steel Cable
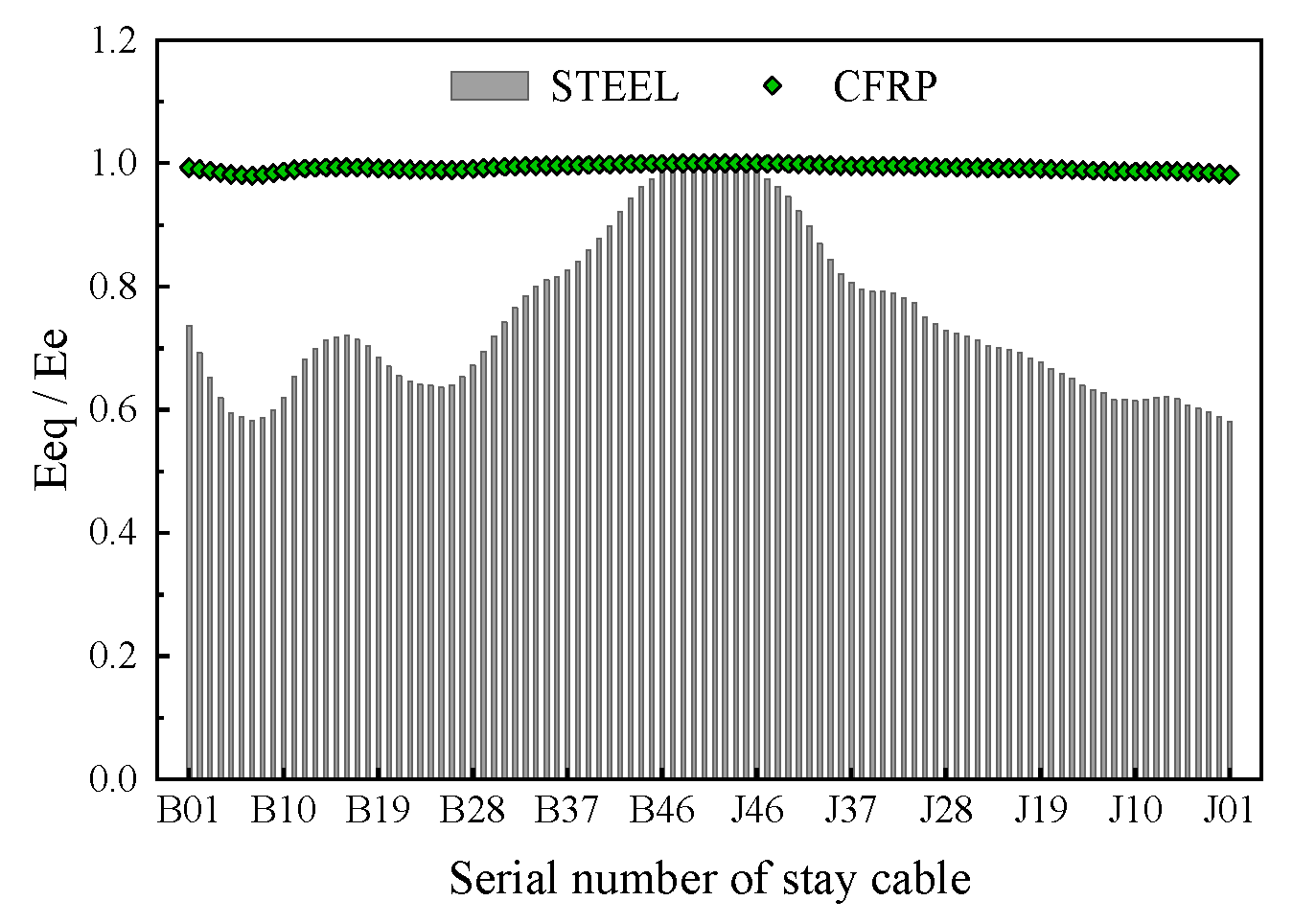
2.2. Bridge Scheme with CFRP Cable
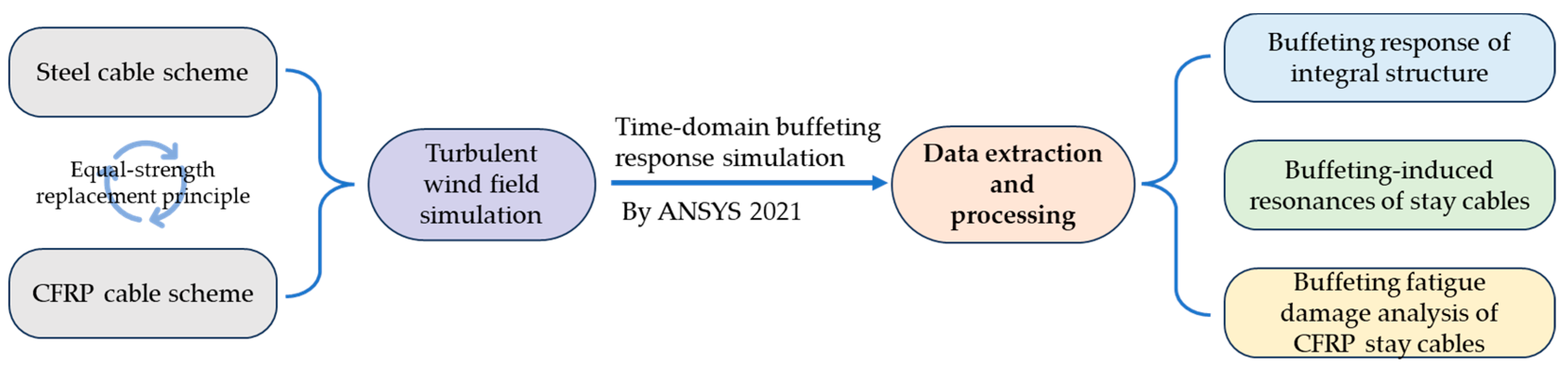
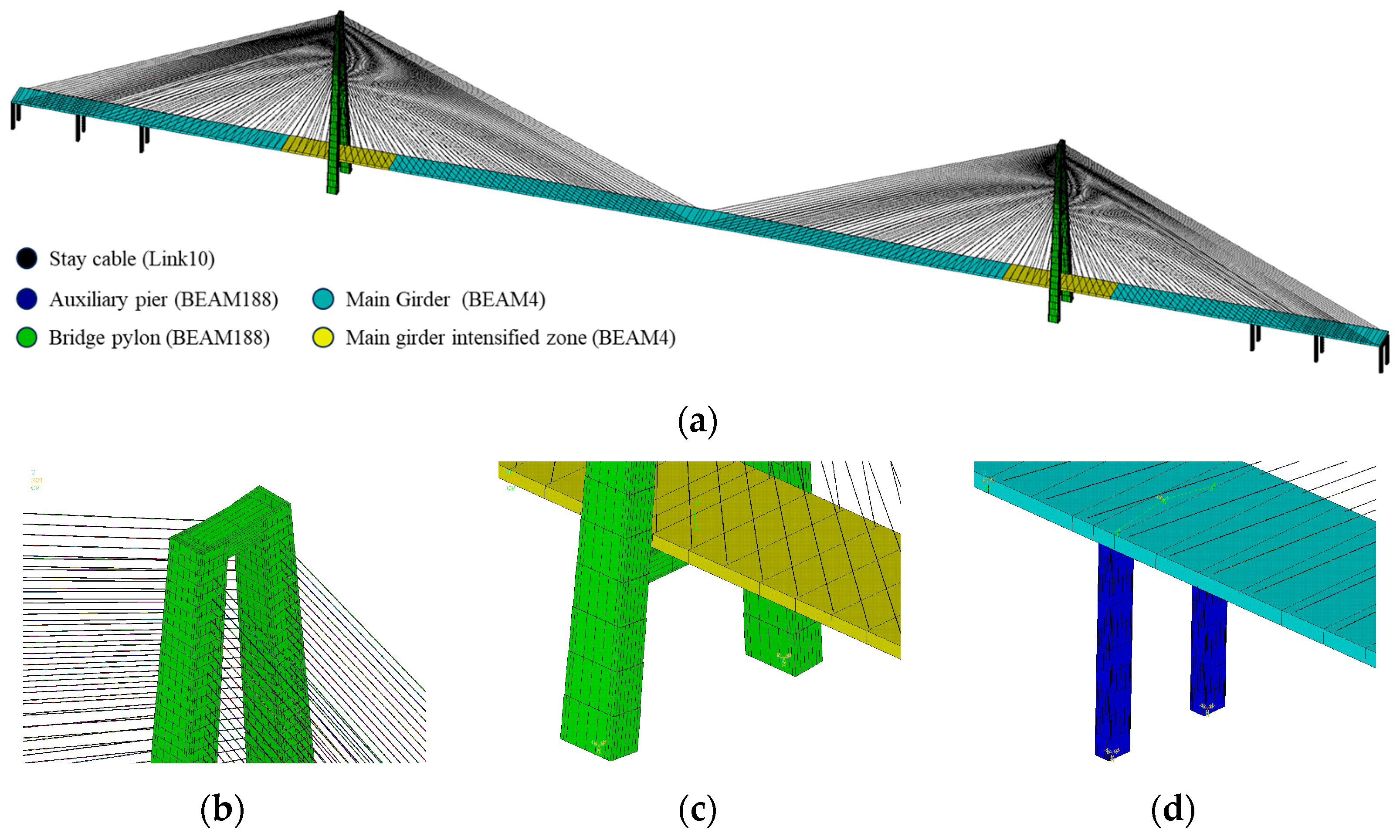
2.3. The FE Model Construction
3. Wind Load Description
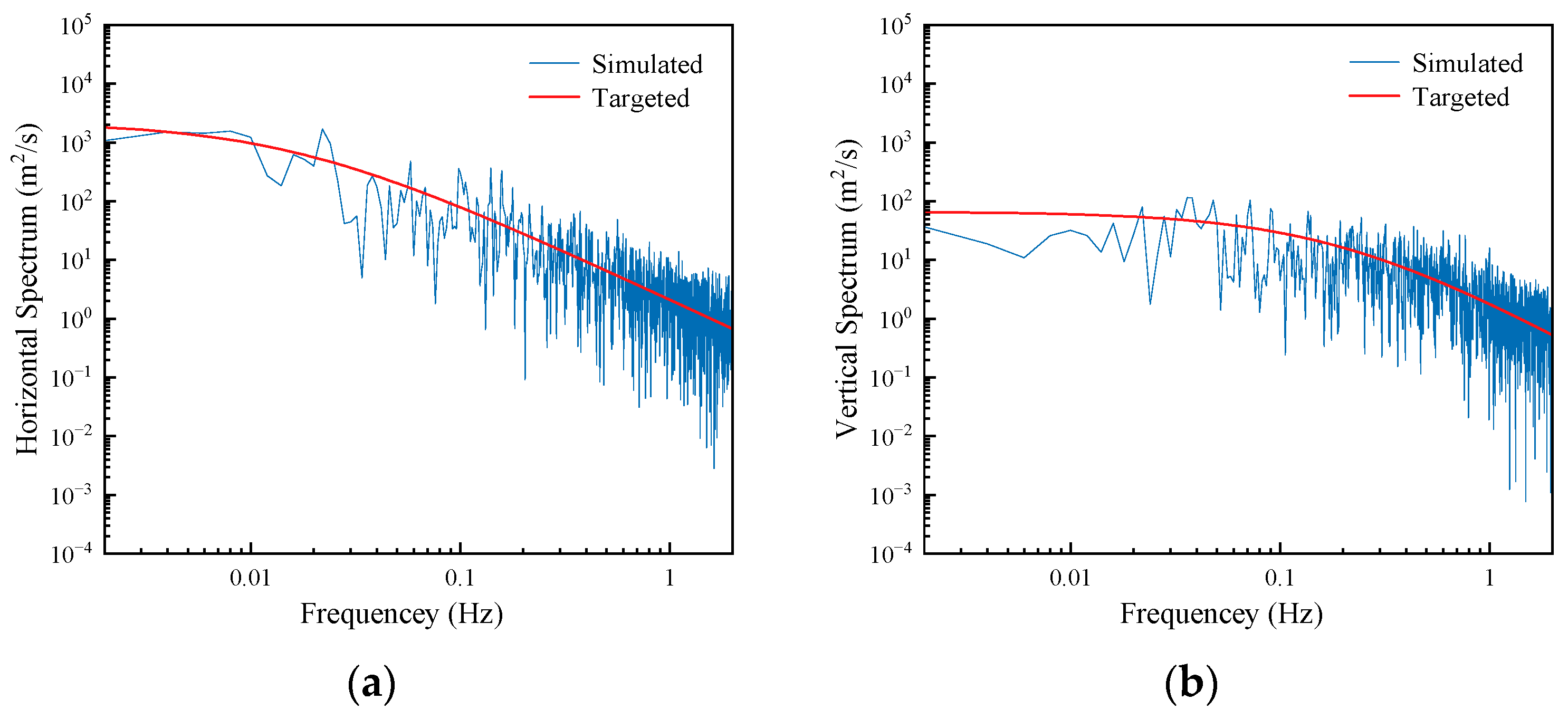
3.1. Turbulent Wind Field Simulation
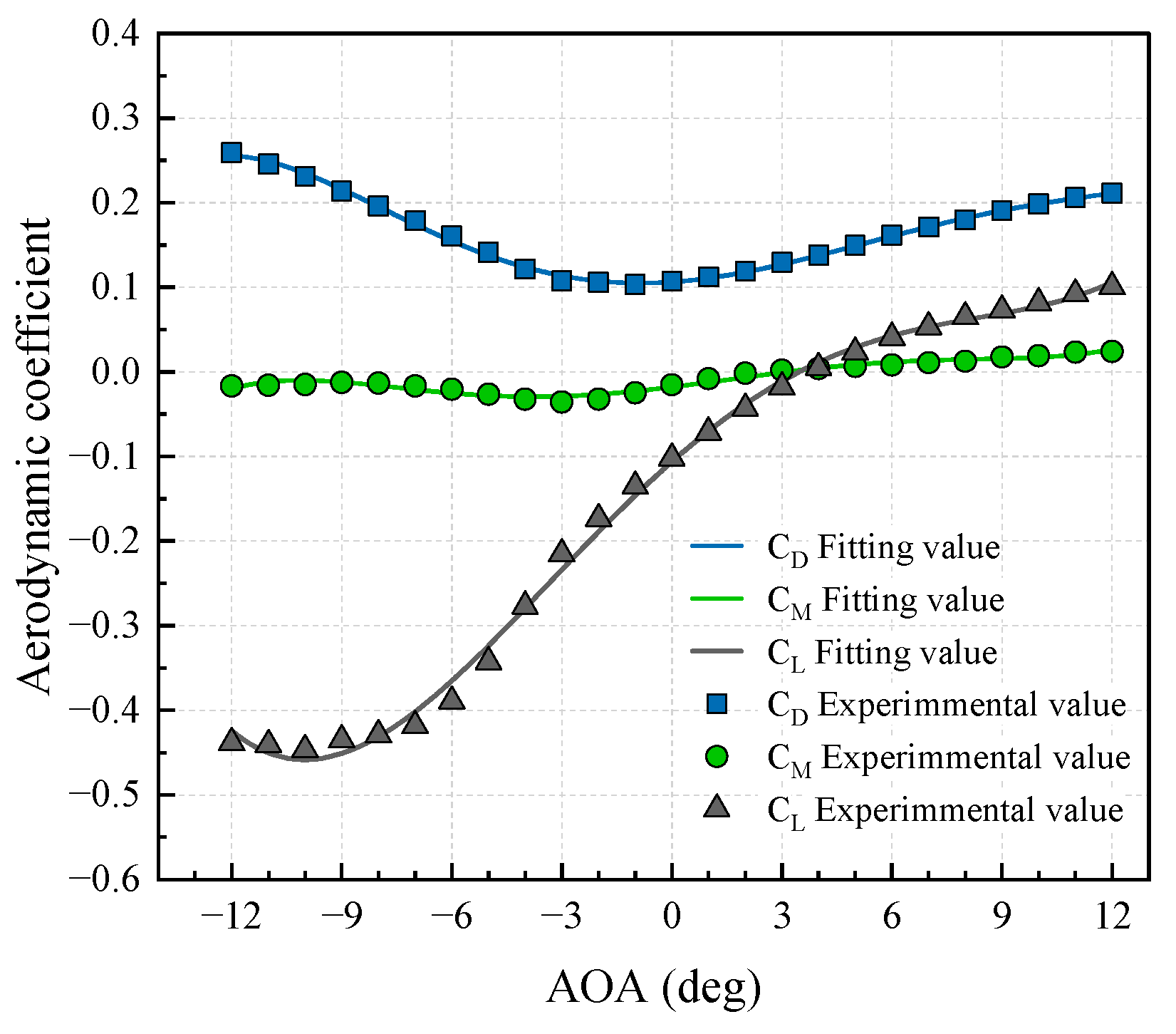
3.2. Wind Load Expression
4. Buffeting Response Analysis
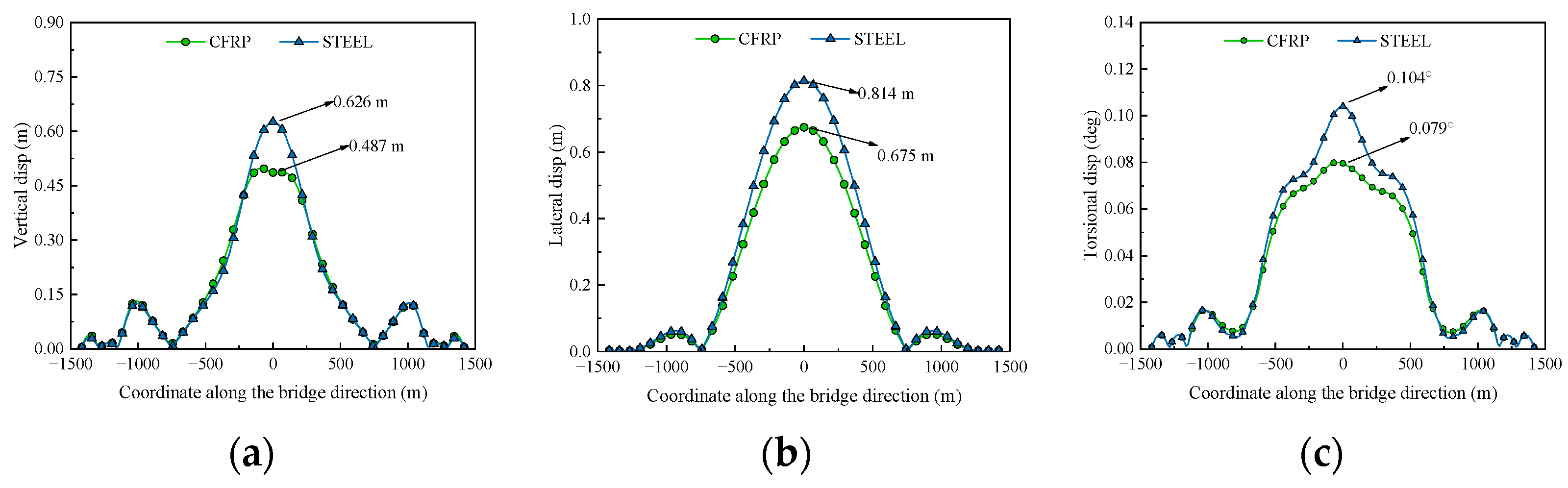
4.1. Buffeting Response of Integral Structure
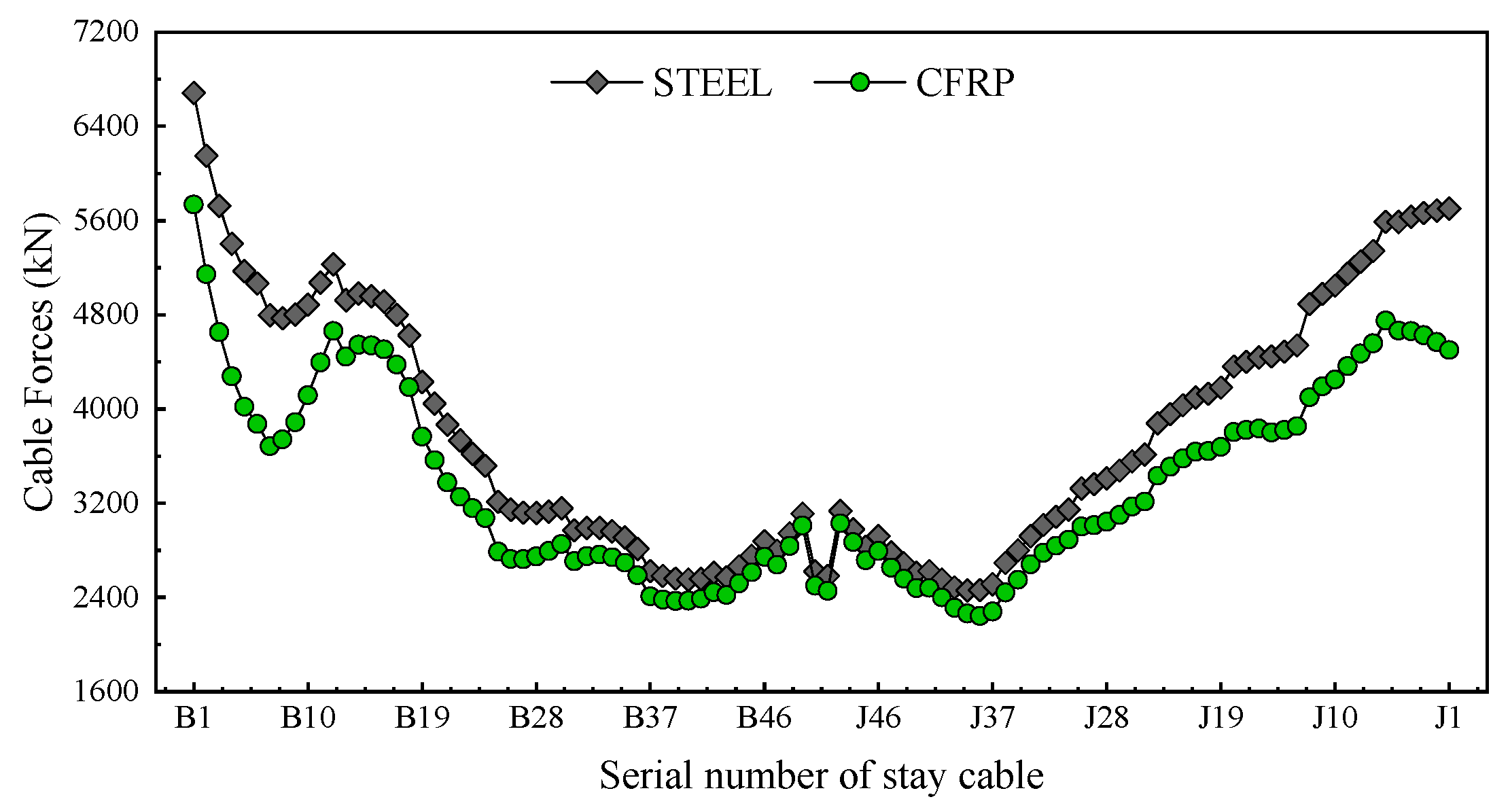
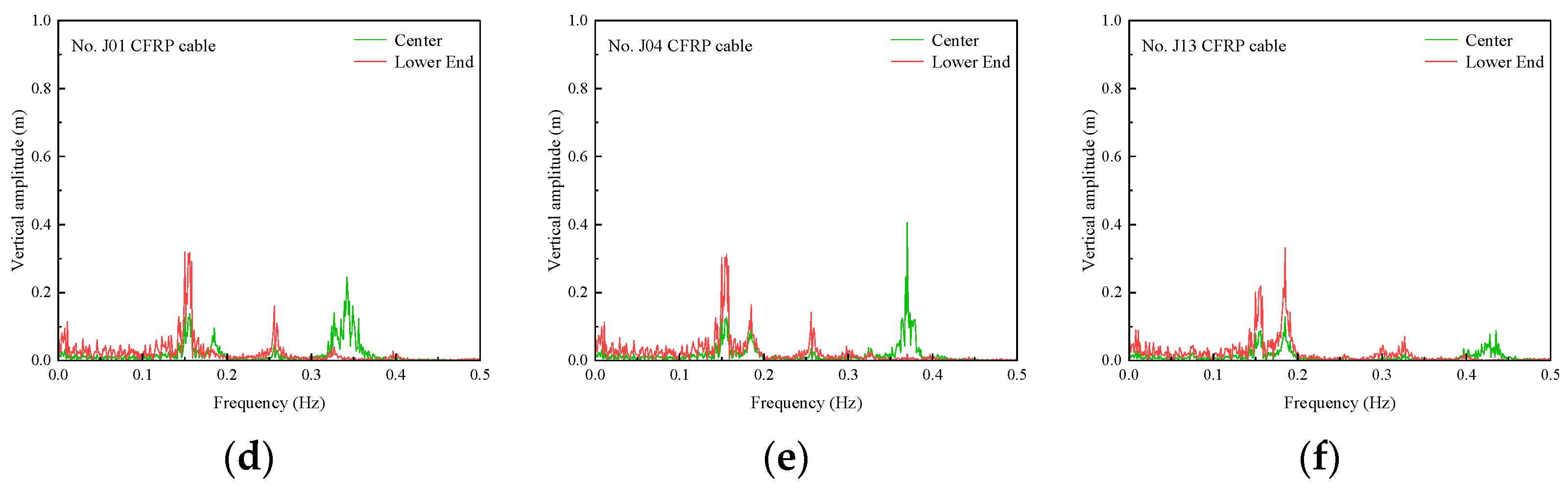
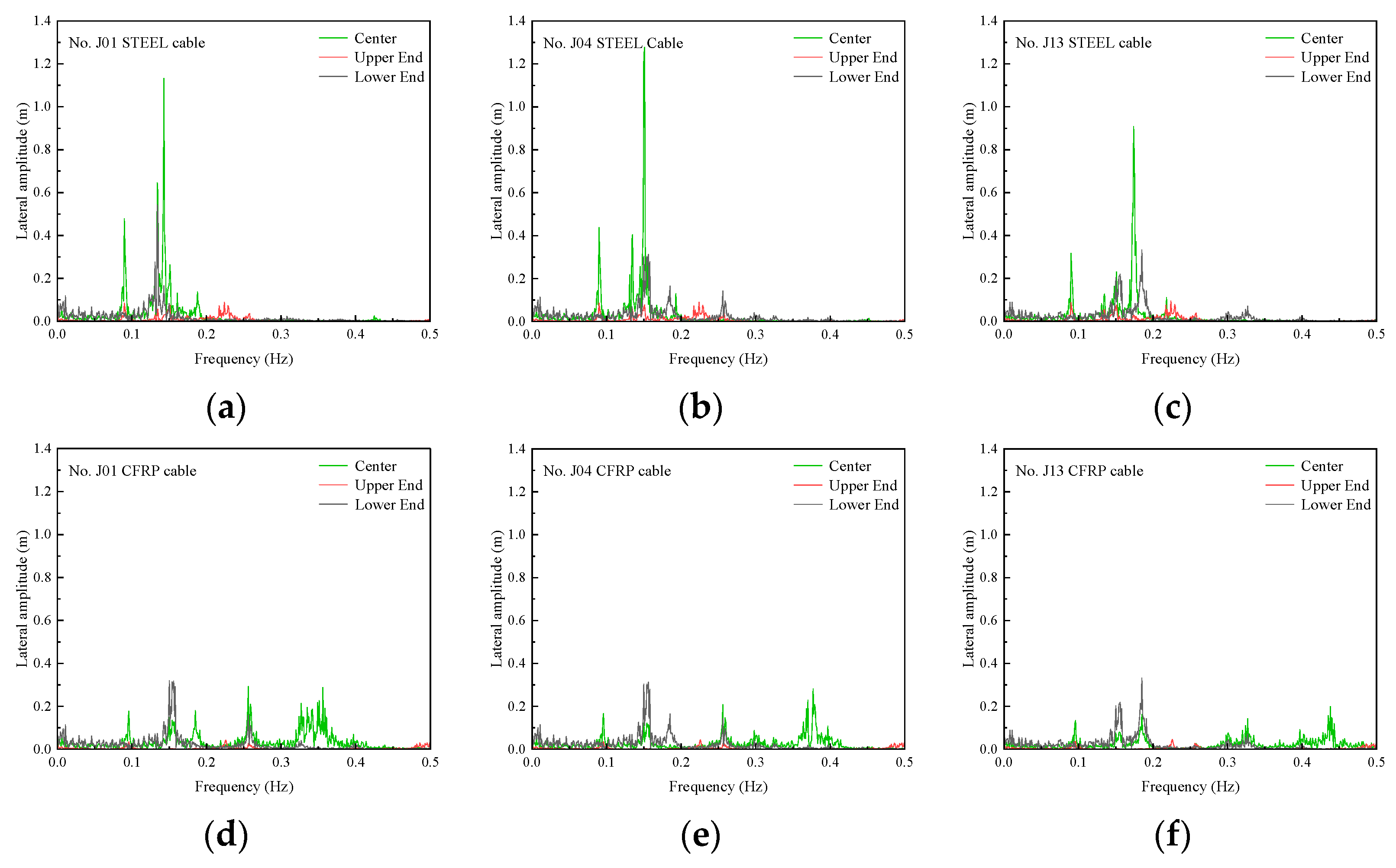
4.2. Buffeting-Induced Resonances of Stay Cables
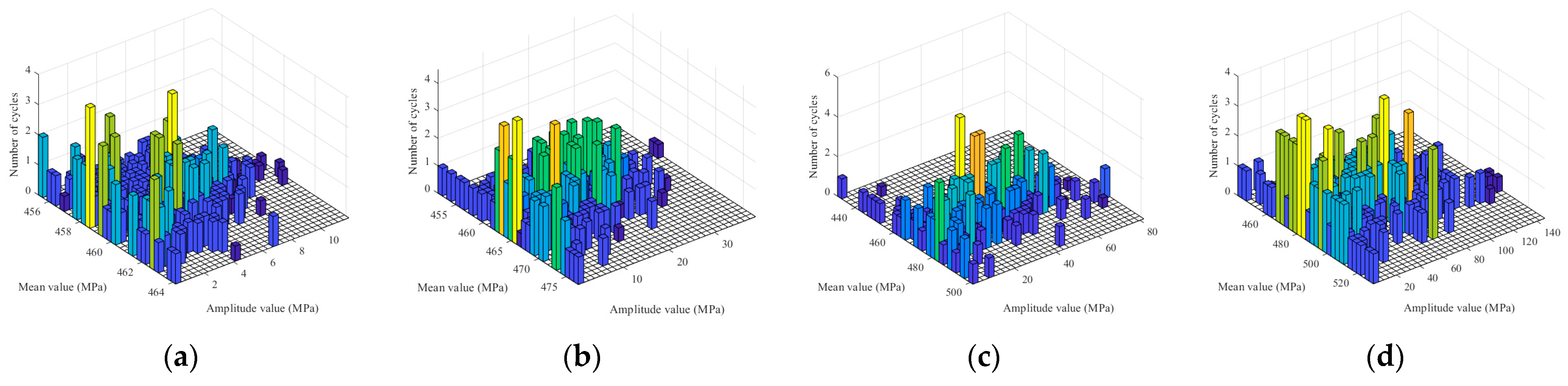
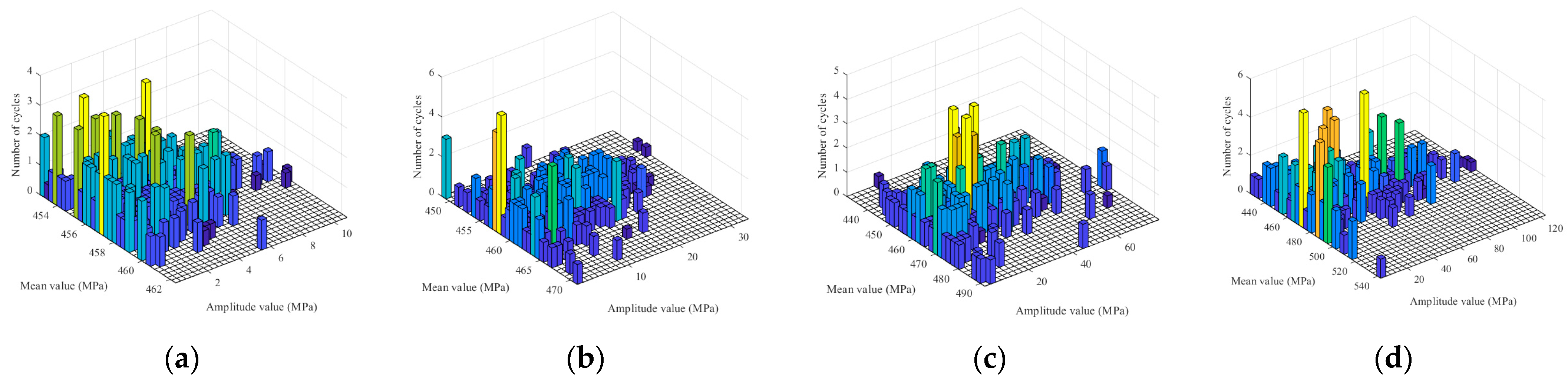
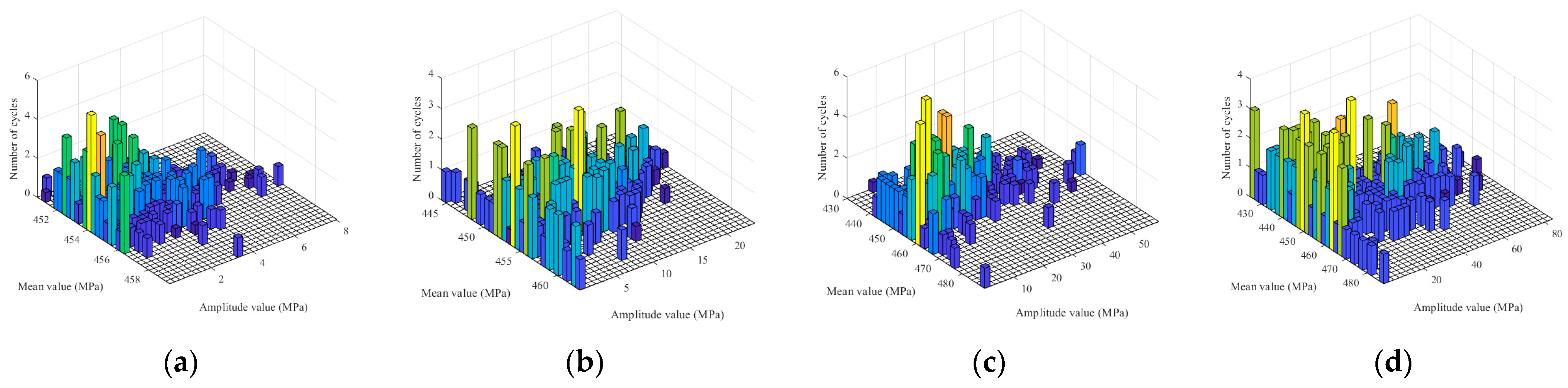
5. Buffeting Fatigue Damage Analysis of CFRP Stay Cables
5.1. Fatigue and Damage Analysis Theory
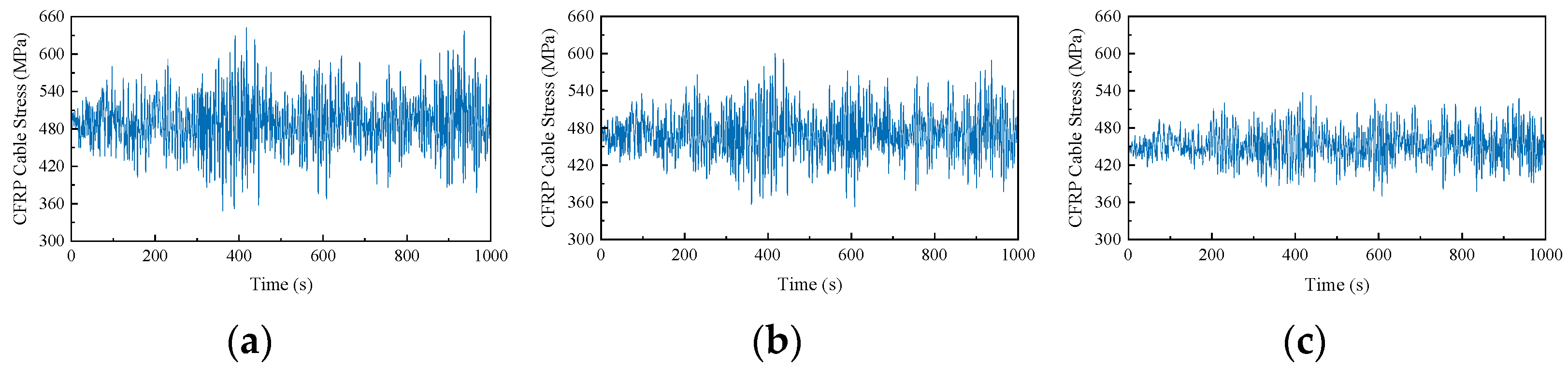
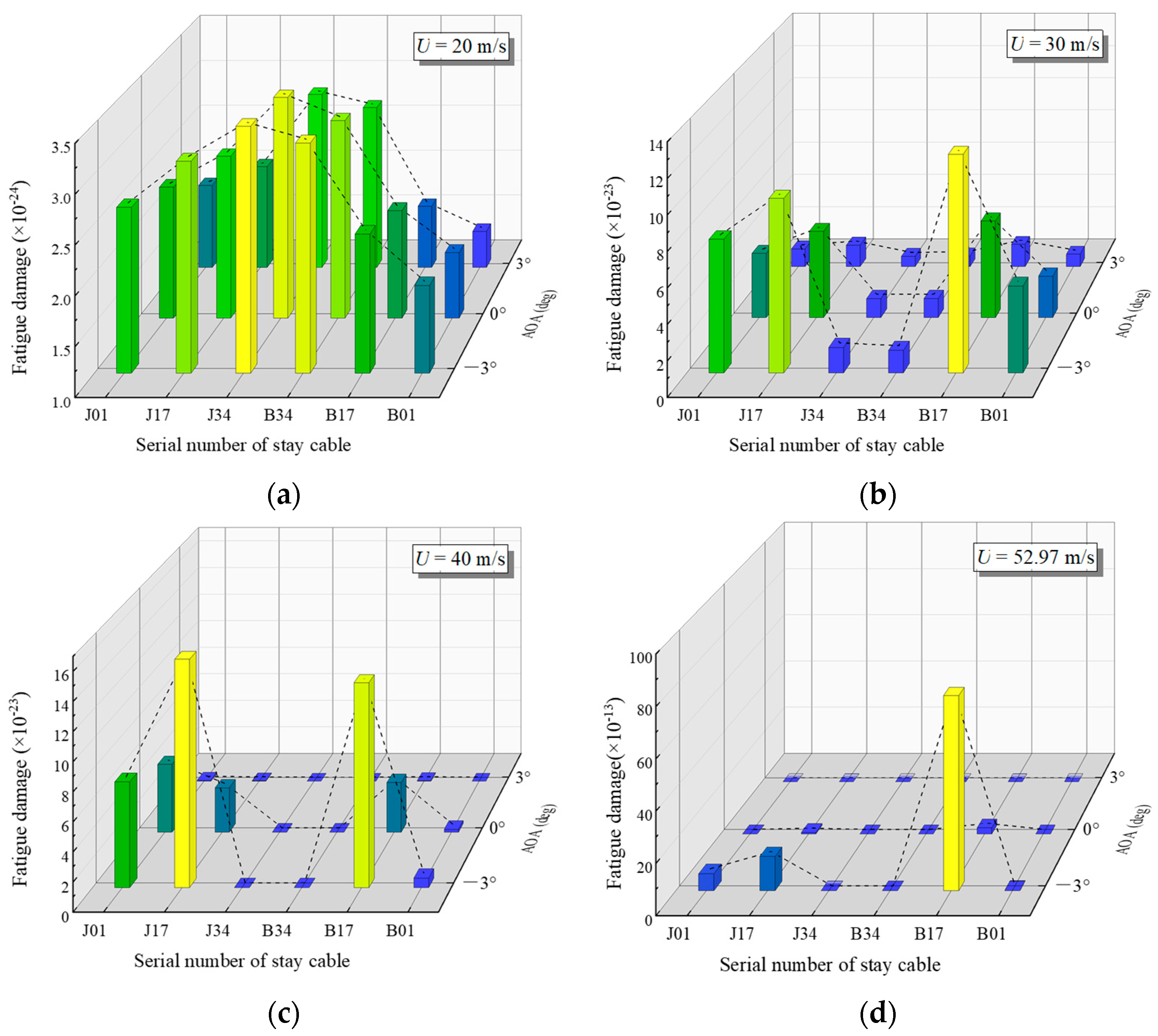
5.2. CFRP Cable Fatigue Damage Analysis
6. Conclusions
- (1)
- The CFRP cable scheme demonstrated superior static wind stability compared with the steel cable scheme, with reduced lateral displacements at equilibrium positions under design wind speeds. The RMS values of vertical, lateral, and torsional buffeting responses in CFRP cables were reduced by 31.6%, 28.5%, and 20.6%, respectively, at mid-span under critical wind angles of attack. This improvement stems from the CFRP’s lower self-weight and higher stiffness, which mitigate sag effects and aerodynamic drag.
- (2)
- The steel cables exhibited significant internal resonance under turbulent wind excitation due to frequency coupling between cable modes and structural vibration frequencies. In contrast, the CFRP cables avoided such resonance phenomena owing to their higher natural frequencies and reduced sensitivity to anchorage-end excitations. The sparser frequency distribution of CFRP cables effectively decoupled cable–girder interactions, suppressing mode transitions and clustered spectral peaks.
- (3)
- Fatigue analysis based on the Palmgren–Miner rule and rainflow counting demonstrated that the CFRP cables exhibited orders-of-magnitude lower cumulative fatigue damage than the steel cables under identical wind conditions. The maximum fatigue damage in CFRP cables remained confined to critical positions but stayed within safe limits, validating the CFRP’s superior durability under stochastic wind loading.
- (4)
- Replacing steel cables with CFRP cables in ultra-long-span cable-stayed bridges significantly enhances wind resistance, reduces maintenance costs associated with fatigue and corrosion, and extends service life. This study provides theoretical and computational support for CFRP cable applications in mega-span bridge engineering, addressing key challenges in aerodynamic stability and fatigue performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFRP | Carbon fiber-reinforced polymer |
| PSD | Power spectral density |
| FEM | Finite element model |
| AOA | Angle of attack |
| RMS | Root mean square |
References
- Nagai, M.; Yamaguchi, H.; Nogami, K.; Fujino, Y. Effect of cable size on static and dynamic instabilities of long-span cable-stayed bridges. In Proceedings of the Cable-Supported Bridges—Challenging Technical Limits, Seoul, Republic of Korea, 12–14 June 2001. [Google Scholar]
- Nagai, M.; Fujino, Y.; Yamaguchi, H.; Iwasaki, E. Feasibility of a 1400 m Span Steel Cable-Stayed Bridge. J. Bridge Eng. 2004, 9, 444–452. [Google Scholar] [CrossRef]
- Xie, G.H.; Yin, J.; Liu, R.G.; Chen, B.; Cai, D.S. Experimental and numerical investigation on the static and dynamic behaviors of cable-stayed bridges with CFRP cables. Compos. Part B Eng. 2017, 111, 235–242. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Z. Evaluation of FRP and hybrid FRP cables for super long-span cable-stayed bridges. Compos. Struct. 2010, 92, 2582–2590. [Google Scholar] [CrossRef]
- Zhang, M.J.; Xu, F.Y. Wind-induced Nonlinearities of Super Long Stay Cables. In Proceedings of the 2015 4th International Conference on Sustainable Energy and Environmental Engineering, Shenzhen, Chian, 20–21 December 2016. [Google Scholar]
- Chen, Z.Q.; Li, S.Y.; Deng, Y.C.; Wang, Y.Y.; An, M.; Yang, C. Recent Challenges and Advances on Study of Wind-induced Vibrations of Bridge Cables. J. Hunan Univ. (Nat. Sci.) 2022, 5, 1–8. [Google Scholar]
- Raeesi, A. Wind-Induced Response of Bridge Stay Cables in Unsteady Wind. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 2015. [Google Scholar]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Carbon Fiber Reinforced Polymer for Cable Structures—A Review. Polymers 2015, 7, 2078–2099. [Google Scholar] [CrossRef]
- Meier, U. Proposal for a Carbon Fiber Reinforced Composite Bridge across the Strait of Gibraltar at its Narrowest Site. Proc. Inst. Mech. Eng. Part B: Manag. Eng. Manuf. 1987, 201, 73–78. [Google Scholar] [CrossRef]
- Meier, H.; Meier, U.; Brönnimann, R. Zwei CFK-Kabel für die Storchenbrücke. Schweiz. Ing. Und Archit.-Schweiz. Bauztg. 1996, 114, 8–13. [Google Scholar]
- Christoffersen, J.; Hauge, L.; Bjerrum, J. Footbridge with Carbon-Fiber-Reinforced Polymers, Denmark. Struct. Eng. Int. 1999, 9, 254–256. [Google Scholar] [CrossRef]
- Geffroy, R.L. The Laroin Footbridge with Carbon Composite Stay-Cables. In Proceedings of the Footbridge 2002, Paris, France, 20–22 November 2002. [Google Scholar]
- Mei, K.H.; Li, Y.J.; Lu, Z.T. Application study on the first cable-stayed bridge with CFRP cables in China. J. Traffic Transp. Eng. (Engl. Ed.) 2015, 2, 242–248. [Google Scholar] [CrossRef]
- Tsay, J. Feasibility Study of Super-Long Span Bridges Considering Aerostatic Instability by a Two-Stage Geometric Nonlinear Analysis. Int. J. Struct. Stab. Dyn. 2021, 21, 2150033. [Google Scholar] [CrossRef]
- Long, G.; Sun, Y.; Shang, Z.; Wang, X.; Xu, X.; Wang, T. Aerodynamic performance and wind-induced response of carbon fiber-reinforced polymer (CFRP) cables. Sci. Rep. 2024, 14, 8154. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.Q.; Wang, X.; Wu, Z.S.; Peng, C. Damping properties of FRP cables for long-span cable-stayed bridges. Mater. Struct. 2016, 49, 2701–2713. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Wu, T.; Fang, Z. Wind-resistance Performance Analysis of Long Span Cable Stayed Bridge Using High Performance Materials. J. Hunan Univ. (Nat. Sci.) 2018, 5, 11–18. [Google Scholar]
- Liu, Z.W.; Chen, A.R.; Zhou, Z.Y.; Ma, R.J. Comparison of Calculation Methods of Static Wind Loading on Stay Cables of Large Span Cable-Stayed Bridges. J. Tongji Univ. (Nat. Sci.) 2005, 5, 575–579. [Google Scholar]
- JTGT 3365-01-2020; Specifications for Design of Highway Cable-stayed Bridge. Ministry of Transport of the People’s Republic of China: Beijing, China, 2018. (In Chinese)
- Wang, X.; Wu, Z.S.; Wu, G.; Zhu, H.; Zen, F.X. Enhancement of basalt FRP by hybridization for long-span cable-stayed bridge. Compos. Part B Eng. 2020, 44, 184–192. [Google Scholar] [CrossRef]
- Zhao, H.X.; Zhang, W.M.; Jiang, X.F.; Liu, Z. Calculation Method for Equivalent Elastic Modulus of Cable Sag Effect Based on Catenary. J. China Foreign Highw. 2020, 02, 62–66. [Google Scholar]
- JTGT 3360-01-2018; Wind-resistant Design Specification for Highway Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2018. (In Chinese)
- Deodatis, G. Simulation of Ergodic Multivariate Stochastic Processes. J. Eng. Mech. 1996, 122, 778–787. [Google Scholar] [CrossRef]
- Luo, J.; Han, D. A fast simulation method of stochastic wind field for long-span structures. Eng. Mech. 2008, 25, 96–101. [Google Scholar]
- Zhang, Z.T.; Ge, Y.J.; Chen, Z.Q. A New Aerodynamic Method For Long-Span Bridge Buffeting Analysis. Eng. Mech. 2006, 23, 94–101. [Google Scholar]
- Qian, C.; Zhu, L.D.; Zhu, Q.; Ding, Q.S.; Yan, L. Pattern and mechanism of wind-induced static instability of super-long-span cable-stayed bridge under large deformation. J. Wind. Eng. Ind. Aerodyn. 2022, 221, 104910. [Google Scholar] [CrossRef]
- Wu, Z.; Wei, J. Nonlinear Analysis of Spatial Cable of Long-Span Cable-Stayed Bridge considering Rigid Connection. Ksce J. Civ. Eng. 2019, 23, 2148–2157. [Google Scholar] [CrossRef]
- Zhang, Z.T.; Zeng, J.D.; Zhu, L.D.; Ge, Y.J. Buffeting-Induced Resonances of Hangers at a Long-Span Suspension Bridge and Mitigation Countermeasure. J. Bridge Eng. 2021, 26, 4021064. [Google Scholar] [CrossRef]
- Khoramishad, H.; Crocombe, A.D.; Katnam, K.B.; Ashcroft, I.A. Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int. J. Fatigue 2010, 32, 1146–1158. [Google Scholar] [CrossRef]
- He, X.H.; Cheng, H.; Li, G.Q. Buffeting-Induced Fatigue Damage Analysis on the Stayed Cables of Long-Span Steel Truss Cable-Stayed Bridge. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2013, 32, 752–755. [Google Scholar]
- Amzallag, C.; Gerey, J.P.; Robert, J.L.; Bahuaud, J. Standardization of the rainflow counting method for fatigue analysis. Int. J. Fatigue 1994, 16, 287–293. [Google Scholar] [CrossRef]




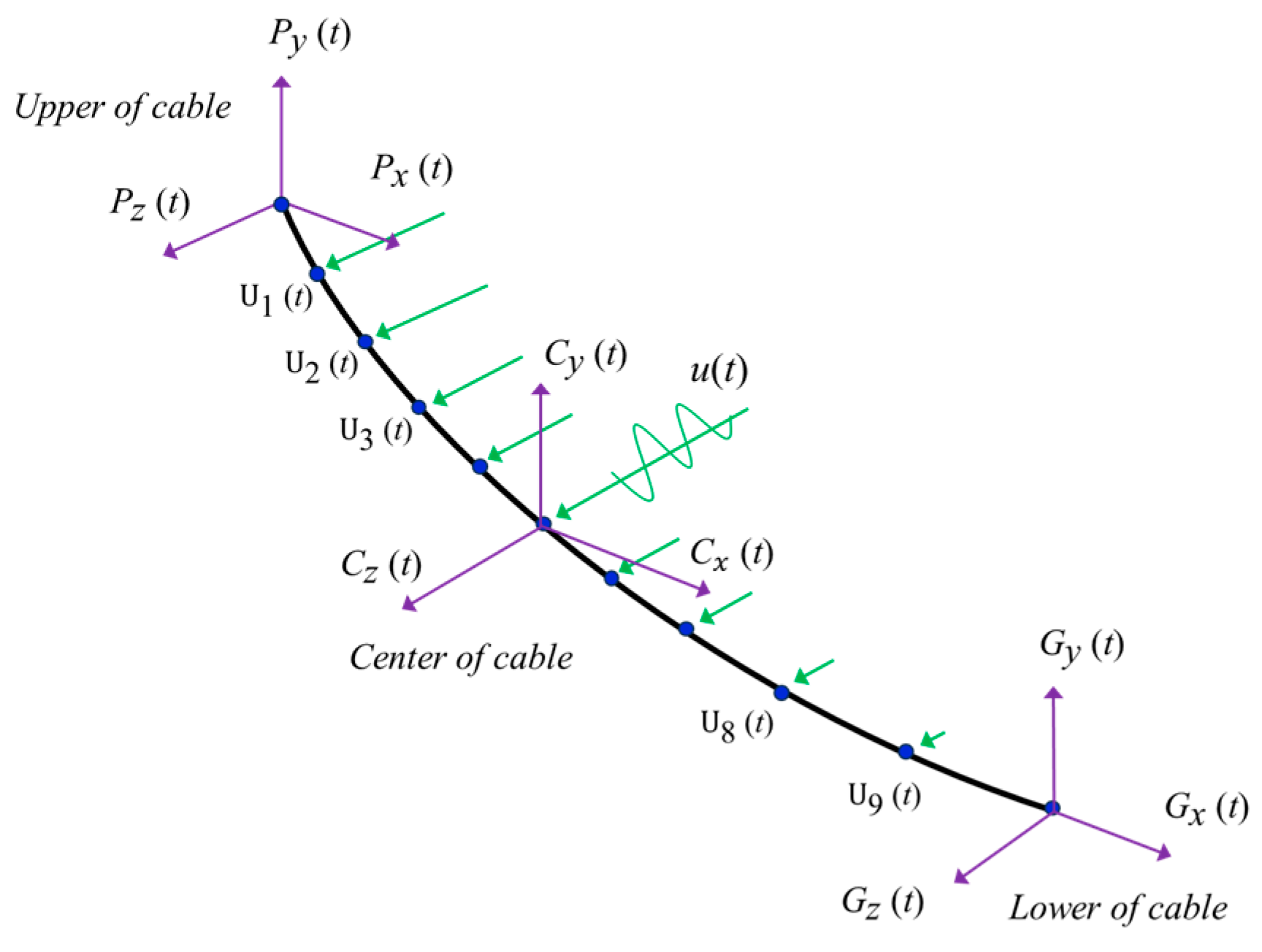
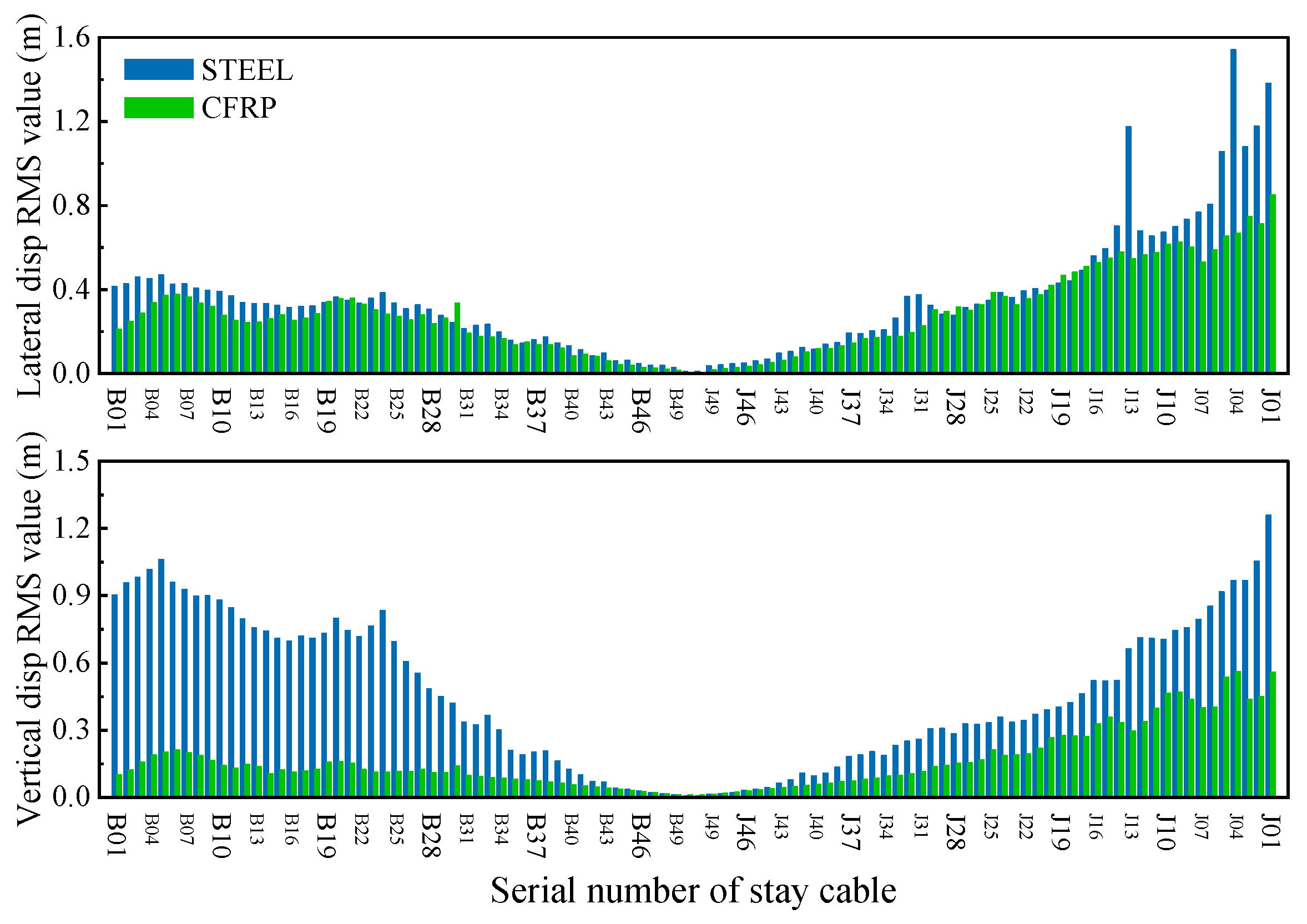

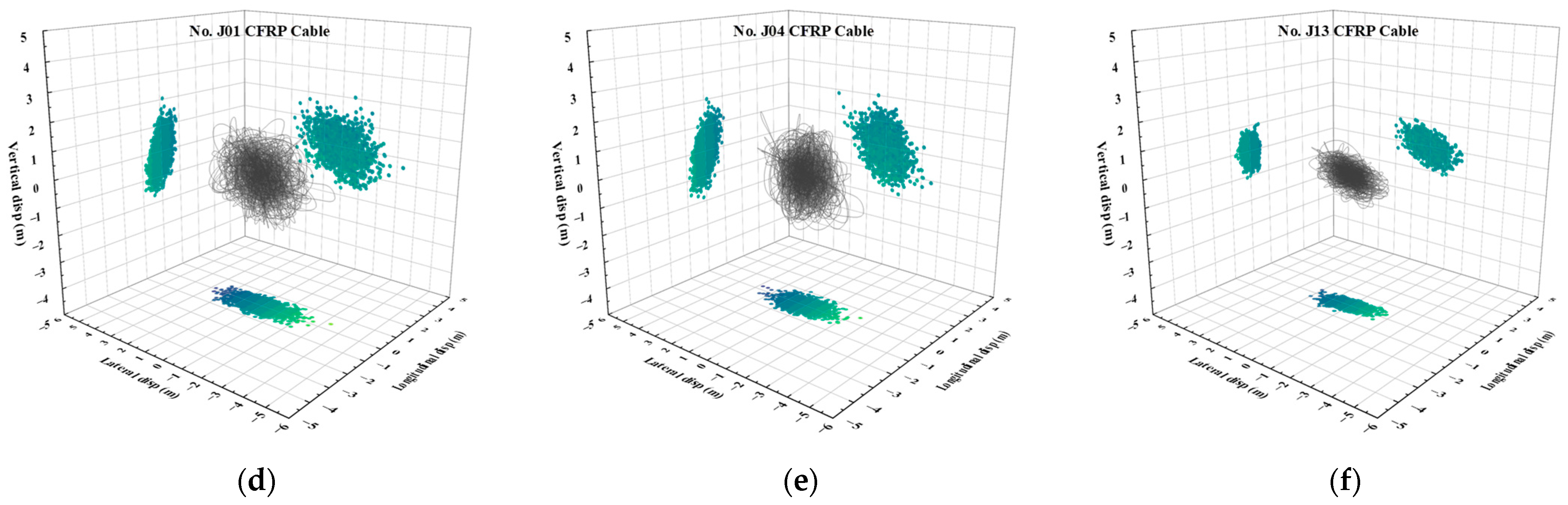
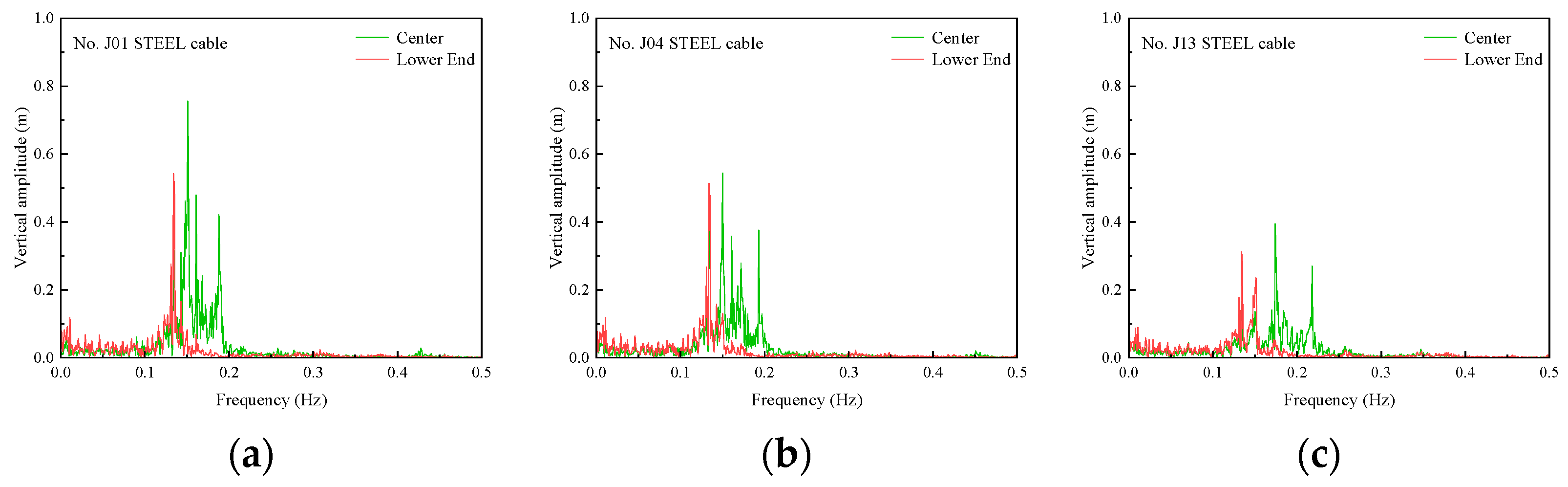
| Location | Material | Tensile Strength (MPa) | Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Area (m2) |
|---|---|---|---|---|---|---|
| Pylon | C60 | / | 36 | 0.2 | 2549 | / |
| Stay cable | 1860 HS steel | 1860 | 195 | 0.3 | 8005 | (0.63~1.41) × 10−2 |
| CFRP | 2550 | 180 | 0.28 | 1500 | (0.55~1.30) × 10−2 | |
| Main girder | Q345 | 345 | 200 | 0.3 | 8005 | 2.1~3.53 |
| Item | Value | Item | Value |
|---|---|---|---|
| Simulated points | 526 | Cutoff frequency | 2 Hz |
| Time span | 1000 s | Frequency segmentation | 2000 |
| Time step length | 0.25 s | Surface roughness Coefficient | 0.16 |
| Equilibrium Position | Scheme | AOA (deg) | ||
|---|---|---|---|---|
| −3 | 0 | 3 | ||
| Lateral (m) | Steel | 2.755 | 2.669 | 2.972 |
| CFRP | 2.578 | 2.488 | 2.786 | |
| Vertical (m) | Steel | −0.395 | 0.133 | 0.546 |
| CFRP | −0.597 | −0.083 | 0.307 | |
| Torsion (deg) | Steel | −0.218 | −0.119 | 0.048 |
| CFRP | −0.242 | −0.146 | 0.008 | |
| AOA (deg) | Scheme | Serial Number of Stay Cable | |||||
|---|---|---|---|---|---|---|---|
| B01 | B17 | B34 | J34 | J17 | J01 | ||
| −3 | STEEL | 3.592 × 10−7 | 3.432 × 10−6 | 2.826 × 10−8 | 9.981 × 10−9 | 7.437 × 10−7 | 3.450 × 10−7 |
| CFRP | 8.604 × 10−15 | 7.595 × 10−12 | 1.587 × 10−17 | 1.492 × 10−18 | 1.335 × 10−12 | 6.641 × 10−13 | |
| 0 | STEEL | 8.368 × 10−8 | 1.786 × 10−6 | 1.543 × 10−8 | 3.064 × 10−9 | 5.903 × 10−7 | 7.542 × 10−7 |
| CFRP | 5.868 × 10−16 | 2.515 × 10−13 | 1.351 × 10−18 | 2.555 × 10−19 | 5.618 × 10−14 | 5.004 × 10−15 | |
| 3 | STEEL | 4.460 × 10−9 | 8.554 × 10−8 | 1.493 × 10−9 | 9.057 × 10−11 | 5.213 × 10−8 | 2.405 × 10−8 |
| CFRP | 2.621 × 10−19 | 1.112 × 10−17 | 5.958 × 10−21 | 2.601 × 10−21 | 1.124 × 10−17 | 6.662 × 10−19 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Zhang, Z.; Zeng, J.; Han, F. Analysis of Buffeting Response and Stay Cable Fatigue Damage in Super-Long-Span Carbon Fiber-Reinforced Polymer (CFRP) Cable-Stayed Bridges. Appl. Sci. 2025, 15, 5267. https://doi.org/10.3390/app15105267
Nie Y, Zhang Z, Zeng J, Han F. Analysis of Buffeting Response and Stay Cable Fatigue Damage in Super-Long-Span Carbon Fiber-Reinforced Polymer (CFRP) Cable-Stayed Bridges. Applied Sciences. 2025; 15(10):5267. https://doi.org/10.3390/app15105267
Chicago/Turabian StyleNie, Yuanqing, Zhitian Zhang, Jiadong Zeng, and Feiyu Han. 2025. "Analysis of Buffeting Response and Stay Cable Fatigue Damage in Super-Long-Span Carbon Fiber-Reinforced Polymer (CFRP) Cable-Stayed Bridges" Applied Sciences 15, no. 10: 5267. https://doi.org/10.3390/app15105267
APA StyleNie, Y., Zhang, Z., Zeng, J., & Han, F. (2025). Analysis of Buffeting Response and Stay Cable Fatigue Damage in Super-Long-Span Carbon Fiber-Reinforced Polymer (CFRP) Cable-Stayed Bridges. Applied Sciences, 15(10), 5267. https://doi.org/10.3390/app15105267







