Discrete Element Simulations of Damage Evolution of NiAl-Based Material Reconstructed by Micro-CT Imaging
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Formulation of the Discrete Element Model
2.1.1. Governing Relations of the Discrete Element Method
2.1.2. The Bonded Particle Model
2.1.3. The Computation of the Forces and Moments for Granular Flows
2.2. Preparation of NiAl Sample for DEM Simulations
2.3. Development of a Geometrical Model of the NiAl Microstructure Based on Micro-CT Images
- Process the micro-CT scan for geometrical reconstruction of the NiAl sample (Figure 2a).
- Define the boundaries of the solid phase by the particles (Figure 2b).
- Fill the volume of the solid phase by irregular highly dense particle packing (Figure 2c).
- Remove the temporal particles from the pores (Figure 2d).
3. Results and Discussion
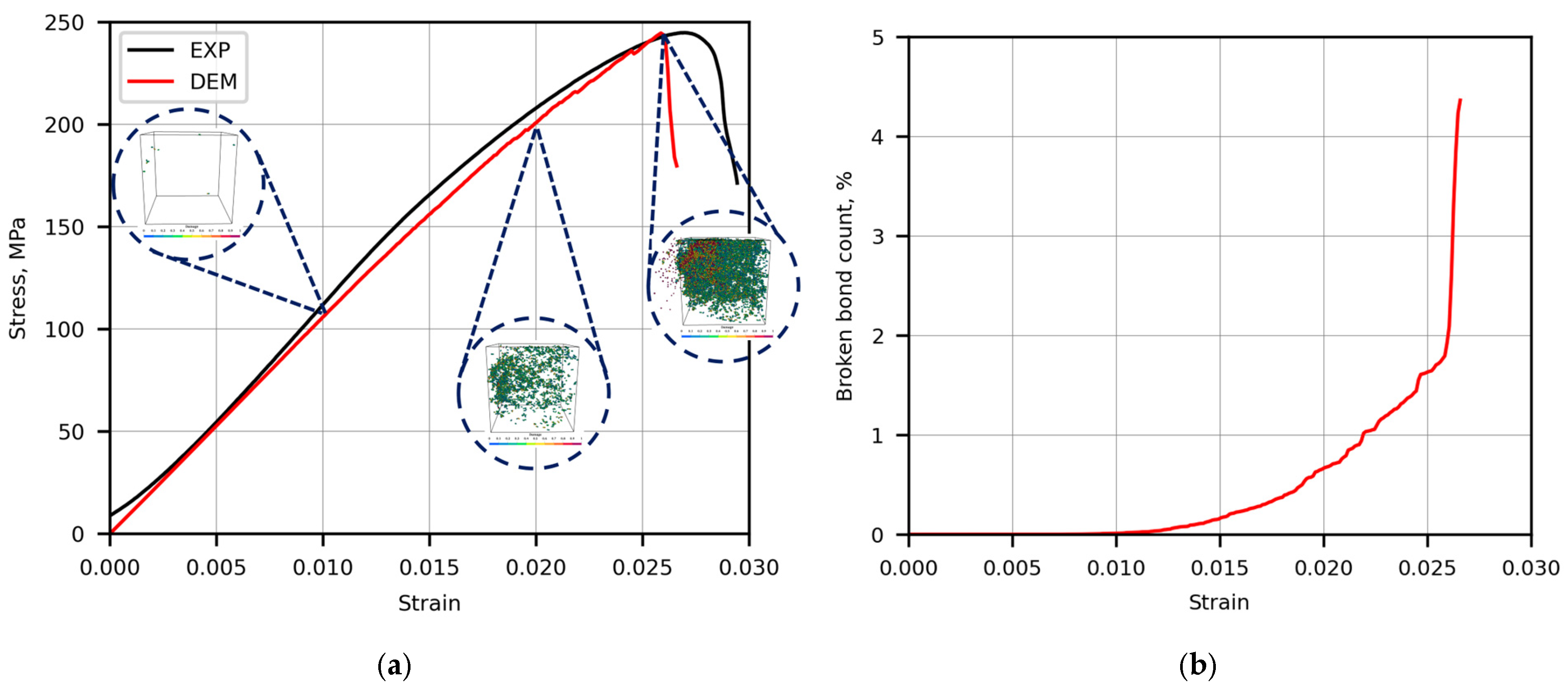
3.1. Stress–Strain Dependency and Comparison with the Experimental Measurements
3.2. Analysis of Damage Evolution
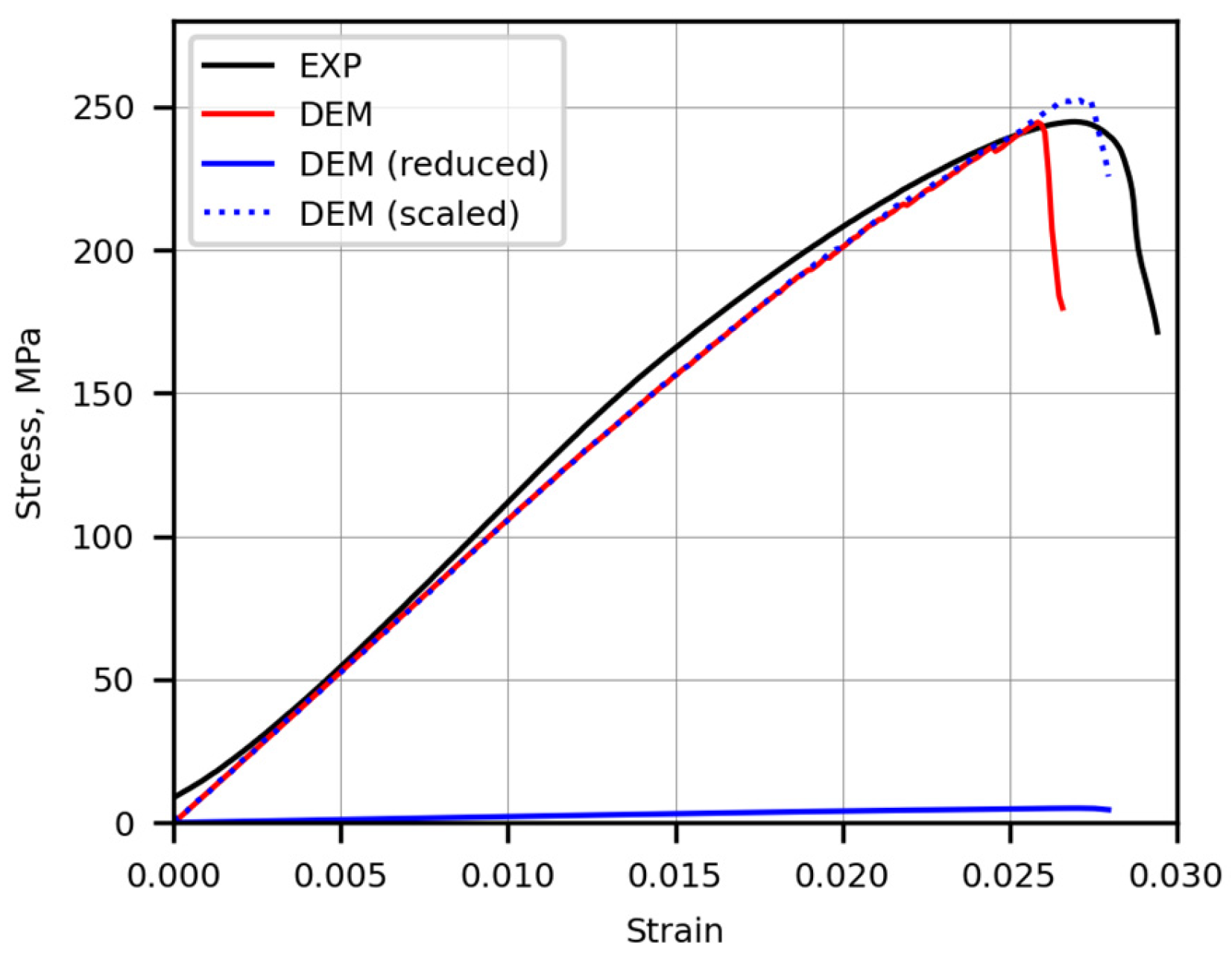
3.3. Proposed Stress Scaling Technique
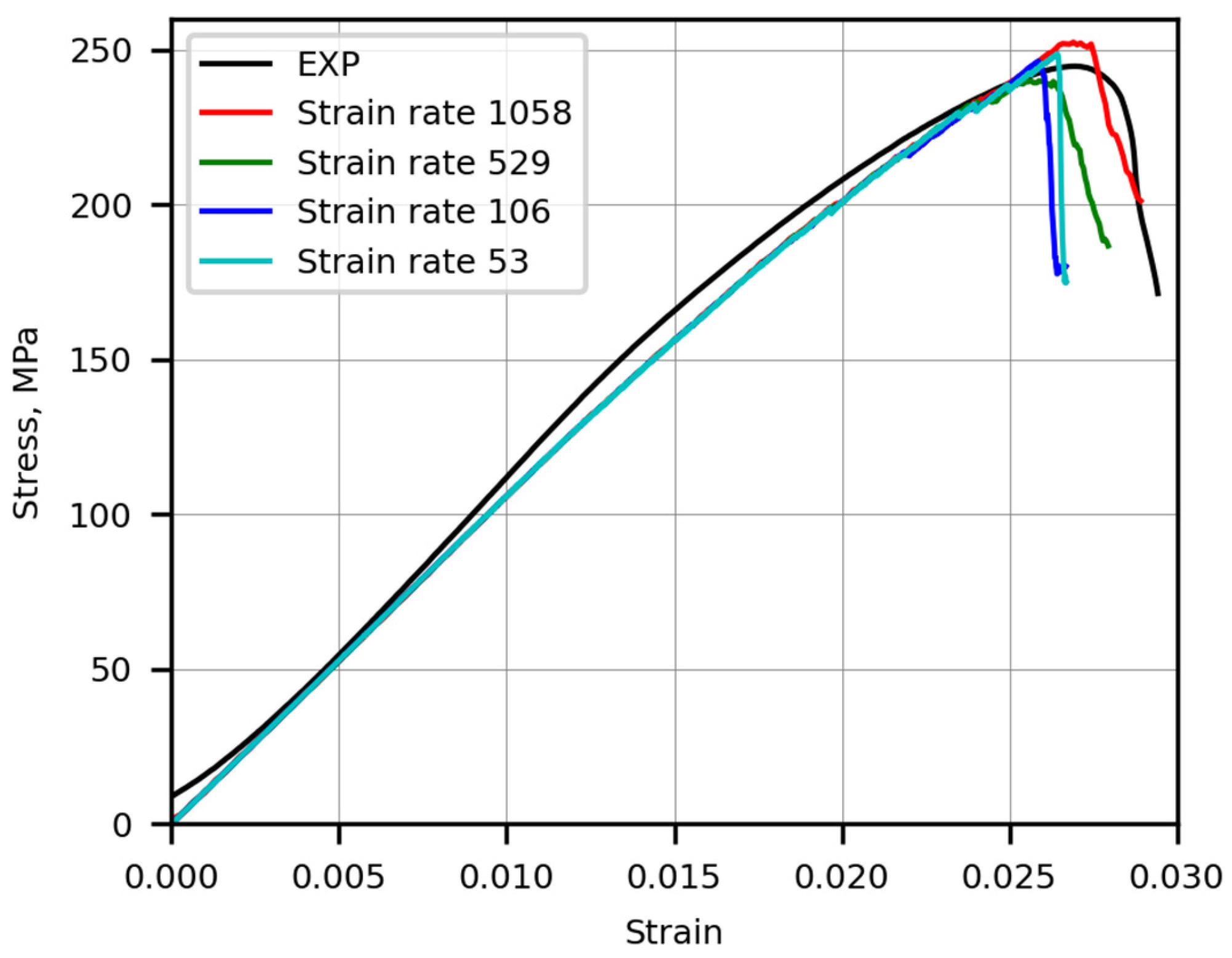
3.4. Compression Strain Rate for Quasi-Static Loading
4. Conclusions
- The DEM supplemented by the micro-CT imaging-based reconstruction of the porous NiAl microstructure revealed a realistic representation of the damage evolution and stress–strain curve.
- While the count of broken bonds was negligibly small, the elastic behavior of the material was dominant, and the numerical stress–strain curve was linear.
- When the strain increased, the count of broken bonds exponentially grew, and some random microcracks initiated, which led to slow weakening of the sample and small deviations of the macroscopic stress–strain curve from the line.
- At the end of the investigated strain interval, the formation and propagation of macroscopic cracks caused the fall-down of the stress–strain curve, which indicated the beginning of the sample failure. The numerically obtained stress and strain of the curve peak differed from the experimentally measured values by 0.1% and 4.2%, respectively.
- At a high compression load, the propagation of macrocracks, caused by a high increase of the broken bond count in the whole macrocrack propagation volume, led to fragmentation of the sample into more than two parts, which is common to failure patterns observed in uniaxial compression experiments of brittle materials.
- The developed stress scaling technique, based on scaled-down elastic moduli with bond breakage parameters and scaled-up stress values, allowed a seven times increase of the size of the time step, which reduced the computing time by seven times. The proposed scaling was very accurate until the time interval of fast macrocrack propagation. However, the stress peaks of the original and scaled curves differed by 3.2% of the highest stress obtained in DEM computations with the original values of parameters.
- The analysis of stress–strain dependencies obtained by using different values of the compression strain rate showed that the computations performed with a compression strain rate close to 53 s−1 approached the quasi-static state and achieved acceptable accuracy within the limits of the available computational resources.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Z.; Wan, Y.; Xin, D.; Zhao, Y.; Zhou, D. Discrete element numerical simulation of the effect of river ice porosity on impact force at bridge abutments. Appl. Sci. 2025, 15, 1738. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, S.; Wang, R.; Ding, B. The vibration response characteristics of neighboring tunnels induced by shield construction. Appl. Sci. 2025, 15, 1729. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Q.; Liang, D.; Ji, S. A novel discrete element method for smooth polyhedrons and its application to modeling flows of concave-shaped particles. Int. J. Numer. Methods Eng. 2024, 126, e7628. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Jiang, M.; Zhang, A.; Shen, Z. Granular soils: From DEM simulation to constitutive modeling. Acta Geotech. 2020, 15, 1723–1744. [Google Scholar] [CrossRef]
- Xia, M. Thermo-mechanical coupled particle model for rock. Trans. Nonferrous Met. Soc. China 2015, 25, 2367–2379. [Google Scholar] [CrossRef]
- Wang, P.; Gao, N.; Ji, K.; Stewart, L.; Arson, C. DEM Analysis on the Role of Aggregates on Concrete Strength. Comput. Geotech. 2020, 119, 103290. [Google Scholar] [CrossRef]
- Le, B.D.; Dau, F.; Charles, J.L.; Iordanoff, I. Modeling damages and cracks growth in composite with a 3D discrete element method. Compos. Part B Eng. 2016, 91, 615–630. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Chen, X.; Peng, D.; Morrisey, J.P.; Ooi, J.Y. Comparative assessment and unification of bond models in DEM simulations. Granul. Matter 2022, 24, 29. [Google Scholar] [CrossRef]
- Beckmann, B.; Schicktanz, K.; Curbach, M. Discrete element simulation of concrete fracture and crack evolution. Beton-Und Stahlbetonbau 2018, 113, 91–95. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.X.; Zhu, L.; Xiong, F.; Liu, J.; Gao, W. A particle-based cohesive crack model for brittle fracture problems. Materials 2020, 13, 3573. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Koval, G.; Chazallon, C. A discrete element model for damage and fatigue crack growth of quasi-brittle materials. Adv. Mater. Sci. Eng. 2019, 2019, 6962394. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yin, P.F.; Huang, Y.H. Experiment and Discrete Element Modelling on Strength, Deformation and Failure Behaviour of Shale Under Brazilian Compression. Rock Mech. Rock Eng. 2019, 52, 4339–4359. [Google Scholar] [CrossRef]
- Tykhoniuk, R.; Tomas, J.; Luding, S.; Kappl, M.; Heim, L.; Butt, H.J. Ultrafine cohesive powders: From interparticle contacts to continuum behaviour. Chem. Eng. Sci. 2007, 62, 2843–2864. [Google Scholar] [CrossRef]
- Long, X.; Ji, S.; Wang, Y. Validation of microparameters in discrete element modeling of sea ice failure process. Part. Sci. Technol. 2019, 37, 550–559. [Google Scholar] [CrossRef]
- Xiang Bo, X.; Wang, X.J. A cohesive strengthening/damage-plasticity model and its application for DEM numerical investigation in hardening/softening of rock and soil. Comput. Geotech. 2023, 159, 105500. [Google Scholar] [CrossRef]
- Horabik, J.; Wiącek, J.; Parafiniuk, P.; Stasiak, M.; Bańda, M.; Kobyłka, R.; Molenda, M. Discrete element method modelling of the diametral compression of Starch Agglomerates. Materials 2020, 13, 932. [Google Scholar] [CrossRef]
- Pacevič, R.; Kačeniauskas, A. The performance analysis of the thermal discrete element method computations on the GPU. Comput. Inform. 2022, 41, 931–956. [Google Scholar] [CrossRef]
- Baniasadi, M.; Baniasadi, M.; Peters, B. Coupled CFD-DEM with heat and mass transfer to investigate the melting of a granular packed bed. Chem. Eng. Sci. 2018, 178, 136–145. [Google Scholar] [CrossRef]
- Xu, T.; Fu, T.-F.; Heap, M.J.; Meredith, P.G.; Mitchell, T.M.; Baud, P. Mesoscopic damage and fracturing of heterogeneous brittle rocks based on three-dimensional polycrystalline discrete element method. Rock Mech. Rock Eng. 2020, 53, 5389–5409. [Google Scholar] [CrossRef]
- Li, X.F.; Li, H.B.; Liu, L.W.; Liu, Y.Q.; Ju, M.H.; Zhao, J. Investigating the crack initiation and propagation mechanism in brittle rocks using grain-based finite-discrete element method. Int. J. Rock Mech. Min. Sci. 2020, 127, 104219. [Google Scholar] [CrossRef]
- Jin, C.; Yang, X.; You, Z. Automated real aggregate modelling approach in discrete element method based on X-Ray computed tomography images. Int. J. Pavement Eng. 2017, 18, 837–850. [Google Scholar] [CrossRef]
- Suchorzewski, J.; Tejchman, J.; Nitka, M. Discrete element method simulations of fracture in concrete under uniaxial compression based on its real internal structure. Int. J. Damage Mech. 2018, 27, 578–607. [Google Scholar] [CrossRef]
- Xue, B.; Pei, J.; Zhou, B.; Zhang, J.; Li, R.; Guo, F. Using random heterogeneous DEM model to simulate the SCB fracture behavior of asphalt concrete. Constr. Build. Mater. 2020, 236, 117580. [Google Scholar] [CrossRef]
- Suchorzewski, J.; Nitka, M. Size effect at aggregate level in microCT scans and DEM simulation—Splitting tensile test of concrete. Eng. Fract. Mech. 2022, 264, 108357. [Google Scholar] [CrossRef]
- Nguyen, N.H.T.; Bui, H.H.; Kodikara, J.; Arooran, S.; Darve, F. A discrete element modelling approach for fatigue damage growth in cemented materials. Int. J. Plast. 2019, 112, 68–88. [Google Scholar] [CrossRef]
- Nosewicz, S.; Jurczak, G.; Wejrzanowski, T.; Ibrahim, S.H.; Grabias, A.; Węglewski, W.; Kaszyca, K.; Rojek, J.; Chmielewski, M. Thermal conductivity analysis of porous NiAl materials manufactured by spark plasma sintering: Experimental studies and modelling. Int. J. Heat Mass Transf. 2022, 194, 123070. [Google Scholar] [CrossRef]
- Liu, G.; Marshall, J.S.; Li, S.Q.; Yao, Q. Discrete element method for particle capture by a body in an electrostatic field. Int. J. Numer. Methods Eng. 2010, 84, 1589–1612. [Google Scholar] [CrossRef]
- Džiugys, A.; Peters, B. An approach to simulate the motion of spherical and non-spherical fuel particles in combustion chambers. Granul. Matter 2001, 3, 231–266. [Google Scholar] [CrossRef]
- Kačeniauskas, A.; Kačianauskas, R.; Maknickas, A.; Markauskas, D. Computation and visualization of discrete particle systems on gLite-based grid. Adv. Eng. Softw. 2011, 42, 237–246. [Google Scholar] [CrossRef]
- Wiśniewska, M.; Laptev, A.M.; Marczewski, M.; Krzyżaniak, W.; Leshchynsky, V.; Celotti, L.; Szybowicz, M.; Garbiec, D. Towards homogeneous spark plasma sintering of complex-shaped ceramic matrix composites. J. Eur. Ceram. Soc. 2024, 44, 7139–7148. [Google Scholar] [CrossRef]
- Laptev, A.M.; Bram, M.; Vanmeensel, K.; Gonzalez-Julian, J.; Guillon, O. Enhancing efficiency of field assisted sintering by advanced thermal insulation. J. Mater. Process. Technol. 2018, 262, 326–339. [Google Scholar] [CrossRef]
- Guillon, O.; Gonzalez-Julian, J.; Dargatz, B.; Kessel, T.; Schierning, G.; Räthel, J.; Herrmann, M. Field-assisted sintering technology/Spark plasma sintering: Mechanisms, materials, and technology developments. Adv. Eng. Mater. 2014, 16, 830–849. [Google Scholar] [CrossRef]
- Santanach, J.G.; Weibel, A.; Estournès, C.; Yang, Q.; Laurent, C.; Peigney, A. Spark plasma sintering of alumina: Study of parameters, formal sintering analysis and hypotheses on the mechanism(s) involved in densification and grain growth. Acta Mater. 2011, 59, 1400–1408. [Google Scholar] [CrossRef]
- Roselló, R.; Pérez, I.; Vanmaercke, S.; Recarey Morfa, C.; Cortés, L.; Casañas, H. Modified algorithm for generating high volume fraction sphere packings. Comput. Part. Mech. 2015, 2, 161–172. [Google Scholar] [CrossRef]
- Govender, N. Study on the effect of grain morphology on shear strength in granular materials via GPU based discrete element method simulations. Powder Technol. 2021, 387, 336–347. [Google Scholar] [CrossRef]
- Zheng, Z.; Zang, M.; Chen, S.; Zeng, H. A GPU-based DEM-FEM computational framework for tire-sand interaction simulations. Comput. Struct. 2018, 209, 74–92. [Google Scholar] [CrossRef]
- Bystrov, O.; Pacevič, R.; Kačeniauskas, A. Performance of communication-and computation-intensive Saas on the OpenStack cloud. Appl. Sci. 2021, 11, 7379. [Google Scholar] [CrossRef]
- Decheng, Z.; Ranjith, P.G.; Perera, M.S.A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: A review. J. Pet. Sci. Eng. 2016, 143, 158–170. [Google Scholar] [CrossRef]
- Wang, Y.; Mora, P.; Liang, Y. Calibration of discrete element modeling: Scaling laws and dimensionless analysis. Particuology 2022, 62, 55–62. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kačeniauskas, A.; Pacevič, R.; Stupak, E.; Rojek, J.; Chmielewski, M.; Grabias, A.; Nosewicz, S. Discrete Element Simulations of Damage Evolution of NiAl-Based Material Reconstructed by Micro-CT Imaging. Appl. Sci. 2025, 15, 5260. https://doi.org/10.3390/app15105260
Kačeniauskas A, Pacevič R, Stupak E, Rojek J, Chmielewski M, Grabias A, Nosewicz S. Discrete Element Simulations of Damage Evolution of NiAl-Based Material Reconstructed by Micro-CT Imaging. Applied Sciences. 2025; 15(10):5260. https://doi.org/10.3390/app15105260
Chicago/Turabian StyleKačeniauskas, Arnas, Ruslan Pacevič, Eugeniuš Stupak, Jerzy Rojek, Marcin Chmielewski, Agnieszka Grabias, and Szymon Nosewicz. 2025. "Discrete Element Simulations of Damage Evolution of NiAl-Based Material Reconstructed by Micro-CT Imaging" Applied Sciences 15, no. 10: 5260. https://doi.org/10.3390/app15105260
APA StyleKačeniauskas, A., Pacevič, R., Stupak, E., Rojek, J., Chmielewski, M., Grabias, A., & Nosewicz, S. (2025). Discrete Element Simulations of Damage Evolution of NiAl-Based Material Reconstructed by Micro-CT Imaging. Applied Sciences, 15(10), 5260. https://doi.org/10.3390/app15105260






