Dynamic Heterogeneous Search-Mutation Structure-Based Equilibrium Optimizer
Abstract
1. Introduction
2. Equilibrium Optimizer (EO)
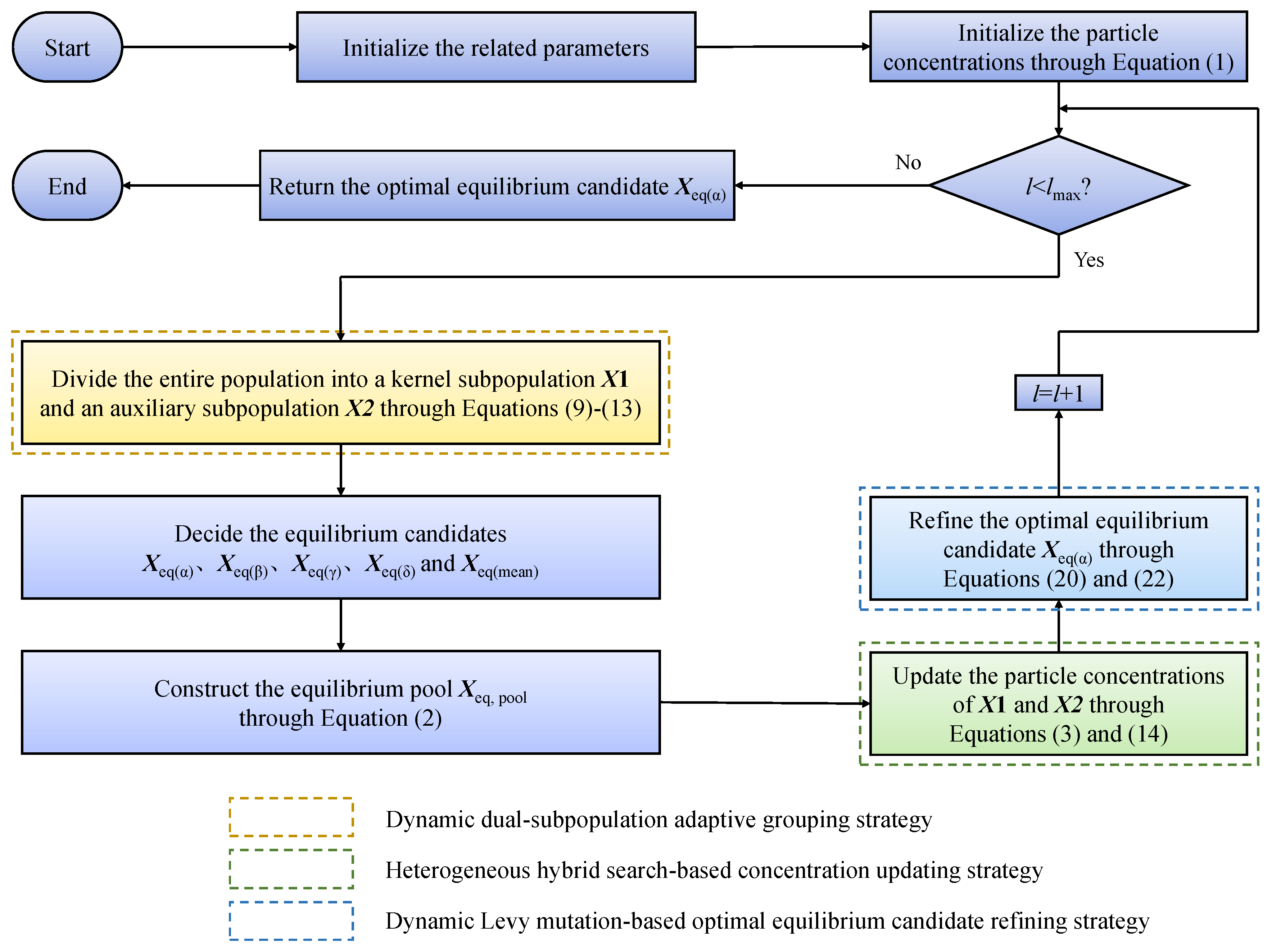
3. Dynamic Heterogeneous Search-Mutation Structure-Based Equilibrium Optimizer (DHSMEO)
3.1. Dynamic Dual-Subpopulation Adaptive Grouping Strategy
3.2. Heterogeneous Hybrid Search-Based Concentration-Updating Strategy
3.3. Dynamic Levy Mutation-Based Optimal Equilibrium Candidate-Refining Strategy
| Algorithm 1 Pseudocode of DHSMEO |
|
3.4. Computational Complexity of DHSMEO
4. Numerical Experiments and Discussion for DHSMEO
4.1. Benchmark Functions, Experimental Configurations, and Performance Indicators
4.2. Parameter Sensitivity Analysis
4.3. Scalability Analysis
4.4. Impacts of Improvement Strategies on EO
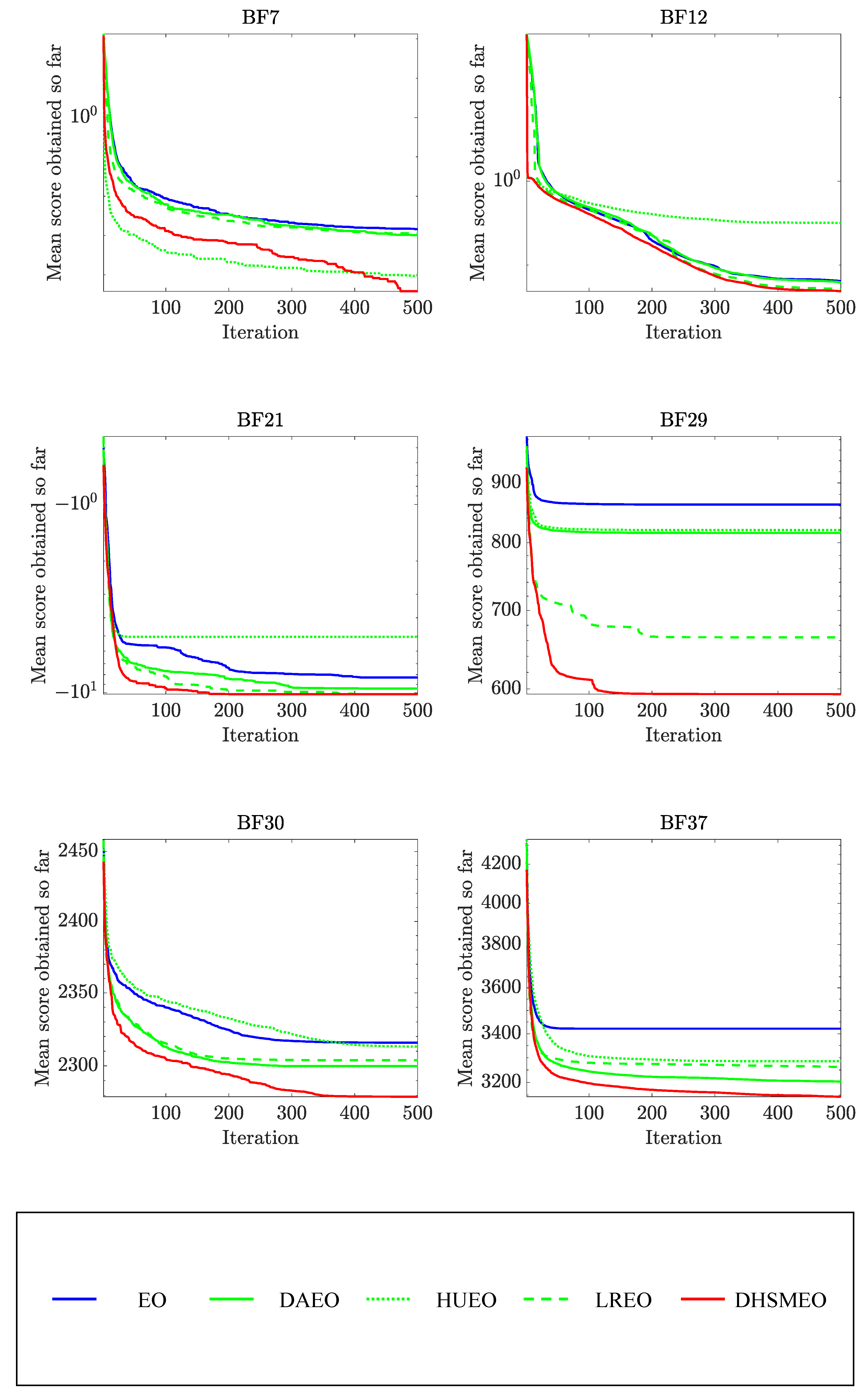
4.5. Comparative Test of DHSMEO and Other Algorithms
5. DHSMEO for UAV Mountain Path-Planning Problem
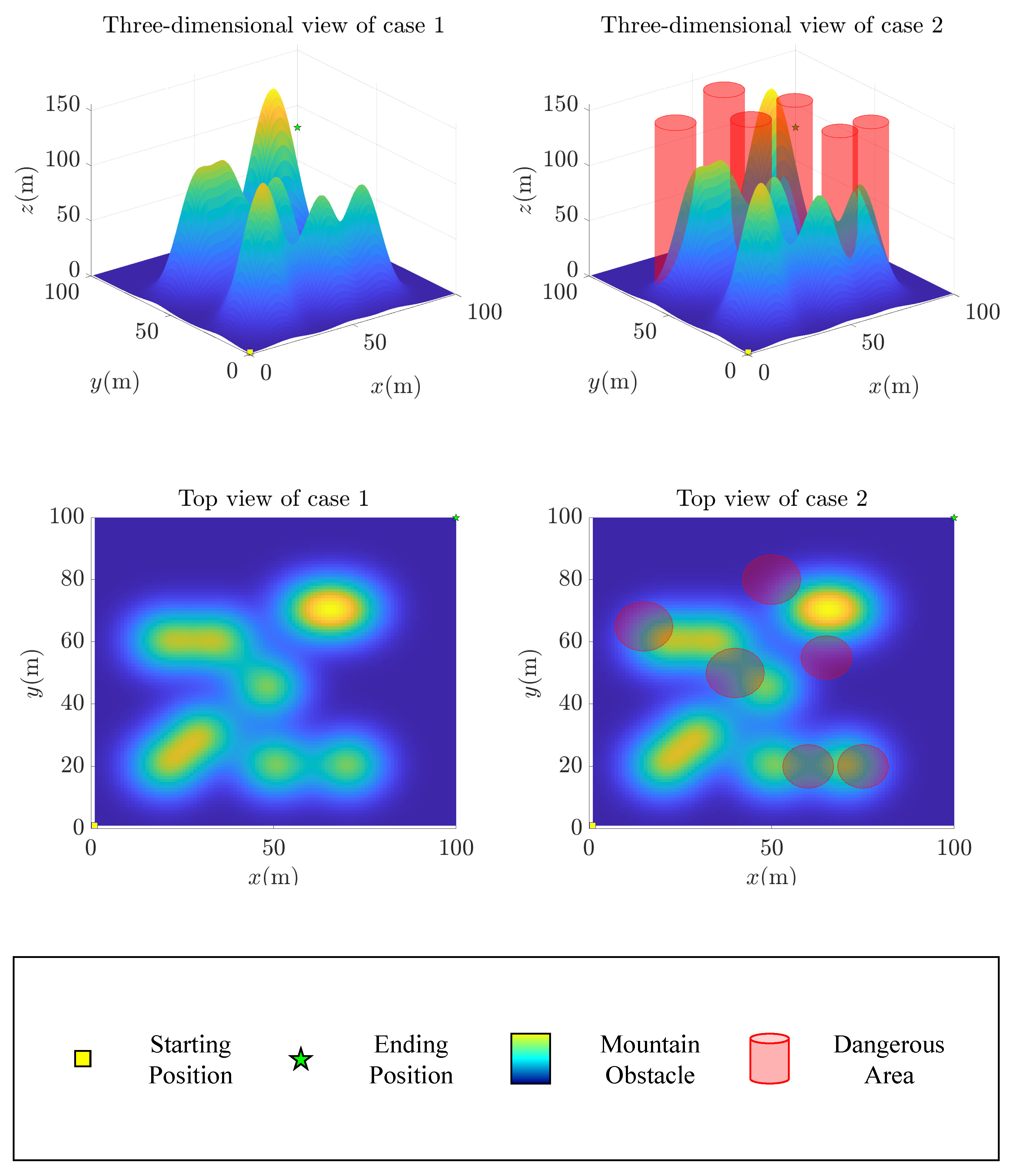
5.1. Problem Description
5.2. DHSMEO-Based UAV Mountain Path-Planning Method
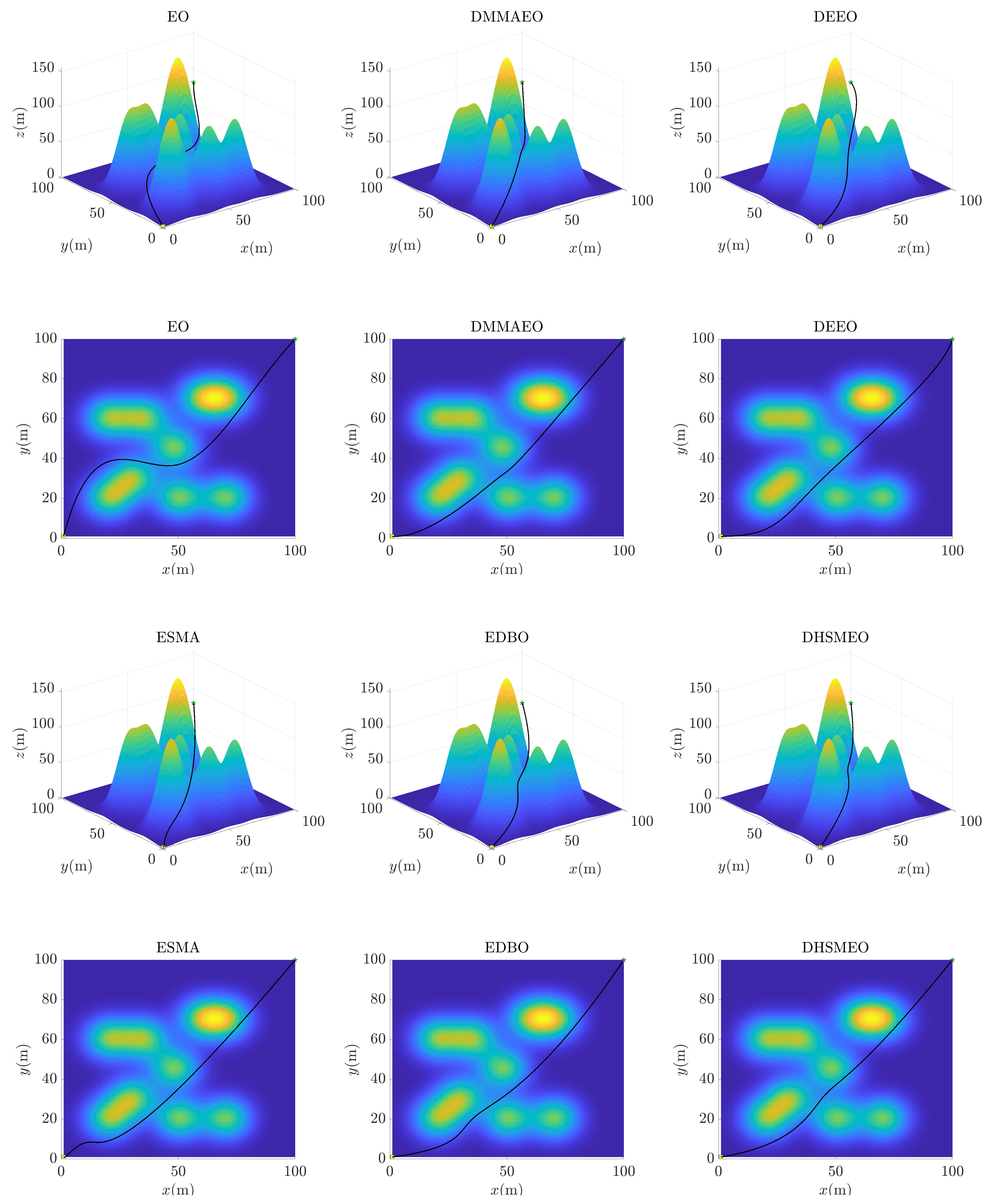
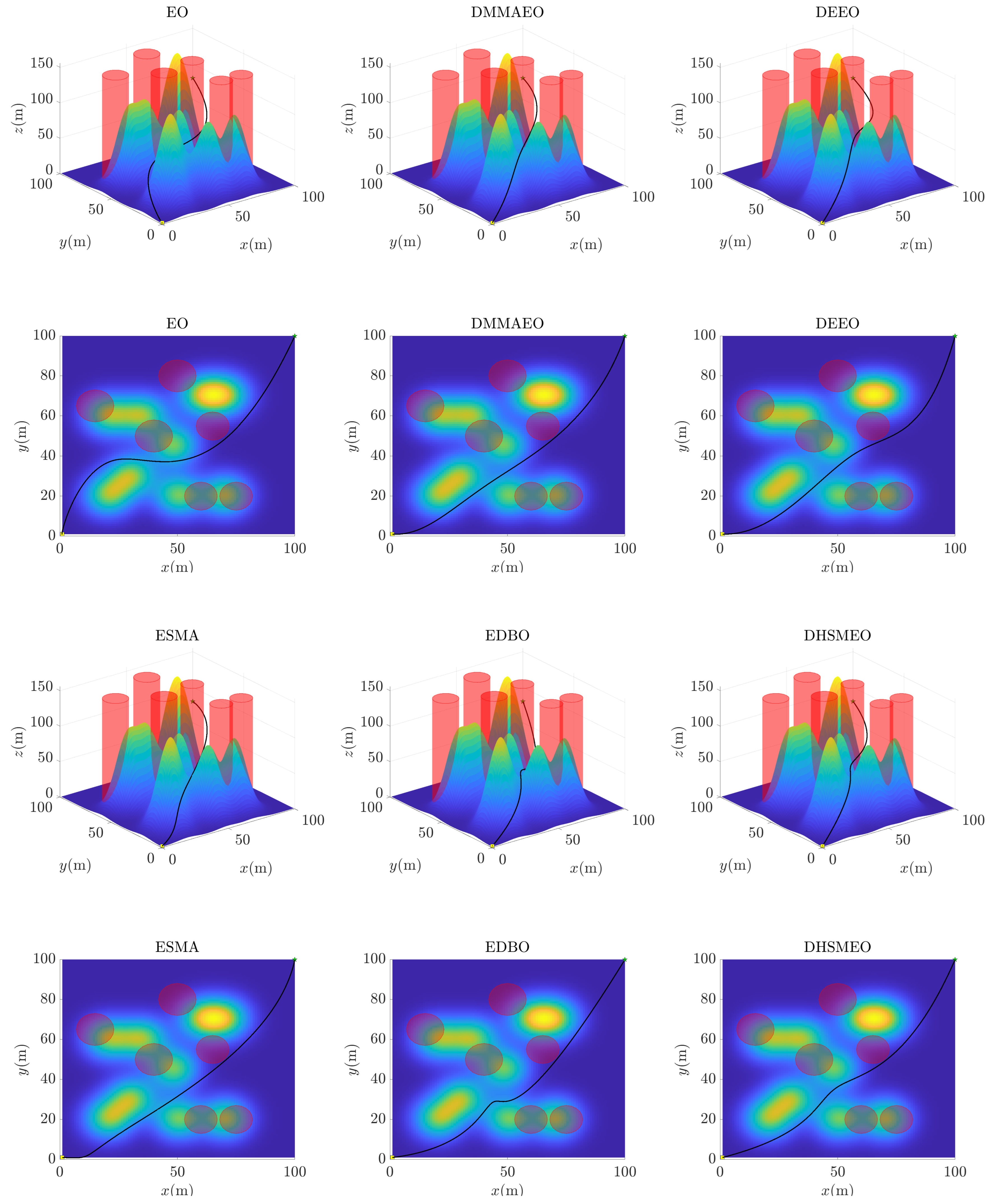
5.3. Results and Analysis of UAV Mountain Path Planning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, W.; Liu, H.; Zhang, Y.; Mi, R.; Tong, C.; Xiao, W.; Shuai, B. Railway dangerous goods transportation system risk identification: Comparisons among SVM, PSO-SVM, GA-SVM and GS-SVM. Appl. Soft Comput. 2021, 109, 107541. [Google Scholar] [CrossRef]
- Avalos, O.; Haro, E.H.; Camarena, O.; Díaz, P. Improved crow search algorithm for optimal flexible manufacturing process planning. Expert Syst. Appl. 2024, 235, 121243. [Google Scholar] [CrossRef]
- Alweshah, M.; Alkhalaileh, S.; Al-Betar, M.A.; Bakar, A.A. Coronavirus herd immunity optimizer with greedy crossover for feature selection in medical diagnosis. Knowl.-Based Syst. 2022, 235, 107629. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.D.; Fang, Y.M.; Liu, L.; Xu, M.; Zhang, P. Ameliorated moth-flame algorithm and its application for modeling of silicon content in liquid iron of blast furnace based fast learning network. Appl. Soft Comput. 2020, 94, 106418. [Google Scholar] [CrossRef]
- Xie, X.; Yang, Y.L.; Zhou, H. Multi-Strategy Hybrid Whale Optimization Algorithm Improvement. Appl. Sci. 2025, 15, 2224. [Google Scholar] [CrossRef]
- Chen, Q.; Qu, H.; Liu, C.; Xu, X.; Wang, Y.; Liu, J. Spontaneous coal combustion temperature prediction based on an improved grey wolf optimizer-gated recurrent unit model. Energy 2025, 314, 133980. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Ucan, A.; Ibrikci, T.; Arasteh, B.; Isik, G. Slime mould algorithm: A comprehensive survey of its variants and applications. Arch. Comput. Methods Eng. 2023, 30, 2683–2723. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Yang, Y.T.; Chen, H.L.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evol. Comput. 2021, 63, 100868. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Shaik, M.A.; Mareddy, P.L. Enhancement of Voltage Profile in the Distribution system by Reconfiguring with DG placement using Equilibrium Optimizer. Alex. Eng. J. 2022, 61, 4081–4093. [Google Scholar] [CrossRef]
- Wu, X.D.; Hirota, K.; Jia, Z.Y.; Ji, Y.; Zhao, K.X.; Dai, Y.P. Ameliorated equilibrium optimizer with application in smooth path planning oriented unmanned ground vehicle. Knowl.-Based Syst. 2023, 260, 110148. [Google Scholar] [CrossRef]
- Rabehi, A.; Nail, B.; Helal, H.; Douara, A.; Ziane, A.; Amrani, M.; Akkal, B.; Benamara, Z. Optimal estimation of Schottky diode parameters using advanced swarm intelligence algorithms. Semiconductors 2020, 54, 1398–1405. [Google Scholar] [CrossRef]
- Fan, Q.S.; Huang, H.S.; Yang, K.; Zhang, S.S.; Yao, L.G.; Xiong, Q.Q. A modified equilibrium optimizer using opposition-based learning and novel update rules. Expert Syst. Appl. 2021, 170, 114575. [Google Scholar] [CrossRef]
- Tang, A.D.; Han, T.; Zhou, H.; Xie, L. An improved equilibrium optimizer with application in unmanned aerial vehicle path planning. Sensors 2021, 21, 1814. [Google Scholar] [CrossRef]
- Dinkar, S.K.; Deep, K.; Mirjalili, S.; Thapliyal, S. Opposition-based Laplacian equilibrium optimizer with application in image segmentation using multilevel thresholding. Expert Syst. Appl. 2021, 174, 114766. [Google Scholar] [CrossRef]
- Wunnava, A.; Naik, M.K.; Panda, R.; Jena, B.; Abraham, A. A novel interdependence based multilevel thresholding technique using adaptive equilibrium optimizer. Eng. Appl. Artif. Intel. 2020, 94, 103836. [Google Scholar] [CrossRef]
- Wu, X.D.; Hirota, K.; Dai, Y.P.; Shao, S. Dynamic Multi-Population Mutation Architecture-Based Equilibrium Optimizer and Its Engineering Application. Appl. Sci. 2025, 15, 1795. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.K.; Ryan, M.J. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 2020, 209, 694–708. [Google Scholar] [CrossRef]
- Hemavathi, S.; Latha, B. HFLFO: Hybrid fuzzy levy flight optimization for improving QoS in wireless sensor network. Ad Hoc Networks 2023, 142, 103110. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Heidari, A.A.; Luo, J.; Zhang, Q.; Zhao, X.; Li, C. An efficient chaotic mutative moth-flame-inspired optimizer for global optimization tasks. Expert Syst. Appl. 2019, 129, 135–155. [Google Scholar] [CrossRef]
- Muthusamy, H.; Ravindran, S.; Yaacob, S.; Polat, K. An improved elephant herding optimization using sine–cosine mechanism and opposition based learning for global optimization problems. Expert Syst. Appl. 2021, 172, 114607. [Google Scholar] [CrossRef]
- Feng, Z.; Duan, J.; Niu, W.; Jiang, Z.; Liu, Y. Enhanced sine cosine algorithm using opposition learning, adaptive evolution and neighborhood search strategies for multivariable parameter optimization problems. Appl. Soft Comput. 2022, 119, 108562. [Google Scholar] [CrossRef]
- Zhong, C.T.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Shami, T.M.; Mirjalili, S.; Al-Eryani, Y.; Daoudi, K.; Izadi, S.; Abualigah, L. Velocity pausing particle swarm optimization: A novel variant for global optimization. Neural Comput. Appl. 2023, 35, 9193–9223. [Google Scholar] [CrossRef]
- Liang, J.J.; Suganthan, P.N.; Deb, K. Novel Composition Test Functions for Numerical Global Optimization. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005; pp. 68–75. [Google Scholar]
- Maharana, D.; Kommadath, R.; Kotecha, P. Dynamic Yin-Yang Pair Optimization and Its Performance on Single Objective Real Parameter Problems of CEC 2017. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC 2017), San Sebastián, Spain, 5–8 June 2017; pp. 2390–2396. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Moharam, A.; Haikal, A.Y.; Elhosseini, M. Economically optimized heat exchanger design: A synergistic approach using differential evolution and equilibrium optimizer within an evolutionary algorithm framework. Neural Comput. Appl. 2024, 36, 14999–15026. [Google Scholar] [CrossRef]
- Almotairi, K.H.; Abualigah, L. Hybrid reptile search algorithm and remora optimization algorithm for optimization tasks and data clustering. Symmetry 2022, 14, 458. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Abraham, A. An entropy minimization based multilevel colour thresholding technique for analysis of breast thermograms using equilibrium slime mould algorithm. Appl. Soft Comput. 2021, 113, 107955. [Google Scholar] [CrossRef]
- Mahajan, S.; Abualigah, L.; Pandit, A.K. Hybrid arithmetic optimization algorithm with hunger games search for global optimization. Multimed. Tools Appl. 2022, 81, 28755–28778. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.J.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inform. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inform. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Wang, P.W.; Yang, J.S.; Zhang, Y.L.; Wang, Q.W.; Sun, B.B.; Guo, D. Obstacle-Avoidance Path-Planning Algorithm for Autonomous Vehicles Based on B-Spline Algorithm. World Electr. Veh. J. 2022, 13, 233. [Google Scholar] [CrossRef]
- Yu, M.Y.; Du, J.; Xu, X.X.; Xu, J.; Jiang, F.; Fu, S.W.; Zhang, J.; Liang, A. A multi-strategy enhanced Dung Beetle Optimization for real-world engineering problems and UAV path planning. Alex. Eng. J. 2025, 118, 406–434. [Google Scholar] [CrossRef]

| Variant | Description | Problem | Reference |
|---|---|---|---|
| m-EO | Incorporate a novel concentration-updating equation and opposition learning | Enhance the accuracy of the algorithm | Fan et al. [17] |
| MHEO | Incorporate a Gaussian distribution estimation method to leverage population-advantage information in guiding evolutionary processes | Strengthen the optimization capability | Tang et al. [18] |
| OB-L-EO | Integrate a Laplace distribution-based random walk and opposition learning | Enhance acceleration in convergence | Dinkar et al. [19] |
| AEO | Introduce an adaptive decision-based modified concentration-updating equation | Enhance the global search capability | Wunnava et al. [20] |
| DMMAEO | Construct the dynamic multi-population mutation architecture | Strengthen search capability and population multiformity | Wu et al. [21] |
| IEO | Integrate a local minimum elimination mechanism and a linear diversity reduction mechanism | Enhance the convergence | Abdel-Basset et al. [22] |
| Problem | ||||||
|---|---|---|---|---|---|---|
| BF1 | Avg | |||||
| Std | ||||||
| BF2 | Avg | |||||
| Std | ||||||
| BF3 | Avg | |||||
| Std | ||||||
| BF4 | Avg | |||||
| Std | ||||||
| BF5 | Avg | |||||
| Std | ||||||
| BF6 | Avg | |||||
| Std | ||||||
| BF7 | Avg | |||||
| Std | ||||||
| BF8 | Avg | − | − | − | − | − |
| Std | ||||||
| BF9 | Avg | |||||
| Std | ||||||
| BF10 | Avg | |||||
| Std | ||||||
| BF11 | Avg | |||||
| Std | ||||||
| BF12 | Avg | |||||
| Std | ||||||
| BF13 | Avg | |||||
| Std | ||||||
| Friedman mean rank | 3.923 | 2.846 | 3.154 | 3.000 | 2.077 | |
| Final rank | 5 | 2 | 4 | 3 | 1 | |
| Problem | ||||||
|---|---|---|---|---|---|---|
| BF1 | Avg | |||||
| Std | ||||||
| BF2 | Avg | |||||
| Std | ||||||
| BF3 | Avg | |||||
| Std | ||||||
| BF4 | Avg | |||||
| Std | ||||||
| BF5 | Avg | |||||
| Std | ||||||
| BF6 | Avg | |||||
| Std | ||||||
| BF7 | Avg | |||||
| Std | ||||||
| BF8 | Avg | − | − | − | − | − |
| Std | ||||||
| BF9 | Avg | |||||
| Std | ||||||
| BF10 | Avg | |||||
| Std | ||||||
| BF11 | Avg | |||||
| Std | ||||||
| BF12 | Avg | |||||
| Std | ||||||
| BF13 | Avg | |||||
| Std | ||||||
| Friedman mean rank | 3.846 | 3.231 | 2.923 | 2.923 | 2.077 | |
| Final rank | 5 | 4 | 2 | 2 | 1 | |
| Problem | Dim 30 | Dim 50 | Dim 100 | ||||
|---|---|---|---|---|---|---|---|
| DHSMEO | EO | DHSMEO | EO | DHSMEO | EO | ||
| BF1 | Avg | ||||||
| Std | |||||||
| BF2 | Avg | ||||||
| Std | |||||||
| BF3 | Avg | ||||||
| Std | |||||||
| BF4 | Avg | ||||||
| Std | |||||||
| BF5 | Avg | ||||||
| Std | |||||||
| BF6 | Avg | ||||||
| Std | |||||||
| BF7 | Avg | ||||||
| Std | |||||||
| BF8 | Avg | − | − | − | − | − | − |
| Std | |||||||
| BF9 | Avg | ||||||
| Std | |||||||
| BF10 | Avg | ||||||
| Std | |||||||
| BF11 | Avg | ||||||
| Std | |||||||
| BF12 | Avg | ||||||
| Std | |||||||
| BF13 | Avg | ||||||
| Std | |||||||
| Problem | EO | DAEO | HUEO | LREO | DHSMEO | ||
|---|---|---|---|---|---|---|---|
| Unimodal | BF1 | Avg | |||||
| Std | |||||||
| BF2 | Avg | ||||||
| Std | |||||||
| BF3 | Avg | ||||||
| Std | |||||||
| BF4 | Avg | ||||||
| Std | |||||||
| BF5 | Avg | ||||||
| Std | |||||||
| BF6 | Avg | ||||||
| Std | |||||||
| BF7 | Avg | ||||||
| Std |
| Problem | EO | DAEO | HUEO | LREO | DHSMEO | ||
|---|---|---|---|---|---|---|---|
| Multimodal | BF8 | Avg | − | − | − | − | − |
| (High | Std | ||||||
| dimension) | BF9 | Avg | |||||
| Std | |||||||
| BF10 | Avg | ||||||
| Std | |||||||
| BF11 | Avg | ||||||
| Std | |||||||
| BF12 | Avg | ||||||
| Std | |||||||
| BF13 | Avg | ||||||
| Std |
| Problem | EO | DAEO | HUEO | LREO | DHSMEO | ||
|---|---|---|---|---|---|---|---|
| Multimodal | BF14 | Avg | |||||
| (Fixed- | Std | ||||||
| dimension) | BF15 | Avg | |||||
| Std | |||||||
| BF16 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF17 | Avg | ||||||
| Std | |||||||
| BF18 | Avg | ||||||
| Std | |||||||
| BF19 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF20 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF21 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF22 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF23 | Avg | − | − | − | − | − | |
| Std |
| Problem | EO | DAEO | HUEO | LREO | DHSMEO | ||
|---|---|---|---|---|---|---|---|
| Composition | BF24 | Avg | |||||
| Std | |||||||
| BF25 | Avg | ||||||
| Std | |||||||
| BF26 | Avg | ||||||
| Std | |||||||
| BF27 | Avg | ||||||
| Std | |||||||
| BF28 | Avg | ||||||
| Std | |||||||
| BF29 | Avg | ||||||
| Std | |||||||
| BF30 | Avg | ||||||
| Std | |||||||
| BF31 | Avg | ||||||
| Std | |||||||
| BF32 | Avg | ||||||
| Std | |||||||
| BF33 | Avg | ||||||
| Std | |||||||
| BF34 | Avg | ||||||
| Std | |||||||
| BF35 | Avg | ||||||
| Std | |||||||
| BF36 | Avg | ||||||
| Std | |||||||
| BF37 | Avg | ||||||
| Std | |||||||
| BF38 | Avg | ||||||
| Std | |||||||
| BF39 | Avg | ||||||
| Std |
| EO | DAEO | HUEO | LREO | DHSMEO | ||
|---|---|---|---|---|---|---|
| Friedman mean rank | 4.436 | 2.769 | 3.462 | 2.872 | 1.462 | |
| Final rank | 5 | 2 | 4 | 3 | 1 | |
| 1/0/−1 | 32/6/1 | 32/6/1 | 28/11/0 | 31/7/1 | ∼ | |
| Problem | EO | RSA | SMA | HGS | DMMAEO | ||
| Unimodal | BF1 | Avg | |||||
| Std | |||||||
| BF2 | Avg | ||||||
| Std | |||||||
| BF3 | Avg | ||||||
| Std | |||||||
| BF4 | Avg | ||||||
| Std | |||||||
| BF5 | Avg | ||||||
| Std | |||||||
| BF6 | Avg | ||||||
| Std | |||||||
| BF7 | Avg | ||||||
| Std | |||||||
| Problem | DEEO | HRSA | ESMA | AOAHGS | DHSMEO | ||
| BF1 | Avg | ||||||
| Std | |||||||
| BF2 | Avg | ||||||
| Std | |||||||
| BF3 | Avg | ||||||
| Std | |||||||
| BF4 | Avg | ||||||
| Std | |||||||
| BF5 | Avg | ||||||
| Std | |||||||
| BF6 | Avg | ||||||
| Std | |||||||
| BF7 | Avg | ||||||
| Std |
| Problem | EO | RSA | SMA | HGS | DMMAEO | ||
| Multimodal | BF8 | Avg | − | − | − | − | − |
| (High | Std | ||||||
| dimension) | BF9 | Avg | |||||
| Std | |||||||
| BF10 | Avg | ||||||
| Std | |||||||
| BF11 | Avg | ||||||
| Std | |||||||
| BF12 | Avg | ||||||
| Std | |||||||
| BF13 | Avg | ||||||
| Std | |||||||
| Problem | DEEO | HRSA | ESMA | AOAHGS | DHSMEO | ||
| BF8 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF9 | Avg | ||||||
| Std | |||||||
| BF10 | Avg | ||||||
| Std | |||||||
| BF11 | Avg | ||||||
| Std | |||||||
| BF12 | Avg | ||||||
| Std | |||||||
| BF13 | Avg | ||||||
| Std |
| Problem | EO | RSA | SMA | HGS | DMMAEO | ||
| Multimodal | BF14 | Avg | |||||
| (Fixed- | Std | ||||||
| dimension) | BF15 | Avg | |||||
| Std | |||||||
| BF16 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF17 | Avg | ||||||
| Std | |||||||
| BF18 | Avg | ||||||
| Std | |||||||
| BF19 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF20 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF21 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF22 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF23 | Avg | − | − | − | − | − | |
| Std | |||||||
| Problem | DEEO | HRSA | ESMA | AOAHGS | DHSMEO | ||
| BF14 | Avg | ||||||
| Std | |||||||
| BF15 | Avg | ||||||
| Std | |||||||
| BF16 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF17 | Avg | ||||||
| Std | |||||||
| BF18 | Avg | ||||||
| Std | |||||||
| BF19 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF20 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF21 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF22 | Avg | − | − | − | − | − | |
| Std | |||||||
| BF23 | Avg | − | − | − | − | − | |
| Std |
| Problem | EO | RSA | SMA | HGS | DMMAEO | ||
| Composition | BF24 | Avg | |||||
| Std | |||||||
| BF25 | Avg | ||||||
| Std | |||||||
| BF26 | Avg | ||||||
| Std | |||||||
| BF27 | Avg | ||||||
| Std | |||||||
| BF28 | Avg | ||||||
| Std | |||||||
| BF29 | Avg | ||||||
| Std | |||||||
| BF30 | Avg | ||||||
| Std | |||||||
| BF31 | Avg | ||||||
| Std | |||||||
| BF32 | Avg | ||||||
| Std | |||||||
| BF33 | Avg | ||||||
| Std | |||||||
| BF34 | Avg | ||||||
| Std | |||||||
| BF35 | Avg | ||||||
| Std | |||||||
| BF36 | Avg | ||||||
| Std | |||||||
| BF37 | Avg | ||||||
| Std | |||||||
| BF38 | Avg | ||||||
| Std | |||||||
| BF39 | Avg | ||||||
| Std | |||||||
| Problem | DEEO | HRSA | ESMA | AOAHGS | DHSMEO | ||
| BF24 | Avg | ||||||
| Std | |||||||
| BF25 | Avg | ||||||
| Std | |||||||
| BF26 | Avg | ||||||
| Std | |||||||
| BF27 | Avg | ||||||
| Std | |||||||
| BF28 | Avg | ||||||
| Std | |||||||
| BF29 | Avg | ||||||
| Std | |||||||
| BF30 | Avg | ||||||
| Std | |||||||
| BF31 | Avg | ||||||
| Std | |||||||
| BF32 | Avg | ||||||
| Std | |||||||
| BF33 | Avg | ||||||
| Std | |||||||
| BF34 | Avg | ||||||
| Std | |||||||
| BF35 | Avg | ||||||
| Std | |||||||
| BF36 | Avg | ||||||
| Std | |||||||
| BF37 | Avg | ||||||
| Std | |||||||
| BF38 | Avg | ||||||
| Std | |||||||
| BF39 | Avg | ||||||
| Std |
| EO | RSA | SMA | HGS | DMMAEO | ||
| Friedman mean rank | 6.487 | 8.526 | 6.077 | 6.410 | 3.462 | |
| Final rank | 8 | 10 | 6 | 7 | 2 | |
| 1/0/−1 | 32/6/1 | 30/7/2 | 31/5/3 | 30/6/3 | 27/10/2 | |
| DEEO | HRSA | ESMA | AOAHGS | DHSMEO | ||
| Friedman mean rank | 4.821 | 7.192 | 4.231 | 5.538 | 2.256 | |
| Final rank | 4 | 9 | 3 | 5 | 1 | |
| 1/0/−1 | 28/9/2 | 32/7/0 | 31/5/3 | 31/5/3 | ∼ | |
| Algorithm | Best | Avg | Worst | Std |
|---|---|---|---|---|
| EO | 179.1639 | 181.5920 | 188.3981 | 2.504409 |
| DMMAEO | 176.0768 | 179.1847 | 183.0997 | 1.957168 |
| DEEO | 176.2221 | 180.8633 | 185.6625 | 2.120665 |
| ESMA | 176.6373 | 180.6428 | 185.6273 | 2.013366 |
| EDBO | 175.7928 | 180.0901 | 185.5089 | 1.897720 |
| DHSMEO | 174.7972 | 177.2150 | 179.5667 | 1.750398 |
| Algorithm | Best | Avg | Worst | Std |
|---|---|---|---|---|
| EO | 180.4039 | 187.0131 | 188.6926 | 1.807976 |
| DMMAEO | 178.7315 | 186.2725 | 187.9656 | 1.721200 |
| DEEO | 180.3755 | 186.6118 | 187.6417 | 2.118246 |
| ESMA | 180.3311 | 186.3473 | 188.0306 | 1.834329 |
| EDBO | 178.5452 | 184.9253 | 186.3825 | 2.306150 |
| DHSMEO | 176.4555 | 178.8353 | 182.1692 | 1.692046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Hirota, K.; Dai, Y.; Shao, S. Dynamic Heterogeneous Search-Mutation Structure-Based Equilibrium Optimizer. Appl. Sci. 2025, 15, 5252. https://doi.org/10.3390/app15105252
Wu X, Hirota K, Dai Y, Shao S. Dynamic Heterogeneous Search-Mutation Structure-Based Equilibrium Optimizer. Applied Sciences. 2025; 15(10):5252. https://doi.org/10.3390/app15105252
Chicago/Turabian StyleWu, Xiangdong, Kaoru Hirota, Yaping Dai, and Shuai Shao. 2025. "Dynamic Heterogeneous Search-Mutation Structure-Based Equilibrium Optimizer" Applied Sciences 15, no. 10: 5252. https://doi.org/10.3390/app15105252
APA StyleWu, X., Hirota, K., Dai, Y., & Shao, S. (2025). Dynamic Heterogeneous Search-Mutation Structure-Based Equilibrium Optimizer. Applied Sciences, 15(10), 5252. https://doi.org/10.3390/app15105252





