Abstract
This study improves existing protection strategies for image processing models by embedding invisible watermarks into model outputs to verify the sources of images. Most current methods rely on CNN-based architectures, which are limited by their local perception capabilities and struggle to effectively capture global information. To address this, we introduce the Swin-UNet, originally designed for medical image segmentation tasks, into the watermark embedding process. The Swin Transformer’s ability to capture global information enhances the visual quality of the embedded image compared to CNN-based approaches. To defend against surrogate attacks, data augmentation techniques are incorporated into the training process, enhancing the watermark extractor’s robustness specifically against surrogate attacks. Experimental results show that the proposed watermarking approach reduces the impact of watermark embedding on visual quality. On a deraining task with color images, the average PSNR reaches 45.85 dB, while on a denoising task with grayscale images, the average PSNR reaches 56.60 dB. Additionally, watermarks extracted from surrogate attacks closely match those from the original framework, with an accuracy of 99% to 100%. These results confirm the Swin Transformer’s effectiveness in preserving visual quality.
1. Introduction
In recent years, the rapid advancement of deep learning technology has demonstrated remarkable application potential in various fields [1,2,3]. For instance, deep learning has brought about revolutionary changes in medical diagnostics [4], autonomous driving [5], and natural language processing [6], achieving significant success in each domain. However, as deep learning technology becomes more widespread, issues surrounding the copyright protection of deep learning models are becoming increasingly prominent. Model creators face difficulties in verifying whether others have copied or extracted their models without authorization. Training a high-performance deep learning model typically requires substantial computational resources and high-quality data, along with time-intensive processes for model design, training, and parameter tuning. These models often constitute a company’s core competitive advantage, yet even sharing a model through an application programming interface (API) can lead to potential misuse. Unauthorized users can input their own datasets through the API, generating data pairs and utilizing them to train their own models, thereby significantly reducing their training costs. This process is known as surrogate model attacks [7,8]. Such actions are highly unfair to the original model creator. Even when infringement is detected, pursuing legal action is often costly and time-consuming, and it rarely leads to an effective solution.
To address the aforementioned issues, various model copyright protection strategies have been proposed, such as weight matching [9], trigger-based watermarking [10], and visible watermarking [11]. Weight matching compares model parameters to identify ownership, while trigger-based watermarking embeds specific triggers into the model to verify its source. These methods are primarily designed for deep learning classification tasks, where the model analyzes input data and outputs a corresponding category. However, they can still be applied to other deep learning tasks, such as image processing. Due to the nature of image output, however, these methods can significantly degrade the resulting visual quality. For image processing models, visible watermarking is a more common approach, involving embedding logo information directly into output images. However, this method clearly impacts visual quality, making it unsuitable for applications that require high-quality results. As a result, researchers have begun exploring alternative methods to balance copyright protection with visual quality [12], particularly in image processing tasks like denoising [13], super-resolution [14], and style transfer [15].
Traditional copyright protection methods for images often involve digital watermarking, which embeds imperceptible watermark information, such as a logo or the author’s name, within the image to achieve copyright protection. Common traditional watermarking techniques include discrete cosine transform (DCT) [16] and discrete wavelet transform (DWT) [17]. DCT embeds watermarks by transforming image data into the frequency domain, while DWT decomposes the image into sub-bands at different scales and orientations. These methods use spatial transformation techniques to achieve the high invisibility of the watermark and can withstand certain types of attacks on the image. However, the watermark capacity in these methods is limited, as the amount of information that can be embedded usually depends on the size of the original image. Moreover, these methods primarily protect the image itself rather than the model.
To overcome limitations related to watermark capacity and robustness, researchers have started applying digital watermarking technology to safeguard the copyright of deep learning models [18,19]. Quan [20] introduced the trigger-based watermarking method mentioned earlier into image processing tasks, generating a watermark output based on a predefined input. Jing [21] proposes an invertible neural network that embeds watermarks in the wavelet domain, leveraging neural networks for both embedding and extraction. Guan [22] adopts a similar invertible neural network framework, extending it to multiple watermarks by analyzing inter-watermark relationships to optimize embedding locations and prevent excessive intensity in any single area. Tancik [23] designs an end-to-end trainable neural network architecture that embeds and extracts digital watermarks directly in the pixel space, using adversarial training to enhance robustness against geometric transformations and image distortions. Wu’s [24] method follows a similar idea to Tancik’s [23], using convolutional neural networks (CNNs) to embed and extract watermarks directly in the pixel space. However, Wu further integrates the watermark embedding process into the primary image processing task, making it more seamless. Additionally, a key-based mechanism is introduced in the extractor to conceal the presence of the watermark, reducing the risk of unauthorized detection and removal. Compared to traditional methods, deep learning models show greater potential for watermark embedding capacity and robustness.
Despite the advancements in deep learning watermarking strategies, many existing methods rely on custom-designed neural networks for embedding and extraction. In contrast, Zhang’s method [25] adopts a more generalizable approach by leveraging UNet, a well-established architecture for image segmentation, to achieve effective watermark embedding with minimal degradation to visual quality. Additionally, Zhang’s [25] method incorporates noise augmentation during the training of the extractor, improving its robustness against surrogate attacks. This combination of high-quality image preservation and improved resistance to surrogate attacks makes Zhang’s [25] method a solid foundation for watermarking tasks.
However, while Zhang’s [25] method achieves impressive performance, CNN architectures are inherently limited in capturing long-range dependencies due to their localized receptive fields. This shortcoming can compromise the invisibility of embedded watermarks and degrade overall visual quality, as critical global information may be lost during feature extraction. To overcome this limitation, we introduce the Swin Transformer into our framework. The Swin Transformer utilizes a hierarchical structure and shifted window-based self-attention, enabling it to model both local and global relationships more effectively. It has demonstrated strong performance in various vision tasks. For example, in iNatAg [26], it is used for the large-scale image classification of over 2900 crop and weed species. Similarly, in medical image segmentation, such as retinal vessel delineation [27], it achieves pixel-level precision in distinguishing microvascular and macrovascular structures. These applications highlight the Swin Transformer’s capability to maintain fine-grained detail while capturing global context, making it particularly suitable for complex image tasks. Building on this, we adopt Swin-UNet as our watermark embedding backbone. This architecture integrates Swin Transformer blocks into the encoder–decoder framework of UNet, which is well suited for image-to-image translation tasks requiring consistent input–output resolution. The Swin-UNet reconnects spatially fragmented patches, effectively overcoming the locality constraints of CNNs. This not only reduces the information loss during processing, but also enhances visual fidelity, resulting in a more seamless and imperceptible watermark embedding.
Although replacing the original CNN-based UNet with Swin-UNet initially resulted in decreased robustness against surrogate models, this was because adversaries could use different architectures or objective functions to approximate the original model. To address this issue, we employed extensive training with data augmentation, which significantly improved the model’s robustness and extraction success rate under various adversarial conditions. Experimental results further confirm that Swin-UNet, as an attention-based watermark embedding strategy, not only preserves visual quality better than conventional convolutional networks, but also provides enhanced robustness against surrogate attacks. These advantages make it a more reliable and effective solution for practical watermarking applications.
2. Literature Review
As mentioned in the introduction, the method proposed by Zhang et al. [25] performs exceptionally well in preserving visual quality and effectively resisting surrogate model attacks. Zhang’s [25] watermark embedding architecture, as shown in Figure 1, is structured into two main stages: the initial training stage and the adversarial training stage.
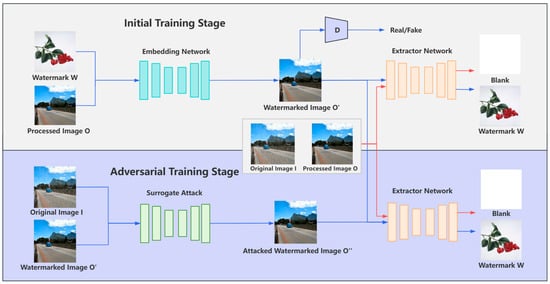
Figure 1.
Overview of Zhang’s watermarking framework.
In the initial training stage, the required images include the original image I, the processed image O obtained by inputting I into the image processing model, and the watermark W. First, the embedder learns to embed the W into the O through an embedding network. To enhance the perceptual quality and invisibility of watermarked images, a discriminator D is introduced during training. The discriminator is designed to distinguish between unwatermarked and watermarked images. It takes both unwatermarked images and watermarked images O’ as input and produces a probability score between 0 and 1, representing the likelihood that the input image is unwatermarked. The discriminator is trained using binary cross-entropy loss, where unwatermarked images are labeled as 1, and watermarked images are labeled as 0. Simultaneously, the embedding network is trained adversarially to generate watermarked images that the discriminator classifies as unwatermarked, thus improving the invisibility of the watermark. In this adversarial setup, the embedding network aims to maximize the discriminator’s misclassification, encouraging it to assign a probability close to 1 for watermarked images. The output of the discriminator serves not only to compute the loss but also as a guiding signal for the embedding network to produce more visually indistinguishable results.
Subsequently, the training of the extractor network takes place. In this phase, the inputs include three types of images the watermarked image O′, along with the original image I and the processed image O, where neither I nor O contain the watermark. Incorporating unwatermarked images into the extractor’s training helps the network differentiate whether an image contains a watermark. Without this ability to distinguish, the extractor might attempt to extract a watermark from an image that does not have one, which would be meaningless. Therefore, it is specified that, when the extractor receives I or O, the output should be a blank image. Only when the input is O′ should the extractor attempt to extract the watermark. However, when faced with surrogate model attacks, the extractor’s watermark extraction performance significantly decreases due to the introduction of noise.
In the adversarial training of the second stage, surrogate attacks are simulated. During training, the surrogate attack learns to transform I into O′. However, due to differences in the training process, the generated images do not perfectly match O′ and instead contain additional noise. In this work, we refer to these images as attacked watermarked images O″. This added noise alters image details and affects the extractor’s performance, so the extractor fine-tuned from the initial stage undergoes further independent training. In this phase, three types of images, I, O′, and O″, are used. O″ is included to help the extractor adapt to extracting watermarks from attacked watermarked images. Meanwhile, I and O′ are included to ensure that the extractor retains its original capabilities, including distinguishing whether an image contains a watermark and extracting watermarks from clean watermarked images. The final embedder and extractor constitute the complete watermarking solution, capable of reliably extracting watermark information under complex conditions.
The experimental results demonstrate that this watermarking strategy effectively prevents the degradation of image quality, ensuring that the watermarked image closely resembles the processed image. The average peak signal-to-noise ratio (PSNR) for grayscale images is 46 dB, while for color images, it is approximately 41.32 dB. PSNR is a metric used to measure the quality of an image by comparing the difference between the original and the distorted watermarked or processed image. Higher PSNR values indicate better image quality, with less distortion. Furthermore, this strategy is one of the few watermarking solutions at the time that considers robustness against surrogate attacks, even when facing noisy distortions in O″.
3. Materials and Methods
3.1. Overall Organizational Structure
This study builds upon the watermarking framework proposed by Zhang et al. [25], whose core idea is embedding watermarks into the processed image O generated by an image processing model, such as deraining and denoising, to protect authorship. This design helps prevent surrogate attacks because, if someone trains their own model using watermarked images, their model will also learn the watermark, making it traceable. As illustrated in Figure 2, the framework consists of two stages: the initial training stage, which jointly trains the embedding and extraction networks, and the adversarial training stage, designed to enhance robustness through simulated attacks. The dashed regions in the figure indicate two critical improvements proposed in this work, which involve upgrading the embedding network architecture and integrating adversarial data augmentation strategies.
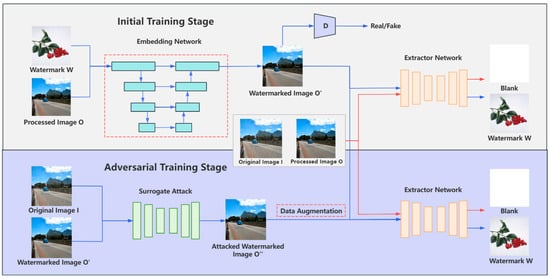
Figure 2.
The framework of proposed watermarking method. The optimized section is highlighted with a dashed box.
The watermark framework operates in two sequential phases. During the initial stage, the following components are prepared: the watermark W, the processed image O generated by the image processing model, and the original image I. The embedding network, Swin-UNet, takes O and the watermark image as inputs to produce the watermarked image O′, which is constrained to maintain high visual fidelity with O. To enhance watermark invisibility, a discriminator D is introduced to classify whether an image contains a watermark, thereby guiding the embedder to minimize perceptual distortions.
Concurrently, the extraction network is trained on three types of inputs: O′, I, and O, ensuring it distinguishes between watermarked and non-watermarked images. Specifically, when fed with I or O, the extractor outputs a blank image, ensuring it does not attempt to extract nonexistent watermarks. After initial training, the extractor achieves near-lossless watermark extraction from O′ under noise-free conditions.
In practice, surrogate attacks may result in noisy and compromised watermarked images. To address this, the adversarial training stage simulates such attacks by perturbing O′ using a surrogate model, such as UNet with L2 loss. The generated attacked watermarked images O″ is further augmented with composite distortions, including Gaussian noise, motion blur, and JPEG compression, to broaden the attack coverage and improve the extractor’s generalization capabilities.
Crucially, the extractor is retrained on a mixed dataset containing both watermarked images O′ and attacked watermarked images O″, alongside non-watermarked images I and O. This approach ensures that the extractor maintains high accuracy on unaltered watermarked images O′ while adapting to diverse noise patterns, enabling robust watermark extraction, even from attacked watermarked images.
The above outlines the overall process of the architecture. This work focuses on optimizing the following two aspects:
- Embedding Network Upgrade by Replacing UNet with Swin-UNet
Zhang’s [25] framework employs a UNet as the embedding network. However, due to the limited receptive field of convolutional operations, it struggles to capture the global context, resulting in reduced similarity between the watermarked and processed images. To overcome this, we adopt Swin-UNet, which enhances feature representation through window-based self-attention and multiscale fusion. This design better preserves local details while capturing long-range dependencies, improving overall structural consistency.
- 2.
- Data Augmentation to Enhance Robustness Against Surrogate Attacks
While the upgraded embedding network enhances visual quality, it inadvertently reduces the extractor’s robustness against attacked watermarked images. When directly applying Zhang’s [25] adversarial training strategy, which generates attacked images via UNet with L2-Ladv loss, the extraction success rate drops from the 99% benchmark to 93% in our experiments. Further analysis reveals that Swin-UNet generates more complex high-frequency feature distributions, making original attack simulations based solely on UNet perturbations insufficient for real-world scenarios. To address this, we apply multimodal data augmentation during adversarial training.
3.2. Embedding Network Based on Swin-Unet
The improvement in the watermarking framework primarily focuses on embedding. While traditional CNN-based methods like Zhang’s [25] employ UNet for watermark embedding, they are limited by the small receptive field of convolutional operations. This restricts the network’s ability to capture global context, potentially leading to information loss and reduced visual quality. These limitations motivate the integration of the Transformer, which has proven effective in various image processing tasks [28,29], into the watermark embedding process.
In the early stages of research, during the dimensionality reduction phase of the original UNet network, attempts were made to integrate lightweight attention modules such as ECA [30] and SENet [31]. These modules were chosen because they can enhance the CNN’s sensitivity to channel information and improve feature reconstruction without significantly increasing computational overhead. SENet adaptively adjusts channel weights to emphasize important features, while ECA achieves efficient channel interaction. In the context of watermark embedding, these properties were expected to better extract and reinforce local features during the downsampling phase, thereby preserving critical information. However, experimental results revealed that these lightweight attention mechanisms did not significantly enhance the model’s performance. This limitation arises because these modules are constrained by the local characteristics of convolutional neural networks (CNNs). The receptive field of convolutional kernels is limited, and the attention mechanisms primarily focus on local features within the image. Although these modules can strengthen feature correlations within local regions, they fall short in capturing global information. Furthermore, CNNs tend to lose global context and long-range dependencies during downsampling, and lightweight attention modules are not effective in addressing this issue. As a result, the quality of the generated images did not meet expectations, and, in some cases, was even inferior to that of the original UNet.
Based on the aforementioned limitations, the research focus shifted to the transformer architecture, culminating in the adoption of Swin-UNet. This decision was motivated by the fact that the original watermark embedding network employed a UNet-based structure, which is recognized for its ability to maintain both overall architectural integrity and fine-grained details. Swin-UNet retains the inherent strengths of UNet while incorporating Swin Transformer modules to effectively address the challenge of global information capture. A distinguishing feature of the Swin Transformer is its shifted window mechanism. This mechanism partitions the image into local patches and applies self-attention within each window, while simultaneously facilitating inter-window interactions, thereby enabling the capture of long-range dependencies. Through this shifted window approach, Swin-UNet not only preserves local feature details but also integrates comprehensive global context information at each layer, thereby expanding the receptive field. In addition, this layered global information capture mechanism proves particularly advantageous for watermark embedding strategies, as it helps preserve subtle watermark details while maintaining overall image integrity. By balancing local precision with global context, the approach offers a robust solution for ensuring that both the embedded watermark and the overall visual quality are effectively maintained. In summary, the comparison between CNN-based UNet and the Swin Transformer is illustrated in Table 1, which highlights the architectural differences and further clarifies the motivation behind adopting the Transformer-based design in this study.

Table 1.
CNN-based vs. Swin Transformer-based models.
Inspired by these studies, Swin-UNet is believed to be well suited for analyzing image details while ensuring global information capture through attention mechanisms. Additionally, Swin-UNet is designed for image-to-image tasks, where the input and output share structural similarities. This aligns with the objective of watermark embedding, ensuring that the watermarked image remains visually similar to the original.
In the embedding network component illustrated in Figure 3, which is built upon the Swin-UNet architecture, the watermark embedding process is executed on the processed image O produced by the image processing model through the following detailed steps:
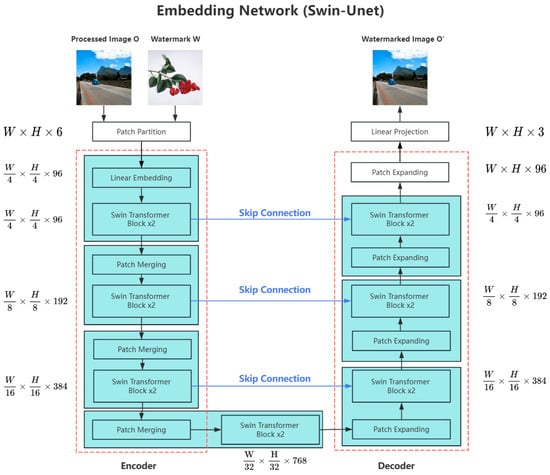
Figure 3.
The embedding network pipeline of the proposed method.
Step 1. Input Image Preprocessing
In this step, two inputs are prepared for feeding into the Swin-UNet embedding network. These inputs include the processed image O generated by the image processing model and the watermark image. To ensure consistency with common practices in image processing tasks and facilitate the comparison with existing models, both images are resized and cropped to a fixed resolution of 256 × 256 pixels. This size is widely used in the field for balancing computational efficiency and preserving essential image features. Additionally, both images are normalized to the range [−1, 1], a standard practice that stabilizes gradient updates and accelerates convergence. This normalization also ensures the compatibility with the discriminator in a later module, contributing to stable training dynamics. Finally, the normalized O and watermark image are concatenated along the channel dimension, forming a six-channel input tensor. Concatenating these along the channel dimension yields a six-channel tensor represented as:
denotes the normalized processed image and denotes the normalized watermark image. The preprocessed tensor, the merged image with a size of 256 × 256 × 6 (width × height × channel), is then passed to the Swin-UNet for watermark embedding.
Step 2. Patch Partition and Encoder Phase
First, the merged image undergoes a patch partition operation, dividing it into non-overlapping patches of size 4 × 4 × 6, as shown in Figure 4. This process reduces computational complexity and prepares the data for Transformer architectures, which are designed to process sequential inputs. Each patch is then passed through the linear embedding layer, where it is flattened into a feature vector and meaningful features are extracted. This operation reshapes the image into , achieving dimensionality compression while converting spatial information into a serialized representation suitable for Transformer processing. The subsequent encoder and decoder operations completely adhere to the original Swin-UNet structure, with no modifications made in this approach.
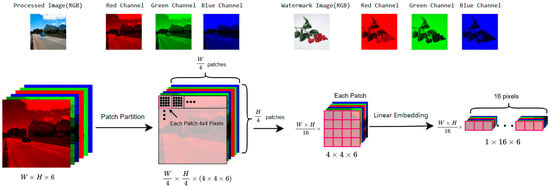
Figure 4.
Patch partition and linear embedding of embedding pipeline.
The embedded feature sequence is then fed into the Swin Transformer module for feature extraction and attention computation. It is important to note that the Swin Transformer employs a hierarchical windowed attention mechanism, which must be used in pairs: the first Swin Transformer block partitions the feature map into non-overlapping fixed-size windows and computes local self-attention within each window. The subsequent Swin Transformer block adopts a shifted window strategy, where the window positions are shifted by 50% to create overlapping regions with the previous stage. This alternating window partitioning mechanism overcomes the global computation limitations of conventional Transformers, ensuring computational efficiency through local attention while enabling cross-region feature interaction via inter-layer window shifts. To extract multi-level features effectively, multiple Swin Transformer blocks are stacked, progressively establishing global feature relationships through a deep network.
Subsequently, a feature downscaling module is employed, combining patch merging and Swin Transformer blocks. This module is represented by the blue block in Figure 4. Patch merging merges adjacent 2 × 2 patches by concatenating their feature representations along the channel dimension, followed by a linear projection. This operation reduces the spatial resolution of the feature map by half while increasing the channel dimension, similar to downsampling in CNNs, but with a better preservation of structured information. Specifically, given an input feature map of size W × H × C, where H denotes the height, W the width, and C the number of channels, the patch merging transformation follows this process:
Here, the 1 × 1 convolution is applied to reduce the merged 4C channels to 2C, a process analogous to channel compression in CNNs. This operation reduces computational complexity while retaining sufficient feature representation capacity. In this approach, three feature downscaling modules are used in total, progressively transforming the shape from to .
It is worth noting that, although progressive downsampling inevitably leads to some loss of low-level spatial information, the multi-scale features extracted at each encoder stage are transmitted to the decoder through skip connections. This design maintains the multi-scale representation of the feature pyramid while effectively compensating for information loss during downsampling through cross-layer feature fusion, which is crucial for subsequent watermark embedding and processed image reconstruction.
Step 3. Decoder Stage
The decoder adopts a symmetric architecture to progressively reconstruct image features, with the core operations being feature upsampling and cross-layer feature fusion. First, for each decoding layer, the input feature map undergoes a 1 × 1 convolution operation to expand the channel dimension from C to 2C. This process can be represented as:
The purpose of channel expansion is to enhance the feature representation, providing richer features for subsequent upsampling operations. Next, a feature upscaling module is employed, combining patch expanding and Swin Transformer blocks. The expanded feature map undergoes spatial dimension reconstruction by rearranging the 2C channels of features in adjacent 2 × 2 patches, thereby generating a feature map with doubled resolution. This operation ensures that the output feature map’s channel count remains consistent with the corresponding encoder layer’s skip connection feature, facilitating subsequent feature fusion.
The skip connection features from the encoder are then element-wise added to the upsampled output features to achieve cross-layer feature fusion. The fused features are fed into the Swin Transformer module, whose core task is to effectively integrate watermark features with host image features. Through the shifted window attention mechanism, the Swin Transformer computes attention weights within local windows, thereby precisely controlling the embedding strength and spatial distribution of watermark features: enhancing the watermark feature weights in texture-rich regions to improve invisibility, while reducing the weights in smooth regions to preserve visual quality. Furthermore, the Swin Transformer establishes global dependencies through cross-window connections, ensuring that the watermark embedding strength is coordinated across different regions, thereby maintaining the continuity and integrity of the watermark pattern. The Swin Transformer also plays a crucial role in reconstructing image details, preserving the structural information and texture features of the host image while embedding the watermark, thereby balancing watermark invisibility and visual quality.
These operations are performed across decoding layers, progressively reconstructing the feature maps. Through three feature upscaling module, the feature dimensions are transformed from to . Finally, interpolation techniques are applied to restore the spatial dimensions to W × H × 96, ensuring that the output image maintains the same resolution as the input while preserving rich feature information.
Step 4. Output Processing
After a series of operations performed by the decoder, the output image is adjusted to a size of W × H × 96. To convert this output into a standard image, a linear projection is applied to reduce the number of channels from 96 to 3, representing the RGB channels of the image. Subsequently, the pixel values are mapped to the range of [−1, 1]. This step ensures that the network operates within a consistent range, which is important for maintaining the stability of the network during training. Finally, a reverse normalization operation is applied to remap the pixel values back to the [0, 255] range, completing the watermark embedding process.
In the design of the watermark embedding network, the primary objective is to ensure that the processed image and the watermarked image remain as similar as possible, thereby preserving the visual quality to the greatest extent. To achieve this, we refer to the approach proposed by Zhang et al. [25] and adopt a combination of commonly used image loss functions, primarily the mean squared error (), visual geometry group (), and generative adversarial network (). The overall loss function is formulated as follows:
where , represent the weights of each loss term, and these three losses constrain visual quality from different perspectives. The MSE loss measures pixel-wise differences between the processed and watermarked images, ensuring that the embedded watermark does not significantly distort the original image’s structure and details. The VGG loss compensates for the limitations of MSE loss by focusing on high-level image features, effectively preserving texture details and better aligning with human perceptual judgments of visual quality. The GAN loss incorporates an adversarial learning mechanism, where a discriminator detects the presence of a watermark in the image, encouraging the embedded watermark to be more imperceptible. By jointly considering pixel-level similarity (MSE), perceptual quality (VGG), and realism (GAN), our loss design effectively balances visual quality, detail preservation, and imperceptibility in watermark embedding.
3.3. Data Augmentation for Adversarial Training Stage
In the design of the adversarial training strategy, this study first draws on Zhang et al.’s methods [25], using UNet_L2 as a surrogate model to simulate attacks by generating attacked watermarked images for training the extractor. However, after replacing the embedding network with Swin-UNet, although the visual quality of the watermarked image improved, the method experienced a significant drop in extraction robustness when subjected to surrogate attacks with specific loss combinations (e.g., L2 + Ladv). The lowest extraction success rate dropped to 93%, which is notably lower than the 99% success rate of Zhang’s approach [25]. This phenomenon can be attributed to the visual quality optimization process driven by the Ladv loss, where the discriminator tends to suppress watermark features, treating them as secondary information, thus leading to insufficient embedding strength.
To enhance the system’s robustness against surrogate attacks, this study applies a data augmentation strategy. Compared to directly increasing the embedding strength or adjusting the loss function, data augmentation enables the extractor to adapt to a variety of potential attack methods without compromising visual quality. This approach is particularly beneficial in real-world scenarios, where different surrogate models may introduce various damage patterns.
Initial attempts to apply augmentation in the initial training stage, where both the embedding network and the extractor are trained together, showed that it forced the embedding network to excessively reinforce watermark features in response to interference, significantly increasing the watermark visibility and compromising the visual quality. Therefore, the final strategy limits augmentation to the adversarial training stage, applying interference simulation training only to the attacked watermarked images to enhance the extractor’s robustness without compromising visual quality.
The augmentation methods include five basic disturbance modes: Gaussian blur to simulate image detail loss; Gaussian noise to simulate training error accumulation; JPEG compression to simulate lossy storage effects; random occlusion to simulate partial information loss; and color distortion to simulate data distribution shifts. These augmentation methods effectively simulate the noise that different surrogate models may introduce during training, improving the extractor’s ability to adapt to surrogate attacks.
Furthermore, this study introduces a probability-triggered augmentation mechanism, where each type of augmentation is assigned an independent Usage Probability. During training, for each incoming image, each augmentation independently determines whether to be applied based on its assigned probability. This ensures that different samples undergo varying combinations of augmentations, creating a more diverse training set. By exposing the extractor to a wide range of watermark degradations, this approach improves its generalization ability against various attack scenarios. Experimental results demonstrate that the probability-triggered mechanism, which better reflects real-world conditions, effectively reduces extraction loss and improves the extraction success rate compared to a non-probability-triggered approach.
4. Results
4.1. Implementation Details
The dataset consisted of 12,200 images for both deraining and denoising tasks. For deraining, 6100 images were sampled from PASCAL VOC 2012 and paired with synthetic rainy versions using a rain synthesis algorithm, following Zhang’s [25] protocol, with 6000 images used for training and 100 for testing.
To train the surrogate model, 6100 images from COCO 2017 were embedded with watermarks via a pretrained network, generating watermarked images O′. These were used to train a surrogate attack model, which was then applied to the 6100 PASCAL images to produce attacked versions O″. This resulted in two parallel datasets: COCO-derived O′ and PASCAL-derived O″.
For adversarial training, 6000 samples from each dataset were combined into a 12,000-image training set with a 1:1 ratio, and 100 samples from each formed a 200-image validation set. All images were resized to 256 × 256. The denoising task followed the same pipeline, but images were converted to grayscale to evaluate robustness under monochrome input.
The embedder and extractor were trained jointly for 150 epochs using a batch size of 4, followed by 50 epochs of fine-tuning for the denoising task using transfer learning. The Swin-UNet embedder was set with a depth of 4. Training was conducted using the Adam optimizer. The learning rate was dynamically reduced by a factor of 0.2 if the validation performance did not improve for three consecutive epochs.
To improve the robustness against surrogate model attacks, we applied targeted data augmentations during training, simulating common distortions introduced by such attacks. These included moderate color jittering (±20% brightness/contrast), Gaussian noise, partial masking, JPEG compression, and Gaussian blur, all with controlled probabilities (see Table 2). These transformations were carefully calibrated to maintain perceptual quality while enhancing model robustness.

Table 2.
Parameter setting and associated usage probabilities in data augmentation transformation.
To assess visual quality, we used two common metrics: PSNR and SSIM. PSNR reflects overall image quality, with higher values indicating better results. SSIM measures structural similarity between images, aligning more closely with human perception, where values closer to 1 indicate higher similarity. These metrics compare watermarked images to the originals to evaluate visual impact.
In addition to evaluating the quality of the watermark, its robustness also needs to be verified. To ensure fairness, we adopted two methods used by Zhang [25]: a classifier and normalized correlation (NC). The classifier, implemented as a three-layer convolutional neural network (CNN), is responsible for determining the presence of watermarks in an image. It is trained using binary cross-entropy loss, where the output is a probability value between 0 and 1. A threshold of 0.5 is applied: if the output exceeds 0.5, the image is classified as containing a watermark; otherwise, it is classified as watermark-free. This classifier does not require extracting the watermark itself, and thus its judgment is likely to be more accurate than the normalized classifier (NC), especially in robust attack scenarios. The success rate of the classifier and the normalized classifier are used to evaluate the effectiveness of the watermark detection mechanism.
4.2. Visual Quality of Watermarked Image and Extracted Watermark
This section presents the results of the initial training stage, focusing on watermark invisibility, visual quality, and watermark extraction performance without noise interference. To ensure consistency and reliability, five distinct watermark images, including both color and grayscale images, were selected. Among them are simpler grayscale images such as a single character and a QR code, as well as more complex color images featuring patterns, such as flowers, portraits, and fruits, as shown in Figure 5. Even when faced with complex color images, the improved embedder exhibited good performance across different watermark images.

Figure 5.
Embedding results for five watermark types, evaluating visual impact, and extraction effectiveness. (a) Original image, (b) Watermarked image, (c) Difference map (×10), (d) Embedded watermark, and (e) Extracted watermark.
Figure 5 demonstrates the embedding effects of the proposed watermarking approach across two distinct image processing tasks: deraining for color images, displayed on the left, and denoising for grayscale images, displayed on the right. For the original and watermarked images, visual comparison shows that the differences are imperceptible to the human eye, demonstrating the high invisibility of the watermark. This indicates that the embedding process does not compromise the quality of the original image. To further validate the embedding effects, the pixel-wise differences between the original and watermarked images were amplified by a factor of 10. The amplified results appear as dark images with only sparse bright spots, confirming that the differences are minimal and the embedding process is highly effective. The extracted watermarks from the watermarked images are also presented, showcasing their consistency with the original watermarks used during embedding. Under clean conditions, where the watermarked images are not subjected to any attacks or noise interference, the extraction results visually match the original watermark closely, reflecting excellent performance. However, success under clean conditions alone is insufficient. The robustness of the watermark against surrogate model attacks is crucial. A detailed evaluation of the watermark’s robustness under such conditions is provided in Section 4.3. Additionally, the inference time for embedding the watermark is approximately 0.013 s, whereas Zhang’s method takes about 0.007 s for the same task.
Table 3 provides a clear and concise comparison of the effects of different watermark choices across various tasks. To ensure a fair comparison with Zhang’s work [25], the same datasets (PASCAL VOC and COCO), and watermark were adopted for the deraining task on color images. To maintain consistency, the denoising task, which involves a D image processing model for grayscale images in Zhang’s work [25], which used a private debone dataset, was substituted with a denoising task due to the limited availability of publicly accessible datasets for this task. However, the primary comparison focuses on the deraining task, where improvements were achieved using Swin-UNet.

Table 3.
Quantitative results of the proposed deep image-based invisible watermarking algorithm.
Due to the inherent fluctuation in PSNR values, which is largely influenced by the specific image and watermark used, we express the PSNR results of our method as a mean ± standard deviation. This approach provides a clearer representation of the variability in performance across different test images. From Table 3, it is evident that, even when embedding different watermark images, the overall visual quality in the deraining task remains significantly improved. On average, the PSNR values increased by approximately 4.5 dB. Despite the already high quality of Zhang’s methods [25], our method further minimized the visual impact of the watermark while enhancing overall image fidelity. In the denoising task, the PSNR average exceeded 53 dB, indicating that our method effectively maintains the integrity of the original image. Additionally, the SSIM values improved by approximately 0.01, further confirming the superior visual quality of the proposed method.
The NC values, along with the subsequent and results, remained consistent with Zhang [25]. With NC values close to 1, the extracted watermarks were nearly identical to the originals. Moreover, both and achieved 100% accuracy, demonstrating that, under noise-free conditions, the proposed watermarking approach not only ensures flawless extraction, but also maintains better visual quality after embedding.
4.3. Robustness Against Surrogate Attacks
As mentioned earlier, while the quality of the images is indeed very important, it is equally crucial to ensure that the model effectively protects the watermarks. This section focuses on the robustness of the watermark. Referring to the surrogate model attacks discussed in the first chapter, an adversary can use their own dataset to generate input–output pairs by accessing the original image processing model through an API. They can then use these generated pairs to train their own model. To simulate these scenarios, this study selected several commonly used models in image processing, including CNet, ResNet, and UNet. Various combinations of loss functions, such as L1, L2, perceptual, and adversarial, were also tested to closely mimic the behavior of the adversary.
As shown in Figure 6 and Figure 7, the performance of watermark extraction using different surrogate models and loss function combinations is presented. The first image represents the original image I, a rainy image, where the extracted watermark appears as a blank image. This is because the original image I itself does not contain any embedded watermark. The second image corresponds to the watermarked image O′, where the watermark is perfectly extracted in the absence of additional noise. Subsequent images depict the extraction results after surrogate attacks using different networks, which are employed to evaluate the robustness of the proposed watermark extraction method. Due to limited computational resources, not all model and loss function combinations were tested. Specifically, CNet, ResNet9, and ResNet16 were evaluated using only the L2 loss to establish a consistent baseline for comparison. This ensures that variations in extraction performance are attributed to the differences in network architectures rather than the influence of different loss functions. In contrast, UNet was tested with multiple loss combinations because different loss functions introduce varying levels of noise, helping to demonstrate the robustness of the watermark extraction process. The results demonstrate that, although noise introduced by the surrogate models affected the extraction process, the overall contours of the watermark were successfully extracted, allowing the presence of the watermark to be clearly identified.

Figure 6.
Watermark extraction results on the deraining task with surrogate models using different networks and loss functions. (a) Original image. (b) Watermarked image without noise. (c–f) Results from CNet, ResNet9, ResNet16, and UNet with L2 loss. (g–j) Results from UNet with L2 + Ladv, L1, L1 + Ladv, and Lperc + Ladv losses.

Figure 7.
Watermark extraction results on the denoising task with surrogate models using different networks and loss functions. (a) Original image. (b) Watermarked image without noise. (c–f) Results from CNet, ResNet9, ResNet16, and UNet with L2 loss. (g–j) Results from UNet with L2 + Ladv, L1, L1 + Ladv, and Lperc + Ladv losses.
Figure 6 illustrates the watermark extraction performance on the deraining task under attacks from surrogate models. For each pair from (a) to (j), the watermarked image (left) is juxtaposed with its extracted watermark (right): (a) represents the original image without an embedded watermark, resulting in a blank image when extraction is performed; (b) illustrates the watermark extraction performance in the absence of attacks, showing that the watermark can be extracted with minimal distortion; (c)–(j) showcase the extraction results after applying surrogate attacks, where different network architectures and loss function configurations are used. These variations lead to subtle differences in the extracted watermarks, resulting in varying degrees of degradation in quality. For instance, in case (c), the watermark extracted by the model trained under the CNet attack exhibits noticeable blurring artifacts on the leaf regions. Similarly, in (g), UNet with L2 + Ladv loss also produces a blurry watermark on the leaves, but the blurriness is less pronounced compared to (c). Other combinations, however, yield extracted watermarks on the leaves that are much closer to the original image in quality. While the presence of noise causes some loss of watermark details, the overall contours of the watermark are still accurately extracted. The extracted NC values across all tested combinations remain consistently high, ranging from 0.96 to 0.99, indicating a near-perfect extraction success rate. Since NC values above 0.95 are considered successful extractions, the can be regarded as 100%. A more detailed comparison can be found in Table 4.

Table 4.
The success rate () of Ours method resisting the attack from surrogate models.
Figure 7 presents the watermark extraction performance on the grayscale denoising task under attacks from surrogate models: (a) shows the original image without an embedded watermark, resulting in blank extraction; (b) illustrates the watermark extraction performance without attacks, where the watermark is extracted with minimal distortion; (c)–(j) unlike the deraining task, the extracted watermarks in the denoising task remain consistent across different network and loss function combinations. Regardless of the surrogate attack used, the extracted watermarks exhibit blurriness in the same regions, particularly on the leaves. This can be attributed to the inherent differences in the characteristics of the tasks. The denoising task involves removing global noise, leading to more uniform processing across the image, while the deraining task requires the handling of structured, localized streaks. As a result, surrogate models in denoising tend to produce more consistent watermark extraction patterns, whereas in deraining, the variations in learned features across different networks and loss functions lead to differences in the extracted watermark quality.
Figure 8 illustrates several cases where the watermark extraction results are suboptimal. Typically, when the surrogate attack incorporates adversarial loss (Ladv) during training, the performance of the extractor declines. This is expected, as the adversarial loss encourages the surrogate model to learn transformations that are less direct and more perturbation-driven, thereby diminishing the recognizability of the embedded watermark and increasing the extraction difficulty.

Figure 8.
Examples of watermarks extracted after surrogate attack, showing cases where the extraction quality is significantly degraded.
As shown in Table 4, the success rates of watermark extraction are evaluated using and . considers a watermark extraction successful if the NC value exceeds 0.95, while measures the proportion of successfully extracted watermarks based on a 0.5 threshold. The comparisons included three methods: Zhang’s method [25], Ours†, and Ours. Ours† refers to the version without data augmentation during the adversarial training phase of the extractor, while Ours indicates the version that incorporates data augmentation. Incorporating data augmentation during training provides more diverse samples, which helps improve the generalization ability of the extractor. The results in Our† demonstrate that UNet_L2 exhibits a certain level of generalizability. Even though the extractor was trained only with noise generated by UNet_L2, it still demonstrated a certain degree of robustness against other untrained network-loss combinations. However, compared to Zhang’s method [25], the extraction success rate was slightly reduced. Specifically, the UNet_L2_Ladv combination exhibited noticeable declines in extraction performance. In the deraining task, the success rate dropped to 93%, whereas, in the denoising task, it remained at 99%. This difference can be attributed to the varying complexity of the tasks. The denoising task primarily removes random noise while preserving the overall structure, allowing the surrogate attack model to better approximate the original model’s transformation, including the embedded watermark. Consequently, the watermarked features are more likely to be retained, facilitating extraction. In contrast, the deraining task involves structured rain streaks and complex transformations, which may inadvertently distort the watermark, reducing the extraction performance after a surrogate attack.
To mitigate the decline in extraction performance, data augmentation techniques were introduced during adversarial training. These augmentations simulate various interference scenarios, helping the model better adapt to different attack conditions. As shown in Ours, data augmentation significantly improved the surrogate attack robustness and extraction performance of the model. Notably, the UNet_L2_Ladv combination, which had the most significant drop in Ours†, showed improved extraction performance after augmentation, reaching 99% in deraining and 100% in denoising, closely resembling Zhang’s findings [25]. This highlights that data augmentation helps the extractor better adapt to untrained network-loss combinations in surrogate attacks.
These results confirm that and remain consistently high under different network attacks, with the lowest success rate still reaching 99%. This demonstrates the reliability of the proposed method in maintaining robustness against surrogate attacks. Overall, this showcases the effectiveness of data augmentation in enhancing both the robustness and training efficiency of watermark extraction, particularly in more challenging tasks.
4.4. Comparison with Existing Works
The previous sections primarily compared the proposed method with Zhang’s approach [25], as it builds upon his framework. This section presents a comprehensive comparison with other watermarking methods, focusing on image quality and robustness against surrogate model attacks, with testing conducted on the denoising task.
Four models were selected for comparison. J. Zhu’s HiDDeN [34] is one of the pioneering deep learning-based watermarking methods, designed to embed a predefined number of bits as binary data. It has two versions, differing by the inclusion of a noise layer during training. The noise layer improves watermark extraction fidelity but degrades the image quality. Despite embedding binary data instead of images, HiDDeN [34] serves as a fundamental benchmark for evaluating deep learning-based watermarking strategies. Jing’s HiNet [21] integrates traditional watermarking algorithms with neural networks. It applies discrete wavelet transform (DWT) to convert the image into the frequency domain before performing watermark embedding and extraction via a neural network. Currently, open source watermarking strategies explicitly designed for surrogate attacks are very limited. Although HiNet [21] does not specifically address surrogate attacks, it is trained against other types of attacks. More importantly, it embeds a watermark image of the same size as the host image, making it structurally aligned with our approach and a suitable baseline for comparison. Zhang’s method [25] is described in detail in Section 2 and will not be reiterated here.
Since HiDDeN [34] is limited to embedding binary data, a 64-bit randomly generated binary sequence was used as the watermark for fair comparison. For models that embed an entire image as a watermark, this binary sequence was repeatedly expanded to form a 256 × 256 binary image before embedding.
Figure 9 illustrates the watermark extraction performance of different methods under the surrogate attacks applied to the same image. HiDDeN [34] is excluded from the figure since it does not embed an image watermark but instead embeds binary data. Processed refers to the image after denoising, watermarked indicates the processed image with an embedded watermark, and watermark represents the embedded watermark itself. The columns labeled CNet, Res9, Res16, and UNet represent the extraction results after surrogate model attacks. The red box in the extracted watermark from Res16 is enlarged for better visibility. The results indicate that HiNet [21] fails to recover the watermark after an attack. This can be attributed to its frequency-domain-embedding strategy, which does not directly map to spatial domain features. If the surrogate model learns only pixel-level spatial mappings, it may fail to capture the frequency-domain watermark structure, leading to the loss of watermark information during training. In contrast, Zhang’s method [25] and the proposed approach embed the watermark in the spatial domain and incorporate noise resilience training to counter surrogate attacks. As a result, both methods can still extract the watermark after attacks, albeit with some minor distortions. The extracted watermarks achieve a normalized correlation (NC) score exceeding 0.95 in most cases, meeting the criteria for successful extraction.

Figure 9.
Comparison of the extraction performance across different watermarking strategies [21,25] under surrogate attacks with repeated 64-bit binary watermarks.
Upon observing Zhang’s method, it can be seen that the extracted watermark exhibits slight distortions compared to the original watermark after the surrogate attack. However, the distortions in the proposed approach are less noticeable. This is due to the introduction of data augmentation during the extraction training process in the proposed approach, which helps the extractor adapt to more challenging conditions, thereby improving its generalization and robustness in watermark extraction.
In addition to using repeated 64-bit binary data as a watermark, we also experimented with enlarging each bit to form a watermark. The main purpose of this approach was to create watermarks that resemble QR codes, enabling us to test the watermark extractor’s ability to recover high-frequency data, particularly the boundary regions, after the image has been subjected to attacks. As it has already been demonstrated that HiNet lacks robustness when handling images subjected to surrogate attacks, we limit the comparison in this part to Zhang’s method.
By observing Figure 10, it can be seen that the black blocks corresponding to each bit are largely extracted accurately. However, the primary issue arises at the boundaries. This result is straightforward to interpret: since the surrogate model primarily learns image-to-image transformations, its focus is on low-frequency components, such as structure or contours. High-frequency components, like the boundaries, are more easily neglected, leading to the less accurate extraction of watermark boundary information compared to other parts of the image.

Figure 10.
Comparison of the extraction performance across different watermarking strategy [25] under surrogate attacks. The embedded watermark consists of a 64-bit binary sequence, where each bit is expanded into a 256 × 256 image.
Table 5 provides a quantitative comparison of different watermarking strategies. Peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are used to measure the visual quality degradation caused by watermark embedding. The proposed method achieves the highest PSNR in denoising tasks, indicating minimal impact on image quality. The NC value measures watermark extraction performance in the absence of attacks. As mentioned earlier, the only difference between HiDDeN [34] and HiDDeN† [34] is the inclusion of the noise layer. HiDDeN [34] refers to the version trained without a noise layer, while HiDDeN† [34] includes the noise layer during training. From the table, it can be observed that, without the noise layer, the watermark is easier to extract, making HiDDeN [34] more advantageous in terms of image quality. However, adding the noise layer enhances the extraction capability, meaning that HiDDeN† [34] provides superior watermark extraction performance, albeit with a slight reduction in image quality. Next, when compared to other methods, all methods, except HiDDeN [34] and HiDDeN† [34], achieve an NC of 0.9999, signifying nearly lossless watermark extraction. The columns labeled CNet, Res9, Res16, and UNet represent different surrogate attack models trained with L2 loss. The results demonstrate that only Zhang’s method [24] and the proposed approach remain robust against such attacks, while other watermarking strategies fail to recover the watermark.

Table 5.
The comparison of image quality and watermark extraction performance of different watermarking strategies under surrogate model attacks.
It is worth noting that HiNet [21] exhibits lower PSNR and SSIM scores. Further analysis suggests that this is due to the nature of the watermark image. HiNet [21] performs better with natural images, as their structure and frequency characteristics align with those of the host image. However, the binary watermark used in this study consists of high-frequency noise, which affects HiNet’s [21] embedding performance. To eliminate potential biases from watermark image quality, an alternative watermark more suitable for HiNet [21] was used in additional experiments. However, its robustness against surrogate attacks remained unchanged, confirming that HiNet [21] is inherently ineffective in countering such attacks.
5. Conclusions
The main contribution of this research lies in successfully introducing Swin-UNet to watermarking tasks and exploring its potential for watermark hiding. Compared to the traditional CNN networks used in previous studies, the attention mechanism of Swin-UNet significantly enhances the quality of watermarked images. Specifically, the peak signal-to-noise ratio of the watermarked images has improved by approximately 4 dB compared to Zhang’s method [25], demonstrating a notable enhancement in visual quality. This improved performance makes the watermark embedding process more effective and contributes to the increased invisibility of the watermark.
In the context of utilizing watermarks for image protection, Swin-UNet exhibits notable advantages. However, experiments indicate that directly substituting the embedding network with Swin-UNet reduces robustness against surrogate attack models. Nevertheless, this limitation can be mitigated through alternative techniques, such as data augmentation, to enhance robustness. By incorporating data augmentation during adversarial training, the model becomes more resilient to various attack scenarios, thereby improving the overall extraction performance. These findings suggest that Swin-UNet holds significant potential for further advancements in watermark embedding.
Future research can focus on enhancing the model’s robustness. The proposed methods primarily addresses robustness against surrogate attacks, but in real-world scenarios, adversaries may employ various techniques to compromise watermarks in images. Common attacks include cropping, scaling, compression, and more recent AI-based transformations that alter image elements, such as changing faces. Future studies could explore a reduction in the size of embedded watermark information to achieve increased robustness, employing strategies like repeated embedding or multi-dimensional embedding. Only when the watermark extractor can withstand a broader range of attacks will the technology’s broader applicability and success be ensured. Additionally, integrating Swin-UNet with other advanced deep learning architectures could significantly advance watermarking technology. In conclusion, the results of this study suggest that Swin-UNet is a promising solution for watermark embedding tasks, providing a strong foundation for future research and practical applications.
Author Contributions
Conceptualization, C.-H.U.; methodology, C.-H.U.; writing—original draft preparation, C.-H.U.; writing—review and editing, K.-C.C.; supervision, K.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The authors sincerely appreciate all technical support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the 26th International Conference on Neural Information Processing Systems-Volume 1, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Parisi, L.; Neagu, D.; Ma, R.; Campean, F. QReLU and m-QReLU: Two novel quantum activation functions to aid medical diagnostics. arXiv 2020, arXiv:2010.08031. [Google Scholar]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. Yolox: Exceeding yolo series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Rush, A.M. Huggingface’s transformers: State-of-the-art natural language processing. arXiv 2019, arXiv:1910.03771. [Google Scholar]
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–6 April 2017; pp. 506–519. [Google Scholar]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (sp), San Jose, CA, USA, 22–24 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 39–57. [Google Scholar]
- Uchida, Y.; Nagai, Y.; Sakazawa, S.; Satoh, S. Embedding watermarks into deep neural networks. In Proceedings of the 2017 ACM on International Conference on Multimedia Retrieval, Bucharest, Romania, 6–9 June 2017; pp. 269–277. [Google Scholar]
- Adi, Y.; Baum, C.; Cisse, M.; Pinkas, B.; Keshet, J. Turning Your Weakness Into a Strength: Watermarking Deep Neural Networks by Backdooring. arXiv 2018. [Google Scholar] [CrossRef]
- Dekel, T.; Rubinstein, M.; Liu, C.; Freeman, W.T. On the Effectiveness of Visible Watermarks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6864–6872. [Google Scholar] [CrossRef]
- Choi, K.-C.; Pun, C.-M. Difference Expansion Based Robust Reversible Watermarking with Region Filtering. In Proceedings of the 2016 13th International Conference on Computer Graphics, Imaging and Visualization (CGiV), Beni Mellal, Morocco, 29 March–1 April 2016; pp. 278–282. [Google Scholar] [CrossRef]
- Liu, Y. Multilingual denoising pre-training for neural machine translation. arXiv 2020, arXiv:2001.08210. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision And Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Alomoush, W.; Khashan, O.A.; Alrosan, A.; Attar, H.H.; Almomani, A.; Alhosban, F.; Makhadmeh, S.N. Digital image watermarking using discrete cosine transformation based linear modulation. J. Cloud Comput. 2023, 12, 96. [Google Scholar] [CrossRef]
- Islam, S.M.M.; Debnath, R.; Hossain, S.K.A. DWT Based Digital Watermarking Technique and its Robustness on Image Rotation, Scaling, JPEG compression, Cropping and Multiple Watermarking. In Proceedings of the 2007 International Conference on Information and Communication Technology, Dhaka, Bangladesh, 7–9 March 2007; pp. 246–249. [Google Scholar] [CrossRef]
- Kandi, H.; Mishra, D.; Gorthi, S.R.S. Exploring the Learning Capabilities of Convolutional Neural Networks for Robust Image Watermarking. Comput. Secur. 2017, 65, 247–268. [Google Scholar] [CrossRef]
- Vukotic, V.; Chappelier, V.; Furon, T. Are Deep Neural Networks good for blind image watermarking? In Proceedings of the 2018 IEEE International Workshop on Information Forensics and Security (WIFS), Singapore, 11–13 December 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Quan, Y.; Teng, H.; Chen, Y.; Ji, H. Watermarking Deep Neural Networks in Image Processing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1852–1865. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Deng, X.; Xu, M.; Wang, J.; Guan, Z. HiNet: Deep Image Hiding by Invertible Network. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 4713–4722. [Google Scholar] [CrossRef]
- Guan, Z.; Jing, J.; Deng, X.; Xu, M.; Jiang, L.; Zhang, Z.; Li, Y. DeepMIH: Deep Invertible Network for Multiple Image Hiding. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 372–390. [Google Scholar] [CrossRef] [PubMed]
- Tancik, M.; Mildenhall, B.; Ng, R. Stegastamp: Invisible hyperlinks in physical photographs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2117–2126. [Google Scholar]
- Wu, H.; Liu, G.; Yao, Y.; Zhang, X. Watermarking Neural Networks With Watermarked Images. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2591–2601. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Liao, J.; Zhang, W.; Feng, H.; Hua, G.; Yu, N. Deep model intellectual property protection via deep watermarking. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4005–4020. [Google Scholar] [CrossRef]
- Jain, N.; Joshi, A.; Earles, M. iNatAg: Multi-Class Classification Models Enabled by a Large-Scale Benchmark Dataset with 4.7 M Images of 2959 Crop and Weed Species. arXiv 2025, arXiv:2503.20068. [Google Scholar]
- Yang, R.; Zhang, S. Enhancing Retinal Vascular Structure Segmentation in Images with a Novel Design Two-Path Interactive Fusion Module Model. arXiv 2024, arXiv:2403.01362. [Google Scholar]
- Tian, Y.; Han, J.; Chen, H.; Xi, Y.; Ding, N.; Hu, J. Instruct-ipt: All-in-one image processing transformer via weight modulation. arXiv 2024, arXiv:2407.00676. [Google Scholar]
- Ju, R.-Y.; Chen, C.-C.; Chiang, J.-S.; Lin, Y.-S.; Chen, W.-H. Resolution enhancement processing on low quality images using swin transformer based on interval dense connection strategy. Multimed. Tools Appl. 2024, 83, 14839–14855. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Zhang, H.; Patel, V.M. Density-aware single image de-raining using a multi-stream dense network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 695–704. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 1833–1844. [Google Scholar]
- Zhu, J. HiDDeN: Hiding data with deep networks. arXiv 2018, arXiv:1807.09937. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).