Study on Influence of Grouting on Mechanical Characteristics and Stress Concentration in Hole-Containing Rock
Abstract
1. Introduction
2. Materials and Testing Methods
2.1. Marble Specimens
2.2. Test Equipment
3. Analysis of Test Results
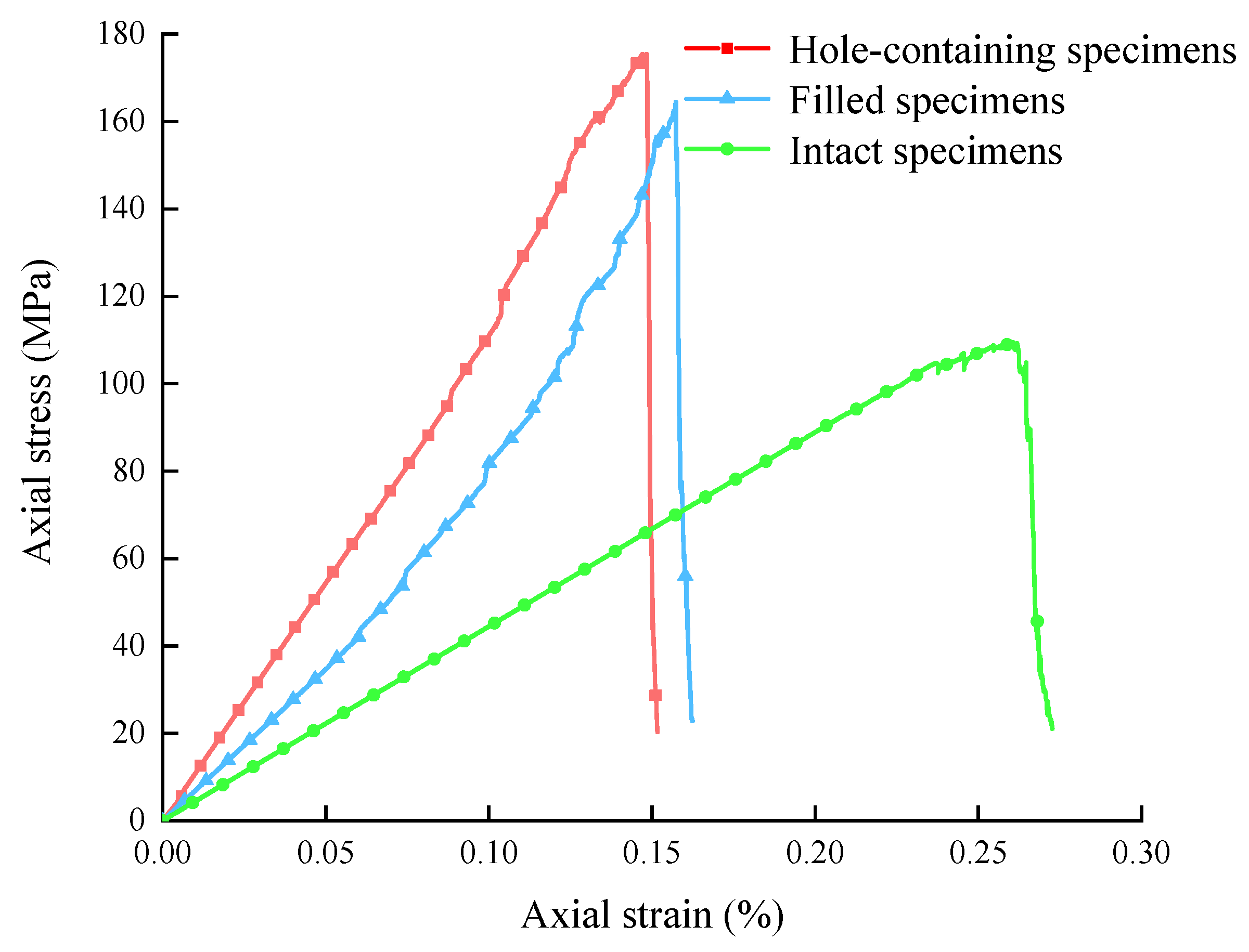
3.1. Stress–Strain Curve
3.2. Failure Mode
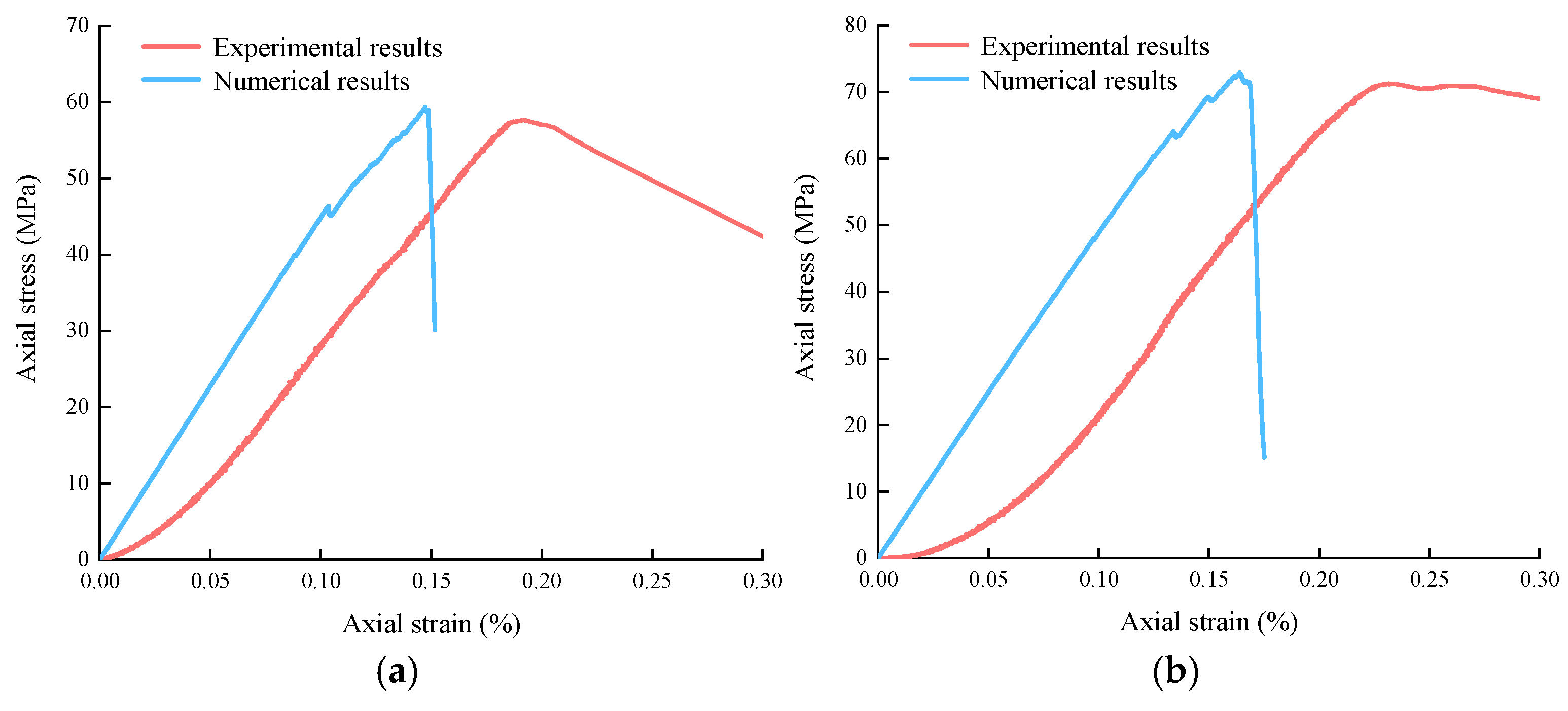
4. Numerical Simulation
4.1. Numerical Modeling
4.2. Model Parameter Calibration
5. Experimental Study with Numerical Methods
5.1. Adaptation Studies of Models
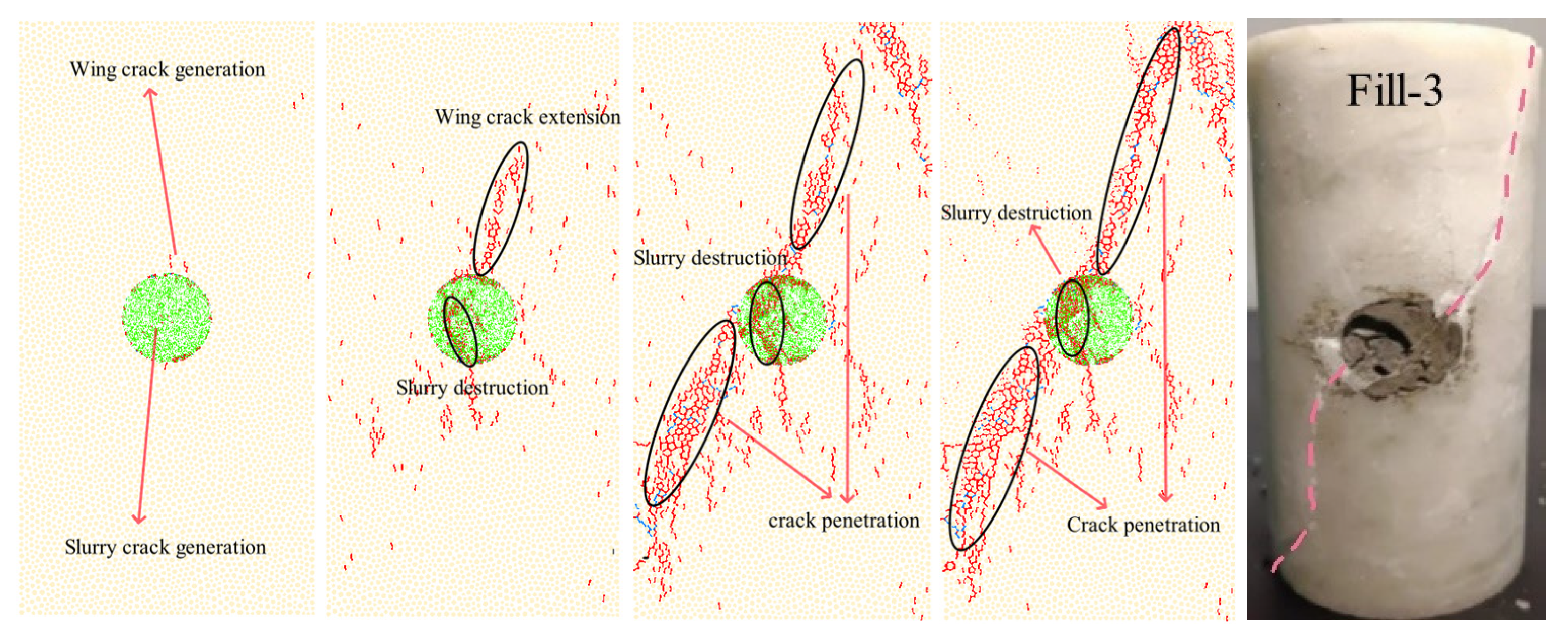
5.2. Failure Pattern
5.3. Crack Type and Number Analysis
6. Stress Analysis Around the Hole
6.1. Stress Problem of Plane Containing a Hole
6.2. Stress Monitoring
7. Conclusions
- (1)
- In terms of strength, the mean uniaxial compressive strength of cement paste-filled specimens increased by 22.38% compared with the unfilled specimens but remained significantly lower than that of the intact specimens. The residual strengths of the intact and cement paste-filled samples were nearly equal, while the residual strength of the hole-containing samples was almost negligible.
- (2)
- Regarding the failure mode, specimen damage primarily originated from the stress concentration area, which promoted crack extension and penetration, ultimately leading to failure. The final macroscopic cracks exhibited an inverted “Y” distribution. The failure mode of the cement paste-filled specimens closely resembled that of the intact specimens, transitioning from tensile to shear damage.
- (3)
- In the numerical simulation, microcracking in the hole-containing specimens initiated near the top and bottom ends of the circular hole. In contrast, the microcracks in the cement slurry-filled specimens first emerged around the filler. These microcracks then propagated axially towards both ends. Microcracking initiated at approximately 67% of peak stress in the hole-containing specimens, compared with 33% in the cement paste-filled specimens. The vast majority of microcracks in both specimens appeared after the peak strength was reached, and both were dominated by tensile microcracks.
- (4)
- Regarding stress concentration, the average stress levels in the designated monitoring area decreased sequentially for the hole-containing, cement slurry-filled, and intact specimens. The stress concentration factor decreased from 2.96 to 2.3 after filling. The cement paste filling shortened stress concentration duration, reduced its intensity, and enhanced material strength.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| R | Hole radius |
| q | Unidirectional pressure |
| θ | Angle with vertical direction |
| ρ | Boundary condition |
| R1 | Radius of outer boundary conditions |
| σθ | Maximum shear stress around hole |
| σc | Axial principal stress |
| k | Stress concentration factor |
| σyy | Average stress of marble grains in yy direction |
References
- Lajtai, E.Z. Brittle fracture in compression. J. Int. J. Fract. 1974, 10, 525–536. [Google Scholar] [CrossRef]
- Carter, B.J.; Lajtai, E.Z.; Petukhov, A. Primary and remote fracture around underground cavities. J. Int. J. Numer. Anal. Methods Geomech. 1991, 15, 21–40. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression. J. Int. J. Rock Mech. Min. Sci. 2009, 46, 239–249. [Google Scholar] [CrossRef]
- Yang, S.Q.; Lu, C.H.; Qu, T. Investigations of Crack Expansion in Marble Having a Single Pre-existing Hole: Experiment and Simulations. J. China Univ. Min. Technol. 2009, 38, 774–781. [Google Scholar]
- Yang, S.Q.; Jing, H.W.; Xu, T. Mechanical Behavior and Failure Analysis of Brittle Sandstone Specimens Containing Combined Flaws under Uniaxial Compression. J. Cent. South Univ. 2014, 21, 2059–2073. [Google Scholar] [CrossRef]
- Janeiro, R.P.; Einstein, H.H. Experimental study of the cracking behavior of specimens containing inclusions (under uniaxial compression). J. Int. J. Fract. 2010, 164, 83–102. [Google Scholar]
- Zhao, G.Y.; Wang, E.J.; Wu, H.; Qiu, J.; Dai, Y.W. Micro-fracture Evolution Rule of Sandstone Specimens with a Single Hole under Uniaxial Compression. J. Cent. South Univ. (Sci. Technol.) 2019, 50, 1891–1900. [Google Scholar]
- Li, C.J.; Li, X.B.; Li, D.Y. Particle Flow Analysis of Fracture Characteristics of Marble with a Single Hole. Chin. J. Eng. 2017, 39, 1791–1801. [Google Scholar]
- Liu, P.; Liu, Q.S.; Xia, M.T.; Luo, Y.; Chen, Z.T. Effect of Hole Shapes on Mechanical Behavior of Layered Rocks Using FDEM Numerical Method. J. Cent. South Univ. (Sci. Technol.) 2024, 55, 595–606. [Google Scholar]
- Li, D.Y.; Zhu, Q.Q.; Li, X.B. Research on the Effect of Cavity Shapes for the Progressive Failure and Mechanical Behavior of Marble. Chin. J. Undergr. Space Eng. 2018, 14, 58–66. [Google Scholar]
- Zhang, Q.W.; Gao, B.B.; Ma, L.J.; Yuan, D.S. Study on Crack Propagation in Sandstone Containing Double Circular Opening. Chin. J. Undergr. Space Eng. 2016, 12, 432–437. [Google Scholar]
- Zhou, Z.W.; Ma, W.B. Study on the Damage Mechanism of Rock-like Materials Containing Bicircular Holes under Uniaxial Compression. Chinese J. Appl. Mech. 2024, 1–12. [Google Scholar]
- Zhang, C.; Tang, J.X.; Teng, J.Y.; Li, C.L. Experimental Study of Influences of Pore Number and Pore Size on Mechanical Properties of Marble. Rock Soil Mech. 2017, 38, 41–50. [Google Scholar]
- Jespersen, C.; MacLaughlin, M.; Hudyma, N. Strength, deformation modulus and failure modes of cubic analog specimens representing macroporous rock. J. Int. J. Rock Mech. Min. Sci. 2010, 47, 1349–1356. [Google Scholar] [CrossRef]
- Lin, P.; Wong, R.H.; Tang, C.A. Experimental study of coalescence mechanisms and failure under uniaxial compression of granite containing multiple holes. J. Int. J. Rock Mech. Min. Sci. 2015, 77, 313–327. [Google Scholar] [CrossRef]
- Zhu, Q.Q.; Li, D.Y.; Li, X.B. Experimental Study on Failure and Mechanical Characteristics of Marble Containing a Prefabricated Elliptical Hole. Chin. J. Rock Mech. Eng. 2019, 38, 2724–2733. [Google Scholar]
- Zhu, T.T.; Jing, H.W.; Su, H.J.; Yin, Q. Experimental Investigation on Mechanical Behavior of Sandstone with Coupling Effects under Uniaxial Compression. J. China Coal Soc. 2015, 40, 1518–1525. [Google Scholar]
- Tang, J.X.; Liu, Q.; Dai, Z.Y.; Wang, Y.L. Research on Mechanical Properties and Failure Modes of Sandy Mudstone with Grouting Fractures. Chin. J. Undergr. Space Eng. 2021, 17, 1028–1037. [Google Scholar]
- Zhang, P.S.; Xu, D.Q.; Lu, T.H.; Hu, X.; Zhao, C.Y. Experimental Study of Seepage Characteristics Before and After Grouting and Mechanical Characteristics After Grouting of Fractured Sandstone. Rock Soil Mech. 2023, 44, 12–26. [Google Scholar]
- Wang, Z.; Li, L.; Wang, C.Y. Experimental Study on Failure of Cracked Rock-like Material After Grouting Reinforcement. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 957–963. [Google Scholar]
- Shen, J.; Liu, B.G.; Chen, J.; Li, Y.F.; Cheng, Y.; Song, Y. Experimental Study on Mechanical Properties of Diabase Fracture-grouting Mass. Chin. J. Rock Mech. Eng. 2020, 39, 2804–2817. [Google Scholar]
- Zuo, J.J.; Li, C.L.; Teng, J.Y.; Zhang, C. Experimental Study of the Influence of the Filling Material on the Mechanical Properties of Marble with Holes. Chin. J. Eng. 2018, 40, 776–782. [Google Scholar]
- Zhou, Y.N.; Zhu, Q.Q.; Li, D.Y.; Ma, C.D. Experimental Study on Mechanical and Failure Characteristics of Sandstone with a Filled Elliptical Hole. J. Railw. Sci. Eng. 2019, 16, 1938–1946. [Google Scholar]
- Zhang, K.; Liu, X.H.; Yang, H.X.; Fan, W.C. Experimental and Numerical Simulation of the Mechanical Characteristics of Rocks Containing Hole and Flaw After Grouting. Hydrogeol. Eng. Geol. 2019, 46, 79–85, 110. [Google Scholar]
- Lu, H.F.; Zhu, C.D.; Liu, Q.S. Study on Shear Mechanical Properties of Structural Planes Grouted with Different Materials. Chin. J. Rock Mech. Eng. 2021, 40, 1803–1811. [Google Scholar]
- Liu, X.W.; Wang, S.; Liu, B.; Liu, Q.S.; Yao, W.J.; Jia, C. Effect of Filling Grouting Material on Mechanical Properties and Mechanism of Rock-like Samples with Double-crack. Chin. J. Rock Mech. Eng. 2024, 43, 623–638. [Google Scholar]
- Shi, S.Y.; Hu, S.Y.; Liu, W.; Liang, D.X.; Qiao, H. Ordovician Paleokarst Cave System and It′s Controlling Factor in Xekar, Tarim Basin. Chin. J. Nat. Gas Geosci. 2014, 25, 167–177. [Google Scholar]
- Howland, R.C. On the stresses in the neighbourhood of a circular hole in a strip under tension. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character. 1930, 229, 49–86. [Google Scholar]
- Zhang, G.S.; Xiao, M.L.; Zhang, Y.D.; Liu, H.Z.; Zhuo, L.; Xie, H.Q. Experimental and numerical study on the mechanical properties of compressively precracked sandstone repaired by grouting. J. Constr. Build. Mater. 2022, 350, 128816. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A Clumped Particle Model for Rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Park, J.W.; Song, J.J. Numerical Simulation of a Direct Shear Test on a Rock Joint Using a Bonded-particle Model. Int. J. Rock Mech. Min. Sci. 2009, 46, 1315–1328. [Google Scholar] [CrossRef]
- Li, W.; Shaikh, F.U.; Wang, L.; Lu, Y.; Wang, B.; Jiang, C.; Su, Y. Experimental study on shear property and rheological characteristic of superfine cement grouts with nano-SiO2 addition. J. Constr. Build. Mater. 2019, 228, 117046. [Google Scholar] [CrossRef]
- Chen, P.Y.; Kong, Y.; Yu, H.M. Research on the Calibration Method of Microparameters of a Uniaxial Compression PFC~(2D) Model for Rock. Chin. J. Undergr. Space Eng. 2018, 14, 1240–1249. [Google Scholar]
- Hao, B.Q.; Zhang, C.S.; Wang, C.L.; Ren, C. Study on Determination Micro-parameters of Rock PFC~(2D) Model. Coal Sci. Technol. 2022, 50, 132–141. [Google Scholar]
- Tang, C.A.; Wong, R.H.; Chau, K.T.; Lin, P. Modeling of compression-induced splitting failure in heterogeneous brittle porous solids. J. Eng. Fract. Mech. 2005, 72, 597–615. [Google Scholar] [CrossRef]
- Yang, S.Q.; Liu, X.R.; Li, Y.S. Experimental Analysis of Mechanical Behavior of Sandstone Containing Hole and Fissure under Uniaxial Compression. Chin. J. Rock Mech. Eng. 2012, 31, 3539–3546. [Google Scholar]
- Li, D.; Zhu, Q.; Zhou, Z.; Li, X.; Ranjith, P.G. Fracture analysis of marble specimens with a hole under uniaxial compression by digital image correlation. J. Eng. Fract. Mech. 2017, 183, 109–124. [Google Scholar] [CrossRef]
- Wei, M.; Qiao, L.; Li, L.; Li, Q.; Chen, L. Crack coalescence and failure behaviors in slate specimens containing a circular cavity and a pre-existing flaw pair under uniaxial compression. J. Theor. Appl. Fract. Mech. 2024, 134, 104721. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Mechanism of brittle fracture of rock: Part I—Theory of the fracture process. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1967, 4, 395–406. [Google Scholar] [CrossRef]
- Zhang, D.F.; Zhu, W.S.; Li, S.C.; Guo, Y.S. Influence of Confining Pressure and Fissure Water Pressure on Initial Opening for Ellipse Fracture. Chin. J. Rock Mech. Eng. 2004, 23, 4721–4725. [Google Scholar]
- Pu, C.Z.; Yang, S.J.; Zhang, C.Y. Fracture Mechanism of Pre-cracked Specimens Influenced by Opening Width. Chin. J. Geotech. Eng. 2019, 41, 1836–1844. [Google Scholar]










| Number | Peak Strength, MPa | Average Peak Intensity, MPa | Peak Strain, % | Average Peak Strain, % | Average Modulus of Elasticity, GPa | Average Residual Strength, MPa |
|---|---|---|---|---|---|---|
| Int-1 | 131.85 | 131.91 | 0.338 | 0.325 | 51.31 | 28.19 |
| Int-2 | 129.35 | 0.317 | ||||
| Int-3 | 134.53 | 0.321 | ||||
| Fla-1 | 75.39 | 73.78 | 0.291 | 0.265 | 45.04 | 20.09 |
| Fla-2 | 74.69 | 0.273 | ||||
| Fla-3 | 71.27 | 0.232 | ||||
| Fill-1 | 57.64 | 60.28 | 0.192 | 0.195 | 41.89 | 2.65 |
| Fill-2 | 60.29 | 0.199 | ||||
| Fill-3 | 62.93 | 0.194 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Density (kg·m−3) | 2700.00 | Porosity | 0.36 |
| Particle size ratio | 1.66 | Radius multiplier | 1.0 |
| Minimum particle size (mm) | 0.40 | Parallel bond modulus (GPa) | 33.2 |
| Particle contact modulus (GPa) | 33.2 | Parallel bond stiffness ratio | 3.5 |
| Particle contact stiffness ratio | 3.5 | Parallel bond normal strength (MPa) | 58 |
| Friction coefficient | 0.4 | Parallel bond tangential strength (MPa) | 62 |
| Parameter | Peak Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|
| Laboratory test | 131.85 | 49.34 |
| Simulation test | 130.12 | 50.65 |
| Error | 1.31% | 2.66% |
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| q | 0 | −q | −2q | −3q |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Kang, Z.; Qiu, S.; Yan, L.; Peng, J. Study on Influence of Grouting on Mechanical Characteristics and Stress Concentration in Hole-Containing Rock. Appl. Sci. 2025, 15, 5245. https://doi.org/10.3390/app15105245
Yang Y, Kang Z, Qiu S, Yan L, Peng J. Study on Influence of Grouting on Mechanical Characteristics and Stress Concentration in Hole-Containing Rock. Applied Sciences. 2025; 15(10):5245. https://doi.org/10.3390/app15105245
Chicago/Turabian StyleYang, Yanshuang, Zhaopeng Kang, Shili Qiu, Lei Yan, and Jiancheng Peng. 2025. "Study on Influence of Grouting on Mechanical Characteristics and Stress Concentration in Hole-Containing Rock" Applied Sciences 15, no. 10: 5245. https://doi.org/10.3390/app15105245
APA StyleYang, Y., Kang, Z., Qiu, S., Yan, L., & Peng, J. (2025). Study on Influence of Grouting on Mechanical Characteristics and Stress Concentration in Hole-Containing Rock. Applied Sciences, 15(10), 5245. https://doi.org/10.3390/app15105245






