Abstract
Object detection in remote sensing imagery plays a pivotal role in various applications, including aerial surveillance and urban planning. Despite its significance, the task remains challenging due to cluttered backgrounds, the arbitrary orientations of objects, and substantial scale variations across targets. To address these issues, we proposed RFE-FCOS, a novel framework that synergizes rotation-invariant feature extraction with adaptive multi-scale fusion. Specifically, we introduce a rotation-invariant learning (RIL) module, which employs adaptive rotation transformations to enhance shallow feature representations, thereby effectively mitigating interference from complex backgrounds and boosting geometric robustness. Furthermore, a rotation feature fusion (RFF) module propagates these rotation-aware features across hierarchical levels through an attention-guided fusion strategy, resulting in richer, more discriminative representations at multiple scales. Finally, we propose a novel dual-aspect RIoU loss (DARIoU) that simultaneously optimizes horizontal and angular regression tasks, facilitating stable training and the precise alignment of arbitrarily oriented bounding boxes. Evaluated on the DIOR-R and HRSC2016 benchmarks, our method demonstrates robust detection capabilities for arbitrarily oriented objects, achieving competitive performance in both accuracy and efficiency. This work provides a versatile solution for advancing object detection in real-world remote sensing scenarios.
1. Introduction
With the rapid advancement of technology, computer vision, especially object detection, has become an essential field with significant applications in various areas of daily life [1,2,3,4,5] thanks to improved algorithms and computational power. Important examples include autonomous driving systems and medical image analysis, highlighting the broad societal and technological impacts of object detection. Furthermore, as drones become more widely utilized, object detection in remote sensing imagery has become a prominent research area, significantly contributing to various fields, including the understanding of natural processes and environmental phenomena [6,7].
Recent developments in deep learning, particularly the widespread adoption of convolutional neural networks (CNNs), have greatly improved performance in various computer vision tasks, including object detection. Numerous sophisticated methods have emerged, typically classified into two categories based on their structural differences: one-stage and two-stage detection techniques. Two-stage detectors, such as faster R-CNN [8], Mask R-CNN [9], and cascade R-CNN [10], initially propose candidate regions through a region proposal network (RPN) and subsequently refine these regions using classification and regression. Although these approaches achieve higher accuracy, they usually require substantial computational resources and processing time. On the other hand, one-stage detectors, including YOLO [11] and SSD [12], directly predict bounding boxes and class labels simultaneously, offering faster detection at the expense of lower accuracy in complex scenarios. Among the one-stage methods, FCOS [13] (fully convolutional one-stage object detection) introduces an innovative, anchor-free detection approach, as shown in Figure 1. This method directly predicts object locations and categories through fully convolutional layers at every pixel location, which achieves great results in many scenarios. Nonetheless, certain challenges persist, particularly in identifying rotated objects within remote sensing images. Compared to ground-level images, remote sensing images often exhibit characteristics such as the (1) arbitrary direction of the target arrangement, (2) interference from cluttered backgrounds, and (3) both inter-class similarity and intra-class diversity. To address these unique challenges, current research extensively focuses on specialized techniques such as rotated representations and rotation-invariant feature learning. Specifically, oriented bounding boxes (OBBs), which include an angular parameter , offer significantly improved accuracy compared to traditional horizontal bounding boxes (HBBs).
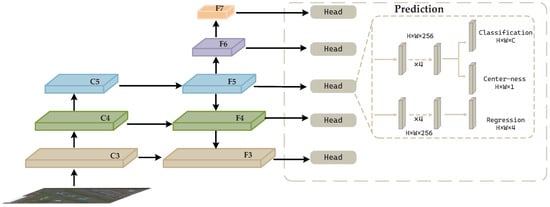
Figure 1.
The overall architecture of FCOS. denotes the feature maps from backbone network at stage i and denotes the feature level used for final prediction. The decoupled detection head consists of separate branches for classification, bounding-box regression, and centerness prediction, where the centerness branch outputs a score that helps suppress low-quality predictions.
To address these challenges above, we introduce an improved version of the FCOS model, named rotated feature enhancement FCOS (RFE-FCOS). Our approach integrates two specially designed modules: a rotation-invariant learning module (RIL) and a rotation-invariant feature fusion module (RFE), which enhance the model’s adaptability to different object orientations by combining feature information across multiple rotation angles. The combined use of these modules allows the model to extract comprehensive rotation-invariant features, leading to a significant improvement in detection accuracy. Additionally, we propose a novel loss function called dual-aspect RIoU loss, which simultaneously leverages rotational and horizontal feature information to optimize the model performance. Extensive experiments conducted on the DIOR-R and HRSC2016 datasets validate the effectiveness of our method, demonstrating substantial enhancements in rotated object detection accuracy.
The primary contributions of this paper are as follows.
- •
- A rotation-invariant module and a rotated feature fusion module are proposed to enhance the adaptability of FCOS to detect rotated objects, which can better counter the interference of complex backgrounds on foreground objects.
- •
- The dual-aspect RIoU loss function is introduced to improve detection performance by integrating both rotational and horizontal information, addressing the complexities introduced by arbitrary orientations.
- •
- Extensive experiments conducted on the DIOR-R [14] and HRSC2016 [15] datasets validate the superiority of the proposed method.
2. Related Works
2.1. Anchor-Free Methods for Remote Sensing
Traditional anchor-based object detection methods, which rely on predefined anchor boxes, have inherent limitations, including imbalanced sampling of positive and negative samples and significant computational complexity. To overcome those drawbacks, anchor-free methods have been proposed, eliminating predefined anchors and providing more flexibility and efficiency. Consequently, anchor-free methods have gained increasing attention, with numerous innovative approaches emerging in recent years. CornerNet [16], an early anchor-free method, detects objects by regressing their top–left and bottom–right corners, subsequently pairing them using a distance-based metric. CenterNet [17] improves upon this by introducing additional predictions of object center points, enhancing detection accuracy through geometric validation. ExtremeNet [18] further advances this concept by identifying four extreme points (top, bottom, left, right) alongside the center point and employing a center-aware grouping strategy for precise instance assembly. FCOS significantly simplifies detection by performing pixel-level bounding box regression and classification, achieving high accuracy and efficiency. RepPoints [19] employs deformable convolutions to dynamically select representative points, which subsequently form bounding boxes through geometric transformations. CentripetalNet [20] introduces a novel method for matching corners, establishing connections based on their positional relationships, which helps overcome the uncertainties seen in previous methods. CPNDet [21] identifies candidate bounding boxes by connecting keypoints and applies dual classifiers to enhance the accuracy and reduce false positives.
2.2. Rotation-Invariant Learning
The Fourier transform, one of the earliest methods for achieving rotation invariance, has been extensively used in computer vision due to its ability to preserve image features in the frequency domain under rotation [22,23]. Then, The SIFT algorithm [24], introduced by Lowe, further refines this by assigning orientations to keypoints, making it robust to both rotation and scale variations. Nowadays, with the advancement of modern technologies, especially the development of CNN, numerous new methods for rotation-invariant learning have been developed. RRPN [25] integrates rotation RoI pooling to align features with oriented bounding boxes (OBBs), mitigating direction mismatches and facilitating accurate detection. The RoI Transformer [26] applies spatial transformation networks to predict and correct region orientations dynamically, enhancing detection precision. ReDet [27] leverages rotation-equivariant networks that robustly extract rotation-invariant features, thereby improving the reliability of object orientation predictions. Additionally, rotation-invariant RoI Align further facilitates adaptive extraction of features tailored to rotated bounding boxes. Moreover, group convolutional networks [28] (G-CNN) implement group-equivariant operations to preserve geometric relationships under rotation transformations, thus improving the network performance in detecting rotated objects.
2.3. Loss Functions for Bounding Box Regression
losses, such as L1 Loss and L2 Loss, primarily optimize the target by minimizing the positional difference between the predicted box and the target box. Considering their sensitivity to outliers and anomalies, Girshick et al. [29] introduced Smooth L1 Loss, which alleviates gradient explosion while retaining sensitivity to large errors. Nevertheless, none of these losses explicitly consider geometric relationships, making them less suitable for bounding-box regression in complex object detection scenarios. Consequently, Intersection over Union (IoU)-based loss functions, which directly consider the overlap between two bounding boxes, have become more widely adopted in object detection. The IoU loss [30], introduced as the earliest IoU-based loss function, enhances the detection accuracy by minimizing the difference between the intersection and union ratio of the ground truth and predicted boxes. Although IoU loss effectively measures the overlap between two bounding boxes, it becomes ineffective when there is no overlap, degenerating to a constant value of 1. This limitation hampers the ability to update the network parameters efficiently, thus impacting training efficiency. To overcome this challenge, enhanced IoU losses such as DIoU [31], GIoU [32], and CIoU [33] have been developed by introducing additional penalty terms that address cases with no overlap.
Among these, CIoU loss extends DIoU loss by integrating factors such as IoU, centroid distance, and aspect ratio, thereby improving bounding box regression accuracy. It has been proven to improve the accuracy of bounding-box regression by taking into account multiple geometric factors, such as location, shape, and size, which is particularly advantageous for complex object detection tasks.
3. Rotational Feature Enhancement FCOS
In this section, we present the architecture of our proposed RFE-FCOS model, with an overview of the framework shown in Figure 2. We begin by detailing the rotation-invariant learning (RIL) module for extracting rotation-invariant features in Section 3.1, followed by an introduction to the rotation feature fusion (RFF) module in Section 3.2. Next, we describe our novel DARIoU loss function in Section 3.3, and finally, we conclude with the objective function in Section 3.4.
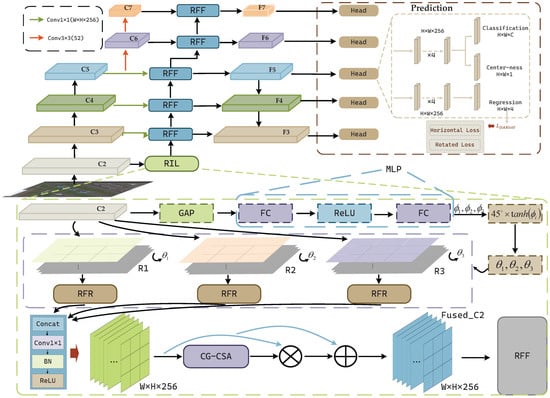
Figure 2.
Overall architecture of our proposed RFE-FCOS, which integrates the backbone network, rotational feature enhancement (RIL and RFF) modules, FPN, and the prediction head. Starting from an input image, the backbone generates multi-scale feature maps. Next, the shallow feature map C2 is directed to the RIL module for rotation-invariant learning, while the remaining deep feature are blended with the extracted rotation features in RFF module before being passed to the FPN. In both the classification and regression branch, centerness and classifier predictions follow FCOS-O defaults, while the localization branch utilizes the proposed DARIoU loss for improved OBB regression. The RFR and CG-CSA components are utilized as sub-modules within the RIL module.
3.1. Rotation-Invariant Learning Module
In the process of multi-scale feature extraction, a common strategy is to disregard shallow features in order to minimize computational complexity. However, shallow features are particularly effective at capturing edge and texture information, which is critical to learning rotation invariance. Motivated by this observation, our approach incorporates a rotation operation applied to the feature map C2, which facilitates the extraction of rotation-invariant features, thereby enhancing the robustness of the network to geometric transformations.
Given the shallow feature C2 , we first generate three adaptive rotation angles through a lightweight angle prediction module. Specifically, the global average pooling (GAP) condenses spatial information into a channel descriptor , which is then passed through a compact multilayer perceptron (MLP) composed of two fully connected layers. The resulting output is further constrained by a scaled activation (bounded by ) to ensure that rotation angles remain within a reasonable range. Equation (1) shows the process of generating the adaptive rotation angles.
where denote the learned rotation angles, adaptively determined from the input feature statistics. With the learned angles , we perform explicit rotation transformations on C2 through a grid sampling procedure, producing three rotated feature maps :
where GS denotes the grid sampling operation, and the affine rotation matrix is defined as:
Each rotated feature is further individually processed by our proposed rotated feature refinement (RFR) module (Section 3.1.1), which aims to mitigate redundant channels while accentuating rotation-sensitive details, thereby delivering more discriminative representations for subsequent processing. The resulting refined characteristics are concatenated along the channel dimension, forming an intermediate aggregated characteristic . Subsequently, a convolution is employed to revert the original channel dimensions, yielding the fused feature map , which not only preserves the global semantic information but also effectively captures the local rotational variations at multiple directions and scales.
To selectively highlight informative features crucial for rotation invariance, is conveyed to our Cross-Gated Channel-Spatial Attention (CG-CSA) module (Section 3.1.2), where cross-gating reinforces complementary interactions between channel and spatial attention maps. As a result, the module produces an attention feature map , which is element-wise multiplied with to emphasize essential rotational cues. Ultimately, a residual link reintegrates the original with the attention-weighted features, maintaining global semantic coherence while enhancing rotation-invariant representations. Equation (4) illustrates the outcome of the RIL module.
where the resulting , enriched by rotation-aware attention guidance, is forwarded to the subsequent rotation feature fusion (RFF) module for multi-scale integration. The structure of our RIL module is presented in Figure 2.
3.1.1. Rotated Feature Refinement Module
The direct concatenation of rotated feature maps inevitably introduces redundant channel information and limits the discriminability of features. To alleviate this, we propose the rotated feature refinement (RFR) module, designed to refine each rotated feature individually.
Specifically, each rotated feature map first undergoes a convolution for channel reduction, pruning superfluous dimensions while retaining the most salient rotation-sensitive cues. Then, the reduced feature map is directed into three parallel branches of depthwise separable convolutions, each set with a distinct dilation rate (1, 2, and 3). This multi-branch architecture captures multi-scale rotational fluctuations, as distinct dilation factors correlate to diverse receptive field dimensions. Utilizing depthwise separable convolutions, we concurrently reduce computing demands while maintaining intricate spatial details—both crucial for precisely capturing rotation-specific attributes. The outputs from these parallel branches are then concatenated, yielding a composite feature map that integrates diverse rotational patterns.
Finally, a convolution consolidates the concatenated channels into , followed by a residual connection that adds the intermediate feature back to the refined output. This design retains essential semantic cues, stabilizes training, and boosts rotation-specific representations without introducing excessive redundancy. The structure and detailed process of our RFR module are presented in Figure 3.
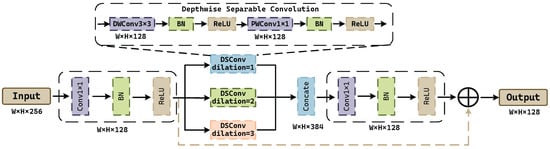
Figure 3.
The structure of the RFR module.
3.1.2. Cross-Gated Channel-Spatial Attention Module
To adaptively highlight critical rotation-related regions and channels, we propose the cross-gated channel-spatial attention (CG-CSA) module. Given the input feature map , we concurrently compute the channel attention map and the spatial attention map through separate attention pathways:
where denotes sigmoid activation. Furthermore, we introduce the cross-gating operation to enhance the synergy between channel and spatial attention branches. Specifically, calculating the mean of across the spatial dimension produces the gating factor , utilized to modify the channel attention; concurrently, calculating the mean of across the channel dimension generates the gating factor , employed to adjust the spatial attention. Equations (7) and (8) demonstrate the generation of the gating factors and the modified attention maps.
Ultimately, the updated channel attention and spatial attention are multiplied element-wise to produce an integrated attention representation :
where is directly treated as the output of the CG-CSA module. This module utilizes cross-gating to strengthen sensitive information in each attention branch, efficiently diminishing unnecessary features and highlighting rotation-critical signals, hence improving the discriminability and robustness of the resulting feature. The structure of our CG-CSA module is presented in Figure 4.
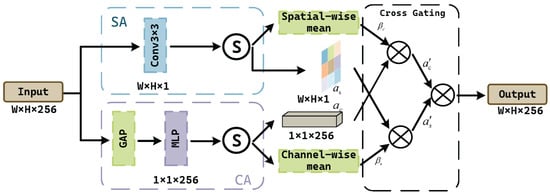
Figure 4.
The structure of the CG-CSA module.
3.2. Rotation Feature Fusion Module
To enable subsequent feature maps to learn rotational features, we apply pooling operations to the fused feature map , aligning it with deeper feature maps (where ). For the aligned , we combine it with by channel-wise concatenation, merging shallow spatial details from pooled features with deep semantic information. These operations are formally represented as follows.
To selectively emphasize these rotation-critical patterns, an additional convolution with sigmoid activation is used on to generate a spatial attention mask . Finally, the mask is multiplied in element terms with the original feature map and combined with its residual connection. Equations (12) and (13) demonstrate the generation of the attention mask and the final result.
where the enhanced features propagate directly to subsequent network layers, with the structure of the RFF module shown in Figure 5.
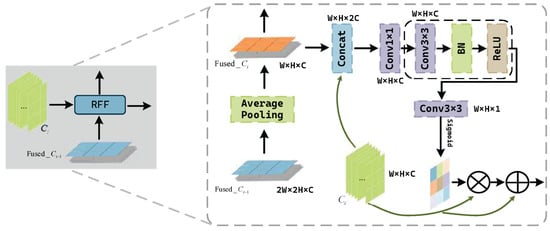
Figure 5.
The structure of the RFF module.
3.3. Dual-Aspect RIoU Loss
Traditional object detection methods primarily focus on the processing of horizontal bounding boxes, which require the prediction of only four parameters . In contrast, remote sensing images often feature objects that appear in various orientations, necessitating the inclusion of rotational parameters such as . This introduces a more complex multi-dimensional regression task, where the model must handle both the dimensions of the horizontal bounding box and the angle of rotation.
To address the complexities introduced by arbitrary orientations, Raisi et al. [34] extended the GIoU loss by incorporating a rotated bounding box representation, which allows for the better handling of rotated targets. Similarly, we propose a loss function that integrates the losses from both the horizontal bounding box and the rotated bounding box dimensions. This design enables the model to first minimize the discrepancies in the horizontal bounding box and then focus on optimizing the rotation angle. The process is presented in Figure 6 and our loss function is designed as follows:
where CRIoU is a variant of the CIoU loss, adapted to include rotational information, and the term represents the penalty component that combines both horizontal and rotational intersection over union (), offering complementary insights to improve prediction accuracy. This dual-component loss provides complementary insights, enhancing the accuracy of the bounding box predictions. The CRIoU loss function is formulated as follows:
where is the centroid distance between the predicted and ground truth boxes, c is the diagonal length of the minimum enclosing box, and the aspect ratio difference term v and the balance factor are determined as follows.
where is adapted to help with the regression of the oriented bounding box. The penalty term is designed to combine the influence of both horizontal and rotational IoU components and is defined as:
where and are hyperparameters that regulate the relative significance of the horizontal and rotational IoU. The penalty term allows the network to adjust its focus between the horizontal and rotational components based on their alignment. In particular, when either or is close to 1, the effort of the penalty term diminishes, resulting in the loss function degenerating to the CRIoU. In this scenario, only minor refinements to the bounding box are required to achieve a satisfactory result. Conversely, when both and are significantly low, the penalty term exerts a stronger influence, causing the network to make more substantial adjustments to both the horizontal and rotated bounding box parameters, thereby accelerating the improvement process. Figure 6 shows the content of our proposed loss function.
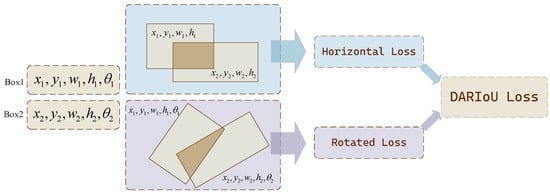
Figure 6.
The concise summary of the proposed loss function. The goal is to minimize the loss in both horizontal and rotational dimensions. As can be imagined, when the two bounding boxes align horizontally, achieving an alignment in the rotational aspect becomes simpler, as only the angle requires adjustment.
3.4. Objective Function
As depicted in Figure 2, the network structure comprises three distinct output branches: the classification branch, the centerness branch, and the regression branch. In the regression branch, we incorporate the proposed DARIoU loss function to optimize the bounding box regression task. The classification and centerness losses are computed using the focal loss and binary cross-entropy loss, respectively, as defined in the baseline model. The final objective function is defined as follows:
where represents the number of positive samples, represents the predicted category score, with indicating the corresponding true category label. signifies the classification of the target as either foreground or background, denoted by the values 1 and 0, respectively. Additionally, refers to the predicted bounding box information, and corresponds to the true bounding box information; indicates the predicted centrality score, with representing the true centrality score.
4. Datasets and Experimental Settings
4.1. Dataset
DIOR-R: The DIOR-R dataset is a large-scale dataset designed for remote sensing object detection, featuring a wide range of object classes commonly found in satellite and aerial imagery. This dataset contains 20 object categories across 23,463 images with 192,472 labeled instances. It includes 5862 images for training, 5863 for verification, and 11,738 for testing, allowing researchers to systematically evaluate the generalization and robustness of detection models.
HRSC2016: The HRSC2016 dataset focuses on ship detection in high-resolution remote sensing images, includes 1061 annotated images—617 for training and 444 for testing. Image resolutions range from 300 × 300 to 1500 × 900 pixels, yielding 2976 labeled instances within a single “ship” category, which captures ships of varying sizes, shapes, and orientations.
4.2. Experimental Platform and Evaluation Metrics
Sometimes, the performance of the model can be influenced to varying degrees by different experimental configurations. Table 1 summarizes the configuration used in our experiments.

Table 1.
Experiment environment for model training.
In our experiments, we employed two datasets with distinct hyperparameter configurations. The detailed settings are presented in Table 2.

Table 2.
Parameter settings for two datasets.
During DIOR-R training, the learning rate was reduced ten-fold in epochs 8 and 11, while for HRSC2016, the same reduction occurred in epochs 24 and 33.
For performance evaluation, we employed three standard object-detection metrics: frame per second () to gauge inference speed, average precision () to quantify detection accuracy for each category, and mean average precision ()—the average of all APs—to provide an overall measure of the multiclass performance of our model.
The calculation equations of , , and are defined as follows:
where represents the total number of frames, represents the total time, and N represents the total number of categories; precision (P) and recall (R) are calculated as:
where is the count of true positives, signifies false positives, and denotes false negatives, referring to detections the model fails to identify.
5. Experimental Results and Analysis
5.1. Comparative Experiment
(1) Comparative analysis on DIOR-R: We compare our method against six advanced techniques on the DIOR-R dataset, as shown in Table 3. Our models, using ResNet50-FPN and ResNet101-FPN as backbones, achieve mAP scores of 61.88% and 62.35%, respectively, surpassing all other methods listed. Notably, with ResNet101-FPN, our method achieves the best AP in nine categories and the second-best in four. Figure 7 illustrates the qualitative performance of our method in detecting rotated objects against challenging backgrounds, which effectively demonstrates the robustness and practicality of our approach. Meanwhile, we also observe that in a few specific categories, our method exhibits slightly lower performance compared to the original baseline. To better understand and address this issue, we conduct an in-depth analysis in the subsequent sections, exploring the potential causes and discussing possible directions for improvement.

Table 3.
Comparison results on DIOR-R. The cells highlighted in red and blue indicate the highest and second-highest values in each column, respectively.
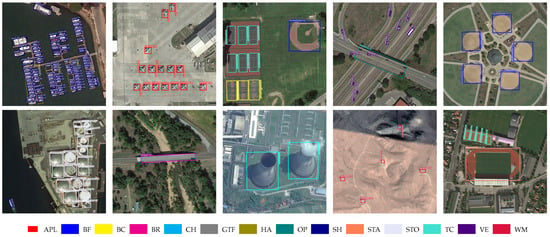
Figure 7.
Visualization results of our method for DIOR-R.
(2) Comparative analysis on HRSC2016: Similarly, we conducted a comparative analysis on the HRSC2016 dataset, with the results presented in Table 4. Our method achieved AP scores of 90.03% and 90.20% with ResNet50-FPN and ResNet101-FPN backbones, respectively, surpassing the performance of all other methods. Despite the significant aspect ratio variations in the HRSC2016 dataset, our method consistently produced accurate bounding box predictions. Selected results are shown in Figure 8.

Table 4.
Comparison results on HRSC2016. The cells highlighted in red and blue indicate the highest and second-highest values in each column, respectively.

Figure 8.
Visualization results of our method for HRSC2016.
The Figure 9 presents the confusion matrix detailing the prediction outcomes for each individual category. Regarding the categories where our model exhibits relatively weaker performance, such as APO and GF, we hypothesize that the rotation features we extracted may not positively contribute to the detection of these categories. Figure 10 shows sample images from these categories and provides a detailed explanation of this observation.
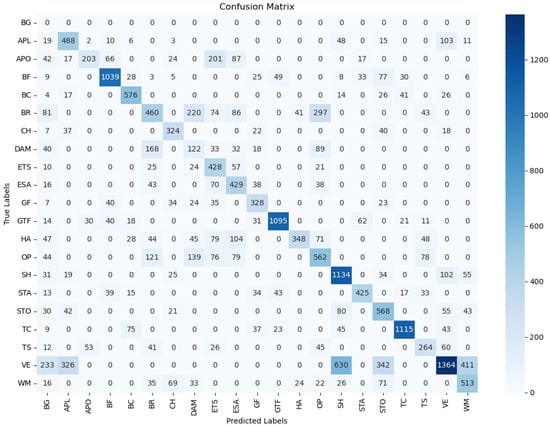
Figure 9.
Confusion matrix of multi-class classification performance on the DIOR-R dataset.

Figure 10.
Sample images from the APO and GF categories.
In Figure 9, the confusion matrix—extended to include all 21 output classes (with ‘no prediction’ as class 0)—provides a fine-grained evaluation of the performance per category of our model. The pronounced diagonal dominance attests to the strong discriminative power of our network, while off-diagonal entries reveal residual confusions, most notably between visually or semantically adjacent classes (e.g., DAM [Dam] vs. BR [Bridge] vs. OP [overpass]).
Figure 10 shows two sample images from the APO and GF categories. The APO category consists of long, strip-like airplane runways in the sample images, which blend seamlessly with the surrounding environment, making it difficult for the model to accurately distinguish them. Detection performance for this category is generally poor across various models, and the rotation information introduced by our method may have disrupted the effectiveness of this structure, further complicating the detection process. As for the GF category, the detection issues likely arise from the irregular and complex shape of golf courses. The rotation features do not align well with these complex layouts, making it challenging for the model to accurately detect the targets.
5.2. Ablation Experiment
To assess the contribution of each component in our proposed method, we performed a series of ablation experiments. Notably, the RIL and RFF modules were integrated to form the rotation feature enhancement module, and the analysis was conducted as a whole.
(1) Effectiveness of RIL+RFF: To verify the efficacy of our rotation feature enhancement module, we integrated the RIL and RFF modules into two baseline models and evaluated their performance on the DIOR-R dataset. The results in Table 5 show that the two models achieved mAP scores of 60.66% and 58.89%, representing improvements of 2.24% and 1.34% over the original method, respectively. These results clearly demonstrate that our module significantly enhances the model’s ability to adapt to rotational features.

Table 5.
Ablation studies of different components on the DIOR-R. The values in bold indicate the highest performance in each column.
(2) Effectiveness of Dual-Aspect RIoU Loss: To investigate the effectiveness of our DARIoU Loss, we replaced the IoU loss from FCOS-O with our loss function, while not making any other modifications. The results on the DIOR-R dataset, presented in Table 5, show that the two models achieved increases of 1.41% and 0.67% in mAP over the baseline model, respectively. These results confirm the effectiveness of our approach in addressing the rotation box regression task. In addition, we compared DARIoU with several advanced regression loss functions (IoU loss, GIoU loss, DIoU loss, and CIoU loss) on the HRSC2016 dataset. As shown in Table 6, DARIoU outperforms the other loss functions, achieving 89.92% AP50, beating the others by 0.81%, 0.40%, 0.06%, and 0.28% mAP, respectively. Furthermore, the accuracy on AP95 improved by 2.5%, significantly outperforming other methods.

Table 6.
Ablation studies of different bounding box regressions on HRSC2016 in terms of , and metrics. The values in bold indicate the highest performance in each column.
To further evaluate the effectiveness of the DARIoU, we compared its performance with the baseline (IoU loss) over the training epochs for both the HRSC2016 and DIOR-R datasets, as shown in Figure 11. On the HRSC2016 dataset, the curve for DARIoU exhibits a much smoother progression in AP50, with a faster and more consistent increase throughout the training. Similarly, for the DIOR-R dataset, DARIoU results in a steadier and faster rise in mAP across 12 epochs, achieving a higher final value compared to the baseline. These observations indicate that DARIoU not only accelerates convergence but also leads to more stable and reliable performance during training.
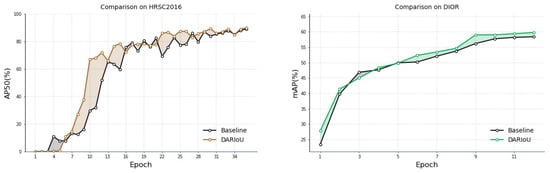
Figure 11.
Training trajectories of AP50 (HRSC2016) and mAP (DIOR-R) for DARIoU and baseline. DARIoU shows faster convergence and higher stability compared to Baseline, with an improved final performance on both datasets.
(3) Combination of two components: After integrating the two modules, the comparative results of our method and the baseline model are shown in Table 5. The data indicate improvements of 3.46% and 2.39% in mAP when applying the two methods individually, both of which outperform the isolated application of each module. This suggests that the proposed modules facilitate the model’s adaptation to rotational characteristics from various perspectives, thereby generating more precise outcomes. Visual examples comparing FCOS-O and our method on the DIOR-R dataset are presented in Figure 12, demonstrating that our method detects more instances compared to the baseline.

Figure 12.
Comparison of the visualization results between baseline and our method on DIOR-R.
5.3. Hyperparameter Selection
In the proposed DARIoU loss function, two hyperparameters, denoted by and control the overall and local weight of the penalty term, respectively. To investigate their impact on model performance, we conducted ablation experiments on the DIOR-R dataset, testing various values for (0.3, 0.7, 1.0, and 1.5) and (0.05, 0.1, 0.3, 0.7, and 1.0). The results, shown in Table 7, indicate that the model performs optimally when = 0.3 and = 1.0, providing the best balance of performance.

Table 7.
Ablation studies of two hyperparameters and for the regression loss on DIOR-R. The values in bold indicate the highest performance in each column.
6. Conclusions
In the field of remote sensing detection, complex backgrounds, arbitrary object orientations and vast scale variations persist as major barriers to both accuracy and efficiency. To tackle these challenges, this paper proposes a novel oriented object detection method that learns multiscale rotational features through an adaptive feature-fusion scheme. Specifically, we introduce the rotation-invariant learning (RIL) and the rotation feature fusion (RFF) modules, which enable the model to learn shallow features from multiple angles, enhancing its ability to handle rotated objects. To further optimize the model, we propose the dual-aspect RIoU loss, which integrates both rotational and horizontal information, overcoming the limitations of existing IoU-based loss functions that are not invariant to the orientation of bounding boxes. Experiments conducted on two remote sensing datasets demonstrate that the incorporation of these strategies into a simple one-stage detector achieves a novel balance between computational efficiency and detection precision.
Author Contributions
Conceptualization, Z.H., X.M. and X.L.; methodology, Z.H., X.M. and X.L.; software, Z.H. and Z.S.; validation, Z.H., X.L. and Z.S.; formal analysis, Z.H. and X.L.; investigation, Z.H. and Z.S.; resources, X.M.; data curation, X.L.; writing—original draft preparation, Z.H.; writing—review and editing, Z.H., X.M. and X.L.; visualization, Z.H.; supervision, X.M. and X.L.; project administration, X.M.; funding acquisition, X.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fundamental Research Project of the Liaoning Provincial Department of Education (Grant No.JYTQN2023203). The authors thank the editorial office and reviewers for dedicating their time and effort to evaluating this manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Both datasets used in this article are publicly available. DIOR-R: https://gcheng-nwpu.github.io/#Datasets (accessed on 13 February 2025); HRSC2016: https://paperswithcode.com/dataset/hrsc2016 (accessed on 13 February 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feng, D.; Harakeh, A.; Waslander, S.L.; Dietmayer, K. A review and comparative study on probabilistic object detection in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2021, 23, 9961–9980. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Pi, Y.; Nath, N.D.; Behzadan, A.H. Convolutional neural networks for object detection in aerial imagery for disaster response and recovery. Adv. Eng. Inf. 2020, 43, 101009. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep-learning-based information mining from ocean remote-sensing imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef] [PubMed]
- Pavel, M.I.; Tan, S.Y.; Abdullah, A. Vision-based autonomous vehicle systems based on deep learning: A systematic literature review. Appl. Sci. 2022, 12, 6831. [Google Scholar] [CrossRef]
- Cerrillo-Cuenca, E.; Bueno-Ramírez, P. Predictive Archaeological Risk Assessment at Reservoirs with Multitemporal LiDAR and Machine Learning (XGBoost): The Case of Valdecañas Reservoir (Spain). Remote Sens. 2025, 17, 1306. [Google Scholar] [CrossRef]
- Durlević, U.; Srejić, T.; Valjarević, A.; Aleksova, B.; Deđanski, V.; Vujović, F.; Lukić, T. GIS-Based Spatial Modeling of Soil Erosion and Wildfire Susceptibility Using VIIRS and Sentinel-2 Data: A Case Study of Šar Mountains National Park, Serbia. Forests 2025, 16, 484. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. Available online: https://openaccess.thecvf.com/content_iccv_2017/html/He_Mask_R-CNN_ICCV_2017_paper.html (accessed on 23 February 2025).
- Cai, Z.; Vasconcelos, N. Cascade r-cnn: Delving into high quality object detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 6154–6162. Available online: https://openaccess.thecvf.com/content_cvpr_2018/html/Cai_Cascade_R-CNN_Delving_CVPR_2018_paper.html (accessed on 13 February 2025).
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. Available online: https://www.cv-foundation.org/openaccess/content_cvpr_2016/html/Redmon_You_Only_Look_CVPR_2016_paper.html (accessed on 8 February 2025).
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. Available online: https://link.springer.com/chapter/10.1007/978-3-319-46448-0_2 (accessed on 13 February 2025).
- Tian, Z.; Shen, C.; Chen, H.; He, T. Fcos: Fully convolutional one-stage object detection. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9627–9636. Available online: https://openaccess.thecvf.com/content_ICCV_2019/html/Tian_FCOS_Fully_Convolutional_One-Stage_Object_Detection_ICCV_2019_paper.html (accessed on 13 February 2025).
- Li, K.; Wan, G.; Cheng, G.; Meng, L.; Han, J. Object detection in optical remote sensing images: A survey and a new benchmark. Isprs. J. Photogramm. 2020, 159, 296–307. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Weng, L.; Yang, Y. Ship rotated bounding box space for ship extraction from high-resolution optical satellite images with complex backgrounds. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1074–1078. [Google Scholar] [CrossRef]
- Law, H.; Deng, J. Cornernet: Detecting objects as paired keypoints. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 734–750. Available online: https://openaccess.thecvf.com/content_ECCV_2018/html/Hei_Law_CornerNet_Detecting_Objects_ECCV_2018_paper.html (accessed on 13 February 2025).
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. Centernet: Keypoint triplets for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6569–6578. Available online: https://openaccess.thecvf.com/content_ICCV_2019/html/Duan_CenterNet_Keypoint_Triplets_for_Object_Detection_ICCV_2019_paper.html (accessed on 1 February 2025).
- Zhou, X.; Zhuo, J.; Krahenbuhl, P. Bottom-up object detection by grouping extreme and center points. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 850–859. Available online: https://openaccess.thecvf.com/content_CVPR_2019/html/Zhou_Bottom-Up_Object_Detection_by_Grouping_Extreme_and_Center_Points_CVPR_2019_paper.html (accessed on 15 February 2025).
- Yang, Z.; Liu, S.; Hu, H.; Wang, L.; Lin, S. Reppoints: Point set representation for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9657–9666. Available online: https://openaccess.thecvf.com/content_ICCV_2019/html/Yang_RepPoints_Point_Set_Representation_for_Object_Detection_ICCV_2019_paper.html (accessed on 12 February 2025).
- Dong, Z.; Li, G.; Liao, Y.; Wang, F.; Ren, P.; Qian, C. Centripetalnet: Pursuing high-quality keypoint pairs for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10519–10528. Available online: https://openaccess.thecvf.com/content_CVPR_2020/html/Dong_CentripetalNet_Pursuing_High-Quality_Keypoint_Pairs_for_Object_Detection_CVPR_2020_paper.html (accessed on 22 February 2025).
- Duan, K.; Xie, L.; Qi, H.; Bai, S.; Huang, Q.; Tian, Q. Corner proposal network for anchor-free, two-stage object detection. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 399–416. Available online: https://link.springer.com/chapter/10.1007/978-3-030-58580-8_24 (accessed on 3 February 2025).
- Guo, C.; Ma, Q.; Zhang, L. Spatio-temporal saliency detection using phase spectrum of quaternion fourier transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, Alaska, 23–28 June 2008; pp. 1–8. Available online: https://ieeexplore.ieee.org/abstract/document/4587715 (accessed on 9 February 2025).
- Ell, T.A.; Sangwine, S.J. Hypercomplex Fourier transforms of color images. IEEE Trans. Image Process. 2006, 16, 22–35. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the IEEE International Conference on Information Visualization, London, UK, 14–16 July 1999; Volume 2, pp. 1150–1157. Available online: https://link.springer.com/article/10.1023/B:VISI.0000029664.99615.94 (accessed on 15 February 2025).
- Nabati, R.; Qi, H. Rrpn: Radar region proposal network for object detection in autonomous vehicles. In Proceedings of the IEEE International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 3093–3097. Available online: https://ieeexplore.ieee.org/abstract/document/8803392 (accessed on 23 February 2025).
- Ding, J.; Xue, N.; Long, Y.; Xia, G.S.; Lu, Q. Learning RoI transformer for oriented object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2849–2858. Available online: https://openaccess.thecvf.com/content_CVPR_2019/html/Ding_Learning_RoI_Transformer_for_Oriented_Object_Detection_in_Aerial_Images_CVPR_2019_paper.html (accessed on 1 February 2025).
- Han, J.; Ding, J.; Xue, N.; Xia, G.S. Redet: A rotation-equivariant detector for aerial object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2786–2795. Available online: https://openaccess.thecvf.com/content/CVPR2021/papers/Han_ReDet_A_Rotation-Equivariant_Detector_for_Aerial_Object_Detection_CVPR_2021_paper.pdf (accessed on 13 February 2025).
- Cohen, T.; Welling, M. Group equivariant convolutional networks. In Proceedings of the International Conference on Machine Learning PMLR, New York, NY, USA, 20–22 June 2016; pp. 2990–2999. Available online: https://proceedings.mlr.press/v48/cohenc16.html (accessed on 8 February 2025).
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. Available online: https://openaccess.thecvf.com/content_iccv_2015/html/Girshick_Fast_R-CNN_ICCV_2015_paper.html (accessed on 23 February 2025).
- Yu, J.; Jiang, Y.; Wang, Z.; Cao, Z.; Huang, T. Unitbox: An advanced object detection network. In Proceedings of the ACM MM, Amsterdam, The Netherlands, 15–19 October 2016; pp. 516–520. [Google Scholar]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU loss: Faster and better learning for bounding box regression. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 9–11 February 2020; Volume 34, pp. 12993–13000. Available online: https://ojs.aaai.org/index.php/AAAI/article/view/6999 (accessed on 8 February 2025).
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 658–666. Available online: https://openaccess.thecvf.com/content_CVPR_2019/html/Rezatofighi_Generalized_Intersection_Over_Union_A_Metric_and_a_Loss_for_CVPR_2019_paper.html (accessed on 20 February 2025).
- Zheng, Z.; Wang, P.; Ren, D.; Liu, W.; Ye, R.; Hu, Q.; Zuo, W. Enhancing geometric factors in model learning and inference for object detection and instance segmentation. IEEE T. Cybern 2021, 52, 8574–8586. Available online: https://ieeexplore.ieee.org/abstract/document/9523600 (accessed on 19 February 2025). [CrossRef] [PubMed]
- Raisi, Z.; Naiel, M.A.; Younes, G.; Wardell, S.; Zelek, J.S. Transformer-based text detection in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, online, 20–25 June 2021; pp. 3162–3171. Available online: https://openaccess.thecvf.com/content/CVPR2021W/VOCVALC/html/Raisi_Transformer-Based_Text_Detection_in_the_Wild_CVPRW_2021_paper.html (accessed on 20 March 2025).
- Zhou, Y.; Yang, X.; Zhang, G.; Wang, J.; Liu, Y.; Hou, L.; Jiang, X.; Liu, X.; Yan, J.; Lyu, C.; et al. Mmrotate: A rotated object detection benchmark using pytorch. In Proceedings of the ACM MM, Lisboa, Portugal, 10–14 October 2022; pp. 7331–7334. Available online: https://dl.acm.org/doi/abs/10.1145/3503161.3548541 (accessed on 21 March 2025).
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. Available online: https://openaccess.thecvf.com/content_iccv_2017/html/Lin_Focal_Loss_for_ICCV_2017_paper.html (accessed on 24 March 2025).
- Xu, Y.; Fu, M.; Wang, Q.; Wang, Y.; Chen, K.; Xia, G.S.; Bai, X. Gliding vertex on the horizontal bounding box for multi-oriented object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 1452–1459. [Google Scholar] [CrossRef] [PubMed]
- Ming, Q.; Miao, L.; Zhou, Z.; Yang, X.; Dong, Y. Optimization for arbitrary-oriented object detection via representation invariance loss. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Ming, Q.; Miao, L.; Zhou, Z.; Dong, Y. CFC-Net: A critical feature capturing network for arbitrary-oriented object detection in remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Qian, W.; Yang, X.; Peng, S.; Yan, J.; Guo, Y. Learning modulated loss for rotated object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, online, 11–15 October 2021; Volume 35, pp. 2458–2466. Available online: https://ojs.aaai.org/index.php/AAAI/article/view/16347 (accessed on 2 March 2025).
- Yang, X.; Yan, J. Arbitrary-oriented object detection with circular smooth label. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 677–694. Available online: https://link.springer.com/chapter/10.1007/978-3-030-58598-3_40 (accessed on 13 March 2025).
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3det: Refined single-stage detector with feature refinement for rotating object. In Proceedings of the AAAI Conference on Artificial Intelligence, online, 11–15 October 2021; Volume 35, pp. 3163–3171. Available online: https://ojs.aaai.org/index.php/AAAI/article/view/16426 (accessed on 9 March 2025).
- Yang, X.; Yang, X.; Yang, J.; Ming, Q.; Wang, W.; Tian, Q.; Yan, J. Learning high-precision bounding box for rotated object detection via kullback-leibler divergence. Adv. Neural Inf. Process. Syst. 2021, 34, 18381–18394. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).