Hybrid Uncertainty Metrics-Based Privacy-Preserving Alternating Multimodal Representation Learning
Abstract
1. Introduction
- We propose a hybrid uncertainty metric that integrates KL divergence and entropy to comprehensively evaluate modality quality, optimize cross-modal fusion, and enhance robustness in noisy or imbalanced scenarios.
- We incorporate differential privacy into alternating training with gradient clipping and noise injection to effectively safeguard sensitive data and mitigate privacy attack risks.
- We demonstrate through extensive experiments on the MVSA and CREMA-D datasets that PAMRL achieves a robust balance of predictive accuracy, robustness, and privacy protection, offering significant practical value.
2. Related Work
2.1. Multimodal Learning
2.2. Privacy Protection in Multimodal Learning
2.3. Uncertainty Quantification
3. Materials and Methods
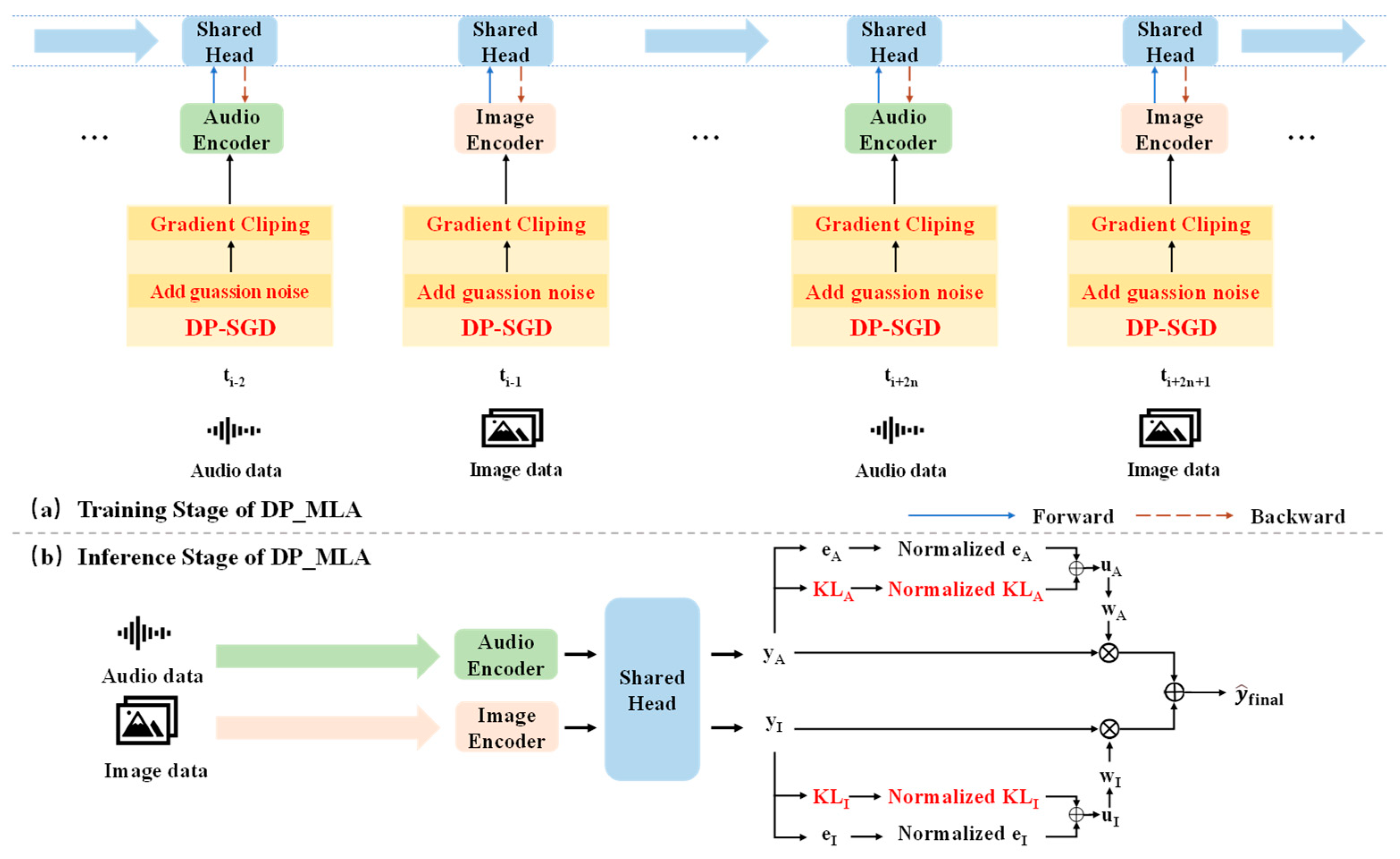
3.1. Overview of Our Proposed PAMRL
3.2. Dynamic Fusion Mechanism
- (1)
- Entropy Calculation .
- (2)
- KL Divergence Calculation .
- (3)
- Normalized Entropy.
- (4)
- Normalized KL Divergence.
- (5)
- Hybrid Uncertainty Metric .
- (6)
- Fusion Weight .
- (7)
- Final Prediction .
3.3. Privacy-Preserving Training
- (1)
- Gradient Clipping.
- (2)
- Noise Injection.
- (3)
- Differential Privacy.
4. Results and Discussion
4.1. Experimental
4.1.1. Datasets
- (1)
- CREMA-D: CREMA-D [2] is an audio–visual dataset for emotion recognition research, containing 7442 video clips of 2–3 s duration, featuring facial and vocal emotional expressions from 91 actors. The emotional states are categorized into six classes: happy, sad, angry, fearful, disgusted, and neutral. The dataset is randomly split into a training set of 6698 samples and a test set of 744 samples at a ratio of 9:1.
- (2)
- MVSA: MVSA-Single [9] is a standardized image-text dataset for multimodal sentiment analysis, comprising 5129 Twitter-derived social media pairs (4511 validated samples after curation). Each entry includes an image and its corresponding textual tweet, annotated via a single-annotator protocol with ternary sentiment labels (positive/negative/neutral). Through a systematic curation process involving eliminating inter-modal polarity conflicts and prioritizing the adoption of non-neutral labels when either modality exhibits neutrality, the dataset ensures label consistency while preserving authentic cross-modal interaction patterns.
4.1.2. Experiment Settings
4.1.3. Evaluation Metrics
- (1)
- Accuracy (ACC): Accuracy measures the proportion of correctly classified samples out of the total samples. It is calculated aswhere is the total number of samples, is the predicted class for sample , is the true class, and is the indicator function (1 if , 0 otherwise).
- (2)
- Precision: Precision measures the proportion of samples predicted as positive that are actually positive, reflecting the model’s prediction precision. It is calculated aswhere is the number of classes, is the proportion of samples in class , is the number of true positives for class , and is the number of false positives for class .
- (3)
- Recall: Recall measures the proportion of actual positive samples correctly identified by the model, reflecting the model’s coverage ability. The weighted average recall is calculated aswhere is the number of false negatives for class .
- (4)
- F1 score: The F1 score is the harmonic mean of precision and recall, providing a balanced measure of model performance. The weighted average F1 score is calculated aswhere and are the precision and recall for class , respectively.
- (5)
- Expected Calibration Error (ECE): ECE measures the difference between the model’s predicted confidence and its actual accuracy, reflecting the model’s calibration quality. ECE divides the predicted confidences into bins (typically ) and computes the weighted average of the absolute difference between accuracy and confidence in each bin:where is the set of samples in the -th confidence bin, is the number of samples in bin , is the total number of samples, is the accuracy in bin , and is the average confidence in bin . A lower ECE indicates better calibration.
- (6)
- Confidence-Stratified Accuracy Low (ConfAcc_Low): ConfAcc_Low measures the model’s accuracy in the low-confidence interval (confidence range [0, 0.5]), reflecting the reliability of low-confidence predictions. It is calculated aswhere is the set of samples with confidence in [0, 0.5], is the predicted class for sample , is the true class, is the indicator function (1 if , 0 otherwise), and is the number of samples in .
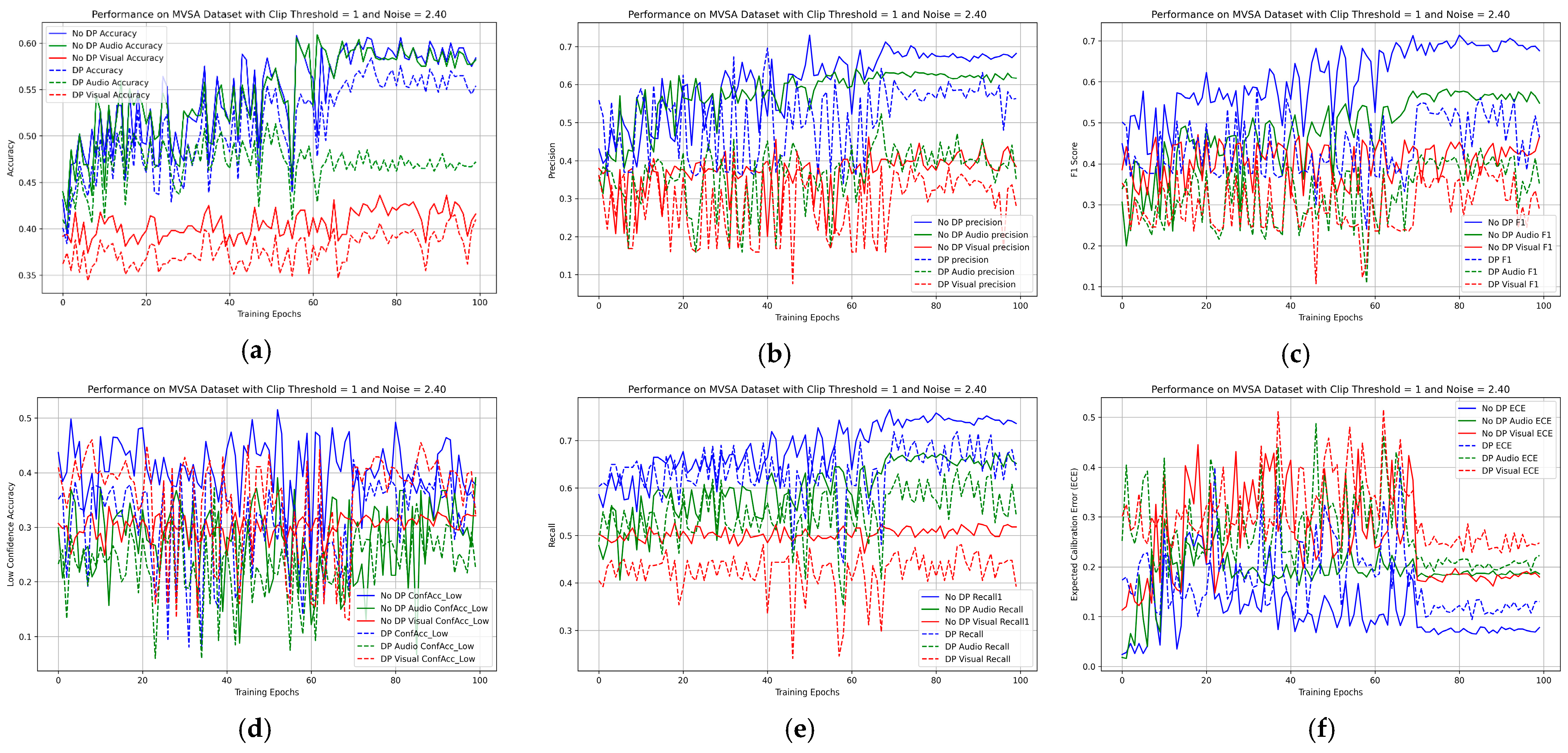
4.2. Main Result for the PAMRL
4.3. Comparison Between PAMRL and MLA Models Against Membership Inference Attacks
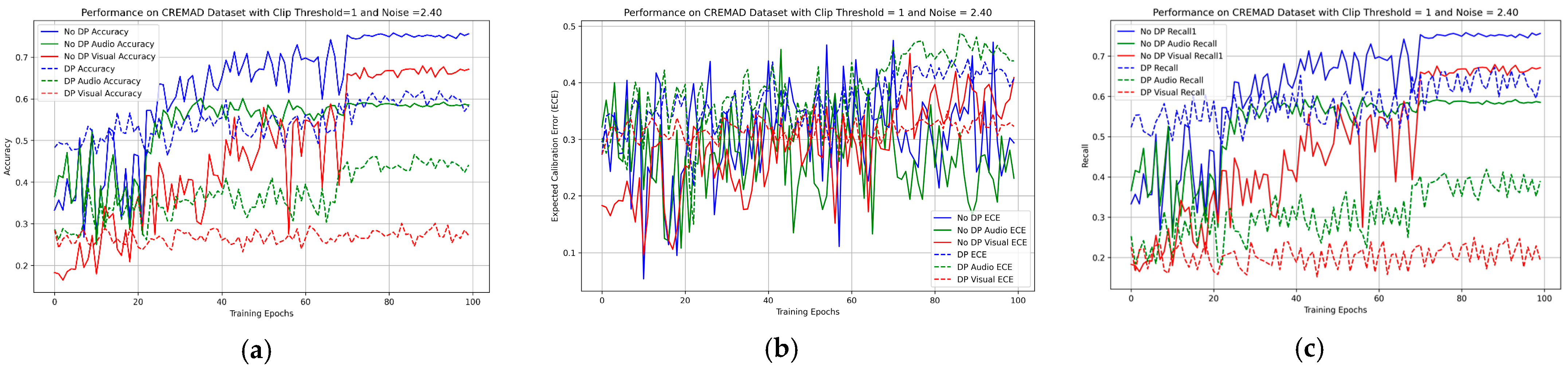
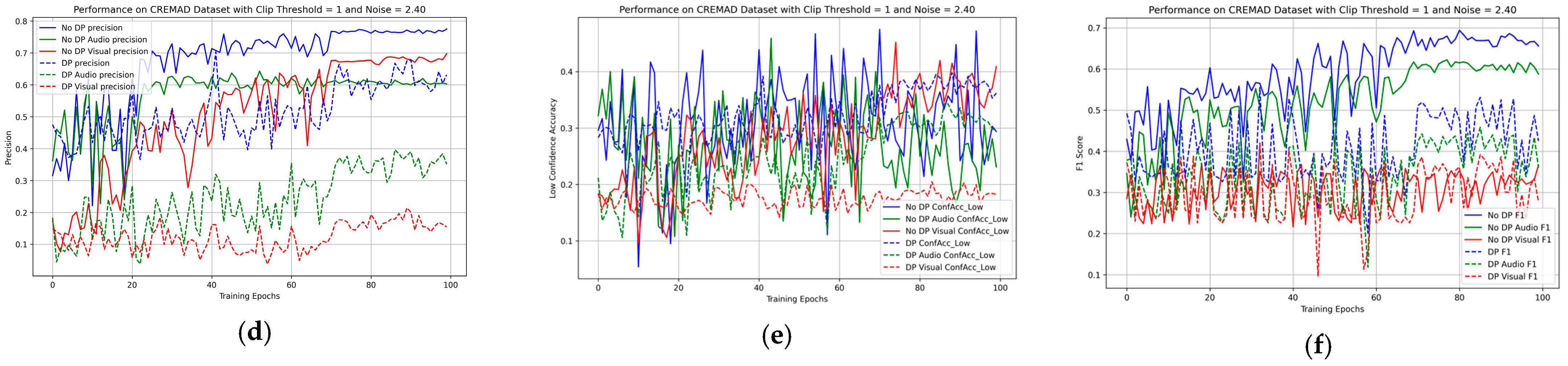
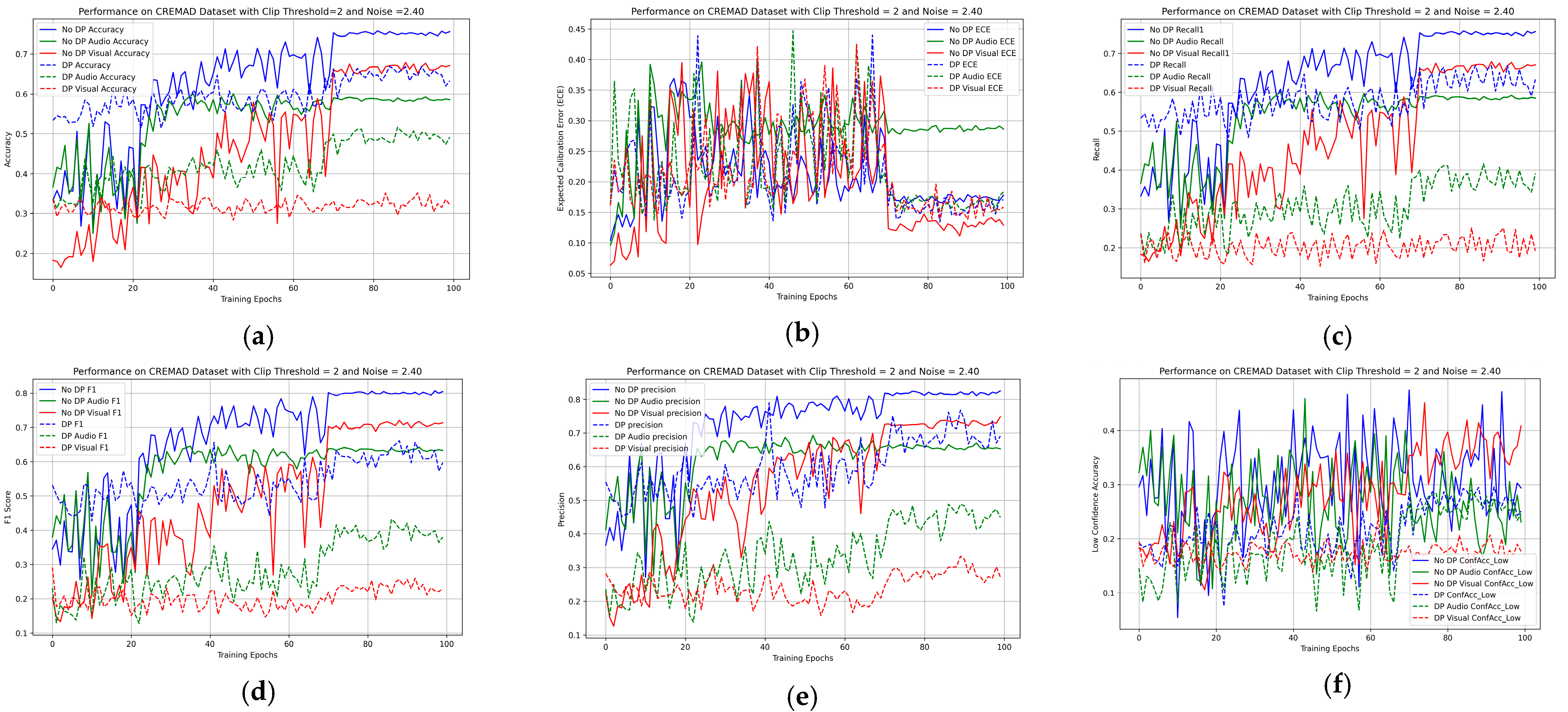
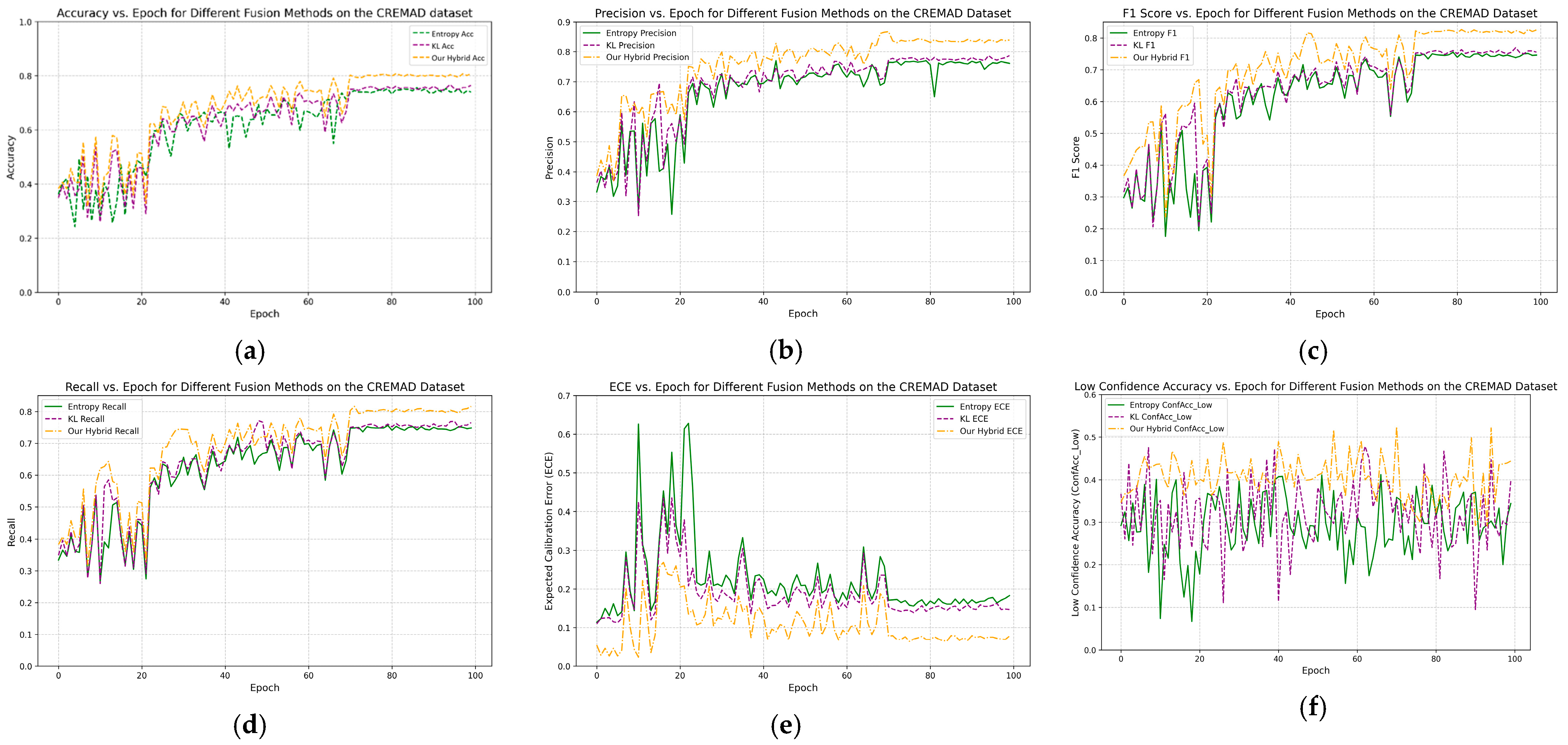
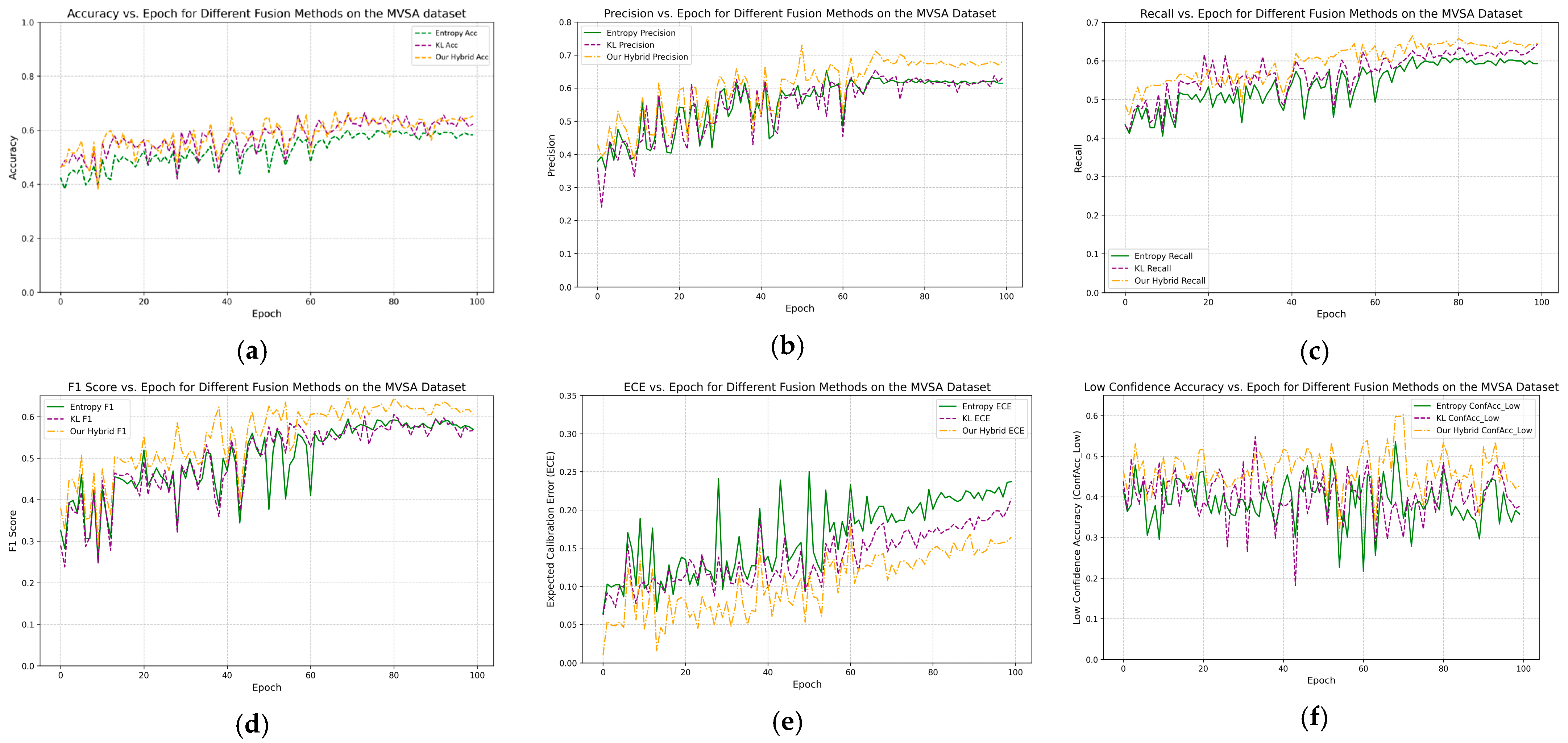
4.4. Ablation Study on Hybrid Uncertainty Metrics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baltrusaitis, T.; Ahuja, C.; Morency, L. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Cooper, D.G.; Keutmann, M.K.; Gur, R.C.; Nenkova, A.; Verma, R. CREMA-D: Crowd-Sourced Emotional Multimodal Actors Dataset. IEEE Trans. Affect. Comput. 2014, 5, 377–390. [Google Scholar] [CrossRef] [PubMed]
- Feng, D.; Haase-Schutz, C.; Rosenbaum, L.; Hertlein, H.; Glaser, C.; Timm, F.; Wiesbeck, W.; Dietmayer, K. Deep Multi-Modal Object Detection and Semantic Segmentation for Autonomous Driving: Datasets, Methods, and Challenges. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1341–1360. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Advances in Neural Information Processing Systems; Cornell University: Ithaca, NY, USA, 2017; Volume 30, pp. 5998–6008. Available online: https://arxiv.org/pdf/1706.03762v5 (accessed on 25 February 2025).
- Cai, C.; Sang, Y.; Tian, H. A Multimodal Differential Privacy Framework Based on Fusion Representation Learning. Connect. Sci. 2022, 34, 2219–2239. [Google Scholar] [CrossRef]
- Zhang, X.; Yoon, J.; Bansal, M.; Yao, H. Multimodal Representation Learning by Alternating Unimodal Adaptation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; IEEE: Piscataway, NJ, USA, 2024; pp. 27446–27456. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Xu, N.; Mao, W.; Chen, G. Multi-Interactive Attention Network for Fine-Grained Feature Learning in Multimodal Sentiment Analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 8–15 February 2022; AAAI Press: Palo Alto, CA, USA, 2022; Volume 36, pp. 12345–12353. [Google Scholar]
- Peng, X.; Wei, Y.; Deng, A.; Yang, Y. Balanced Multimodal Learning via On-the-Fly Gradient Modulation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 8238–8247. [Google Scholar]
- Wang, H.; Zhang, J.; Chen, Y.; Ma, C.; Avery, J.; Hull, L.; Carneiro, G. Uncertainty-Aware Multi-Modal Learning via Cross-Modal Random Network Prediction. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; pp. 200–217. [Google Scholar]
- Alfasly, S.; Lu, J.; Xu, C.; Zou, Y. Learnable Irrelevant Modality Dropout for Multimodal Action Recognition on Modality-Specific Annotated Videos. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 20176–20185. [Google Scholar]
- Park, S.; Kim, Y. A Metaverse: Taxonomy, Components, Applications, and Open Challenges. IEEE Access 2022, 10, 4209–4251. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep Learning with Differential Privacy. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; ACM: New York, NY, USA, 2016; pp. 308–318. [Google Scholar]
- Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership Inference Attacks against Machine Learning Models. In Proceedings of the 38th IEEE Symposium on Security and Privacy (S&P), San Jose, CA, USA, 22–24 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3–18. [Google Scholar]
- Feng, J.; Wu, Y.; Sun, H.; Zhang, S.; Liu, D. Panther: Practical Secure Two-Party Neural Network Inference. In IEEE Transactions on Information Forensics and Security; IEEE: Piscataway, NJ, USA, 2025; pp. 1–11. [Google Scholar]
- Zhang, P.; Fang, X.; Zhang, Z.; Fang, X.; Liu, Y.; Zhang, J. Horizontal Multi-Party Data Publishing via Discriminator Regularization and Adaptive Noise under Differential Privacy. Inf. Fusion 2025, 120, 103046. [Google Scholar] [CrossRef]
- Zhang, P.; Cheng, X.; Su, S.; Wang, N. Effective Truth Discovery under Local Differential Privacy by Leveraging Noise-Aware Probabilistic Estimation and Fusion. Knowl.-Based Syst. 2023, 261, 110213. [Google Scholar] [CrossRef]
- Li, Y.; Yang, S.; Ren, X.; Shi, L.; Zhao, C. Multi-Stage Asynchronous Federated Learning with Adaptive Differential Privacy. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 1243–1256. Available online: https://pubmed.ncbi.nlm.nih.gov/37956007/ (accessed on 25 February 2025). [CrossRef]
- Pan, K.; Ong, Y.S.; Gong, M.; Li, H.; Qin, A.K.; Gao, Y. Differential privacy in deep learning: A literature survey. Neurocomputing 2024, 589, 127663. Available online: https://www.sciencedirect.com/science/article/abs/pii/S092523122400434X (accessed on 25 February 2025). [CrossRef]
- Xue, Y.; Cheng, S.; Li, Y.; Tian, L. Reliable Deep-Learning-Based Phase Imaging with Uncertainty Quantification. Optica 2019, 6, 618–626. [Google Scholar] [CrossRef] [PubMed]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; Bach, F., Blei, D., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1050–1059. [Google Scholar]
- Tian, J.; Song, Q.; Wang, H. Blockchain-Based Incentive and Arbitrable Data Auditing Scheme. In Proceedings of the 2022 52nd Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Baltimore, MD, USA, 27–30 June 2022; pp. 170–177. [Google Scholar] [CrossRef]
- Li, Y.; Daho, M.E.; Conze, P.H.; Zeghlache, R.; Le Boité, H.; Tadayoni, R.; Cochener, B.; Lamard, M.; Quellec, G. A review of deep learning-based information fusion techniques for multimodal medical image classification. Comput. Biol. Med. 2024, 177, 108635. Available online: https://www.sciencedirect.com/science/article/pi-i/S0010482524007200 (accessed on 25 February 2025). [CrossRef] [PubMed]
- Geng, X.; Zhang, H.; Song, B.; Yang, S.; Zhou, H.; Keutzer, K. Multimodal Masked Autoencoders Learn Transferable Representations. arXiv 2022, arXiv:2205.14204. [Google Scholar]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Ye, J.; Maddi, A.; Murakonda, S.K.; Bindschaedler, V.; Shokri, R. Enhanced Membership Inference Attacks against Machine Learning Models. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; ACM: New York, NY, USA, 2022; pp. 3093–3106. [Google Scholar]


| Dataset | Model | Accuracy | Precision | F1 Score | Recall | ECE | ConfAcc_Low |
|---|---|---|---|---|---|---|---|
| CREMAD | MLA [6] | 72.21% | 77.11% | 69.45% | 75.41% | 5.54% | 46.75% |
| PAMRL (ϵ = 1) | 62.58% | 68.54% | 53.35% | 67.78% | 18.34% | 30.12% | |
| PAMRL (ϵ = 2) | 65.69% | 74.65% | 62.24% | 69.56% | 14.35% | 32.34% | |
| MVSA | MLA [6] | 62.23% | 72.65% | 71.67% | 76.23% | 4.76% | 51.54% |
| PAMRL (ϵ = 1) | 55.56% | 61.48% | 54.42% | 61.94% | 9.45% | 40.16% | |
| PAMRL (ϵ = 2) | 58.45% | 63.45% | 58.65% | 64.34% | 6.43% | 45.87% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Huang, Y.; Zhang, A.; Li, C.; Jiang, L.; Liao, X.; Li, R.; Wan, J. Hybrid Uncertainty Metrics-Based Privacy-Preserving Alternating Multimodal Representation Learning. Appl. Sci. 2025, 15, 5229. https://doi.org/10.3390/app15105229
Sun Z, Huang Y, Zhang A, Li C, Jiang L, Liao X, Li R, Wan J. Hybrid Uncertainty Metrics-Based Privacy-Preserving Alternating Multimodal Representation Learning. Applied Sciences. 2025; 15(10):5229. https://doi.org/10.3390/app15105229
Chicago/Turabian StyleSun, Zhe, Yaowei Huang, Aohai Zhang, Chao Li, Lifan Jiang, Xiaotong Liao, Ran Li, and Junping Wan. 2025. "Hybrid Uncertainty Metrics-Based Privacy-Preserving Alternating Multimodal Representation Learning" Applied Sciences 15, no. 10: 5229. https://doi.org/10.3390/app15105229
APA StyleSun, Z., Huang, Y., Zhang, A., Li, C., Jiang, L., Liao, X., Li, R., & Wan, J. (2025). Hybrid Uncertainty Metrics-Based Privacy-Preserving Alternating Multimodal Representation Learning. Applied Sciences, 15(10), 5229. https://doi.org/10.3390/app15105229






