Crack Defect Detection Method for Plunge Pool Corridor Based on the Improved U-Net Network

Abstract

Crack defects pose a significant threat to the safe operation of the foundational structures of hydropower stations. Therefore, crack detection in a plunge pool corridor is crucial for the safe operation and maintenance of hydropower hubs. Addressing challenges such as missing crack datasets, complex and diverse crack shapes, and difficulties in feature extraction, this paper proposes an improved U-Net model. The model integrates the CDIAM attention module within the U-Net architecture and is optimized through the incorporation of the MIDConv convolutional block. The enhanced U-Net model demonstrates outstanding performance on a self-constructed plunge pool corridor crack dataset, achieving an MIoU, F1-score, MPA, and accuracy of 84.44%, 93.05%, 89.75%, and 99.46%, respectively. Compared to the original U-Net model, these metrics show improvements of 5.34%, 4.90%, 3.39%, and 0.36%, respectively. The improved U-Net model exhibits higher detection accuracy in corridor crack segmentation tasks, effectively extracting feature information from irregular shapes, and provides a superior solution for crack defect detection in a plunge pool corridor, thereby enhancing the safety and efficient maintenance of hydropower stations.

1. Introduction

The corridors of hydropower stations are critical components of hydraulic hubs, directly affecting the safety and economic benefits of the hydropower station. The appearance of cracks threatens structural integrity and can lead to water leakage and equipment damage. Therefore, regular crack detection is crucial as it enables the timely identification and resolution of potential risks, ensuring the health and stability of the corridors and thereby safeguarding the safe operation and efficient maintenance of the hydropower station. Conventional manual inspection not only involves substantial consumption of human and material resources but also suffers from extremely low detection efficiency, being unable to meet the requirement of rapid detection [1]. Alongside the rapid advancement of computer science, the accurate detection of concrete cracks via computer vision has emerged as a primary research goal.

Yu et al. [2] employed the Sobel operator to detect crack edges in images, identifying genuine cracks through region filling, labeling, and adjacent region connection operations. Li et al. [3] utilized a wavelet-based algorithm to eliminate noise from images and integrated the C-V model with a Canny edge detector for crack segmentation. Through comparison with the original Canny edge detector, the proposed method outperforms the original Canny edge detector in performance. Likewise, Li et al. [4] employed the Canny edge detector to extract cracks from images and optimized crack shapes with a region-based active contour model. Subsequently, support vector machines (SVM) and a greedy search strategy were applied to eliminate noise induced by crack surface contamination and uneven lighting, ultimately yielding pixel-level crack detection results with distinct shapes. Despite extensive research on crack detection using conventional digital image processing techniques, their limitations are evident. Conventional image processing techniques depend on manual feature extraction and segmentation, restricting their applicability to specific scenarios.

In recent years, convolutional neural networks (CNN) [5] have been widely applied in various tasks, with segmentation techniques based on fully convolutional networks demonstrating exceptional performance in infrastructure inspection, such as concrete crack detection, providing strong technical support for crack recognition and monitoring. The U-Net model [6], originally developed for the medical field, along with its improved variants, has been widely applied in concrete infrastructure inspection, including residential building crack detection [7,8,9,10,11], bridge surface crack detection [12,13,14], and highway surface crack detection [15,16,17,18,19,20,21]. For instance, Ren et al. [22] integrated dilated convolution and spatial pyramid pooling modules into the deep fully convolutional neural network to enable efficient multi-scale feature extraction, aggregation, and resolution reconstruction, demonstrating high precision and generalization capability in crack detection. Aiming at complex scenarios in tunnel images, including water stains, scratches, and structural joints, QING et al. [23] developed an objective and fast recognition algorithm for tunnel cracks via computer vision-based semantic segmentation. Wooram et al. [24] developed the SDDNet network, comprising standard convolution, a DenSep module, an improved atrous spatial pyramid pooling (ASPP) module, and a decoder module. Experimental results indicate that SDDNet is highly effective for segmented crack segmentation. Liu et al. [25] opted to learn and aggregate multi-scale and multi-level features from low to high convolutional layers during training, followed by guided filtering and conditional random fields (CRFs) for model optimization, resulting in the DeepCrack deep neural network with an F1-score of 86.5%. The CrackU-Net proposed by Ju et al. [26] enhances the depth of the U-Net model and surpasses the original U-Net in pavement crack detection. To tackle the issue of crack discontinuities in segmentation outcomes, Cao et al. [27] introduced the HC-Unet++ network segmentation model for road crack detection. SUN et al. [28] incorporated a multi-scale attention module into the decoder of DeepLabv3+, which effectively reduces the instances of missed crack detections.

• Semantic segmentation approaches are capable of achieving detailed identification of specified objects, showcasing notable advantages in concrete crack detection. Yet most current mainstream crack detection networks are tailored for scenarios like building walls, road surfaces, or bridges. Plunge pool corridors, long-term exposed to high-speed water flow erosion, thermal stress, and wet–dry cycles, exhibit concrete cracks with morphological features, spatial distributions, and data distributions that differ substantially from target objects in conventional public datasets. This makes it challenging for generic models to accurately differentiate targets from backgrounds. Additionally, the nonlinear morphology and multi-scale characteristics of cracks in plunge pool corridors render traditional fixed-size convolution kernels ineffective in capturing edge details. While techniques like deformable convolutions attempt to dynamically adjust the receptive field, existing approaches lack the exploitation of crack morphological priors, making them susceptible to feature deviation in complex backgrounds and resulting in segmentation issues such as discontinuities and missed detections.
• To address the aforementioned research gaps, this study develops a specialized dataset for crack segmentation in plunge pool corridors via on-site data collection and presents an improved U-Net model incorporating morphology-aware dynamic convolution and cross-dimensional interactive attention. The contributions of this work are as follows:

  (1)

  Development of a scenario-specific dataset: Using an inspection robot outfitted with a multi-angle vision system, we acquired crack images of plunge pool corridors with complex backgrounds and constructed a high-quality dataset comprising 4075 images via data augmentation techniques, addressing the lack of data for plunge pool corridor scenarios.

  (2)

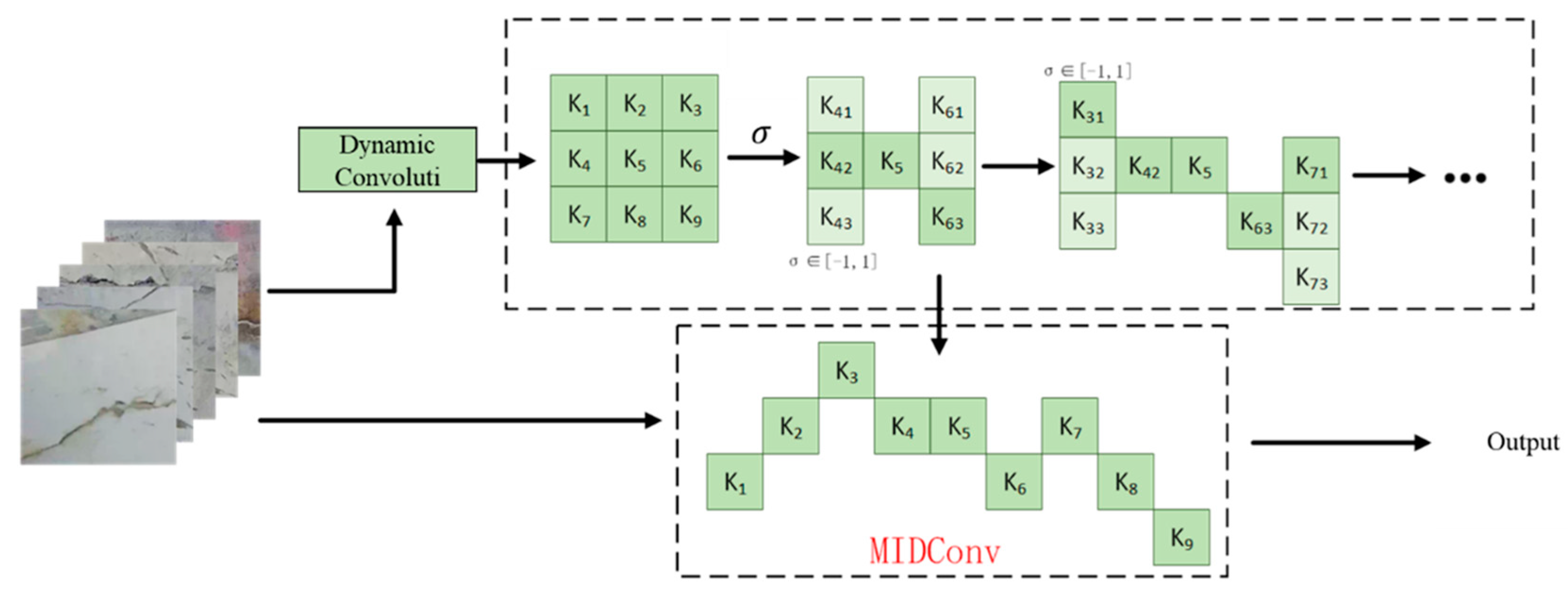
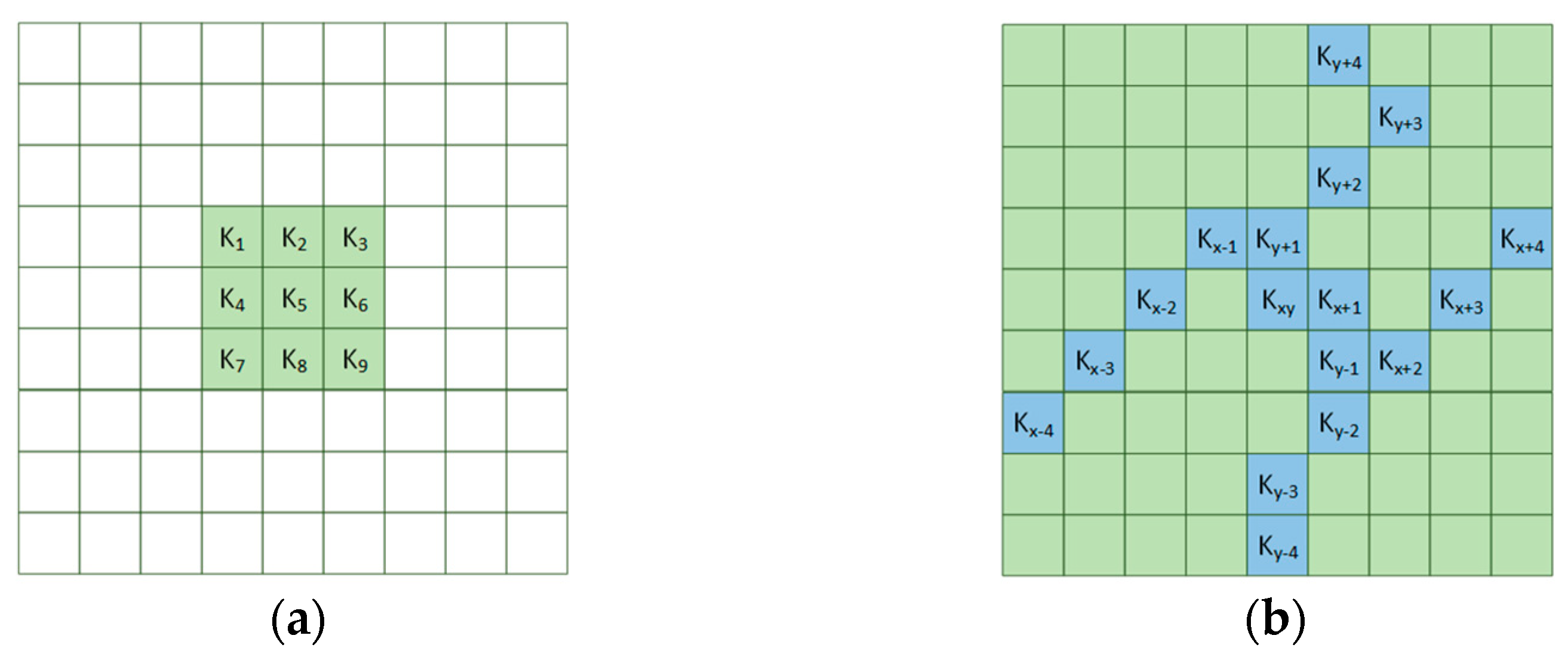
  Proposing morphology-integrated irregular dynamic convolution (MIDConv): By integrating the linear morphological features of cracks and constraining the offset accumulation of deformable convolutions, the receptive field of the convolution kernel is dynamically expanded along the crack orientation, effectively enhancing the ability to extract features of irregular edges.

  (3)

  Development of cross-dimensional interactive attention module (CDIAM): By partitioning channels into groups and introducing a global information calibration mechanism, semantic interaction between channel and spatial dimensions is established, enhancing the model’s capacity to model pixel-level relationships of cracks in complex backgrounds and markedly reducing misdetections and omissions.

  (4)

  Substantial enhancement in detection performance: On the self-constructed dataset, the improved model achieves an MIoU, F1-Score, MPA, and accuracy of 84.44%, 93.05%, 89.75%, and 99.46%, reflecting improvements of 5.34%, 4.90%, 3.39%, and 0.36% compared to the original U-Net, effectively resolving the problem of inadequate detection accuracy of traditional methods in complex scenarios. Additionally, to validate the generalization capability of the proposed approach, experiments were performed on two public datasets, both yielding promising results.

2. Methods

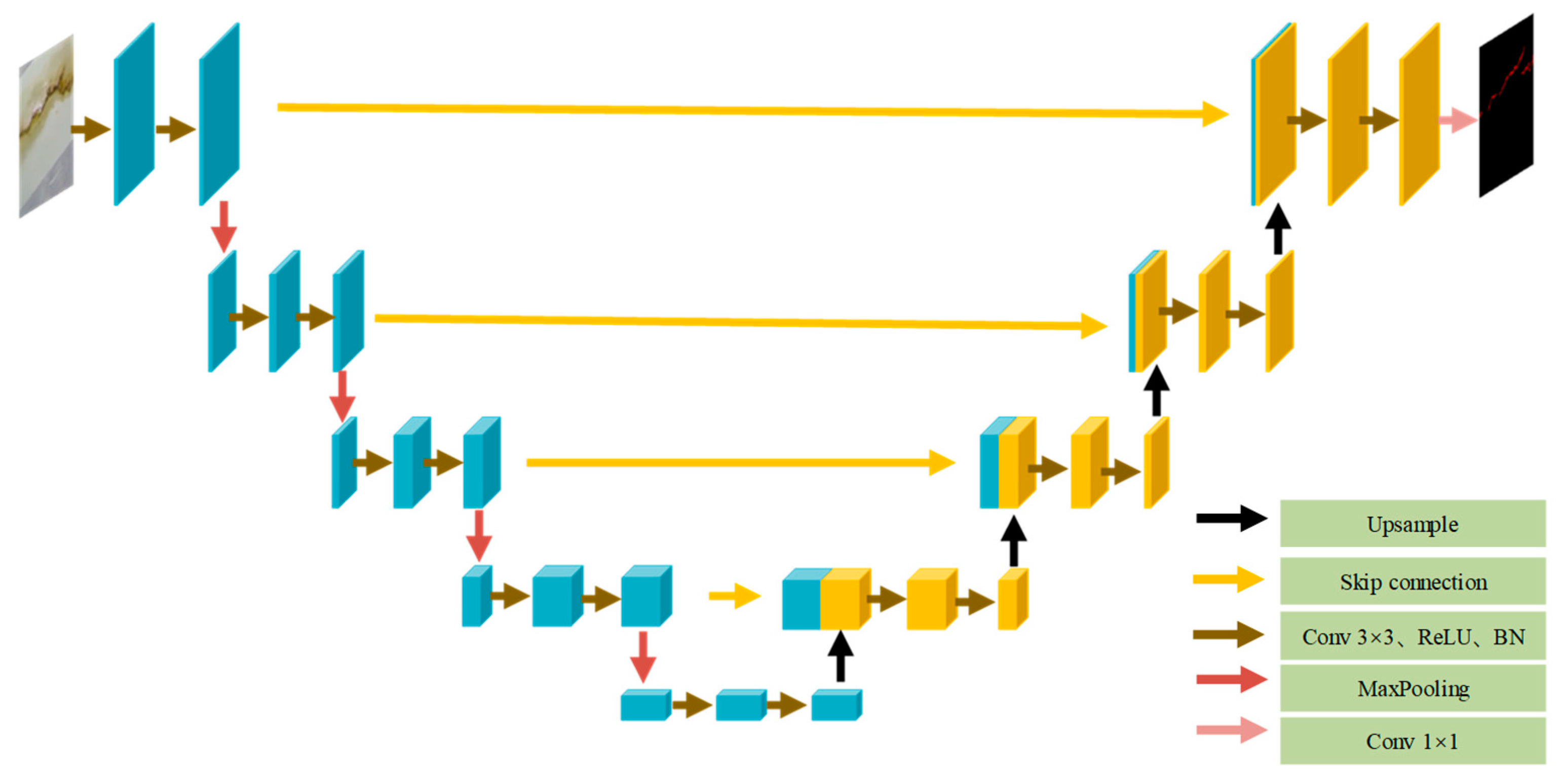
2.1. Crack Segmentation Model for Plunge Pool Corridors Based on the Improved U-Net

U-Net, proposed by O. Ronneberger in 2015, is a general-purpose semantic segmentation model with a typical symmetric encoder–decoder network architecture, which has shown outstanding performance in the field of semantic segmentation for medical images. The U-Net model performs feature extraction of target objects through four down-sampling operations and then restores the spatial resolution of the image through four up-sampling operations and skip connections, ultimately achieving the semantic segmentation task. The original U-Net model is shown in Figure 1.

The crack images in plunge pool corridors have complex backgrounds and diverse target pixel shapes. The original U-Net model uses traditional convolution, where the fixed kernel shape and size result in poor performance when processing different receptive field sizes. Additionally, using the same convolutional kernel for the entire image limits the feature extraction capability in different regions, which affects the segmentation results. The up-sampling and down-sampling structure makes the network insensitive to the precise location of the target, leading to positional deviations. To address these issues, this paper proposes the integration of morphological irregular dynamic convolution (MIDConv) to capture the morphological features of cracks and extract edge feature information. Furthermore, a cross-dimensional interaction attention module (CDIAM) is incorporated to enhance the model’s ability to extract spatial semantic information of cracks. The improved model is shown in Figure 2.

2.2. Morphological Irregular Dynamic Convolution Method

The morphological irregular dynamic convolution (MIDConv) method is a feature extraction approach, based on deformable convolution [29], aimed at extracting features according to the morphological characteristics of cracks. Deformable convolution enhances feature extraction by introducing offsets to the original convolution operation, allowing the convolutional kernel to dynamically adjust according to the input feature map, thereby improving the model’s ability to handle irregular shapes and structures. Inspired by deformable convolution, this paper integrates the morphological features of cracks into the convolution process, introducing deformable offsets to enhance the model’s ability to extract crack features. However, if the convolution kernel can freely deform and shift, the feature extraction area may gradually deviate from the target, especially in images of cracks with complex shapes. Therefore, it is necessary to restrict the introduced offsets to ensure that the feature extraction process does not deviate from the target region. The process is shown in Figure 3.

In MIDConv, the convolution kernel is straightened along the X-axis and Y-axis. Taking a convolution kernel of size $3\times 3$ as an example, the coordinates of the convolution kernel along the X-axis are $K_{i\pm b}=\left(x_{i\pm b},y_{i\pm b}\right),b=\left(0,1,2,3,4\right)$, where $b$ represents the horizontal distance from each convolution grid to the center grid. The selection of each grid position in the convolution kernel is progressively accumulated, starting from the central grid position of the kernel. The position of the kernel center grid is determined by the previous grid position. Compared to the central grid $K_i$, the grid position $K_{i+1}$ is offset by a value of $\mathsf{\sigma }\left\{\mathsf{\sigma }\in -1,1\right\}$. The offset values in different convolution kernel positions need to be continually accumulated to ensure that the convolution kernel conforms to a linear morphological structure. Therefore, the coordinates of each grid position in the convolution kernel along the X-axis can be represented as follows:

$$K_{i\pm b}=\left\{\begin{array}{c}\left(x_{i+b},y_{i+b}\right)=\left(x_{i+b},y_i+{{\displaystyle \sum }}_i^{i+b}\sigma y\right)\\ \left(x_{i-b},y_{i-b}\right)=\left(x_{i-b},y_i-{{\displaystyle \sum }}_{i-b}^i\sigma y\right)\end{array}\right.$$

(1)

From the above equation, the coordinates of each grid position in the convolution kernel along the Y-axis can be represented as follows:

$$K_{j\pm b}=\left\{\begin{array}{c}\left(x_{j+b},y_{j+b}\right)=\left(x_{j+b}+{{\displaystyle \sum }}_j^{j+b}\sigma x,y_j\right)\\ \left(x_{j-b},y_{j-b}\right)=\left(x_{j-b}-{{\displaystyle \sum }}_{j-b}^j\sigma x,y_j\right)\end{array}\right.$$

(2)

Since the offset $\mathsf{\sigma }\left\{\mathsf{\sigma }\in -1,1\right\}$ is usually not an integer, the coordinates of the convolution kernel $K$ can be obtained through bilinear interpolation and are represented as follows:

$$K={{\displaystyle \sum }}_K{B}_I\left(K^{\prime },K\right)\cdot K^{\prime }$$

(3)

where $K$ represents the fractional part of the coordinate offset along the X-axis and Y-axis, $K^{\prime }$ denotes the integer spatial coordinates of the corresponding grid point in the convolution kernel, and $B_I$ represents the bilinear interpolation operation.

As shown in Figure 4, after processing the input features using the morphological irregular dynamic convolution method, the receptive field of the features is expanded, allowing for more detailed information about the crack features to be obtained, thereby enhancing the model’s ability to extract crack features.

2.3. Cross-Dimensional Interaction Attention Module

The attention module [30] primarily enhances the model’s detection performance of target features through spatial information, channel information of the feature data, and their combination. Currently, the widely acknowledged attention modules that effectively enhance feature detection capabilities mainly consist of CBAM [31], SE [32], ECA [33], and CA [34]. In the crack segmentation task, the channel or spatial attention mechanism has been demonstrated to be highly effective in extracting crack features. Nevertheless, when handling cross-dimensional information, the approach of channel dimensionality reduction may result in information loss during the extraction of higher-dimensional features. To address this issue, this paper, based on the existing research of the attention mechanism, puts forward a cross-dimensional interaction attention module (CDIAM). This attention module remolds part of the channel information into the batch-processing dimension, divides the channel dimension into multiple sub-feature groups, and guarantees the even distribution of spatial semantic features. Meanwhile, this module utilizes global information to calibrate the weights of the channel dimension, integrates the features output from parallel branches, captures pixel-level relationships, and enhances the model’s crack feature extraction capacity and crack recognition precision. The architecture of the cross-dimensional interaction attention module is shown in Figure 5.

To enable the model to better differentiate between foreground and background pixels, the input feature map is subjected to cross-dimensional division, splitting it into N sub-feature groups. Suppose the input feature map is $\mathrm{X}\in {ℝ}^{\mathrm{C}\times \mathrm{H}\times \mathrm{W}}$. Following cross-dimensional division, the feature map can be denoted as $\mathrm{X}=\left[{\mathrm{X}}_0,{\mathrm{X}}_1,{\mathrm{X}}_2\cdots {\mathrm{X}}_{\mathrm{N}}\right]$, of which ${\mathrm{X}}_{\mathrm{i}}ϵ{ℝ}^{C//N\times \mathrm{H}\times \mathrm{W}}$, typically $\mathrm{N}\ll C$. Meanwhile, it is hypothesized that the learned attention weight descriptor will be employed to enhance the feature representation of the regions of interest within each sub-feature. This implies that the model can concentrate its attention on specific areas, thus enhancing the quality and significance of the feature representation in those areas. By this means, the network can capture the crucial information in the input data more efficiently, thereby enhancing the performance and expressivity of the task.

The attention module consists of three parallel branches, which are the H-direction feature map-processing branch (the first branch), the W-direction feature map-processing branch (the second branch), and the input sub-feature-group-processing branch (the third branch). After the features of average pooling and convolution in the first and second branches are concatenated, weight redistribution is carried out with the input sub-feature group, thus obtaining the output features. Subsequently, the output features are interactively integrated across dimensions with the feature map of the third branch that has undergone $3\times 3$ convolution processing, and ultimately, the output feature map is acquired.

To realize diverse cross-channel feature interactions between the first and second branches, the product operation is utilized to aggregate the channel features of these two branches. Meanwhile, to capture local cross-channel interactions and broaden the feature space, the third branch conducts processing on the input features with a $3\times 3$ convolution. By means of the above operations, the cross-dimensional interaction attention module is capable of not only encoding the inter-channel information to adjust the weights of various channel features but also of precisely retaining the spatial structure information within the channels. The output features in the H and W directions after going through the first and second branches are denoted, respectively, as follows:

$$Z_c^H\left(H\right)={\displaystyle \frac{1}{W}}{\displaystyle \sum }_{0\le i\le W}{x}_c\left(H,i\right)$$

(4)

$$Z_c^W\left(W\right)={\displaystyle \frac{1}{H}}{\displaystyle \sum }_{0\le j\le H}{x}_c\left(j,W\right)$$

(5)

Cross-dimensional interaction can well establish a relationship between the channel-position features and spatial-position features of the input feature map. To better integrate these two types of features to obtain a feature map with more abundant semantic information, cross-dimensional interaction is performed between the features processed by the first and second branches and the features of the third branch after a regular $3\times 3$ convolution. Global average pooling is employed to encode the global spatial information in the output of the $1\times 1$ branch. Prior to the joint activation mechanism of channel features, the output of the smallest branch is directly transformed into the corresponding dimensional form, namely, ${ℝ}_1^{1\times \mathrm{C}//\mathrm{N}}\times {ℝ}_3^{\mathrm{C}//\mathrm{N}\times \mathrm{HW}}$. Two-dimensional global average pooling is expressed as the formula below:

$$Z_c={\displaystyle \frac{1}{H\times W}}{\displaystyle \sum }_J^H{\displaystyle \sum }_I^W{x}_c\left(i,j\right)$$

(6)

Two-dimensional global average pooling is capable of establishing the reliance between global and dimensional information. Employing a two-dimensional Gaussian map to approximate the linear transformation of the global average pool’s output by Softmax renders the calculation more efficient. The multiplication of the parallel-processed output and the matrix dot-product operation results in the first spatial attention and integrates multi-scale spatial information. Likewise, global average pooling is employed to encode the global information of the $3\times 3$ branch, while the $1\times 1$ branch changes the dimensional form to ${ℝ}_3^{1\times \mathrm{C}//\mathrm{N}}\times {ℝ}_1^{\mathrm{C}//\mathrm{N}\times \mathrm{HW}}$. We generate the second spatial attention map to preserve the accurate spatial location information. The output feature map represents the combination of the two spatial-attention weight values. Following Sigmoid processing, the global context is emphasized.

3. Dataset

3.1. Data Collection

The corridor crack data in this study were collected by an inspection robot fitted with a visible-light camera and a fill light. This inspection robot is equipped with a mechanical arm system, allowing the acquisition device to be mounted on the mechanical arm to achieve omnidirectional rotation and multi-position control at the transverse central position of the standard corridor. Regarding hardware parameters, the visible-light camera features a pixel resolution of 2 megapixels, with a horizontal field of view of 65° and a vertical field of view of 63°. At the software control level, taking full account of on-site conditions and practical requirements, in the horizontal direction, upon reaching each data acquisition point, the inspection robot extends the mechanical arm to the front and positions it at the transverse central position of the standard corridor (e.g., point P1 or P2 in Figure 6a below). Additionally, an overlapping image area of approximately 5° is designed to ensure image overlap between acquisition points. In the cross-sectional direction, the mechanical arm is set at a height of approximately 1 m from the ground. To ensure full coverage of the corridor side walls and vault, a total of five images are designed to be captured, with an overlap of approximately 5° employed to achieve image overlap in the cross-sectional direction.

3.2. Data Augmentation

Given the limitations of manual inspection during flood-discharge operations, the structural damage is often concealed, making it difficult for regular manual inspections to promptly and accurately identify corridor defects and operating states. Additionally, the scarcity of effective defect data in the early stage makes it challenging to support the design of concrete-defect identification methods. This paper adopts the data augmentation algorithm. The collected data were processed with random flipping and random color adjustment, the effect is shown in Figure 7 and Figure 8, including horizontal flipping, transposed flipping, vertical flipping, brightness enhancement, and brightness reduction, resulting in a plunge pool corridor crack dataset consisting of 4075 images in total.

4. Experiment

4.1. Experimental Environment

All experiments in this paper were conducted under the Windows operating system, using PyTorch 1.11.0 on a personal server equipped with an Intel i5-13600kf processor, 32 GB of RAM, and an NVIDIA GeForce RTX 4070 GPU (12GB). In the experiments, the SGD optimizer was employed to update the weight parameters of the plunge pool corridor crack detection model. The DiceLoss [35] was used as the loss function. The number of training epochs was 200, the batchsize was 8, the initial learning rate was 0.007, and the learning rate decayed by 0.0001 every 10 epochs. Throughout the model training process, the loss change curve and pixel accuracy change curve are depicted in the Figure 9.

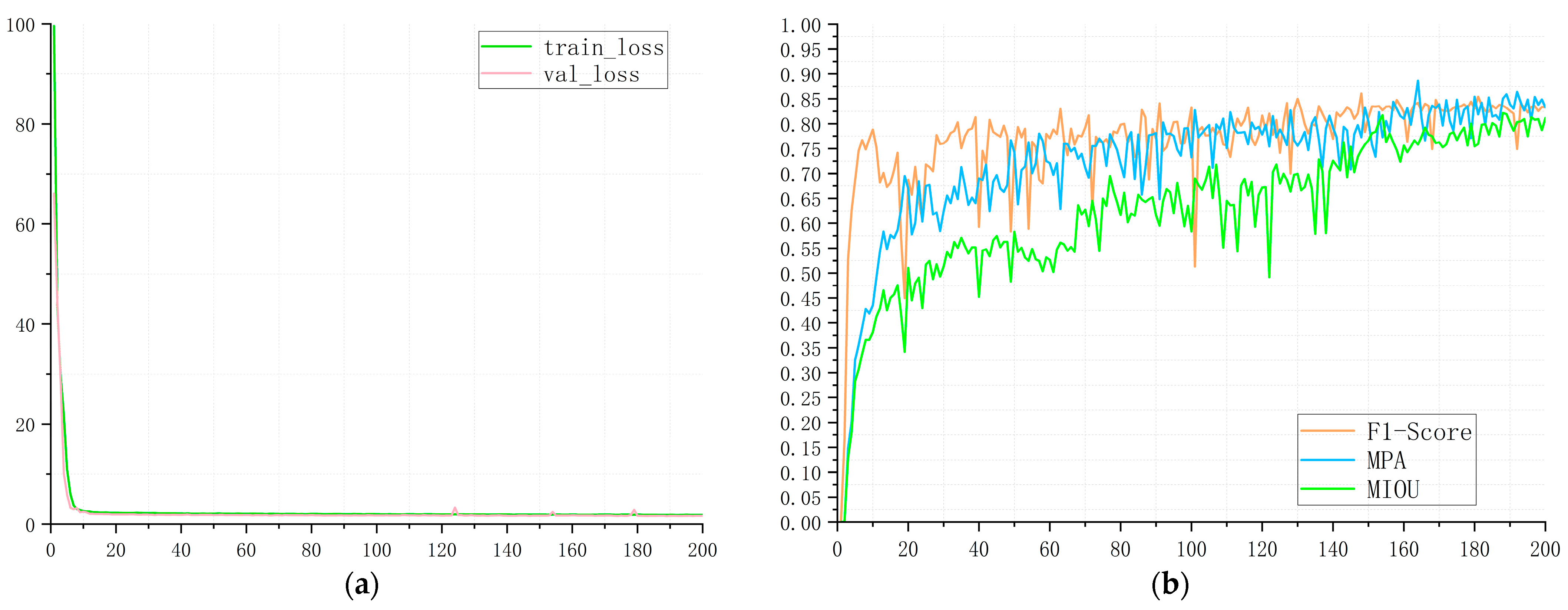
4.2. Evaluation Metrics

Evaluation metrics refer to the use of various data indicators to determine the detection performance of the model. The metrics adopted in this paper include mean intersection over union (MIoU), F1-score, mean pixel accuracy (MPA), and accuracy.

In crack detection, the MIoU metric can help evaluate the performance of the model in image segmentation, especially in capturing the degree of overlap between the detected crack area and the actual label. Its calculation formula is as follows:

$$MIoU={\displaystyle \frac{1}{N}}{\displaystyle \sum }_{I=1}^N{\displaystyle \frac{T{P}_i}{T{P}_i+F{P}_i+F{N}_i}}$$

(7)

Among them, N denotes the total number of categories; $T{P}_i$ denotes the true positives of the i-th category, that is, the number of pixels that the model correctly predicts as this category; $F{P}_i$ denotes the false positives of the i-th category, namely, the number of pixels that the model wrongly predicts as this category; and $F{N}_i$ denotes the false negatives of the i-th category, which means the number of pixels that the model fails to predict as this category.

The F1-score represents the balance coefficient between the precision and recall of the model, providing a comprehensive evaluation of the overall performance of the trained model.

$$Precision={\displaystyle \frac{T{P}_i}{T{P}_i+F{P}_i}}$$

(8)

$$Recall={\displaystyle \frac{T{P}_i}{T{P}_i+F{N}_i}}$$

(9)

$$F1-score=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(10)

As an intuitive and straightforward evaluation metric, mean pixel accuracy (MPA) can comprehensively consider the classification accuracy of an image segmentation model at the pixel level. It provides an intuitive understanding of the overall performance of the model and is applicable to the evaluation and comparison of various image segmentation tasks.

$$MPA={\displaystyle \frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{TP}}_{\mathrm{i}}}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}({\mathrm{TP}}_{\mathrm{i}}+{\mathrm{FP}}_{\mathrm{i}})}}$$

(11)

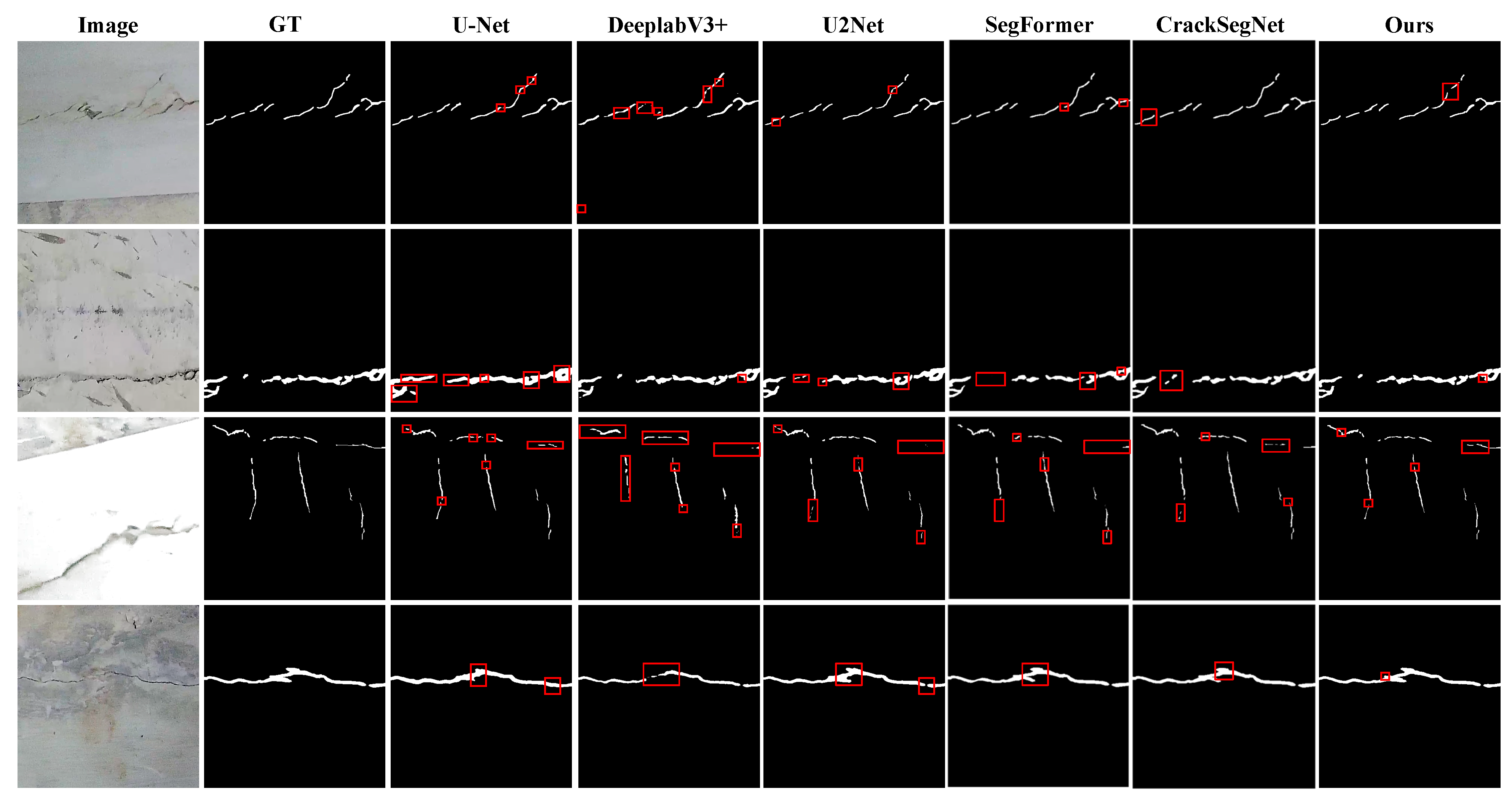
4.3. Comparative Experiment

This paper verifies the superiority of the improved model by comparing three segmentation models: U-Net, DeepLabV3+ [36], U2Net [37], SegFormer [38], and CrackSegNet [39]. The figure below shows the detection results of U-Net, DeepLabV3+, U2Net, and the improved model on the plunge pool corridor crack dataset. The visual comparison is shown in Figure 10, The red box represents a relatively large difference, the comparison of evaluation metrics are shown in

Table 1. Comparative experiments of different detection models.

Model	MIOU (%)	MPA (%)	F1-Score (%)	Accuracy (%)
U-Net	79.1	87.15	84.36	99.1
DeepLabV3+	80.5	88.04	84.79	99.2
U2Net	82.11	89.45	85.52	99.11
SegFormer	82.64	89.69.	85.78	99.32
CrackSegNet	81.37	88.53	84.94	99.23
Ours	84.44	92.05	87.75	99.46

.

In Figure 10, the U-Net and DeepLabV3+ models show little overall difference in performance within this dataset. Nevertheless, DeepLabV3+ uses spatial pyramid pooling, allowing it to achieve a larger receptive field. As a result, it performs better in crack-feature extraction, with fewer occurrences of crack breakpoints, undetected cracks, and misidentifications. By introducing the residual module, U2Net can acquire more diverse crack features; SegFormer integrates the transformer with a lightweight multi-layer perceptron (MLP) decoder, allowing the encoder to produce high-resolution fine-grained features and low-resolution coarse-grained features; and the CrackSegNet decoder incorporates a spatial attention module to improve the feature representation of cracks. Yet there are still instances of crack breakpoints, undetected cracks, and misidentifications. In comparison to the previous models, the improved U-Net network model in this paper can capture crack features more effectively, and there is a significant reduction in the number of crack breakpoints, misidentifications, and undetected cracks.

By calculating the four metrics of MIOU, MPA, F1-score, and accuracy for the test dataset, the statistical results are presented in the table below. The U-Net and DeepLabV3+ models exhibit similar performances, and U2Net shows an improvement compared to the previous two. Compared with the pre-improvement U-Net model, the improved model in this paper has an increase of 5.34% in MIOU, 4.90% in MPA, 3.39% in F1-score, and 0.36% in accuracy. This shows that the improved model has improved in terms of both the extraction of crack features in different channel dimensions and the handling of the features of irregular shapes.

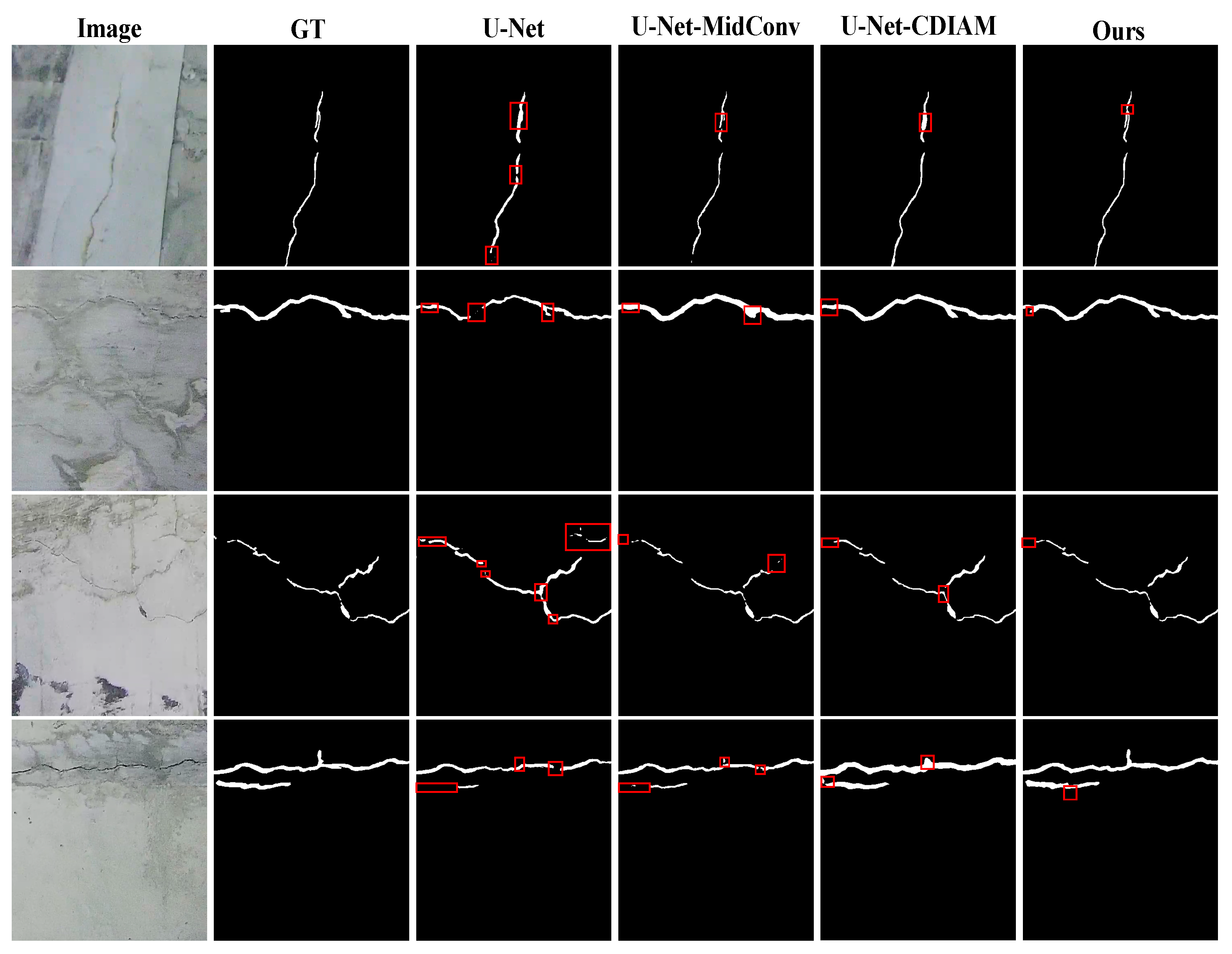
4.4. Ablative Experiment

To more effectively validate the performance of the morphology-integrated irregular dynamic convolution (MIDConv) and the cross-dimensional interactive attention module (CDIAM) in corridor crack detection, an ablation experiment was devised to examine the effectiveness of these two improvements in extracting crack features, as show in Figure 11, the red box represents a relatively large difference. The comparison of evaluation metrics are shown in

Table 2. Comparative experiments of different model structures.

Model	MIOU (%)	MPA (%)	F1-Score (%)	Accuracy (%)
U-Net	79.1	87.15	84.36	99.1
U-Net+CDIAM	82.36	89.54	85.68	99.27
U2Net+MIDConv	82.78	91.56	87.02	99.30
Ours	84.44	92.05	87.75	99.46

.

Figure 11 indicates that by introducing irregular dynamic convolution to expand the fixed-shaped and sized convolution kernels in the original U-Net network architecture, the receptive field of the improved network is correspondingly enlarged. During crack feature extraction, U-Net-MIDConv acquires more abundant feature information, allowing the segmentation model to identify more crack features in the prediction map. It can be easily observed that while the crack segmentation results of U-Net-MIDConv are more effective than the original U-Net network and visually more comprehensive, U-Net-MIDConv still exhibits slight omissions in some details. In this case, by incorporating the cross-dimensional interactive attention module, pixel-level relationships between cracks are reconstructed using global channel information, minimizing information loss during high-dimensional feature extraction. Additionally, experimental results from adding the cross-dimensional interactive attention module to the original U-Net network alone validate its ability to handle details at a fine-grained level.

After computing the four metrics of MIOU, MPA, F1-score, and accuracy for the test dataset, the results are presented in the table. The results indicate that for the original U-Net network, independently adopting the morphology-integrated irregular dynamic convolution method (MIDConv) or adding the cross-dimensional interactive attention module (CDIAM) both improve the model’s detection performance, demonstrating that while MIDConv or CDIAM alone are effective in corridor crack feature extraction, they also have shortcomings. By combining the two, the model can both extract features according to the morphological features of the cracks and also, remarkably, extract crack features across different dimensions.

Additionally, to further validate the generalization ability of the algorithm proposed in this paper, the crack dataset used in the literature DeepCrack and the public crack dataset Crack500 were trained and tested using the method in this paper. The indicators of the test set are shown in

Table 3. Comparison table of model generalization capability indicators.

Dataset	MIOU (%)	MPA (%)	F1-Score (%)	Accuracy (%)
DeepCrack	83.64	88.83	86.34	99.37
Crack500	84.37	89.20	87.36	99.41

. Through comparative analysis of metrics results, it is evident that the improved algorithm proposed herein demonstrates strong generalization capability under the same environmental configuration.

5. Discussion

5.1. Validity and Scenario Adaptability of Data Acquisition Scheme

The multi-angle data acquisition scheme proposed herein achieves full-area coverage of the side walls and vaults in plunge pool corridors via the mechanical arm system integrated with the inspection robot. The 5° overlapping region design in the horizontal direction and stratified shooting strategy with five images in the cross-sectional direction effectively address the issue of detection blind spots arising from traditional single-view acquisition, ensuring the integrity and diversity of crack samples. In comparison to manual handheld device acquisition, this scheme notably enhances the standardization and efficiency of data collection while eliminating the influence of human perspective bias on subsequent model training. Furthermore, data augmentation techniques, including random flipping and color adjustment, expand the original dataset from limited samples to 4075 images, effectively mitigating the typical small-sample learning issue in water conservancy engineering and enhancing the model’s robustness to complex backgrounds.

5.2. The Synergy of Improved Modules

The ablation experiments and visual analyses in Section 4.4 demonstrate that MIDConv and CDIAM achieve effective synergy via the complementarity of their feature extraction mechanisms. MIDConv adjusts convolution kernel offsets to enable dynamic expansion of the network’s receptive field, improving the capability to capture features of irregularly shaped cracks. CDIAM employs channel grouping and global information calibration to enhance pixel-level semantic relationships in complex backgrounds and suppress interference from similar textures. In their combination, the dynamic spatial features provided by MIDConv at the encoder stage and the cross-dimensional semantic enhancement realized by CDIAM at the decoder stage form hierarchical complementarity, jointly resolving the issues of geometric feature extraction for irregular morphologies and semantic ambiguity in complex backgrounds. Quantitative results indicate that the joint use of the two modules raises MIoU to 84.44%, representing increases of 2.08% and 1.66% over single modules, respectively, which validates the positive impact of the two modules’ synergy on improving crack detection accuracy.

5.3. Comparison with Existing Methods and Domain Migration Potential

Comparisons with existing semantic segmentation approaches reveal that the improved model in this study exhibits notable advantages in crack detection under complex backgrounds via scenario-tailored design. In contrast to mainstream open-source models, its core distinction lies in the redesign of the feature extraction framework to address the irregular morphologies and cross-dimensional semantic requirements of plunge pool corridor cracks. Regarding cross-domain recognition capabilities, the model achieves promising results on public building wall crack and pavement crack datasets, demonstrating that its core mechanisms possess cross-scenario applicability.

6. Conclusions

In the domain of hydropower station infrastructure safety, traditional manual inspection and crack detection methods based on conventional digital image processing are plagued by issues such as low efficiency and dependence on manual feature design. Current deep learning models encounter challenges in plunge pool corridor crack detection, including a lack of datasets, complex crack morphologies, and inadequate cross-dimensional semantic information extraction capabilities. To tackle these challenges, this study employs an inspection robot to acquire full-area crack data in plunge pool corridors and establishes a plunge pool corridor crack dataset comprising 4075 images through data augmentation algorithms applied to the original data. Through investigating the effects of integrating morphology-integrated irregular dynamic convolution (MIDConv) and the cross-dimensional interactive attention module (CDIAM) on model feature extraction, a pixel-level crack segmentation model based on an improved U-Net network tailored for this corridor dataset is proposed. The performance of the improved U-Net model is thoroughly validated via quantitative metrics and visual analysis.

(1)

Quantitative assessments reveal that the improved model achieves an MIoU, F1-score, MPA, and accuracy of 84.44%, 93.05%, 89.75%, and 99.46%, respectively. When compared with mainstream semantic segmentation models like DeepLabV3+ and U2Net, it exhibits superior fine-grained segmentation capability for overlapping areas between crack regions and backgrounds. The notable enhancement in F1-score signifies that the model has achieved breakthroughs in balancing precision and recall, effectively minimizing the missed detections of slender cracks (e.g., missing bifurcation structures) and misjudgments of complex backgrounds (e.g., stains, uneven lighting areas) of traditional models.

(2)

Visual comparisons further disclose that the improved model, through the morphology-integrated irregular dynamic convolution (MIDConv), binds the convolution kernel’s offsets in the X/Y axis directions with the linear morphological features of cracks, allowing the receptive field to dynamically expand along crack orientations and thus fully capture continuous edges. Simultaneously, the cross-dimensional interactive attention module (CDIAM) significantly enhances the capability to model pixel-level semantic relationships by partitioning channels into sub-feature groups and calibrating cross-dimensional weights via global average pooling, effectively suppressing background interference and retaining crack details.

(3)

Independently introducing the MIDConv or CDIAM module elevates the MIoU to 82.78% and 82.36%, respectively, whereas their combination further boosts the metric to 84.44%, demonstrating significant complementarity between dynamic feature extraction and cross-dimensional semantic enhancement. In generalization capability tests, the improved model validates its accuracy–efficiency balance advantage—achieved via structured feature group partitioning and convolution kernel offset constraints—on public datasets.

For future work, plans involve expanding multimodal datasets, optimizing model architecture, exploring cross-scenario transfer learning, and developing an integrated detection–repair system to further improve model performance and practical application value.