Theoretical and Simulation Study of Suction Force in Wall-Climbing Cleaning Robots with Negative Pressure Adsorption

Abstract

To address the frequent cleaning requirements of casting molds in bridge tower construction, a wall-climbing cleaning robot based on negative pressure adsorption is designed to safely and efficiently replace manual labor for cleaning tasks. The primary focus of this paper is the establishment of a theoretical model for negative pressure adsorption, along with an analysis of potential adhesion hazards. Initially, the robot’s chassis was designed, followed by the development of a theoretical model for the rotational-flow suction unit that incorporates two critical parameters: the number of blades and their thickness. This model was validated through computational fluid dynamics (CFD) and experimental methods. The findings indicate that, with fewer blades, an increase in blade quantity significantly improves the distribution of nonlinear velocity in the z-plane, resulting in a substantial enhancement of suction force up to a certain limit. As the number of blades increases, the thickness of the blades primarily influences the volume of air within the rotating domain, thereby affecting the suction force; thinner blades are preferable. Moreover, this study reveals that square suction units provide greater suction force compared to circular ones, attributable to their superior negative pressure effect and larger adsorption area. The most critical adhesion risk identified is leakage at the edges of the suction unit.

1. Introduction

Wall-climbing robots offer an efficient alternative to manual labor for high-altitude tasks. Examples of such tasks include cleaning, painting, and reconnaissance of high-rise buildings in the construction industry, inspection and diagnosis of pressure vessels in the chemical and nuclear industries, and flaw detection and descaling of ship hulls in the maritime industry [1,2,3,4]. Recently, many researchers have proposed various types of wall-climbing robots, which have been developed and deployed across diverse engineering applications. Wall-climbing robots can be classified into six types based on their adsorption principles: magnetic attraction [5,6,7,8], electrostatic adhesion [9,10,11,12], bionic adsorption [13,14,15,16], propeller thrust adsorption [17,18,19,20], negative pressure adsorption [21,22,23,24], and hybrid adsorption, and the characteristics of each type are shown in

Table 1. Comparison of the characteristics of various adsorption types.

Adsorption Method		Application Scenario	Advantages	Disadvantages
Magnetic attraction	Permanent magnets	Magnetic wall	Strong adsorption Simple structure	Only applicable to the magnetic wall
	Solenoid
Negative pressure adsorption	Suction cups	Smooth flat wall	Strong adsorption	High Sealing Requirements Complex structure
	Rotational-flow adsorption unit	Wide range of applications	Moderate adsorption	Louder noise High power consumption
Propeller thrust adsorption		Wide range of applications	High maneuverability and safety	Inefficient Noisy Susceptible to external influences
Bionic adsorption	Rheum	Clean smooth wall	No need for extra power Lightweight Low noise	Limited maneuverability Complicated design Elevated costs Reduced load-bearing capacity
	The van der Waals forces
	Claws and thorns	Rough wall
Electrostatic adhesion		Wide range of applications	Simple structure Low energy consumption Lightweight	Slow-moving speed Low load capacity Low load carrying capacity
Hybrid adsorption		Wide range of applications	Integrating the advantages of different adsorption methods	Complex structure Complex control

.

Negative pressure adsorption is more commonly used in the development of wall-climbing robots. Its fundamental principle is that the internal air pressure of the suction unit is lower than the external atmospheric pressure, utilizing the pressure differential to achieve adhesion. The first wall-climbing robot [25] employed a fan to extract air from the adsorption device, creating a negative pressure environment to enable the adhesion function. Subsequently, the optimization of adhesion performance in negative pressure adsorption wall-climbing robots has primarily focused on two aspects: the use of multiple suction cups [26,27] and the enhancement of sealing properties [28,29].

The optimization approaches mentioned above primarily focus on traditional adsorption units. While adhesion performance has been significantly improved, drawbacks such as complex structures and high power consumption have emerged. Furthermore, the requirement for traditional adsorption units to maintain close contact with the working surface for effective adhesion limits the widespread application of wall-climbing robots.

Li and Dong introduced a novel electrically activated sucker [30], which utilizes a motor to drive blades that create a rotating airflow within the suction unit, generating a cup-shaped negative pressure distribution and consequently producing suction force. The rotating airflow effectively obstructs the circulation of air at the edges of the suction unit, solving the traditional vacuum leakage problem. This enables the electromechanical suction cup to adhere to rough, uneven, and even gap-ridden surfaces. Zhou [31] applied the electromechanical suction cup to wall-climbing robots, incorporating a square adsorption chamber and designing a flexible skirt structure to improve adhesion performance. This wall-climbing robot is capable of traversing rough walls and easily navigating larger recesses and protrusions. Chen [32] examined the effect of blade height on the performance of the electromechanical suction unit, finding that an increase in blade height significantly increases the maximum suction force and reduces the rate of decline in suction force with changing gaps. However, this improvement diminishes with further increases in blade height. Furthermore, experiments and CFD analyses indicated that the relationship between power consumption and suction force is primarily determined by the gap size rather than the blade height. Shi [33] developed and validated a theoretical model for the torque and suction force of the electrically activated sucker. By adding a disk at the tip of the blades and installing a flexible skirt around the suction unit, resistance torque was reduced, thereby optimizing adhesion performance and improving the efficiency of the electrically activated sucker.

The impact of blade quantity and thickness on the adsorption performance of cyclone suction units has not been extensively studied, nor has significant research been conducted on wall-climbing cleaning robots equipped with such units. This paper focuses on the robot’s design, the development of a theoretical model, and an analysis of potential adhesion hazards. The robot’s main body was designed first, followed by the development of a theoretical model for the cyclone suction unit, which incorporates the critical parameters of blade quantity and thickness. The model was validated using computational fluid dynamics and experimental methods. This study designs four fan configurations with varying blade quantities to examine their effect on the internal flow field of the suction unit. The findings reveal that, within a certain range, the number of blades is a dominant factor, and increasing blade quantity significantly improves the distribution of nonlinear velocity in the z-plane, resulting in a substantial enhancement in suction force. As the number of blades increases, the thickness of the blades primarily affects the air volume within the rotating domain, suggesting that thinner blades are preferable. Moreover, this study finds that square suction units provide greater suction force than circular ones, owing to their superior negative pressure effect and larger adsorption area. The most critical adhesion risk identified is leakage at the edges of the suction unit.

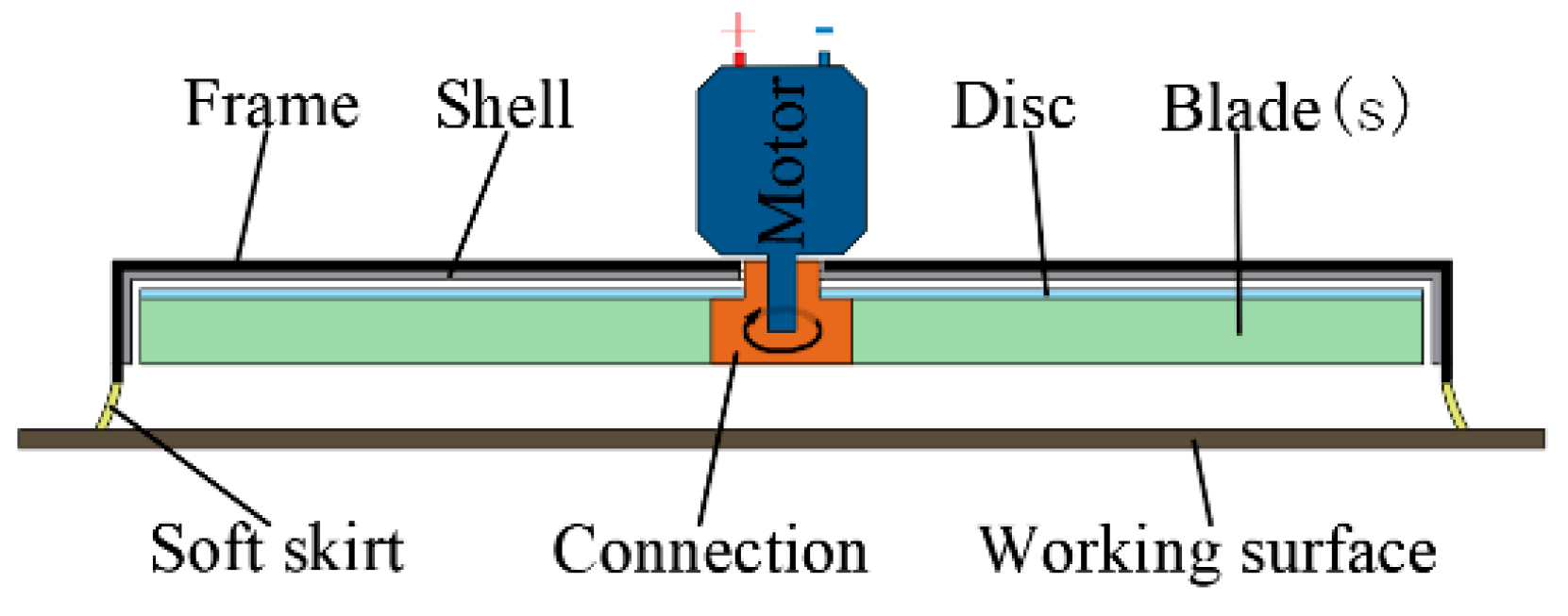
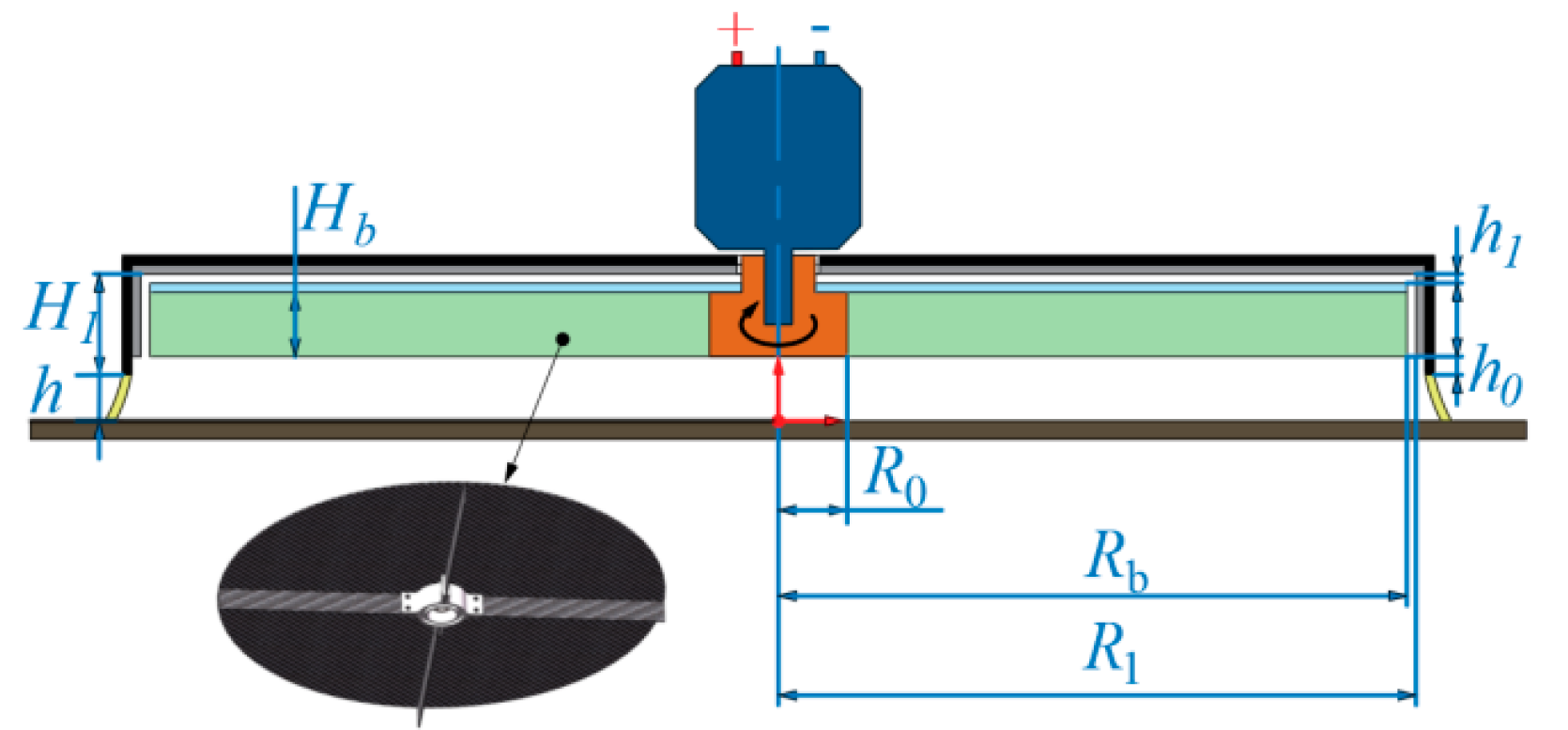
2. Structural Design and Methods

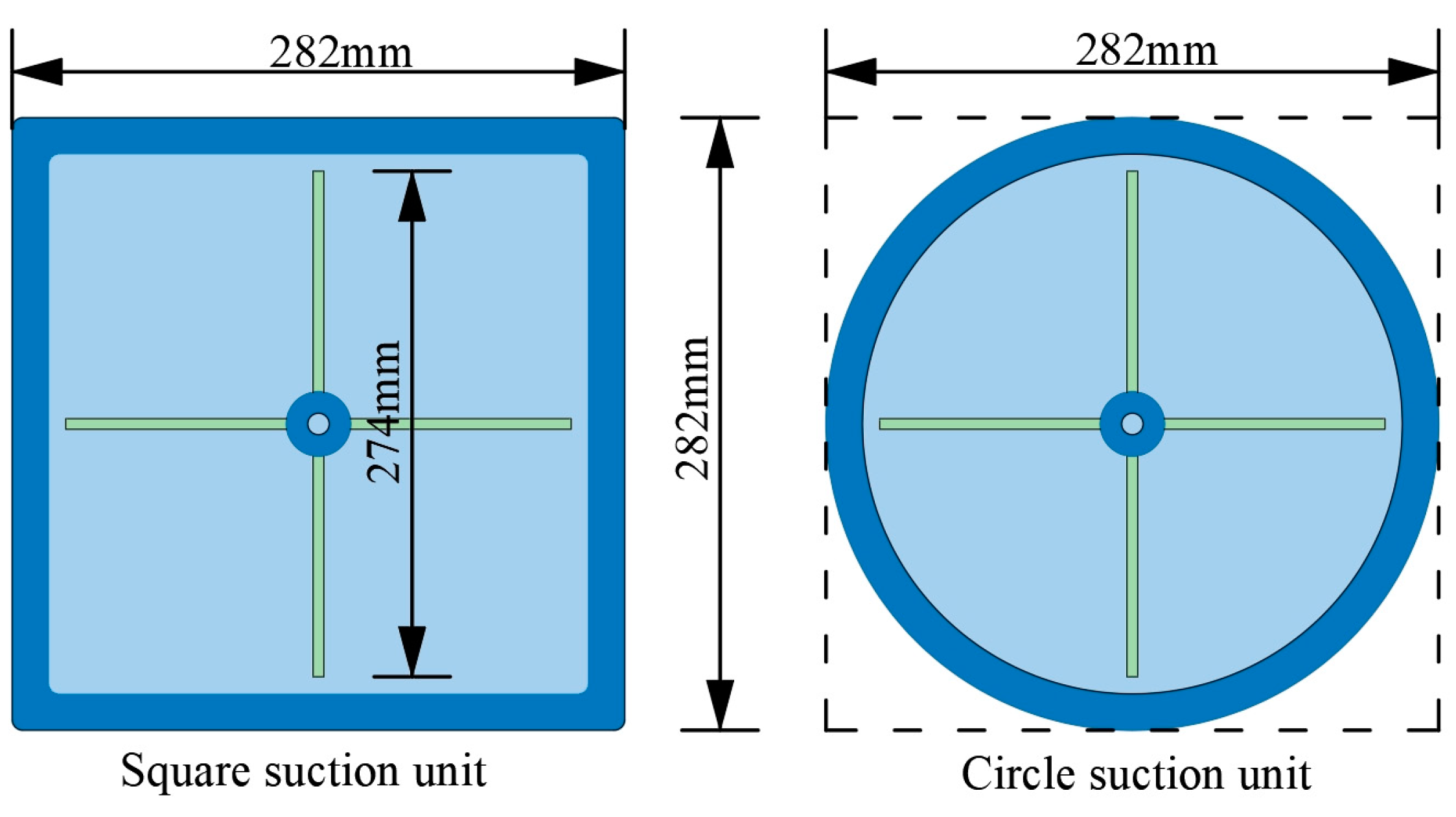
2.1. Structural Design

This paper presents the design of a wall-climbing cleaning robot equipped with an electrically activated rotation-flow suction unit. As illustrated in Figure 1, the robot is composed of five main components: the moving unit, suction unit, cleaning unit, control unit, and frame. The robot features a four-wheel drive mechanism that utilizes differential rotation to facilitate turning, with the four wheels and the carbon fiber frame collectively forming the moving unit.

The electrically activated rotation-flow suction unit is mounted onto the carbon fiber frame, as shown in Figure 2. This unit consists of a brushless motor, a straight-blade fan, a square adsorption chamber, a disk, and a flexible skirt. The brushless motor drives the straight-blade fan to rotate at high speed within the square adsorption chamber, creating a rotating airflow at the edges of the chamber and generating an internal negative pressure. The pressure differential between the internal low pressure and the external atmospheric pressure presses the wall-climbing robot against the surface. The cleaning unit, as shown in Figure 3, includes stands, bearings, a shaft, a motor base, a brushless motor, a cross pin, a roller, and a brush. The brushless motor inside the roller drives the roller and brush to achieve the cleaning effect.

2.2. Apparatus and Method for Measuring Adhesion Force

The suction force is always perpendicular to the suction unit, so measuring the suction force in a horizontal position is also feasible. The suction force measurement platform consists of a frame, a working surface, pressure sensors, sensor seats, and support plates. The key parameters of the suction unit include rotation speed, blade radius, blade height, the gap between the shell and the working surface, and suction force. Blade dimensions are determined during the design phase, rotation speed is measured using an encoder, and motor power is directly measured using a power meter. A data acquisition card is employed to capture signals from the force sensors. The measurement platform is shown in Figure 4, where the wall-climbing robot is mounted on two force sensors, and suction force is derived from the data returned by the sensors. The experimental procedure is as follows: (1) Install the suction unit onto the experimental platform; (2) confirm the gap between the bottom of the suction unit and the working surface; (3) record the current values from the two force sensors to obtain the gravitational force $G$ of the suction unit; (4) activate the brushless motor and set the rotation speed; (5) after stabilization of the rotation speed, record the rotation speed ω and the aggregate values of the force sensors $F_2$; (6) calculate the suction force $F_s=F_2-G$.

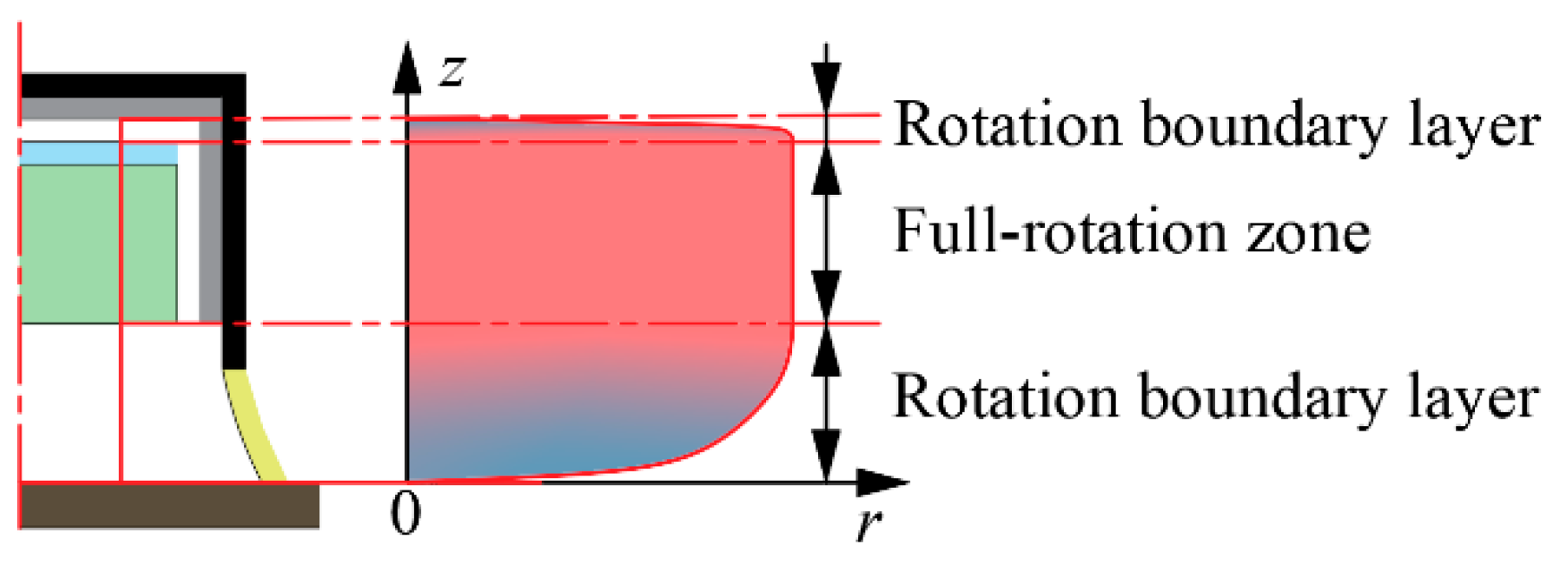
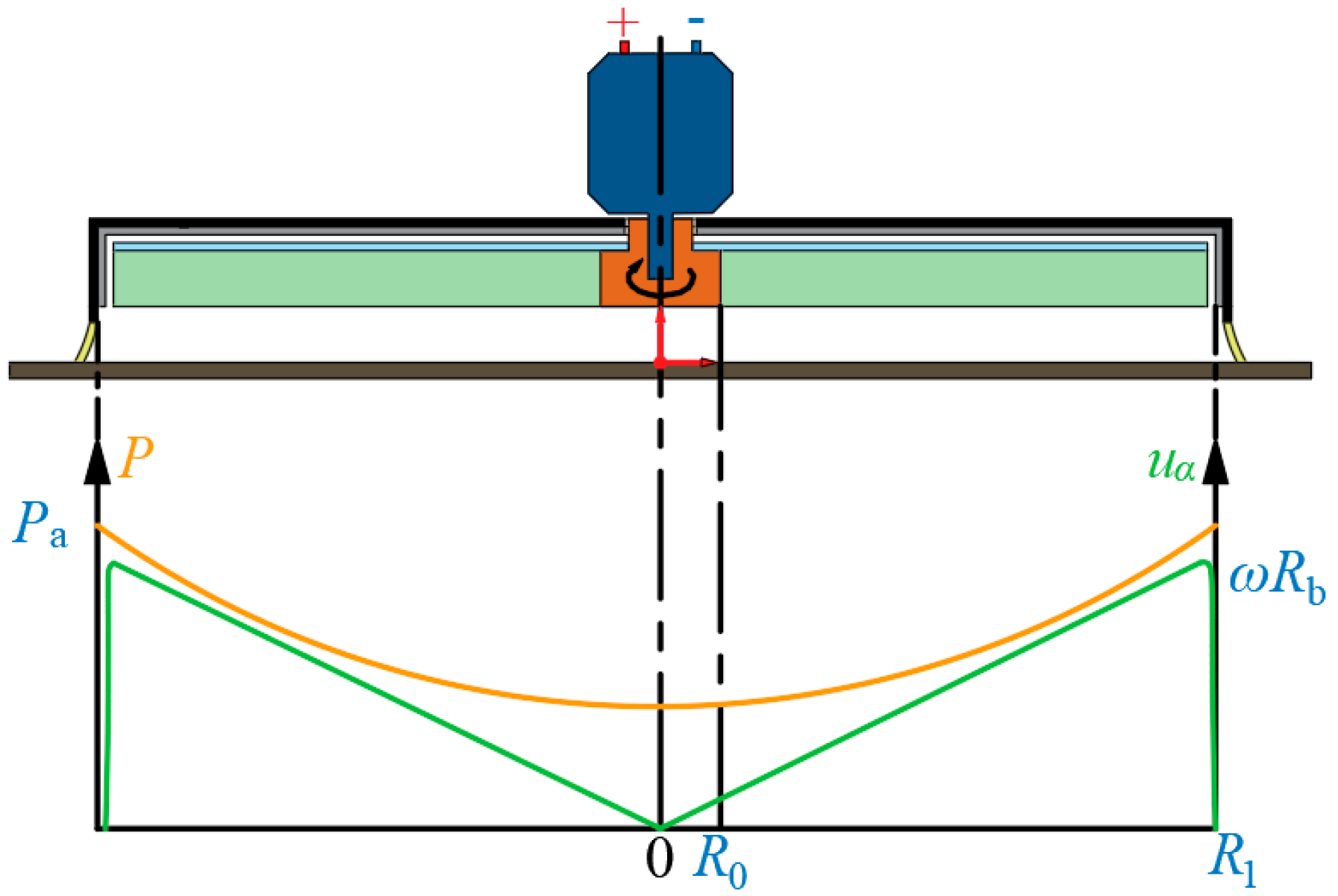
3. Theoretical Modeling

Suction force directly determines the adhesion performance of wall-climbing cleaning robots, and the theoretical model of suction force plays a critical role in research.

The geometric parameters of the suction unit are depicted in Figure 5. In order to establish a theoretical model for suction force, the following assumptions are made:

• The continuum assumption, which posits that a fluid is composed of a continuous distribution of fluid particles.
• The incompressible flow assumption, which holds when the Mach number is within the range of 0–0.3, and the density and temperature of the airflow within the adhesion chamber are considered constants. The maximum Mach number in this suction unit is 0.22.
• Only the tangential air velocity generated by the fan rotation is considered, with the vertical and radial air velocities being neglected.

Based on the assumptions stated above, and by neglecting the viscous and external force terms, the Navier–Stokes equations can be simplified to the following form:

$${\displaystyle \frac{\rho u_{\alpha }^2}{r}}={\displaystyle \frac{\mathsf{\partial }P}{\mathsf{\partial }r}},$$

(1)

In this equation, $\rho$ denotes the air density, $u_a$ represents the circumferential velocity of the airflow, $r$ signifies the radius, and $P$ refers to the pressure.

Within the suction unit, the airflow is not fully developed in the fan region, where $u_a$ represents the tangential velocity at that location, caused by the rotation of the fan blades. In the regions between the fan blades and the shell surface, as well as between the fan blades and the working surface, the flow remains undeveloped and can be characterized by the $1/n$ power law, as shown in Figure 6. This region is referred to as the rotational boundary layer. Some researchers have demonstrated that as the air flow velocity increases, the degree of turbulence intensifies, and, typically, $n$ is assumed to be 7, which is considered a reasonable approximation. Additionally, Chen’s [32] research indicated the presence of secondary flow between the blades, suggesting that the air velocity within this interval cannot reach the rotational speed of the blades, and the airflow in the z-plane does not undergo complete rotation. This paper proposes that the velocity distribution in the z-direction can be expressed as follows:

$$u_{\alpha }=\left\{\begin{array}{cc}(1-e^{-{\displaystyle \frac{N_b}{4}}}){({\displaystyle \frac{z}{h+h_0}})}^{1/n}\omega r& (0\le z<h+h_0)\\ (1-e^{-{\displaystyle \frac{N_b}{4}}})\omega r& (h+h_0\le z<h+H_1-h_1)\\ (1-e^{-{\displaystyle \frac{N_b}{4}}}){({\displaystyle \frac{H_1+h-z}{h_1}})}^{1/n}\omega r& (h+H_1-h_1\le z<h+H_1)\end{array}\right.,$$

(2)

Substituting (2) into (1) and integrating (1) over $0\le z<h+H_1$ gives

$${\displaystyle \frac{\mathsf{\partial }P}{\mathsf{\partial }r}}=(1-e^{-{\displaystyle \frac{N_b}{4}}})({\displaystyle \frac{n}{n+2}}+{\displaystyle \frac{2}{n+2}}{\displaystyle \frac{H_b}{H_1+h}})\rho {\omega }^{2}r=\epsilon \sigma \rho {\omega }^{2}r$$

(3)

In this equation, ε represents the degree of flow development within the z-plane of the suction unit, where σ represents the degree of flow development along the z-axis. It can be observed that both ε and σ are less than 1, indicating that the flow within the suction unit is not fully developed. By integrating the above equation and applying the boundary condition $r=R_1$, $P=P_a$, we can derive the expression for the internal negative pressure P:

$$P={\displaystyle \frac{1}{2}}\epsilon \sigma \rho {\omega }^2\left(r^2-R_1^2\right)$$

(4)

The pressure and velocity distribution within the suction unit are shown in Figure 7. Finally, considering the effects of blade thickness and quantity, the suction force can be expressed as follows:

$$F_S={\displaystyle \frac{1}{2}}\epsilon \sigma \pi \rho {\omega }^2[{\displaystyle \frac{1}{2}}\pi (R_1^4-R_0^4)-{\displaystyle \frac{1}{3}}{N}_{b}t(R_1^3-R_0^3)-\pi R_1^2(R_1^2-R_0^2)+N_{b}t{R}_1^2(R_1-R_0)]$$

(5)

In this equation, $R_0$ represents the connection radius, $R_1$ denotes the radius at which the fan blades rotate, $N_b$ is the number of blades, and $t$ is the blade thickness. All parameter details can be found in

Table 2. Parameter table.

Symbol	Quantity	SI Unit
Fs	Suction force	N
g	Gravitational acceleration	m/s2
G	Gravitational force	N
ρ	Air density	kg/m3
h	Clearance between the surface and the suction unit	m
ω	Rotation speed	Rad/s
Hb	Height of blades	m
H1	Height of the shell	m
R0	The radius of the connector	m
Rb	The radius of the fan blade	m
R1	Inner radius of the shell	m
Nb	The number of fan blades
t	The thickness of the fan blades	m

.

4. Results

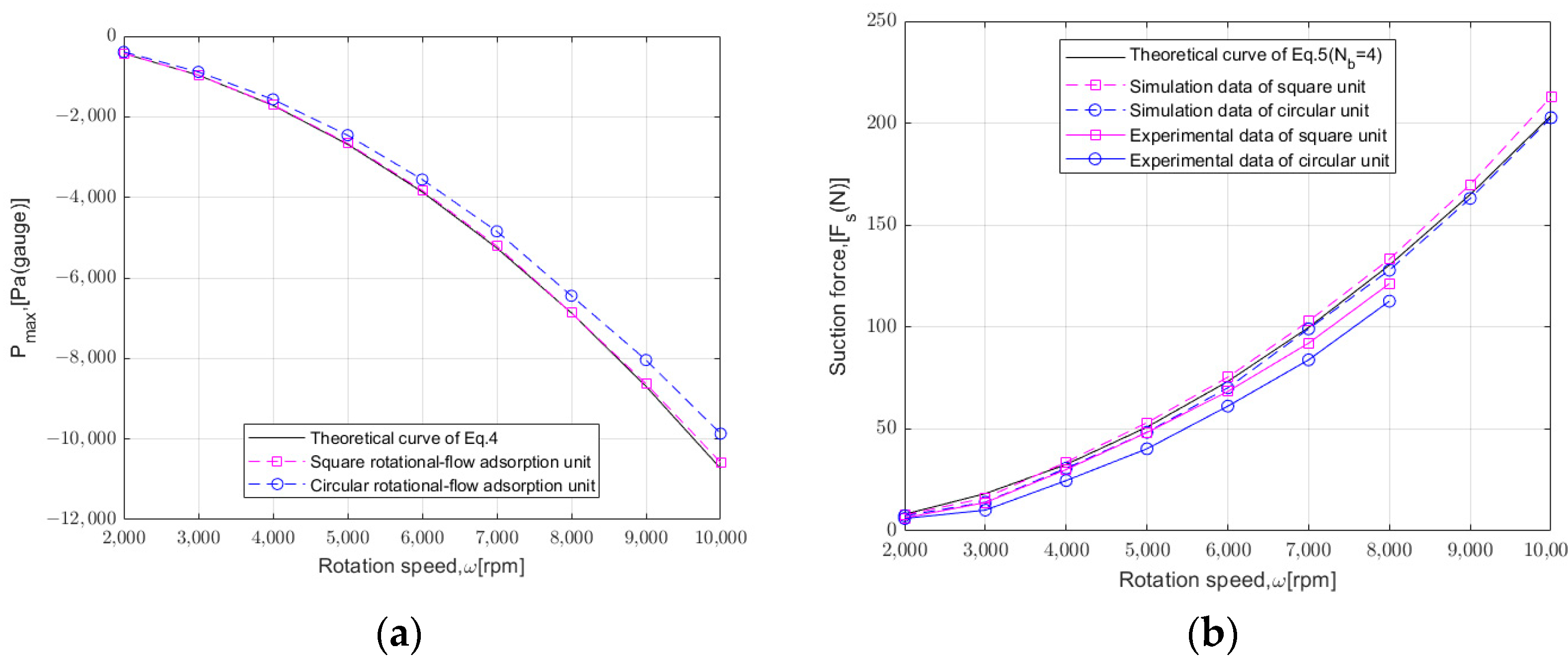
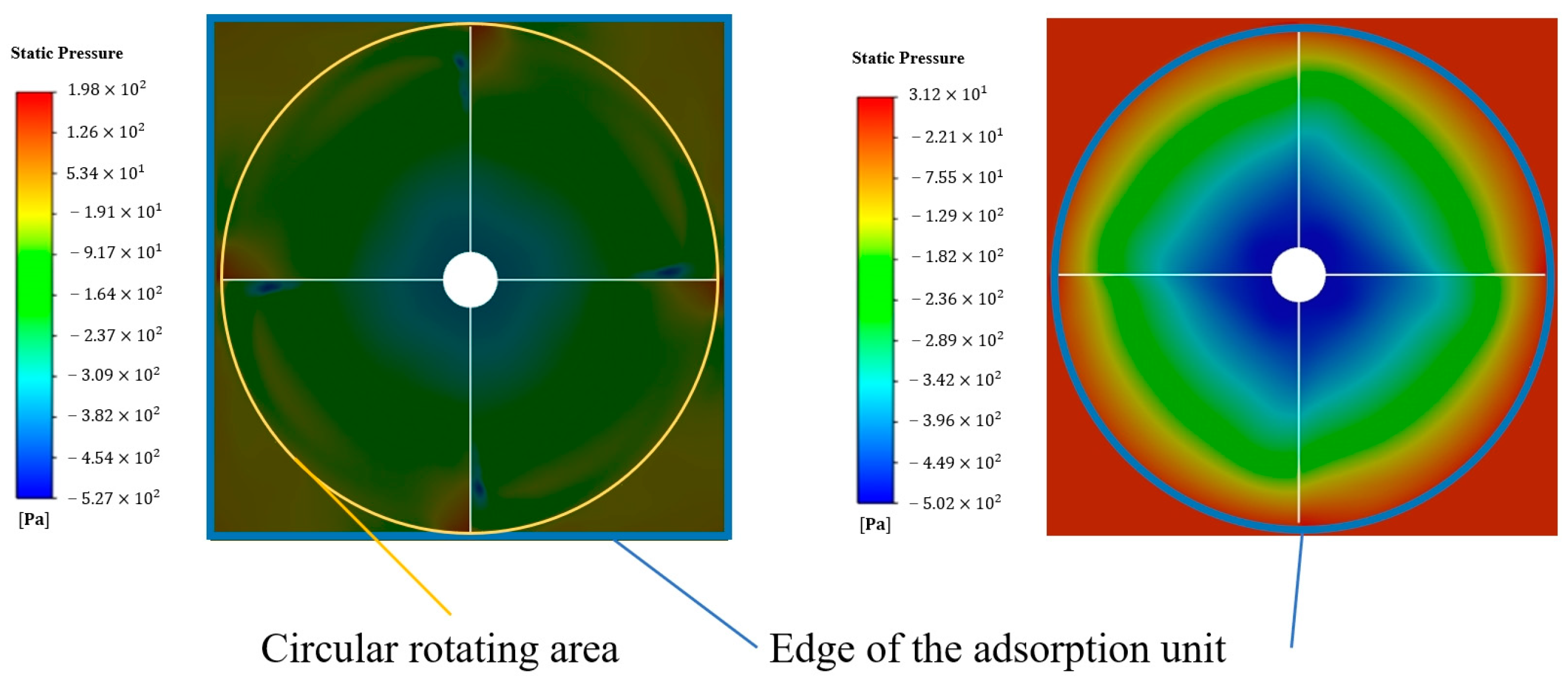
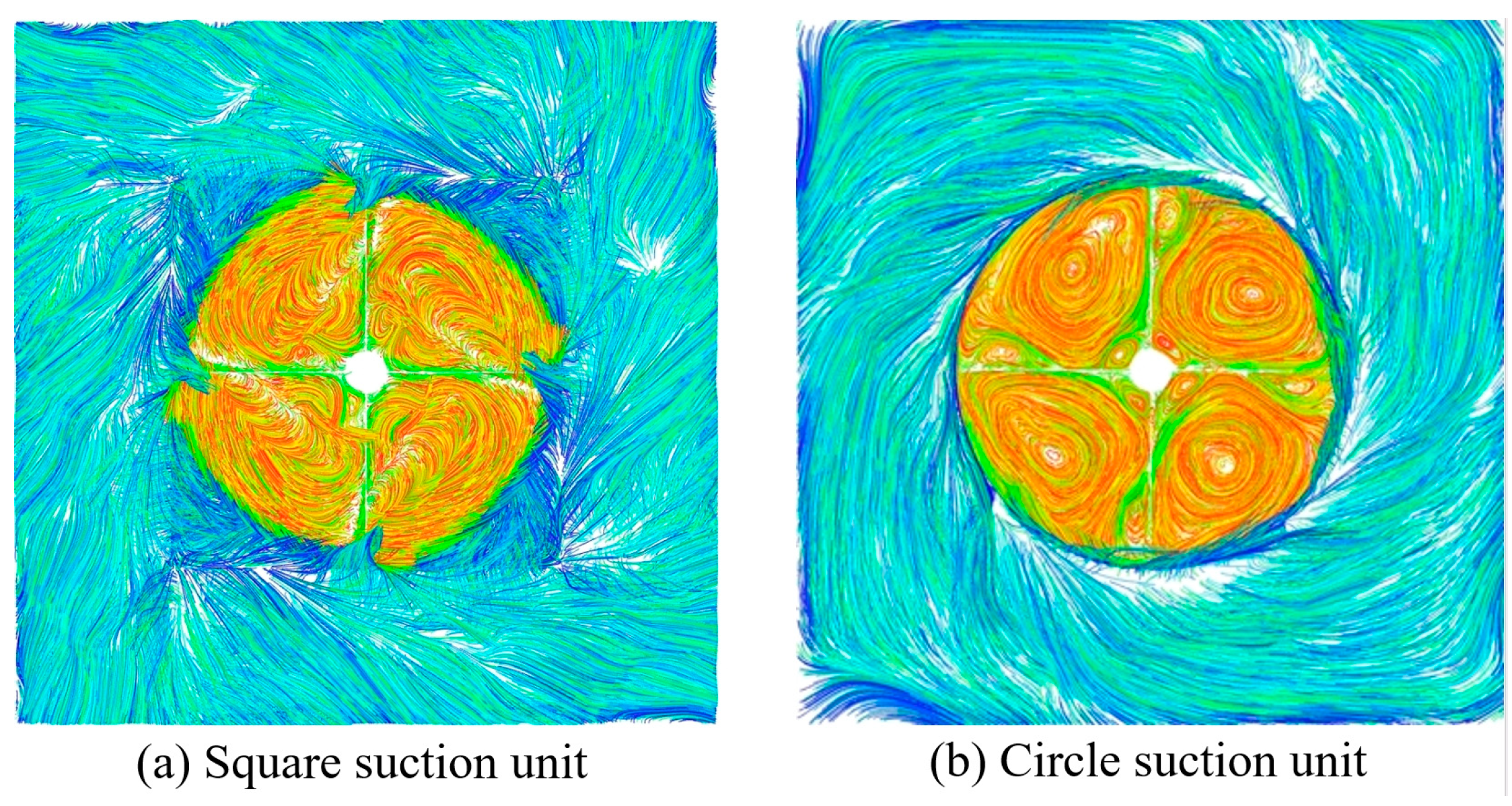
4.1. Comparison of Square and Circular Suction Units

As shown in Figure 8, during the experimental procedure, the dimensions of the two suction units are as follows: the square suction unit measures 282 × 282 mm, and the circular suction unit has a radius of $R=141$ mm. The shell height is 22 mm, and its thickness is 2 mm. The blades have a length of 137 mm, a height of 14 mm, and a thickness of 1 mm. Figure 9 illustrates the negative pressure versus rotation speed and suction force versus rotation speed curves for both square and circular suction units, with a gap height of 10 mm, including both simulation and experimental data. The data indicate that the square suction unit generates a greater suction force compared to the circular suction unit.

As shown in Figure 10, although the maximum negative pressure in the central area of the square suction unit is lower than that of the circular suction unit, the negative pressure gradient in the square suction unit is smaller along the $r$-direction, and the four corners can also provide negative pressure. Calculations indicate that the suction force of the square suction unit increases by approximately 16%, which is in close agreement with the experimental results.

As shown in Figure 11, flow field visualization analysis reveals that the square suction unit has a larger adhesion area with more negative pressure regions. Additionally, the boundary layer of the internal rotating airflow in the square suction unit is larger, resulting in better sealing effects compared to the circular suction unit.

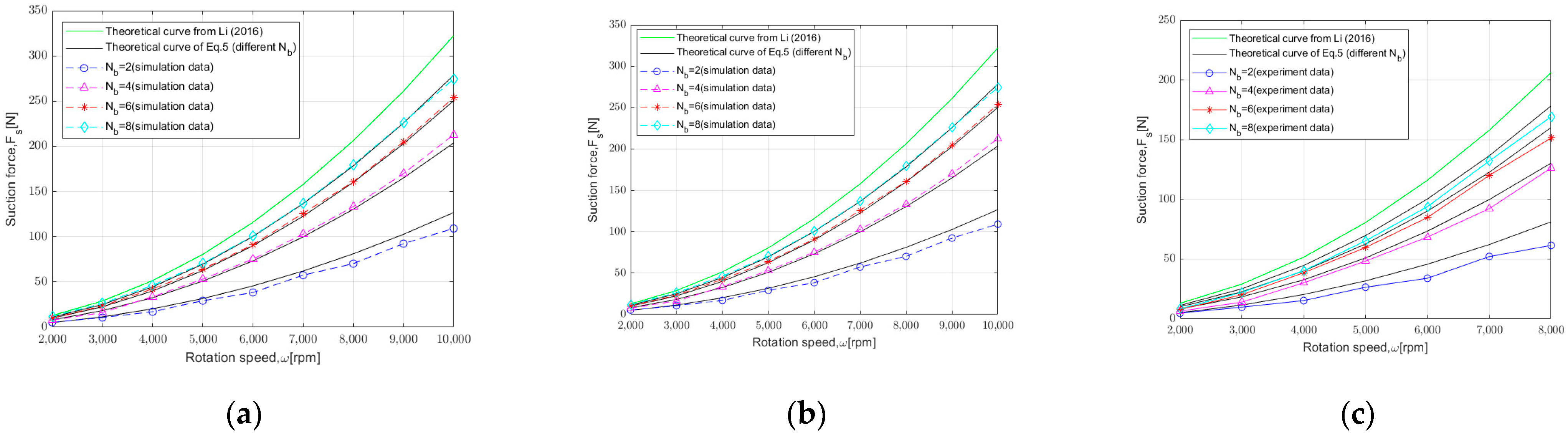
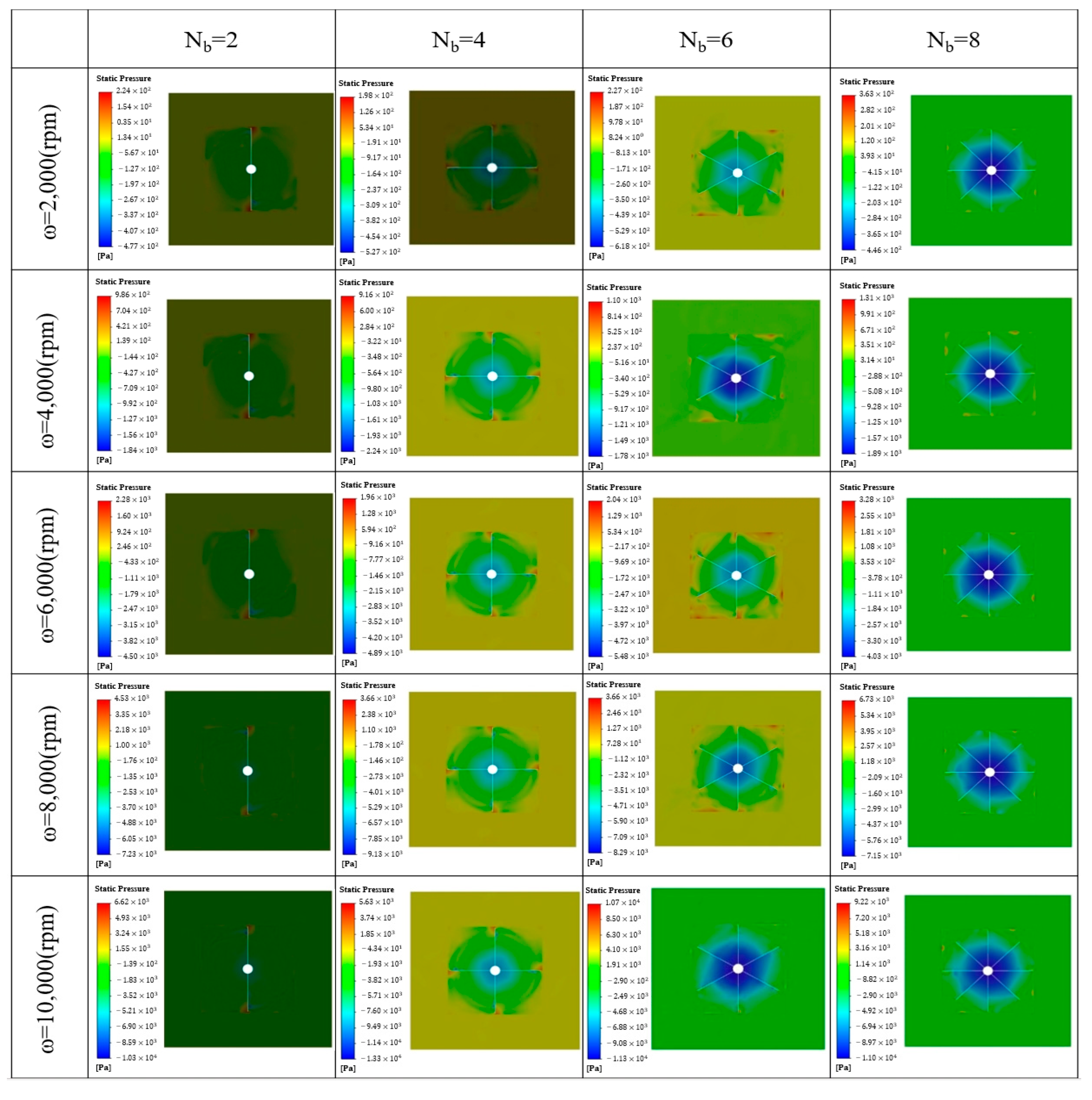
4.2. The Effect of Blade Quantity on Adsorption

Li [30] mentioned that, with all else being equal, the suction force provided by six blades is the highest. However, she only presents this conclusion without providing specific justifications. This paper uses Fluent software (v.5.1.0) to simulate the internal flow field of the suction unit with varying numbers of blades and conducts experiments.

Further analysis of the simulation and experimental data, as shown in Figure 12, reveals that the effect of blade quantity on negative pressure and suction force diminishes with increasing blade numbers. Figure 13 displays the internal negative pressure under different blade quantities and rotation speeds. It can be observed that as the number of blades increases, the negative pressure area expands, leading to a significant improvement in the negative pressure value. Once the number of blades reaches a critical value, the improvement effect becomes negligible. It can also be observed that, compared to Li’s [30] model, the model presented in this paper more accurately reflects the relationship between the number of blades and the suction force.

Through flow field visualization analysis, as shown in Figure 14, an increase in the number of blades results in a reduction in secondary flow recirculation between the blades. This reduction in secondary flow recirculation is the primary reason why an increase in blade number enhances suction force.

In theory, without considering the blade thickness, the more blades, the better. However, in practical applications, blades have thickness, and factors such as manufacturing, installation, and motor power must be taken into account. This study concludes that the optimal number of blades is four or six, with a blade thickness of 1 mm.

4.3. The Impact of Blade Thickness on Adsorption

Blade thickness significantly influences suction force, with an increase in thickness leading to a reduction in the adhesion performance of the suction unit. This paper compares simulation results to generate pressure contour plots and suction force data for different blade thicknesses. As shown in Figure 15, an increase in blade thickness decreases the negative pressure value at the center of the suction unit. The data in

Table 3. Flow field visualization under different blade counts.

	Thicknesses/mm	a	b	c	d	e
Air proportion	t = 1	98.4%	98.0%	97.5	97.1%	90.5%
	t = 10	94.7%	90.5%	86.3%	82.2%	27.9%
Suction force/N	t = 1	5.4	7.8	10.2	11.9	14.5
	t = 10	3.8	8.1	9.4	10.3	5.6

indicate that with a larger number of blades, the effect of blade thickness on suction force is more pronounced. When the blade volume fully occupies the rotational area of the suction unit, it ceases to generate negative pressure. The weight of the wall-climbing robot is 1.98 kg. In the experiment ($N_b=4, t=1$), the maximum suction force obtained was 133.3 N. The ratio of the maximum suction force to the gravitational force was 6.73.

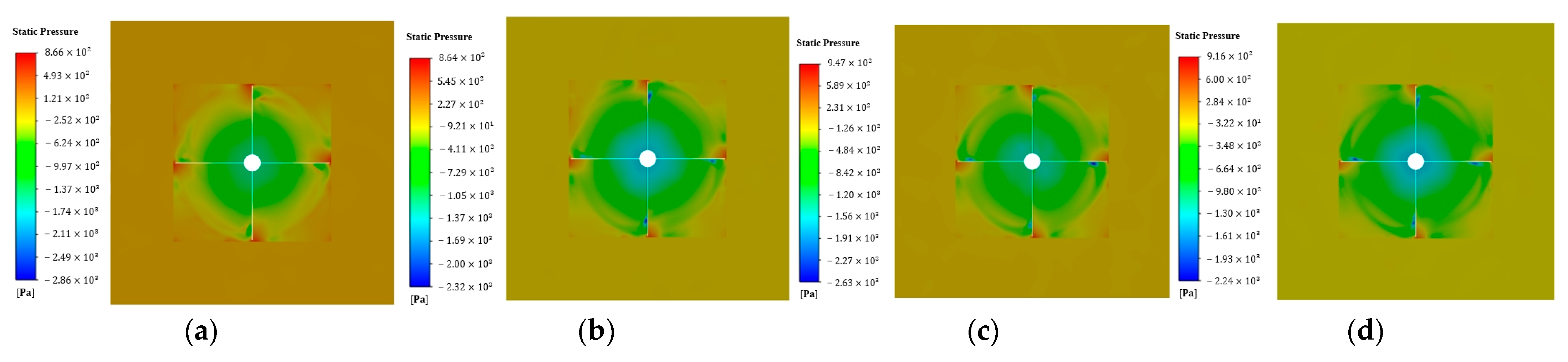
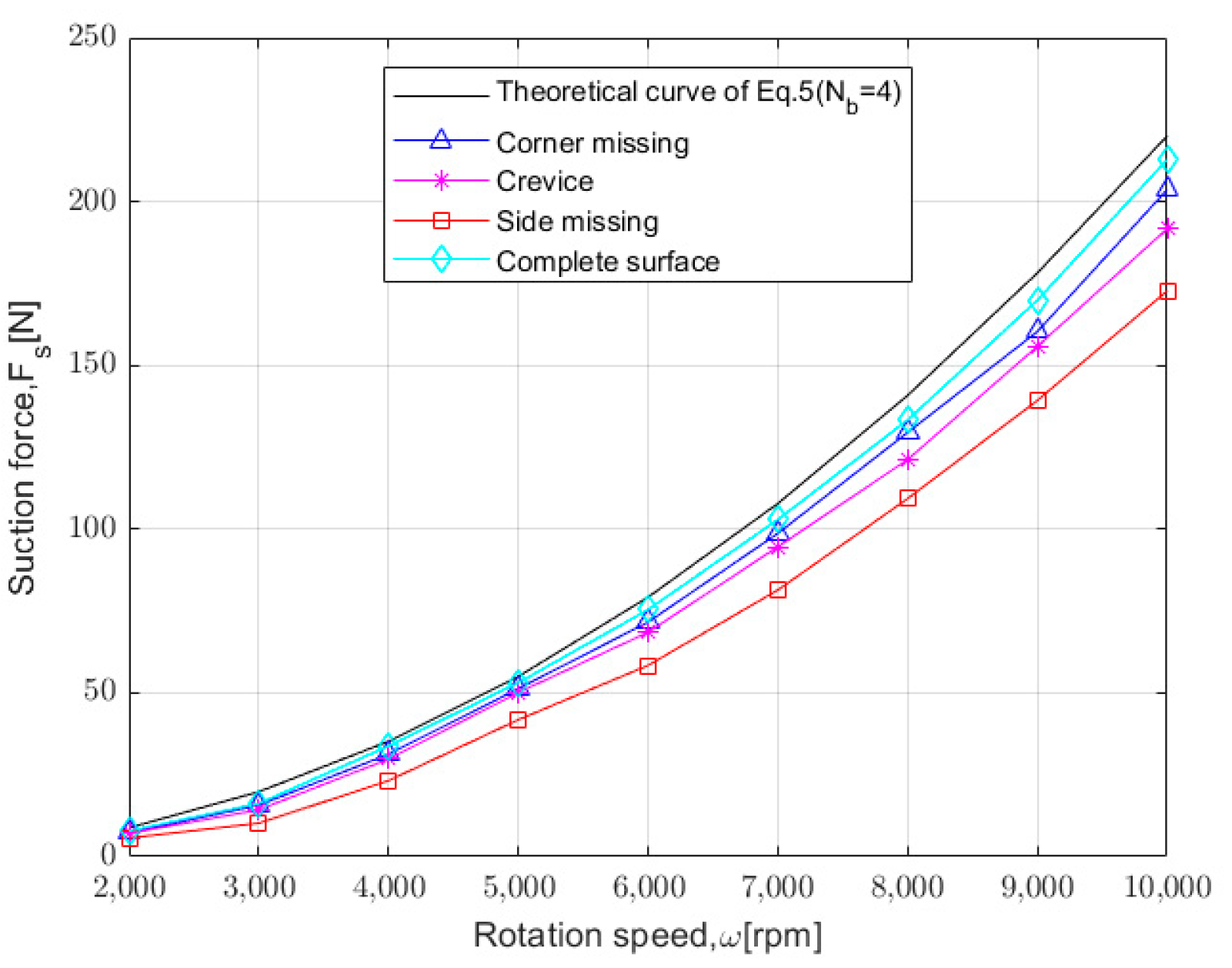
4.4. The Impact of Leakage Zones on Adsorption

Although the new suction unit has addressed the leakage issues of traditional suction cups, permitting a small gap between the suction unit and the working surface, attention must still be given to leaks from areas where the surface is missing, as a loss of internal negative pressure could pose a risk of the wall-climbing cleaning robot falling. Figure 16 illustrates several dangerous operating conditions encountered by the wall-climbing robot, with Figure 16a showing leakage on one side of the suction unit, Figure 16b showing leakage at one corner, and Figure 16c showing leakage when the robot passes through a gap, with all three having the same leakage area. Figure 17 shows that when the missing area does not compromise the integrity of the rotating airflow, the internal negative pressure of the suction unit remains largely unaffected and can still maintain negative pressure. It can be observed that, compared to the intact surface condition, the size of the blue area near the center is largest for corner leakage, followed by gap leakage, and smallest for side leakage. This indicates that, among the three leakage scenarios, side leakage is the most dangerous, as it compromises the integrity of the rotating airflow.

To further investigate the leakage conditions under different scenarios, this paper presents the airflow patterns for various leakage conditions, as shown in Figure 18. The red box highlights the leakage area. When there is a side gap, external airflow enters the fan blade rotation area; when there is a corner gap, external airflow creates a vortex at the corner of the suction unit; and when encountering a gap, a vortex is generated inside the gap, facilitating air exchange with the external atmosphere.

The suction force data under leakage conditions are shown in Figure 19, with results consistent with previous scenarios. Therefore, the wall-climbing cleaning robot can easily handle corner leakage and gap situations during operation, but the risk is greatest with side leakage, particularly when it compromises the integrity of the rotating area. Hence, the robot should avoid leakage in the rotating area during operation.

5. Conclusions

In this study, a wall-climbing robot equipped with a rotating airflow suction unit was designed to clean wall surfaces. The internal fan of the suction unit, driven by a DC brushless motor, generates negative pressure to facilitate adhesion. This paper primarily investigates the impact of the number of fan blades, blade thickness, and adhesion leakage area on the adhesion effect, and presents the following conclusions:

(1)

Compared to circular suction units, square suction units provide greater suction force for two main reasons: a larger adhesion area and reduced loss of the internal pressure gradient.

(2)

An increase in the number of blades improves the distribution of nonlinear velocity in the z-plane. Suction force increases significantly with the number of blades up to a certain point, after which further improvements are minimal. In practical applications, four or six blades are appropriate.

(3)

As the number of blades increases, the thickness of the blades primarily affects the air volume in the rotating domain, influencing suction force; thinner blades are preferable.

(4)

This paper analyzes three dangerous working conditions that the wall-climbing cleaning robot may encounter, with edge leakage being the most dangerous, followed by corner leakage, and gap leakage having the least impact.

6. Future Work

Research on wall-climbing cleaning robots holds significant practical engineering implications, and continued investigation is necessary. Future research can focus on the following areas:

(1)

The design of wall-climbing cleaning robots requires further refinement, including balancing the load (cleaning equipment) with cleaning effectiveness, developing more efficient mobility strategies, and achieving lightweight and low-noise operation.

(2)

This study found that the internal airflow in the square suction unit is more turbulent, particularly near the blades, which negatively impacts adhesion. Optimizing blade design and the internal structure of the square suction unit to enhance the integrity of the rotating airflow is a promising area for further research.

(3)

A comprehensive and systematic analysis should be conducted, considering factors such as the mechanics, kinematics, and motor power of the wall-climbing robot on the wall surface.

(4)

The most critical issue for negative pressure adhesion is vacuum leakage. Further investigation into the anti-leakage theory of suction units and the development of safety measures to mitigate leakage are essential.

(5)

Overcoming obstacles is a critical function of wall-climbing robots. The impact of protruding obstacles on wall-climbing robots, as well as the influence of the internal flow field of the suction unit, are important areas for further investigation.