Abstract
With the rapid advancement of aerospace technology, the maneuverability of spacecraft has increasingly improved, creating a pressing demand for star sensors with a high attitude update rate and high precision. Star identification, as the most complex and time-consuming algorithm of star sensors, faces stringent requirements for enhanced identification speed and an enhanced identification rate. Furthermore, as the space environment is becoming more complex, the need for star sensors with heightened detection sensitivity is growing to facilitate real-time and accurate alerts for various non-cooperative targets, which has led to a sharp increase in the number of high-magnitude navigation stars in the star catalog, significantly impeding the speed and rate of star identification. Traditional methods are no longer adequate to meet the current demand for star sensors with high identification speed and a high identification rate. Addressing these challenges, a voting-based star identification algorithm using a partitioned star catalog is proposed. Initially, a uniform partitioning method for the star catalog is introduced. Building on this, a navigation feature library using partitioned catalog neighborhoods as a basic unit is constructed. During star identification, a method based on a voting decision is employed for feature matching in the basic unit. Compared to conventional methods, the proposed algorithm significantly simplifies the navigation feature library and narrows the retrieval region during star identification, markedly enhancing identification speed while effectively reducing the probability of redundant and false matching. The performance of the proposed algorithm is validated through a simulation experiment and nighttime star observation experiment. Experimental results indicate an average identification rate of 99.760% and an average identification time of 8.861 milliseconds, exhibiting high robustness against position errors, magnitude errors, and false stars. The proposed algorithm presents a clear advantage over other common star identification methods, meeting the current requirement for star sensors with high star identification speed and a high identification rate.
1. Introduction
A star sensor is one kind of high-precision, highly reliable autonomous attitude measurement instrument that uses stars as measurement objects and is now widely used in space payloads such as spacecraft [1]. When first activated or experiencing being lost in space, the star sensor needs to image the starry sky, and achieves attitude measurement after star extraction, centroid positioning, and star identification. The primary working principle of star sensors involves imaging the starry sky using an optical system and image sensor, extracting stars and locating centroids to obtain the position and brightness information of stars on the image sensor, and identifying corresponding navigation stars in the star catalog through a star identification algorithm. Then, the attitude of the star sensor relative to the inertial coordinate system is measured [2]. With the rapid development of aerospace technology and the increasing maneuverability of spacecraft, the demand for star sensors with a high attitude update rate and precision is quite urgent. Since star identification represents the algorithmically most complex and time-consuming step in the working process of star sensors [3], heightened demand for the identification speed and rate of the star identification algorithm has been put forward. Additionally, as the space environment becomes increasingly complex and the need to provide real-time, accurate warnings for various non-cooperative targets grows, the demand for the detection sensitivity of star sensors also increases, leading to a rapid increase in the number of high-magnitude navigation stars in the star catalog [4], severely impacting the speed and rate of star identification. Consequently, star identification algorithms with fast identification speed and a high identification rate are the crucial technology in the current research field of star sensors.
Depending on the recognition strategy, star identification algorithms are primarily divided into three categories: subgraph isomorphism, pattern recognition, and neural network methods [5]. The subgraph isomorphism methods match the geometrics of stars in the star image with navigation stars in the star catalog. The pattern recognition methods use pattern features of stars in the star image with navigation stars in the star catalog. The neural network methods employ a trained network structure to match stars in the star image with navigation stars in the star catalog based on distribution features [6].
The most fundamental method of the subgraph isomorphism methods is the triangle algorithm, characterized by its requirement for fewer stars and strong portability in embedded systems. Theoretically, star identification can be performed with no fewer than three stars in the star image. However, the features of the triangle algorithm are simplistic, easily leading to redundant and false matching during star identification, and a large number of feature matches influences the identification speed. Plenty of scholars have proposed different subgraph isomorphism methods based on the triangle algorithm, mainly divided into two categories: One involves increasing the dimensionality of features to enhance the identification rate. Mortari et al. [7] introduced the pyramid algorithm, which added an angular distance feature to the triangle algorithm. Fan et al. [8] proposed the double-triangle algorithm, doubling the feature dimensionality compared to the triangle algorithm. Hernández et al. [9] used a polygonal algorithm to increase feature dimensionality. The other involves reducing the number of feature matches to improve identification speed. You et al. [10], Liu et al. [11], Wang et al. [12], Fan et al. [13], and Mehta et al. [14] each proposed different subgraph isomorphism algorithms, but their star identification strategies are broadly similar, dividing star identification into coarse and fine identification stages. Stars are coarsely identified first within a constrained range of the star catalog, and then stars are finely identified based on the results of the coarse identification. Kim et al. [15] introduced a method to improve identification speed through linked-list matching. Wang et al. [16] used a hash table to enhance retrieval speed.
The most fundamental pattern recognition method is the grid algorithm [17], noted for its robustness against position errors. However, the need to rotate the star image during star identification significantly impacts the speed of the algorithm. Many scholars have developed different pattern recognition methods based on the grid algorithm, which can be broadly categorized into two types: One establishes different pattern features to improve the performance of the grid algorithm. Liao et al. [18] improved the grid algorithm based on redundant coding and Li et al. [19] introduced a grid algorithm combined with angular distance. Kim et al. [20] and Wei et al. [21] suggested using matrix singular values as pattern features. Mehta et al. [22], Zhu et al. [23], Schiattarella et al. [24], Zhao et al. [25], and Luo et al. [26] introduced methods using vectors composed of star positions as pattern features. Samirbhai et al. [27] and Sun et al. [28] employed Hamming distance as a pattern feature, while Roshanian et al. [29] used Euclidean distance as a pattern feature for identification. The other uses different star image segmentation methods from the grid algorithm. Jiang et al. [30] initially proposed a polygonal grid algorithm that segments the star image using polygonal grids. Following this, Jiang et al. [31] introduced a radial and circular grid algorithm that segments the star image using radial and circular grids. Zhao et al. [32], Wei et al. [33], Liu et al. [34], and Du et al. [35] proposed improvements based on the radial and circular grid algorithm. Notably different from the grid algorithm, the radial and circular algorithm features rotational invariance, thus eliminating the need to rotate the star image during identification and significantly enhancing identification speed.
With the rapid development and widespread application of neural network algorithms, lots of scholars have proposed star identification algorithms based on various network structures. Hongchi et al. [36] used an LVQ network structure for star identification. Jiang et al. [37] employed an ant colony algorithm, Xu et al. [38] utilized an RPNet network structure, and Wang et al. [39] applied a CNN structure for star identification. Rijlaarsdam et al. [40] adopted a simple network structure, Jiang et al. [41] implemented a Hierarchical CNN structure, and Yang et al. [42] applied a 1D-CNN structure in star identification.
Comparative analysis of various star identification algorithms reveals the following conclusions [43]: Subgraph isomorphism methods have relatively low algorithmic complexity and strong portability in embedded systems, but low feature dimensionality often leads to redundant and false matching, and they require a large number of feature matches, resulting in slow identification speed. Pattern recognition methods have moderate algorithmic complexity and portability, but the construction of pattern features is limited by the number of stars in the star image. Insufficient stars can lead to redundant and false matching during the feature matching. Neural network methods have high algorithmic complexity and poor portability in generic star sensor platforms, and the performance is greatly influenced by the star dataset, leading to low stability and weak robustness.
In light of the shortcomings present in each category of star identification algorithms, and after considering the performance and portability, we propose a voting-based star identification algorithm using a partitioned star catalog based on subgraph isomorphism methods. Initially, a method for uniform partitioning of the star catalog is introduced. Building on this, a navigation feature library using partitioned catalog neighborhoods as a basic unit is constructed. During star identification, a method based on a voting decision is employed for feature matching in the basic unit. Different from other star identification algorithms, the proposed algorithm significantly simplifies the navigation feature library and narrows the retrieval region during star identification, markedly enhancing identification speed while effectively reducing the probability of redundant and false matching.
The paper is organized as follows: A method for uniform partitioning of the star catalog is put forward in Section 2. Based on the partitioned star catalog, the construction of the navigation feature library is explained in Section 3.1, and then a voting-based star identification algorithm is proposed in Section 3.2. A simulation experiment and nighttime star observation experiment are conducted in Section 4 and Section 5, respectively, to validate the performance of the proposed algorithm. Finally, in Section 6, the methodology and experimental results are summarized.
2. Star Catalog Partitioning
In this section, the star catalog and its preprocessing method are firstly introduced. Then, a method for uniform partitioning of the star catalog is put forward.
2.1. Star Catalog Preprocessing
A star catalog is a database containing information such as the number, right ascension, declination, and brightness of stars. Generally, the brightness of a star is indicated by its apparent magnitude, which relates to the irradiance and the distance from Earth. The irradiance of Vega is denoted as . Defining the apparent magnitude of Vega as zero, the irradiance of the star with apparent magnitude is given by the following:
It is evident from Formula (1) that, with apparent magnitude increases, the irradiance of the star decreases by a factor of 2.512, and a higher apparent magnitude indicates lower irradiance.
Figure 1 shows the distribution of the right ascension and declination of stars in the star catalog supplied by the National Astronomical Observatory of the Chinese Academy of Sciences, which includes 77,189 stars with an apparent magnitude of up to 10, detailing their number, right ascension, declination, and brightness.
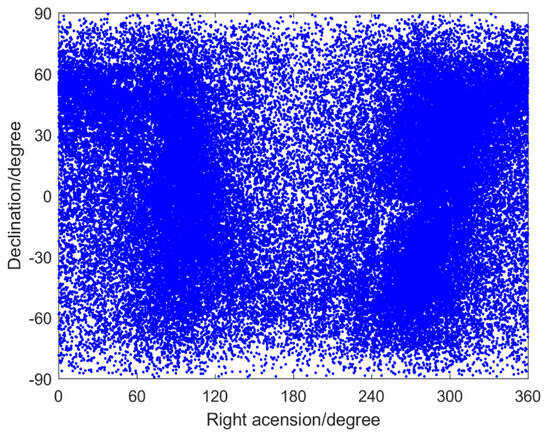
Figure 1.
The distribution of the right ascension and declination of stars in the star catalog.
As shown in Figure 1, there are a large number of stars in the star catalog. However, stars of high apparent magnitude or with small angular distance will reduce the identification speed and rate during star identification. Therefore, star catalog preprocessing is necessary before it is used.
Due to the limitation of the detection sensitivity, stars in the star catalog with brightness below the detection sensitivity cannot be detected during the imaging process of the star sensor. Thus, it is necessary to eliminate stars whose magnitude exceeds the detection sensitivity of the star sensor. Moreover, to ensure the position accuracy of stars in the star image, the energy of the stars is dispersed across multiple pixels of the image sensor by a defocusing technique. If two stars in the star catalog are too close in angular distance, the two stars may be merged into a single star on the image sensor, thus degrading position accuracy and affecting the identification rate. Therefore, it is crucial to eliminate double stars with angular distances that are too small.
2.2. A Method for Uniform Partitioning of the Star Catalog
Generally, in a star catalog, the right ascension is in the range of , and the declination is in the range of . During the work of the star sensor, its field of view limits it to capturing only a portion of the sky, meaning only a subset of stars in the star catalog is included in the field of view of the star sensor. However, the majority of algorithms require repeated retrieval of stars from the entire star catalog during the star identification process. This frequent retrieval increases the time taken for feature matching, which easily leads to redundant and false matching and significantly affects the identification speed and rate. Therefore, we propose a method for uniform partitioning of the star catalog which approximates the entire celestial region as a celestial sphere, evenly divides the celestial sphere into several regions, and maps them to the stars in the star catalog.
As illustrated in Figure 2, depicts a celestial coordinate system, and connections between the center of the celestial sphere and the vertices of an arbitrary face in a regular icosahedron form a pyramid. The pyramid intersects with the celestial sphere, uniformly dividing it into 20 regions, each of which is numbered . Each of these 20 regions is uniformly further subdivided into zones, resulting in a total of zones across the entire celestial sphere. The theoretical range for is , but the appropriate value should be chosen based on the field of view of the star sensor in practical applications. Once parameter is determined, the stars in the star catalog are mapped to the corresponding celestial sphere zones to complete the star catalog partitioning.
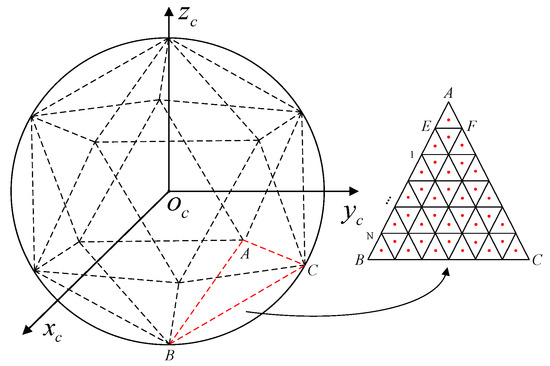
Figure 2.
Uniform partitioning of celestial sphere. The points A, B and C are the vertices of the regular icosahedron described by dotted lines.
Taking the regular triangle in Figure 2 as an example, let the spatial coordinates of vertex be , vertex be , and vertex be . Then, the spatial coordinate of any point within the triangle can be expressed as follows:
where and are the weight values.
Defining the spatial coordinate of a star on the celestial sphere as , the ray equation from the center of the celestial sphere to the star can be represented as follows:
where is a weight value.
If the star belongs to the celestial sphere zone corresponding to triangle , then the ray intersects with triangle , meaning that there is a common solution between Formulas (2) and (3), which implies the existence of a set of weight values , , that satisfy the following:
Letting , and , Formula (4) is updated to the following:
Solving Equation (5) results in the following:
If the solution of Equation (6) satisfies and , the star belongs to the celestial sphere zone corresponding to triangle ; conversely, the star X does not belong to the zone. Figure 3 visually demonstrates the scenario in which the star belongs to the celestial sphere zone. The ray from the center of the celestial sphere to the star intersects with the equilateral triangle in the regular icosahedron corresponding to the celestial sphere zone.
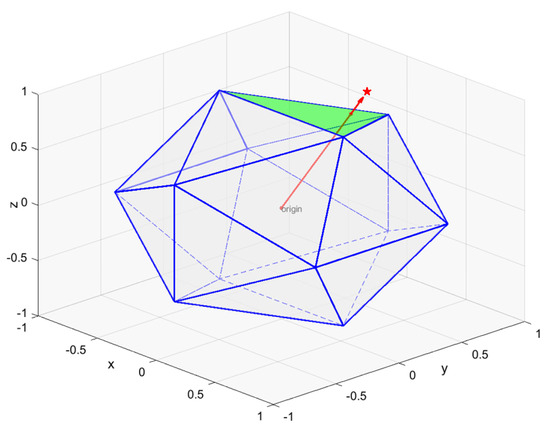
Figure 3.
The star belongs to the celestial sphere zone. The red star represents a star randomly selected from the star catalog. The blue polyhedron is a regular icosahedron and the green region is one of its surfaces.
Following the described method, the star catalog can be partitioned. Firstly, a zone from the celestial sphere zones is selected and the vertex coordinates of its corresponding equilateral triangle are obtained. The star catalog is traversed and the zone number is assigned to the star that belongs to the celestial sphere zone. The above process is repeated until each star in the star catalog owns a unique zone number. Figure 4 visually demonstrates the result of the star catalog partitioning when . As shown in the figure, the star catalog is uniformly divided into 20 regions, labeled .
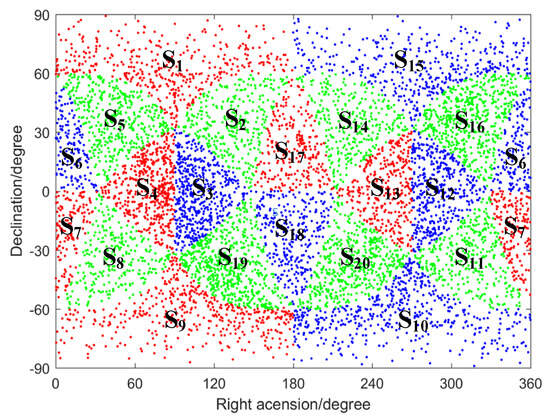
Figure 4.
The result of star catalog partitioning. Different colors are used to distinguish 20 divided regions of the star catalog.
3. Star Identification
Based on the partitioned star catalog, the method for the construction of the navigation feature library is explained in Section 3.1, and then a voting-based star identification algorithm is proposed in Section 3.2.
3.1. Construction of Navigation Feature Library
The navigation feature library is a database that characterizes the information of the stars in a star catalog and their positional relationships, serving as the foundation for star identification. The construction quality of the navigation feature library directly impacts the performance of star identification algorithms. Subgraph isomorphism methods typically use the angular distances between two stars as a feature to build the navigation feature library. However, due to the vast number of stars in the star catalog, the navigation feature library generated from angular distances between any two stars will be extremely large. In the process of star identification, the high number of feature matches leads to slow matching speed and a high probability of redundant and false matching, significantly affecting the identification speed and rate. Therefore, we propose a method for constructing a navigation feature library based on the partitioned star catalog.
In Figure 5, the red circle represents the field of view (FOV) of the star sensor. By selecting an appropriate parameter , the celestial sphere zone could include the FOV of the star sensor. The stars within the FOV of the star sensor generally belong to several celestial sphere zones rather than one zone, but it is evident from Figure 5 that the thirteen partitions around partition 0 can definitively contain all stars within the FOV. Therefore, by using thirteen partitions as a basic unit to construct the navigation feature library, the all-sky star identification can be simplified to star identification within the local celestial sphere, which will significantly simplify the navigation feature library and narrow the retrieval region during star identification, thereby markedly enhancing identification speed while effectively reducing the probability of redundant and false matching. The basic unit is constructed using the angular distance between two stars.
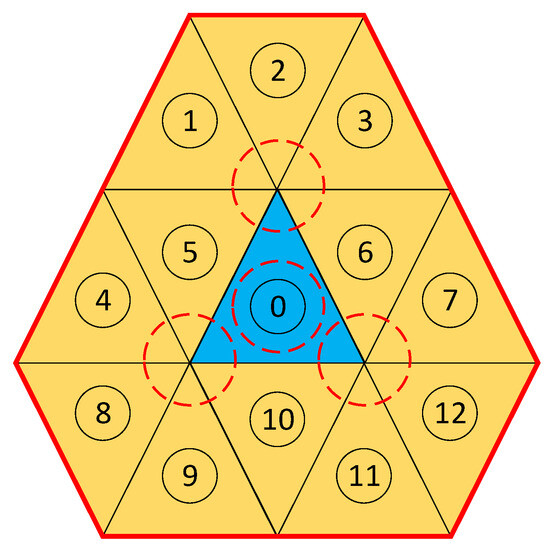
Figure 5.
Construction of navigation feature library. The blue region represents the center of the thirteen partitions in a basic unit.
Firstly, two stars and are randomly selected from thirteen partitions. Then, the reference vectors of two stars are defined as follows:
where and are the right ascension and declination of stars and .
The angular distance between stars and is given by the following:
where the symbol ‘’ represents the dot product of the vectors, and ‘| |’ is the norm of the vector.
Due to the limitation imposed by the FOV of star sensor, any angular distance within the basic unit that exceeds the FOV is considered as invalid information. Therefore, the constructed basic unit can be optimized based on Formula (9) by filtering out angular distances greater than the FOV.
where represents the FOV, and refers to the basic unit .
Since the arrangement of angular distances within the basic unit is somewhat disorganized, it makes it difficult to perform fast retrieval during star identification. To enhance the retrieval speed of angular distances in the basic unit, we sort the angular distances in ascending order and divide the basic unit into blocks. Then, an index function as defined in Formula (10) is established to quickly locate the block of the angular distance.
where denotes rounding to the nearest integer, and and represent the minimum and maximum values of the angular distances in the basic unit, respectively. The result refers to the block number where the angular distance is located, and its range satisfies .
3.2. Star Identification Algorithm Based on Voting Decision
The core of star identification uses an algorithm to match the features of stars between the star image and the navigation feature library, thus obtaining information about the stars. The navigation feature library uses the angular distance between stars as a feature; therefore, obtaining the angular distance between stars in the star image is necessary.
The imaging model of the star sensor can be approximated as a pinhole model. The starlight from infinity is treated as parallel light, which is projected onto the surface of the image sensor through the optical system, and then the stars on the image sensor are created. Figure 6 shows the imaging model of the star sensor.
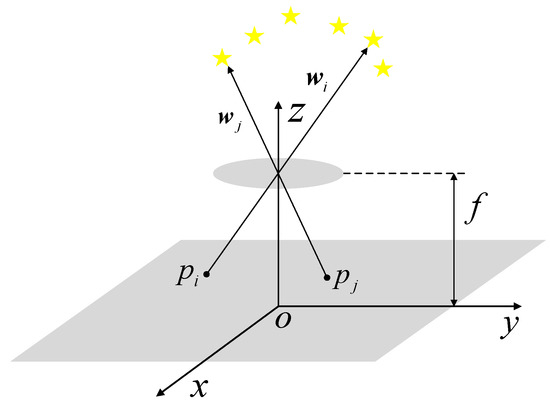
Figure 6.
The imaging model of the star sensor. The yellow stars represent the stars within the FOV of the star sensor.
As shown in Figure 6, depicts a coordinate system of a star sensor, and and are the projections of stars on the surface of the image sensor, with their centroid coordinates being and , respectively. The observation vectors for the stars and are and , which are calculated as follows:
where represents the focal length of the star sensor.
Similar to Formula (8), the angular distance between stars and is given by the following:
To effectively match the features of stars between the star image and the navigation feature library, a star identification algorithm based on a voting decision is proposed. During the optical system manufacturing of the star sensor, distortion is inevitable and the closer it is to the edge of the FOV, the greater the distortion will be. Therefore, selecting the stars closer to the center of the FOV is advisable during star identification, which could reduce the impact of distortion. As shown in the schematic star image in Figure 7, we choose those stars within the 3/4 FOV for star identification, and the stars near the edge of the FOV are discarded.
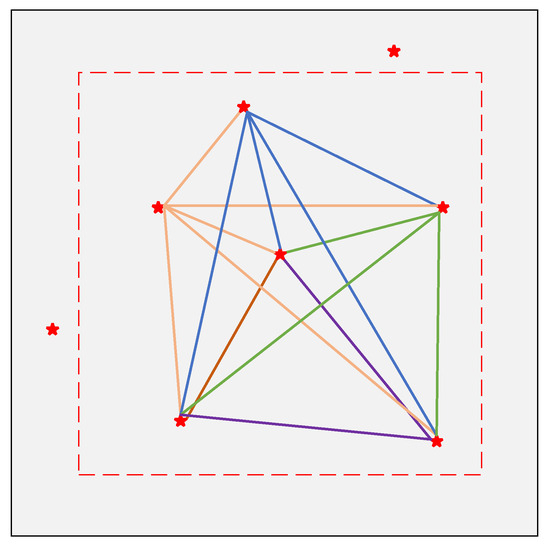
Figure 7.
Schematic star image. The red stars represent the stars within the FOV of the star sensor. The colored lines represent the valid angular distances between two stars without repetition.
Assuming there are stars within the 3/4 FOV of the star sensor, the angular distances between these stars form the set . In the basic unit of the navigation feature library, all the angular distances in the set are sequentially searched. Based on the search results, voting is conducted for by the following method:
where represents the voting score of the basic unit , represents the angular distance between stars and in , represents the angular distance between stars and in the basic unit , and is the error threshold.
As shown in Formula (13), if two stars and in the basic unit could obtain the angular distance and , equal within the error threshold , then the stars and match the stars and . In this case, the voting score of the basic unit increases; otherwise, remains unchanged.
Since the number of angular distances in set is , the theoretical maximum voting score for the basic unit is . However, considering the potential presence of false stars in the FOV, when the voting score of basic unit satisfies , which indicates that at least two sets of feature triangles in the star image belong to the basic unit , the decision can be made that the basic unit matches the angular distance set and is the subset of . Based on this, the basic unit is continually used to identify other stars in the star image. On the contrary, if all angular distances in the set have been traversed and the voting score of basic unit satisfies , which indicates that no feature triangle in the star image belongs to the basic unit , the decision can be made that the basic unit does not match the angular distance set , and it is necessary to select another basic unit and repeat the process above.
4. Simulation Experiment
In this section, a simulation experiment is conducted to verify the identification rate and speed of the proposed algorithm. Firstly, the algorithm is applied to multiple star images containing position errors, magnitude errors, and false stars to test its identification rate under different conditions. Additionally, the algorithm is used to identify multiple star images with various numbers of stars to verify its identification speed in different scenarios. During the experiment, the identification performance of the proposed algorithm is preliminarily evaluated by comparison with other typical subgraph isomorphism algorithms, such as those of Mortari [7], You [10], Liu [11], and Wang [12].
4.1. Impact of Position Errors on Identification Rate
The centroid positions of stars in the star image are calculated using the centroid algorithm, and a position error is generally caused by the imaging quality of the star sensor and the signal-to-noise ratio (SNR) of the star image. During the process of star identification, a position error affects the accuracy of the angular distance by altering the observation vector, which can result in redundant and false matching when compared to the navigation feature library. To assess the impact of position errors on the identification rate of the proposed algorithm, different position errors are added to the centroid positions of stars from 1000 frames of actual star images. The average identification rate under different position error conditions is then recorded and compared with other subgraph isomorphism algorithms. The experimental results are shown in Figure 8.
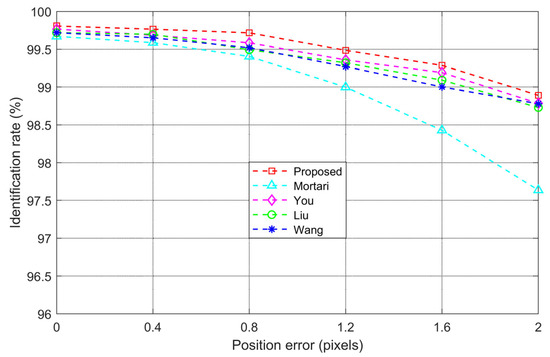
Figure 8.
Identification rate with different position errors.
The results in Figure 8 demonstrate that, under the same experimental conditions, the average identification rate of the proposed algorithm is significantly higher than that of the other algorithms. As the position error increases, the average identification rate of all algorithms declines, but the proposed algorithm has the slowest declining speed. Moreover, under the same position error conditions, the average identification rate of the proposed algorithm remains higher than that of the others. The analysis of the experimental results is explained below. The Mortari algorithm performs star identification across the entire celestial sphere, making it more susceptible to position errors, and thus exhibits weaker robustness. The You, Liu, and Wang algorithms perform coarse identification across the entire celestial sphere and fine identification in localized areas, providing some robustness to position errors. However, the proposed algorithm matches only within the basic unit of the navigation feature library, significantly reducing the probability of redundant and false matching compared to algorithms that operate on the entire celestial sphere. Consequently, the proposed algorithm demonstrates stronger robustness to position errors.
4.2. Impact of Magnitude Errors on Identification Rate
Affected by the meteorological conditions, optical spectrum, and image sensor, it is possible in the star image that the gray value of a star does not correspond to the apparent magnitude, which is called a magnitude error. This means that stars with low magnitude and high brightness may appear to have a low gray value, while stars with high magnitude and low brightness may appear to have a high gray value. To evaluate the impact of magnitude errors on the identification rate of the proposed algorithm, different brightness errors are added to 1000 frames of actual star images. The average identification rate under various magnitude error conditions is then recorded and compared with other subgraph isomorphism algorithms. The experimental results are shown in Figure 9.
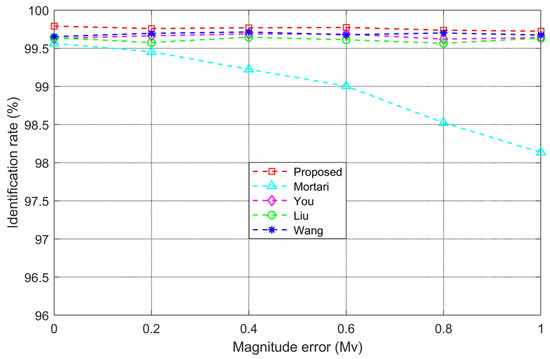
Figure 9.
Identification rate with different magnitude errors.
As shown in Figure 9, as the magnitude error increases, the identification rates of the proposed algorithm as well as that of the You, Liu, and Wang algorithms remain largely unaffected by the magnitude error, while the Mortari algorithm shows a significant decline in identification rate. The analysis of the experimental results is explained below. The Mortari algorithm selects the brightest star in the star image as the primary star and the next three brightest stars as accompanied stars to form a matching group. During the process of star identification, the algorithm also selects stars from the navigation feature library according to the strategy of primary and accompanied stars, which is highly susceptible to the brightness error of the primary star. In contrast, the proposed algorithm, as well as the You, Liu, and Wang algorithms, does not use brightness as a feature during the process of star identification and thus would not reference the brightness when selecting stars. As a result, these algorithms are less affected by the magnitude error and exhibit stronger robustness.
4.3. Impact of False Stars on Identification Rate
When a star sensor images the sky, the star image may contain not only stars but also false stars such as satellites, planets, and other celestial bodies which are not included in the star catalog. These false stars could lead to redundant and false matching during the process of star identification. To evaluate the impact of false stars on the identification rate of the proposed algorithm, varying numbers of false stars are added to 1000 frames of actual star images. The average identification rate under different false star conditions is recorded and compared with other subgraph isomorphism algorithms. The experimental results are shown in Figure 10.
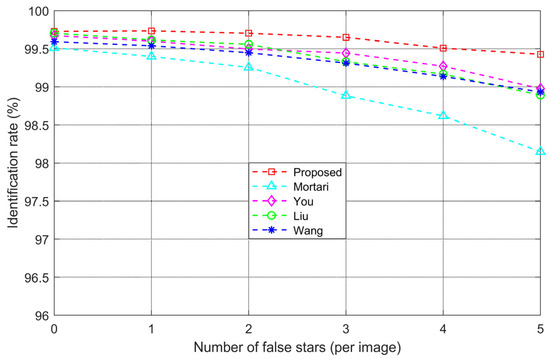
Figure 10.
Identification rate with different numbers of false stars.
The results in Figure 10 show that, under the same experimental conditions, the identification rate of the proposed algorithm is significantly higher than that of the other algorithms. As the number of false stars increases, the identification rate of all algorithms decreases, but the decline is slowest with the proposed algorithm. Moreover, with the same number of false stars, the identification rate of the proposed algorithm remains higher than the others. The analysis of the experimental results is explained below. The Mortari algorithm performs star identification across the entire celestial sphere, using the matching group composed of primary and accompanied stars. When a bright false star is treated as the primary or accompanied star, it easily causes redundant and false matching, making the algorithm less robust against false stars. The You, Liu, and Wang algorithms perform coarse identification over the entire celestial sphere first, then fine identification within a localized area, reducing the retrieval range for navigation stars during the fine identification, which offers some robustness to false stars. However, the proposed algorithm only performs star identification within the basic unit of the navigation feature library, significantly reducing the retrieval range compared to other algorithms, making the algorithm less susceptible to false stars and resulting in fewer redundant and false matches and stronger robustness.
4.4. Impact of Number of Stars on Identification Speed
Identification speed is also a key parameter for evaluating the performance of a star identification algorithm. Typically, identification speed is closely related to the number of stars in the star image. More stars correspond to more feature matching, resulting in longer identification time and slower identification speed. To assess the impact of number of stars on the identification speed, the proposed algorithm is applied to 1000 frames of actual star images containing different numbers of stars. The identification time for star images with the same number of stars is recorded and compared with other subgraph isomorphism algorithms. The experimental results are shown in Figure 11.
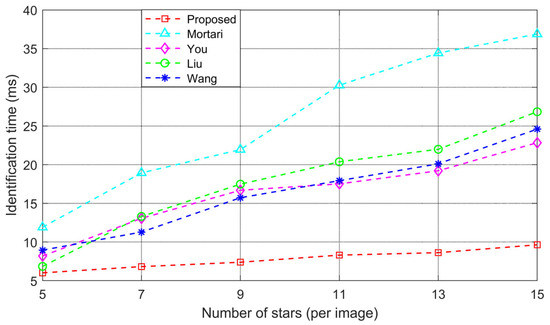
Figure 11.
Identification time with different numbers of stars.
The results in Figure 11 show that, under the same experimental conditions, the identification time of the proposed algorithm is significantly lower than that of the other algorithms. As the number of stars increases, the identification time of the proposed algorithm rises at the slowest rate. Furthermore, for the same number of stars, the identification time of the proposed algorithm is shorter than that of the other algorithms. The analysis of the experimental results is explained below. The Mortari algorithm performs star identification across the entire celestial sphere, with a wide retrieval range for navigation stars and a high number of feature matches, leading to a longer identification time. The You, Liu, and Wang algorithms firstly perform coarse identification across the celestial sphere and then fine identification within a local area, reducing the retrieval range for navigation stars, which somewhat decreases the number of feature matches and shortens the identification time. However, the proposed algorithm only performs star identification within the basic unit of the navigation feature library, leading to a smaller retrieval range for navigation stars and fewer feature matches, which results in a shorter identification time.
Moreover, since the basic unit of the navigation feature library contains all features of stars within the FOV, even as the number of stars increases, the retrieval range for navigation stars remains unchanged, making the identification time of the proposed algorithm less sensitive to the number of stars.
5. Nighttime Stargazing Experiment
In this section, the performance of the proposed algorithm is verified through a nighttime stargazing experiment. To reduce the interference of stray light on the experiment, the observation site is selected at the Xinglong Station of the National Astronomical Observatory, Chinese Academy of Sciences, located in Xinglong County, Chengde City, Hebei Province. The geographical coordinates are 117°34′30″ E longitude, 40°23′36″ N latitude, and the site is located at an altitude of 960 m. The experiment is conducted on a clear night, and the equipment mainly includes a large-aperture telescope and a star sensor. The key parameters of the star sensor are listed in Table 1.

Table 1.
The key parameters of the star sensor.
As shown in Figure 12, the star sensor is fixed on the telescope, ensuring that the coaxial and star sensor are unobstructed. The telescope provides directional guidance to the star sensor based on star catalog information from the control software of the telescope.

Figure 12.
Nighttime stargazing experiment.
During the experiment, a celestial region is firstly selected in the star catalog from the control software, and then the telescope and star sensor are guided to point at the selected region. As shown in Figure 13, the star sensor captures a star image and the stars are identified using the star identification algorithm.

Figure 13.
Star image captured by star sensor. The numbers respectively represent the number of each star in the star image.
The information of the identified stars is explained in Table 2, and includes centroids, average gray value, right ascension, declination, and magnitude.

Table 2.
The information of the identified stars.
Based on the right ascension and declination information listed in Table 2, the corresponding celestial region of the star image is captured and shown in Figure 14.

Figure 14.
Corresponding celestial region of the star image. The numbers respectively represent the number of each star in the star image.
It is pretty obvious that the relative positions of the stars in Figure 13 and Figure 14 are virtually identical, and the right ascension, declination, and magnitude of the stars shown in Figure 14 are largely consistent with the information in Table 2, which confirms the validity of the proposed star identification algorithm.
In addition, the star information in Table 2 has been sorted in the sequence of ascending magnitude. Based on this, the histogram regarding the gray value and magnitude of the stars is generated and shown in Figure 15.
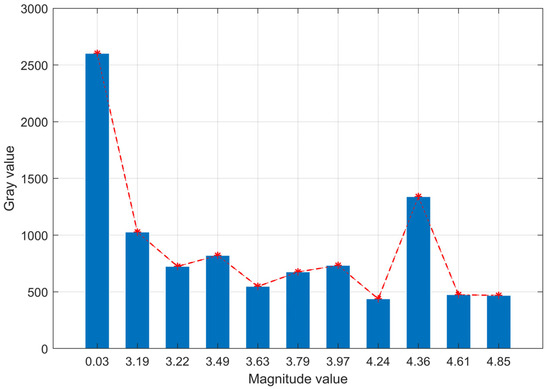
Figure 15.
The histogram regarding gray values and magnitude values. The asterisks represent the gray values corresponding to the magnitude values. The red dashed line represents the variation trend of the gray value when the magnitude value increases. With the increasing magnitude value, the disorder of the gray value indicates the presence of a magnitude error in the captured star image.
Generally, higher magnitude corresponds to lower brightness; however, as shown in Figure 15, the gray values of stars do not consistently decrease as the magnitude increases. Specifically, star 9, with a magnitude of only 4.36, has a significantly higher gray value than star 2, which has a magnitude of 3.19. This indicates that a magnitude error is indeed present in the star image when the star sensor works in practice. Nevertheless, the proposed algorithm successfully identifies the star image, even with significant brightness interference, further demonstrating the robustness of the proposed algorithm against the magnitude error. The robustness is attributed to the fact that the brightness of star is not used as a feature during the process of star identification, making the algorithm less susceptible to the effect of magnitude errors. To thoroughly validate the identification performance of the proposed algorithm, the rotation of the telescope is controlled and the star sensor is guided to capture 5000 frames of star images corresponding to different celestial regions. Different star identification algorithms are applied to identify the stars in the star images, and the average identification rate and average identification time for each algorithm are recorded and listed in Table 3.

Table 3.
The performance of star identification algorithms.
The results in Table 3 demonstrate that, under the same experimental conditions, the proposed algorithm achieves an average identification rate of 99.760% and an average identification time of 8.861 milliseconds. Both the identification rate and time are significantly better than those of the other algorithms, further confirming the effectiveness of the proposed star identification algorithm in the application of a star sensor.
6. Conclusions
Aiming at the problem wherein traditional methods cannot meet the current demand for star sensors with high identification speed and a high identification rate, a voting-based star identification algorithm using a partitioned star catalog is proposed. Compared to conventional methods, the proposed algorithm significantly simplifies the navigation feature library and narrows the retrieval region during star identification, markedly enhancing identification speed while effectively reducing the probability of redundant and false matching. A simulation experiment and nighttime stargazing experiment verify that the proposed algorithm can exhibit high robustness against position errors, magnitude errors, and false stars. Additionally, when compared with other subgraph isomorphism algorithms, the average identification rate and average identification time of the proposed algorithm are 99.760% and 8.861 milliseconds, respectively, presenting a clear advantage over other methods and meeting the current requirement for star sensors with a high star identification rate and high identification speed. The proposed algorithm could be applied in many fields that use star sensors for astronomical navigation, such as in the navy, aviation, and aerospace, and it is especially effective under lost-in-space conditions. Take the famous satellite network plan for instance. When thousands of satellites are launched into space, the satellites are lost in space and it is time consuming to obtain the attitude of each satellite as well as establish the attitude relationships among them. The proposed algorithm would help to improve the attitude acquisition speed and accuracy of the satellites, and ultimately contribute to the chain establishment efficiency of the whole satellite network.
Author Contributions
Conceptualization, X.H.; methodology, X.H.; software, X.H.; validation, X.H., J.W. and Z.L.; formal analysis, X.H., Z.L. and Z.M.; investigation, X.H. and J.W.; resources, L.Z. and J.H.; data curation, X.H.; writing—original draft preparation, X.H. and J.W.; writing—review and editing, L.Z. and J.H.; visualization, X.H.; supervision, L.Z. and J.H.; project administration, X.H. and Z.M.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the Changchun Scientific and Technological Development Program (19SS008).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Christian, J.A.; Crassidis, J.L. Star identification and attitude determination with projective cameras. IEEE Access 2021, 9, 25768–25794. [Google Scholar] [CrossRef]
- Izadmehr, M.; Ghomi, M.K. Design and construction of a portable high resolution positioner using star patterns. Astrophys. Space Sci. 2019, 364, 75. [Google Scholar] [CrossRef]
- Liang, X.; Ma, W.; Zhou, J.; Kong, S. Star identification algorithm based on image normalization and Zernike moments. IEEE Access 2020, 8, 29228–29237. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, J.; Zhang, G. Stellar instrument magnitude estimation in infinite-dimensional space. IEEE Sens. J. 2019, 20, 1422–1432. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. A survey of lost-in-space star identification algorithms since 2009. Sensors 2020, 20, 2579. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.A.; Saif, M. A fast fault detection and identification approach in power distribution systems. In Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; IEEE: New York, NY, USA, 2019; pp. 1–4. [Google Scholar]
- Mortari, D.; Samaan, M.A.; Bruccoleri, C.; Junkins, J.L. The pyramid star identification technique. Annu. Navig. 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Fan, Q.; Zhong, X. A triangle voting algorithm based on double feature constraints for star sensors. Adv. Space Res. 2018, 61, 1132–1142. [Google Scholar] [CrossRef]
- Hernández, E.A.; Alonso, M.A.; Chávez, E.; Covarrubias, D.H.; Conte, R. Robust polygon recognition method with similarity invariants applied to star identification. Adv. Space Res. 2017, 59, 1095–1111. [Google Scholar] [CrossRef]
- You, Z.; Li, J.; Zhang, H.; Yang, B.; Le, X. An accurate star identification approach based on spectral graph matching for attitude measurement of spacecraft. Complex Intell. Syst. 2022, 8, 1639–1652. [Google Scholar] [CrossRef]
- Liu, H.; Wei, X.; Li, J.; Wang, G. A star identification algorithm based on simplest general subgraph. Acta Astronaut. 2021, 183, 11–22. [Google Scholar] [CrossRef]
- Wang, X.; Sun, C.; Sun, T. A novel two-step validation algorithm for lost-in-space star identification. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2272–2279. [Google Scholar] [CrossRef]
- Fan, Q.; Zhong, X.; Sun, J. A voting-based star identification algorithm utilizing local and global distribution. Acta Astronaut. 2018, 144, 126–135. [Google Scholar] [CrossRef]
- Mehta, D.S.; Chen, S.; Low, K.S. A robust star identification algorithm with star shortlisting. Adv. Space Res. 2018, 61, 2647–2660. [Google Scholar] [CrossRef]
- Kim, S.; Cho, M. New star identification algorithm using labelling technique. Acta Astronaut. 2019, 162, 367–372. [Google Scholar] [CrossRef]
- Wang, G.; Li, J.; Wei, X. Star identification based on hash map. IEEE Sens. J. 2017, 18, 1591–1599. [Google Scholar] [CrossRef]
- Padgett, C.; Kreutz-Delgado, K. A grid algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 202–213. [Google Scholar] [CrossRef]
- Liao, J.; Wei, X.; Niu, A.; Zhang, Y.; Kweon, I.S.; Qi, C. Redundant-Coded Masked Grid Pattern for Full-sky Star Identification. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4343–4355. [Google Scholar] [CrossRef]
- Li, J.; Wei, X.; Wang, G.; Zhou, S. Improved grid algorithm based on star pair pattern and two-dimensional angular distances for full-sky star identification. IEEE Access 2019, 8, 1010–1020. [Google Scholar] [CrossRef]
- Kim, K.; Bang, H. Algorithm with patterned singular value approach for highly reliable autonomous star identification. Sensors 2020, 20, 374. [Google Scholar] [CrossRef]
- Wei, X.; Wen, D.; Song, Z.; Xi, J. Star identification algorithm based on oriented singular value feature and reliability evaluation method. Trans. Jpn. Soc. Aeronaut. Space Sci. 2019, 62, 265–274. [Google Scholar] [CrossRef]
- Mehta, D.S.; Chen, S.; Low, K.S. A rotation-invariant additive vector sequence based star pattern recognition. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 689–705. [Google Scholar] [CrossRef]
- Zhu, H.; Liang, B.; Zhang, T. A robust and fast star identification algorithm based on an ordered set of points pattern. Acta Astronaut. 2018, 148, 327–336. [Google Scholar] [CrossRef]
- Schiattarella, V.; Spiller, D.; Curti, F. A novel star identification technique robust to high presence of false objects: The multi-poles algorithm. Adv. Space Res. 2017, 59, 2133–2147. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, X.; Li, J.; Wang, G. Star identification algorithm based on K–L transformation and star walk formation. IEEE Sens. J. 2016, 16, 5202–5210. [Google Scholar] [CrossRef]
- Luo, L.; Xu, L.; Zhang, H. An autonomous star identification algorithm based on one-dimensional vector pattern for star sensors. Sensors 2015, 15, 16412–16429. [Google Scholar] [CrossRef]
- Samirbhai, M.D.; Chen, S.; Low, K.S. A hamming distance and spearman correlation based star identification algorithm. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 17–30. [Google Scholar] [CrossRef]
- Sun, L.; Jiang, J.; Zhang, G.; Wei, X. A discrete HMM-based feature sequence model approach for star identification. IEEE Sens. J. 2015, 16, 931–940. [Google Scholar] [CrossRef]
- Roshanian, J.; Yazdani, S.; Ebrahimi, M. Star identification based on euclidean distance transform, voronoi tessellation, and k-nearest neighbor classification. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2940–2949. [Google Scholar] [CrossRef]
- Jiang, D.; Zhang, K.; Debeir, O. A graph based algorithm for star recognition. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; IEEE: New York, NY, USA, 2017; pp. 159–162. [Google Scholar]
- Jiang, J.; Ji, F.; Yan, J.; Sun, L.; Wei, X. Redundant-coded radial and neighbor star pattern identification algorithm. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2811–2822. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, X.; Wang, G.; Li, J. Real-time star identification using synthetic radial pattern and its hardware implementation. Acta Astronaut. 2017, 131, 1–9. [Google Scholar] [CrossRef]
- Wei, X.; Wen, D.; Song, Z.; Xi, J.; Zhang, W.; Liu, G.; Li, Z. A star identification algorithm based on radial and dynamic cyclic features of star pattern. Adv. Space Res. 2019, 63, 2245–2259. [Google Scholar] [CrossRef]
- Liu, H.; Wei, X.; Li, J.; Wang, G. A star identification algorithm based on recommended radial pattern. IEEE Sens. J. 2022, 22, 8030–8040. [Google Scholar] [CrossRef]
- Du, J.; Wei, X.; Li, J.; Wang, G.; Zang, C. Star identification based on radial triangle mapping Matrix. IEEE Sens. J. 2022, 22, 8795–8807. [Google Scholar] [CrossRef]
- Hongchi, S.; Rongjun, M.; Huajun, D. A star identification method based on mixed characteristics and lvq neural network. In Proceedings of the 2018 10th International Conference on Modelling, Identification and Control (ICMIC), Guiyang, China, 2–4 July 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Jiang, D.; Zhang, K.; Debeir, O. Star recognition based on path optimization in star sensor with multiple fields of view. Adv. Astron. 2018, 2018, 8261068. [Google Scholar] [CrossRef]
- Xu, L.; Jiang, J.; Liu, L. RPNet: A representation learning-based star identification algorithm. IEEE Access 2019, 7, 92193–92202. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.-Y.; Wang, B.-D.; Yu, Z.-Q.; Jin, Z.-H.; Crassidis, J.L. An artificial intelligence enhanced star identification algorithm. Front. Inf. Technol. Electron. Eng. 2020, 21, 1661–1670. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. Efficient star identification using a neural network. Sensors 2020, 20, 3684. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, L.; Zhang, G. Star identification based on spider-web image and hierarchical CNN. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 3055–3062. [Google Scholar] [CrossRef]
- Yang, S.; Liu, L.; Zhou, J.; Zhao, Y.; Hua, G.; Sun, H.; Zheng, N. Robust and efficient star identification algorithm based on 1-D convolutional neural network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4156–4167. [Google Scholar] [CrossRef]
- Toloei, A.; Zahednamazi, M.; Ghasemi, R.; Mohammadi, F. A comparative analysis of star identification algorithms. Astrophys. Space Sci. 2020, 365, 63. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).