The Application of Structural Reliability and Sensitivity Analysis in Engineering Practice
Abstract
1. Introduction
2. Materials and Methods
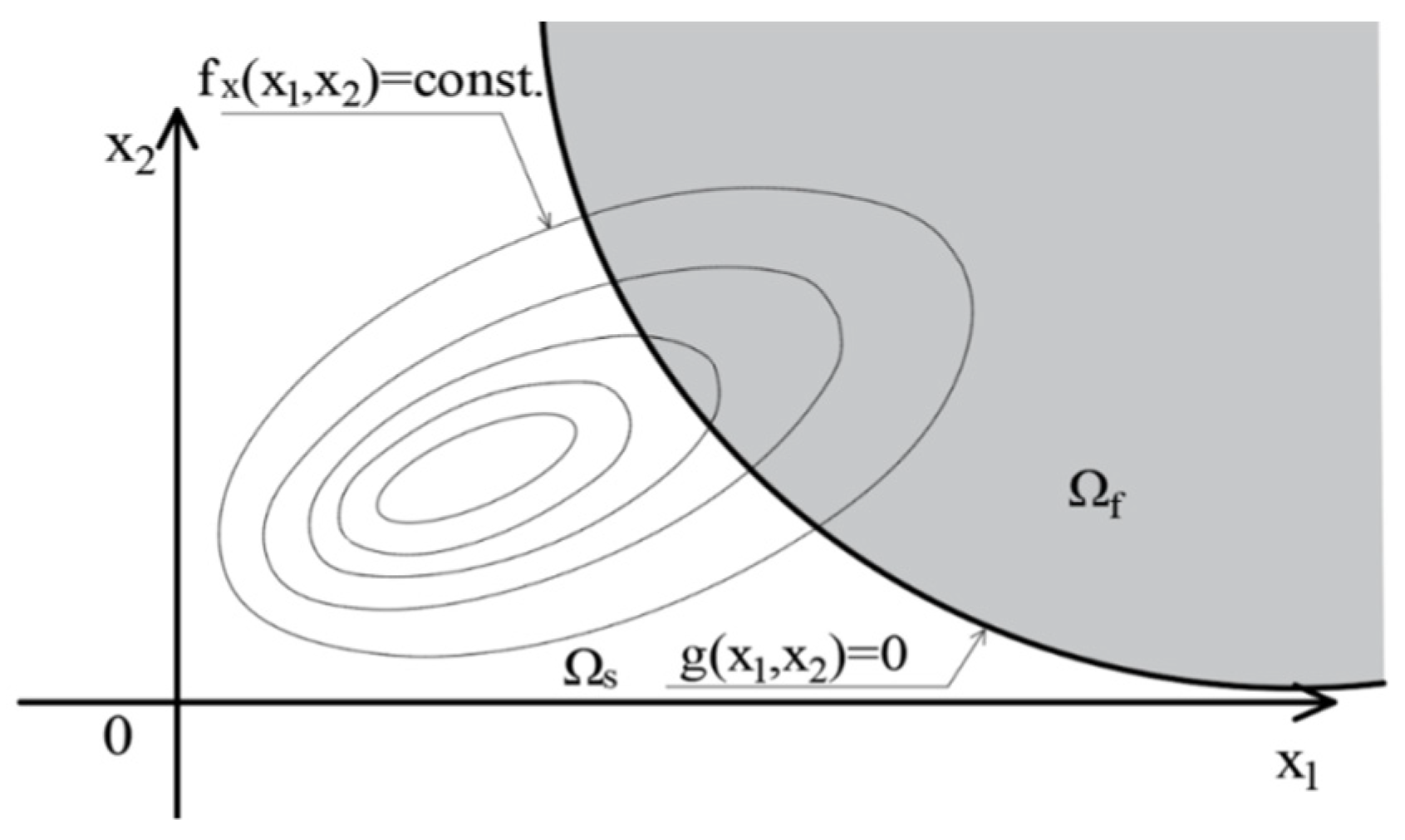
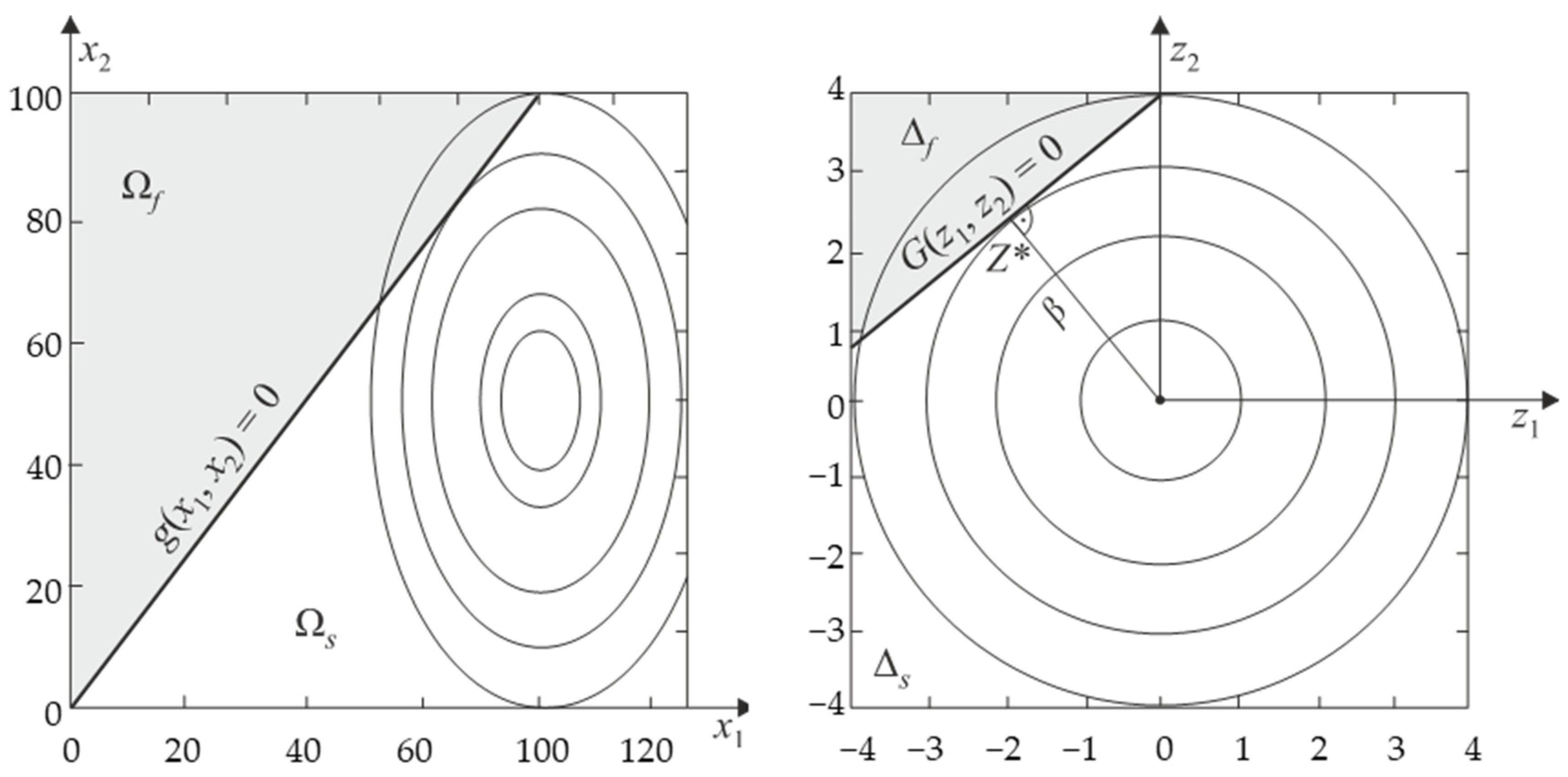
2.1. First-Order Reliability Method—FORM, Hasofer–Lind Reliability Index
- Define the limit state function and determine the corresponding parameters of the distributions of the random variables Xi.
- Find the initial design point by assigning initial values to n − 1 variables Xi (mean value consideration is often used). Solve the equation g(X) = 0 with respect to the remaining random variable. This ensures that the initial point belongs to the boundary of the failure area.
- Determine the values of the standard variables that correspond to the design point:
- Determine the partial derivatives of the limit state function with respect to standard random variables. The column vector {K} should be defined as follows:
- Calculate the approximation β using the formula below:
- Calculate the column vector of sensitivity coefficients:
- Determine a new design point in the space of reduced random variables for n − 1 variables:
- Determine the corresponding design point in origin coordinates for n − 1 variables from step 7:
- Calculate the values of the remaining random variable (i.e., undefined in steps 7 and 8) by solving the equation g(X) = 0. Steps 3–9 are repeated until β and the coordinates of the design point converge.
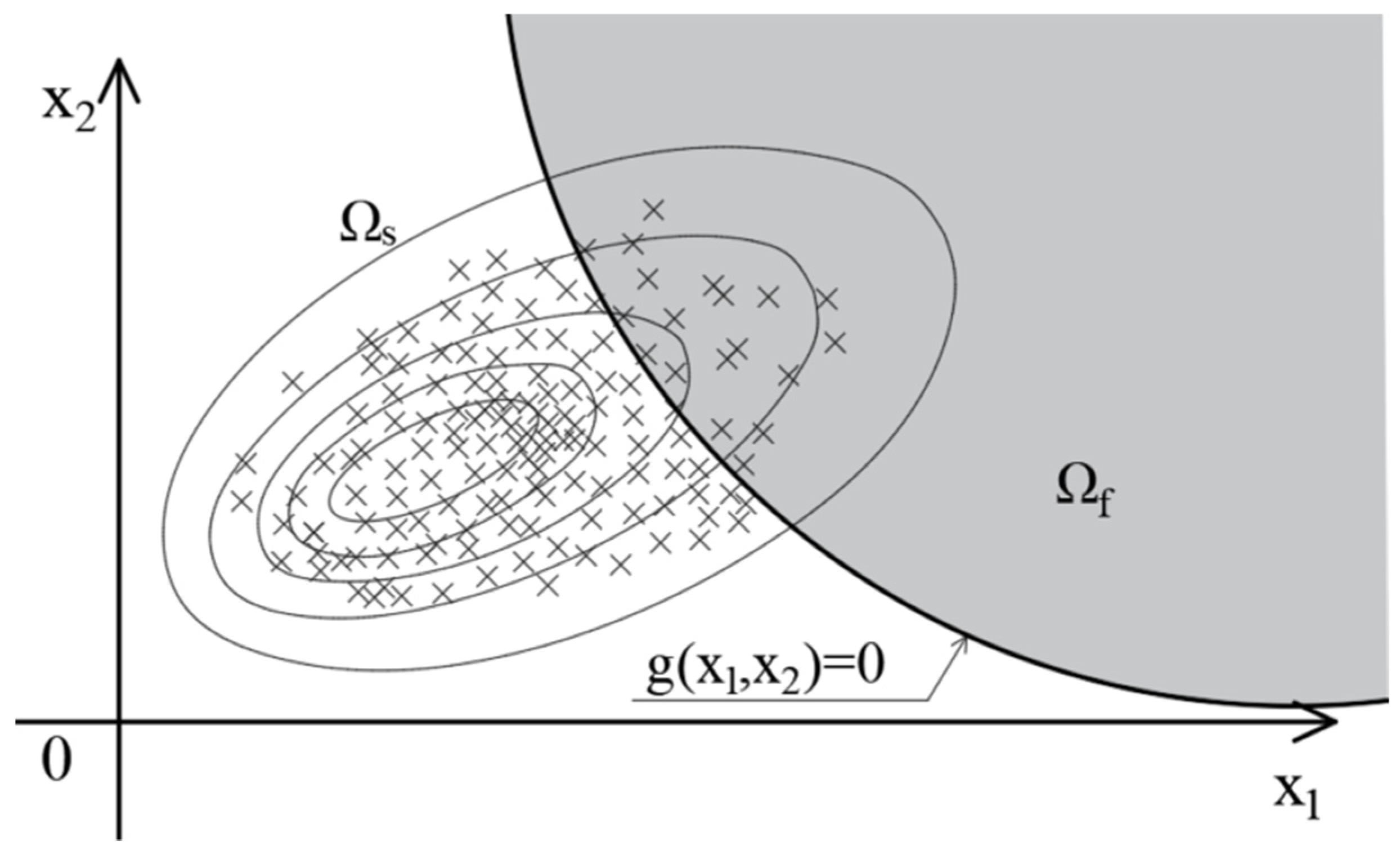
2.2. Monte Carlo Method
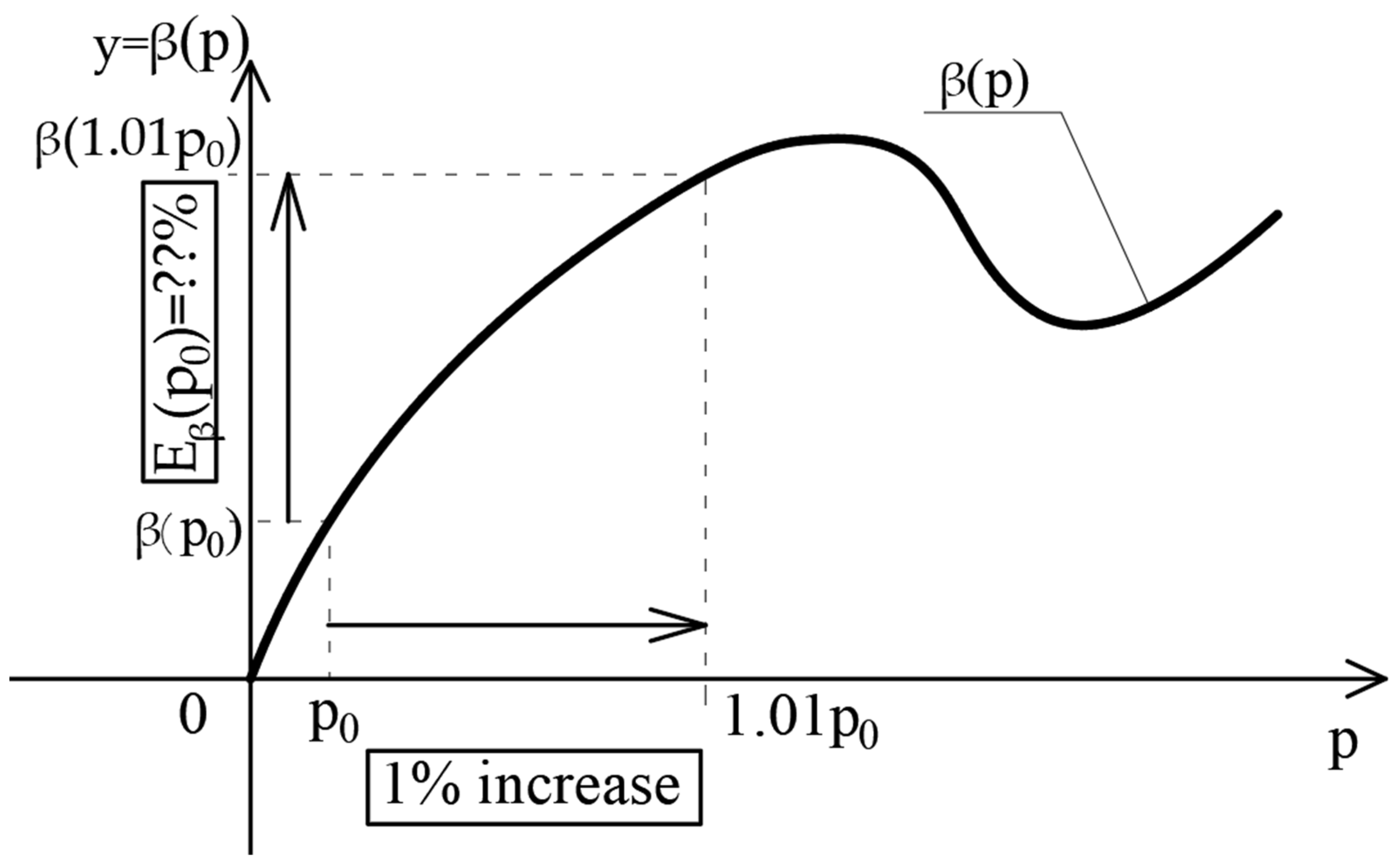
2.3. Sensitivity Measures of Probability of Failure
3. Case Study
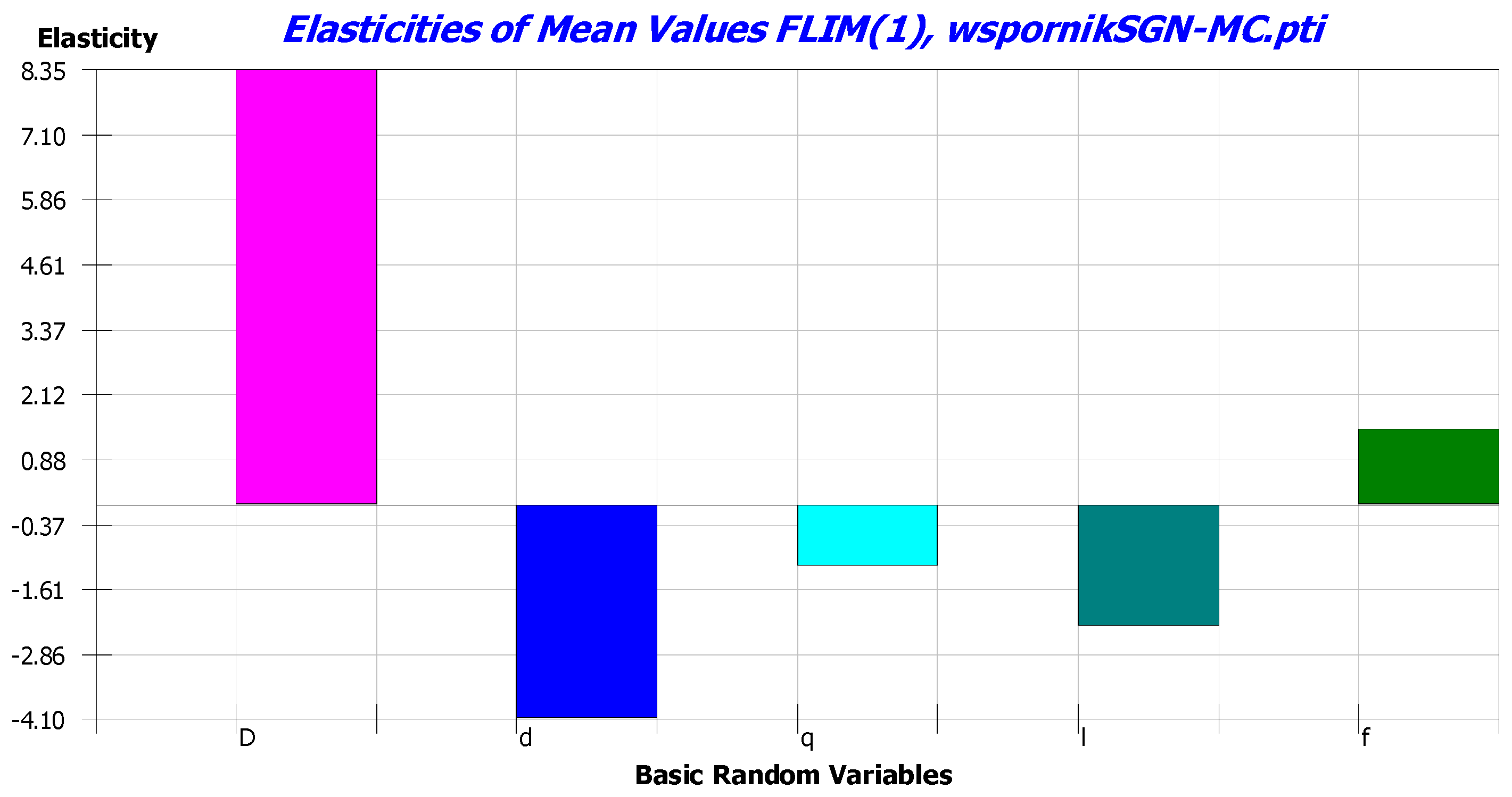
| ################################### Monte Carlo Sampling | Statistics ################################### Total number of samples: 1,000,000 Total number of failed samples: 52,502 Beta reliability index: 1.621 Estimated probability of failure: 5.3 × 10−2 =================================== Bayesian credible intervals =================================== upper bound ----------------------------------- probability that the actual probability of failure does not exceed the indicated value 50%: p_f 5.3 × 10−2 75%: p_f 5.3 × 10−2 90%: p_f 5.3 × 10−2 95%: p_f 5.3 × 10−2 99%: p_f 5.3 × 10−2 ----------------------------------- equal tail ----------------------------------- probability that the actual probability of failure is within the specified interval 50%: [5.2 × 10−2 p_f 5.3 × 10−2] 75%: [5.2 × 10−2 p_f 5.3 × 10−2] 90%: [5.2 × 10−2 p_f 5.3 × 10−2 95%: [5.2 × 10−2 p_f 5.3 × 10−2] 99%: [5.2 × 10−2 p_f 5.3 × 10−2] =================================== Variance based sensitivity analysis =================================== ----------------------------------- first-order sensitivity index ----------------------------------- Mean of LSF values: 2.1 × 10−1 Variance of LSF values: 1.5 × 10−2 Standard deviation of LSF values: 1.2 × 10−1 C.o.V. of LSF values: 5.7 × 10−1 Variable|S_i -------------------------- D|6.1 × 10−1 d|6.3 × 10−2 q|1.7 × 10−2 l|2.7 × 10−1 E|3.8 × 10−2 -------------------------- Sum of S_i|1.0 × 100 ========================== |
| Monte Carlo Sampling | Statistics ################################### Total number of samples: 1,000,000 Total number of failed samples: 8 Beta reliability index: 4.388 Estimated probability of failure: 8.0 × 10−6 =================================== Bayesian credible intervals =================================== upper bound ----------------------------------- probability that the actual probability of failure does not exceed the indicated value 50%: p_f 8.7 × 10−6 75%: p_f 1.1 × 10−5 90%: p_f 1.3 × 10−5 95%: p_f 1.4 × 10−5 99%: p_f 1.7 × 10−5 ----------------------------------- equal tail ----------------------------------- probability that the actual probability of failure is within the specified interval 50%: [6.8 × 10−6 p_f 1.1 × 10−5] 75%: [5.7 × 10−6 p_f 1.2 × 10−5] 90%: [4.7 × 10−6 p_f 1.4 × 10−5] 95%: [4.1 × 10−6 p_f 1.6 × 10−5] 99%: [3.1 × 10−6 p_f 1.9 × 10−5] =================================== Variance based sensitivity analysis =================================== ----------------------------------- first-order sensitivity index ----------------------------------- Mean of LSF values: 7.0 × 102 Variance of LSF values: 3.3 × 104 Standard deviation of LSF values: 1.8 × 102 C.o.V. of LSF values: 2.6 × 10−1 Variable|S_i -------------------------- D|5.3 × 10−1 d|7.8 × 10−2 q|5.4 × 10−3 l|2.2 × 10−2 f|3.6 × 10−1 -------------------------- Sum of S_i|1.0 × 100 |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, S.; Lu, Z.; Qiao, H. Subset Simulation for Structural Reliability Sensitivity Analysis. Reliab. Eng. Syst. Saf. 2009, 94, 658–665. [Google Scholar] [CrossRef]
- Dubourg, V.; Sudert, B. Meta-Model-Based Importance Sampling for Reliability Sensitivity Analysis. Struct. Saf. 2014, 49, 27–36. [Google Scholar] [CrossRef]
- Papaioannou, I.; Breitung, K.; Straub, D. Reliability Sensitivity Estimation with Sequential Importance Sampling. Struct. Saf. 2018, 75, 24–34. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of Sampling-Based Method for Uncertainty and Sensitivity Analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Chun, M.H.; Han, S.J.; Tak, N.I. An Uncertainty Importance Measure Using a Distance Metric for the Change in a Cumulative Distribution Function. Reliab. Eng. Syst. Saf. 2009, 94, 596–603. [Google Scholar] [CrossRef]
- Borgonovo, E. Measuring Uncertainty Importance: Investigation and Comparison of Alternative Approaches. Risk Anal. 2006, 26, 1349–1361. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Lu, Z.; Feng, J.; Wang, B. Moment Independent Importance Measure of Basic Variable and Its State Dependent Parameter Solution. Struct. Saf. 2012, 38, 40–47. [Google Scholar] [CrossRef]
- Wang, Q.A.; Liu, Q.A.; Ma, Z.G.; Wang, J.F.; Ni, Y.Q.; Ren, W.X.; Wang, H.B. Data Interpretation and Forecasting of SHM Heteroscedastic Measurements Under Typhoon Conditions Enabled by an Enhanced Hierarchical Sparse Bayesian Learning Model with High Robustness. Measurement 2024, 230, 114509. [Google Scholar] [CrossRef]
- Wang, Q.-A.; Dai, Y.; Ma, Z.-G.; Ni, Y.Q.; Tang, J.Q.; Xu, X.Q.; Wu, Z.Y. Towards Probabilistic Data-Driven Damage Detection in SHM Using Sparse Bayesian Learning Scheme. Struct. Control. Health Monit. 2022, 29, e3070. [Google Scholar] [CrossRef]
- Zheng, X.-W.; Li, H.-N.; Lv, H.-L.; Huo, L.-S.; Zhang, Y.-Y. Bayesian-Based Seismic Resilience Assessment for High-Rise Buildings with the Uncertainty in Various Variables. J. Build. Eng. 2022, 51, 104321. [Google Scholar] [CrossRef]
- Zheng, X.-W.; Li, H.-N.; Shi, Z.-Q. Hybrid AI-Bayesian-Based Demand Models and Fragility Estimates for Tall Buildings Against Multi-Hazard of Earthquakes and Winds. Thin Walled Struct. 2023, 187, 110749. [Google Scholar] [CrossRef]
- Zheng, X.-W.; Li, H.-N.; Gardoni, P. Hybrid Bayesian-Copula-Based Risk Assessment for Tall Buildings Subject to Wind Loads Considering Various Uncertainties. Reliab. Eng. Syst. Saf. 2023, 233, 109100. [Google Scholar] [CrossRef]
- Sobol, I.M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Estimates for Nonlinear Mathematical Models. Math. Modell. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Iman, R.L.; Hora, S.C. A Robust Measure of Uncertainty Importance for Use in Fault Tree System Analysis. Risk Anal. 1990, 10, 401–406. [Google Scholar] [CrossRef]
- Szepietowska, K.; Magnain, B.; Lubowiecka, I.; Florentin, E. Sensitivity Analysis Based on Non-Intrusive Regression-Based Polynomial Chaos Expansion for Surgical Mesh Modelling. Struct. Multidisc. Optim 2018, 57, 1391–1409. [Google Scholar] [CrossRef]
- Szepietowska, K.; Lubowiecka, I.; Magnain, B.; Florentin, E. Modelling of Abdominal Wall Under Uncertainty of Material Properties. In Computer Methods, Imaging and Visualization in Biomechanics and Biomedical Engineering, Lecture Notes in Computational Vision and Biomechanics, 36, Proceedings of the 16th International Symposium on Computer Methods in Biomechanics and Biomedical Engineering, New York, NY, USA, 14–16 August 2019; Ateshian, G., Myers, K., Tavares, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Sudret, B. Global Sensitivity Analysis Using Polynomial Chaos Expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Crestaux, T.; Le Maître, O.; Martinez, J.M. Polynomial Chaos Expansion for Sensitivity Analysis. Reliab. Eng. Syst. Saf. 2009, 94, 1161–1172. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Hao, W.; Feng, J.; Wang, B. Efficient Sampling Methods for Global Reliability Sensitivity Analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
- Papaioannou, I.; Straub, D. Variance-Based Reliability Sensitivity Analysis and the FORM α-Factors. Reliab. Eng. Syst. Saf. 2021, 210, 107496. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Schuëller, G.I. Efficient Monte Carlo Simulation Procedures in Structural Uncertainty and Reliability Analysis—Recent Advances. Struct. Eng. Mech. 2009, 32, 1–20. [Google Scholar] [CrossRef]
- Pradlwarter, H.J.; Schuëller, G.I.; Koutsourelakis, P.S.; Charmpis, D.C. Application of Line Sampling Simulation Method to Reliability Benchmark Problems. Struct. Saf. 2007, 29, 208–221. [Google Scholar] [CrossRef]
- Papaioannou, I.; Straub, D. Combination Line Sampling for Structural Reliability Analysis. Struct. Saf. 2021, 88, 102025. [Google Scholar] [CrossRef]
- Papaioannou, I.; Papadimitriou, C.; Straub, D. Sequential Importance Sampling for Structural Reliability Analysis. Struct. Saf. 2016, 62, 66–75. [Google Scholar] [CrossRef]
- Rackwitz, R.; Flessler, B. Structural Reliability Under Combined Random Load Sequences. Comput. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and Invariant Second Moment Code Format. J. Eng. Mech. Div. ASCE 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Gollwitzer, S.; Kruse, W.; Rackwitz, R. New Light on First and Second Order Reliability Thods. Struct. Saf. 1987, 4, 267–284. [Google Scholar] [CrossRef]
- Breitung, K.; Hohenbichler, M. Asymptotic Approximations for Multivariate Integrals with an Application to Multinormal Probabilities. J. Multivar. Anal. 1989, 30, 80–97. [Google Scholar] [CrossRef][Green Version]
- Fiessler, B.; Neumann, H.-J.; Rackwitz, R. Quadratic Limit States in Structural Reliability. J. Eng. Mech. Div. ASCE 1979, 105, 661–676. [Google Scholar] [CrossRef]
- Abdo, T.; Rackwitz, R. Reliability of Uncertain Structural Systems. Proc. Finite Elem. Eng. Appl. 1990, 805, 161–176. [Google Scholar]
- Schittkowski, K. The Nonlinear Programming Method of Wilson, Han and Powell with an Augmented Lagrangian Type Line Search Function, Part 1: Convergence Analysis. Numer. Math. 1982, 38, 83–114. [Google Scholar] [CrossRef]
- Schittkowski, K. User’s Guide for the Nonlinear Programming Code NLPQL, Handbook to Optimization Program Package NLPQL; University of Stuttgart: Stuttgart, Germany, 1985. [Google Scholar]
- Schittkowski, K.; Zillober, C.; Zotemantel, R. Numerical Comparison of Nonlinear Programming Algorithms for Structural Optimization. Struct. Multidiscip. Optim. 1994, 7, 1–19. [Google Scholar] [CrossRef]
- Arora, J.S. Introduction to Optimum Design; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Zabojszcza, P.; Radoń, U. Optimization of Steel Roof Framing Taking into Account the Random Nature of Design Parameters. Materials 2022, 15, 5017. [Google Scholar] [CrossRef]
- Zabojszcza, P.; Radoń, U. Stability Analysis of the Single-Layer Dome in Probabilistic Description by the Monte Carlo Method. J. Theor. Appl. Mech. 2020, 58, 425–436. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. Improvement of Second-Order Reliability Estimates by Importance Sampling. J. Eng. Mech. ASCE 1988, 114, 2195–2199. [Google Scholar] [CrossRef]
- Doliński, K. Importance Sampling Techniques in Reliability Calculations; IPPT: Warsaw, Poland, 1988; Volume 37. [Google Scholar]
- Fujita, M.; Rackwitz, R. Updating First and Second Order Reliability Estimates by Importance Sampling. Proc. Jpn. Soc. Civ. Eng. 1988, 392, 53–59. [Google Scholar] [CrossRef]
- de Angelis, M.; Patelli, E.; Beer, M. Advanced Line Sampling for Efficient Robust Reliability Analysis. Struct. Saf. 2015, 52, 170–182. [Google Scholar] [CrossRef]
- Bucher, C.G. Adaptive Sampling—An Iterative Fast Monte Carlo Procedure. Struct. Saf. 1988, 5, 119–126. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Pradlwarter, H.J. Computational Stochastic Structural Analysis (COSSAN)—Software Tool. Struct. Saf. 2006, 28, 68–82. [Google Scholar] [CrossRef]
- Reh, S.; Beley, J.D.; Mukherjee, S.; Khor, E.H. Probabilistic Finite Element Analysis Using ANSYS. Struct. Saf. 2006, 28, 17–43. [Google Scholar] [CrossRef]
- Pellissetti, M.F.; Schuëller, G.I. On General Purpose Software in Structural Reliability—An Overview. Struct. Saf. 2006, 28, 3–16. [Google Scholar] [CrossRef]
- Lemaire, M.; Pendola, M. Phimeca-Soft. Struct. Saf. 2006, 28, 130–149. [Google Scholar] [CrossRef]
- Lin, H.Z.; Khalessi, M.R. General Outlook of UNIPASSV5.0: A General-Purpose Probabilistic Software System. Struct. Saf. 2006, 28, 196–216. [Google Scholar] [CrossRef]
- Gollwitzer, S.; Kirchgabner, B.; Fischer, R.; Rackwitz, R. PERMAS-RA/STRUREL System of Programs for Probabilistic Reliability Analysis. Struct. Saf. 2006, 28, 108–129. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Haukaas, T.; Fujimura, K. Structural Reliability Software at the University of California, Berkeley. Struct. Saf. 2006, 28, 44–67. [Google Scholar] [CrossRef]
- Thacker, B.H.; Riha, D.S.; Fitch, S.K.H.; Huyse, L.J.; Pleming, J.B. Probabilistic Engineering Analysis Using the NESSUS Software. Struct. Saf. 2006, 28, 83–107. [Google Scholar] [CrossRef]
- Tvedt, L. Proban-Probabilistic Analysis. Struct. Saf. 2006, 28, 150–163. [Google Scholar] [CrossRef]
- Wu, Y.T.; Shin, Y.; Sues, R.H.; Cesare, M.A. Probabilistic Function Evaluation System (ProFES) for Reliability-Based Design. Struct. Saf. 2006, 28, 164–195. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]

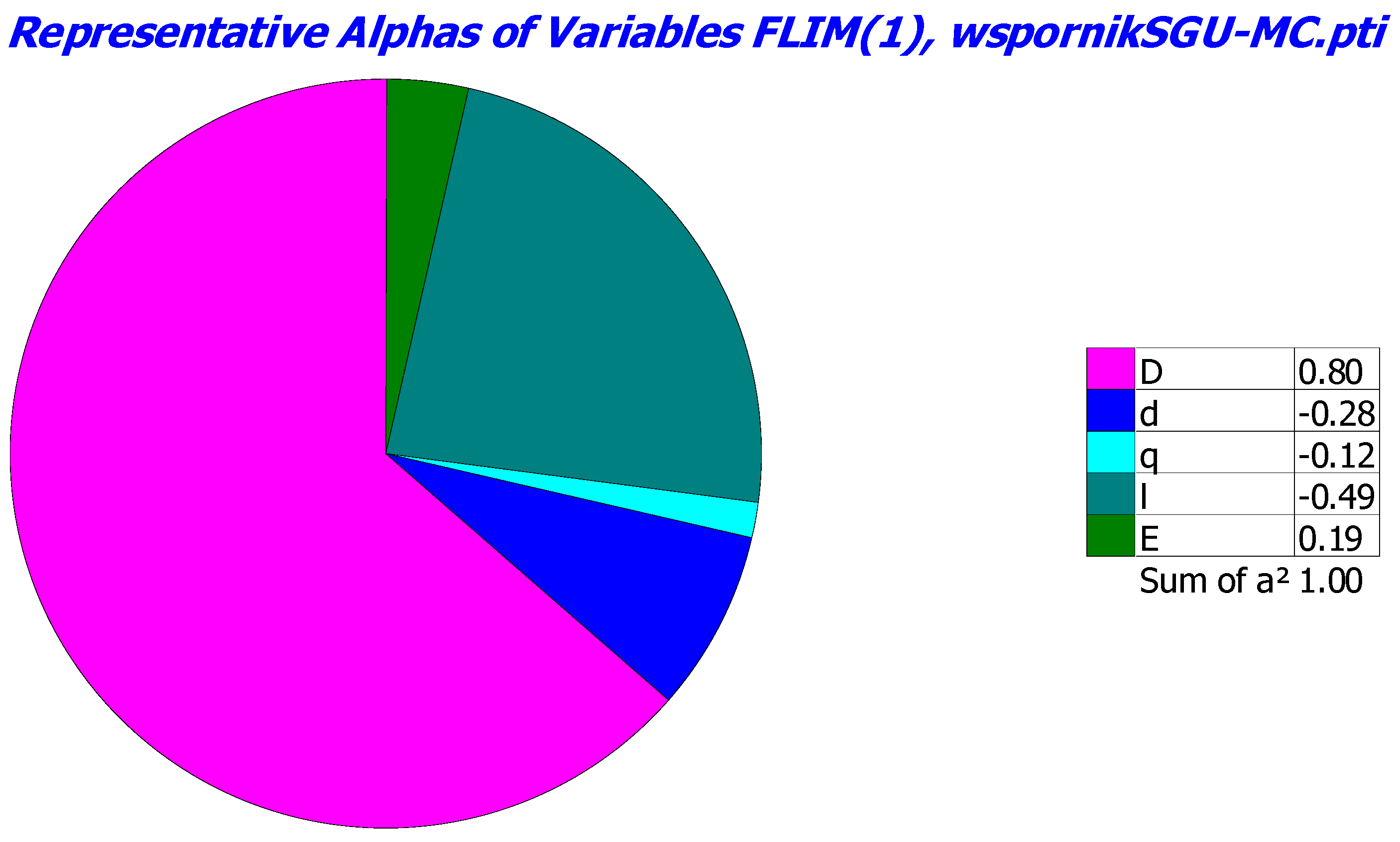
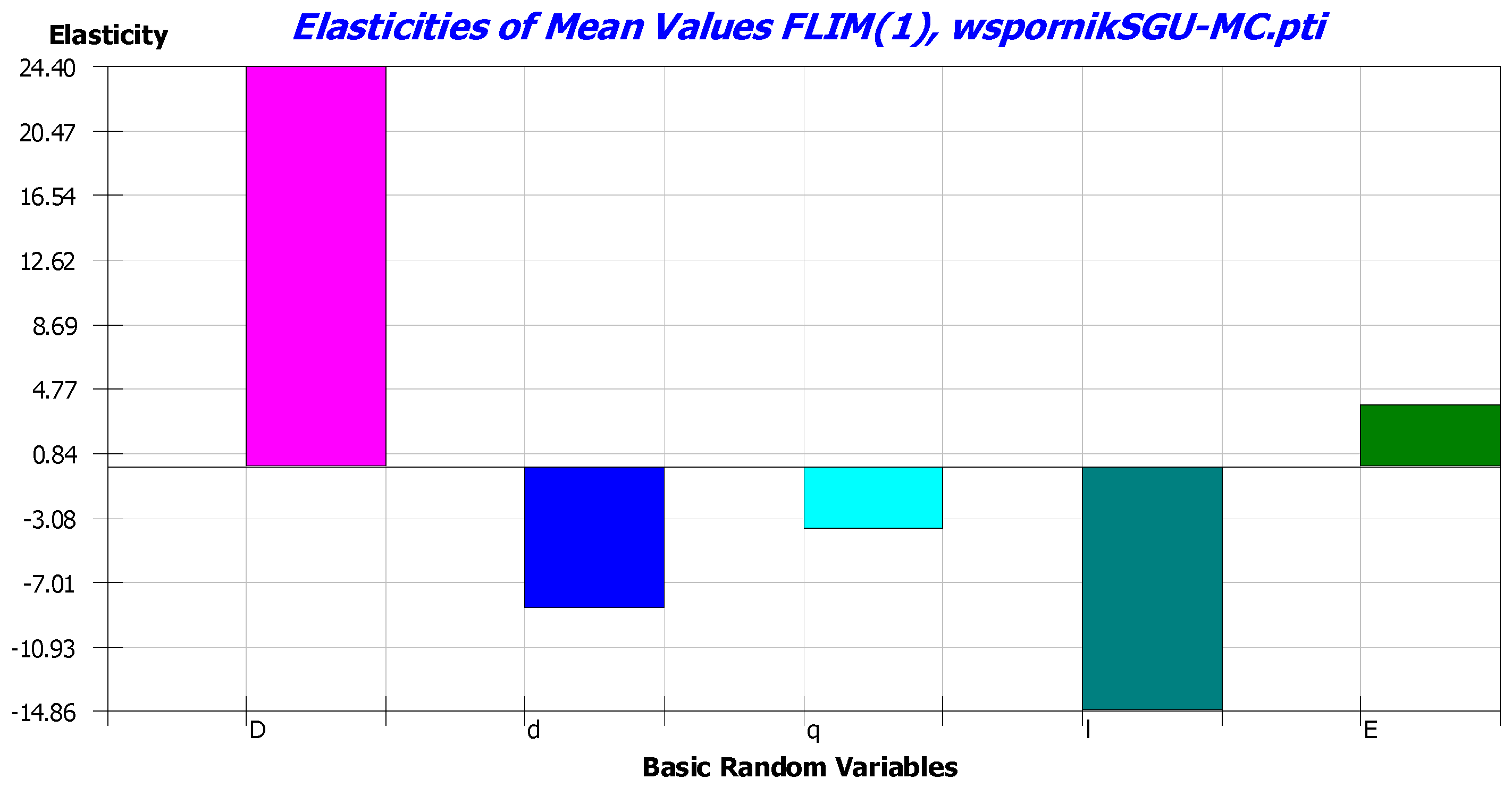
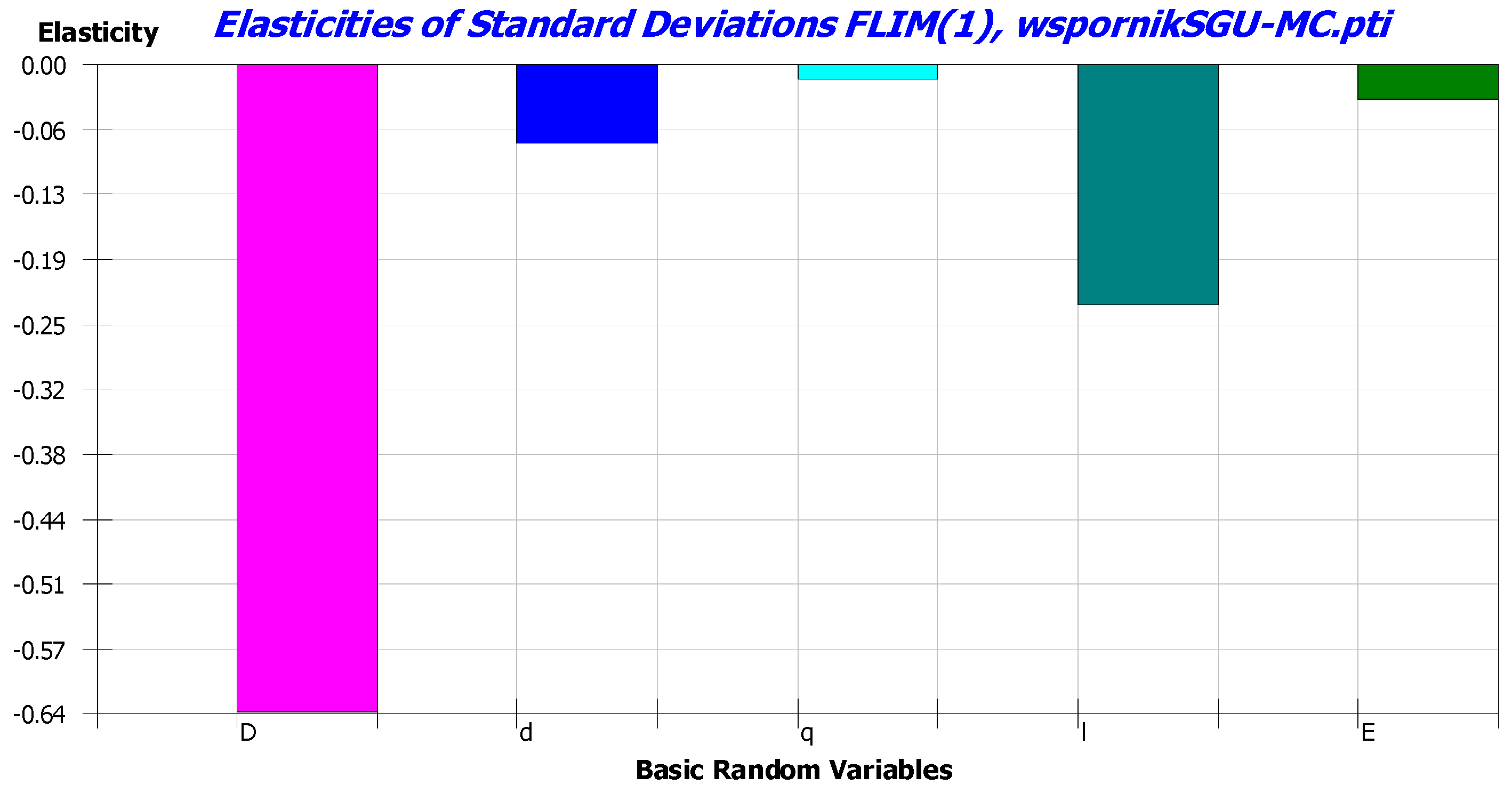
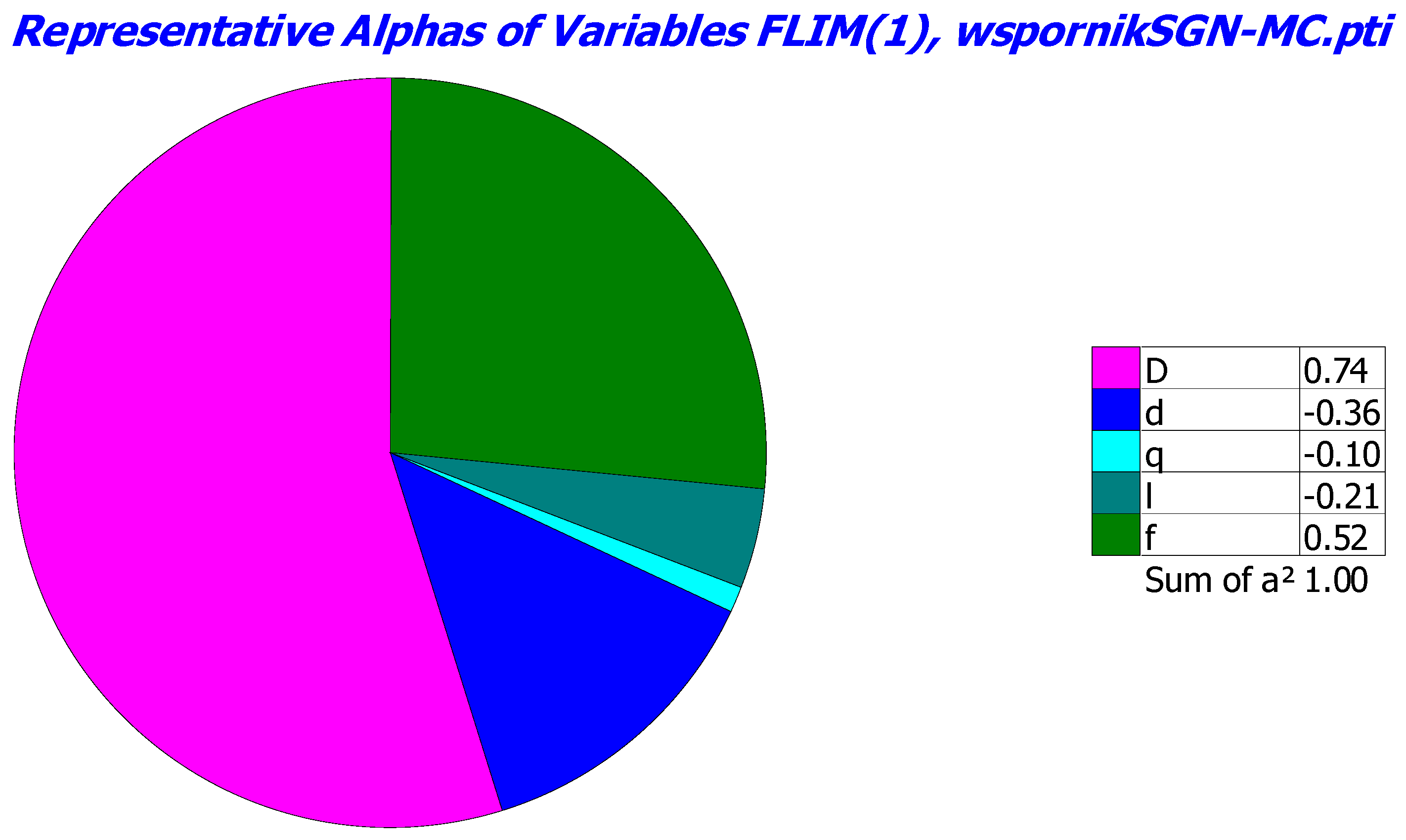

| Random Variable | Mean Value | Standard Deviation | Coefficient of Variation |
|---|---|---|---|
| D | 8 cm | 0.16 cm | 2% |
| d | 6 cm | 0.12 cm | 2% |
| E | 21,000 kN/cm2 | 630 kN/cm2 | 3% |
| q | 0.06 kN/cm | 0.0012 kN/cm | 2% |
| l | 150 cm | 3 cm | 2% |
| fy | 23.5 kN/cm2 | 1.88 kN/cm2 | 8% |
| FORM | SORM | |
|---|---|---|
| reliability index | 1.634 | 1.62 |
| failure probability | 5.11 × 10−2 | 5.26 × 10−2 |
| FORM | SORM | |
|---|---|---|
| reliability index | 4.434 | 4.388 |
| failure probability | 4.62 × 10−6 | 5.73 × 10−6 |
| Variable | SLS | ULS | ||
|---|---|---|---|---|
| Sobol Index Si | Coordinate α Vector | | | Sobol Index Si | Coordinate α Vector | | | |
| D | 6.1 × 10−1 | 8.0 × 10−1 | 5.3 × 10−1 | 7.9 × 10−1 |
| l | 2.7 × 10−1 | 4.9 × 10−1 | 2.2 × 10−2 | 2.1 × 10−1 |
| d | 6.3 × 10−2 | 2.8 × 10−1 | 7.8 × 10−2 | 3.6 × 10−1 |
| E | 3.8 × 10−2 | 1.9 × 10−1 | - | - |
| fy | - | - | 3.6 × 10−1 | 5.2 × 10−1 |
| q | 1.7 × 10−2 | 1.2 × 10−1 | 5.4 × 10−3 | 1.0 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radoń, U.; Zabojszcza, P. The Application of Structural Reliability and Sensitivity Analysis in Engineering Practice. Appl. Sci. 2025, 15, 342. https://doi.org/10.3390/app15010342
Radoń U, Zabojszcza P. The Application of Structural Reliability and Sensitivity Analysis in Engineering Practice. Applied Sciences. 2025; 15(1):342. https://doi.org/10.3390/app15010342
Chicago/Turabian StyleRadoń, Urszula, and Paweł Zabojszcza. 2025. "The Application of Structural Reliability and Sensitivity Analysis in Engineering Practice" Applied Sciences 15, no. 1: 342. https://doi.org/10.3390/app15010342
APA StyleRadoń, U., & Zabojszcza, P. (2025). The Application of Structural Reliability and Sensitivity Analysis in Engineering Practice. Applied Sciences, 15(1), 342. https://doi.org/10.3390/app15010342





