Wireless May Benefit Blockchain †
Abstract
1. Introduction
1.1. Motivation
1.2. State of the Art
1.2.1. Consensus Mechanisms
1.2.2. Blockchain Trilemma
1.2.3. Blockchain over Wirelessly Connected Nodes
1.3. Contributions
- It provides an analytical framework for calculation of scalability and decentralization of a blockchain consensus process.
- It quantifies the impacts of wireless connections on the scalability and decentralization by adopting a probabilistic analysis.
- It presents a comparative study among PoW, PoS, vs. PoC with respect to scalability and decentralization.
2. System Model
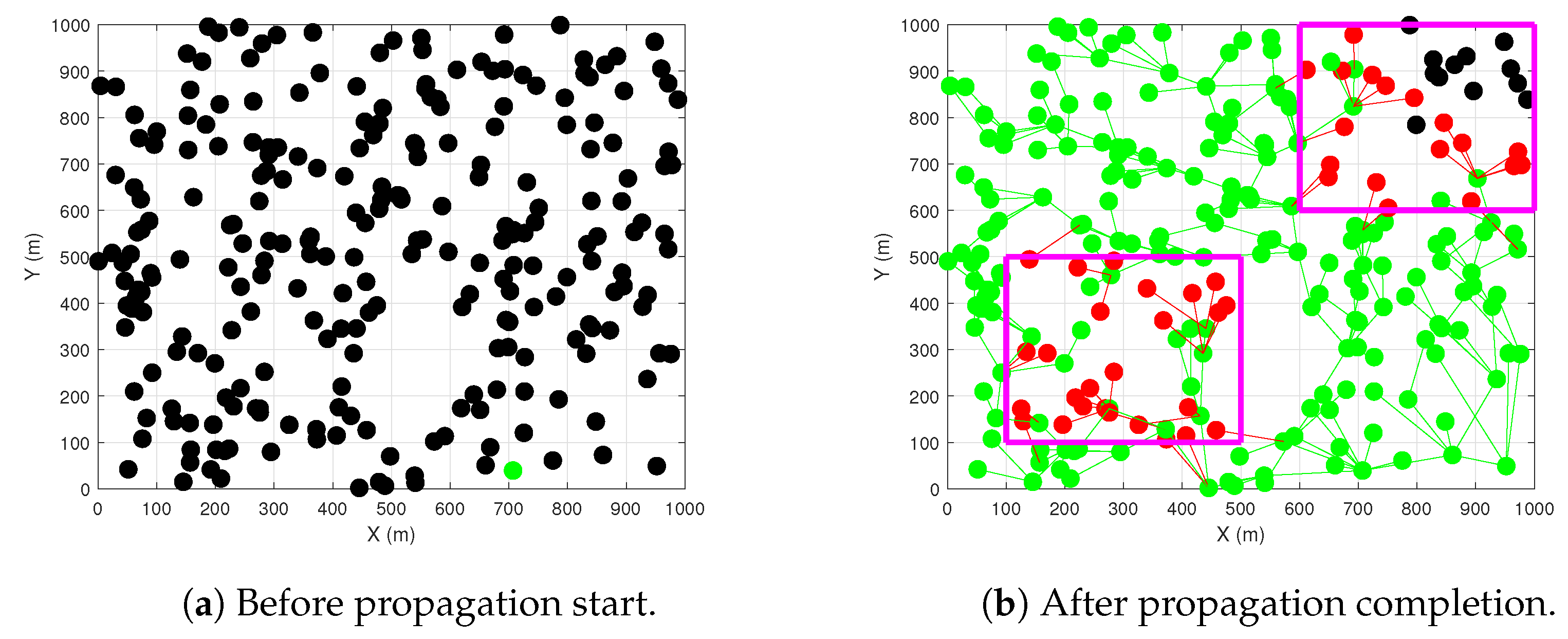
2.1. Spatial Distribution of Wireless Nodes
2.2. Communication Among Wireless Nodes
2.3. Byzantine Faults and Wireless Connection
3. Consensus Among Wireless Nodes
3.1. PoW
3.2. PoS
- A user initiates a transaction by generating and signing it using their private key. The user specifies the gas amount they are willing to pay as a tip to incentivize a validator for including the transaction in a block.
- The transaction is then submitted to an Ethereum execution client, where its validity is verified. This verification includes checking if the sender has sufficient ETH for the transaction and if it has been correctly signed with the corresponding key.
- Upon confirming the transaction’s validity, the execution client adds it to its local mempool (a list of pending transactions) and broadcasts it to other nodes through the execution layer gossip network. Other nodes, upon receiving the transaction, also add it to their mempool.
- A node is randomly selected as the block proposer for the current slot via the pseudo-random RANDAO process. This proposer is responsible for constructing and broadcasting the next block to be appended to the chain, along with updating the global state.
- Other nodes receive the new beacon block through the consensus layer gossip network. They forward it to their execution client, where transactions are re-executed locally to verify the proposed state change’s validity. The validator client then attests to the block’s validity, confirming that it logically follows the chain with the highest weight of attestations as defined in the fork choice rules. The block is added to the local database in each attesting node.
- The transaction achieves a state of being “finalized” when it becomes part of a chain with a supermajority link between two checkpoints, indicating agreement from 66% of the total staked ETH on the network regarding two specific checkpoints.
3.3. PoC
4. Analysis on Consensus Performance
4.1. Scalability
4.2. Decentralization
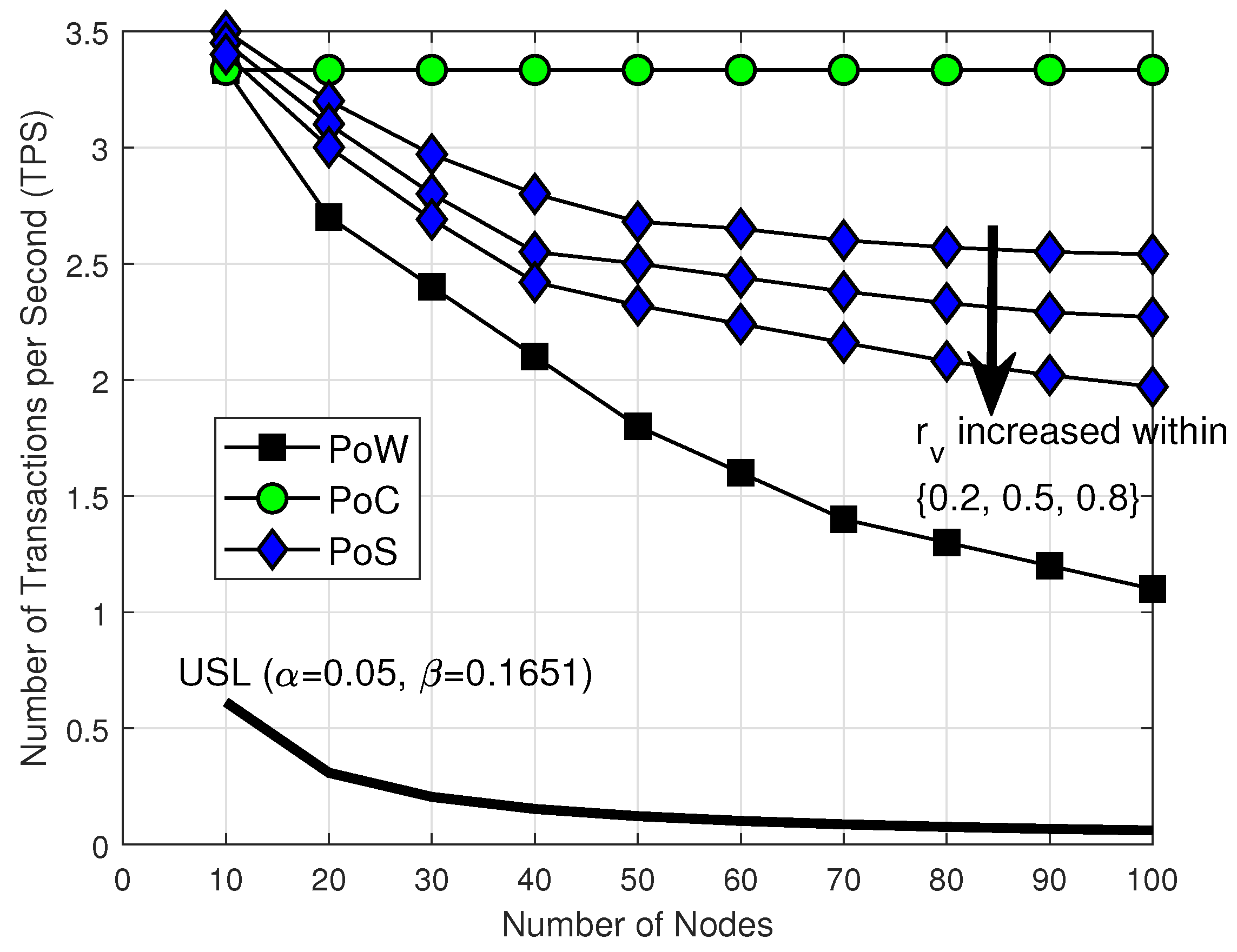
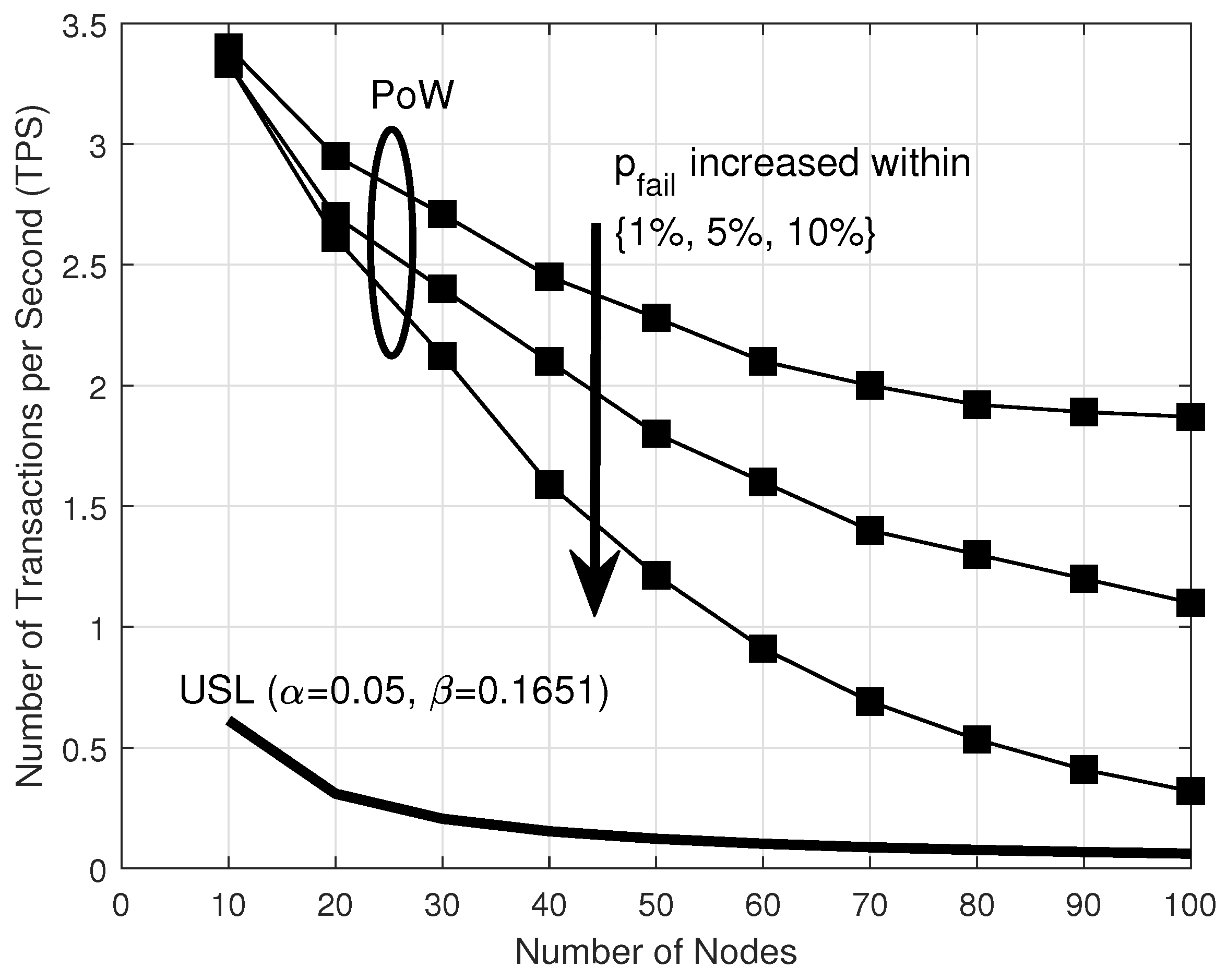
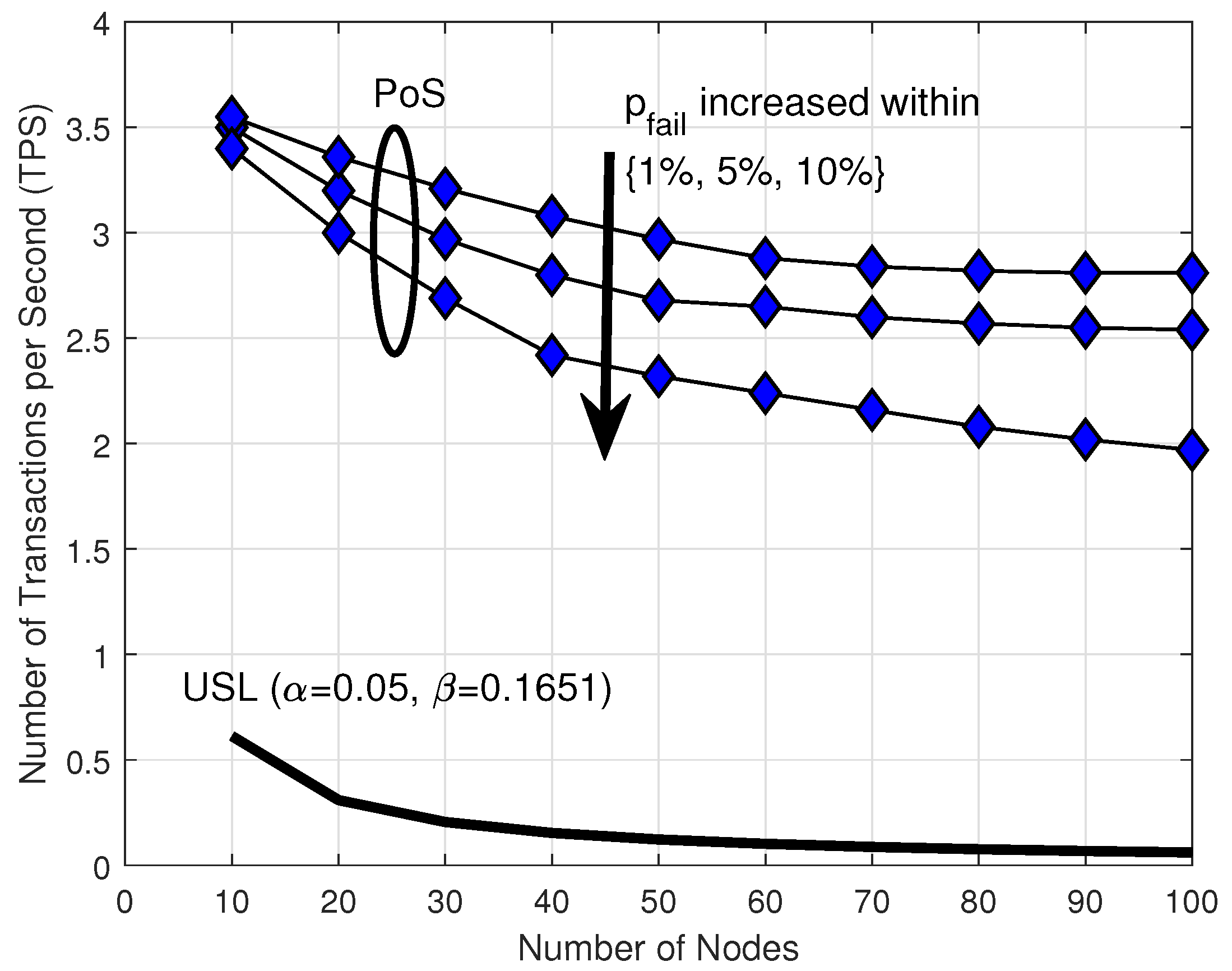
5. Numerical Results
5.1. Parameters and Setup
5.2. Results and Discussion
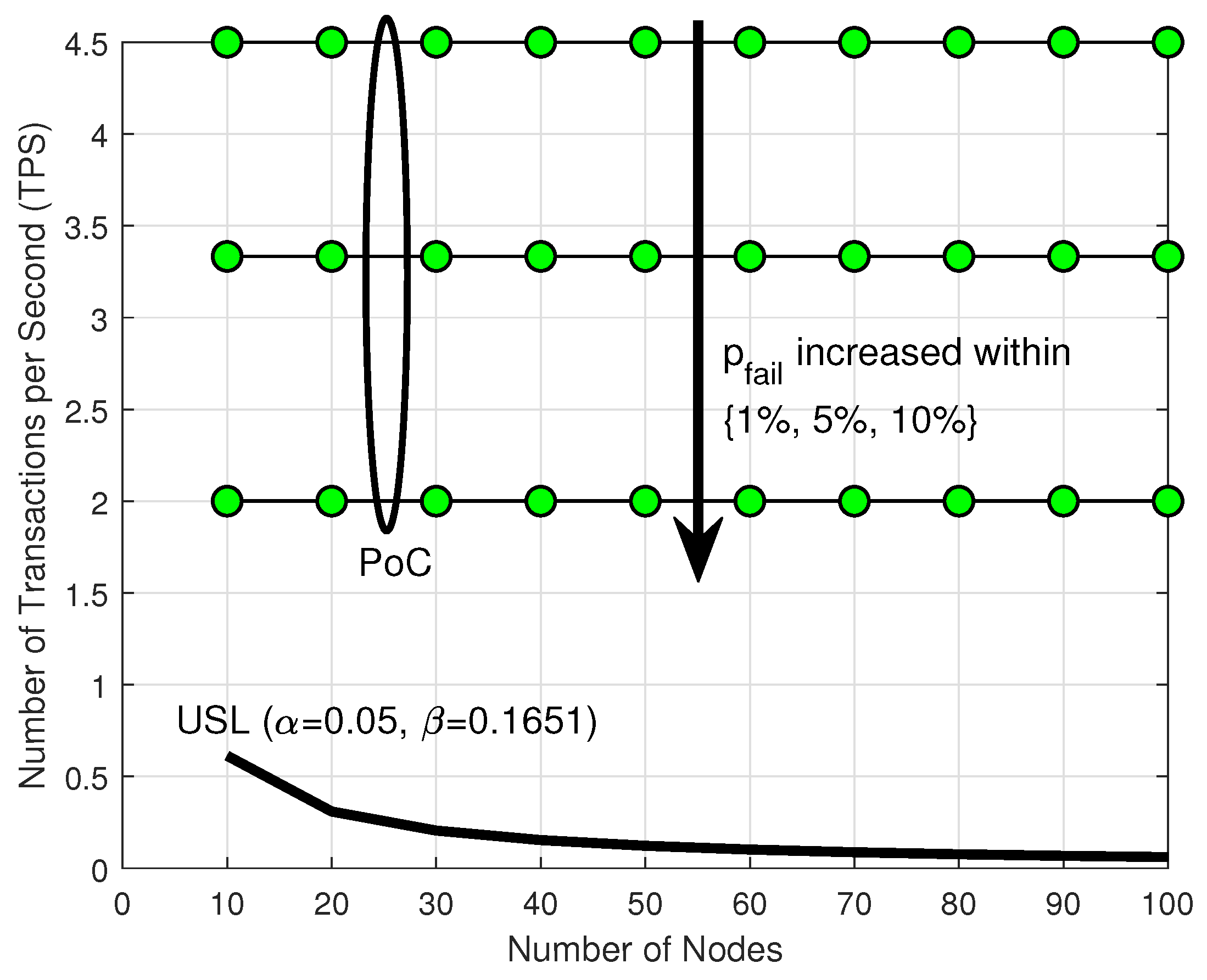
5.2.1. Scalability
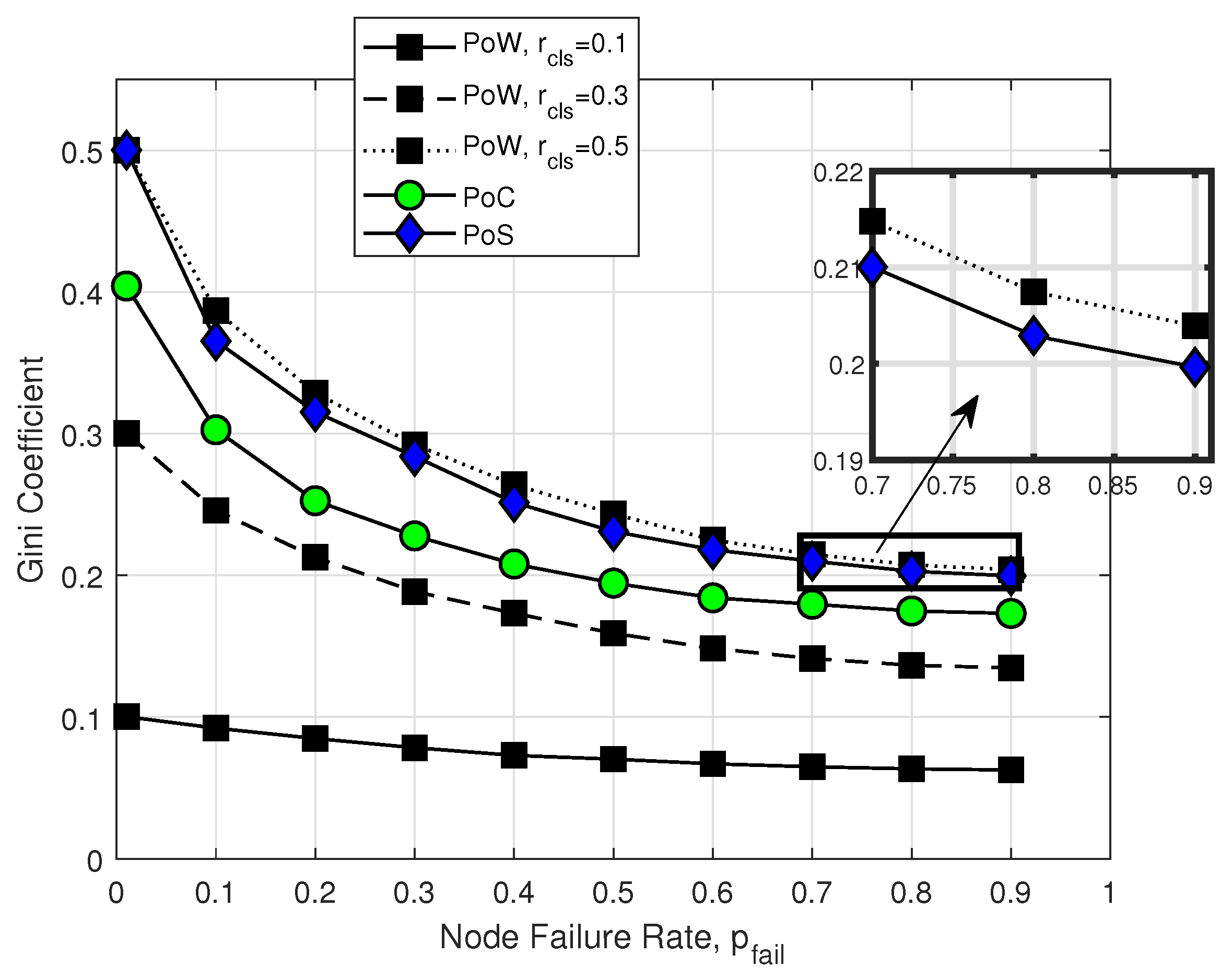
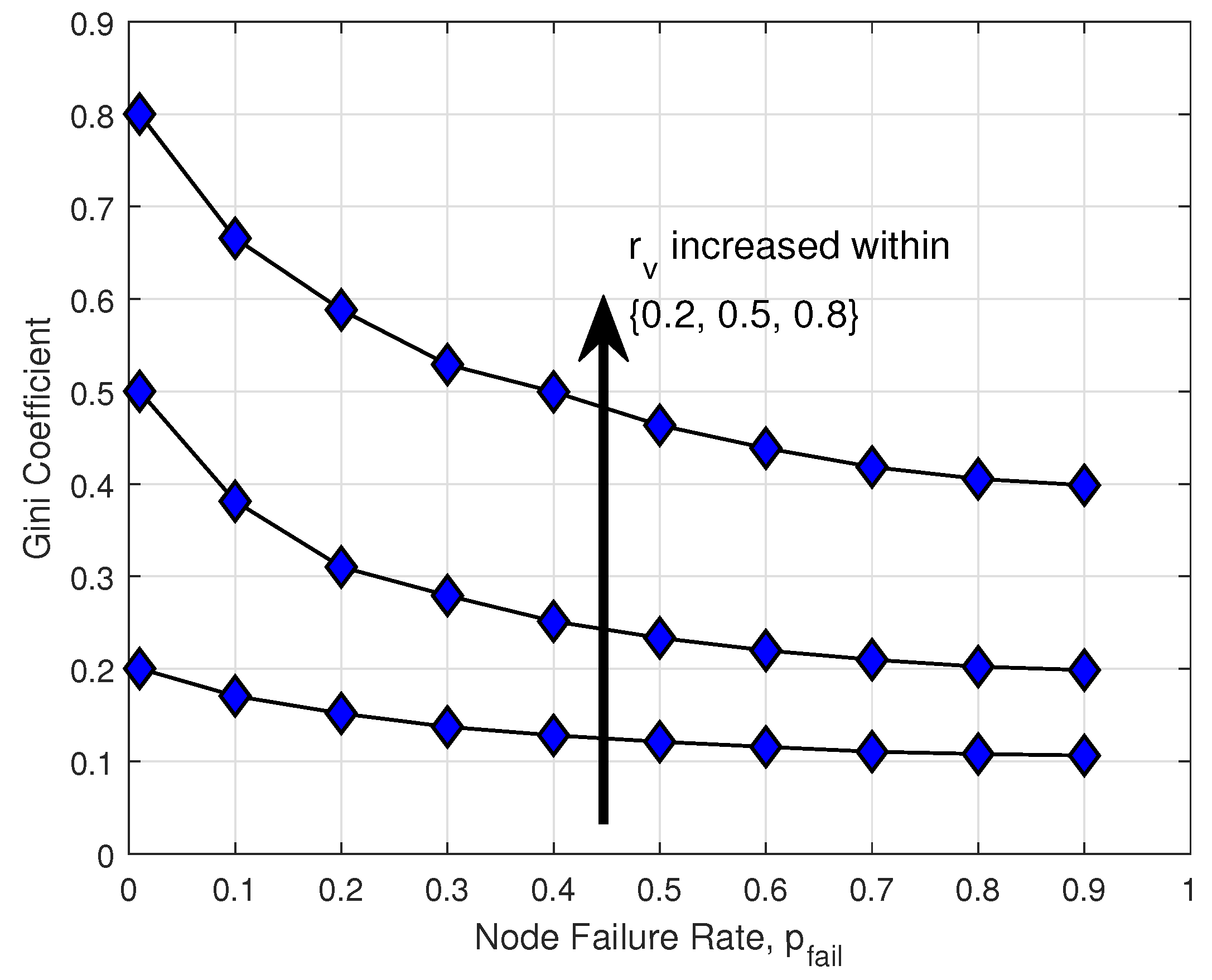
5.2.2. Decentralization
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Howarth, J. Internet Traffic from Mobile Devices. 2023. Available online: https://explodingtopics.com/blog/mobile-internet-traffic (accessed on 1 December 2024).
- Kim, S.; Choi, J.; Dietrich, C. PSUN: An OFDM—Pulsed radar coexistence technique with application to 3.5 GHz LTE. Mobile Inf. Syst. 2016, 2016, 7480460. [Google Scholar] [CrossRef]
- Kim, S.; Visotsky, E.; Moorut, P.; Bechta, K.; Ghosh, A.; Dietrich, C. Coexistence of 5G with the incumbents in the 28 and 70 GHz bands. IEEE J. Sel. Areas Commun. 2017, 35, 1254–1268. [Google Scholar] [CrossRef]
- Kim, S.; Dietrich, C. Coexistence of outdoor Wi-Fi and radar at 3.5 GHz. IEEE Wirel. Commun. Lett. 2017, 6, 522–525. [Google Scholar] [CrossRef]
- Kim, S.; Kim, B.J. Novel backoff mechanism for mitigation of congestion in DSRC broadcast. arXiv 2020, arXiv:2005.08921. [Google Scholar]
- Kim, S.; Sharif, Y.; Nasim, I. Human electromagnetic field exposure in wearable communications: A review. arXiv 2019, arXiv:1912.05282. [Google Scholar] [CrossRef]
- Nasim, I.; Kim, S. Human EMF exposure in wearable networks for internet of battlefield things. arXiv 2020, arXiv:2003.01552. [Google Scholar]
- Banerjee, D.D.D.S.; Chatterjee, P.; Ghosh, U.; Biswas, U. Blockchain for intelligent transportation systems: Applications, challenges, and opportunities. IEEE Internet Things J. 2023, 10, 18961–18970. [Google Scholar]
- Junaidi, N.; Abdullah, M.; Alharbi, B.; Shaaban, M. Blockchain-based management of demand response in electric energy grids: A systematic review. Energy Rep. 2023, 9, 5075–5100. [Google Scholar] [CrossRef]
- Ullah, Z.; Naeem, M.; Coronato, A.; Ribino, P.; Pietro, G.D. Blockchain applications in sustainable smart cities. Sustain. Cities Soc. 2023, 97, 104697. [Google Scholar] [CrossRef]
- Hawashin, D.; Nemer, M.; Gebreab, S.; Salah, K.; Jayaraman, R.; Khan, M.; Damiani, E. Blockchain applications in UAV industry: Review, opportunities, and challenges. J. Netw. Comput. Appl. 2024, 230, 103932. [Google Scholar] [CrossRef]
- Al-Nbhany, W.; Zahary, A.; Al-Shargabi, A. Blockchain-IoT healthcare applications and trends: A review. IEEE Access 2024, 12, 4178–4212. [Google Scholar] [CrossRef]
- Jordan, R.; Abdallah, C. Wireless communications and networking: An overview. IEEE Antennas Propag. Mag. 2002, 44, 185–193. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, W.; Cui, Q.; Tao, X.; Liu, R. Efficient and trusted data sharing in a sharding-enabled vehicular blockchain. IEEE Netw. 2022, 37, 230–237. [Google Scholar] [CrossRef]
- Okegbile, S.; Cai, J.; Alfa, A. Performance analysis of blockchain-enabled data-sharing scheme in cloud-edge computing-based IoT networks. IEEE Internet Things J. 2022, 9, 21520–21536. [Google Scholar] [CrossRef]
- Bedawala, M. A Deeper Dive into Consensus Mechanisms. Available online: https://usa.visa.com/solutions/crypto/consensus-mechanisms.html#:~:text=In%20blockchains%2C%20reaching%20consensus%20is,distributed%20nature%20of%20the%20network (accessed on 1 December 2024).
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 1 December 2024).
- Ethereum Foundation. Proof-of-Stake (PoS). 2023. Available online: https://ethereum.org/en/developers/docs/consensus-mechanisms/pos/ (accessed on 1 December 2024).
- European Parliament. Cryptocurrencies and Blockchain. PE 619.024. 2018. Available online: https://www.europarl.europa.eu/cmsdata/150761/TAX3%20Study%20on%20cryptocurrencies%20and%20blockchain.pdf (accessed on 1 December 2024).
- Dwork, C.; Naor, M. Pricing via processing or combatting junk mail. LNCS Adv. Cryptol. 1992, 740, 1993. [Google Scholar]
- Monte, G.; Pennino, D.; Pizzonia, M. Scaling blockchains without giving up decentralization and security: A solution to the blockchain scalability trilemma. In Proceedings of the Workshop on Cryptocurrencies and Blockchains for Distributed Systems, London, UK, 25 September 2020. [Google Scholar]
- Reno, S.; Haque, M. Solving blockchain trilemma using off-chain storage protocol. IET Inf. Secur. 2023, 17, 681–702. [Google Scholar] [CrossRef]
- Kim, S.; Ibrahim, A.S. Byzantine-fault-tolerant consensus via reinforcement learning for permissioned blockchain implemented in a V2X network. IEEE Trans. Intell. Veh. 2023, 8, 172–183. [Google Scholar] [CrossRef]
- Trifecta Blockchain Team. Trifecta: The Blockchain Trilemma Solved. White Paper. 2019. Available online: https://pramodv.ece.illinois.edu/pubs/Whitepaper2019-9.pdf (accessed on 1 December 2024).
- Khatoon, A.; Verma, P.; Southernwood, J.; Massey, B.; Corcoran, P. Blockchain in energy efficiency: Potential applications and benefits. Energies 2019, 12, 3317. [Google Scholar] [CrossRef]
- Rathod, T.; Jadav, N.; Alshehri, M.; Tanwar, S.; Sharma, R.; Felseghi, R.; Raboaca, M. Blockchain for future wireless networks: A decade survey. Sensors 2022, 22, 4182. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Jia, X. An advanced scheme for range ambiguity suppression of spaceborne SAR based on cocktail party effect. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- Alrubei, S.; Ball, E.; Rigelsford, J.; Willis, C. Latency and performance analyses of real-world wireless IoT-blockchain application. IEEE Sens. J. 2020, 20, 7372–7383. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, H.; Onireti, O.; Imran, M.; Cao, B. How much communication resource is needed to run a wireless blockchain network? IEEE Netw. 2021, 36, 128–135. [Google Scholar] [CrossRef]
- Xie, X.; Hua, C.; Hong, J.; Gu, P.; Xu, W. AirCon: Over-the-air consensus for wireless blockchain networks. IEEE Trans. Mobile Comput. 2023, 23, 4566–4582. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.; Jiao, Y.; Kang, J.; Dai, W.; Xu, Y. Connectivity-aware contract for incentivizing IoT devices in complex wireless blockchain. IEEE Internet Things J. 2023, 10, 10413–10425. [Google Scholar] [CrossRef]
- Zou, Y.; Yang, L.; Jing, G.; Zhang, R.; Xie, Z.; Li, H.; Yu, D. A survey of fault tolerant consensus in wireless networks. High-Confid. Comput. 2024, 4, 100202. [Google Scholar] [CrossRef]
- Bevilacqua-Linn, M.; Byron, M.; Cline, P.; Moore, J.; Muir, S. Sirius: Distributing and coordinating application. In Proceedings of the USENIX Annual Technical Conference, Philadelphia, PA, USA, 17–20 June 2014. [Google Scholar]
- Kim, S. Is wireless bad for consensus in blockchain? arXiv 2024, arXiv:2403.10186. [Google Scholar]
- ElSawy, H.; Hossain, E.; Haenggi, M. Stochastic geometry for modeling, analysis, and design of multi-tier and cognitive cellular wireless networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 996–1019. [Google Scholar] [CrossRef]
- Kim, S.; Choi, W.; Choi, Y.; Lee, J.; Han, Y. Interference reduction of cellular relay networks in multiple-cell environment by spectrum agility. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Tokyo, Japan, 13–16 September 2009. [Google Scholar]
- Kim, S.; Cho, K.S.; Kim, H.S. The capacity of cognitive ad hoc networks. In Proceedings of the 2010 16th Asia-Pacific Conference on Communications (APCC), Auckland, New Zealand, 31 October–3 November 2009. [Google Scholar]
- 3GPP. Universal Mobile Telecommunications System (UMTS); LTE; Proximity-Based Services (ProSe); Stage 2. ETSI TS 123 303, V17.1.0. 2023. Available online: https://www.etsi.org/deliver/etsi_ts/123300_123399/123303/17.01.00_60/ts_123303v170100p.pdf (accessed on 1 December 2024).
- Sunuwar, D.; Kim, S.; Reyes, Z. Is 30 MHz Enough for C-V2X? arXiv 2023, arXiv:2302.09536. [Google Scholar]
- Jelasity, M. Gossip; Springer: Berlin/Heidelberg, Germany, 2011; pp. 139–162. Available online: https://link.springer.com/chapter/10.1007/978-3-642-17348-6_7 (accessed on 1 December 2024).
- Driscoll, K.; Hall, B.; Sivencrona, H.; Zumsteg, P. Byzantine fault tolerance, from theory to reality. In Proceedings of the International Conference on Computer Safety, Reliability, and Security, Edinburgh, UK, 23–26 September 2003. [Google Scholar]
- Cardieri, P. Modeling interference in wireless ad hoc networks. IEEE Commun. Surv. Tutor. 2010, 12, 551–572. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical byzantine fault tolerance. In Proceedings of the Third Symposium on Operating Systems Design and Implementation, New Orleans, LA, USA, 22–25 February 1999. [Google Scholar]
- Lamport, L. Paxos made simple. ACM SIGACT News 2001, 32, 51–58. [Google Scholar]
- Ongaro, D.; Ousterhout, J. In Search of an Understandable Consensus Algorithm (Extended Version). Available online: https://raft.github.io/raft.pdf (accessed on 1 December 2024).
- Ethereum Foundation. Networking Layer. 2023. Available online: https://ethereum.org/en/developers/docs/networking-layer/#connecting-clients (accessed on 1 December 2024).
- Ethereum Foundation. Consensus Mechanisms. 2023. Available online: https://ethereum.org/en/developers/docs/consensus-mechanisms/ (accessed on 1 December 2024).
- Helium Network. Proof of Coverage. Available online: https://docs.helium.com/iot/proof-of-coverage/ (accessed on 1 December 2024).
- Haleem, A. Helium Network (HNT): Decentralizing Wireless Networks. 2023. Available online: https://www.gemini.com/cryptopedia/helium-network-token-map-helium-hotspot-hnt-coin (accessed on 1 December 2024).
- The Wireless Miner. An Introduction to Proof of Coverage for Blockchains. 2022. Available online: https://thewirelessminer.com/2022/02/21/an-introduction-to-proof-of-coverage-for-blockchains/ (accessed on 1 December 2024).
- Gini, C. On the measure of concentration with special reference to income and statistics. Colo. Coll. Publ. 1936, 208, 73–79. [Google Scholar]
- Jogalekar, P.; Woodside, M. Evaluating the scalability of distributed systems. IEEE Trans. Parallel Dist. Syst. 2000, 11, 589–603. [Google Scholar] [CrossRef]
- Lu, N.; Shen, X. Scaling laws for throughput capacity and delay in wireless networks—A survey. IEEE Commun. Surv. Tutor. 2014, 16, 642–657. [Google Scholar] [CrossRef]
- Hunt, P.; Konar, M.; Junqueira, F.; Reed, B. ZooKeeper: Wait-free coordination for internet-scale systems. In Proceedings of the Annual Technical Conference, Berkeley, CA, USA, 23–25 June 2010. [Google Scholar]
- Bandara, E.; Tosh, D.; Foytik, P.; Shetty, S.; Ranasinghe, N.; Zoysa, K. Tikiri–Towards a lightweight blockchain for IoT. Future Gener. Comput. Syst. 2021, 119, 154–165. [Google Scholar] [CrossRef]
- Duan, J.; Karve, A.; Sreedhar, V.; Zeng, S. Service management of blockchain networks. In Proceedings of the International Conference on Cloud Computing, San Francisco, CA, USA, 2–7 July 2018. [Google Scholar]
- Gamal, A.; Mammen, J.; Prabhakar, B.; Shah, D. Throughput-delay trade-off in wireless networks—Part I: The fluid model. IEEE Trans. Inf. Theory 2006, 52, 2568–2592. [Google Scholar] [CrossRef]
- Kim, S.; Kim, B.J. On the Byzantine-fault-tolerant consensus in blockchain built on internet of vehicles. In Proceedings of the 2022 International Conference on Electronics, Information, and Communication (ICEIC), Jeju, Republic of Korea, 6–9 February 2022. [Google Scholar]
- Gochhayat, S.; Shetty, S.; Mukkamala, R.; Foytik, P.; Kamhoua, G.; Njilla, L. Measuring decentrality in blockchain based systems. IEEE Access 2020, 24, 178372–178390. [Google Scholar] [CrossRef]
- Cowell, F. Theil, inequality indices and decomposition. In Dynamics Inequality Poverty; Society for the Study of Economic Inequality: Palma de Mallorca, Spain, 2006; pp. 341–356. [Google Scholar]
- Catalano, M.; Leise, T.; Pfaff, T. Measuring resource inequality: The Gini coefficient. Numeracy 2009, 2, 4. [Google Scholar] [CrossRef]
- Sen, A. On Economic Inequality; Oxford University Press: Oxford, UK, 1977. [Google Scholar]
- Cao, F.; Marshall, N. From the binomial reshuffling model to Poisson distribution of money. arXiv 2022, arXiv:2212.14388v1. [Google Scholar] [CrossRef]
- Grossglauser, M.; Tse, D. Mobility increases the capacity of ad hoc wireless networks. IEEE/ACM Trans. Netw. 2002, 10, 477–486. [Google Scholar] [CrossRef]
- Helium Foundation. HIP-70: Scaling the Helium Network. 2023. Available online: https://github.com/helium/HIP/blob/main/0070-scaling-helium.md (accessed on 1 December 2024).

| Acronym/Symbol | Description |
|---|---|
| Gini coefficient as the decentralization measure | |
| Probability of failure at each node | |
| PoC | Proof of coverage |
| PoS | Proof of stake |
| PoW | Proof of work |
| Scalability | |
| Rate of clustered area | |
| Rate of validators | |
| Universal scalability [52,53] | |
| Set of nodes belonging to consensus type | |
| Length of time taken to complete a consensus | |
| USL | Universal scalability law [52,53] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Choi, J. Wireless May Benefit Blockchain. Appl. Sci. 2025, 15, 334. https://doi.org/10.3390/app15010334
Kim S, Choi J. Wireless May Benefit Blockchain. Applied Sciences. 2025; 15(1):334. https://doi.org/10.3390/app15010334
Chicago/Turabian StyleKim, Seungmo, and Junsung Choi. 2025. "Wireless May Benefit Blockchain" Applied Sciences 15, no. 1: 334. https://doi.org/10.3390/app15010334
APA StyleKim, S., & Choi, J. (2025). Wireless May Benefit Blockchain. Applied Sciences, 15(1), 334. https://doi.org/10.3390/app15010334










