Geometric Detail-Preserved Point Cloud Upsampling via a Feature Enhanced Self-Supervised Network
Abstract
1. Introduction
- Contributions. Our contributions are summarized as follows.
- We design feature enhancement and geometric coordinate reconstruction modules that effectively preserve geometric details of output dense point clouds, such as non-flat regions, which outperforms existing methods in upsampling and related downstream tasks.
- Our end-to-end self-supervised network model considers the relationships between dense and sparse point clouds, including both global shapes and similar local geometric structures. This allows us to obtain more geometric information-rich dense point clouds, as validated by our experiments.
2. Related Works
- Encoding and learning of local features. Yu et al. [6] pioneered the field of point cloud upsampling with their PU-Net, a deep learning approach that leverages PointNet++ [13] for feature enhancement and a fully connected layer for reconstructing upscaled coordinates. Qian et al. [8] introduced a novel approach by representing 3D surfaces using 2D parameter spaces to enrich point data. In their subsequent work, PU-GCN [14], they employed graph convolutional networks (GCNs) in combination with shared multilayer perceptrons (MLPs) and parallel local feature learning networks, effectively processing multiscale features. Qiu et al. [15] integrated the self-attention mechanism into point cloud upsampling, emphasizing the enhancement of local feature distinguishability. Ding et al. [16] took a different approach, learning 2D perturbations through MLPs to estimate coordinate offsets between input and upsampling points. They further refined these offsets through residual learning, combining extracted features with the learned 2D perturbations. More recently, He et al. [9] introduced Grad-PU, an algorithm that seamlessly combines midpoint interpolation in Euclidean space with iterative optimization of distances to the target high-resolution point cloud.
- Upsampling network architectures. In the realm of point cloud upsampling, network architectures can be broadly classified into two categories: supervised and unsupervised (or self-supervised) networks. Supervised networks leverage metrics such as point uniformity [17], point-to-point distance [6], and reconstruction loss [18] to meticulously refine dense point clouds by comparing them to ground truth (GT) data. Li et al. [7] introduce Dis-PU, a two-phase model that combines feature expansion and spatial refinement, delivering high-quality, uniformly distributed point clouds. On the other hand, unsupervised methods, exemplified by GAN networks [17] and the self-supervised SPU-Net [19], focus on learning directly from the inherent structure of the point cloud, without relying on GT comparisons. These methods underscore the significance of feature supervision in network design, particularly in self-supervised learning, for enhancing upsampling quality.
3. Our Methodology
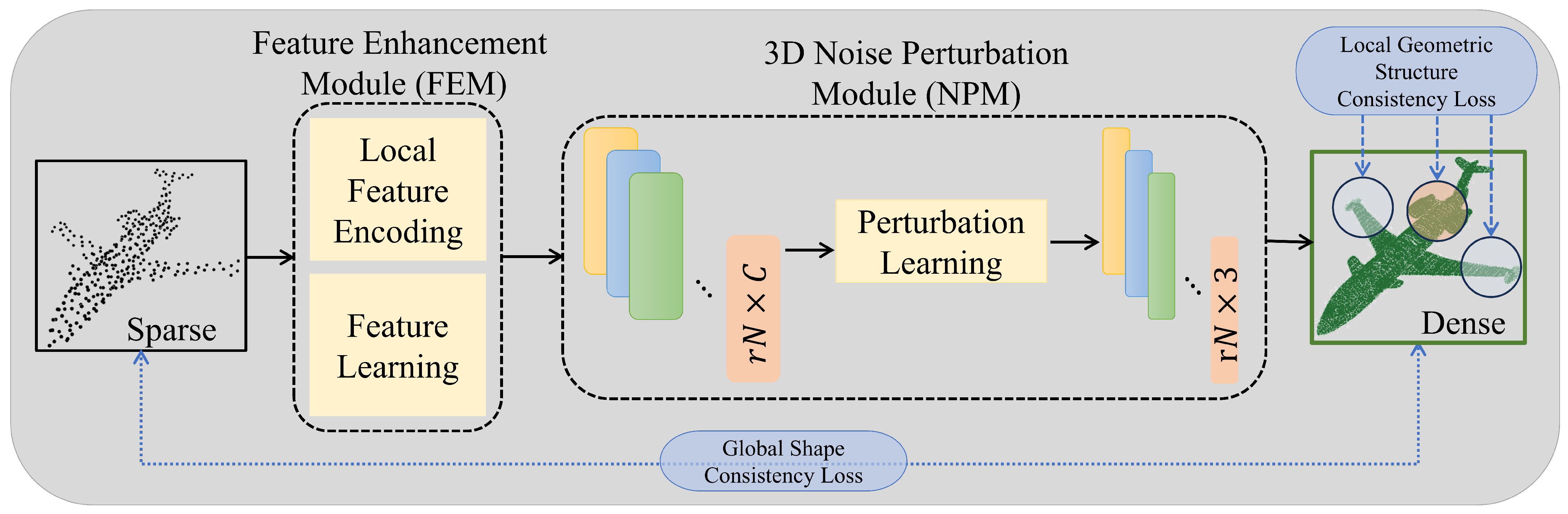
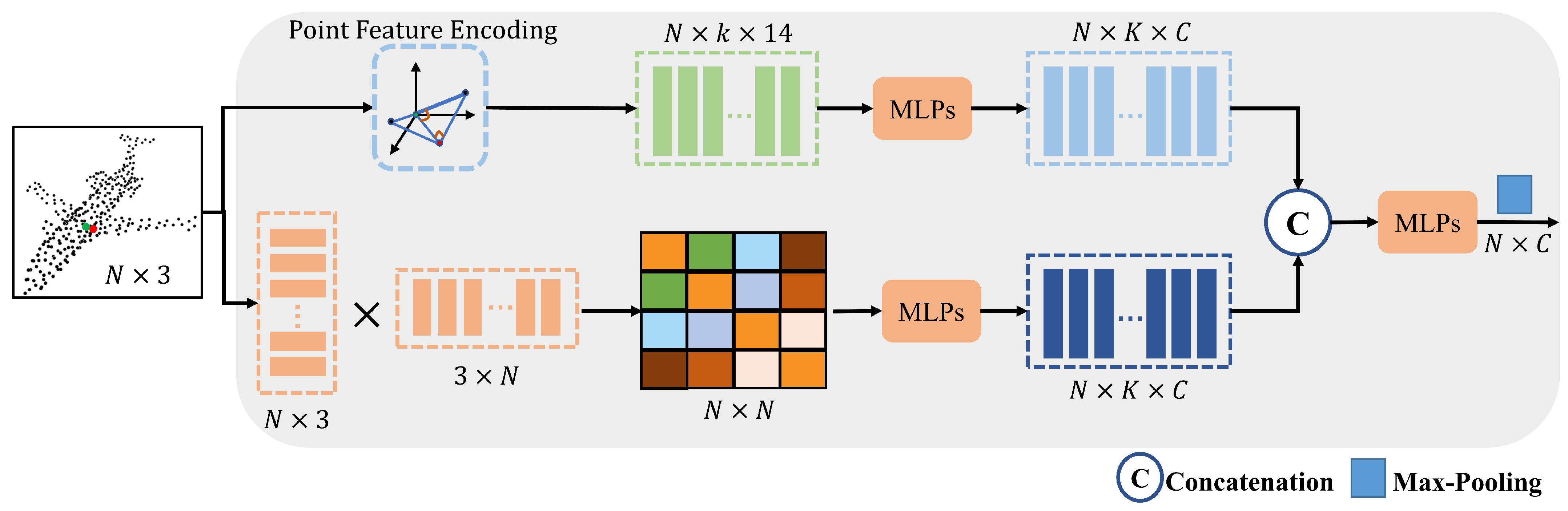
3.1. Feature Enhancement Module (FEM)
3.2. The 3D Noise Perturbation Module (NPM)
3.3. Loss Functions
- Global shape consistency loss. The input sparse point cloud S can generally be considered as a downsampled version of the output dense point cloud D, which shares consistent global shapes. By applying a downsampling function , we obtain the downsampled point cloud from D. The covariance matrices and are computed for and S, respectively, effectively capturing the point cloud structure for applications like 3D detection, similarity analysis, and 2D image matching. The similarity measure between these two covariance matrices is then computed as follows:
- Local geometric structure consistency loss. We introduce the local geometric structure consistency loss for point cloud upsampling tasks, motivated by the observation that 3D models usually share consistent (similar) local geometric structures. An illustration can be seen in Figure 4, where two regions highlighted in red and blue exhibit similar local geometric details. The measurement of such similarity can be computed by their Gram matrices [20,21]. Without loss of generality, assuming that the output dense point cloud is denoted by D, we construct the Gram matrix for any point with the assistance of the KNN algorithm. The local geometric structure consistency loss is thus defined as follows.
4. Experimental Results and Analysis
4.1. Datasets and Experimental Settings
4.2. Ablation Studies
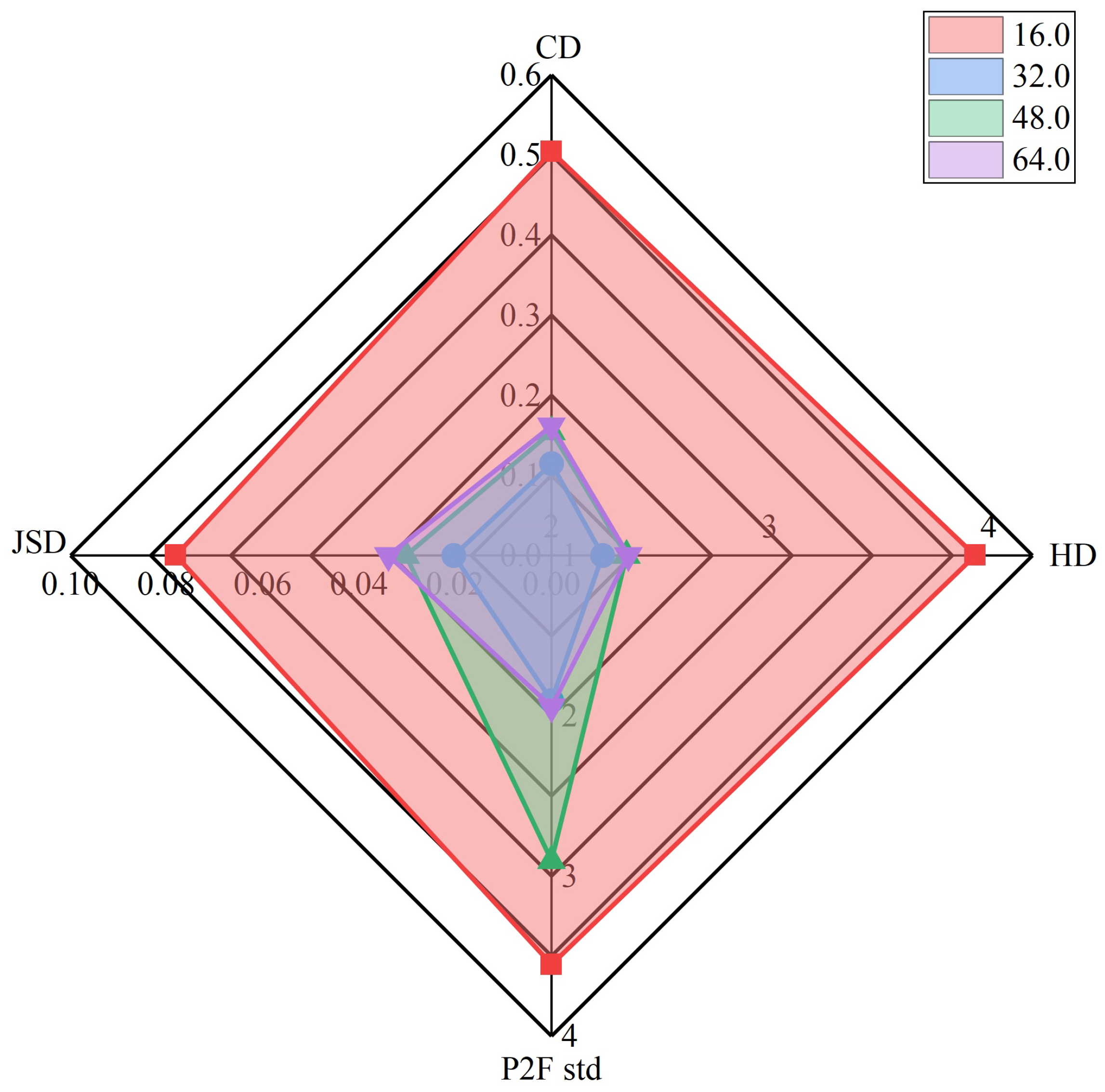
- Analysis of the size of the neighboring range. The neighborhood size significantly influences the performance of local feature encoding and feature learning in point cloud upsampling, as shown in Figure 6, with a point cloud of 512 points as network input and the average results of upsampling on different ratios () as the output. An analysis of the chamfer distance (CD) and Hausdorff distance (HD) reveals that a reduction in these distances corresponds to an enhancement in upsampling quality. Notably, the optimal results are attained at a neighborhood size of 32. Additionally, the point-to-face distance (P2F) represents the importance of a smaller distance, indicating a closer approximation to the geometric surface. Specifically, a neighborhood size of 32 yields the lowest average distance, approximately 1.9. The Jensen–Shannon divergence (JSD) metric provides insights into distribution disparities, while the two uniform metrics assess point alignment, all converging to their minimal values at a neighborhood size of 32. Moreover, whether using 512, 1024, or 4096 points as network input for upsampling, it shows that a neighborhood size of 32 still gives the best results in terms of evaluation metrics; e.g., for 1024 points as network input for upsampling, a neighborhood size of 32 yields the lowest average distance under the P2F metric, 1.9011, and a neighborhood size of 16 yields the distance 3.5910. In summary, this particular setting is crucial for achieving efficient and superior results in point cloud upsampling. For fewer or more points as input, we need to recompute the size of this neighborhood.
- Analysis of network modules. Table 2 shows the average metric results on different upsampling ratios () when inputting point clouds with 512 points to the three distinct networks for upsampling, which are SSPU-FENet, SSPU-FENet without the FEM (where the coordinates are directly fed into the network), and SSPU-FENet without the NPM. The results show that SSPU-FENet exhibits the lowest values across all metrics, clearly demonstrating the significance of each component in enhancing point cloud upsampling. Meanwhile, Figure 7 shows a visualization of the results. When the FEM is omitted, a noticeable increase point-to-face distance (P2F) is observed, rising from 1.9052 (Figure 7b) to 1.9210 (Figure 7a). This indicates that some of the interpolated points (mainly edge and corner points) have not been placed in the proper positions and they are too close to the current center point. It leads to a degradation in upsampling quality. Furthermore, the exclusion of the NPM also results in a significant deterioration of performance. Specifically, the chamfer distance (CD) increases from 0.1148 to 0.2206, indicating a decrease in the accuracy and precision of the upsampled point cloud.
- Analysis of model and time complexity. In Table 3, a comprehensive comparison of various network models is presented, emphasizing key aspects such as network type, network parameter size, inference time, and the incorporation of feature perturbation learning. A method like PU-GAN [17] employs fixed-value perturbation learning, leading to faster inference speeds despite its unique architecture as a generative adversarial network. Conversely, the GC-PCU [16] model employs adaptive perturbation learning, resulting in an increase in both parameters and inference time compared to PU-GAN or non-perturbation methods.
4.3. Results of Point Cloud Upsampling
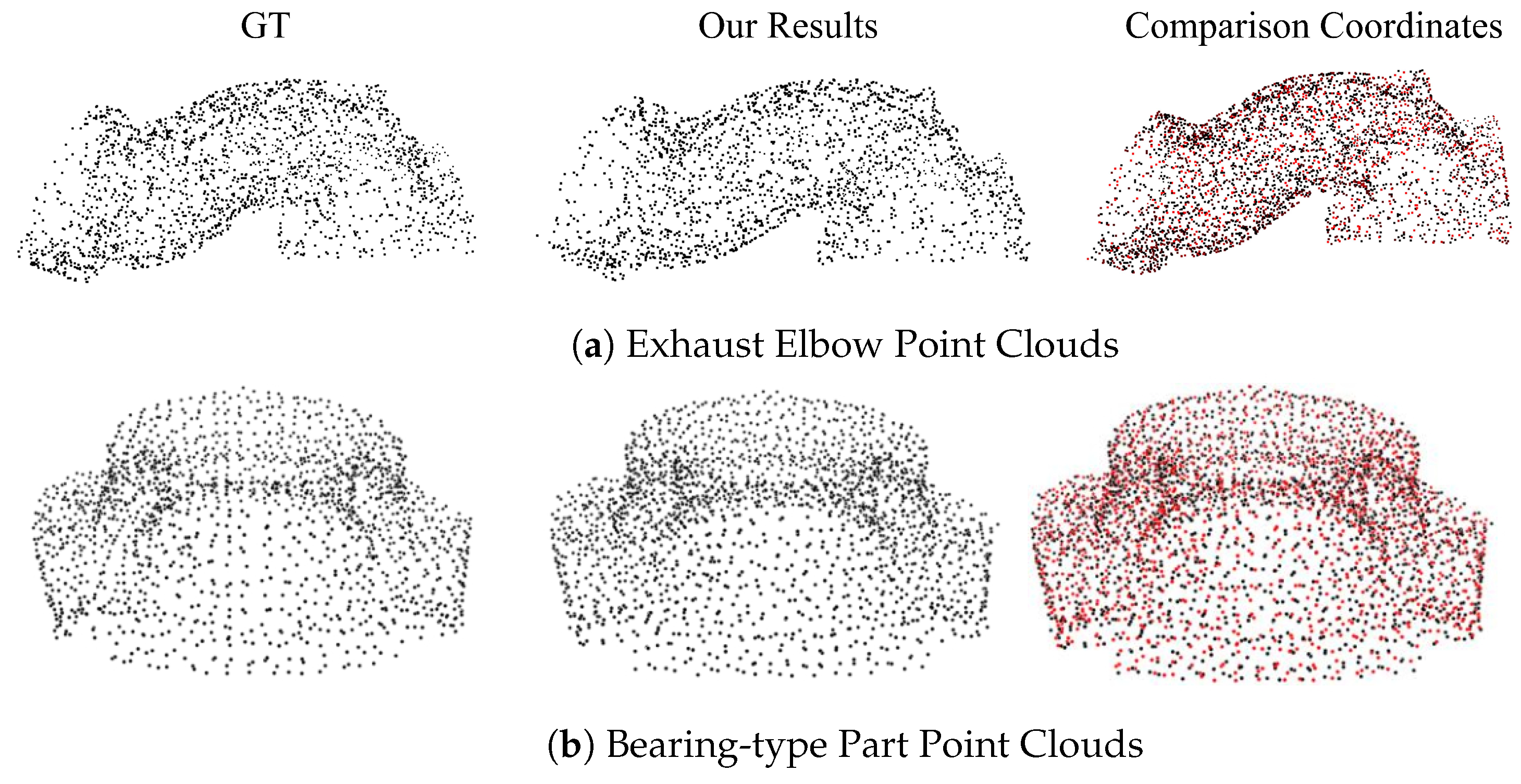
- Results from testing on ESB dataset. Figure 8 validates the performance of our proposed point cloud upsampling method on mechanical CAD models sourced from the ESB dataset. Initially containing 512 points (first column), the point clouds are effectively upsampled to 1024 points (second column) and 2048 points (third column). This quadrupled point density not only enhances the clarity of the point cloud details but also brings the points closer to the geometric surface, ensuring a uniform distribution. Notably, the upsampling process preserves intricate manufacturing details, such as holes, as evident in the bearing seat point clouds presented in Figure 8a. These features remain clear, smooth, and well defined throughout the process.
- Results from tested point clouds collected in ModelNet40 and PU-GAN with various numbers of points. First, it is important to note that the number of points in a point cloud model can vary significantly. Therefore, it is crucial to assess the sampling effectiveness of our method across various point counts. To validate our approach, we randomly select models from the ModelNet40 dataset [23] and present the results in Figure 10. When dealing with sparse point clouds having diverse point inputs, our SSPU-FENet outperforms other methods, such as PU-Refiner [26] and PUFA-GAN [27]. Notably, even with a minimal input of 256 points, our method generates high-quality upsampled point clouds with well-defined boundaries and reduced blurring compared to PU-Mask [12]. Additionally, we observed that unsupervised methods exhibit varying upsampling effects when the input point clouds are sparse. For example, SPU-Net [19] produces some outliers at the edges of the upsampled point clouds. Similarly, SAPCU [25] generates some points to gather together. In addition, U-PVNet [25] blurs some non-flat regions, as shown in Figure 11.
- Mesh reconstruction based on upsampled point clouds. Point cloud upsampling is pivotal in various downstream tasks, such as mesh reconstruction. Firstly, we verify the impact of our upsampled point cloud model on mesh reconstruction using the Poisson surface reconstruction method [28]. As shown in Figure 13, the first column displays randomly selected ground truth (GT) models from the ESB and PU-GAN datasets. The second and third columns are the and upsampling results, respectively, with the 512 input points. The varying colors in the last two columns represent the distance between the points and the GT model, ranging from blue (indicating the smallest distance) to red (representing the largest distance). It is evident that the mesh reconstruction closely resembles the GT model, apart from some minor non-smooth edges observed in the upsampling. Moreover, we randomly select a test sample from the PU1K dataset and generate the corresponding upsampled point cloud. Subsequently, we employ the ball-pivoting method [29] to reconstruct the meshes, as shown in Figure 14. Our method successfully infers the points at the armrests of the chair, significantly contributing to the subsequent mesh reconstruction process. In contrast, other methods [7,8,12,14,17,26,30] yield incomplete results or loss points at the armrests of the chair, demonstrating the superiority of our approach in handling complex geometric features.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, W.; Liu, X.; Zhai, D.; Jiang, J.; Ji, X. Self-Supervised Arbitrary-Scale Implicit Point Clouds Upsampling. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 12394–12407. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Li, M.; Yang, J.; Chen, Z.; Zhang, H.; Liu, W.; Han, F.K.; Liu, J. A Benchmark Dual-Modality Dental Imaging Dataset and a Novel Cognitively Inspired Pipeline for High-Resolution Dental Point Cloud Synthesis. Cogn. Comput. 2023, 15, 1922–1933. [Google Scholar] [CrossRef]
- Fugacci, U.; Romanengo, C.; Falcidieno, B.; Biasotti, S. Reconstruction and Preservation of Feature Curves in 3D Point Cloud Processing. Comput.-Aided Des. 2024, 167, 103649. [Google Scholar] [CrossRef]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image super-resolution via iterative refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4713–4726. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, W.; Li, J.; Zhuang, P.; Sun, H.; Xu, Y.; Li, C. CVANet: Cascaded visual attention network for single image super-resolution. Neural Netw. 2024, 170, 622–634. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Li, X.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. Pu-net: Point cloud upsampling network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2790–2799. [Google Scholar]
- Li, R.; Li, X.; Heng, P.A.; Fu, C.W. Point cloud upsampling via disentangled refinement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 344–353. [Google Scholar]
- Qian, Y.; Hou, J.; Kwong, S.; He, Y. PUGeo-Net: A geometry-centric network for 3D point cloud upsampling. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 752–769. [Google Scholar]
- He, Y.; Tang, D.; Zhang, Y.; Xue, X.; Fu, Y. Grad-PU: Arbitrary-Scale Point Cloud Upsampling via Gradient Descent with Learned Distance Functions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5354–5363. [Google Scholar]
- Han, B.; Zhang, X.; Ren, S. PU-GACNet: Graph attention convolution network for point cloud upsampling. Image Vis. Comput. 2022, 118, 104371. [Google Scholar] [CrossRef]
- Han, B.; Deng, L.; Zheng, Y.; Ren, S. S3U-PVNet: Arbitrary-scale point cloud upsampling via Point-Voxel Network based on Siamese Self-Supervised Learning. Comput. Vis. Image Underst. 2024, 239, 103890. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, H.; Hamzaoui, R.; Liu, Q.; Li, S. PU-Mask: 3D Point Cloud Upsampling via an Implicit Virtual Mask. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 6489–6502. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; ACM: New York, NY, USA, 2017; pp. 5105–5114. [Google Scholar]
- Qian, G.; Abualshour, A.; Li, G.; Thabet, A.; Ghanem, B. Pu-gcn: Point cloud upsampling using graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11683–11692. [Google Scholar]
- Qiu, S.; Anwar, S.; Barnes, N. Pu-transformer: Point cloud upsampling transformer. In Proceedings of the Asian Conference on Computer Vision, Macau, China, 4–8 December 2022; pp. 2475–2493. [Google Scholar]
- Ding, D.; Qiu, C.; Liu, F.; Pan, Z. Point cloud upsampling via perturbation learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4661–4672. [Google Scholar] [CrossRef]
- Li, R.; Li, X.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. Pu-gan: A point cloud upsampling adversarial network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7203–7212. [Google Scholar]
- Ye, S.; Chen, D.; Han, S.; Wan, Z.; Liao, J. Meta-PU: An arbitrary-scale upsampling network for point cloud. IEEE Trans. Vis. Comput. Graph. 2021, 28, 3206–3218. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Liu, Y.S.; Han, Z. Spu-net: Self-supervised point cloud upsampling by coarse-to-fine reconstruction with self-projection optimization. IEEE Trans. Image Process. 2022, 31, 4213–4226. [Google Scholar] [CrossRef] [PubMed]
- Pumir, T.; Singer, A.; Boumal, N. The generalized orthogonal Procrustes problem in the high noise regime. Inf. Inference J. IMA 2021, 10, 921–954. [Google Scholar] [CrossRef]
- Qin, S.; Li, Z.; Liu, L. Robust 3D Shape Classification via Non-Local Graph Attention Network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5374–5383. [Google Scholar]
- Jayanti, S.; Kalyanaraman, Y.; Iyer, N.; Ramani, K. Developing an engineering shape benchmark for CAD models. Comput.-Aided Des. 2006, 38, 939–953. [Google Scholar] [CrossRef]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Long, C.; Zhang, W.; Li, R.; Wang, H.; Dong, Z.; Yang, B. Pc2-pu: Patch correlation and point correlation for effective point cloud upsampling. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 2191–2201. [Google Scholar]
- Zhao, W.; Liu, X.; Zhong, Z.; Jiang, J.; Gao, W.; Li, G.; Ji, X. Self-Supervised Arbitrary-Scale Point Clouds Upsampling via Implicit Neural Representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1999–2007. [Google Scholar]
- Liu, H.; Yuan, H.; Hamzaoui, R.; Gao, W.; Li, S. PU-refiner: A geometry refiner with adversarial learning for point cloud upsampling. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 22–27 May 2022; pp. 2270–2274. [Google Scholar]
- Liu, H.; Yuan, H.; Hou, J.; Hamzaoui, R.; Gao, W. Pufa-gan: A frequency-aware generative adversarial network for 3d point cloud upsampling. IEEE Trans. Image Process. 2022, 31, 7389–7402. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. (ToG) 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The ball-pivoting algorithm for surface reconstruction. IEEE Trans. Vis. Comput. Graph. 1999, 5, 349–359. [Google Scholar] [CrossRef]
- Yifan, W.; Wu, S.; Huang, H.; Cohen-Or, D.; Sorkine-Hornung, O. Patch-based progressive 3d point set upsampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5958–5967. [Google Scholar]










| Hyperparameter | Value |
|---|---|
| Window sizes of 2D conv layers | 3/3 |
| Values k in two k-max pooling layers | 2/2 |
| Learning rate | 0.001 |
| Batch size | 28 |
| Max epoch | 120 |
| Decay rate | 0.70 |
| Default upsampling ratio | 4 |
| Metric | SSPU-FENet | Removing FEM | Removing NPM |
|---|---|---|---|
| CD | 0.1148 | 0.1943 | 0.2206 |
| HD | 2.2331 | 2.6475 | 2.9116 |
| P2F | 1.9052 | 1.9210 | 1.9223 |
| JSD | 0.0203 | 0.0204 | 0.0234 |
| Model | Supervised? | Perturbation Learning | Params (M) | Time (ms) |
|---|---|---|---|---|
| PU-Net [6] | Yes | No | 3.00 | 4.55 |
| PU-GAN [17] | No | Yes (fixed, 1D) | 2.07 | 7.08 |
| PU-GCN [14] | Yes | No | 0.29 | 5.51 |
| Dis-PU [7] | Yes | No | 3.99 | 12.77 |
| PC2-PU [24] | Yes | No | 1.71 | 4.19 |
| GC-PCU [16] | Yes | Yes (adaptive, 2D) | 5.01 | 858.9 |
| SPU-Net [19] | No | No | 0.68 | 130.9 |
| SAPCU [25] | No | No | 26.48 | 11,607.0 |
| U-PVNet [11] | No | No | 19.64 | 1047.0 |
| SSPU-FENet | No | Yes (adaptive, 3D) | 8.71 | 900.1 |
| Models | ||||||
|---|---|---|---|---|---|---|
| CD | HD | P2F | CD | HD | P2F | |
| PU-Net [6] | 0.5225 | 4.6083 | 4.3590 | 0.3123 | 3.9111 | 5.0470 |
| PU-GAN [17] | 0.2676 | 4.7379 | 3.6100 | 0.2232 | 6.3243 | 4.5690 |
| PU-GCN [14] | 0.2724 | 3.0455 | 3.3760 | 0.1657 | 3.8224 | 3.5060 |
| Dis-PU [7] | 0.2560 | 4.7277 | 3.1780 | 0.1484 | 6.0934 | 3.7660 |
| PC2-PU [24] | 0.2321 | 2.5942 | 2.7250 | 0.0998 | 2.8692 | 2.9440 |
| Grad-PU [9] | 0.2500 | 2.3700 | 1.8900 | 0.1080 | 2.3520 | 2.1270 |
| U-PVNet [11] | 0.2800 | 1.6400 | 2.5300 | 0.1212 | 1.5250 | 2.4040 |
| SAPCU [25] | 0.4600 | 9.0600 | 3.4500 | 0.3820 | 9.3550 | 3.2900 |
| SSPU-FENet | 0.1898 | 2.2293 | 2.7034 | 0.0991 | 2.0297 | 2.1435 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, S.; Jin, Y.; Hu, H. Geometric Detail-Preserved Point Cloud Upsampling via a Feature Enhanced Self-Supervised Network. Appl. Sci. 2025, 15, 174. https://doi.org/10.3390/app15010174
Qin S, Jin Y, Hu H. Geometric Detail-Preserved Point Cloud Upsampling via a Feature Enhanced Self-Supervised Network. Applied Sciences. 2025; 15(1):174. https://doi.org/10.3390/app15010174
Chicago/Turabian StyleQin, Shengwei, Yao Jin, and Hailong Hu. 2025. "Geometric Detail-Preserved Point Cloud Upsampling via a Feature Enhanced Self-Supervised Network" Applied Sciences 15, no. 1: 174. https://doi.org/10.3390/app15010174
APA StyleQin, S., Jin, Y., & Hu, H. (2025). Geometric Detail-Preserved Point Cloud Upsampling via a Feature Enhanced Self-Supervised Network. Applied Sciences, 15(1), 174. https://doi.org/10.3390/app15010174






