Energy Management Strategies for Extended-Range Electric Vehicles with Real Driving Emission Constraints
Abstract
1. Introduction
2. Models and Methods
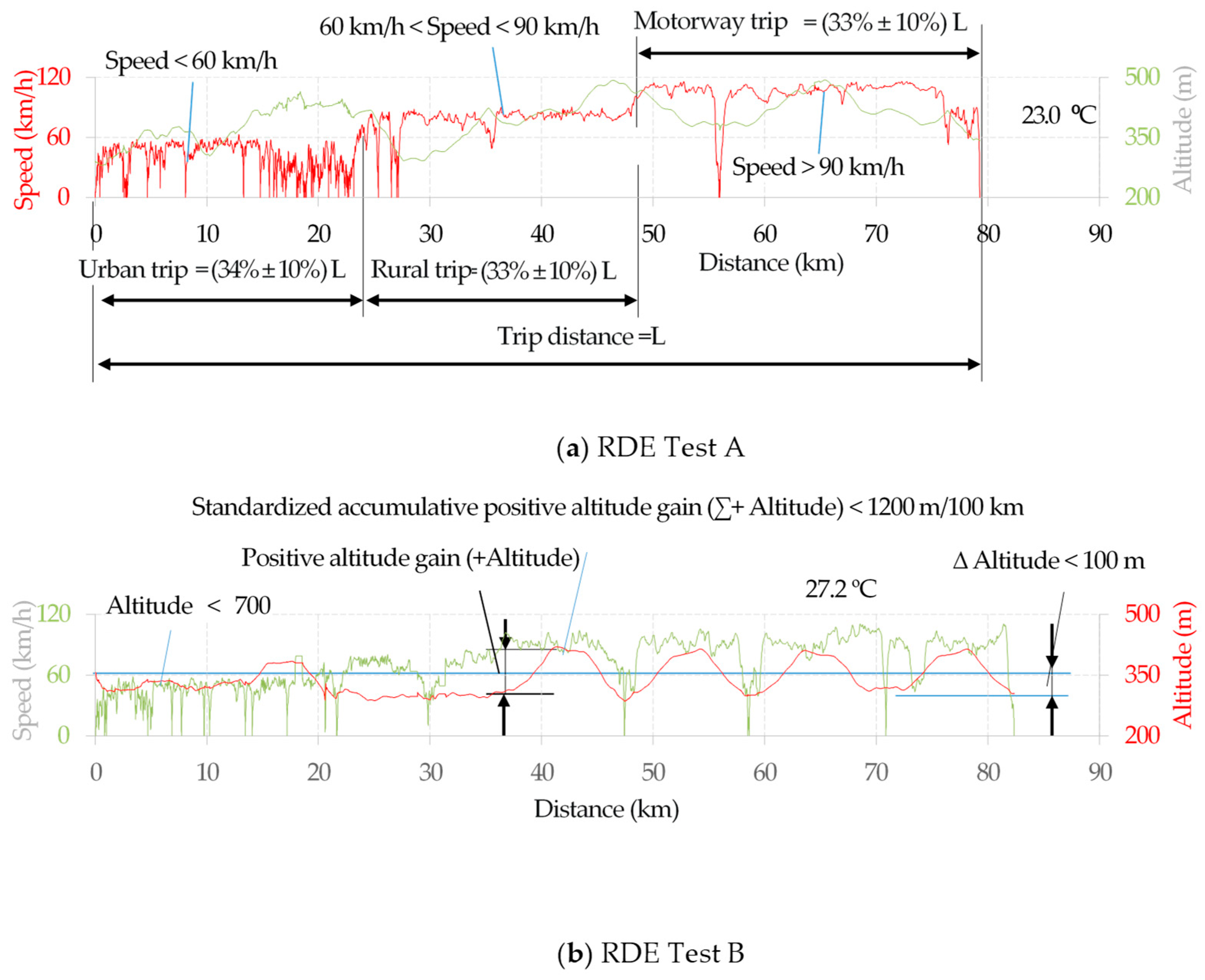
2.1. Real Driving Emission Tests
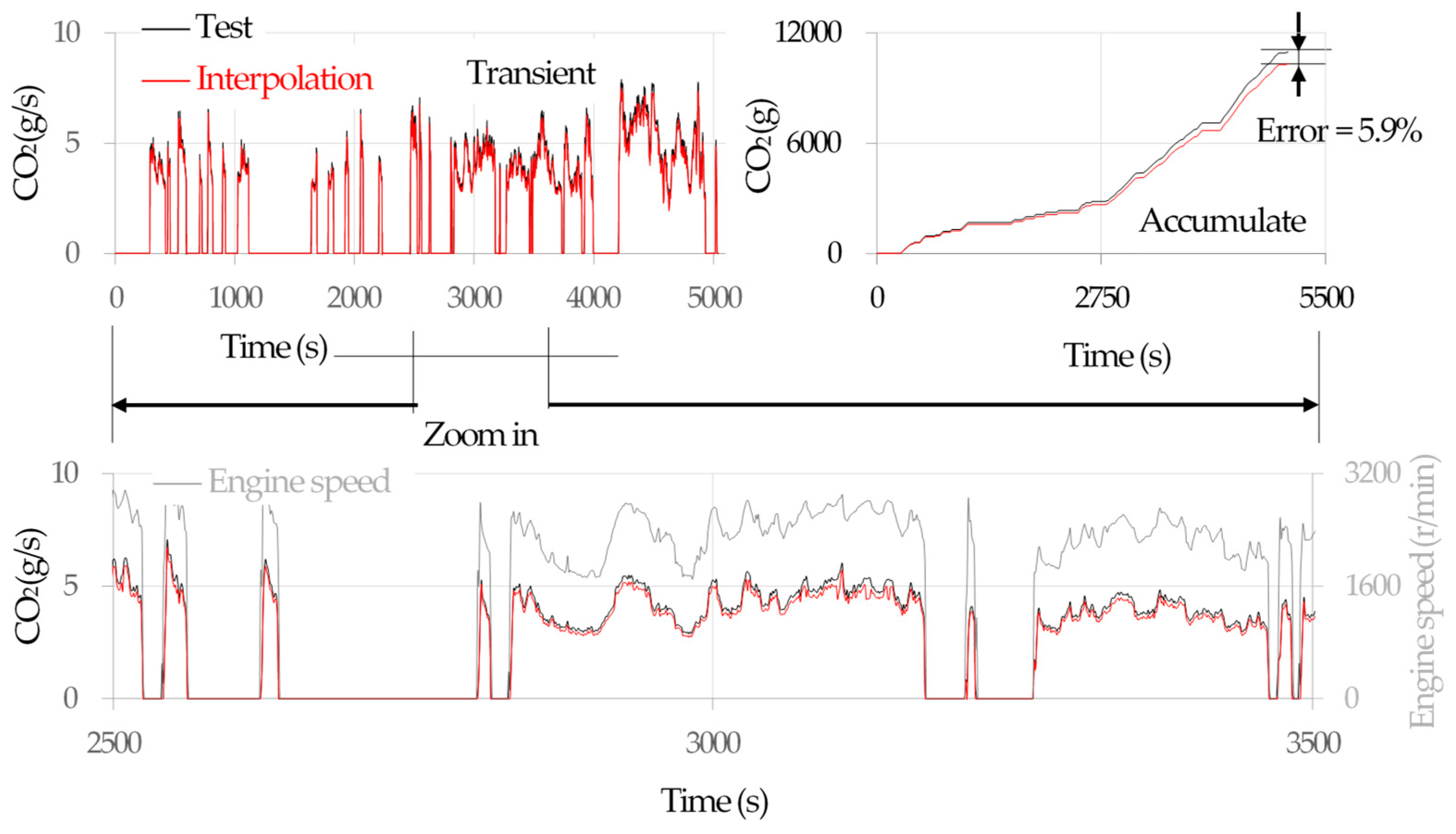
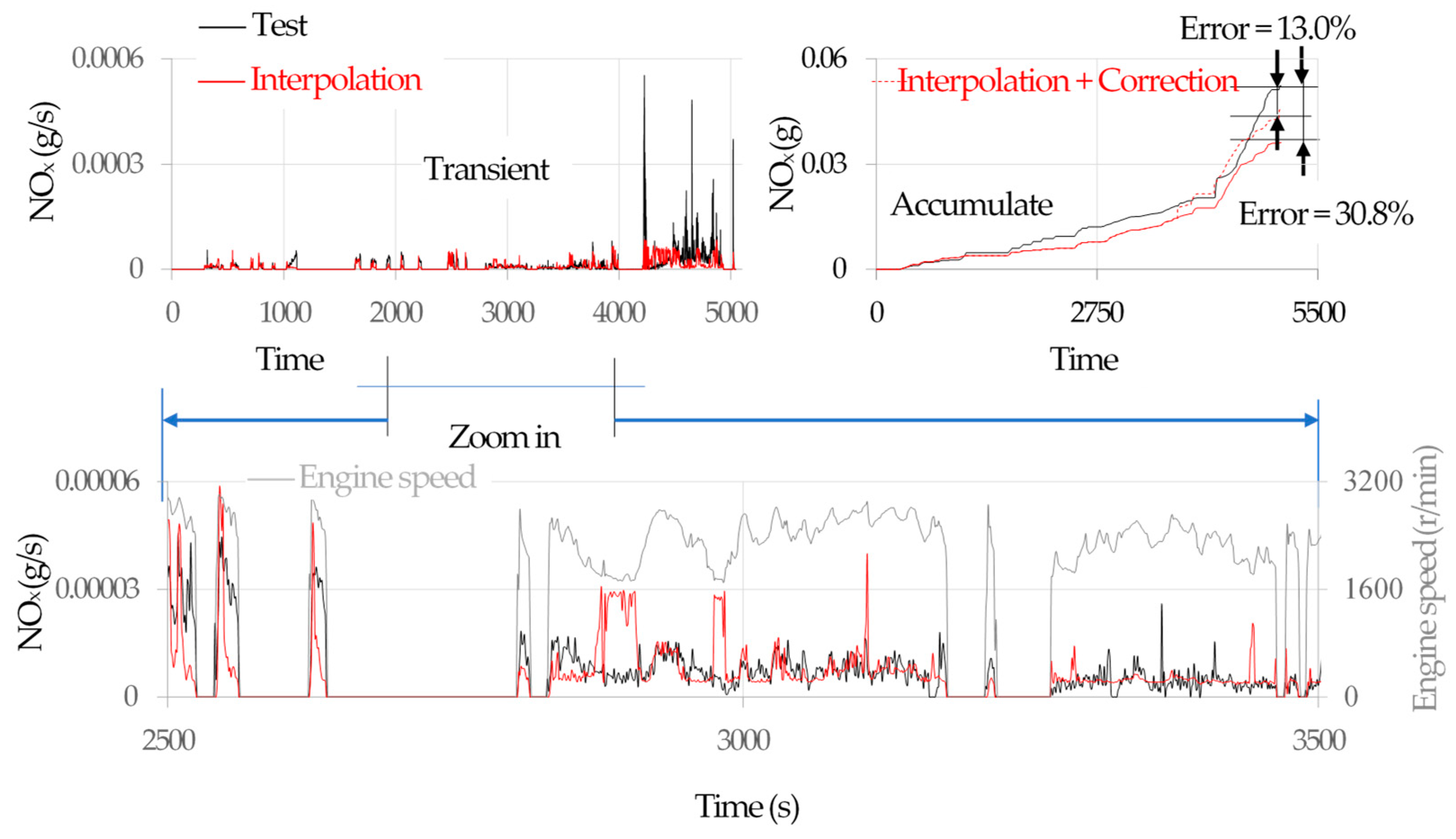
2.2. Real Driving Emission Modeling
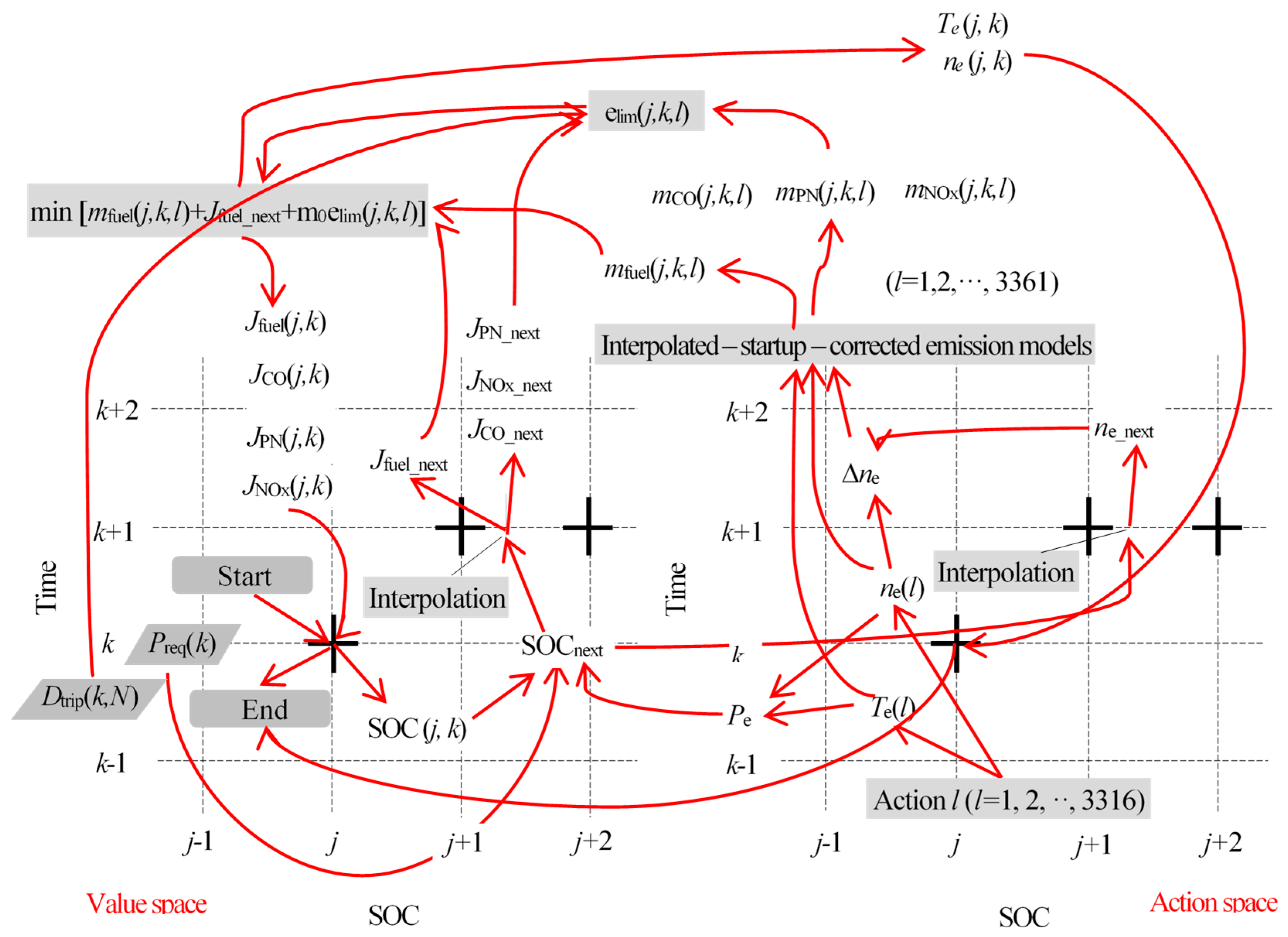
2.3. DP Algorithm with Emission Constraints
3. Results and Discussions
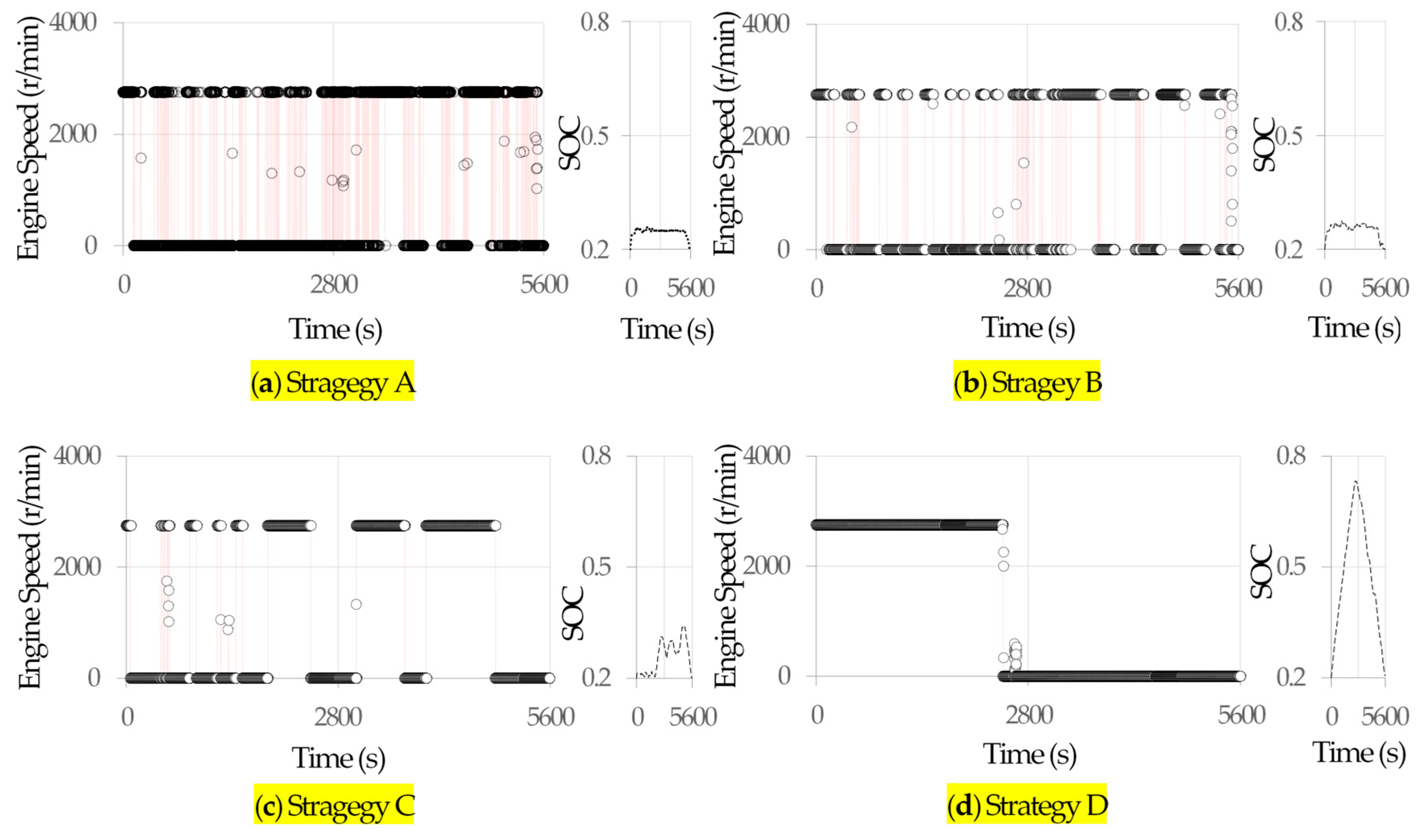
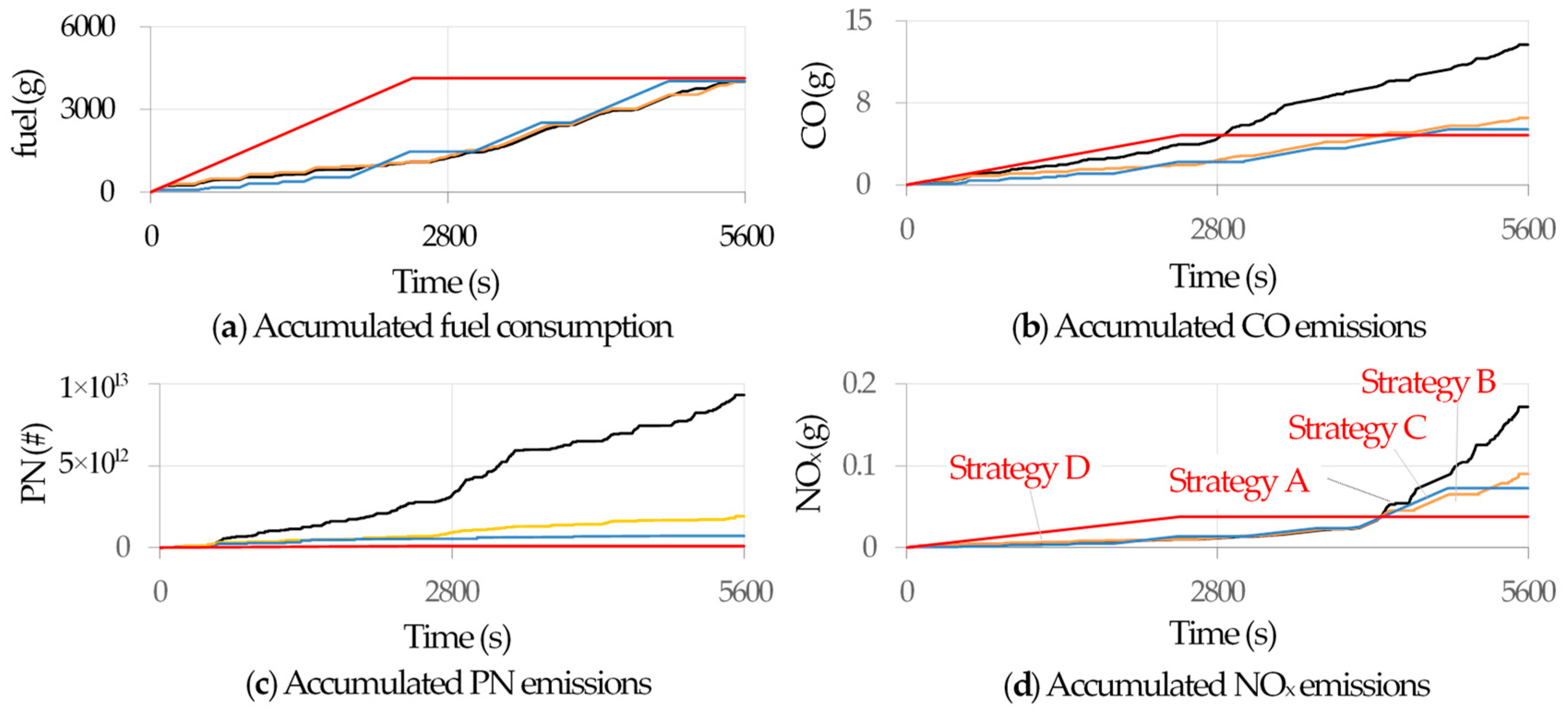
3.1. Start–Stop Reduction Strategies
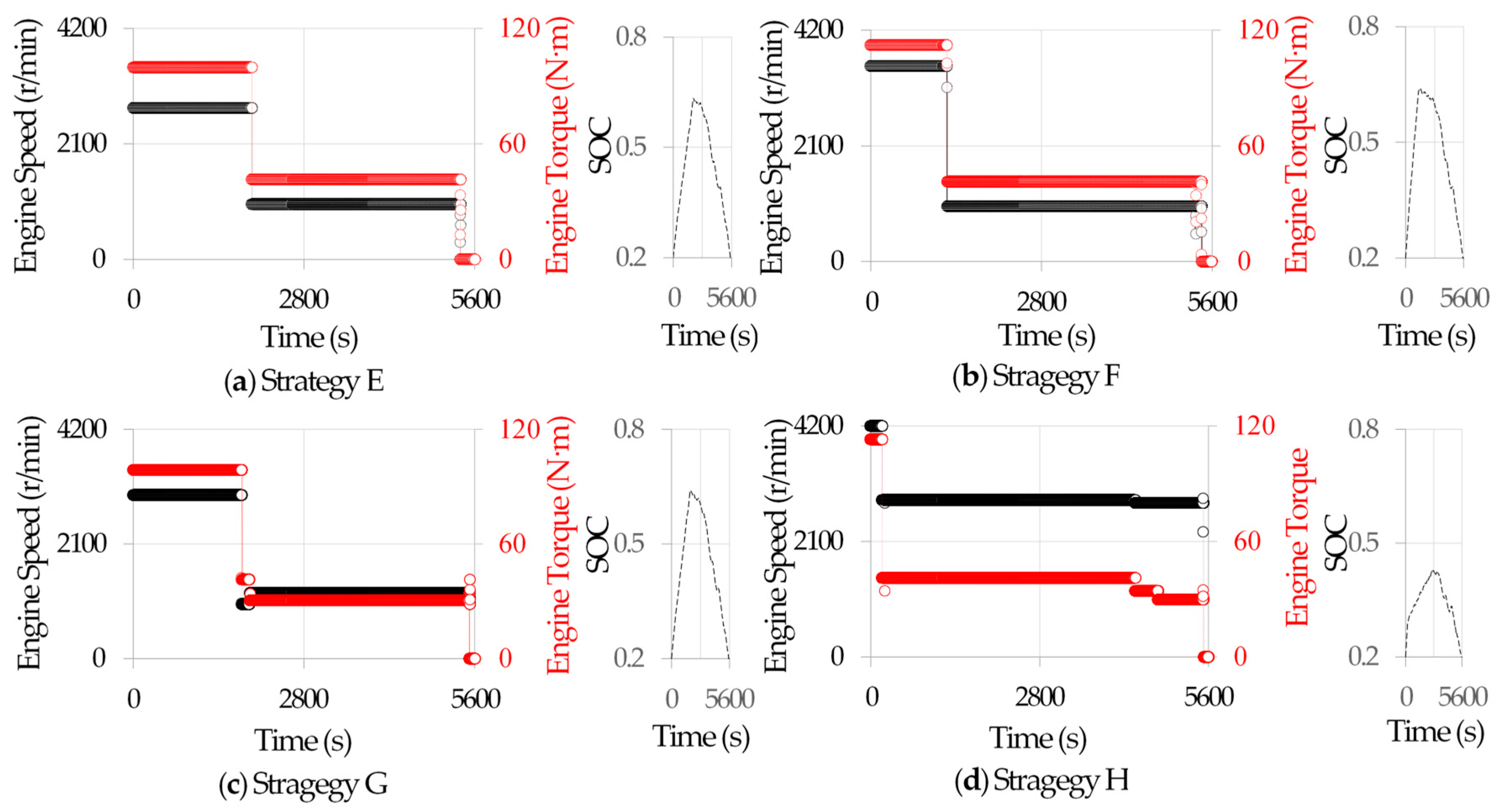
3.2. Condition Migration Strategies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cherp, A.; Jewell, J. The concept of energy security: Beyond the four As. Energy Policy 2014, 75, 415–421. [Google Scholar] [CrossRef]
- Lu, Z.N.; Chen, H.Y.; Hao, Y.; Wang, J.Y.; Song, X.J.; Mok, T.M. The dynamic relationship between environmental pollution, economic development and public health: Evidence from China. J. Clean. Prod. 2017, 166, 134–147. [Google Scholar] [CrossRef]
- Jorgenson, A.K.; Fiske, S.; Hubacek, K.; Li, J.; McGovern, T.; Rick, T.; Schor, J.B.; Solecki, W.; York, R.; Zycherman, A. Social science perspectives on drivers of and responses to global climate change. Wires Clim. Chang. 2019, 10, e554. [Google Scholar] [CrossRef] [PubMed]
- Zelasky, S.E.; Buonocore, J.J. The social costs of health- and climate-related on-road vehicle emissions in the continental United States from 2008 to 2017. Environ. Res. Lett. 2021, 16, 065009. [Google Scholar] [CrossRef]
- Andwari, A.M.; Pesiridis, A.; Rajoo, S.; Martinez-Botas, R.; Esfahanian, V. A review of battery electric vehicle technology and readiness levels. Renew. Sustain. Energy Rev. 2017, 78, 414–430. [Google Scholar] [CrossRef]
- Liu, Z.W.; Hao, H.; Cheng, X.; Zhao, F.Q. Critical issues of energy efficient and new energy vehicles development in China. Energy Policy 2018, 115, 92–97. [Google Scholar] [CrossRef]
- Ku, A.; Kammen, D.M.; Castellanos, S. A quantitative, equitable framework for urban transportation electrification: Oakland, California as a mobility model of climate justice. Sustain. Cities Soc. 2021, 74, 103179. [Google Scholar] [CrossRef]
- Puma-Benavides, D.S.; Izquierdo-Reyes, J.; Calderon-Najera, J.D.; Ramirez-Mendoza, R.A. A Systematic Review of Technologies, Control Methods, and Optimization for Extended-Range Electric Vehicles. Appl. Sci. 2021, 11, 7095. [Google Scholar] [CrossRef]
- Zhao, F.Q.; Liu, X.L.; Hao, H.; Liu, Z.W. A comprehensive study of range-extended electric vehicles from the perspectives of the technology, policy, market, and design concept. Int. J. Vehicle Des. 2023, 92, 190–212. [Google Scholar] [CrossRef]
- Prasad, S.L.; Gudipalli, A. Range-anxiety reduction strategies for extended-range electric vehicle. Int. Trans. Electr. Energy Syst. 2023, 2023, 7246414. [Google Scholar]
- Tate, E.D.; Harpster, M.O.; Savagian, P.J. The electrification of the automobile: From conventional hybrid, to plug-in hybrids, to extended-range electric vehicles. SAE Int. J. Passeng. Cars-Electron. Electr. Syst. 2008, 1, 125–135. [Google Scholar] [CrossRef]
- Pozzato, G.; Formentin, S.; Panzani, G.; Savaresi, S.M. Least costly energy management for extended-range electric vehicles: An economic optimization framework. Eur. J. Control 2020, 56, 218–230. [Google Scholar] [CrossRef]
- Wu, J.L.; Gao, W.H.; Zhang, Y.Q. A new real-time optimal energy management strategy for range extended electric vehicles considering battery degradation and engine start-up. Adv. Mech. Eng. 2024, 16, 16878132241257327. [Google Scholar] [CrossRef]
- Hu, D.; Huang, C.; Yin, G.D.; Li, Y.M.; Huang, Y.; Huang, H.L.; Wu, J.D.; Li, W.F.; Xie, H. A transfer-based reinforcement learning collaborative energy management strategy for extended-range electric buses with cabin temperature comfort consideration. Energy 2024, 290, 130097. [Google Scholar] [CrossRef]
- Xiao, B.; Ruan, J.; Yang, W.; Walker, P.D.; Zhang, N. A review of pivotal energy management strategies for extended range electric vehicles. Renew. Sustain. Energy Rev. 2021, 149, 111194. [Google Scholar] [CrossRef]
- Turker, E.; Bulut, E.; Kahraman, A.; Cakici, M.; Ozturk, F. Estimation of energy management strategy using neural-network-based surrogate model for range extended vehicle. Appl. Sci. 2023, 12, 12935. [Google Scholar] [CrossRef]
- Du, J.Y.; Chen, J.F.; Song, Z.Y.; Gao, M.M.; Ouyang, M.G. Design method of a power management strategy for variable battery capacities range-extended electric vehicles to improve energy efficiency and cost-effectiveness. Energy 2017, 121, 32–34. [Google Scholar] [CrossRef]
- Kalia, A.V.; Fabien, B.C. Comparison of model predictive control and distance constrained-adaptive concurrent dynamic programming algorithms for extended range electric vehicle optimal energy management. J. Dyn. Syst. Meas. Control 2021, 143, 094504. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q.X.; Wen, C.Q.; Liu, M.M.; Yang, X.H.; Xu, H.M.; Li, J. Predictive equivalent consumption minimization strategy based on driving pattern personalized reconstruction. Appl. Energy 2024, 367, 123424. [Google Scholar] [CrossRef]
- Xi, L.H.; Zhang, X.; Sun, C.Y.; Wang, Z.X.; Hou, X.S.; Zhang, J.B. Intelligent energy management control for extended range electric vehicles based on dynamic programming and neural network. Energies 2017, 10, 1871. [Google Scholar] [CrossRef]
- Yu, Y.B.; Jiang, J.Y.; Min, H.T.; Zhang, Z.P.; Sun, W.Y.; Cao, Q.M. Integrated energy and thermal management strategy for extended range electric vehicle based on battery temperature and state-of-charge global planning. Energy Convers. Manag. 2023, 288, 117154. [Google Scholar] [CrossRef]
- Xiao, B.Y.; Yang, W.W.; Wu, J.M.; Walker, P.D.; Zhang, N. Energy management strategy via maximum entropy reinforcement learning for an extended range logistics vehicle. Energy 2022, 253, 124105. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Guo, R.; Xue, X.; Hong, Z.; Luo, M.H.; Wong, P.K.; Liu, J.J.R.; Wang, X.Z. Application-oriented mode decision for energy management of range-extended electric vehicle based on reinforcement learning. Electr. Power Syst. Res. 2024, 226, 109896. [Google Scholar] [CrossRef]
- Yao, M.Y.; Zhu, B.; Zhang, N. Adaptive real-time optimal control for energy management strategy of extended range electric vehicle. Energy Convers. Manag. 2021, 234, 113874. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.T.; Tian, J.Y.; Li, T. Adaptive real-time optimal energy management strategy for extender range electric vehicle. Energy 2022, 197, 117237. [Google Scholar] [CrossRef]
- Krawczyk, P.; Kopczynski, A.; Lasocki, J. Modeling and simulation of extended-range electric vehicle with control strategy to assess fuel consumption and CO2 emission for the expected driving range. Energies 2022, 15, 4187. [Google Scholar] [CrossRef]
- Lin, W.Y.; Zhao, H.; Zhang, B.Z.; Wang, Y.; Xiao, Y.; Xu, K.; Zhao, R. Predictive energy management strategy for range-extended electric vehicles based on ITS information and start-stop optimization with vehicle velocity forecast. Energies 2022, 15, 7774. [Google Scholar] [CrossRef]
- Wang, Y.X.; Lou, D.M.; Xu, N.; Fang, L.; Tan, P.Q. Energy management and emission control for range extended electric vehicles. Energy 2021, 236, 121370. [Google Scholar] [CrossRef]
- Liu, H.W.; Lei, Y.L.; Fu, Y.; Li, X.Z. A novel hybrid-point-line energy management strategy based on multi-objective optimization for range-extended electric vehicle. Energy 2022, 247, 123357. [Google Scholar] [CrossRef]
- Lin, X.Y.; Chen, Z.Y.; Zhang, J.J.; Wu, C.Y. A multi-objective optimization control strategy of a range-extended electric vehicle for the trip range and road gradient adaption. Int. J. Automot. Technol. 2024, 25, 131–145. [Google Scholar] [CrossRef]
- Chang, C.; Fan, Z.K.; Wang, Z.H.; Liu, H.W. Research on adaptive two-point energy management strategy and optimization for range-extended electric vehicle. IEEE Access 2023, 11, 90201–90213. [Google Scholar] [CrossRef]
- Tang, X.L.; Chen, J.X.; Liu, T.; Qin, Y.C.; Cao, D.P. Distributed deep reinforcement learning-based energy and emission management strategy for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 9922–9934. [Google Scholar] [CrossRef]
- Giakoumis, E.G.; Alafouzos, A.I. Study of diesel engine performance and emissions during a transient cycle applying an engine mapping-based methodology. Appl. Energy 2010, 87, 1358–1365. [Google Scholar] [CrossRef]
- Fu, J.Q.; Deng, B.L.; Liu, X.Q.; Shu, J.; Xu, Y.; Liu, J.P. The experimental study on transient emissions and engine behaviors of a sporting motorcycle under world motorcycle test cycle. Energy 2020, 211, 118670. [Google Scholar] [CrossRef]
- Gallus, J.; Kirchner, U.; Vogt, R.; Benter, T. Impact of driving style and road grade on gaseous exhaust emissions of passenger vehicles measured by a portable emission measurement system (PEMS). Transp. Res. Part D Transp. Environ. 2017, 52, 215–226. [Google Scholar] [CrossRef]
- Huang, R.; Ni, J.M.; Zheng, T.; Wang, Q.W.; Shi, X.Y.; Cheng, Z.X. Characterizing and assessing the fuel economy, particle number and gaseous emissions performance of hybrid electric and conventional vehicles under different driving modes. Atmos. Pollut. Res. 2022, 13, 101597. [Google Scholar] [CrossRef]
- Shahariar, G.M.H.; Bodisco, T.A.; Zare, A.; Sajjad, M.; Jahirul, M.I.; Van, T.C.; Bartlett, H.; Ristovski, Z.; Brown, R.J. Impact of driving style and traffic condition on emissions and fuel consumption during real transient operation. Fuel 2022, 319, 123874. [Google Scholar] [CrossRef]
- Khan, T.; Frey, H.C. Comparison of real and certification emission rates for light duty gasoline vehicles. Sci. Total Environ. 2018, 622, 790–800. [Google Scholar] [CrossRef] [PubMed]
- Triantafyllopoulos, G.; Dimaratos, A.; Ntziachristos, L.; Bernard, Y.; Dornoff, J.; Samaras, Z. A study on the CO2 and NOx emissions performance of Euro 6 diesel vehicles under various chassis dynamometer and on-road conditions including latest regulatory provisions. Sci. Total Environ. 2019, 666, 337–346. [Google Scholar] [CrossRef]
- Jimenez, J.L.; Valido, J.; Molden, N. The drivers behind differences between official and actual vehicle efficiency and CO2 emissions. Transp. Res. Part D Transp. Environ. 2019, 67, 628–641. [Google Scholar] [CrossRef]
- Du, B.C.; Zhang, L.; Zou, J.; Han, J.L.; Zhang, Y.; Xu, H.L. Investigating the impact of route topography on real driving emission tests based on large data sample at data window level. Sci. Total Environ. 2022, 809, 151133. [Google Scholar] [CrossRef] [PubMed]
- Barbier, A.; Salavert, J.M.; Palau, C.E.; Guardiola, C. Analysis of the Euro 7 on-board emissions monitoring concept with real-driving data. Transp. Res. Part D Transp. Environ. 2024, 127, 104062. [Google Scholar] [CrossRef]
- European Commission (EC). Commission Regulation (EU) 2023/443 of 8 February 2023 amending Regulation (EU) 2017/1151 as regards the emission type approval procedures for light passenger and commercial vehicles. Off. J. Eur. Union 2023. Available online: https://eur-lex.europa.eu/eli/reg/2023/443/oj/eng (accessed on 24 December 2024).
- GB18352.6-2016; Limits and Measurement Methods for Emissions from Light-Duty Vehicles (CHINA VI). China Environmental Science Press: Beijing, China, 2016.
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Chen, Y.; Zhang, L.; Chen, G.; Han, J.; Zhang, Q.; Li, C. Energy Management Strategies for Extended-Range Electric Vehicles with Real Driving Emission Constraints. Appl. Sci. 2025, 15, 142. https://doi.org/10.3390/app15010142
Xu H, Chen Y, Zhang L, Chen G, Han J, Zhang Q, Li C. Energy Management Strategies for Extended-Range Electric Vehicles with Real Driving Emission Constraints. Applied Sciences. 2025; 15(1):142. https://doi.org/10.3390/app15010142
Chicago/Turabian StyleXu, Hualong, Yang Chen, Li Zhang, Guoliang Chen, Jinlin Han, Qing Zhang, and Chaokai Li. 2025. "Energy Management Strategies for Extended-Range Electric Vehicles with Real Driving Emission Constraints" Applied Sciences 15, no. 1: 142. https://doi.org/10.3390/app15010142
APA StyleXu, H., Chen, Y., Zhang, L., Chen, G., Han, J., Zhang, Q., & Li, C. (2025). Energy Management Strategies for Extended-Range Electric Vehicles with Real Driving Emission Constraints. Applied Sciences, 15(1), 142. https://doi.org/10.3390/app15010142





