Imputing Covariance for Meta-Analysis in the Presence of Interaction
Abstract
1. Introduction
2. Regression with Interaction
3. Meta Analysis for the Main Effect and Interaction Effect
3.1. Fixed-Effect Meta-Analysis
3.2. Random-Effects Meta-Analysis
4. Covariance in Meta-Analysis
4.1. Relationship Between Covariance and Correlation Coefficient r
- For each cohort, extract the standard errors of the two coefficients and their covariance from the regression model.
- Calculate the correlation coefficient for each cohort using Equation (12)where represents the covariance between the two coefficients, and , are the standard errors of and , respectively.
- Perform a random-effects meta-analysis (or fixed-effect meta-analysis) on values to estimate .
4.2. Fixed-Effect Meta-Analysis for Correlation Coefficient r
4.3. Random-Effects Meta-Analysis for Correlation Coefficient r
- Calculate the Q statistic
- Calculate the between-study variancewhereand is the degrees of freedom, equal to .
- Recalculate variance and weightThe variance is updated as.The new weight becomes
- Calculate the overall Fisher’s
- Transform back toOnce is obtained, transform it back to overall using Equation (17).
4.4. Summary of the Meta-Analytic Framework
5. Example: Analyzing the 10 Cohort Studies in Table 1
5.1. Meta-Analysis for
5.2. Meta-Analysis for
5.3. Meta-Analysis for r
5.4. Overall Covariance for and
- Fixed-effect model
- Random-effects model
5.5. Calculating the Effect of Falls on Hip Fracture at Different Ages and 95% Confidence Intervals
6. Comparing the Results with the Multivariate Meta-Analysis
7. An R Package for Calculating Overall Covariance in Meta-Analysis
8. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vandenput, L.; Johansson, H.; McCloskey, E.V.; Liu, E.; Schini, M.; Åkesson, K.E.; Anderson, F.A.; Azagra, R.; Bager, C.L.; Beaudart, C.; et al. A meta-analysis of previous falls and subsequent fracture risk in cohort studies. Osteoporos Int. 2024, 35, 469–494. [Google Scholar] [CrossRef] [PubMed]
- Kanis, J.A.; Johansson, H.; McCloskey, E.V.; Liu, E.; Åkesson, K.E.; Anderson, F.A.; Azagra, R.; Bager, C.L.; Beaudart, C.; Bischoff-Ferrari, H.A.; et al. Previous fracture and subsequent fracture risk: A meta-analysis to update FRAX. Osteoporos Int. 2023, 34, 2027–2045. [Google Scholar] [CrossRef] [PubMed]
- Spineli, L.M.; Pandis, N. Two-stage vs. one-stage meta-analysis. Am. J. Orthod. Dentofac. Orthop. 2024, 166, 295–298. [Google Scholar] [CrossRef] [PubMed]
- Riley, R.D.; Ensor, J.; Hattle, M. Two-stage or not two-stage? That is the question for IPD meta-analysis projects. Res. Synth. Methods 2023, 14, 903–910. [Google Scholar] [CrossRef] [PubMed]
- Haller, B.; Mansmann, U.; Dobler, D.; Ulm, K.; Hapfelmeier, A. Confidence interval estimation for the changepoint of treatment stratification in the presence of a qualitative covariate-treatment interaction. Stat. Med. 2020, 39, 70–96. [Google Scholar] [CrossRef] [PubMed]
- Hattle, M.; Burke, D.L.; Trikalinos, T.; Schmid, C.H.; Chen, Y.; Jackson, D.; Riley, R.D. Multivariate meta-analysis of multiple outcomes: Characteristics and predictors of borrowing of strength from Cochrane reviews. Syst. Rev. 2022, 11, 149. [Google Scholar] [CrossRef] [PubMed]
- Basten, M.; van Tuijl, L.A.; Pan, K.Y.; Hoogendoorn, A.W.; Lamers, F.; Ranchor, A.V.; Dekker, J.; Frank, P.; Galenkamp, H.; Knol, M.J.; et al. Estimating additive interaction in two-stage individual participant data meta-analysis. Am. J. Epidemiol. 2024, kwae325. [Google Scholar] [CrossRef] [PubMed]
- Sauerbrei, W.; Royston, P. Investigating treatment-effect modification by a continuous covariate in IPD meta-analysis: An approach using fractional polynomials. BMC Med. Res. Methodol. 2022, 22, 98. [Google Scholar] [CrossRef] [PubMed]
- Khan, S. Meta-Analysis Methods for Health and Experimental Studies; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Borenstein, M.; Hedges, L.V.; Higgins, J.P.; Rothstein, H.R. Introduction to Meta-Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Schwarzer, G.; James, R. Carpenter, Gerta Rucke. In Meta-Analysis with R; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Bakbergenuly, I.; Hoaglin, D.C.; Kulinskaya, E. Methods for estimating between-study variance and overall effect in meta-analysis of odds ratios. Res. Synth. Methods 2020, 11, 426–442. [Google Scholar] [CrossRef] [PubMed]
- Dufour, J.-M. Covariance, Correlation and Linear Regression Between Random Variables. 2024. Available online: https://www2.cirano.qc.ca/~dufourj/Web_Site/ResE/ECON763_2024W/Dufour_2016_C_Covariances_W_Slides.pdf (accessed on 20 December 2024).
- Schwarzer, G. Meta-Analysis in R. Systematic Reviews in Health Research: Meta-Analysis in Context; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Chen, D.-G.D.; Peace, K.E. Multivariate Meta-Analysis. Applied Meta-Analysis with R and Stata; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Riley, R.D.; Debray, T.P.; Fisher, D.; Hattle, M.; Marlin, N.; Hoogl, J.; Gueyffier, F.; Staessen, J.A.; Wang, J.; Moons, K.G.; et al. Individual participant data meta-analysis to examine interactions between treatment effect and participant-level covariates: Statistical recommendations for conduct and planning. Stat. Med. 2020, 39, 2115–2137. [Google Scholar] [CrossRef] [PubMed]
- Brankovic, M.; Kardys, I.; Steyerberg, E.W.; Lemeshow, S.; Markovic, M.; Rizopoulos, D.; Boersma, E. Understanding of interaction (subgroup) analysis in clinical trials. Eur. J. Clin. Investig. 2019, 49, e13145. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Piantadosi, S.; Le-Rademacher, J.; Mandrekar, S.J. Statistical Considerations for Subgroup Analyses. J. Thorac. Oncol. 2021, 16, 375–380. [Google Scholar] [CrossRef] [PubMed]
- Richardson, M.; Garner, P.; Donegan, S. Interpretation of subgroup analyses in systematic reviews: A tutorial. Clin. Epidemiol. Glob. Health 2019, 7, 192–198. [Google Scholar] [CrossRef]
- Higgins, J.P.T.; López-López, J.A.; Aloe, A.M. Meta-regression. In Handbook of Meta-Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020; pp. 129–150. [Google Scholar]
- Spineli, L.M.; Pandis, N. Problems and pitfalls in subgroup analysis and meta-regression. Am. J. Orthod. Dentofac. Orthop. 2020, 158, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Cuijpers, P.; Griffin, J.W.; Furukawa, T.A. The lack of statistical power of subgroup analyses in meta-analyses: A cautionary note. Epidemiol. Psychiatr. Sci. 2021, 30, e78. [Google Scholar] [CrossRef] [PubMed]
- The Stata News, In the Spotlight: Multivariate Meta-Analysis. Available online: https://www.stata.com/stata-news/news37-1/multivariate-meta-analysis/ (accessed on 28 November 2024).
- Riley, R.D.; Jackson, D.; White, I.R. Multivariate Meta-Analysis Using IPD. In Individual Participant Data Meta-Analysis: A Handbook for Healthcare Research; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 311–346. [Google Scholar]
- Stanley, T.D.; Doucouliagos, H.; Havranek, T. Meta-analyses of partial correlations are biased: Detection and solutions. Res. Synth. Methods 2024, 15, 313–325. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Goldfeld, K.S.; Petkova, E. Developing a Bayesian hierarchical model for a prospective individual patient data meta-analysis with continuous monitoring. BMC Med. Res. Methodol. 2023, 23, 25. [Google Scholar] [CrossRef] [PubMed]
- Geissbühler, M.; Hincapié, C.A.; Aghlmandi, S.; Zwahlen, M.; Jüni, P.; da Costa, B.R. Most published meta-regression analyses based on aggregate data suffer from methodological pitfalls: A meta-epidemiological study. BMC Med. Res. Methodol. 2021, 21, 123. [Google Scholar] [CrossRef] [PubMed]

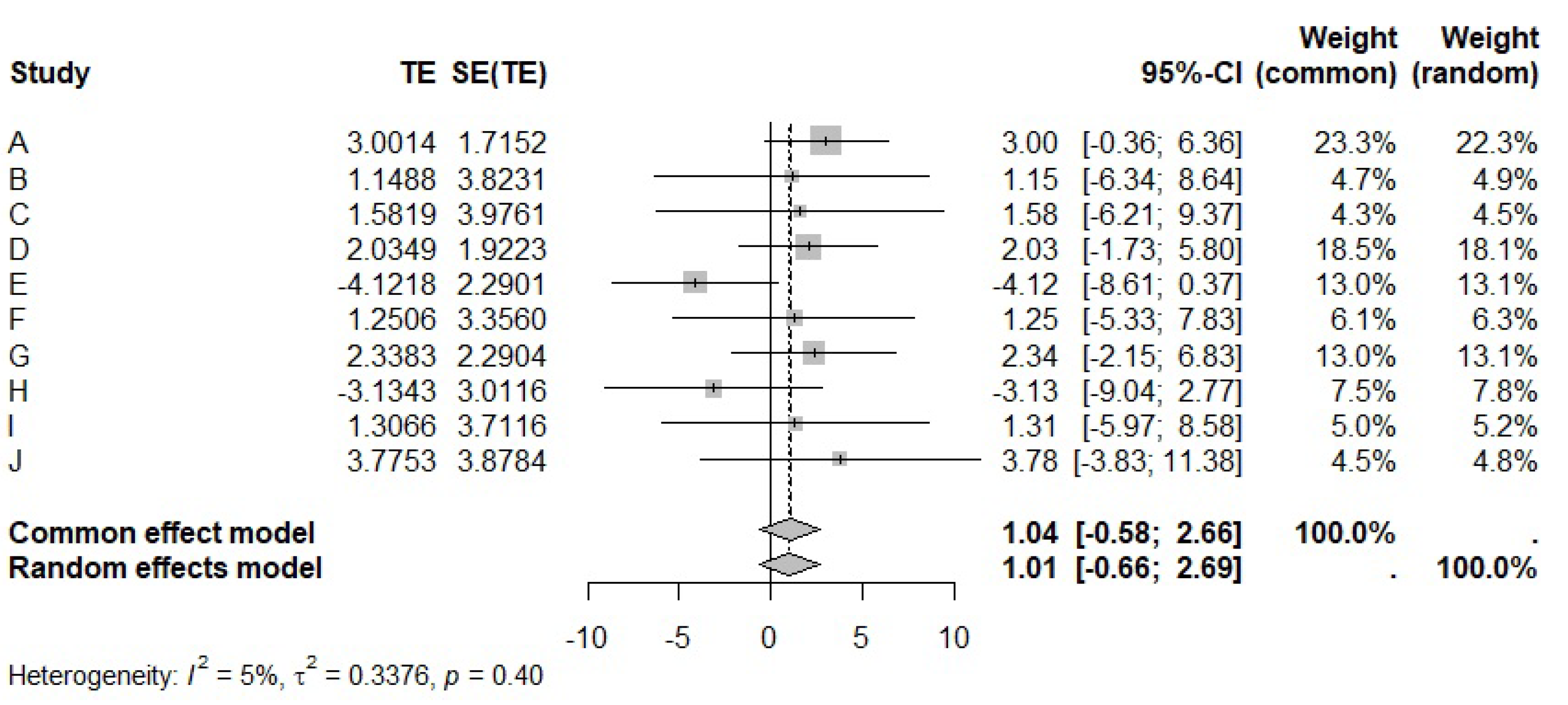
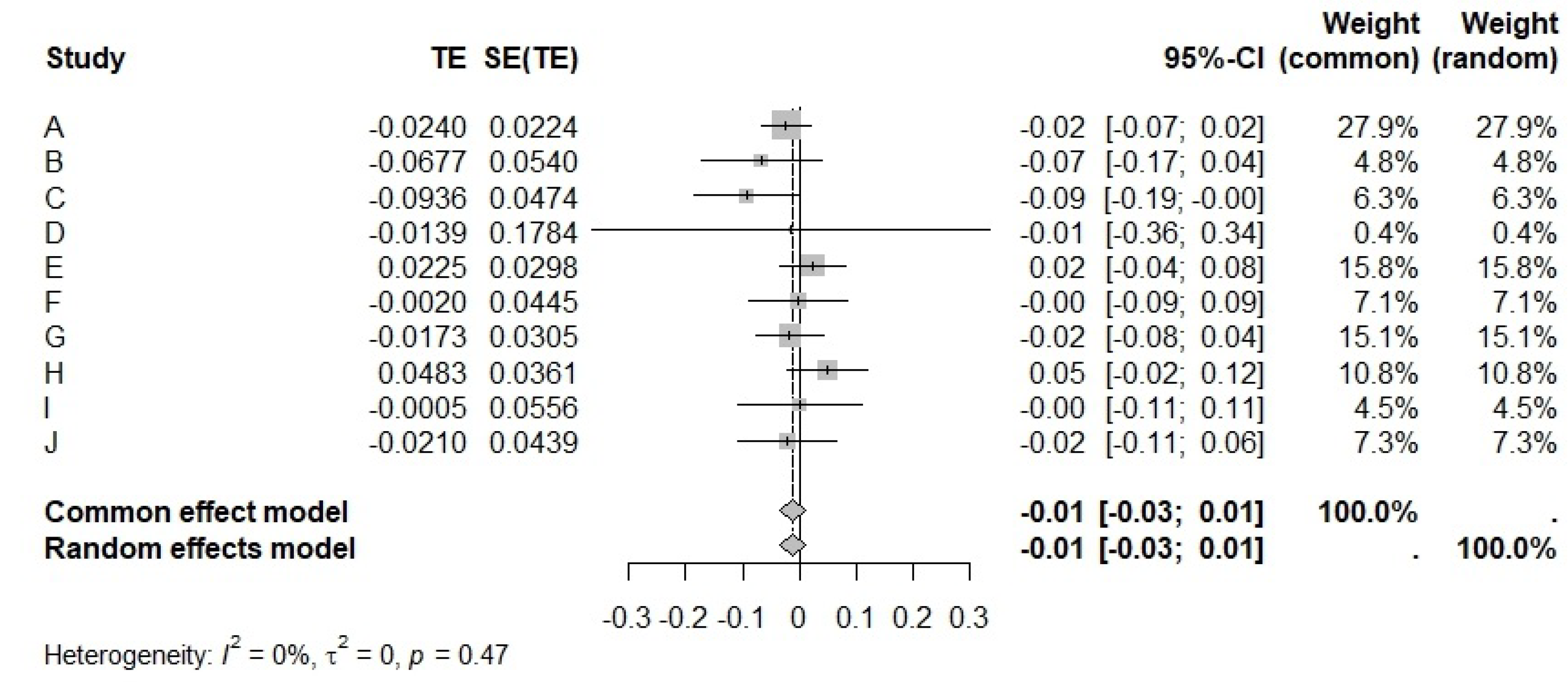


| Cohort | var() | var() | cov() | |||
|---|---|---|---|---|---|---|
| A | 3.0014 | −0.0240 | 2.9419 | 0.0005 | −0.0333 | 5000 |
| B | 1.1488 | −0.0677 | 14.6165 | 0.0029 | −0.2000 | 30,000 |
| C | 1.5819 | −0.0936 | 15.8097 | 0.0022 | −0.1825 | 10,000 |
| D | 2.0349 | −0.0139 | 3.6954 | 0.0318 | −0.3230 | 3000 |
| E | −4.1219 | 0.0225 | 5.2448 | 0.0009 | −0.0629 | 2000 |
| F | 1.2506 | −0.0020 | 11.2628 | 0.002 | −0.144 | 5000 |
| G | 2.3383 | −0.0173 | 5.2458 | 0.0009 | −0.0644 | 1000 |
| H | −3.1343 | 0.0483 | 9.0698 | 0.0013 | −0.103 | 2000 |
| I | 1.3066 | −0.0005 | 13.7763 | 0.0031 | −0.2000 | 800 |
| J | 3.7753 | −0.021 | 15.0422 | 0.0019 | −0.1635 | 3200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, E.; Liu, R.Y. Imputing Covariance for Meta-Analysis in the Presence of Interaction. Appl. Sci. 2025, 15, 141. https://doi.org/10.3390/app15010141
Liu E, Liu RY. Imputing Covariance for Meta-Analysis in the Presence of Interaction. Applied Sciences. 2025; 15(1):141. https://doi.org/10.3390/app15010141
Chicago/Turabian StyleLiu, Enwu, and Ryan Yan Liu. 2025. "Imputing Covariance for Meta-Analysis in the Presence of Interaction" Applied Sciences 15, no. 1: 141. https://doi.org/10.3390/app15010141
APA StyleLiu, E., & Liu, R. Y. (2025). Imputing Covariance for Meta-Analysis in the Presence of Interaction. Applied Sciences, 15(1), 141. https://doi.org/10.3390/app15010141







