Transforming Landslide Prediction: A Novel Approach Combining Numerical Methods and Advanced Correlation Analysis in Slope Stability Investigation
Abstract
1. Introduction
2. Mechanism of Strength Reduction Method
3. Basic Statistical Analysis
3.1. Correlation Analysis
3.1.1. Spearman’s Rank Correlation Coefficient (Spearman’s Rho)
- = For each pair, calculate the difference between the ranks of the displacement and the stability reduction factor
- n = number of observations (or data points) at a monitoring point
- = incorporating the rank differences to assess the correlation.
3.1.2. Kendall’s Tau Coefficient
- reflects the balance between concordant and discordant pairs
- M = tally of the number of concordant pairs
- N = tally of the number of discordant pairs
- n = number of observations (or data points) at a monitoring point.
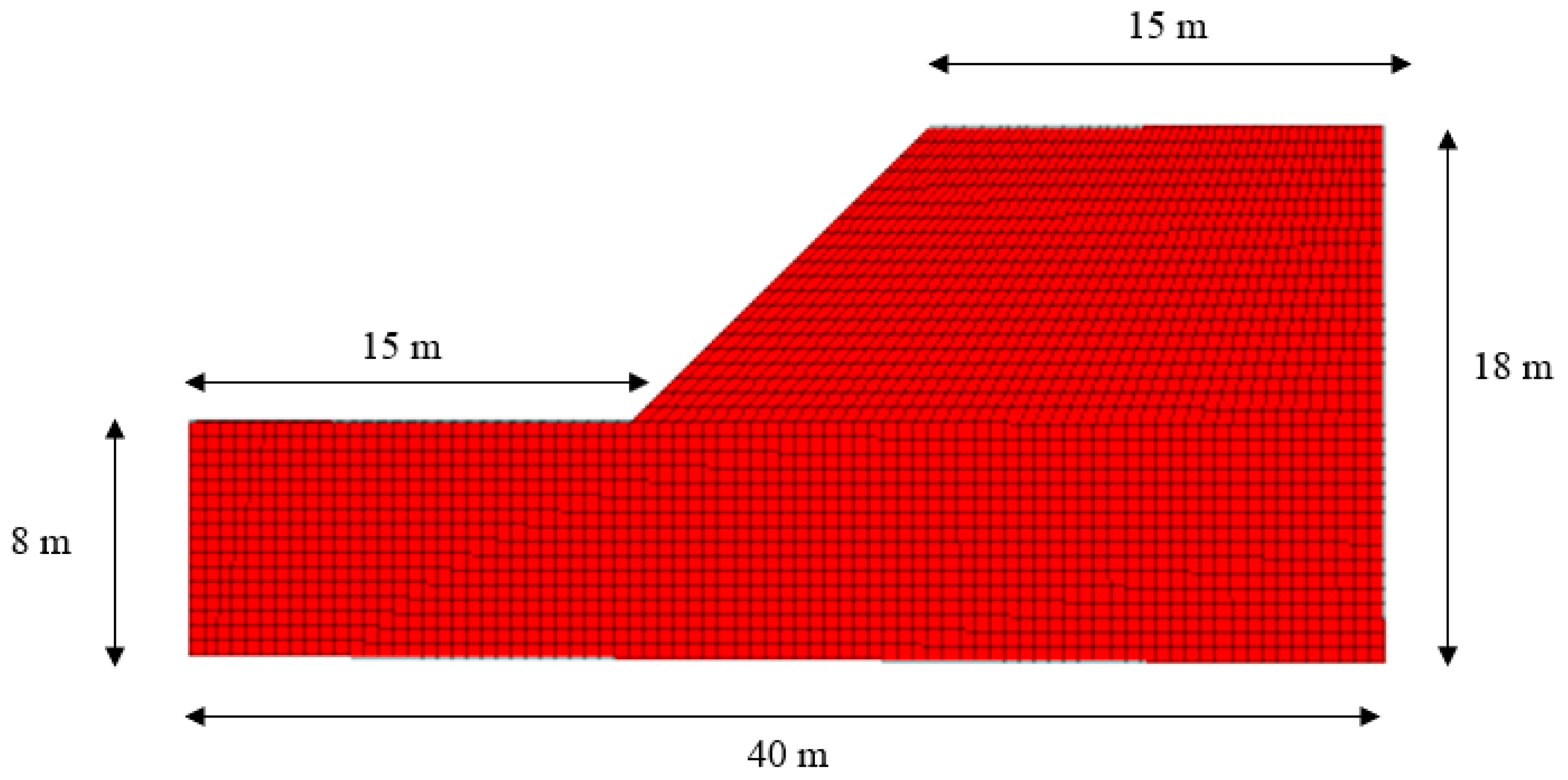
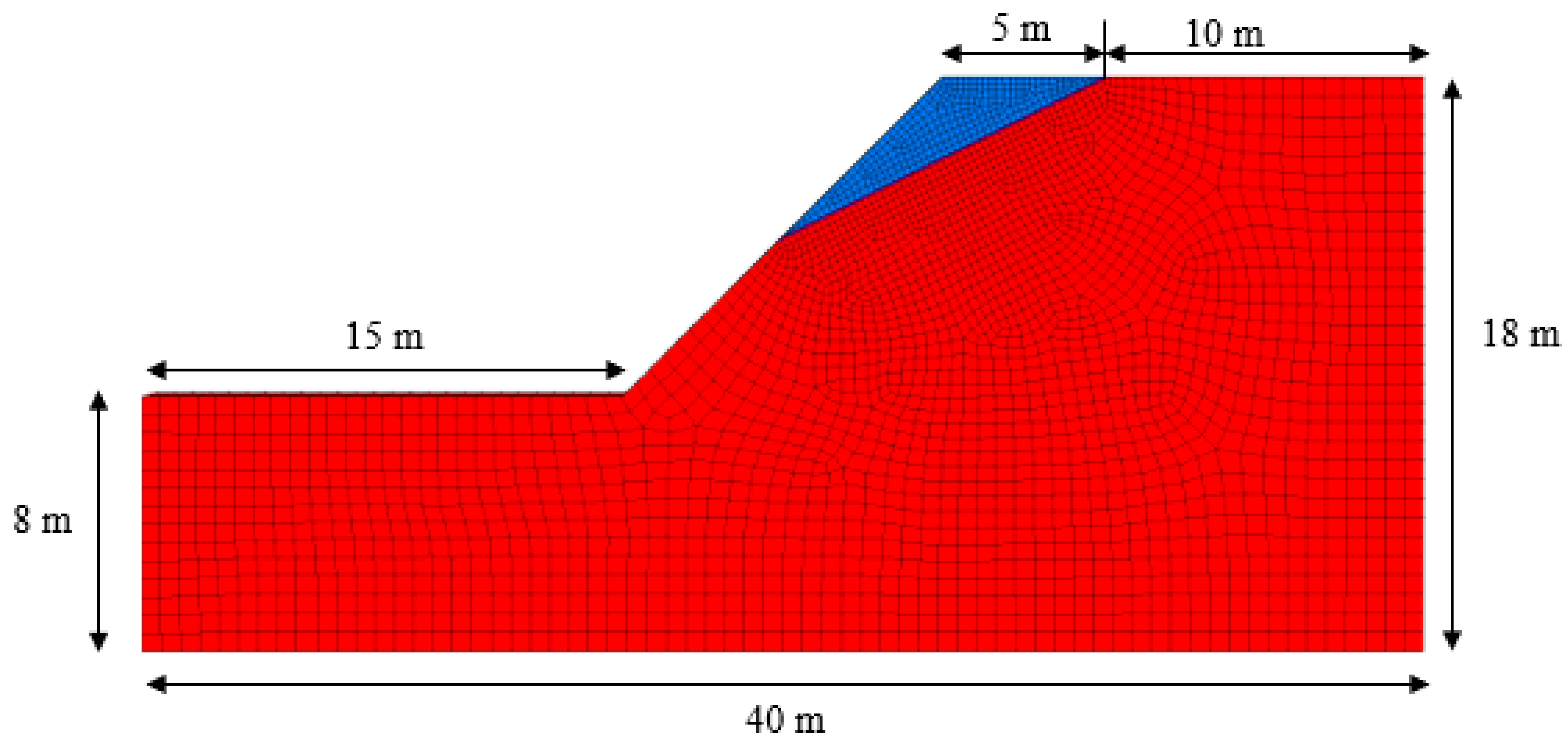
4. Homogeneous Soil Slope (Simple Slope) Stability Analysis Using the FLAC3D Model
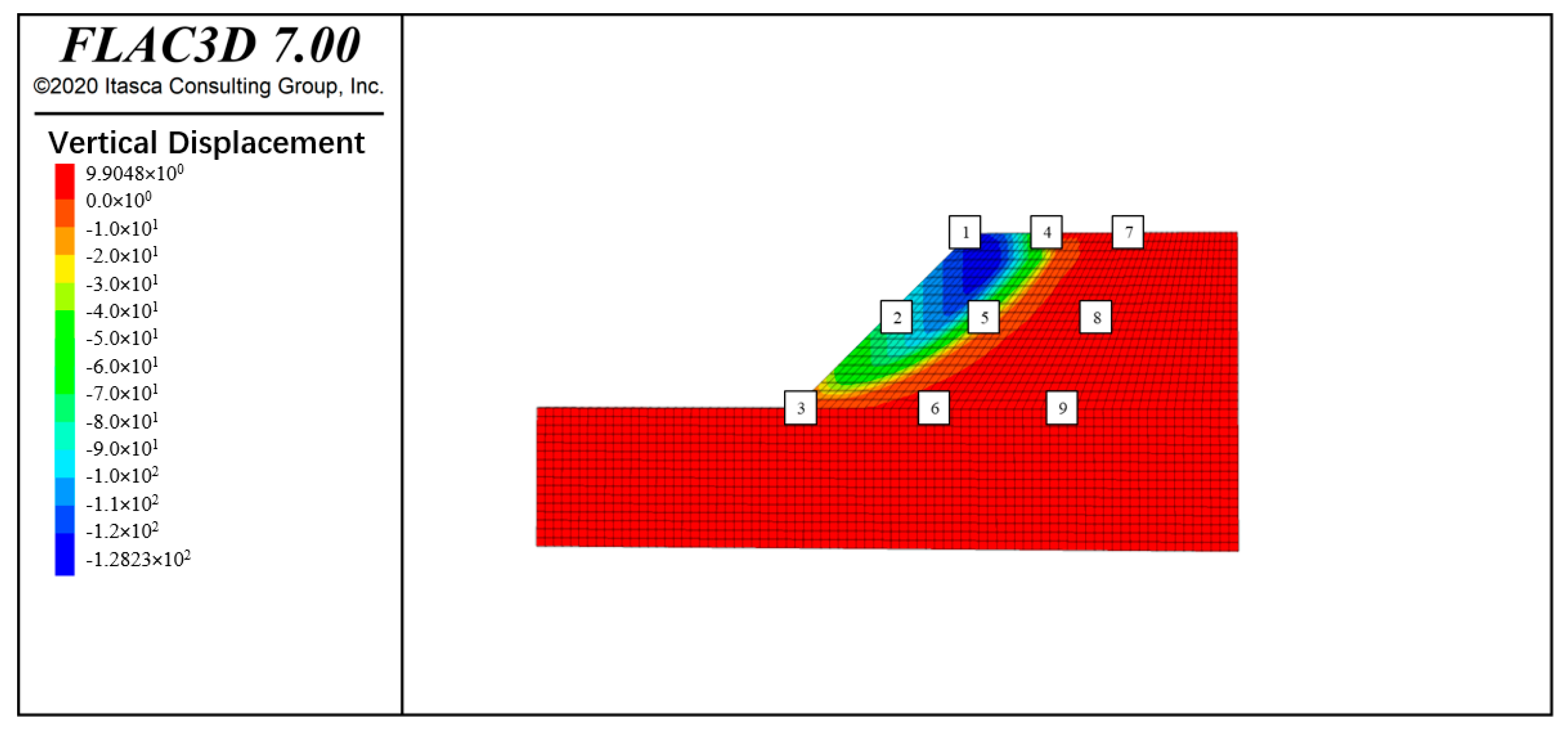
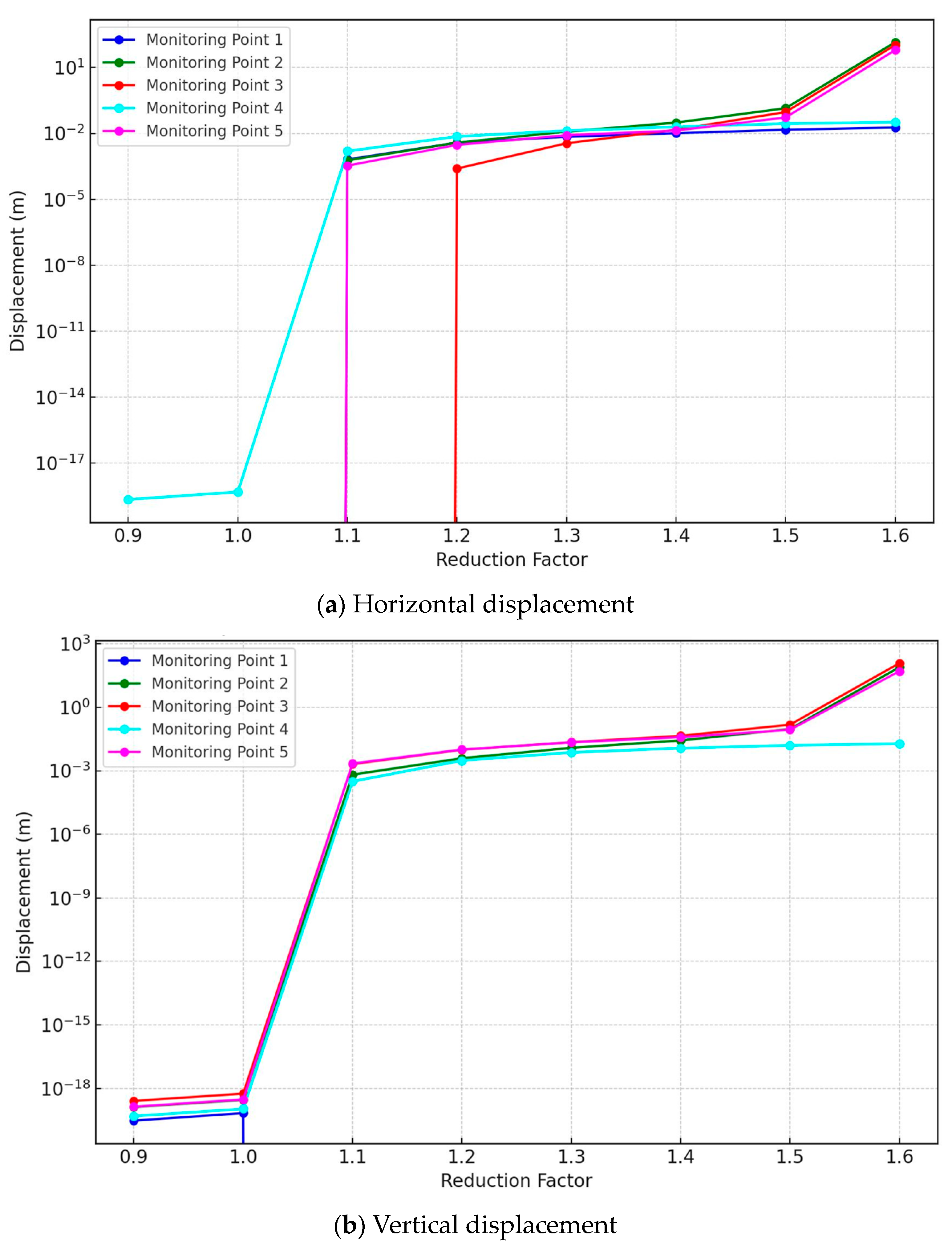
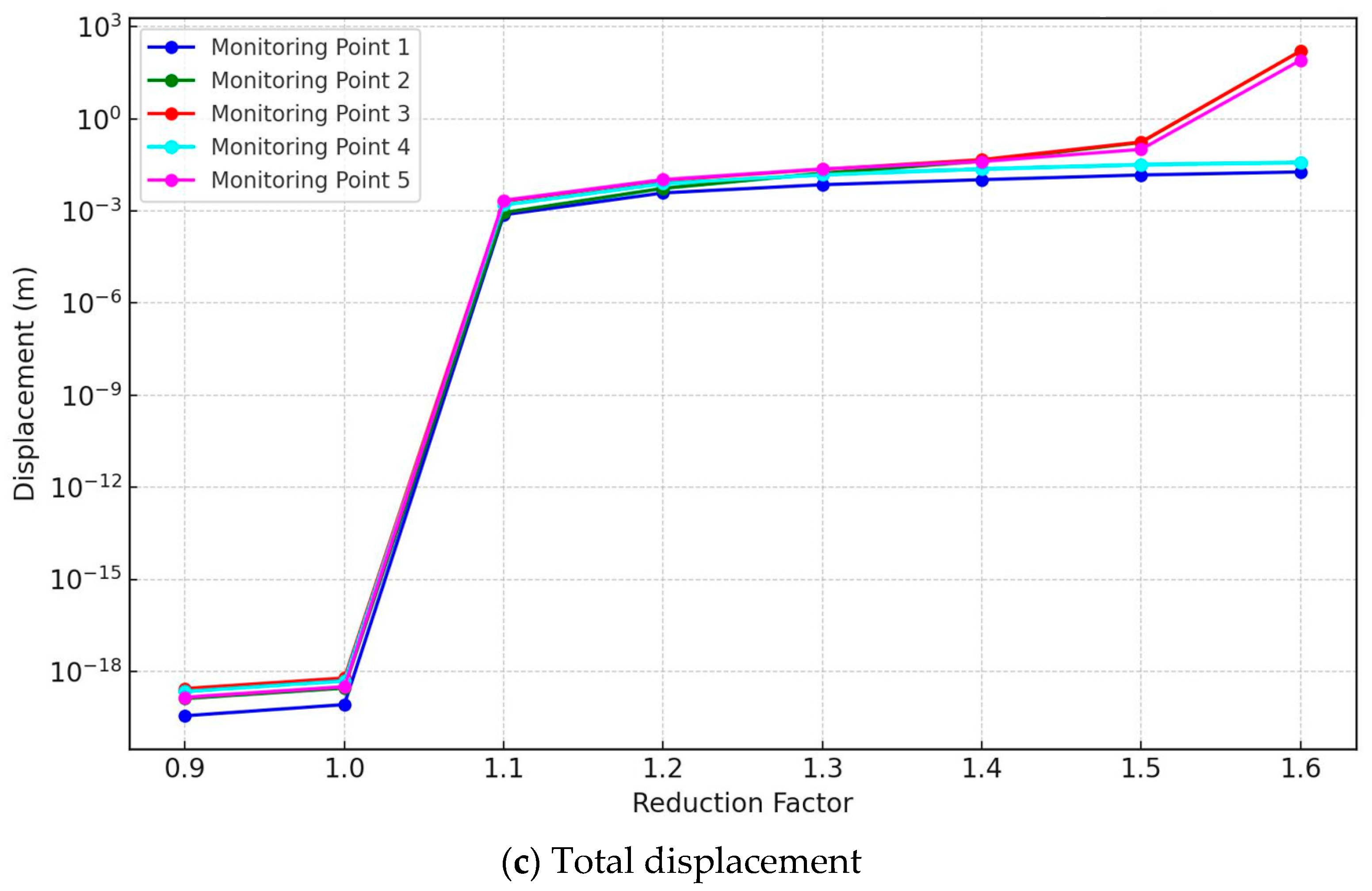
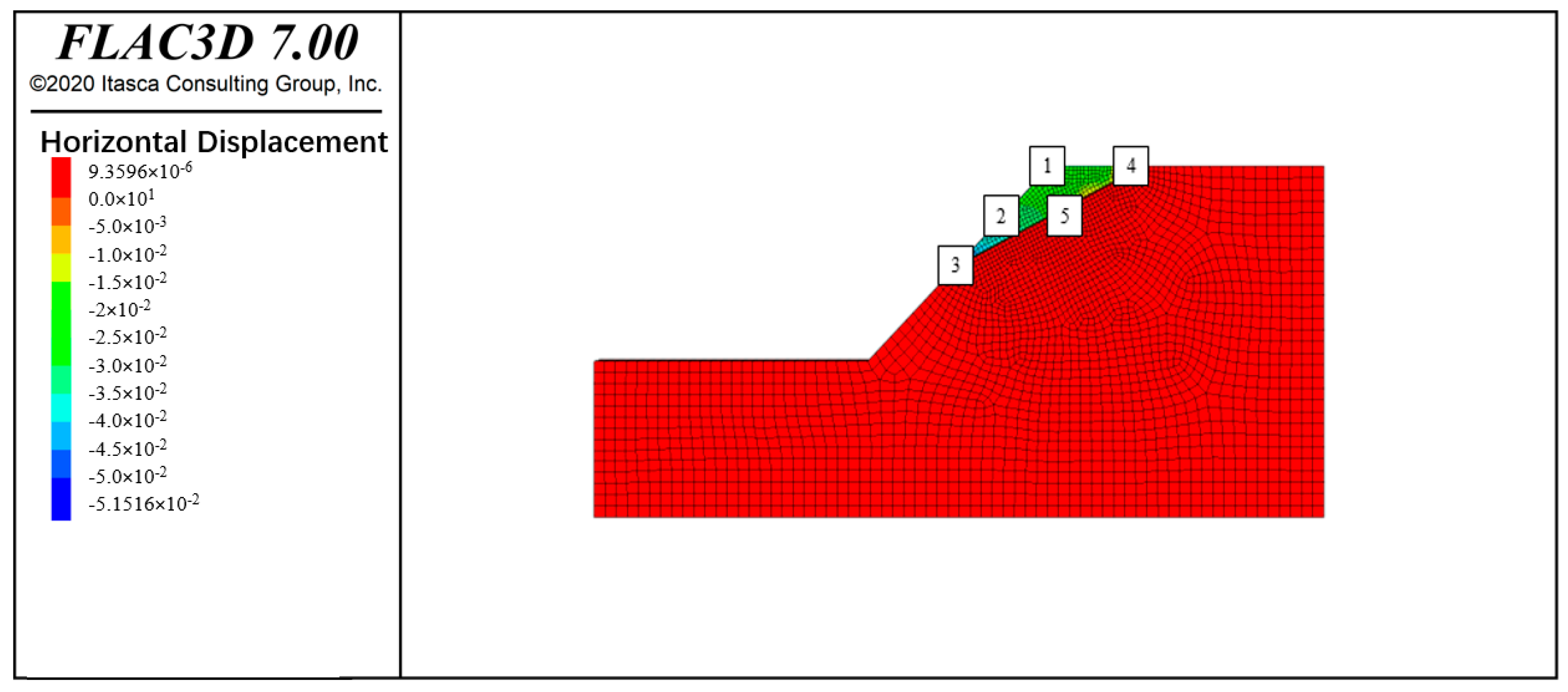
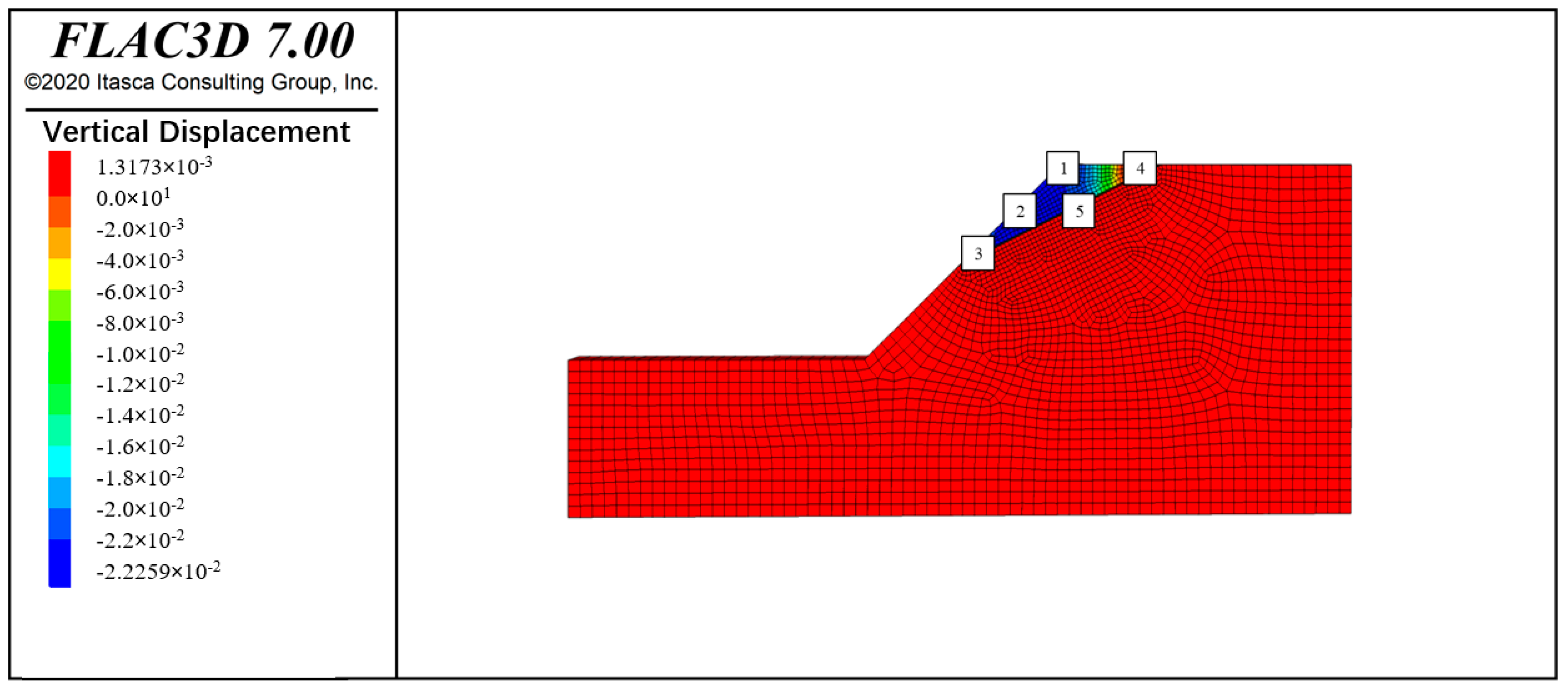
4.1. Analysis of Displacement-Reduction Factor Relationships at Monitoring Points
4.2. Basic Statistical Properties of Simple Slope
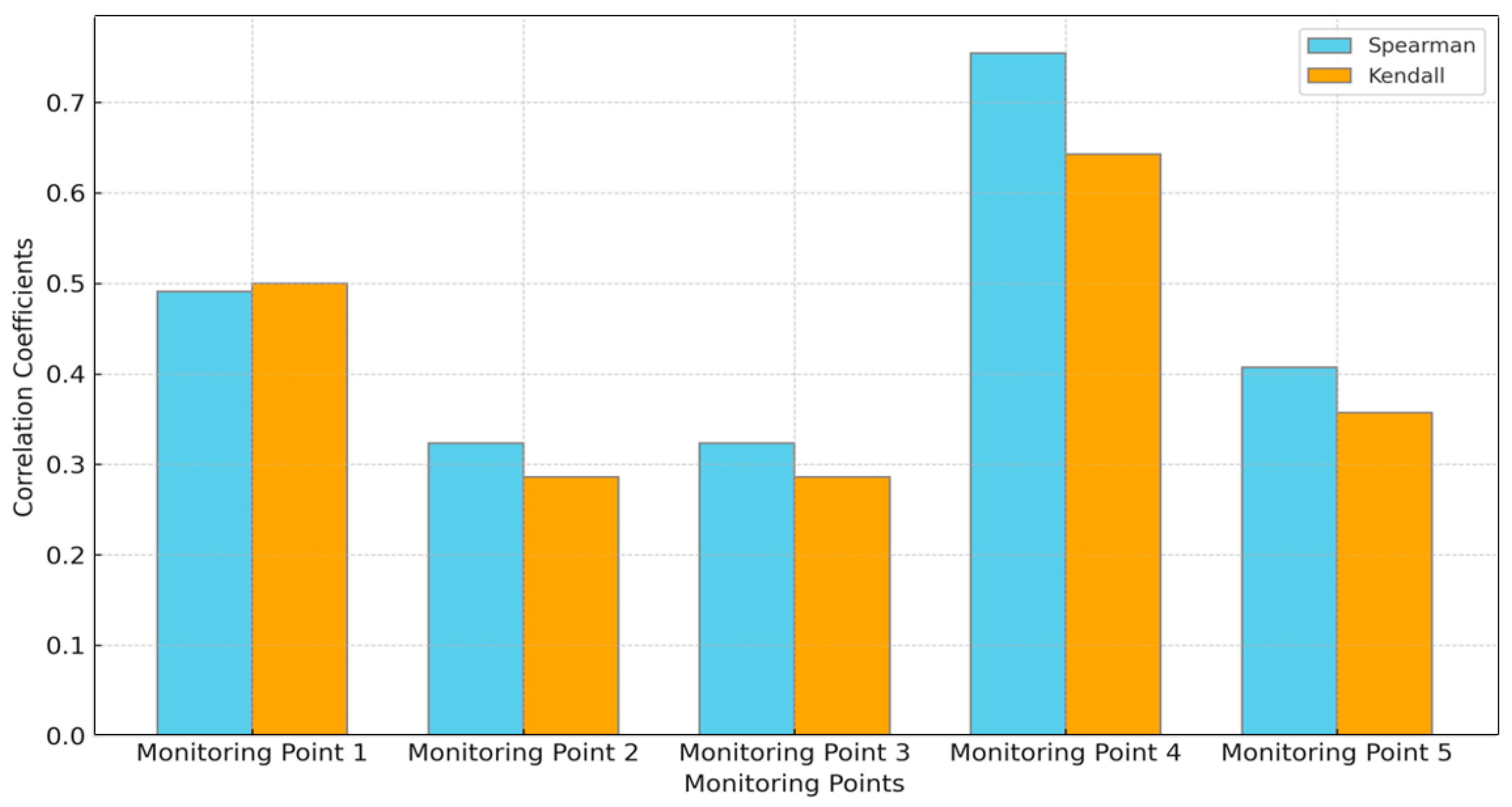
4.3. Spearman and Kendall Correlation Coefficients of Simple Slope
5. Joint Rock Slope Stability Analysis Using the FLAC3D Model
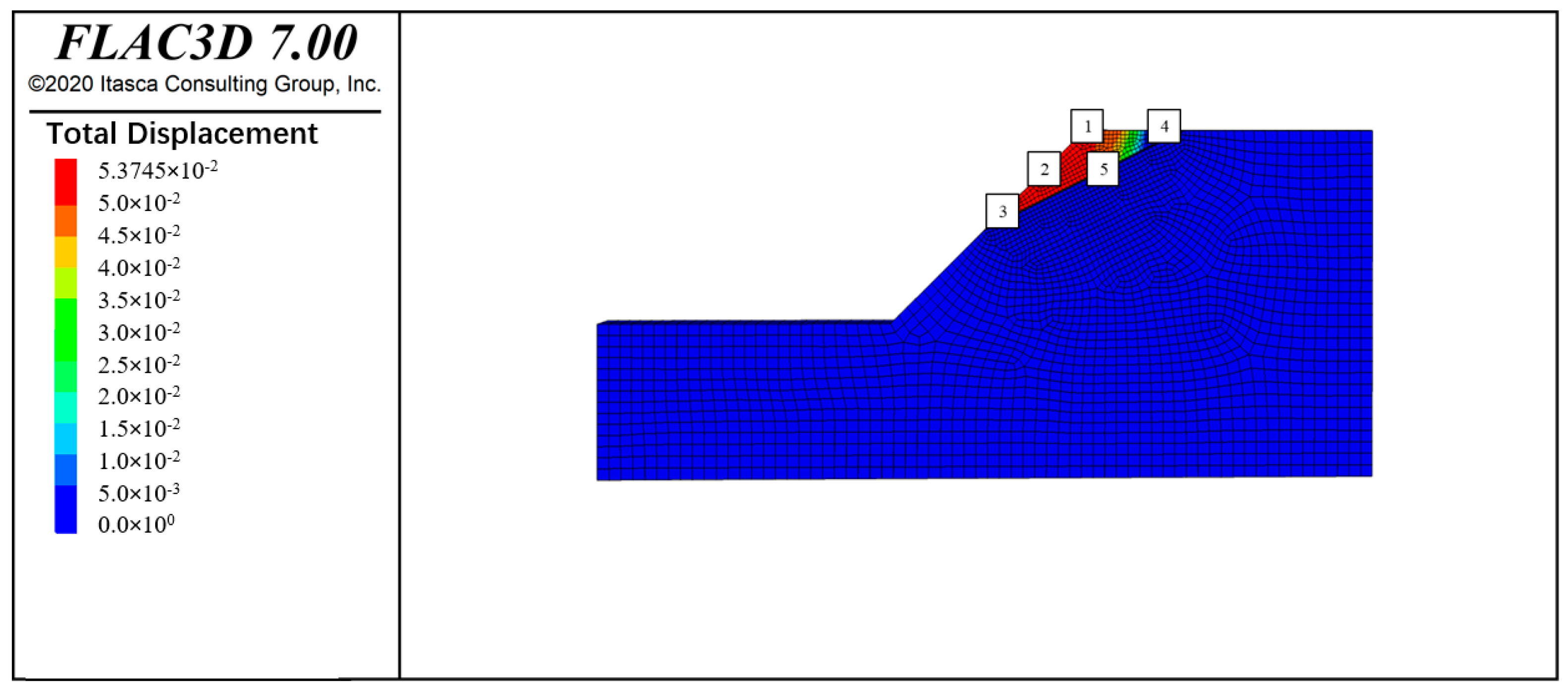
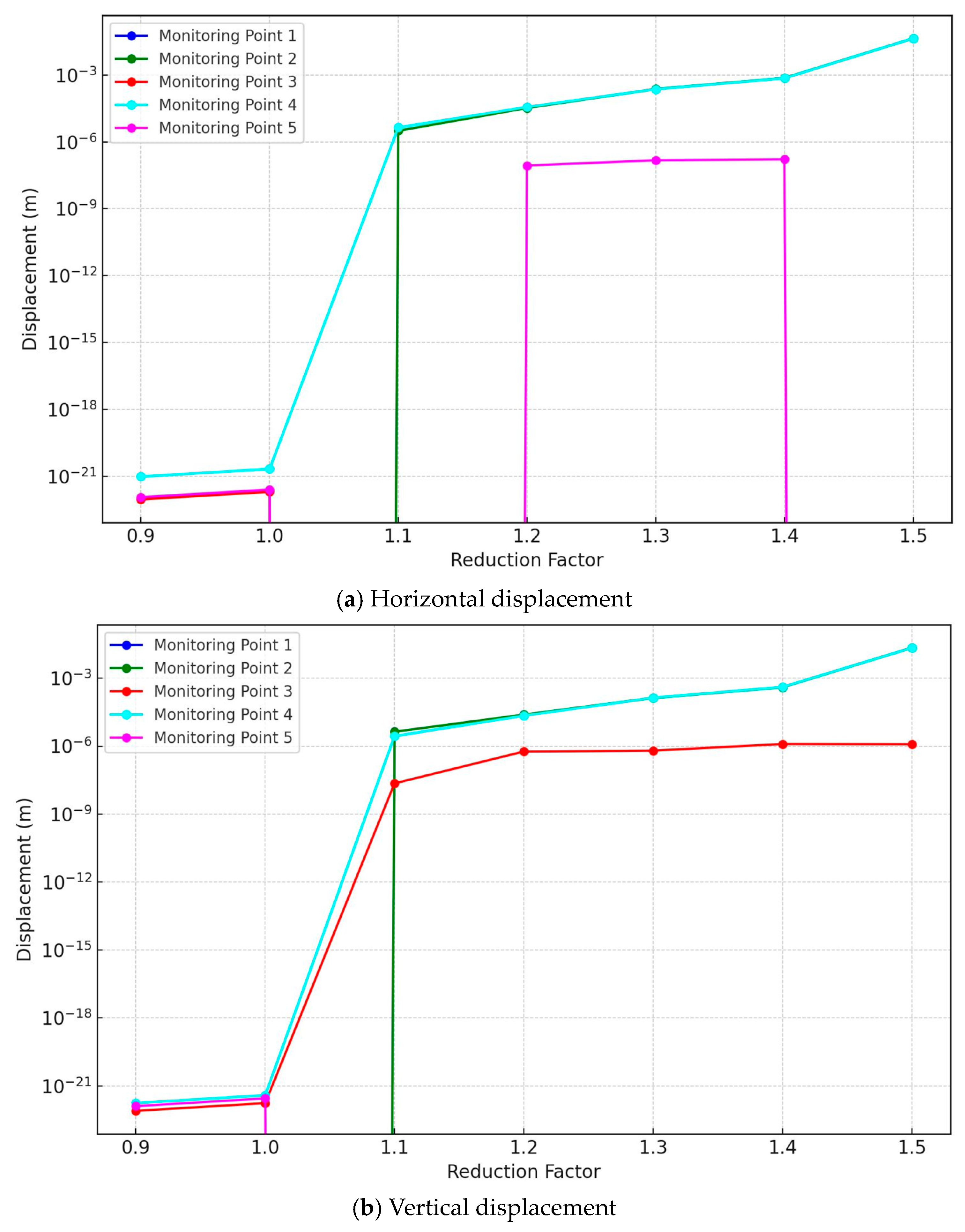
5.1. Analysis of Displacement-Reduction Factor Relationships by Monitoring Point
5.2. Basic Statistical Properties of Joint Slope
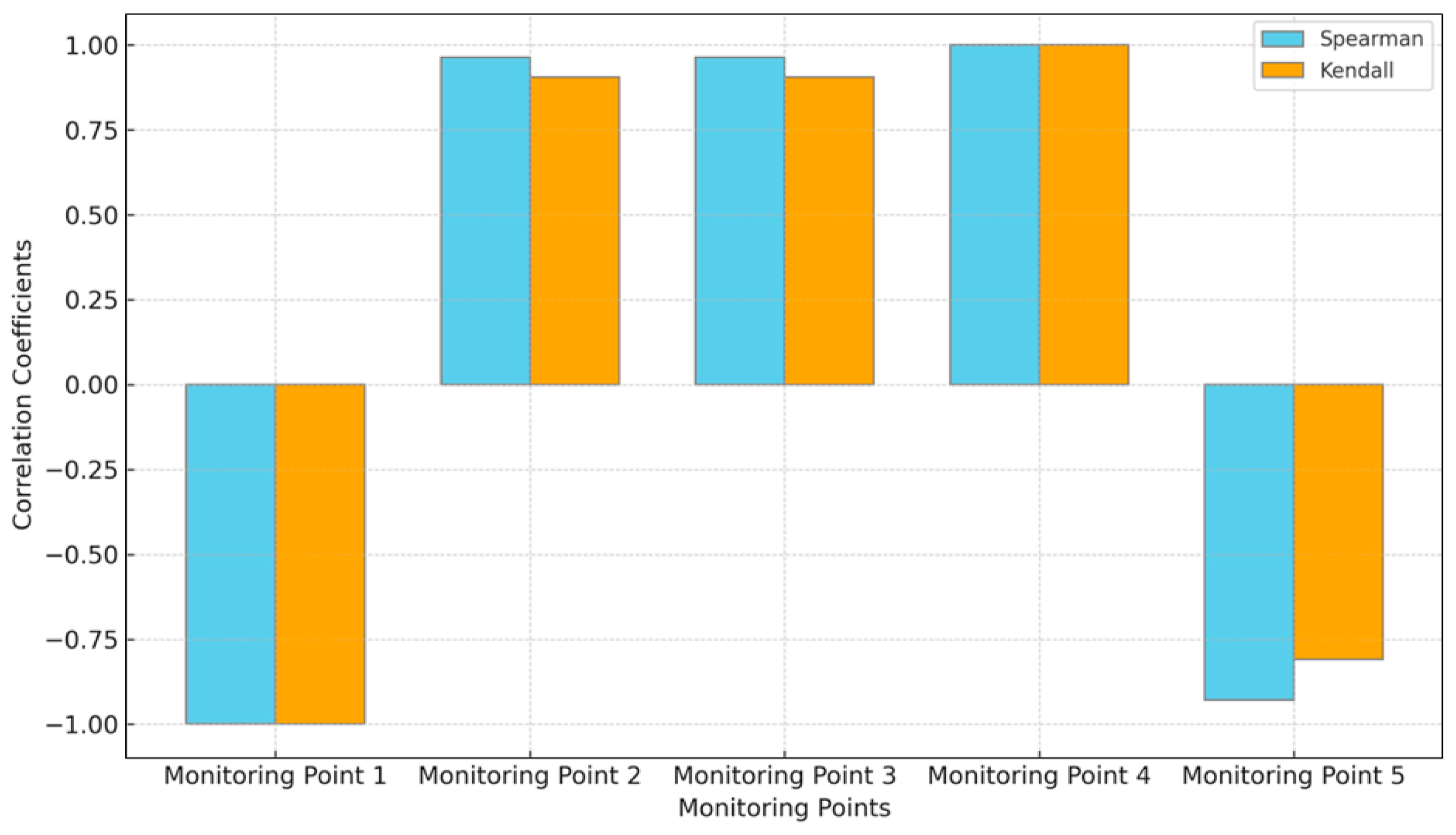
5.3. Spearman and Kendall Correlation Coefficients of Joint Slope
6. Conclusions
- For the homogeneous soil slope model, the results showed Spearman’s rho correlation coefficients ranging from 0.31 to 0.76, and Kendall’s tau values ranging from 0.29 to 0.64, indicating variable displacement–stability relationships across the monitoring points. In contrast, the joint rock slope model exhibited strong positive total displacement correlations, with Spearman’s and Kendall’s coefficients showing ranges close to +1.0 and −1.0 at most monitoring points. The maximum mean horizontal and vertical displacements reached 44.13 mm and 22.17 mm, respectively, at the critical point 2.
- The quantitative correlation analysis allowed the researchers to identify and distinguish between stable and unstable zones on the simulated slopes, providing localized insights into the progression of slope failures. For example, monitoring point 2 on the soil slope showed a mean horizontal displacement of 17.65 mm and a mean vertical displacement of 9.72 mm under stability reduction, indicating it as a critically unstable location.
- By quantifying the strength and directionality of the correlations between displacement measurements and stability reduction factors, the methodology enables more precise identification of areas prone to instability and potential failure. This level of detail can inform targeted remediation efforts and early warning systems, which is a significant improvement over generalized assessments of overall slope stability.
- Future work should focus on further refinement of the proposed correlation analysis methodology through additional physical model testing and field calibration prior to implementation for early warning systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elfass, S.A.; Aczel, R.; Norris, G.M.; Jacobson, E. Physical and Numerical Modeling of Rock Joints and Slope Stability. GeoCongress 2006, 2006, 1–6. [Google Scholar]
- Sun, L.; Liu, Q.; Abdelaziz, A.; Tang, X.; Grasselli, G. Simulating the entire progressive failure process of rock slopes using the combined finite-discrete element method. Comput. Geotech. 2022, 141, 104557. [Google Scholar] [CrossRef]
- Schneider-Muntau, B.; Medicus, G.; Fellin, W. Strength reduction method in Barodesy. Comput. Geotech. 2018, 95, 57–67. [Google Scholar] [CrossRef]
- Tu, Y.; Liu, X.; Zhong, Z.; Li, Y. New criteria for defining slope failure using the strength reduction method. Eng. Geol. 2016, 212, 63–71. [Google Scholar] [CrossRef]
- Umar, I.H.; Lin, H. Marble Powder as a Soil Stabilizer: An Experimental Investigation of the Geotechnical Properties and Unconfined Compressive Strength Analysis. Materials 2024, 17, 1208. [Google Scholar] [CrossRef] [PubMed]
- Haruna, I.U.; Kabir, M.; Yalo, S.G.; Muhammad, A.; Ibrahim, A.S. Quantitative Analysis of Solid Waste Generation from Tanneries in Kano State. J. Environ. Eng. Stud. 2022, 7, 23–30. [Google Scholar] [CrossRef]
- Umar, I.H.; Elif, M.; Firat, O. A Study on Uniaxial Compressive Strength and Ultrasonic Non-Destructive Analysis of Fine- Grained Soil in Seasonally Frozen Regions Mevsimsel Donmuş Bölgelerde İnce Taneli Zeminlerin Tek Eksenli Basınç Dayanımları ve Ultrasonik Tahribatsız Analizleri Üzer. Turk. J. Sci. Technol. 2022, 17, 267–677. [Google Scholar] [CrossRef]
- Umar, I.H.; Firat, M.E.O. Investigation of Unconfined Compressive Strength of Soils Stabilized With Waste Elazig Cherry Marble Powder at Different Water Contents. In Proceedings of the 14th International Conference on Engineering & Natural Sciences, Sivas, Turkey, 18–19 July 2022; pp. 703–711. [Google Scholar]
- Umar, I.H.; Lin, H.; Ibrahim, A.S. Laboratory Testing and Analysis of Clay Soil Stabilization Using Waste Marble Powder. Appl. Sci. 2023, 13, 9274. [Google Scholar] [CrossRef]
- Umar, I.H.; Muhammad, A.; Ahmad, A.; Yusif, M.A.; Yusuf, A. Suitability of Geotechnical Properties of Bentonite-Bagasse Ash Mixtures Stabilized Lateritic Soil as Barrier in Engineered Waste Landfills. In Proceedings of the 7th International Student Symposium; Ondokuz Mayiz University: Samsun, Turkey, 2021. [Google Scholar]
- Umar, I.H.; Muhammad, A.; Yusuf, A.; Muhammad, K.I. Study on the Geotechnical Properties of Road Pavement Failures “(A Case Study of Portion Of Malam Aminu Kano Way, Kano State From Tal-Udu Roundabout To Mambaya House Roundabout)”. J. Geotech. Stud. 2020, 5, 8–15. [Google Scholar] [CrossRef]
- Chen, W.; Wan, W.; Zhao, Y.; Pen, W. Experimental Study of the Crack Predominance of Rock-Like Material Containing Parallel Double Fissures under Uniaxial Compression. Sustainability 2020, 12, 5188. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Mei, G.; Xu, N. A statistics-based discrete element modeling method coupled with the strength reduction method for the stability analysis of jointed rock slopes. Eng. Geol. 2020, 264, 105247. [Google Scholar] [CrossRef]
- Huang, L.; Lin, H.; Cao, P.; Zhao, Q.; Pang, Y.; Yong, W. Investigation of the Degradation Mechanism of the Tensile MechanicalProperties of Sandstone under the Corrosion of Various pH Solutions. Materials 2023, 16, 6536. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, M.R.; Nakata, Y.; Shitano, M.; Kaneko, M. Rainfall-induced unstable slope monitoring and early warning through tilt sensors. Soils Found. 2021, 61, 1033–1053. [Google Scholar] [CrossRef]
- Sztubecki, J.; Mrówczyńska, M. Vertical displacement monitoring using the modified leveling method. Measurement 2023, 206, 112264. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Tan, X. Displacement-based back analysis of mitigating the effects of displacement loss in underground engineering. J. Rock. Mech. Geotech. Eng. 2023, 15, 2626–2638. [Google Scholar] [CrossRef]
- Hammah, R. ‘Open Secret’ Advantages of the Shear Strength Reduction Approach in Slope Stability Analysis; Rocscience: Sydney, Australia, 2022. [Google Scholar]
- Krahn, J. Limit Equilibrium, Strength Summation and Strength Reduction Methods for Assessing Slope Stability; GEO-SLOPE International: Calgary, AB, Canada, 2007. [Google Scholar]
- Hang, L.; Ping, C.; Feng-Qiang, G. Analysis of locations and displacement modes of monitoring points in displacement mutation criteria. Chin. J. Geotech. Eng. 2007, 29, 1435–1438. [Google Scholar]
- Marchigiani, R.; Gordy, S.; Cipolla, J.; Adams, R.C.; Evans, D.C.; Stehly, C.; Galwankar, S.; Russell, S.; Marco, A.P.; Kman, N.; et al. Wind disasters: A comprehensive review of current management strategies. Int. J. Crit. Illn. Inj. Sci. 2013, 3, 130–142. [Google Scholar] [CrossRef] [PubMed]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth-Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, G.; Liang, W. Slope Stability Prediction Using k-NN-Based Optimum-Path Forest Approach. Mathematics 2023, 11, 3071. [Google Scholar] [CrossRef]
- Chaulagain, S.; Choi, J.; Kim, Y.; Yeon, J.; Kim, Y.; Ji, B. A Comparative Analysis of Slope Failure Prediction Using a Statistical and Machine Learning Approach on Displacement Data: Introducing a Tailored Performance Metric. Buildings 2023, 13, 2691. [Google Scholar] [CrossRef]
- Chen, F.; Wang, X.-B.; Du, Y.-H.; Tang, C.-A. Numerical analysis of the precursory information of slope instability process with constant resistance bolt. Sci. Rep. 2021, 11, 21814. [Google Scholar] [CrossRef] [PubMed]
- Barančoková, M.; Šošovička, M.; Barančok, P.; Barančok, P. Predictive Modelling of Landslide Susceptibility in the Western Carpathian Flysch Zone. Land 2021, 10, 1370. [Google Scholar] [CrossRef]
- Nitsche, M.; Rickenmann, D.; Turowski, J.; Badoux, A.; Kirchner, J. Evaluation of bedload transport predictions using flow resistance equations to account for macro-roughness in steep mountain streams. Water Resour. Res. 2011, 47, 1–21. [Google Scholar] [CrossRef]
- Wu, X.Z. Trivariate analysis of soil ranking-correlated characteristics and its application to probabilistic stability assessments in geotechnical engineering problems. Soils Found. 2013, 53, 540–556. [Google Scholar] [CrossRef]
- Hashash, Y.; Song, H. The Integration of Numerical Modeling and Physical Measurements through Inverse Analysis in Geotechnical Engineering. KSCE J. Civ. Eng. 2008, 12, 165–176. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, X.; Esveld, C.; Dollevoet, R.; Molodova, M. An investigation into the causes of squats—Correlation analysis and numerical modeling. Wear 2008, 265, 1349–1355. [Google Scholar] [CrossRef]
- Boels, L.; Bakker, A.; Van Dooren, W.; Drijvers, P. Conceptual difficulties when interpreting histograms: A review. Educ. Res. Rev. 2019, 28, 100291. [Google Scholar] [CrossRef]
- Ozer, M.; Isik, N.S.; Orhan, M. Statistical and neural network assessment of the compression index of clay-bearing soils. Bull. Eng. Geol. Environ. 2008, 67, 537–545. [Google Scholar] [CrossRef]
- Jambu, M. Chapter 3-1-D Statistical Data Analysis. In Exploratory and Multivariate Data Analysis; Jambu, M., Ed.; Academic Press: Boston, MA, USA, 1991; pp. 27–62. [Google Scholar]
- Xiao, C.; Ye, J.; Esteves, R.; Rong, C. Using Spearman’s correlation coefficients for exploratory data analysis on big dataset: Using Spearman’s Correlation Coefficients for Exploratory Data Analysis. Concurr. Comput. Pract. Exp. 2015, 28, 3866–3878. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Ye, J.; Xiao, C.; Esteves, R.; Rong, C. Time Series Similarity Evaluation Based on Spearman’s Correlation Coefficients and Distance Measures. In Proceedings of the International Conference on Cloud Computing and Big Data in Asia, Huangshan, China, 17–19 June 2015; pp. 319–331. [Google Scholar]
- Muñoz-Pichardo, J.M.; Lozano-Aguilera, E.D.; Pascual-Acosta, A.; Muñoz-Reyes, A.M. Multiple Ordinal Correlation Based on Kendall’s Tau Measure: A Proposal. Mathematics 2021, 9, 1616. [Google Scholar] [CrossRef]
- Brossart, D.F.; Laird, V.C.; Armstrong, T.W. Interpreting Kendall’s Tau and Tau-U for single-case experimental designs. Cogent Psychol. 2018, 5, 1518687. [Google Scholar] [CrossRef]
- Svensson, E. Ordinal invariant measures for individual and group changes in ordered categorical data. Stat. Med. 1998, 17, 2923–2936. [Google Scholar] [CrossRef]
- Svensson, E. Concordance between ratings using different scales for the same variable. Stat. Med. 2001, 19, 3483–3496. [Google Scholar]
- Cheng, Q.; Yang, Y.; Du, Y. Failure mechanism and kinematics of the Tonghua landslide based on multidisciplinary pre- and post-failure data. Landslides 2021, 18, 3857–3874. [Google Scholar] [CrossRef]
- Xia, P.; Ying, C. Research on the stability evaluation method of anchored slopes based on group decision making and matter element analysis. Sci. Rep. 2021, 11, 16588. [Google Scholar] [CrossRef] [PubMed]
- Jaboyedoff, M.; Del Gaudio, V.; Derron, M.-H.; Grandjean, G.; Jongmans, D. Characterizing and monitoring landslide processes using remote sensing and geophysics. Eng. Geol. 2019, 259, 105167. [Google Scholar] [CrossRef]
- Luo, H.Y.; Zhang, L.M.; Zhang, L.L.; He, J.; Yin, K.S. Vulnerability of buildings to landslides: The state of the art and future needs. Earth-Sci. Rev. 2023, 238, 104329. [Google Scholar] [CrossRef]
- Liu, W.; Yan, S.; He, S. Landslide damage incurred to buildings: A case study of Shenzhen landslide. Eng. Geol. 2018, 247, 69–83. [Google Scholar] [CrossRef]
- Schulz, W.H.; Coe, J.A.; Ricci, P.P.; Smoczyk, G.M.; Shurtleff, B.L.; Panosky, J. Landslide kinematics and their potential controls from hourly to decadal timescales: Insights from integrating ground-based InSAR measurements with structural maps and long-term monitoring data. Geomorphology 2017, 285, 121–136. [Google Scholar] [CrossRef]
- Lollino, P.; Giordan, D.; Allasia, P.; Fazio, N.L.; Perrotti, M.; Cafaro, F. Assessment of post-failure evolution of a large earthflow through field monitoring and numerical modelling. Landslides 2020, 17, 2013–2026. [Google Scholar] [CrossRef]
- Stumvoll, M.J.; Schmaltz, E.M.; Kanta, R.; Roth, H.; Grall, B.; Luhn, J.; Flores-Orozco, A.; Glade, T. Exploring the dynamics of a complex, slow-moving landslide in the Austrian Flysch Zone with 4D surface and subsurface information. CATENA 2022, 214, 106203. [Google Scholar] [CrossRef]
- Muenchow, J.; Brenning, A.; Richter, M. Geomorphic process rates of landslides along a humidity gradient in the tropical Andes. Geomorphology 2012, 139–140, 271–284. [Google Scholar] [CrossRef]
- Zevgolis, I.E.; Deliveris, A.V.; Koukouzas, N.C. Slope failure incidents and other stability concerns in surface lignite mines in Greece. J. Sustain. Min. 2019, 18, 182–197. [Google Scholar] [CrossRef]
- Heap, M.J.; Violay, M.E.S. The mechanical behaviour and failure modes of volcanic rocks: A review. Bull. Volcanol. 2021, 83, 33. [Google Scholar] [CrossRef]
- Cooksey, R.W. Descriptive Statistics for Summarising Data. In Illustrating Statistical Procedures: Finding Meaning in Quantitative Data; Springer: Singapore, 2020. [Google Scholar]
- Heath, J.P.; Borowski, P. Quantifying proportional variability. PLoS ONE 2013, 8, e84074. [Google Scholar] [CrossRef] [PubMed]
- Crosta, G.; Agliardi, F. A methodology for physically based rockfall hazard assessment. Nat. Hazards Earth Syst. Sci. 2003, 3, 407–422. [Google Scholar] [CrossRef]
- Puth, M.-T.; Neuhäuser, M.; Ruxton, G. Effective use of Spearman’s and Kendall’s correlation coefficients for association between two measured traits. Anim. Behav. 2015, 102, 77–84. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar] [PubMed]
- Kettermann, M.; Urai, J. Changes in structural style of normal faults due to failure mode transition: First results from excavated scale models. J. Struct. Geol. 2015, 74, 105–116. [Google Scholar] [CrossRef]
- Ghalayini, R.; Homberg, C.; Daniel, J.-M.; Nader, F. Growth of layer-bound normal faults under a regional anisotropic stress field. Geol. Soc. Lond. Spec. Publ. 2016, 439, 57–78. [Google Scholar] [CrossRef]
- Gamperl, M.; Singer, J.; Garcia-Londoño, C.; Seiler, L.; Castañeda, J.; Cerón-Hernandez, D.; Thuro, K. An integrated, replicable Landslide Early Warning System for informal settlements—Case study in Medellín, Colombia. Nat. Hazards Earth Syst. Sci. Discuss. 2023, 2023, 1–16. [Google Scholar] [CrossRef]
- Han, Y.; Dong, S.; Chen, Z.; Hu, K.; Su, F.; Huang, P. Assessment of secondary mountain hazards along a section of the Dujiangyan-Wenchuan highway. J. Mt. Sci. 2014, 11, 51–65. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, P.; Lan, T.; Liu, Z.; Ling, S. Resilient and Sustainability Analysis of Flexible Supporting Structure of Expansive Soil Slope. Sustainability 2022, 14, 12813. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Lin, H.; Wang, Y.; Tang, W.; Liao, J.; Li, Y.; Wang, X. A Review of Hydromechanical Coupling Tests, Theoretical and Numerical Analyses in Rock Materials. Water 2023, 15, 2309. [Google Scholar] [CrossRef]
- Pang, J.; Xie, J.; He, Y.; Han, Q.; Hao, Y. Study on the Distribution Trend of Rockburst and Ground Stress in the Hegang Mining Area. Sustainability 2023, 15, 9445. [Google Scholar] [CrossRef]









| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Density | ρ | 27 | kN/m3 |
| Young’s Modulus | E | 12 | MPa |
| Poisson’s Ratio | ν | 0.25 | - |
| Cohesion | c | 25 | kPa |
| Friction Angle | φ | 30 | degrees |
| Monitoring Point | Displacement Type | Mean δ (mm) | Standard Deviation δ (mm) | Range δ (mm) |
|---|---|---|---|---|
| 1 | Horizontal | 0.006846 | 0.007076 | 0.0185 |
| 2 | Horizontal | 17.64841 | 49.84159 | 141 |
| 3 | Horizontal | 13.26401 | 37.47101 | 106 |
| 4 | Horizontal | 0.012809 | 0.012851 | 0.0326 |
| 5 | Horizontal | 7.759776 | 21.91637 | 62 |
| 1 | Vertical | −0.00116 | 0.000966 | 0.00243 |
| 2 | Vertical | 9.717119 | 27.42884 | 77.6 |
| 3 | Vertical | 15.02845 | 42.41494 | 120 |
| 4 | Vertical | 0.007152 | 0.007575 | 0.019 |
| 5 | Vertical | 6.34475 | 17.88184 | 50.6 |
| 1 | Total | 0.006945 | 0.00711 | 0.0186 |
| 2 | Total | 20.15416 | 56.91034 | 161 |
| 3 | Total | 20.03215 | 56.55558 | 160 |
| 4 | Total | 0.014691 | 0.014899 | 0.0377 |
| 5 | Total | 10.0222 | 28.27532 | 80 |
| Material | Density (ρ) | Young’s Modulus (E) | Poisson’s Ratio (ν) | Cohesion (c) | Friction Angle (φ) |
|---|---|---|---|---|---|
| Layer | 29 kN/m3 | 12 GPa | 0.35 | 600 kPa | 37° |
| Joint | 21.5 kN/m3 | 12 MPa | 0.40 | 12 kPa | 20° |
| Monitoring Point | Displacement Type | Mean δ (mm) | Standard Deviation δ (mm) | Range δ (mm) |
|---|---|---|---|---|
| 1 | Horizontal | −6.6 × 10−7 | 6.1 × 10−7 | 0.000002 |
| 2 | Horizontal | 0.006448 | 0.016617 | 0.044128 |
| 3 | Horizontal | −3.8 × 10−7 | 4.15 × 10−7 | 0.000001 |
| 4 | Horizontal | 0.006469 | 0.016675 | 0.044280 |
| 5 | Horizontal | 3.4 × 10−8 | 1.03 × 10−7 | 0.000000 |
| 1 | Vertical | −5.2 × 10−7 | 4.79 × 10−7 | 0.000001 |
| 2 | Vertical | 0.003248 | 0.008346 | 0.022173 |
| 3 | Vertical | 5.29 × 10−7 | 5.52 × 10−7 | 0.000001 |
| 4 | Vertical | 0.003228 | 0.008291 | 0.022028 |
| 5 | Vertical | −7.6 × 10−8 | 8.36 × 10−8 | 0.000000 |
| 1 | Total | 8.39 × 10−7 | 7.75 × 10−7 | 0.000002 |
| 2 | Total | 0.00722 | 0.018596 | 0.049385 |
| 3 | Total | 6.67 × 10−7 | 6.71 × 10−7 | 0.000002 |
| 4 | Total | 0.00723 | 0.018623 | 0.049456 |
| 5 | Total | 1.16 × 10−7 | 9.92 × 10−8 | 0.000000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umar, I.H.; Lin, H.; Hassan, J.I. Transforming Landslide Prediction: A Novel Approach Combining Numerical Methods and Advanced Correlation Analysis in Slope Stability Investigation. Appl. Sci. 2024, 14, 3685. https://doi.org/10.3390/app14093685
Umar IH, Lin H, Hassan JI. Transforming Landslide Prediction: A Novel Approach Combining Numerical Methods and Advanced Correlation Analysis in Slope Stability Investigation. Applied Sciences. 2024; 14(9):3685. https://doi.org/10.3390/app14093685
Chicago/Turabian StyleUmar, Ibrahim Haruna, Hang Lin, and Jubril Izge Hassan. 2024. "Transforming Landslide Prediction: A Novel Approach Combining Numerical Methods and Advanced Correlation Analysis in Slope Stability Investigation" Applied Sciences 14, no. 9: 3685. https://doi.org/10.3390/app14093685
APA StyleUmar, I. H., Lin, H., & Hassan, J. I. (2024). Transforming Landslide Prediction: A Novel Approach Combining Numerical Methods and Advanced Correlation Analysis in Slope Stability Investigation. Applied Sciences, 14(9), 3685. https://doi.org/10.3390/app14093685







