Interactive Airfoil Optimization Using Parsec Parametrization and Adjoint Method
Abstract
Featured Application
Abstract
1. Introduction
2. Theory of Adjoint Optimization
2.1. General Basics of Optimization
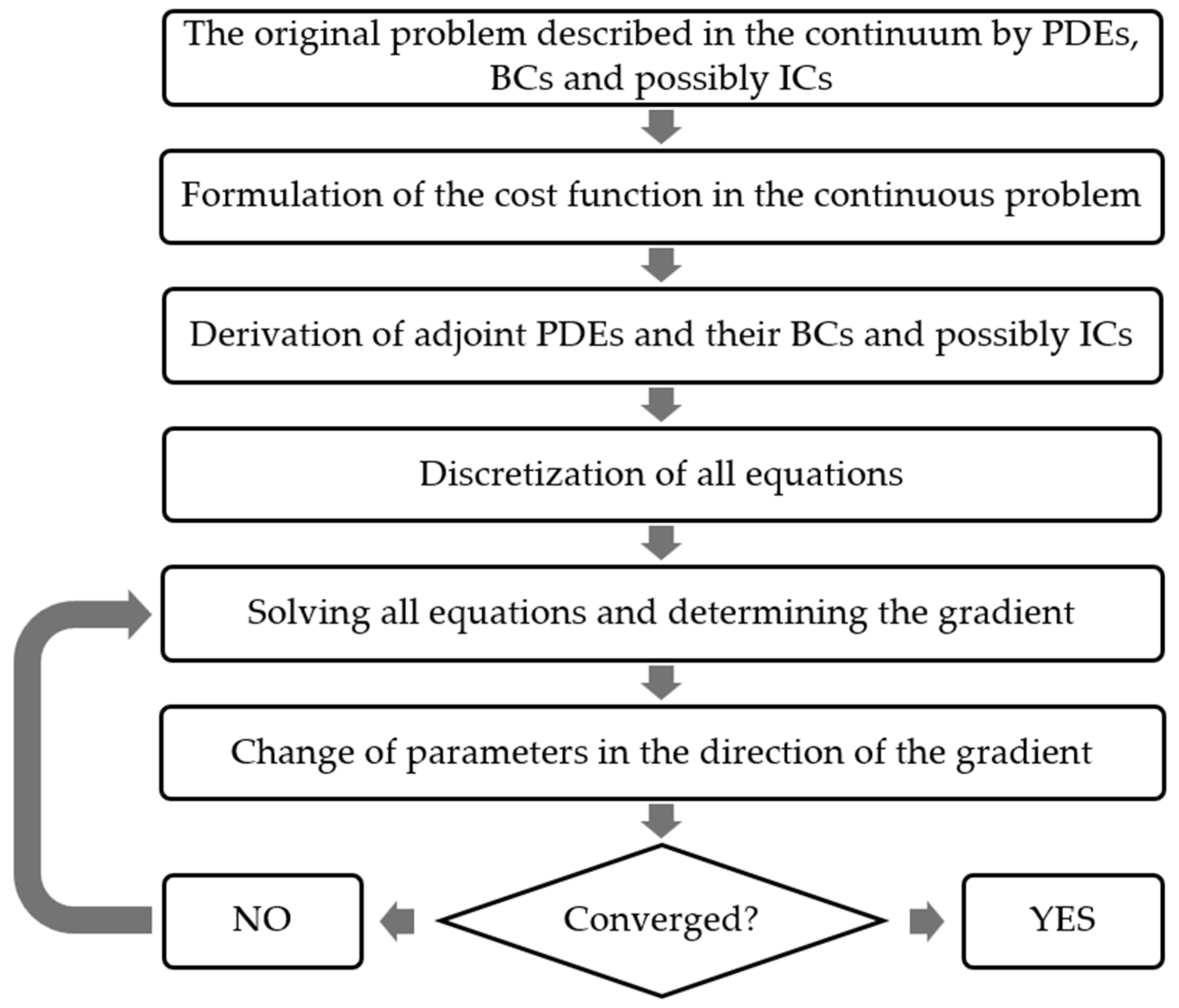
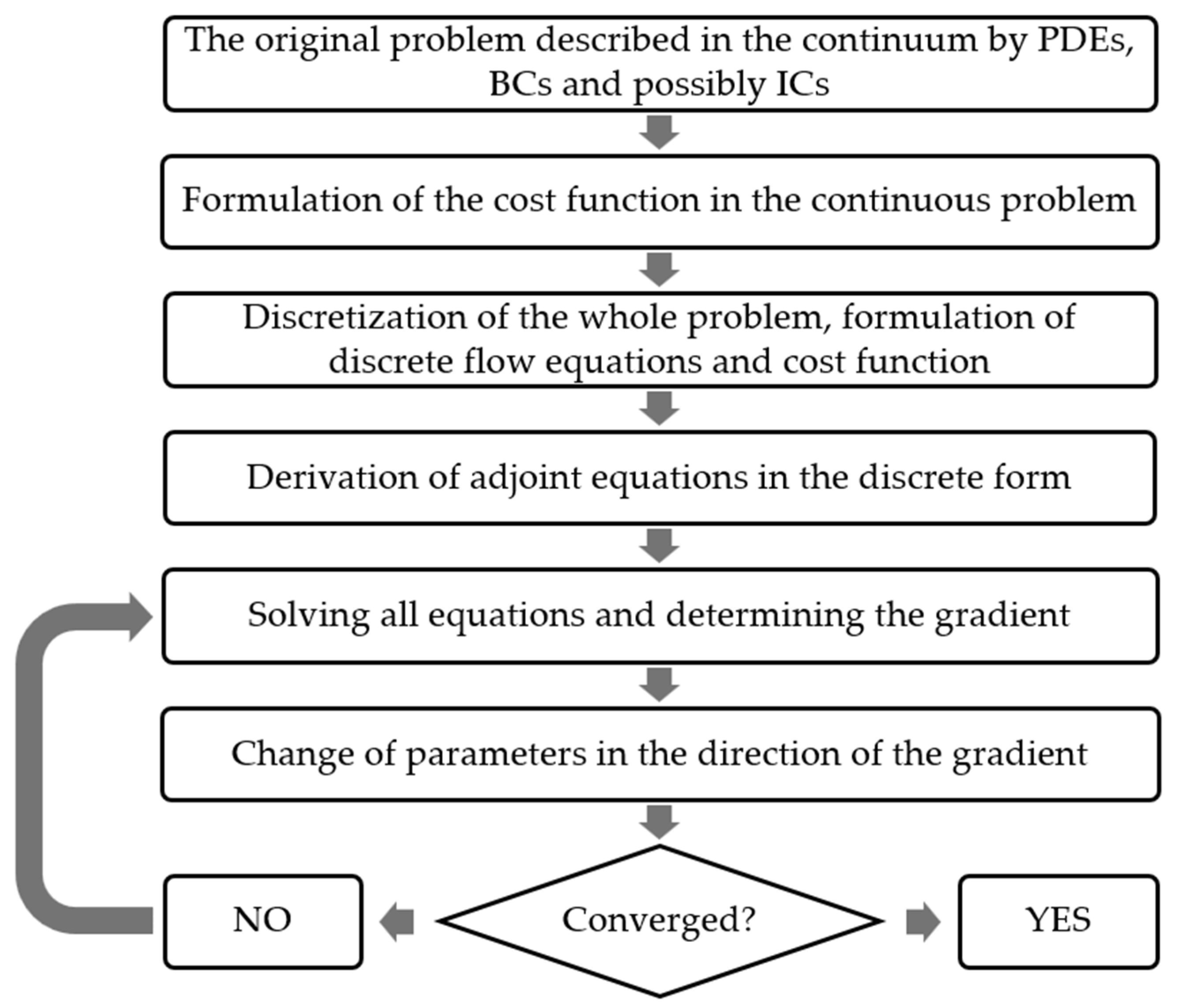
2.2. Adjoint Method: Continuous and Discrete Approach
2.3. Discrete Adjoint Method from the Lagrange Point of View: Governing Equations
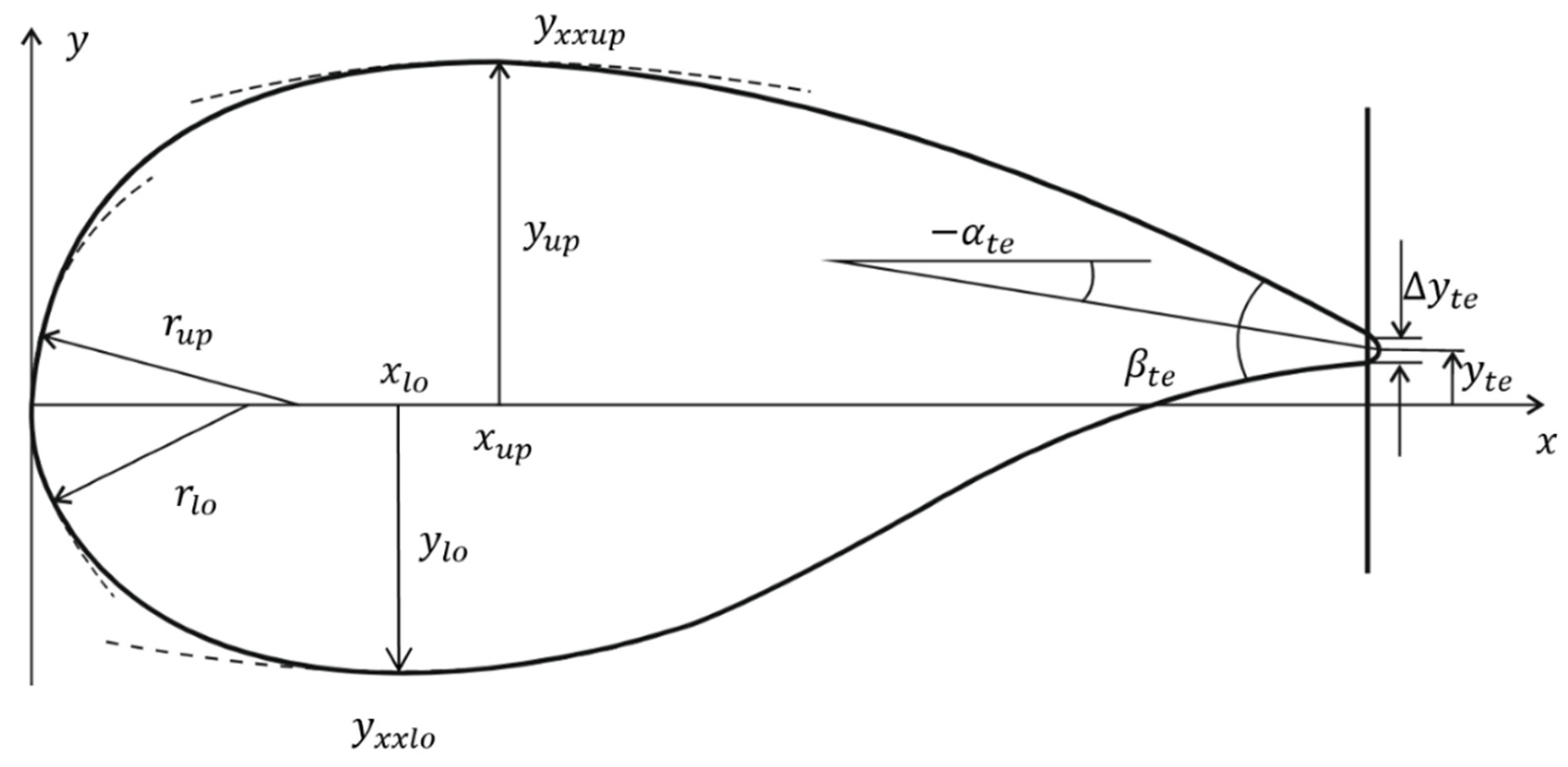
3. Parsec Parametrization
4. Airfoil Optimization: Governing Equations and Implementation
4.1. Potential Flow and Panel Method
4.2. Adjoint-Based Optimization with Panel Method and Parsec Parametrization
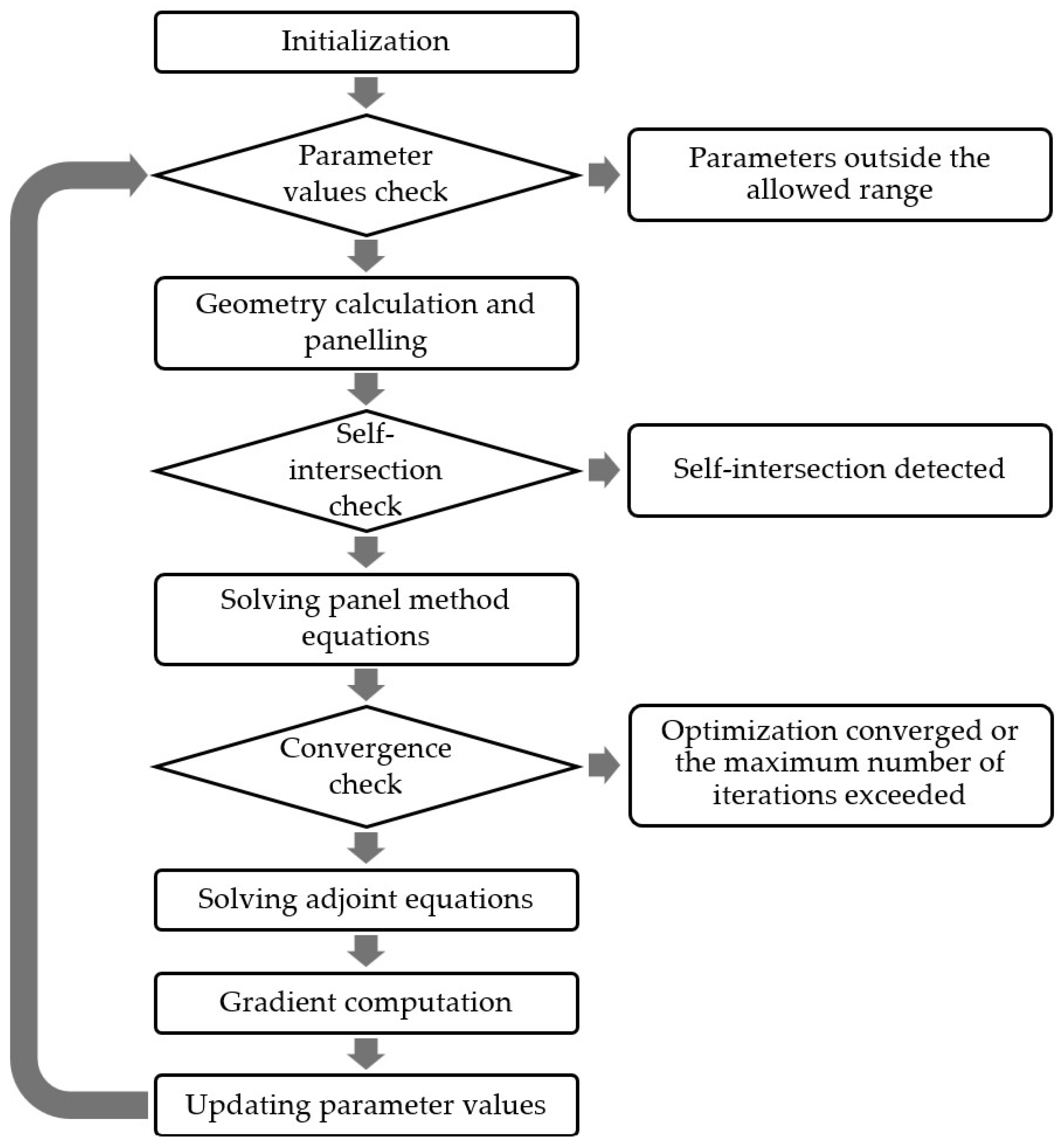
4.3. Resulting Shape Feasibility and Convergence of the Optimization
5. Results and Verification
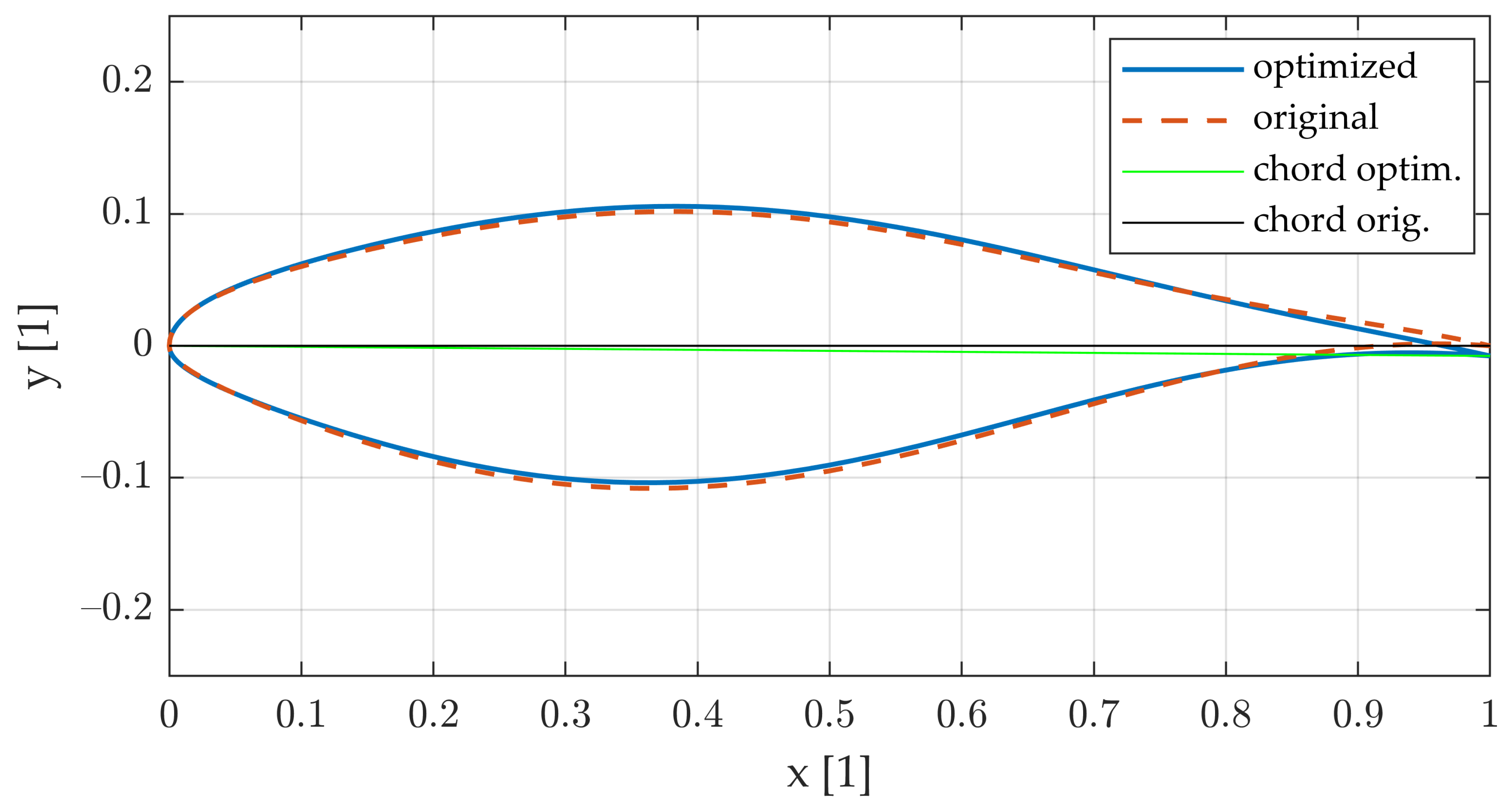
5.1. Adjoint Optimization Results: Incompressible and Inviscid Flow
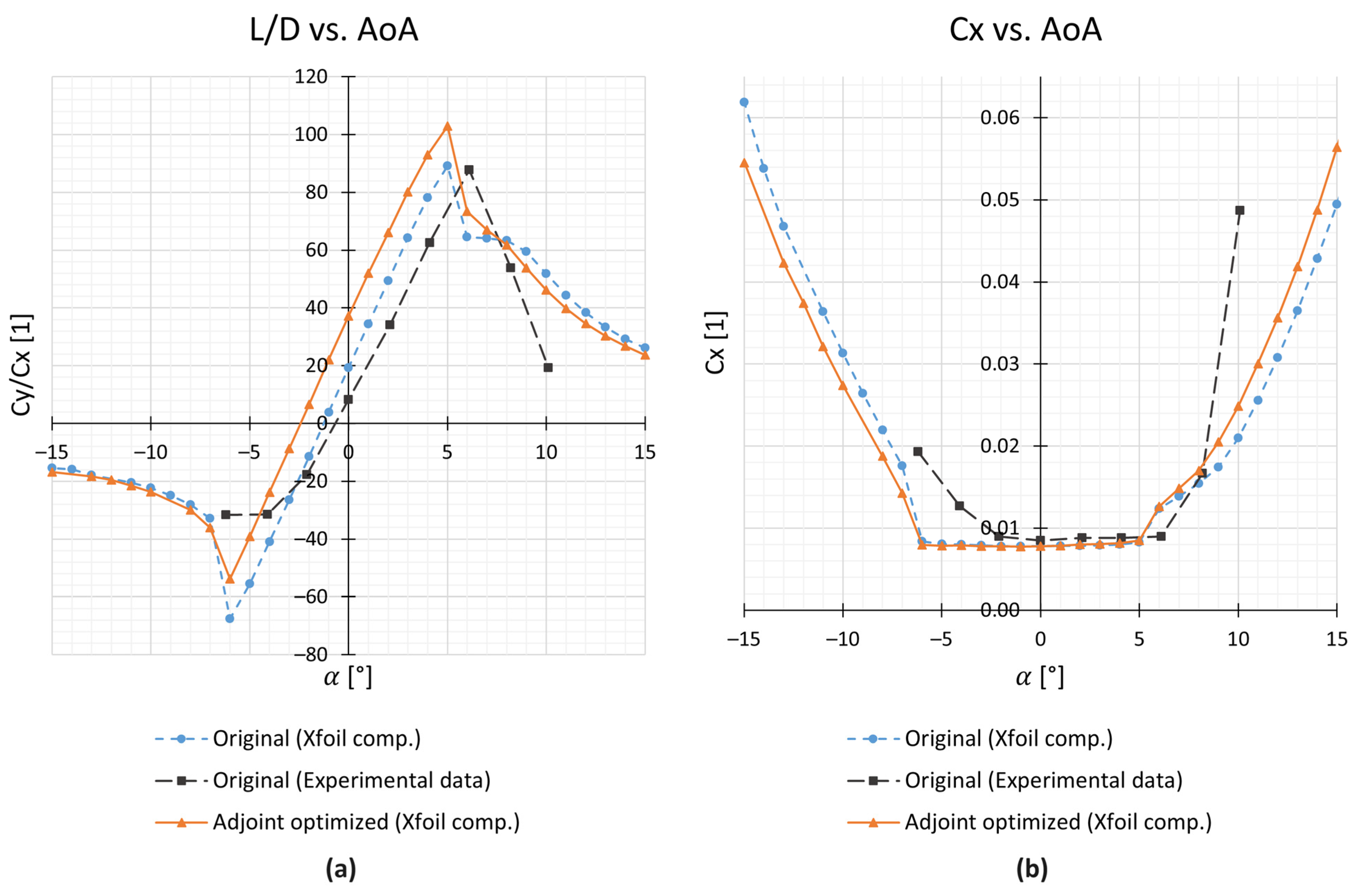
5.2. Xfoil Verification Computations: Compressible and Viscous Flow
6. Conclusions
- The optimization showed a significant improvement to the objective function . For 0 deg AoA, the improvement was 94.7%, and for 6.2 deg AoA, it was 16.1%.
- A big improvement was also observed in the L/D ratio, which matched or even exceeded the improvement to , as the optimization did not noticeably affect the .
- For different AoAs (0 and 10 deg), the resulting shape was almost the same, meaning that the shape optimized for one operating point should work well in a wide range of AoAs, adding to the practical usability of the optimized airfoil.
- The runtime of the adjoint optimization was, for the same airfoil with the same cost function, orders of magnitude shorter than the runtime of the GA coupled with Xfoil while yielding similar results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Du, X.; Martins, J.R.R.A. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Luo, J.; Xiong, J.; Liu, F. Aerodynamic design optimization by using a continuous adjoint method. Sci. China Phys. Mech. Astron. 2014, 57, 1363–1375. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic Shape Optimization Using the Adjoint Method; The von Kármán Institute: Belgium, 2003; Available online: http://aero-comlab.stanford.edu/Papers/jameson.vki03.pdf (accessed on 6 October 2023).
- Giles, M.B.; Pierce, N.A. An Introduction to the Adjoint Approach to Design. Flow Turbul. Combust. 2000, 65, 393–415. [Google Scholar] [CrossRef]
- Monfaredi, M.; Asouti, V.; Trompoukis, X.; Tsiakas, K.; Giannakoglou, K. Aeroacoustic and Aerodynamic Adjoint-Based Shape Optimization of an Axisymmetric Aero-Engine Intake. Aerospace 2023, 10, 743. [Google Scholar] [CrossRef]
- Kim, H.J.; Sasaki, D.; Obayashi, S.; Nakahashi, K. Aerodynamic Optimization of Supersonic Transport Wing Using Unstructured Adjoint Method. AIAA J. 2001, 39, 1011–1020. [Google Scholar] [CrossRef]
- Li, W.; Tian, Y.; Yi, W.; Ji, L.; Shao, W.; Xiao, Y. Study on adjoint-based optimization method for multi-stage turbomachinery. J. Therm. Sci. 2011, 20, 398–405. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic Design via Control Theory. J. Sci. Comput. 1988, 3, 233–245. [Google Scholar] [CrossRef]
- Jameson, A.; Martinelli, L.; Pierce, N.A. Optimum Aerodynamic Design Using the Navier–Stokes Equations. Theor. Comput. Fluid Dyn. 1998, 10, 213–237. [Google Scholar] [CrossRef]
- Salunke, N.P.; Ahamad, R.A.J.; Channiwala, S.A. Airfoil Parameterization Techniques: A Review. Am. J. Mech. Eng. 2014, 2, 99–102. [Google Scholar] [CrossRef]
- Masters, D.A.; Taylor, N.J.; Rendall, T.C.S.; Allen, C.B.; Poole, D.J. Geometric Comparison of Aerofoil Shape Parameterization Methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- Cantwell, B.J. The NACA Airfoil Series. STANFORD UNIVERSITY, Index of /~cantwell/AA200_Course_Material. 2013. Available online: https://web.stanford.edu/~cantwell/AA200_Course_Material/The%20NACA%20airfoil%20series.pdf (accessed on 10 October 2023).
- Akram, M.T.; Kim, M.H. Aerodynamic Shape Optimization of NREL S809 Airfoil for Wind Turbine Blades Using Reynolds-Averaged Navier Stokes Model—Part II. Appl. Sci. 2021, 11, 2211. [Google Scholar] [CrossRef]
- Ziemkiewicz, D. Simple analytic equation for airfoil shape description. arXiv 2016, arXiv:1701.00817. [Google Scholar]
- Sobieczky, H. Parametric Airfoils and Wings. Notes Numer. Fluid Mech. 1998, 68, 71–88. [Google Scholar]
- Khurana, M.; Winarto, H.; Sinha, A. Airfoil Optimisation by Swarm Algorithm with Mutation and Artificial Neural Networks. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; ISBN 978-1-60086-973-0. [Google Scholar] [CrossRef]
- Della Vecchia, P.; Daniele, E.; d’Amato, E. An airfoil shape optimization technique coupling PARSEC parameterization and evolutionary algorithm. Aerosp. Sci. Technol. 2014, 32, 103–110. [Google Scholar] [CrossRef]
- Suprayitno, Y.; Aminnudin, J.C.; Wulandari, R. Airfoil aerodynamics optimization under uncertain operating conditions. J. Phys. Conf. Ser. 2020, 1446, 012014. [Google Scholar] [CrossRef]
- Arias-Montaño, A.; Coello Coello, C.A.; Mezura-Montes, E. Evolutionary Algorithms Applied to Multi-Objective Aerodynamic Shape Optimization. In Computational Optimization, Methods and Algorithms; Koziel, S., Yang, X.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 356, pp. 211–240. ISBN 978-3-642-20858-4. [Google Scholar] [CrossRef]
- Alonso, J.J. Hess-Smith Panel Method: AA200b—Applied Aerodynamics II—Lecture 3. 2005. Available online: http://aero-comlab.stanford.edu/aa200b/lect_notes/lect3-4.pdf (accessed on 8 September 2023).
- Xia, L.; Zou, Z.; Wang, Z.; Zou, L.; Gao, H. Surrogate model based uncertainty quantification of CFD simulations of the viscous flow around a ship advancing in shallow water. Ocean Eng. 2021, 234, 109206. [Google Scholar] [CrossRef]
- Cravero, C.; De Domenico, D.; Marsano, D. The Use of Uncertainty Quantification and Numerical Optimization to Support the Design and Operation Management of Air-Staging Gas Recirculation Strategies in Glass Furnaces. Fluids 2023, 8, 65. [Google Scholar] [CrossRef]
- Broniszewski, J.; Piechna, J.R. Fluid-Structure Interaction Analysis of a Competitive Car during Brake-in-Turn Manoeuvre. Energies 2022, 15, 2917. [Google Scholar] [CrossRef]
- Collicott, S.H.; Valentine, D.T.; Houghton, E.L.; Carpenter, P.W. Potential flow. In Aerodynamics for Engineering Students, 6th ed.; Butterworth-Heinemann: Waltham, MA, USA, 2013; pp. 149–207. ISBN 9780080966328. [Google Scholar]
- Caldwell, A.L. Solutions of the Two-Dimensional, Subsonic Flow About an Airfoil. Master’s Thesis, Oregon State College, Corvallis, OR, USA, 1949. [Google Scholar]
- Ramsay, R.R.; Hoffmann, M.J.; Gregorek, G.M. Effects of Grit Roughness and Pitch Oscillations on the S809 Airfoil; The Ohio State University: Columbus, OH, USA, 1995. [Google Scholar]
- Sommers, D.M. Design and Experimental Results for the S809 Airfoil; National Renewable Energy Laboratory: Golden, CO, USA, 1997. [Google Scholar]


| Optimization Method | RSM | Genetic Algorithm | Finite Difference Method | Adjoint Method | Simplex Method |
|---|---|---|---|---|---|
| Computational complexity |
| Basic Parsec Parametrization [10] | Parsec Variant Used for Optimization [13] | ||
|---|---|---|---|
| Parameter | Meaning | Parameter | Meaning |
| --- | --- | [1] | Lower surface leading edge radius |
| [1] | Lower surface crest location—horizontal position | [1] | Lower surface crest location—horizontal position |
| [1] | Lower surface crest location—vertical position | [1] | Lower surface crest location—vertical position |
| [1] | Lower surface crest curvature | [1] | Lower surface crest curvature |
| [1] | Leading edge radius | [1] | Upper surface leading edge radius |
| [1] | Upper surface crest location—horizontal position | [1] | Upper surface crest location—horizontal position |
| [1] | Upper surface crest location—vertical position | [1] | Upper surface crest location—vertical position |
| [1] | Upper surface crest curvature | [1] | Upper surface crest curvature |
| Trailing edge direction | Trailing edge direction | ||
| Trailing edge wedge angle | Trailing edge wedge angle | ||
| [1] | Trailing edge location—vertical position | [1] | Trailing edge location—vertical position |
| [1] | Trailing edge thickness | [1] | Trailing edge thickness |
| Parameter | Original | Optimized | ||
|---|---|---|---|---|
| [°] | 0 | 10 | 0 | 10 |
| [1] | 0.0100 | 0.0100 | 0.01115 | 0.01168 |
| [1] | 0.3633 | 0.3633 | 0.3630 | 0.3629 |
| [1] | −0.1081 | −0.1081 | −0.1038 | −0.1038 |
| [1] | 1.526 | 1.526 | 1.526 | 1.526 |
| [1] | 0.02160 | 0.02160 | 0.02123 | 0.02167 |
| [1] | 0.3826 | 0.3826 | 0.3829 | 0.3829 |
| [1] | 0.1018 | 0.1018 | 0.1057 | 0.1057 |
| [1] | −1.201 | −1.201 | −1.201 | −1.201 |
| −8.500 | −8.500 | −8.558 | −8.558 | |
| 8.500 | 8.500 | 8.499 | 8.495 | |
| [1] | 0 | 0 | −0.007687 | −0.007616 |
| [1] | 0.2178 | 1.4256 | 0.3507 | 1.5529 |
| [1] | --- | --- | 0.1329 | 0.1273 |
| --- | --- | 61.02 | 8.93 | |
| Type of Xfoil Simulation | Incompressible and Inviscid | Compressible and Viscous | ||||||
|---|---|---|---|---|---|---|---|---|
| Original Airfoil | Optimized Airfoil | Absolute Difference | Relative Difference | Original Airfoil | Optimized Airfoil | Absolute Difference | Relative Difference | |
| α [°] | 0 | 0 | --- | --- | 0 | 0 | --- | --- |
| 0.2137 | 0.3502 | 0.1365 | +63.9% | 0.1480 | 0.2881 | 0.1401 | +94.7% | |
| --- | --- | --- | --- | 0.00883 | 0.00885 | 0.00002 | +0.2% | |
| --- | --- | --- | --- | 16.76 | 32.55 | 15.79 | +94.2% | |
| −0.0578 | −0.0778 | −0.0200 | −34.6% | −0.0425 | −0.0638 | −0.0213 | −50.1% | |
| α [°] | 6.2 | 6.2 | --- | --- | 6.2 | 6.2 | --- | --- |
| 0.9869 | 1.1215 | 0.1346 | +13.6 % | 0.8108 | 0.9415 | 0.1307 | +16.1% | |
| --- | --- | --- | --- | 0.01347 | 0.01337 | −0.00010 | −0.7% | |
| --- | --- | --- | --- | 60.20 | 70.40 | 10.20 | +16.9% | |
| −0.0778 | −0.0974 | −0.0196 | −25.2% | −0.0449 | −0.0641 | −0.0192 | −42.8% | |
| Exp. Data | Xfoil Computation Data | CFD Computation Data | |||||
|---|---|---|---|---|---|---|---|
| Original Airfoil (OSU) | Optimized Airfoil (CST) | Optimized Airfoil (PARSEC) | CST vs. Experiment | PARSEC vs. Experiment | Optimized Airfoil (CST) | CST vs. Experiment | |
| α [°] | 6.2 | 6.2 | 6.2 | --- | --- | 6.2 | --- |
| 0.79 | 0.883 | 0.87 | +11.8% | +10.1% | 0.985 | +24.6% | |
| 0.0131 | 0.0134 | 0.0148 | +2.2% | +12.1% | 0.0147 | +12.2% | |
| 60.3 | 65.9 | 58.8 | +9.6% | −2.0% | 67 | +12.4% | |
| Original Airfoil | |||||||
|---|---|---|---|---|---|---|---|
| MATLAB Inviscid | Xfoil Inviscid | Xfoil Viscous | Experiment [13,26] | MATLAB Inviscid vs. Experiment | Xfoil Inviscid vs. Experiment | Xfoil Viscous vs. Experiment | |
| α [°] | 6.2 | 6.2 | 6.2 | 6.2 | --- | --- | --- |
| 0.9777 | 0.9869 | 0.8108 | 0.79 | +23.8% | +24.9% | +2.6% | |
| --- | --- | 0.01347 | 0.0131 | --- | --- | +2.8% | |
| --- | --- | 60.20 | 60.30 | --- | --- | −0.2% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belda, M.; Hyhlík, T. Interactive Airfoil Optimization Using Parsec Parametrization and Adjoint Method. Appl. Sci. 2024, 14, 3495. https://doi.org/10.3390/app14083495
Belda M, Hyhlík T. Interactive Airfoil Optimization Using Parsec Parametrization and Adjoint Method. Applied Sciences. 2024; 14(8):3495. https://doi.org/10.3390/app14083495
Chicago/Turabian StyleBelda, Marek, and Tomáš Hyhlík. 2024. "Interactive Airfoil Optimization Using Parsec Parametrization and Adjoint Method" Applied Sciences 14, no. 8: 3495. https://doi.org/10.3390/app14083495
APA StyleBelda, M., & Hyhlík, T. (2024). Interactive Airfoil Optimization Using Parsec Parametrization and Adjoint Method. Applied Sciences, 14(8), 3495. https://doi.org/10.3390/app14083495






