Abstract
With the increasing demand for space missions, space robots have become the focus of research and attention. As a typical representative, the free-floating dual-arm space robot has the characteristics of multiple degrees of freedom, a floating base, and dynamic coupling between the manipulator and the base, so its modeling and control are very challenging. To address these challenges, a novel dynamic modeling and control method is proposed for a free-floating dual-arm space robot. First, an explicit dynamic model of a free-floating dual-arm space robot is established based on the explicit canonical multi-rigid-body dynamic modeling theory and combined with the concept of a dynamic equivalent manipulator. The establishment process of this model is not only simple and canonical to avoid the definition and calculation of many intermediate variables, but the symbolic result expression of the model also has the characteristics of iteration, which is convenient for computer automatic modeling. Next, aiming at addressing the problem of trajectory tracking and the base attitude stability of a free-floating dual-arm space robot with parameter perturbation and external disturbance, an improved nonlinear model predictive control method introducing the idea of sliding mode variable structure is proposed. Theoretical analysis shows that the proposed controller has better robustness than the traditional nonlinear model predictive controller. Then, an in-orbit service task is designed to verify the effectiveness of the proposed dynamic modeling and control strategy of the free-floating dual-arm space robot. Finally, the dynamic modeling and control methods proposed are discussed and summarized. The proposed methods can not only realize the tracking of the desired trajectory of the arms of the free-floating space robot, but can also realize the stable control of the base of the free-floating space robot. This paper provides new insights into the difficult problems regarding the dynamics and control of free-floating dual-arm space robots.
1. Introduction
Since the 1990s, space manipulators used to manipulate and capture payloads have received extensive attention [1,2,3,4,5,6]. Space manipulator can not only be installed on a space station to assist astronauts in the maintenance of the space station [7,8,9], but can also be installed on an unmanned satellite to carry out in-orbit maintenance of the satellite and capture space debris [10,11,12,13]. In 2007, the US Orbital Express project carried out capture and maintenance experiments of controlled target satellites using unmanned satellites equipped with a manipulator [14]. Unlike a manipulator with a fixed base on the ground, the base of a small space robot composed of a small unmanned satellite and manipulator is generally movable [15]. This kind of space robot with a movable base is a typical unrooted tree multibody dynamic system, which has the characteristics of many degrees of freedom (DOF), strong nonlinearity and strong coupling [16]. Its dynamic modeling and control are challenging and have attracted increasing attention from researchers in recent years [1,15].
Compared with single-arm space robots, the establishment of the dynamic model of a dual-arm space robot is more complicated. So far, according to the different expressions of dynamic equations, the dynamic modeling methods of multibody systems such as robots are mainly divided into recursive methods based on the Newton–Euler equation and explicit methods based on the Lagrange equation. Recursive methods can obtain efficient recursive equations, but they are not suitable for the derivation of a high control law [17,18]. Compared with recursive methods, the expression of the dynamic equation of explicit methods is more intuitive. The pseudo inertia matrix method [19,20] and the generalized momentum method [21] are two common explicit dynamic modeling methods. However, these two explicit methods both have the problem that many intermediate variables need to be analyzed and calculated. Recently, an explicit multi-rigid-body dynamic modeling method was proposed, which can directly obtain the final canonical expression of a multibody system [22,23].
Unlike ground robots with a fixed base, space robots have dynamic coupling between the arm and the movable base [24,25]. If this is not controlled, it will lead to accidental movement of the base and affect the performance of the space robot [7,26,27]. For example, to ensure reliable communication with the ground or receive solar energy, the base of the satellite needs to accurately point in a fixed position, but the dynamic coupling between the arm and the base will interfere with the attitude of base [7]. Dubowsky and Papadopoulos [28] divided space robots with movable bases into free-flying space robots and free-floating space robots according to the different control problems to be solved. Unlike free-flying space robots that need to control the position and attitude of the base at the same time, free-floating space robots only needs to consider the control of base attitude, which can save energy [29]. In order to simplify the kinematic analysis of free-floating space robots, Vafa and Dubowsky [30] proposed the concept of the virtual manipulator (VM). VM is a fixed base robot with the same kinematic equivalence as a free-floating space robot, and its first joint is a passive spherical joint, which represents the free-floating characteristics of the space robot [31]. Liang [32] extended the concept of VM and proposed the dynamic equivalent manipulator (DEM), which can simultaneously simplify the kinematics and dynamics analysis of free-floating space robots.
In the process of in-orbit service, a space robot will not only be subjected to unknown disturbances from the outside, but will also be constrained by the uncertainty of internal parameters of the system caused by the change in fuel quality and other factors [15]. Therefore, designing controllers for space robots is a challenge which has been studied by many researchers [33,34,35]. Papadopoulos and Dubowsky [29] noted the similarities in control between free-floating space robots and ground fixed-base robots. Since then, many control algorithms designed for ground fixed-base robots have been studied and applied in space robots. Among them, the PID control method, which has been widely studied in ground industrial robots, has also been used in space robots [36]. However, this method has the problem of parameter tuning difficulty when it is applied to control an in-orbit service space robot with complex disturbances. Sliding mode control (SMC) is widely applied in the field of nonlinear systems because of its high precision and fast response [37,38]. Slotine et al. [39] first used SMC to design the controller of a two-DOF manipulator, and then the researchers conducted much research on the SMC of robots, representing a typical nonlinear system [40,41]. In recent years, many novel SMC methods have been proposed for the in-orbit service of space robots [42,43]. Model predictive control (MPC) is an excellent control method based on a system model to obtain a control signal by minimizing the objective function [44]. Raimondo et al. [45,46] improved MPC for the control problem of nonlinear systems and obtained better control performance. In the field of space robots, compared with other control methods, there is relatively less research on MPC. When studying the control problem of dual-arm space robots, Shi [47] found that MPC can achieve higher-precision control performance than SMC when there is no system disturbance, while SMC shows better robustness than MPC when there is system disturbance. Tomasz Rybus [44] discussed the possibility of applying a nonlinear model predictive controller (NMPC) to a free-floating space robot. Tomasz Rybus [11] proposed a new concept for a free-floating space robot control system, in which the NMPC controller introduced a trajectory planning module, but the paper only carried out a numerical simulation on the planar case of the two-DOF manipulator.
In this paper, the dynamic model of a free-floating dual-arm space robot with stylization and high computational efficiency is established by using the concept of DEM and the explicit multi-rigid-body dynamic modeling theory [22,23], and a novel control method is proposed. This method can be effectively applied to the terminal trajectory tracking and base attitude stability control of free-floating space robots under the condition of parameter perturbation and external disturbance. The remainder of this paper is organized as follows: in Section 2, a free-floating dual-arm space robot is modeled and analyzed by using explicit multi-rigid-body dynamic modeling theory and DEM. In Section 3, an improved NMPC controller is designed and its stability is analyzed based on Lyapunov theory. In Section 4, an in-orbit service task is designed and a numerical simulation is performed to verify the proposed controller. In Section 5, the dynamic modeling and control methods for the free-floating space robot are discussed, while the conclusions are provided in Section 6.
2. Dynamic Modeling of Free-Floating Dual-Arm Space Robot
This section mainly introduces and analyzes the dynamic model of a free-floating dual-arm space robot based on the explicit multi-rigid-body dynamic modeling method and combined with the concept of DEM, which is used for subsequent control research. Because kinematics is the foundation of dynamics [17], the kinematic model is introduced first before the dynamic modeling.
2.1. Kinematic Modeling
The free-floating dual-arm space robot used in this study is a typical unrooted tree multibody system [16]. The schematic diagram of the free-floating dual-arm space robot studied in this paper is shown in Figure 1. The topological structure analysis and the establishment of the reference frames of the space robot are introduced below.

Figure 1.
Schematic diagram of the free-floating dual-arm space robot.
The topology of a robot is usually composed of nodes representing the links (except the root node) and arcs representing the joints [48]. The schematic diagram of the free-floating dual-arm space robot is shown in Figure 1, where represents the kinematic pair composed of parent link and child link l. Each arm of the free-floating dual-arm space robot contains three single-DOF revolute pairs. The attitude of the base of the free-floating space robot has three rotational DOF. According to the concept of DEM, after the free-floating base of the space robot is equivalent to three single-DOF revolute pairs, the unrooted free-floating tree-chain space robot can be equivalent to a fixed-base tree-chain ground robot [31]. According to the above analysis, the topology graph of the free-floating dual-arm space robot is shown in Figure 2, where i represents the inertial space, b represents the base, l represents the left arm, r represents the right arm and R represents the revolute pair. Except for the root node, the remaining nine nodes in the topology correspond to the nine DOF of the free-floating dual-arm space robot, and these nodes are numbered in turn. In addition, unless otherwise specified, the rest of the symbols used in this article are shown in Table A1 of Appendix A.
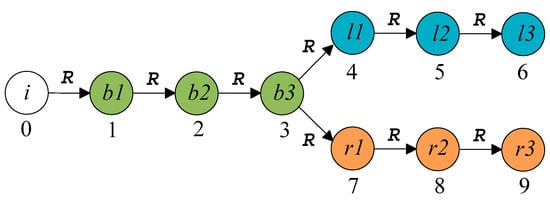
Figure 2.
Topology graph of the free-floating dual-arm space robot.
To improve the calibration accuracy of the robot’s structural parameters, we propose a reference system establishment method based on the Axis-Invariant [49]. The reference frames and the Axis-Invariant of the left arm of the free-floating dual-arm space robot are described in Figure 3. The origin of the inertial reference frame is located at the center of the Earth. The origin of the base reference frame is located at the center of mass of the base. The origins of the joint reference frames are located on the rotation axes of the joints. At the initial moment, the directions of these reference frames are consistent. The Axis-Invariant is defined as the motion axis vector direction of joint l. For more background and applications of the Axis-Invariant, refer to [22,23,49,50,51].
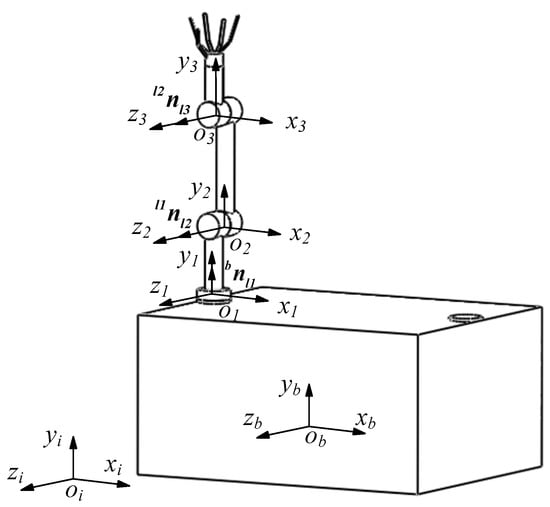
Figure 3.
The reference system and the Axis-Invariant of the left arm.
With the Axis-Invariant as the reference axis, the rotational vector of the rotating joint and the translational vector of the prismatic joint can be expressed as follows [22,23]:
The rotation transformation matrix based on the Axis-Invariant can be expressed as follows [22,23]:
According to the expression of the rotation transformation matrix in Equation (3), the iterative kinematic equations of multi-joint series based on the Axis-Invariant can be expressed as follows:
where the left superscript “i|” of the vector represents the projection of the vector under the inertial reference frame .
The velocity vector and acceleration vector are the derivative and second derivative of the displacement vector, respectively. By taking the derivative and second derivative of Equations (5) and (6), the iterative velocity and iterative acceleration of multi-joint kinematic chain can be expressed as follows:
2.2. Dynamic Modeling
As a classical method of multibody system dynamics modeling, the Lagrange equation is widely used in the field of robot dynamics [52]. When the free-floating dual-arm space robot serving in orbit is running in space, the influence of gravity can be ignored, and the joint type of the robot only contains rotating joints. The Lagrange equation expression of the space robot tree-chain multibody system based on the Axis-Invariant, which only contains rotating joints and ignores gravity, is as follows [22,23]:
where is an energy term,
The iterative partial derivative equation based on the Axis-Invariant is [22,23]
Substituting Equations (1)–(10) and (13) and (14) into Equations (11) and (12), after simplifying the results, the explicit canonical dynamic expression of the space robot tree-chain multibody system that ignores gravity and only contains rotating joints can be obtained:
where is a 3 × 3 inertia matrix for revolute pairs and is a 3D bias force vector for revolute pairs,
According to Equation (15) and the above topological analysis, the explicit canonical dynamic model of the base, left arm and right arm of the free-floating dual-arm space robot can be obtained as follows:
The above Equation (18) can be rewritten as follows:
According to Equations (16) and (17), the inertia matrix M[·][·] and the bias force vector h[·] in Equation (19) can be defined by Equations (A1)–(A9) and Equations (A10)–(A15) in Appendix B, respectively.
3. Design of the Improved NMPC Controller
In this section, an improved NMPC controller is designed for the trajectory tracking control of a free-floating dual-arm space robot serving in orbit. The principle of the improved NMPC controller designed in this paper is shown in Figure 4. As shown in Figure 4, the controller proposed in this paper is mainly composed of a predictive control unit for the rolling optimization of a nominal dynamic model and a sliding mode variable structure control unit for the purposes of weakening the influence of disturbance. The improved NMPC controller introduced the idea of SMC control and added the sliding mode variable structure control technology to suppress the disturbance, which improved the performance of the traditional NMPC controller.
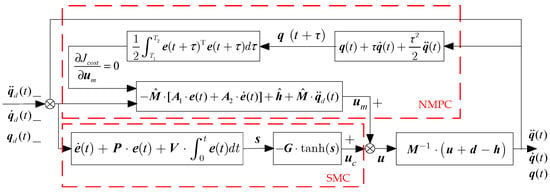
Figure 4.
The principle block diagram of the proposed controller.
According to Figure 4, the control law of the proposed controller can be expressed as follows:
where is the torque generated by the predictive control unit and is the torque generated by the sliding mode variable structure control unit.
3.1. Design of the NMPC Controller
The designed predictive controller refers to the classical NMPC control algorithm developed in [53]. NMPC is essentially a kind of optimal control that aims to minimize the trajectory tracking error during control. Therefore, the cost function of the NMPC is often expressed as [53,54]:
where is the prediction error at time and is the prediction time. and represent the actual and desired joint angles of the system at time , respectively.
The truncated Taylor series is applied to expand as follows:
If , , and are taken, then and can be expressed as:
According to Equation (23), the prediction error can be re-expressed as:
The nominal dynamic model of the free-floating dual-arm space robot under ideal conditions can be expressed as follows:
where and are the nominal inertia matrix and nominal bias force vector of the free-floating dual-arm space robot constructed in the second section of this paper under ideal conditions.
According to Equation (25), the vector can be expressed as
According to Equation (26), the cost function in Equation (21) can be re-expressed as
The matrix in the above formula is expressed as
where the rolling period .
The system control law of the predictive control unit can be solved according to :
According to and , Equation (29) can be re-expressed as
where , .
3.2. Design of an Improved NMPC Controller Based on Sliding Mode Variable Structure
During the in-orbit service of an actual space robot, the dynamic parameters will change due to factors such as fuel consumption, and the space robot will inevitably be affected by external disturbances. Therefore, considering the influence of parameter uncertainty and external disturbances, the practical dynamic model of the in-orbit service free-floating dual-arm space robot is
where and are the actual inertia matrix and the actual bias force vector of the free-floating dual-arm space robot, respectively, and d is the external disturbance.
The sliding mode function is taken as
where , , , , is a positive definite diagonal matrix of size , is a diagonal element of , and .
The sliding mode hyperplane is
According to , Equation (33) can be re-expressed as
The reference acceleration is taken as
Then, Equation (34) can be re-expressed as
According to Equation (31), we can obtain
According to Equation (37), Equation (36) can be re-expressed as
By substituting Equations (20), (30) and (35) into Equation (38), we can obtain
where is the uncertainty of the system.
According to Equation (39), we can obtain
Theorem 1.
Suppose there is a positive definite matrix of and there is a positive real number b > 0 such that holds, where I is the identity matrix of size . Suppose any vector and ; then, for any vector , the following inequality holds:
According to Theorem 1, we can obtain
where is the infimum of M.
Because , then according to Equations (40) and (42), we can obtain
3.3. Analysis of Stability
The sliding mode boundary thickness is denoted as . If the control process of the closed-loop control system from the initial state to the sliding mode surface is expected to satisfy Lyapunov stability, then
Because , according to Equations (43) and (44), to ensure the stability of the system, it is necessary to select to meet the following conditions:
Equation (45) can be re-expressed as
According to Equation (46), the control law of the sliding mode variable structure control unit can be constructed as
where is a positive definite diagonal matrix of size , is a diagonal element of and is a positive definite function; is also a positive definite diagonal matrix of size , and is a diagonal element of .
By substituting Equation (47) into Equation (46), we can obtain
where is the supremum of M.
Theorem 2.
Consider to be a positive definite matrix of size and to be a diagonal positive definite matrix of size . If there exists a positive real number and , then for any vector , the following equation holds:
The proof of Theorem 2 is given in Equations (A16)–(A18) in Appendix C.
According to Theorem 2, we can obtain
According to Equations (48) and (50), to ensure the stability of the system, the following equation needs to be satisfied:
The above Equation (51) can be re-expressed as
The control law of the sliding mode variable structure control unit in Equation (47) is equivalent to
Since the slope of the sign function dsgn() in Equation (53) is infinite, the control signal of the system has a serious jitter problem in the switching process. In this paper, the hyperbolic tangent function tanh() with a gentler slope is introduced to replace the sign function dsgn() to improve it. According to Equations (52) and (53), the improved can be expressed as
According to Equation (54), we can obtain the control law of the sliding mode variable structure control unit of the system as
4. Simulation
In this section, an in-orbit service task as shown in Figure 5 is designed for a free-floating dual-arm space robot, in which one manipulator performs the capture operation on the target object and the other manipulator performs the maintenance operation on the captured object. The parameters of the free-floating dual-arm space robot are shown in Table 1.

Figure 5.
Schematic diagram of the designed in-orbit service task.

Table 1.
Initial parameters of the free-floating dual-arm space robot.
The space robot will inevitably be affected by uncertain dynamic parameters and external disturbance when it performs the in-orbit service task. First, we use the traditional NMPC method to simulate and contrast the trajectory tracking of the space robot under the influence of dynamic parameter uncertainty and external disturbance. The relevant parameter settings of the dynamic parameter uncertainty and external disturbance of the space robot during simulation can be found in Table 1. Taking joint 5 as an example, the traditional NMPC method is used to simulate and compare the actual situation of the free-floating dual-arm space robot affected by parameter uncertainty and external disturbance with the ideal situation that is not affected. The results are shown in Figure 6. It can be seen from Figure 6 that the traditional NMPC method has a good control effect on the robot under ideal conditions, but the control effect of the robot under actual conditions with disturbances needs to be improved.
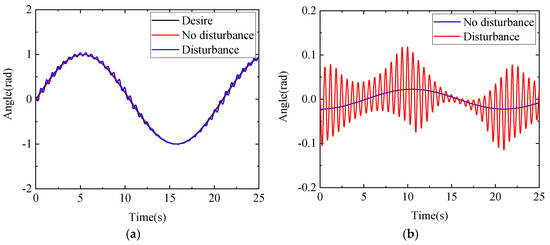
Figure 6.
Simulation comparison of traditional NMPC with and without disturbance. (a) Comparison of desired trajectory tracking for joint 5. (b) Error comparison of desired trajectory tracking for joint 5.
To show the advantages of the proposed improved NMPC method, we next build two controllers based on the traditional NMPC method and the proposed improved NMPC method, respectively. The relevant parameter settings of these two controllers can be found in Table 1. We use these two controllers to simulate the trajectory tracking of the two arms of the free-floating dual-arm space robot under the influence of uncertain dynamic parameters and external disturbances. Figure 7 shows the tracking comparison of each joint of the left arm based on these two controllers to the desired trajectory. As shown in Figure 7, compared with the traditional NMPC controller, the proposed improved NMPC controller is more accurate in tracking the desired trajectory, and can keep the error within the target range, showing an excellent control effect.
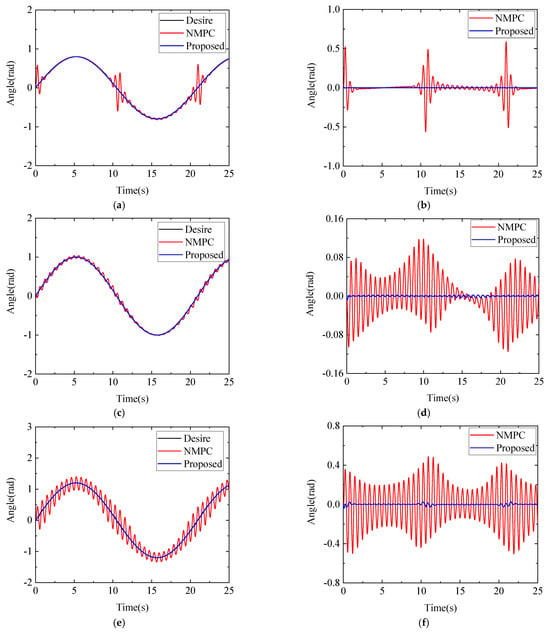
Figure 7.
Simulation comparison between traditional NMPC and proposed improved NMPC. (a) Comparison of desired trajectory tracking for joint 4. (b) Error comparison of desired trajectory tracking for joint 4. (c) Comparison of desired trajectory tracking for joint 5. (d) Error comparison of desired trajectory tracking for joint 5. (e) Comparison of desired trajectory tracking for joint 6. (f) Error comparison of desired trajectory tracking for joint 6.
Unlike the ground fixed manipulator, the attitude of the base of the free-floating dual-arm space robot needs to be controlled stably; otherwise, it will seriously affect the operation accuracy of the two arms, resulting in the failure of the operation task. Therefore, we finally use these two controllers to simulate the stable control of the base attitude of the free-floating dual-arm space robot. In order to further demonstrate the advantages of the designed improved NMPC controller, we increase the amplitude of the external disturbance of the robot base attitude simulation experiment to five times the original to increase the uncertainty of the system to verify the performance of the proposed controller. Figure 8 shows the error comparison of the base attitude stabilization control of the free-floating dual-arm space robot based on these two controllers. It can be seen from Figure 8 that compared with the traditional NMPC controller, the designed improved controller obtains a more stable base attitude. The proposed controller shows excellent stability in conditions of strong disturbance.
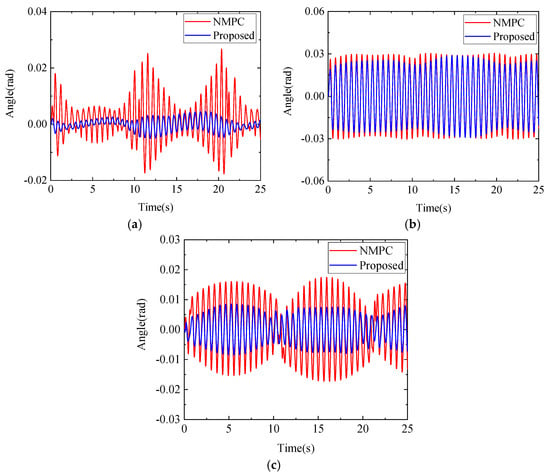
Figure 8.
Error comparison of base attitude stability control. (a) Comparison of the x-axis error of the base. (b) Comparison of the y-axis error of the base. (c) Comparison of the z-axis error of the base.
5. Discussion
This section will discuss the proposed method from two perspectives: dynamic modeling and control.
- Dynamic modeling:
- (1)
- The free-floating dual-arm space robot studied in this paper is a complex multibody system with nine DOF. The modeling efficiency of the traditional explicit multibody system dynamic modeling method needs to be improved. For example, when the pseudo inertia matrix method [19,20] is used, the pseudo inertia matrix, the homogeneous transformation matrix, and other intermediate variables need to be calculated; when the generalized momentum method [21] is used, although the computational efficiency of the inertia matrix is higher than that of the pseudo inertia matrix method, it is also necessary to derive and calculate the intermediate variables such as the Jacobian matrix, and the generalized momentum method cannot explicitly establish the bias force vector. The space robot modeling method in this paper avoids the definition and operation of intermediate variables, and its modeling efficiency is higher than the traditional explicit modeling method. The highest computational complexity is obtained when all joint types of the robot are considered as rotational joints. Table 2 shows the comparison of the computational complexity of the inertia matrix M and the bias force vector h in the calculation of an n-DOF robot with full rotational joints when the three different explicit dynamics modeling methods are adopted. Table 2 shows that the computational complexity of the explicit canonical method in this paper is significantly lower than those of the other two methods.
 Table 2. Comparison of computational complexity.
Table 2. Comparison of computational complexity. - (2)
- Due to the floating characteristics of the base of the free-floating space robot, it is difficult to combine the traditional explicit dynamic modeling method with DEM, because it requires tedious and complex analysis processes, such as the definition and operation of complex intermediate variables. When combined with DEM, our explicit canonical dynamic modeling method can avoid the tedious and complex analysis of intermediate variables.
- (3)
- Due to the inconvenient modeling method, most of the literature in the study of space robot dynamics and control only simulates the plane situation of the two-DOF manipulator, which makes it difficult to reflect the real working state of the complex multi-DOF space robot. When using the proposed explicit dynamic modeling method, it is easy to establish a dynamic model for complex multi-DOF space robot for control research.
- Control:
- (1)
- Compared with other traditional control methods, research on the NMPC method applied to space robots is not extensive enough. Recently, Tomasz Rybus [11,44] explored the possibility of using the NMPC method to control manipulators mounted on free-floating space robots. However, Tomasz Rybus [11,44] only considered the trajectory tracking control of the end manipulator of the free-floating space robot, and did not consider the stable control of the attitude of the base of the free-floating space robot. In addition, Tomasz Rybus [11,44] only carried out dynamic modeling and simulation verification of the NMPC method for a two-DOF planar manipulator. This paper not only considers the trajectory tracking control of the end manipulator of the free-floating space robot, but also considers the stable control of the base attitude of the free-floating space robot. In addition, the dynamic modeling and control simulation of the free-floating dual-arm space robot with nine DOF are carried out in this paper.
- (2)
- The free-floating space robot has high requirements on the accuracy of trajectory tracking and the stability of the base attitude. The traditional NMPC method has difficulty meeting these requirements. This paper innovatively introduces the idea of sliding mode variable structure to improve the traditional NMPC method. The proposed improved NMPC method has better robustness and can better meet the requirements of trajectory tracking accuracy and base attitude stability for free-floating space robots serving in orbit.
- (3)
- Inspired by the literature [15], the control system in this paper consists of a combined controller for the base and the arms, rather than two separate controllers, which can reduce the risk of failure.
6. Conclusions
Based on a new dynamic modeling theory, a novel dynamic control method is proposed for the free-floating dual-arm space robot. This method can not only realize the tracking of the desired trajectory by the two arms of the space robot, but also realize the stable control of the space robot base. The in-orbit service mission of space debris capture was designed and simulated. The main contributions of this paper are as follows:
- (1)
- Based on a new explicit multi-rigid-body dynamic modeling method and employing the concept of DEM, the dynamic model of a free-floating dual-arm space robot is established. The modeling process of the model is simple and standardized, which is convenient for computer programming.
- (2)
- After introducing the control idea of the sliding mode variable structure into the traditional NMPC method, a novel NMPC controller is designed, which effectively solves the problem of tracking the desired trajectory and stabilizing the base attitude of the free-floating dual-arm space robot under unknown model uncertainty and external disturbance.
This article focuses on the challenging problem of dynamic modeling and control of free-floating space robots. The proposed new dynamic modeling and control method can be effectively applied to the on-orbit service tasks of free-floating dual-arm space robots, providing new insights into the challenging problems regarding the dynamics and control of complex multi-DOF space robots. In order to fully verify the method proposed in this paper, a prototype platform of a free-floating dual-arm space robot will be built in the future, and the development and test of hardware system will be carried out. At the same time, in the future, factors such as link flexibility, joint friction and contact collision will be considered to study the dynamic modeling, control and planning of multi-arm space robots.
Author Contributions
Methodology, Z.G. and C.L.; software, Z.G.; writing—original draft preparation, Z.G.; writing—review and editing, Z.G., H.J. and K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (61673010).
Data Availability Statement
The authors will supply the relevant data in response to reasonable requests.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose.
Appendix A

Table A1.
Symbol descriptions.
Table A1.
Symbol descriptions.
| Symbols | Description | Symbols | Description |
|---|---|---|---|
| Angular position along | |||
| Closed subtree of link u | Kinematic chain from i to l | ||
| Mass of link k | Inertia tensor of link k | ||
| Inertial force matrix of revolute joint u | Bias force vector of revolute joint u | ||
| resultant torque on axis except gravity | uth row and kth column element of inertia matrix |
Appendix B
- Because the inertia matrix M[·][·] is a symmetric matrix, and because we are limited by the length of the article, the following are only the explicit expressions of the corresponding elements in the upper left corner of the M[·][·] matrix in Equation (19).
- The explicit expressions of the bias force vector h[·] of the left arm and the right arm of the free-floating dual-arm space robot with symmetrical tree-chain topology are very similar. Since we are limited by the length of the article, the following are only the explicit expressions of the corresponding elements of the base and the left arm in the h[·] vector in Equation (19).
Appendix C
Proof of Theorem 2.
Since , where and is a positive definite matrix, and is a diagonal positive definite matrix, then the following equation holds:
Since M is a positive definite matrix, then is also a positive definite matrix. According to Equation (A16), the following equation holds:
Since is a diagonal positive definite matrix, then and K are interchangeable, so is also positive definite. According to Equation (A17), for any vector , the following equation holds:
Proof done. □
References
- Zong, L.; Emami, M.R.; Luo, J. Reactionless Control of Free-Floating Space Manipulators. ITAES 2019, 56, 1490–1503. [Google Scholar] [CrossRef]
- Chu, X.; Hu, Q.; Zhang, J. Path Planning and Collision Avoidance for a Multi-Arm Space Maneuverable Robot. ITAES 2017, 54, 217–232. [Google Scholar] [CrossRef]
- Wang, D.; Huang, P.; Meng, Z. Coordinated stabilization of tumbling targets using tethered space manipulators. ITAES 2015, 51, 2420–2432. [Google Scholar] [CrossRef]
- Dou, B.; Yue, X. Disturbance observer-based fractional-order sliding mode control for free-floating space manipulator with disturbance. Aerosp. Sci. Technol. 2023, 132, 108061. [Google Scholar] [CrossRef]
- Meng, D.; Xu, H.; Xu, H.; Sun, H.; Liang, B. Trajectory tracking control for a cable-driven space manipulator using time-delay estimation and nonsingular terminal sliding mode. Control Eng. Pract. 2023, 139, 105649. [Google Scholar] [CrossRef]
- Wu, H.; Hu, Q.; Shi, Y.; Zheng, J.; Sun, K.; Wang, J. Space manipulator optimal impedance control using integral reinforcement learning. Aerosp. Sci. Technol. 2023, 139, 108388. [Google Scholar] [CrossRef]
- Jayakody, H.S.; Shi, L.; Katupitiya, J.; Kinkaid, N. Robust Adaptive Coordination Controller for a Spacecraft Equipped with a Robotic Manipulator. J. Guid. Control Dyn. 2016, 39, 2699–2711. [Google Scholar] [CrossRef]
- Sallaberger, C.; Force, S.P.T.; Agency, C.S. Canadian space robotic activities. Acta Astronaut. 1997, 41, 239–246. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Gao, J.; Gan, S.; Kang, E. High performance assembly of complex structural parts in special environments–research on space manipulator assisted module docking method. Robot. Intell. Autom. 2023, 43, 122–131. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, J.; Guo, L. Adaptive Sliding Mode Disturbance Observer-Based Composite Control With Prescribed Performance of Space Manipulators for Target Capturing. ITIE 2018, 66, 1973–1983. [Google Scholar] [CrossRef]
- Rybus, T.; Seweryn, K.; Sasiadek, J.Z. Control System for Free-Floating Space Manipulator Based on Nonlinear Model Predictive Control (NMPC). JIRS 2017, 85, 491–509. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, X.; Xu, Z.; Bai, X. Novel ground microgravity experiment system for a spacecraft-manipulator system based on suspension and air-bearing. Aerosp. Sci. Technol. 2023, 141, 108587. [Google Scholar] [CrossRef]
- Kernot, J.E.; Ulrich, S. Adaptive control of a tendon-driven manipulator for capturing non-cooperative space targets. JSpRo 2022, 59, 111–128. [Google Scholar] [CrossRef]
- Ogilvie, A.; Allport, J.; Hannah, M.; Lymer, J. Autonomous Satellite Servicing Using the Orbital Express Demonstration Manipulator System. In Proceedings of the 9th International Symposium on Artificial Intelligence, Robotics Automation in Space, Los Angeles, CA, USA; 2008; pp. 25–29. [Google Scholar]
- Seddaoui, A.; Saaj, C.M. Combined Nonlinear H∞ Controller for a Controlled-Floating Space Robot. J. Guid. Control Dyn. 2019, 42, 1878–1885. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Chen, Y.; Cai, G.; Wang, X. Dynamics and control of capture of a floating rigid body by a spacecraft robotic arm. Multibody Syst. Dyn. 2015, 33, 315–332. [Google Scholar] [CrossRef]
- Ding, W.H.; Deng, H.; Li, Q.M.; Xia, Y.M. Control-orientated dynamic modeling of forging manipulators with multi-closed kinematic chains. Robot. Comput. Integr. Manuf. 2014, 30, 421–431. [Google Scholar] [CrossRef]
- Xu, X.R.; Chung, W.J.; Choi, Y.H.; Ma, X.F. A new approach for modeling and computation of dynamics of robots containing closed chains. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Victoria, BC, Canada, 17 October 1998. [Google Scholar]
- Uicker, J.J. History of Multibody Dynamics in the U.S. J. Comput. Nonlinear Dyn. 2016, 11, 060302. [Google Scholar] [CrossRef]
- Li, C. A New Lagrangian Formulation of Dynamics for Robot Manipulators. J. Dyn. Syst. Meas. Control 1989, 111, 545. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Yang, Y.; Ju, H.; Wang, K. An innovative joint-space dynamic theory for rigid multi-axis system-Part I: Fundamental principles. Appl. Math. Model. 2022, 110, 28–44. [Google Scholar] [CrossRef]
- Wang, K.; Ju, H.; Yang, Y. An innovative joint-space dynamic theory for rigid multi-axis system—Part II: Canonical dynamic equations. Appl. Math. Model. 2022, 110, 475–492. [Google Scholar] [CrossRef]
- Shao, X.; Sun, G.; Xue, C.; Li, X. Nonsingular terminal sliding mode control for free-floating space manipulator with disturbance. Acta Astronaut. 2021, 181, 396–404. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Gao, Q.; Ju, Z. Adaptive robust decoupling control of multi-arm space robots using time-delay estimation technique. Nonlinear Dyn. 2020, 100, 2449–2467. [Google Scholar] [CrossRef]
- Nguyen-Huynh, T.C.; Sharf, I. Adaptive Reactionless Motion and Parameter Identification in Postcapture of Space Debris. J. Guid. Control Dyn. 2013, 36, 404–414. [Google Scholar] [CrossRef]
- James, F.; Shah, S.V.; Singh, A.K.; Krishna, K.M.; Misra, A.K. Reactionless Maneuvering of a Space Robot in Precapture Phase. JGCD 2016, 39, 2419–2425. [Google Scholar] [CrossRef]
- Dubowsky, S.; Papadopoulos, E. The kinematics, dynamics, and control of free-flying and free-floating space robotic systems. IEEE Trans. Robot. Autom. 1993, 9, 531–543. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Dubowsky, S. On the nature of control algorithms for free-floating space manipulators. ITRA 1991, 7, 750–758. [Google Scholar] [CrossRef]
- Vafa, Z.; Dubowsky, S. The Kinematics and Dynamics of Space Manipulators: The Virtual Manipulator Approach. IJRR 1990, 9, 3–21. [Google Scholar] [CrossRef]
- Pazelli, T.F.P.A.T.; Terra, M.H.; Siqueira, A.A.G. Experimental investigation on adaptive robust controller designs applied to a free-floating space manipulator. Control Eng. Pract. 2011, 19, 395–408. [Google Scholar] [CrossRef]
- Liang, B.; Xu, Y.; Bergerman, M. Dynamically equivalent manipulator for space manipulator system. 1. In Proceedings of the Proceedings of International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997. [Google Scholar]
- Guo, Y.; Chen, L. Robust Control of Dual-Arm Space Robot Systems with Two Objects in Joint Space. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Beijing, China, 9–15 October 2006; pp. 5091–5095. [Google Scholar]
- Flores-Abad, A.; Ou, M.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. PrAeS 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Cocuzza, S.; Pretto, I.; Debei, S. Least-Squares-Based Reaction Control of Space Manipulators. J. Guid. Control Dyn. 2012, 35, 976–986. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, X.X.; Tan, Q.; Tian-Jian, H.U. Fractional-order PID control for teleoperation of a free-flying space robot. Control Theory Appl. 2016, 33, 800–808. [Google Scholar]
- Liu, J.; Vazquez, S.; Wu, L.; Marquez, A.; Gao, H.; Franquelo, L.G. Extended State Observer-Based Sliding-Mode Control for Three-Phase Power Converters. ITIE 2016, 64, 22–31. [Google Scholar] [CrossRef]
- Guanghui; Sun; Ligang; Wu; Zhian; Kuang; Zhiqiang; Ma; Jianxing, Practical tracking control of linear motor via fractional-order sliding mode. Autom 2018, 94, 221–235. [CrossRef]
- Slotine, J.; Li, W.P. Applied Nonlinear Control; China Machine Press: Beijing, China, 1991. [Google Scholar]
- Korayem, M.H.; Taherifar, M.; Tourajizadeh, H. Compensating the flexibility uncertainties of a cable suspended robot using SMC approach. Robot 2015, 33, 578–598. [Google Scholar] [CrossRef]
- Tsuda, S.; Kobayashi, T. Space Robot Control for Unknown Target Handling. In International Conference on Advances in Intelligent Control and Innovative Computing; Springer: New York, NY, USA, 2012; pp. 11–24. [Google Scholar]
- Song, Z.; Chao, D.; Wang, J.; Wu, Q. Chattering-free full-order recursive sliding mode control for finite-time attitude synchronization of rigid spacecraft. J. Frankl. Inst. 2019, 356, 998–1020. [Google Scholar] [CrossRef]
- Gui, H.; Vukovich, G. Adaptive integral sliding mode control for spacecraft attitude tracking with actuator uncertainty. J. Frankl. Inst. 2015, 352, 5832–5852. [Google Scholar] [CrossRef]
- Rybus, T.; Seweryn, K.; Sąsiadek, J.Z. Nonlinear Model Predictive Control (NMPC) for Free-Floating Space Manipulator. In Aerospace Robotics III; Sasiadek, J., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 17–29. [Google Scholar]
- Raimondo, D.M.; Limon, D.; Lazar, M.; Magni, L.; Camacho, E.F. Min-max Model Predictive Control of Nonlinear Systems: A Unifying Overview on Stability. Eur. J. Control 2009, 15, 5–21. [Google Scholar] [CrossRef]
- Rahideh, A.; Shaheed, M.H. Stable model predictive control for a nonlinear system. J. Frankl. Inst. 2011, 348, 1983–2004. [Google Scholar] [CrossRef]
- Shi, L.; Kayastha, S.; Katupitiya, J. Robust coordinated control of a dual-arm space robot. Acta Astronaut. 2017, 138, 475–489. [Google Scholar] [CrossRef]
- Featherstone, R. Rigid Body Dynamics Algorithms; Springer US: New York, NY, USA, 2008. [Google Scholar]
- Xiao, P.; Ju, H.; Li, Q.; Meng, J.; Chen, F. A New Fixed Axis-Invariant Based Calibration Approach to Improve Absolute Positioning Accuracy of Manipulators. IEEE Access 2020, 8, 134224–134232. [Google Scholar] [CrossRef]
- Ju, H. Axis-Invariant Based Multi-Axis Robot System Forward Kinematics Modeling and Solving Method. US16541147, 20 February 2020. [Google Scholar]
- Ju, H. Axis-Invariant Based Multi-Axis Robot Inverse Kinematics Modeling and Solving Method. US16541149, 20 February 2020. [Google Scholar]
- Hollerbach, J.M. A Recursive Lagrangian Formulation of Maniputator Dynamics and a Comparative Study of Dynamics Formulation Complexity. IEEE Trans. Syst. Man Cybern. 1980, 10, 730–736. [Google Scholar] [CrossRef]
- Merabet, A.; Gu, J. Robust nonlinear predictive control based on state estimation for robot manipulator. Int. J. Appl. Math Mech. 2008, 5, 48–49. [Google Scholar]
- Rojas-Moreno, A.; Valdivia-Mallqui, R. Embedded position control system of a manipulator using a robust nonlinear predictive control. In Proceedings of the International Conference on Advanced Robotics, Montevideo, Uruguay, 25–29 November 2013; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).