Application of Artificial Neural Networks to Numerical Homogenization of the Precast Hollow-Core Concrete Slabs
Abstract
1. Introduction
2. Methods and Materials
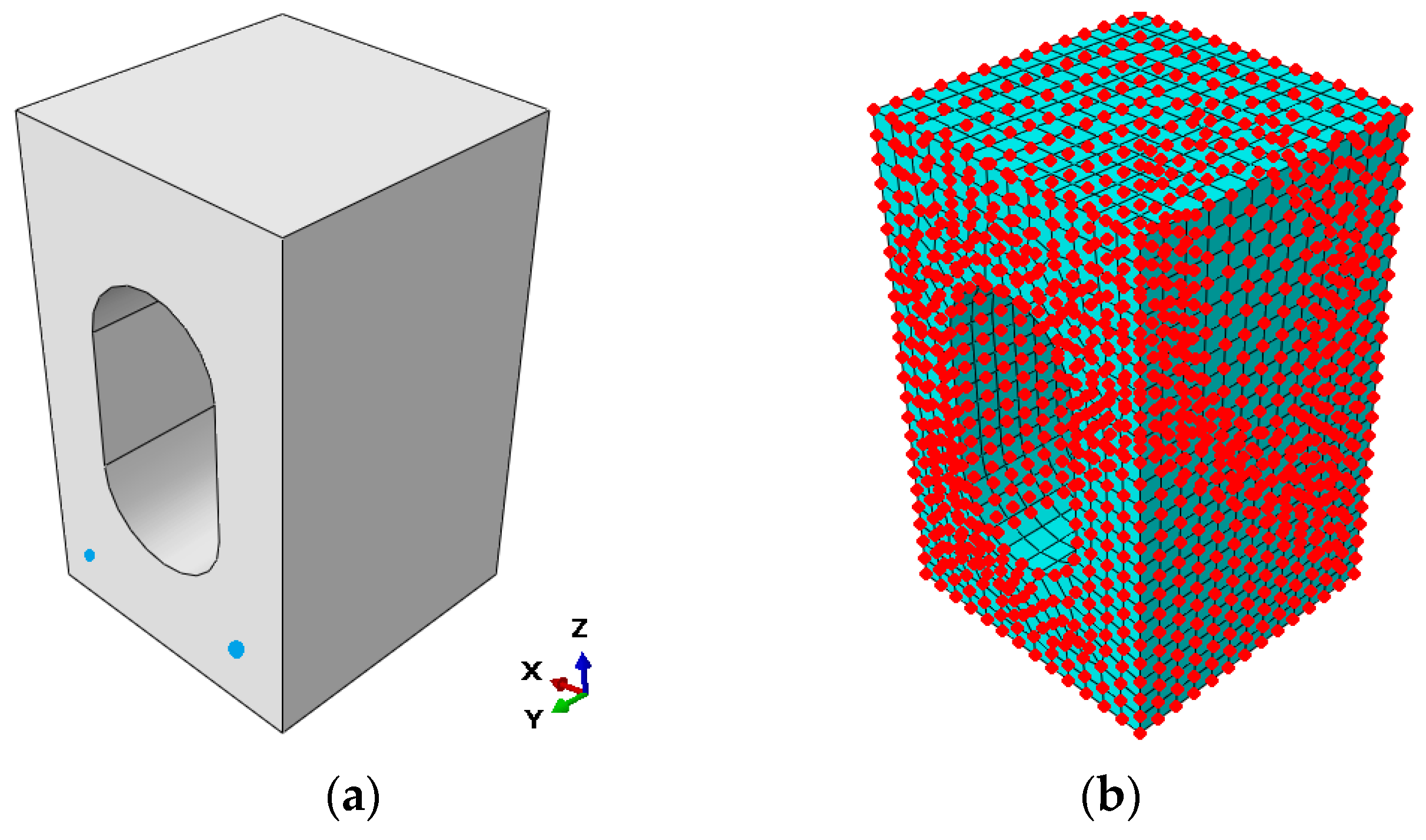
2.1. Representative Volume Element and Structure Parametrization
2.2. Latin Hypercube Sampling
2.3. Numerical Homogenization of Precast Reinforced Concrete Slab
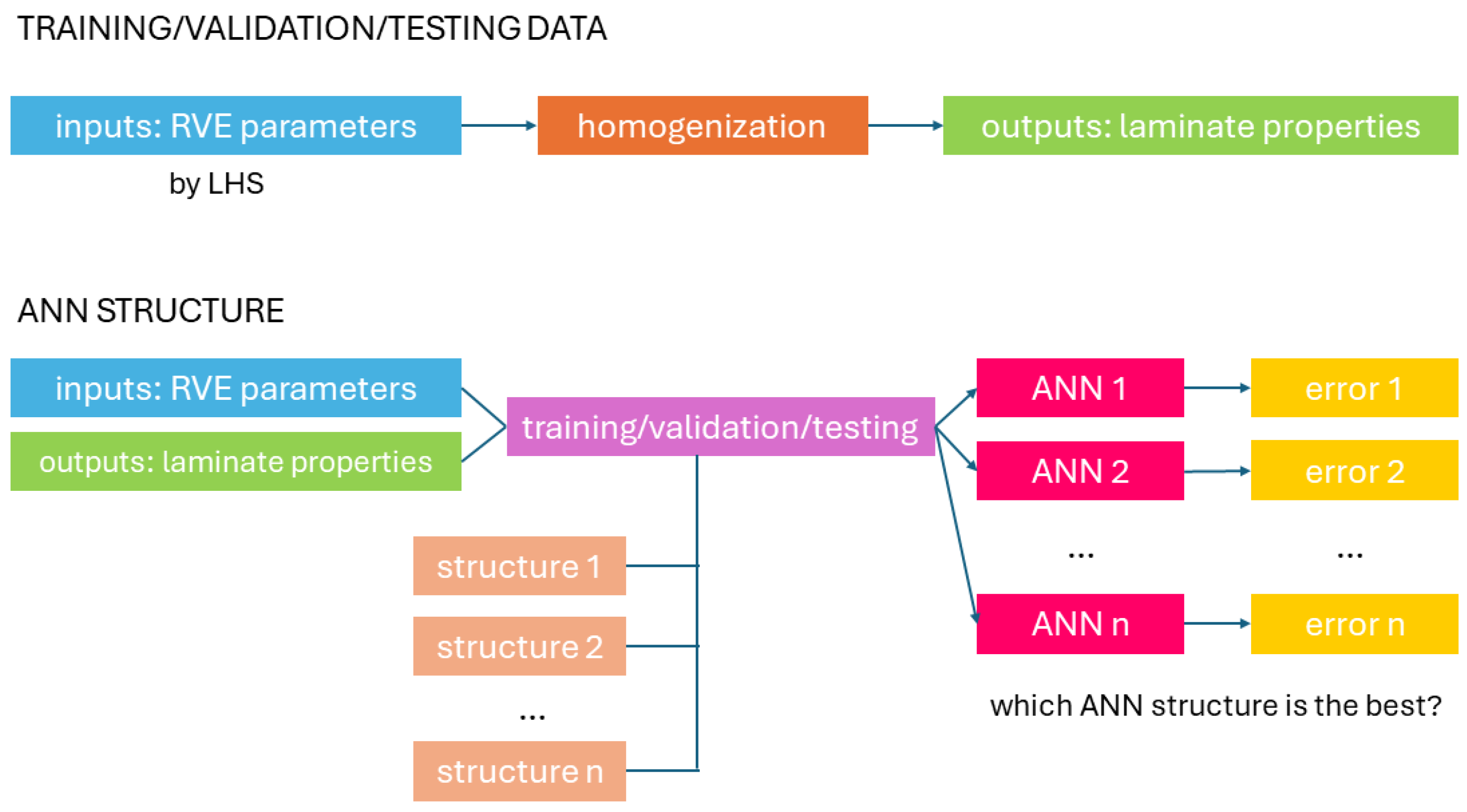
2.4. Artificial Neural Network
| Algorithm 1. The pseudo code of the Adam algorithm. |
| 1: (stepsize) 2: (exponential decay rates for the moment estimates) 3: (stochastic objective function with parameters ) 4: (initial parameter vector) 5: 6: (initialize moment vector) 7: (initialize moment vector) 8: (initialize timestep) 9: 10: not converged : 11: 12: 13: 14: 15: 16: 17: 18: 19: |
2.5. Error Measures
3. Results
3.1. Verification of the Implementation of the Homogenization Algorithm
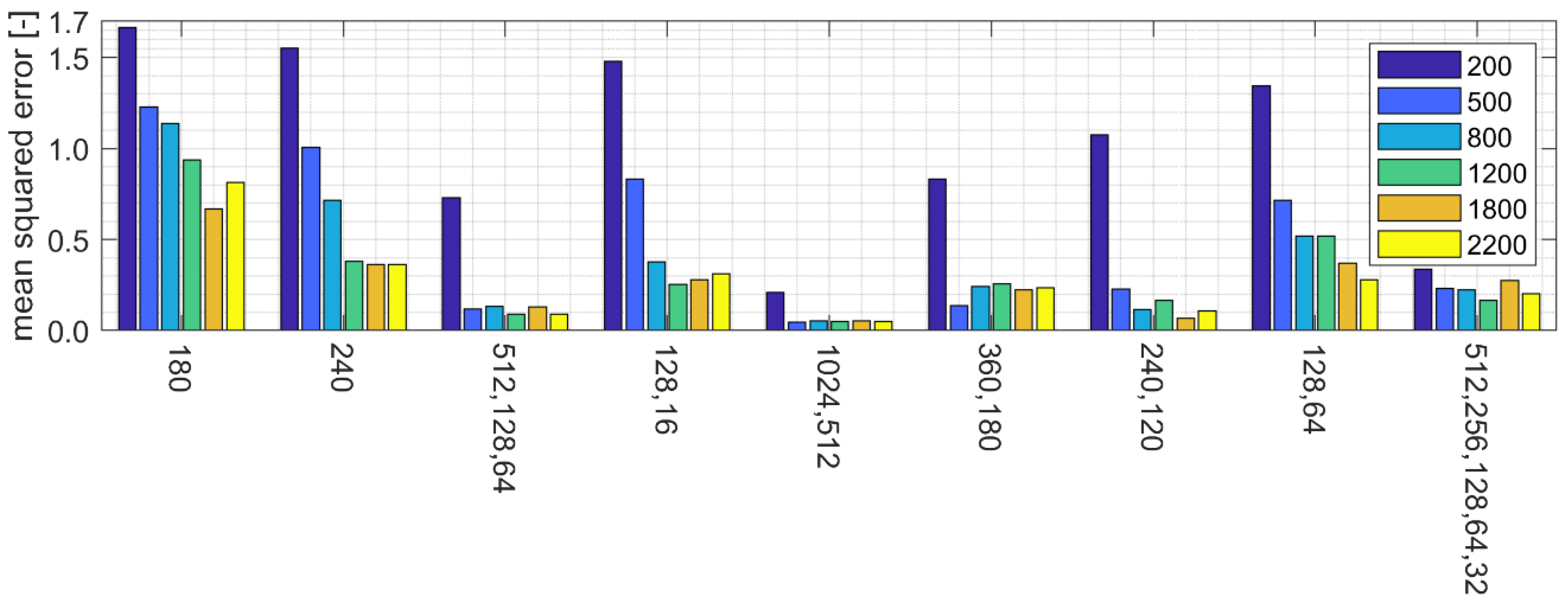
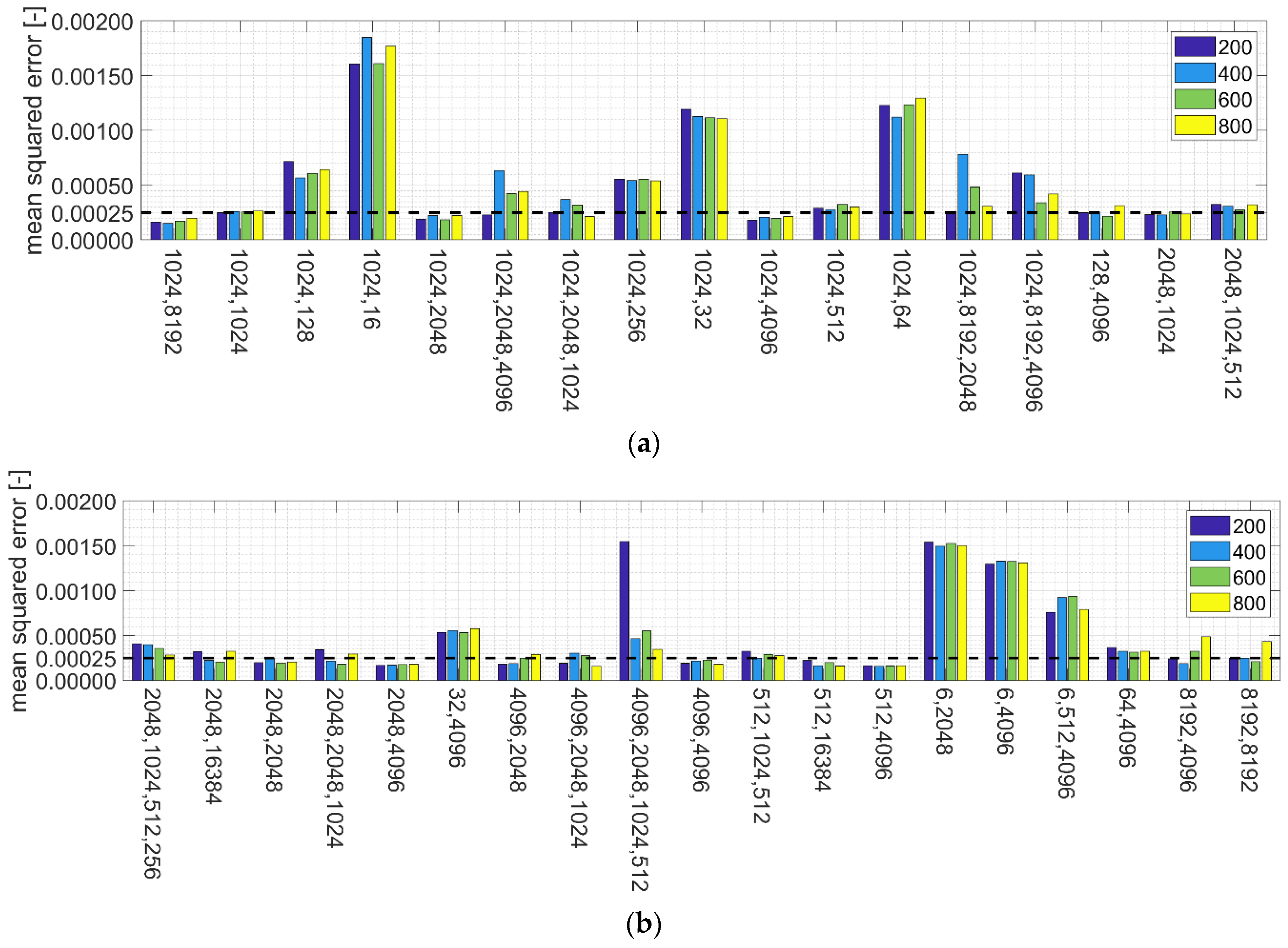
3.2. Selection of Parameter Values of the Artificial Neural Network Due to Approximation Error
3.3. Achieved Accuracy of the Artificial Neural Network
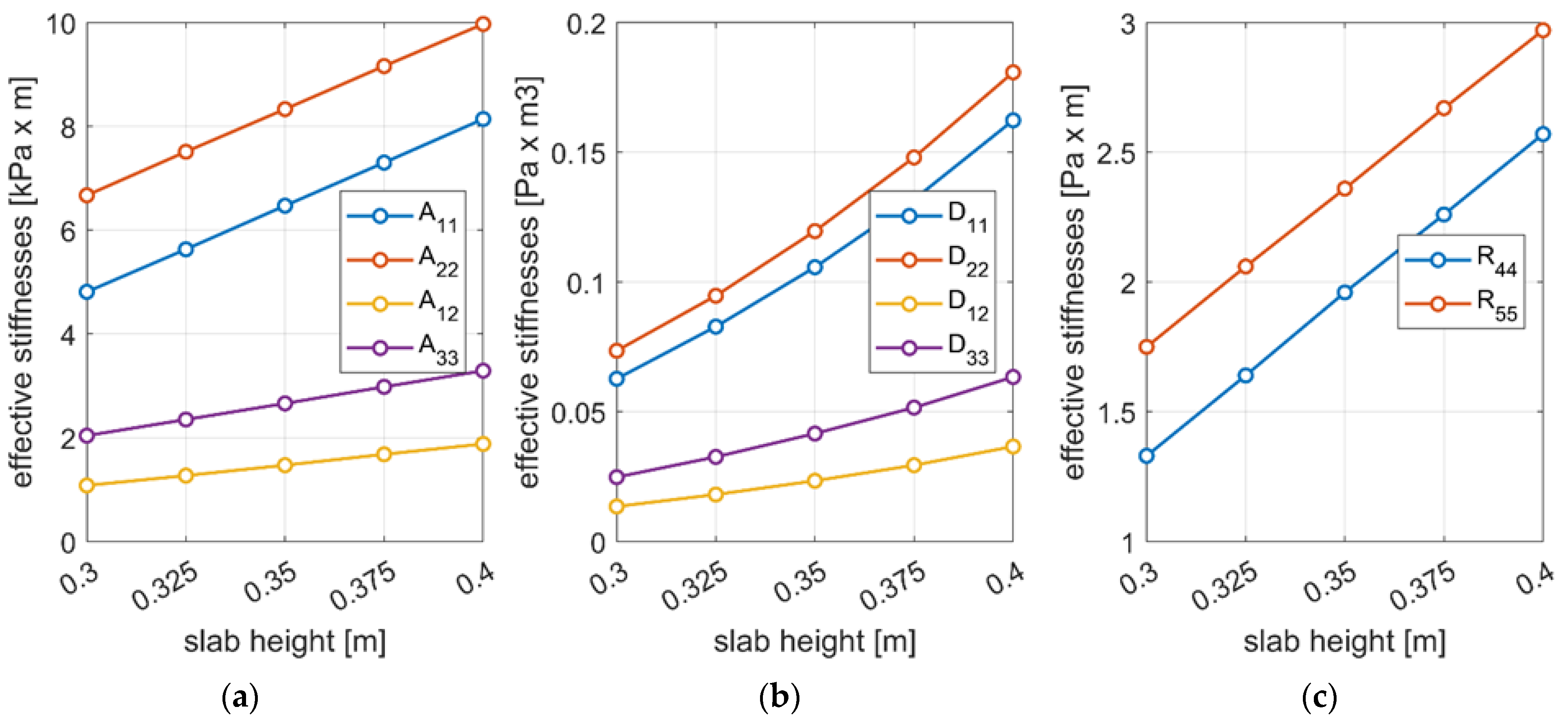
3.4. Influence of Changing Parameters of Prefabricated Concrete Slabs on the Effective Stiffnesses
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Derkowski, W.; Surma, M. Prestressed hollow core slabs for topped slim floors—Theory and research of the shear capacity. Eng. Struct. 2021, 241, 112464. [Google Scholar] [CrossRef]
- Jankowiak, T.; Łodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Hafezolghorani Esfahani, M.; Hejazi, F.; Vaghei, R.; Jaafar, M.; Karimzadeh, K. Simplified Damage Plasticity Model for Concrete. Struct. Eng. Int. 2017, 27, 68–78. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Chrysanidis, T.A.; Panoskaltsis, V.P. Experimental investigation on cracking behavior of reinforced concrete tension ties. Case Stud. Constr. Mater. 2022, 16, e00810. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Predicting the likelihood and extent of reinforced concrete corrosion-induced cracking. J. Struct. Eng. 2005, 131, 1681–1689. [Google Scholar] [CrossRef]
- Arab, A.A.; Badie, S.S.; Manzari, M.T. A methodological approach for finite element modeling of pretensioned concrete members at the release of pretensioning. Eng. Struct. 2011, 33, 1918–1929. [Google Scholar] [CrossRef]
- Staszak, N.; Garbowski, T.; Ksit, B. Application of the generalized nonlinear constitutive law in numerical analysis of hollow-core slabs. Arch. Civ. Eng. 2022, 68, 125–145. [Google Scholar] [CrossRef]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Comp. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T. Determination of transverse shear stiffness of sandwich panels with a corrugated core by numerical homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef]
- Kalita, K.; Haldar, S.; Chakraborty, S. A Comprehensive Review on High-Fidelity and Metamodel-Based Optimization of Composite Laminates. Arch. Comput. Methods Eng. 2022, 29, 3305–3340. [Google Scholar] [CrossRef]
- Staszak, N.; Szymczak-Graczyk, A.; Garbowski, T. Elastic Analysis of Three-Layer Concrete Slab Based on Numerical Homogenization with an Analytical Shear Correction Factor. Appl. Sci. 2022, 12, 9918. [Google Scholar] [CrossRef]
- Staszak, N.; Garbowski, T.; Szymczak-Graczyk, A. Solid Truss to Shell Numerical Homogenization of Prefabricated Composite Slabs. Materials 2021, 14, 4120. [Google Scholar] [CrossRef]
- Archaviboonyobul, T.; Chaveesuk, R.; Singh, J.; Jinkarn, T. An analysis of the influence of hand hole and ventilation hole design on compressive strength of corrugated fiberboard boxes by an artificial neural network model. Packag. Technol. Sci. 2020, 33, 171–181. [Google Scholar] [CrossRef]
- Adamopoulos, S.; Anthony, K.; Rapti, E.; Birbilis, D. Predicting the properties of corrugated base papers using multiple linear regression and artificial neural networks. Drewno 2016, 59, 61–72. [Google Scholar] [CrossRef]
- Gajewski, T.; Grabski, J.K.; Cornaggia, A.; Garbowski, T. On the use of artificial intelligence in predicting the compressive strength of various cardboard packaging. Packag. Technol. Sci. 2023, 37, 97–105. [Google Scholar] [CrossRef]
- Stręk, A.M.; Dudzik, M.; Kwiecień, A.; Wańczyk, K.; Lipowska, B. Verification of application of ANN modelling in study of compressive behaviour of aluminium sponges. Eng. Trans. 2019, 67, 271–288. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Piątkowska, A.; Grabski, J.K. Estimation of the Edge Crush Resistance of Corrugated Board Using Artificial Intelligence. Materials 2023, 16, 1631. [Google Scholar] [CrossRef]
- Gajewski, T.; Staszak, N.; Garbowski, T. Parametric optimization of thin-walled 3D beams with perforation based on homogenization and soft computing. Materials 2022, 15, 2520. [Google Scholar] [CrossRef]
- Adamski, M.; Czechlowski, M.; Durczak, K.; Garbowski, T. Determination of the Concentration of Propionic Acid in an Aqueous Solution by POD-GP Model and Spectroscopy. Energies 2021, 14, 8288. [Google Scholar] [CrossRef]
- Araujo, G.; Andrade, F.A.A. Post-Processing Air Temperature Weather Forecast Using Artificial Neural Networks with Measurements from Meteorological Stations. Appl. Sci. 2022, 12, 7131. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Gajewski, T.; Garbowski, T. Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023, 16, 412. [Google Scholar] [CrossRef]
- Konbet. Dokumentacja Techniczna Sprężone Płyty Kanałowe SPK 15, SPK 20, SPK 26.5, SPK 32, SPK 40, SPK 50. Brochure. Available online: https://www.konbet.com.pl/pliki/Plyty-stropowe-kanalowe-strunobetonowe-SPK_dokumentacja-techniczna.pdf (accessed on 15 February 2023).
- Pekabex. Hollow Core Slab 265. Datasheet. Available online: https://pekabex.pl/wp-content/files/HC265.pdf (accessed on 15 February 2023).
- Dassault Systèmes. Abaqus Documentation. 2019. Available online: https://abaqusdocs.mit.edu/ (accessed on 15 February 2024).
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 42, 55–61. [Google Scholar] [CrossRef]
- Python Library pyDOE2 1.3.0. 2021. Available online: https://pypi.org/project/pyDOE2/ (accessed on 15 June 2021).
- Mindlin, R.D. Influence of Rotatory Inertia and Shear De-formation on Flexural Motion of Isotropic, Elastic Plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Reissner, E. The Effect of Transverse Shear Deformation on the Bending of Elastic Plates. ASME J. Appl. Mech. 1945, 12, 69–77. [Google Scholar] [CrossRef]
- Python Library Scikit-Learn 1.2.1. 2021. Available online: https://scikit-learn.org/stable/ (accessed on 15 June 2021).
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Rogalka, M.; Grabski, J.K.; Garbowski, T. A Comparison of Two Artificial Intelligence Approaches for Corrugated Board Type Classification. Eng. Proc. 2023, 56, 272. [Google Scholar] [CrossRef]
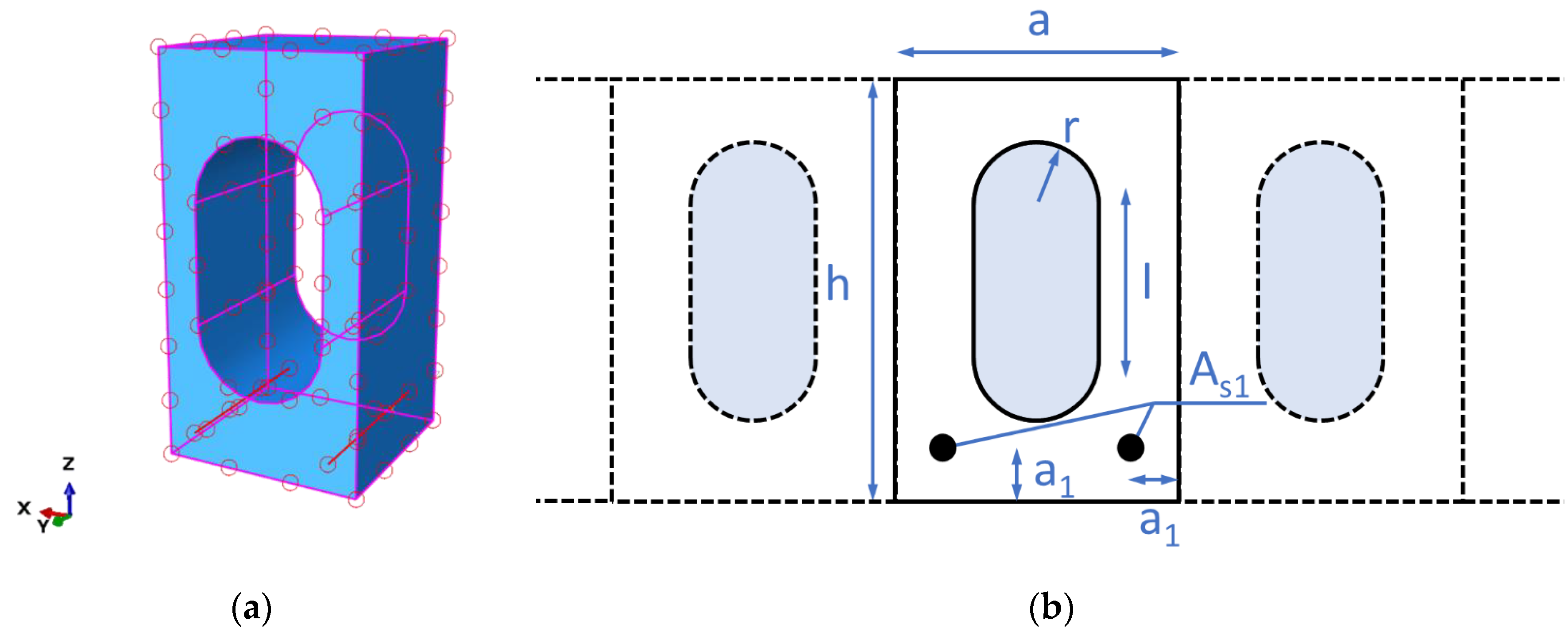
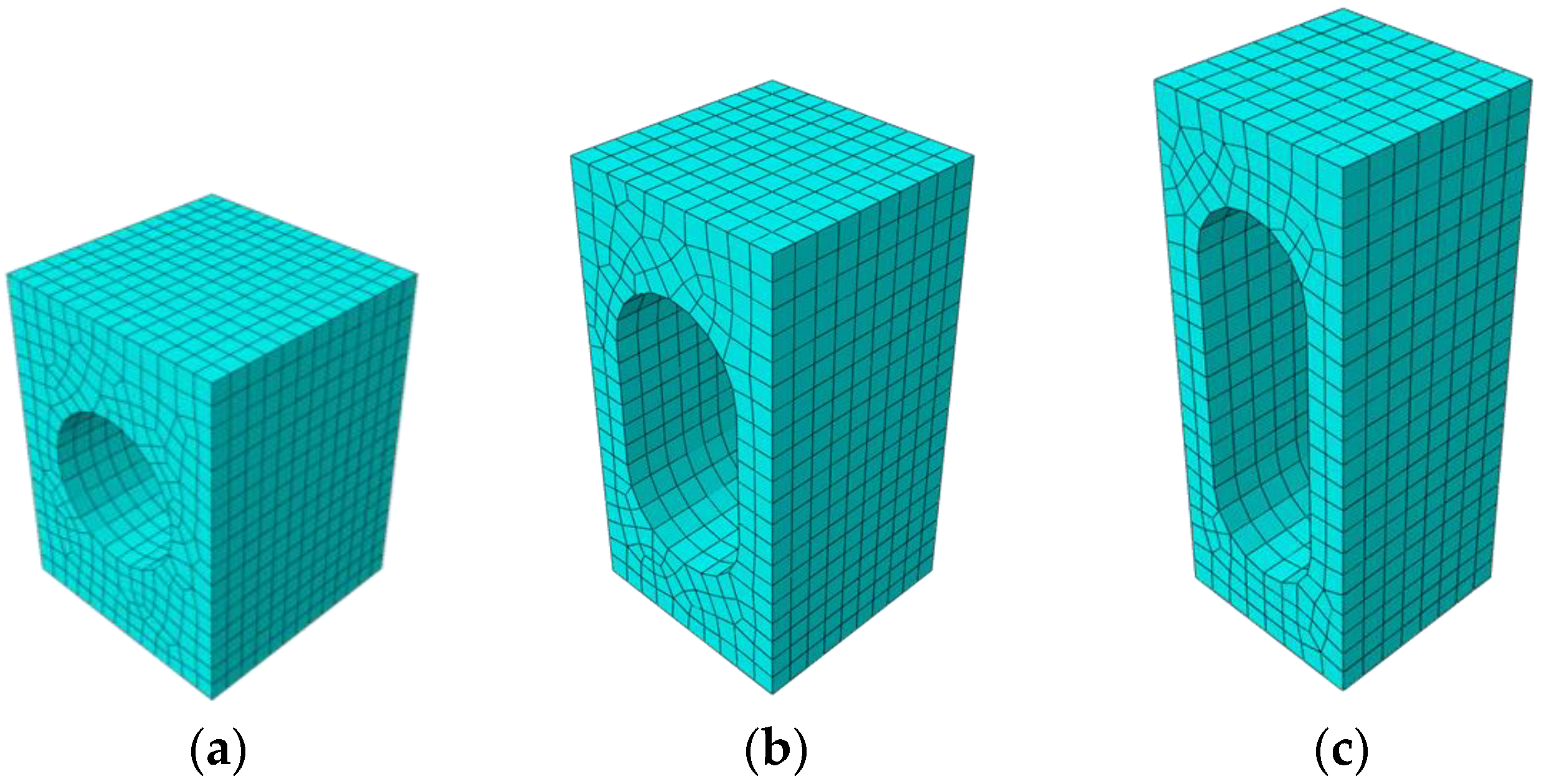
| Parameter | Symbol | Lower Boundary | Upper Boundary |
|---|---|---|---|
| Slab height | [cm] | 15.0 | 50.0 |
| Width of periodic part | [cm] | 10.0 | 18.0 |
| Position of the steel reinforcement | [cm] | 2.0 | 3.0 |
| Hole radius | [cm] | 3.0 | 6.0 |
| Cross-sectional area of steel reinforcement | [cm2] | 0.0 | 6.44 |
| Vertical dimension of the hole | [cm] | 0.0 | 20.0 |
| Effective Stiffness | Implementation of homogenization [10] | Published in [10] | Error |
|---|---|---|---|
| 2139.7 | 2140.0 | 0.01% | |
| 1664.5 | 1665.0 | 0.03% | |
| 382.9 | 382.9 | 0.00% * | |
| 662.5 | 662.5 | 0.00% * | |
| 6.392 | 6.392 | 0.00% * | |
| 3.859 | 3.859 | 0.00% * | |
| 1.115 | 1.115 | 0.00% * | |
| 1.656 | 1.656 | 0.00% * | |
| 202.4 | 202.4 | 0.00% * | |
| 99.0 | 99.0 | 0.00% * |
| Example | [cm] | [cm] | [cm] | [cm] | [cm2] | [cm] |
|---|---|---|---|---|---|---|
| 1 | 45.338 | 17.958 | 2.654 | 4.427 | 5.024 | 6.205 |
| 2 | 41.454 | 17.497 | 2.763 | 4.304 | 2.804 | 0.707 |
| 3 | 49.704 | 15.191 | 2.657 | 3.811 | 4.233 | 17.965 |
| 4 | 34.155 | 17.209 | 2.167 | 4.550 | 1.800 | 12.737 |
| 5 | 43.766 | 17.278 | 2.747 | 5.624 | 3.490 | 9.842 |
| 6 | 42.823 | 17.736 | 2.273 | 5.964 | 3.034 | 4.266 |
| Effective Stiffness | ANN Homogenization | Homogenization [10] | Error |
|---|---|---|---|
| 109.0 | 109.1 | 0.09% | |
| 130.1 | 132.0 | 1.44% | |
| 25.53 | 25.52 | 0.04% | |
| 44.68 | 44.61 | 0.16% | |
| 0.2419 | 0.2441 | 0.9% | |
| 0.2613 | 0.2697 | 3.11% | |
| 0.0543 | 0.0545 | 0.37% | |
| 0.0949 | 0.0952 | 0.32% | |
| 36.15 | 36.2 | 0.14% | |
| 41.08 | 40.86 | 0.54% |
| Effective Stiffness | ANN Homogenization | Homogenization [10] | Error |
|---|---|---|---|
| 113.7 | 113.8 | 0.09% | |
| 126.8 | 126.4 | 0.32% | |
| 26.72 | 26.74 | 0.07% | |
| 45.29 | 45.3 | 0.02% | |
| 0.1867 | 0.1896 | 1.53% | |
| 0.2011 | 0.2007 | 0.2% | |
| 0.0419 | 0.0422 | 0.71% | |
| 0.0734 | 0.0738 | 0.54% | |
| 37.34 | 37.41 | 0.19% | |
| 39.57 | 39.76 | 0.48% |
| Effective Stiffness | ANN Homogenization | Homogenization [10] | Error |
|---|---|---|---|
| 90.64 | 90.33 | 0.34% | |
| 125.8 | 127.6 | 1.41% | |
| 21.23 | 21.1 | 0.62% | |
| 39.05 | 39.1 | 0.13% | |
| 0.2946 | 0.2967 | 0.71% | |
| 0.3296 | 0.3396 | 2.94% | |
| 0.0667 | 0.067 | 0.45% | |
| 0.1164 | 0.1173 | 0.77% | |
| 31.09 | 30.88 | 0.68% | |
| 40.50 | 40.64 | 0.34% |
| Effective Stiffness | ANN Homogenization | Homogenization [10] | Error |
|---|---|---|---|
| 50.32 | 50.08 | 0.48% | |
| 79.67 | 77.78 | 2.43% | |
| 11.3 | 11.25 | 0.44% | |
| 23.26 | 23.19 | 0.3% | |
| 0.0831 | 0.0859 | 3.26% | |
| 0.1001 | 0.0992 | 0.91% | |
| 0.0182 | 0.0186 | 2.15% | |
| 0.035 | 0.0352 | 0.57% | |
| 14.63 | 14.58 | 0.34% | |
| 22.54 | 22.68 | 0.62% |
| Effective Stiffness | ANN Homogenization | Homogenization [10] | Error |
|---|---|---|---|
| 82.52 | 82.4 | 0.15% | |
| 106.0 | 106.1 | 0.09% | |
| 18.9 | 18.89 | 0.05% | |
| 34.36 | 34.2 | 0.47% | |
| 0.2069 | 0.206 | 0.44% | |
| 0.2274 | 0.2275 | 0.04% | |
| 0.0461 | 0.0456 | 1.1% | |
| 0.0817 | 0.0812 | 0.62% | |
| 25.55 | 25.42 | 0.51% | |
| 31.31 | 31.36 | 0.16% |
| Effective Stiffness | ANN Homogenization | Homogenization [10] | Error |
|---|---|---|---|
| 94.79 | 94.91 | 0.13% | |
| 112.5 | 112.5 | 0.0% * | |
| 21.88 | 21.86 | 0.09% | |
| 38.43 | 38.43 | 0.0% * | |
| 0.1997 | 0.2025 | 1.38% | |
| 0.2162 | 0.2179 | 0.78% | |
| 0.0447 | 0.0449 | 0.45% | |
| 0.0786 | 0.0792 | 0.76% | |
| 29.69 | 29.65 | 0.13% | |
| 33.55 | 33.54 | 0.03% |
| Effective Stiffnesses | h [m] | ||||
|---|---|---|---|---|---|
| 0.300 | 0.325 | 0.350 | 0.375 | 0.400 | |
| 4.81 | 5.63 | 6.47 | 7.30 | 8.14 | |
| 6.67 | 7.51 | 8.33 | 9.16 | 9.97 | |
| 1.08 | 1.27 | 1.47 | 1.68 | 1.88 | |
| 2.04 | 2.35 | 2.66 | 2.98 | 3.29 | |
| 0.0627 | 0.0828 | 0.1057 | 0.1318 | 0.1623 | |
| 0.0735 | 0.0947 | 0.1196 | 0.1480 | 0.1808 | |
| 0.0135 | 0.0181 | 0.0234 | 0.0294 | 0.0366 | |
| 0.0248 | 0.0326 | 0.0416 | 0.0516 | 0.0634 | |
| 1.33 | 1.64 | 1.96 | 2.26 | 2.57 | |
| 1.75 | 2.06 | 2.36 | 2.67 | 2.97 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajewski, T.; Skiba, P. Application of Artificial Neural Networks to Numerical Homogenization of the Precast Hollow-Core Concrete Slabs. Appl. Sci. 2024, 14, 3018. https://doi.org/10.3390/app14073018
Gajewski T, Skiba P. Application of Artificial Neural Networks to Numerical Homogenization of the Precast Hollow-Core Concrete Slabs. Applied Sciences. 2024; 14(7):3018. https://doi.org/10.3390/app14073018
Chicago/Turabian StyleGajewski, Tomasz, and Paweł Skiba. 2024. "Application of Artificial Neural Networks to Numerical Homogenization of the Precast Hollow-Core Concrete Slabs" Applied Sciences 14, no. 7: 3018. https://doi.org/10.3390/app14073018
APA StyleGajewski, T., & Skiba, P. (2024). Application of Artificial Neural Networks to Numerical Homogenization of the Precast Hollow-Core Concrete Slabs. Applied Sciences, 14(7), 3018. https://doi.org/10.3390/app14073018







