Strength Reduction Method for the Assessment of Existing Large Reinforced Concrete Structures
Abstract
1. Introduction
2. Why Strength Reduction for Large RC Structures?
2.1. FE and ANFE in the Field of Large RC Structures
2.2. Strength Reduction
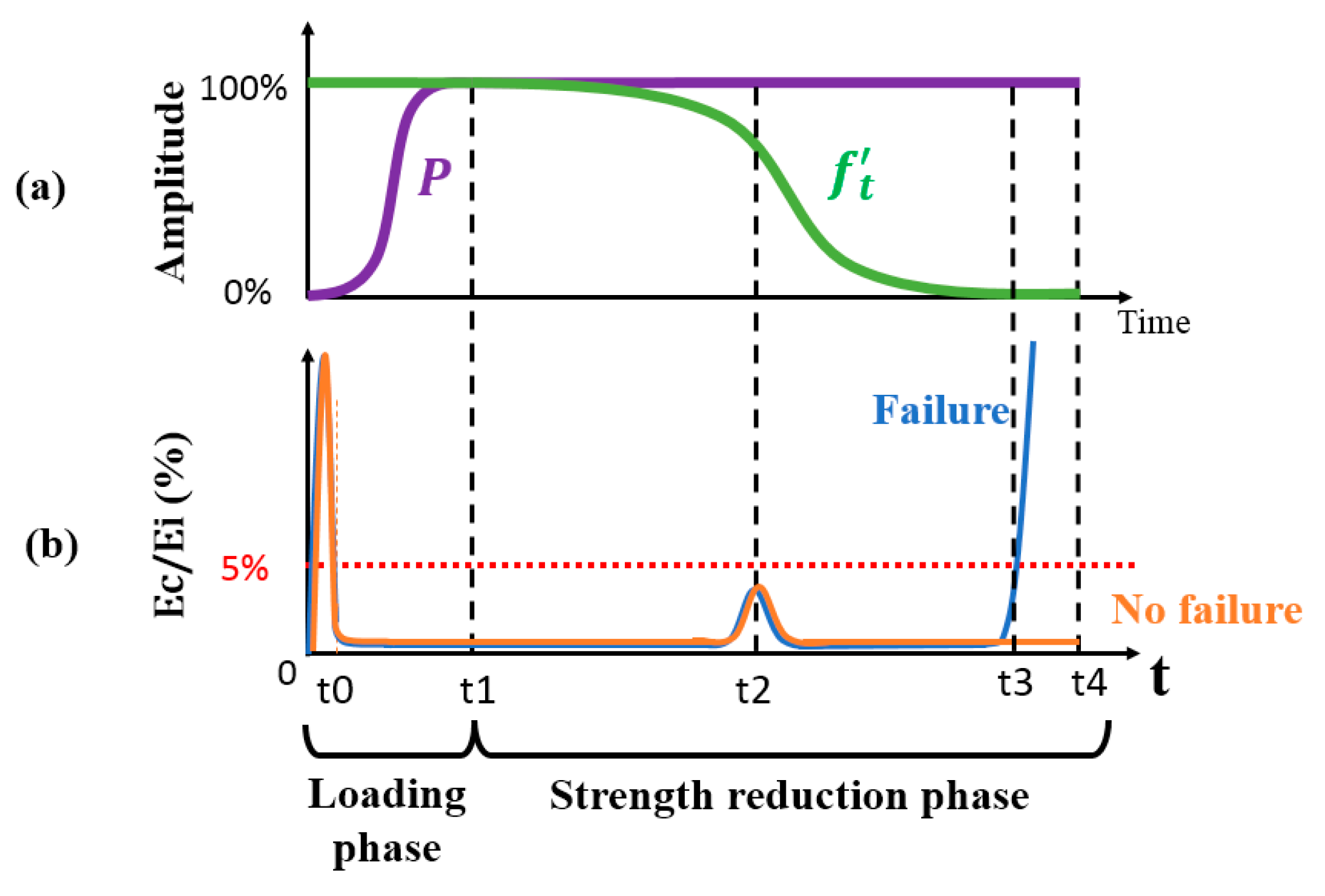
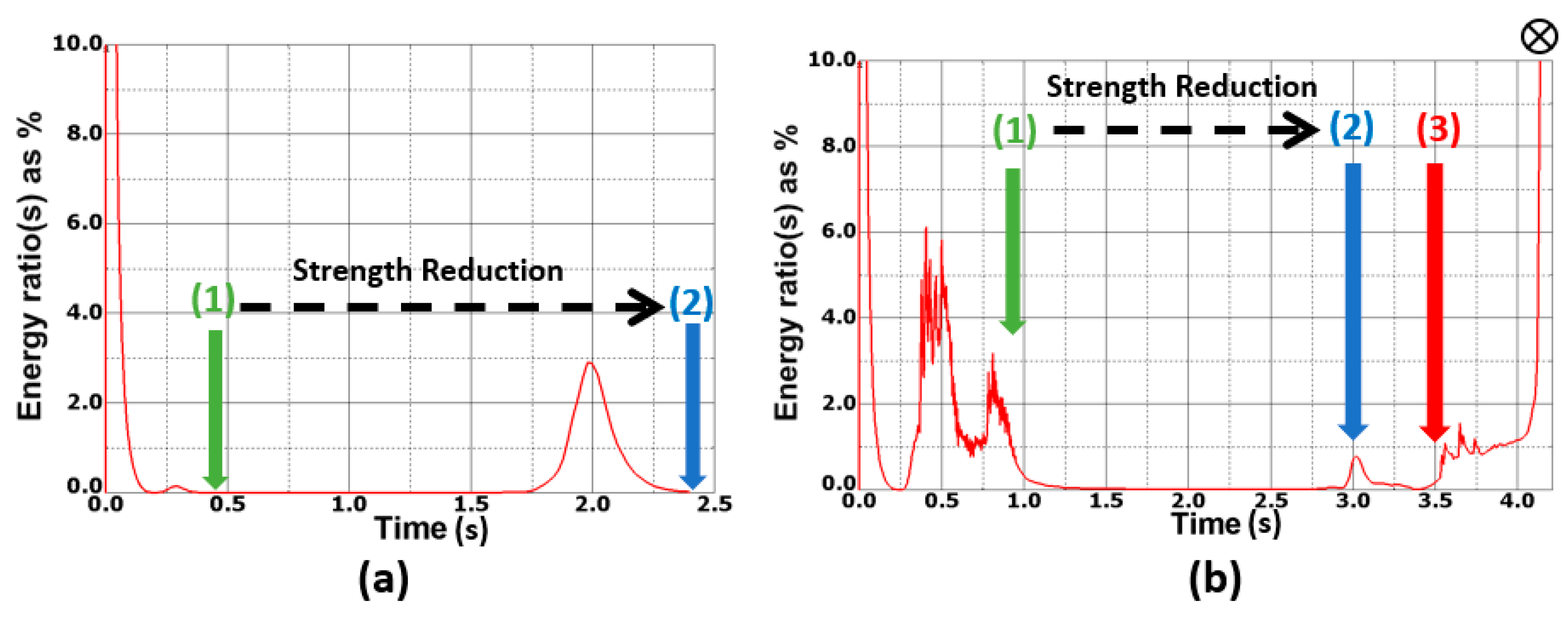
3. Strength Reduction Assessment Methodology
3.1. The Reloading Phase
3.2. Service Load Condition
3.3. Reliability Framework
- -
- m is the moment order (e.g., m = 1 for the mean value). To compute the variance of R, Equation (6) is used twice to compute and . Subsequently, the variance is determined using the equation: ;
- -
- is the resistance evaluated at a given sampling point i, N is the number of random input variables, and is the discrete mass probability. In case of uncorrelated input variables: .
4. Validations
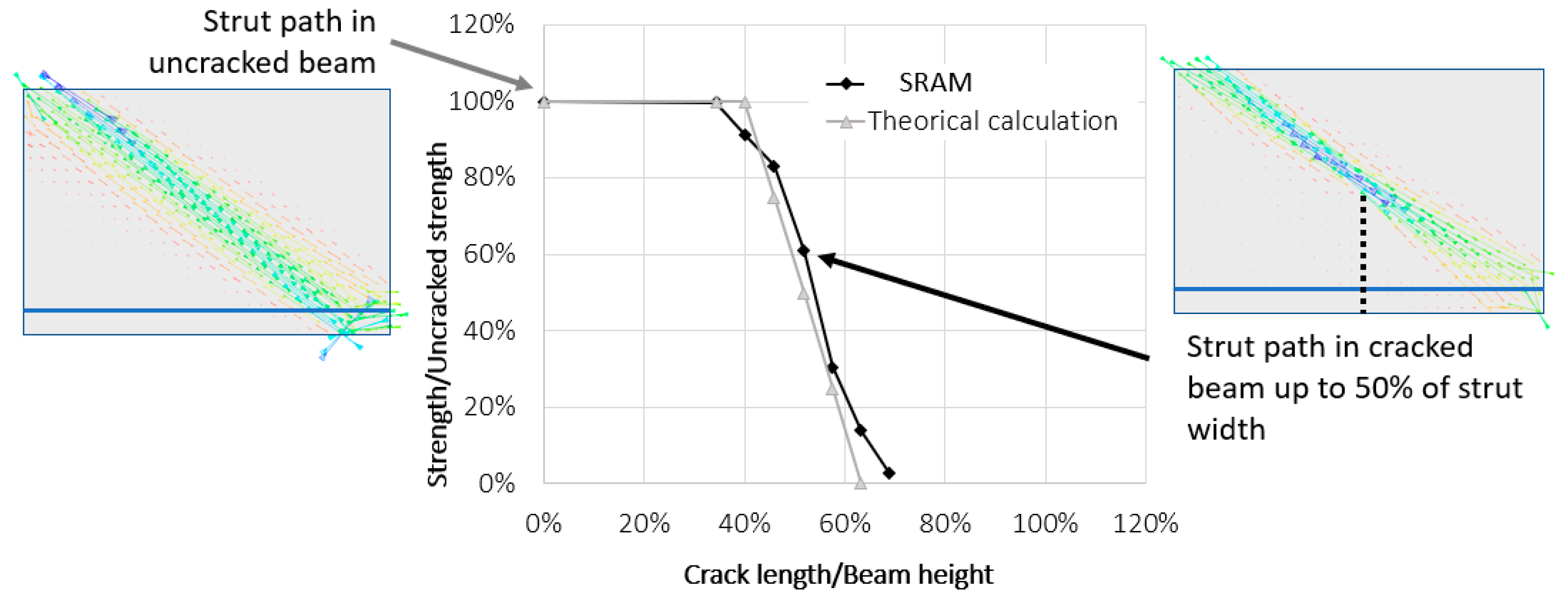
4.1. Example 1: RC Beam with Pre-Existing Crack
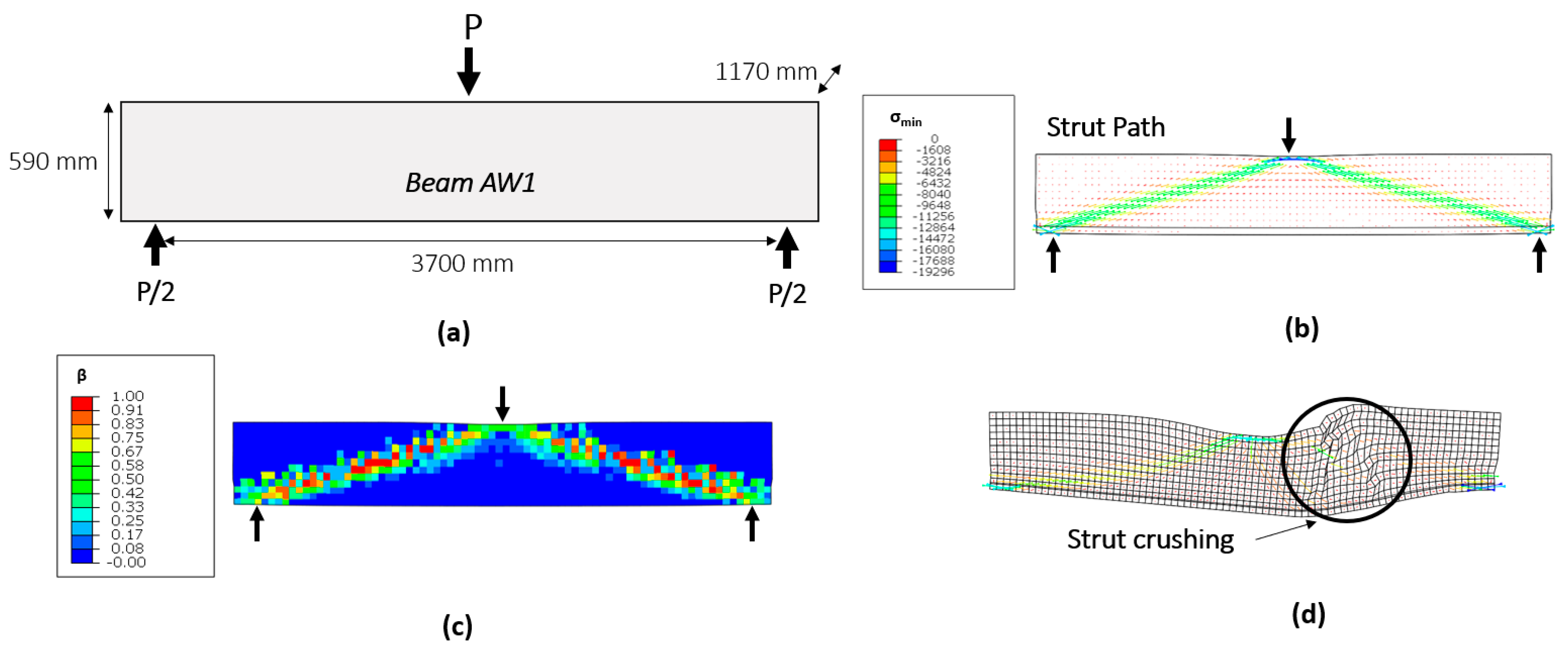
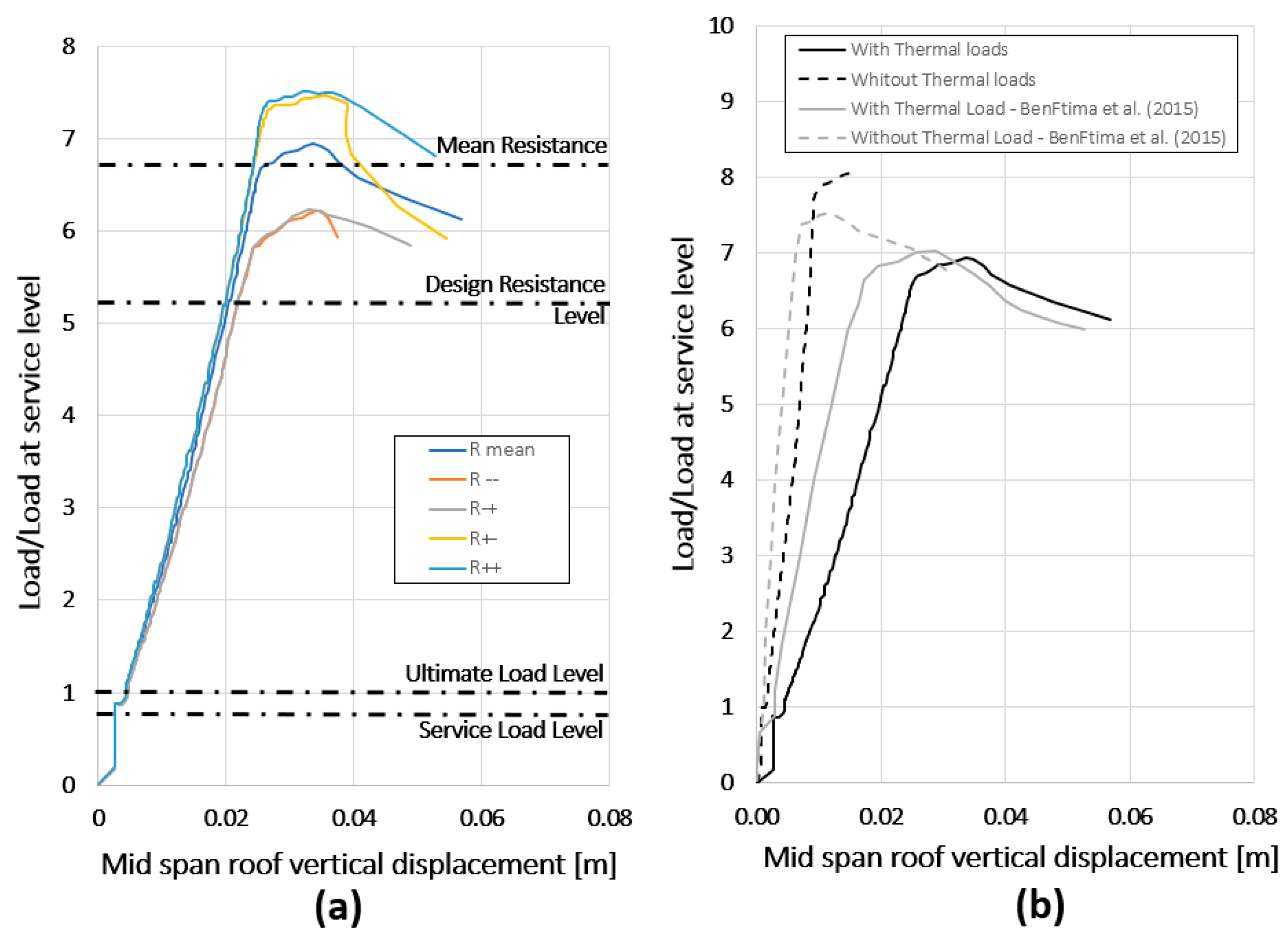
4.2. Example 2: RC Beam Falling in Shear (AW1 from [26])
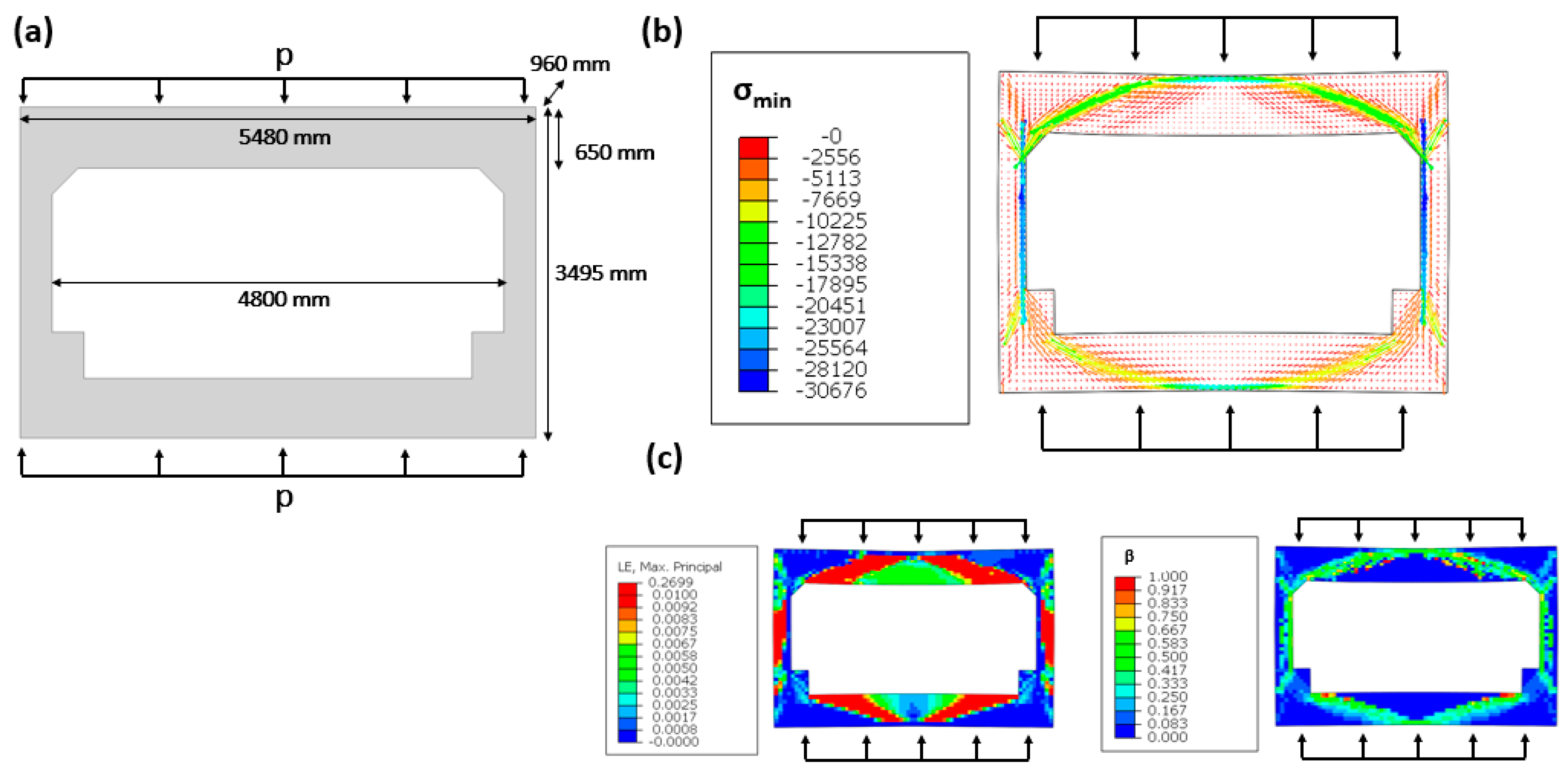
4.3. Example 3: RC Tunnel Section (from [27])
5. Applications
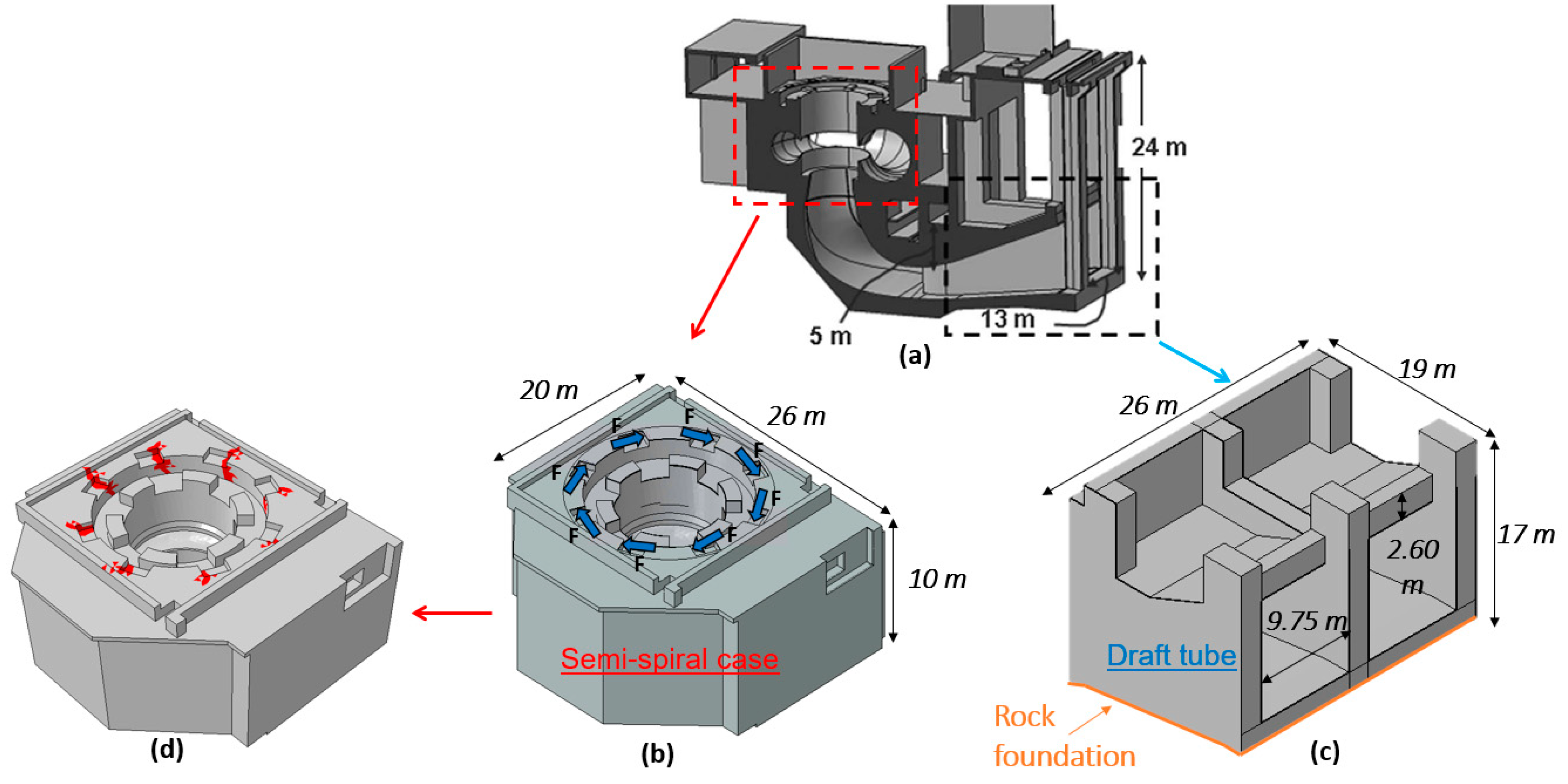
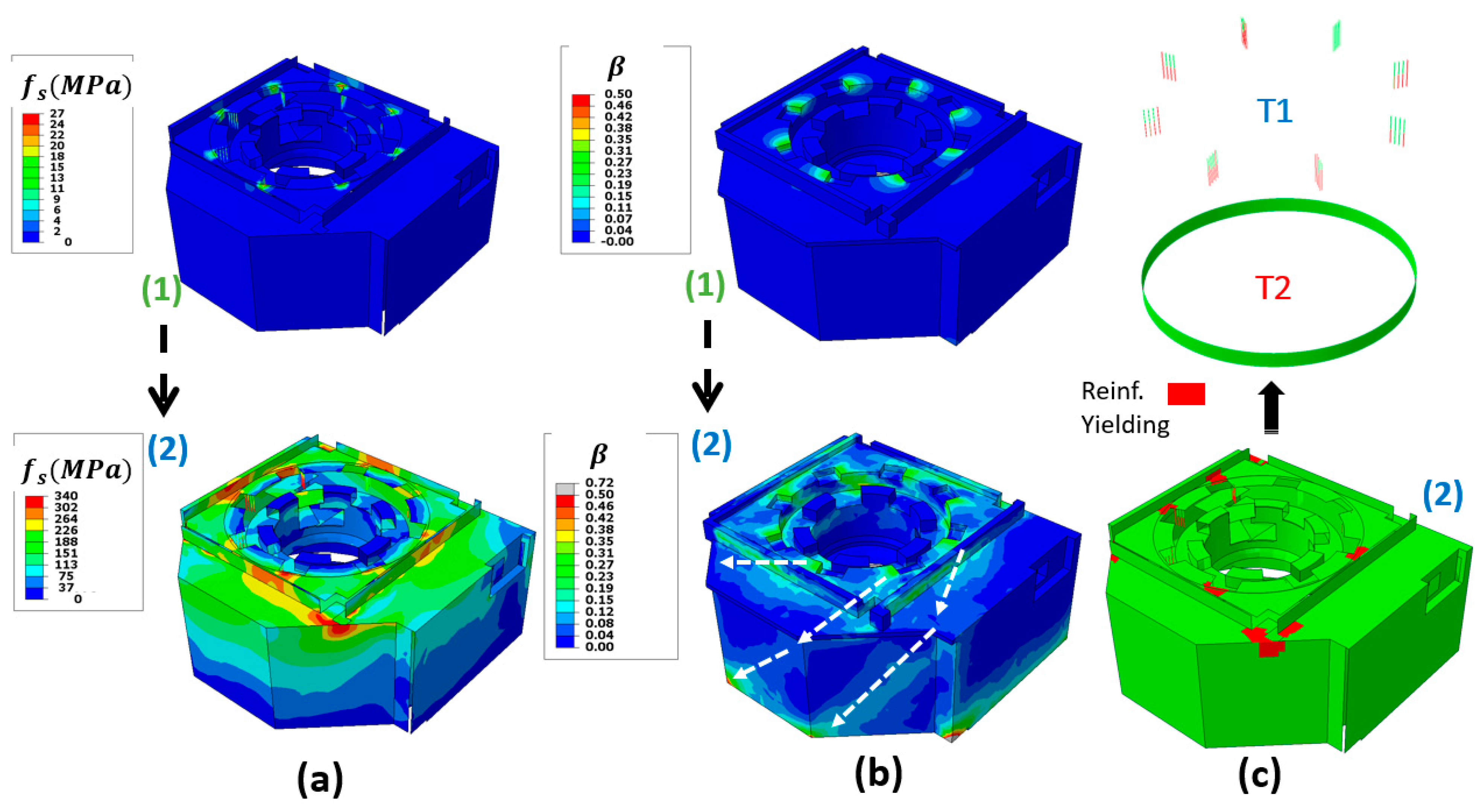
5.1. Application 1: Spiral Case
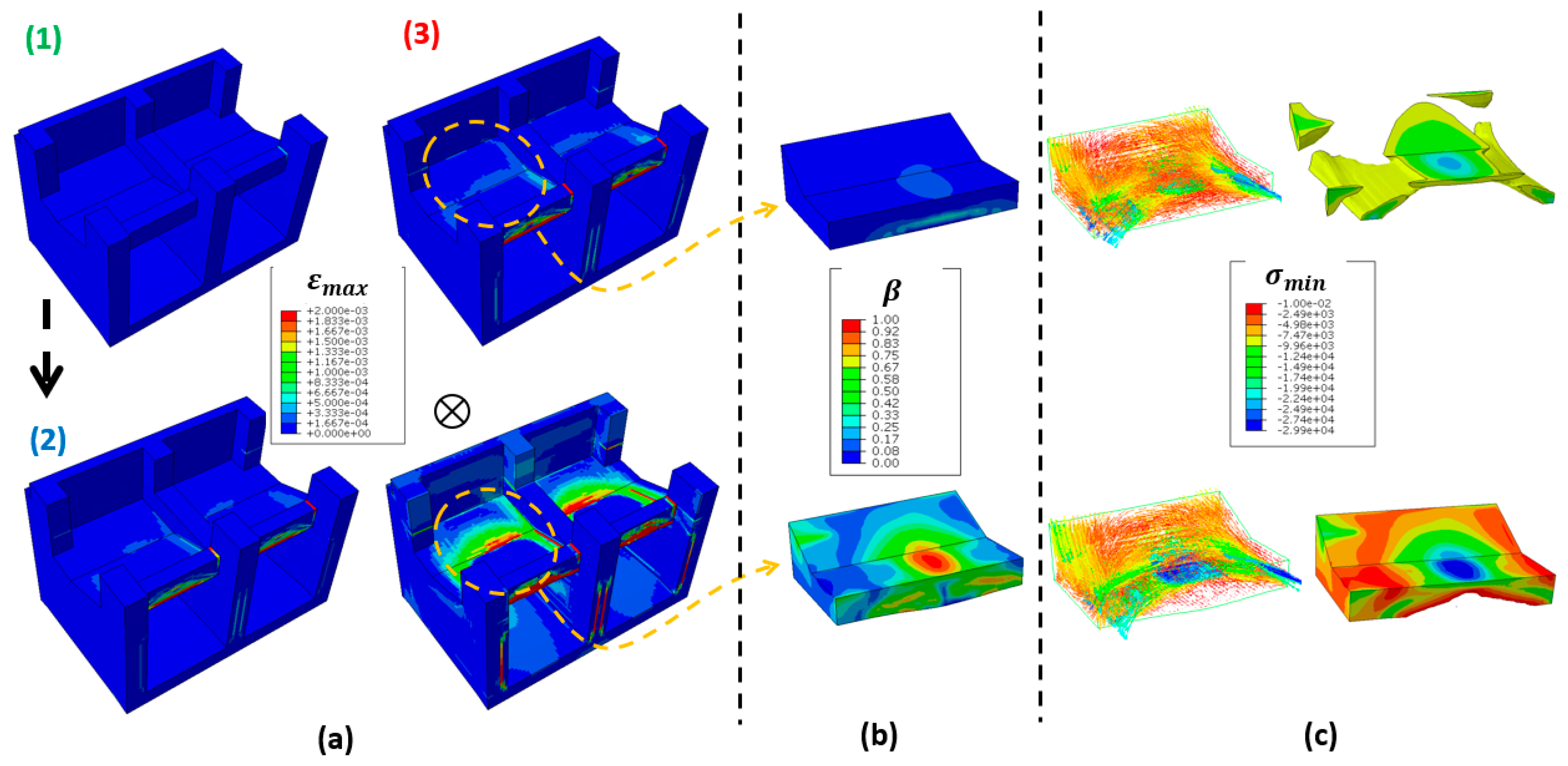
5.2. Application 2: Draft Tube
6. Conclusions
- -
- Compared to sophisticated non-linear finite element analysis, the method is simpler, more robust and allows to compute conservative value of structural resistance, excluding any contribution in tension from concrete;
- -
- The methodology is well-suited for the assessment of existing large RC structures, particularly complex 3D hydraulic structures.
- -
- The methodology can be used to assess disturbed 3D regions, with important advantages over conventional Strut & Tie model: possibility to include loads other than mechanical loads and to consider the structural effects of pre-existing cracks.
- -
- While the focus of this paper is on large RC structures, SRAM's applicability extends to various types of RC structures and can be seamlessly integrated into future design and assessment codes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Couland, R. Concrete Planet: The Strange and Fascinating Story of the World's Most Common Man-Made Material; Prometheus Books; Rowman & Littlefield: Lanham, MD, USA, 2011; 396p. [Google Scholar]
- FIB Task Group 4.4. Practitioners’ Guide to Finite Element Modelling of Reinforced Concrete Structures, State-of-the-Art Report- Bulletin 45; FIB: Lausanne, Switzerland, 2008; pp. 1–337. [Google Scholar]
- Ftima, B.M.; Massicotte, B. Utilization of nonlinear finite elements for the design and assessment of large concrete structures: Part I: Calibration and validation, part II: Applications. ASCE J. Struct. Eng. 2015, 141, 04014218. [Google Scholar] [CrossRef]
- Antoniou, M.; Mantakas, A.; Nikitas, N.; Fuentes, R. A numerical case study on the long-term seismic assessment of reinforced concrete tunnels in corrosive environments. J. Rock Mech. Geotech. Eng. 2023, 15, 551–572. [Google Scholar] [CrossRef]
- Wang, G.; Shu, Y.; Lu, W.; Chen, M.; Pan, X.; Lu, A. Damage prediction of concrete gravity dams subjected to penetration explosion. Eng. Fail. Anal. 2023, 143, 106855. [Google Scholar] [CrossRef]
- Fu, Q.L.; Tan, L.; Long, B.; Kang, S.B. Numerical investigations of progressive collapse behaviour of multi-storey reinforced concrete frames. Buildings 2023, 13, 533. [Google Scholar] [CrossRef]
- Chauhan, A.; Desai, M.D.; Banerjee, S.; Sharma, U.K. 3D simulation of non-uniform corrosion induced damage in reinforced concrete exposed to real climate. Structures 2023, 56, 104852. [Google Scholar] [CrossRef]
- Thacker, B.H.; Doebling, S.W.; Hemez, F.M.; Anderson, M.C.; Pepin, J.E.; Rodriguez, E.A. Concepts of Model Verification and Validation; Report LA-14167-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 2004. [Google Scholar]
- Schlaich, J.; Schafer, K.; Jennewein, M. Toward a consistent design of structural concrete. J. Prestress. Concr. Inst. 1987, 32, 74–150. [Google Scholar] [CrossRef]
- Muttoni, A.; Schwartz, J.; Thürlimann, B. Design of Concrete Structures with Stress Fields; Birkhaüser Verlag: Basel, Switzerland, 1997. [Google Scholar]
- Bentz, D.P. A Review of Early-Age Properties of Cement-Based Materials. Cem. Concr. Res. 2008, 38, 196–204. [Google Scholar] [CrossRef]
- Pimentel, M.; Bruhwiler, E.; Figueiras, J. Safety examination of existing concrete structures using the global resistance safety factor concept. Eng. Struct. 2014, 70, 130–143. [Google Scholar] [CrossRef]
- Ben Ftima, M.; Massicotte, B. Development of a reliability framework for the use of advanced nonlinear finite elements in the design of concrete structures. ASCE J. Struct. Eng. 2012, 138, 1054–1064. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Figueiras, J.A. Automatic design of reinforcement in concrete plates and shells. Eng. Comput. 1993, 10, 519–541. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and non-associated visco- plasticity and plasticity in soil mechanics. Geotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Abra, O.; Ftima, M.B. Development of a new design approach of reinforced concrete structures based on strength reduction method. Eng. Struct. 2020, 207, 110192. [Google Scholar] [CrossRef]
- Abra, O.; Ftima, M.B. Strength reduction design method for reinforced concrete structures: Generalization. Eng. Struct. 2022, 258, 114134. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. Modified compression field theory for reinforced concrete elements subjected to shear. ACI J. 1986, 83, 219–231. [Google Scholar]
- CSA A23.3; Design of Concrete Structures. Canadian Standards Association: Toronto, ON, Canada, 2016.
- Hibbitt, H.D.; Karlson, B.I.; Sorensen, E.P. ABAQUS, version 6.14; Finite Element Program; Hibbitt, Karlson and Sorensen: Providence, RI, USA, 2014. [Google Scholar]
- ACI Committee. ACI231 R-10 Report. In Report on Early-Age Cracking: Causes, Measurement, and Mitigation; ACI Committee: Farmington Hills, MI, USA, 2010; Volume 231. [Google Scholar]
- Ellingwood, B.R.; Galambos, T.V.; MacGregor, J.G.; Cornell, C.A. Development of a Probability-Based Load Criterion for American National Standard A58, National Bureau of Standards; Department of Commerce: Washington, DC, USA, 1980. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Prediction, 2nd ed.; John Wiley & Sons: Chichester, England, 2001. [Google Scholar]
- Červenka, V. Global Safety Format for Nonlinear Calculation of Reinforced Concrete. In Beton- und Stahlbetonbau 103, Special ed.; Ernst & Sohn: Berlin, Germany, 2008; pp. 37–42. [Google Scholar]
- Rosenblueth, E. Point estimates for probability moments. Proc. Nat. Acad. Sci. USA 1975, 72, 3812–3814. [Google Scholar] [CrossRef]
- Lubell, A.S. Shear in Wide Reinforced Concrete Members. Ph.D. Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2006. [Google Scholar]
- Kuzmanovic, S. An Investigation of the Shear Design of a Reinforced Concrete Box Structure. Master’s Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 1998. [Google Scholar]





| Material Property | Value | |
|---|---|---|
| Compressive strength of concrete | 30 MPa | |
| Tensile strength of concrete | 2.9 MPa | |
| Young modulus of concrete | Ec | 26,600 MPa |
| Poisson coefficient of concrete | v | 0.18 |
| Reinforcement ratio | ρ | 0.011 |
| Reinforcement yield stress | fy | 400 MPa |
| Reinforcement Young modulus | Es | 200,000 MPa |
| Input Data | Exp Result | SRAM | ANFE [3] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Example | f′c (MPa) | fy (MPa) | COV (f′c) | COV (fy) | Vexp (kN) | Rm = Vu (kN) | VANFE (kN) | ||||||
| Beam AW1 | 37 | 465 | 0.2 | 0.09 | 585 | 424 | 460 | 460 | 353 | 353 | 0.13 | 535 | 0.10 |
| Tunnel Box | 45 | 490 | 0.2 | 0.09 | 805 | 722 | 798 | 714 | 663 | 691 | 0.07 | 885 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abra, O.; Ben Ftima, M. Strength Reduction Method for the Assessment of Existing Large Reinforced Concrete Structures. Appl. Sci. 2024, 14, 1614. https://doi.org/10.3390/app14041614
Abra O, Ben Ftima M. Strength Reduction Method for the Assessment of Existing Large Reinforced Concrete Structures. Applied Sciences. 2024; 14(4):1614. https://doi.org/10.3390/app14041614
Chicago/Turabian StyleAbra, Oumaima, and Mahdi Ben Ftima. 2024. "Strength Reduction Method for the Assessment of Existing Large Reinforced Concrete Structures" Applied Sciences 14, no. 4: 1614. https://doi.org/10.3390/app14041614
APA StyleAbra, O., & Ben Ftima, M. (2024). Strength Reduction Method for the Assessment of Existing Large Reinforced Concrete Structures. Applied Sciences, 14(4), 1614. https://doi.org/10.3390/app14041614






