Abstract
The free-flowing traffic environment of the freeway is an important application scenario for automatic driving. In this scenario, the freeway’s geometric design is an important factor because no other vehicle affects the driving process of the target vehicle. The freeway’s combined curves have more safety problems, but there are no quantitative guidelines for their geometric design. They present more challenges for automatic driving or driver assistance functions. If the relationship between human-drivers’ micro-behavior and the geometric design of combined curves is examined, it could provide theoretical support for the enhancement of automated driving and driver assistance functions as well as the quantitative design of combined curves. The paper analyzed the speed change and lane departure behaviors of combined curves, considering downslope curves, upslope curves, sag curves, and crest curves. The relationship between micro-driving behaviors and combined curves’ geometric design were determined using random forest models. The SHAP values of each variable were calculated. The results showed that (1) on a downslope curve and sag curve the speed change behavior should be paid more attention; on an upslope curve and crest curve, the lane departure behavior should be paid more attention; (2) the priority of geometric design parameters for four types of combined curves were different. Based on the results, drivers and autonomous vehicles can pay different levels of attention to their speed change and departure behavior on different combination curves, and take targeted improvement measures in time according to the driving status of the vehicles. Road designers can also prioritize more important road design parameters in the design process to avoid serious accidents caused by excessive speed changes and departures.
1. Introduction
Autonomous vehicles (AVs) and advanced driver assistance systems (ADASs) have the potential to decrease the likelihood of accidents. Lidar and camera technology, among others, are currently used by AVs and ADASs to detect roadway geometry designs and the surrounding environment. The free-flowing traffic environment of the freeway is a crucial application scenario for both AVs and ADASs. In this scenario, the geometric design of the roadway plays a key role in ensuring driver safety and comfort, especially considering the absence of surrounding vehicles.
For example, when driving around a curve, human drivers tend to feel uncomfortable if the AV or ADAS regulates the level of speed beyond what they would expect. Additionally, if the AVs are too close to the lane boundary in a curve, the human driver would experience discomfort. These problems arise from the insufficient analysis of drivers’ micro-driving behavior and habits. Understanding how roads’ geometric design impacts on drivers’ behavior is essential for enhancing human-like automated driving from the perspectives of safety and comfort. And, it can provide a basis for improving the control strategies of AVs and optimizing ADASs [1,2].
Particularly for combined curves (combining the horizontal and vertical curves), previous research indicates that there is a greater risk of accidents on combined curves compared to single horizontal and vertical curves [3,4]. When approaching combined curves, drivers tend to be more cautious and alert. They control the vehicle’s speed and trajectory in a more complex way and adjust the driving process more frequently. AVs and ADASs will help drivers reduce driving risks in combined curves. Improving these systems requires a thorough understanding of human drivers’ micro-driving behavior and habits in combined curves, as well as comprehension of how the geometric design of combined curves affects human micro-driving behavior.
Micro-driving behavior is typically quantified through indicators such as vehicle speed, trajectory, acceleration, and deceleration, which can reveal the driver’s cognitive and perceptive abilities, as well as their capacity to navigate the road safely. Ensuring both lateral and longitudinal safety is crucial when driving. In this study, both the lateral micro-driving behavior and the longitudinal micro-driving behavior in the combined curve are focused on.
Drivers’ speed change is a crucial metric for evaluating the feasibility of a proposed design because it is a key predictor of both operational efficiency and safety [5,6]. When the geometric design calls for speed variations beyond safe limits, drivers may engage in unsafe maneuvers. Given the relatively high speeds on highways, such maneuvers may result in severe accidents. Some studies, however, have neglected the increase in speed [5,7], which poses a more significant danger than driving at slower speeds. Consequently, this study places significant emphasis on analyzing substantial speed increases.
Lane departure, which occurs when a vehicle moves out of its current lane is a critical surrogate measure for evaluating road safety. On divided roadways, lane departure can cause rear-end and side-swipe collisions, while on undivided roadways, it can result in head-on crashes. Lane departure is the primary cause of single-vehicle crashes [8]. The Louisiana Department of Transportation and Development’s accident database shows a total of 83,843 accidents on Louisiana’s R2L highways from 2008 to 2017. These accidents were mainly caused by lane departure, which accounts for about 65%. The Louisiana Strategic Highway Safety Plan (SHSP) has identified lane departure as one of the five key areas to address [9]. In China, approximately 42% of traffic crashes over the past 15 years have been linked to lane departure [10]. Nonetheless, the correlation between lane departure behavior and combined curve geometric design remains uncertain.
Previous studies have investigated the relationship between combined curve design and micro-driving behavior. Kazemzadehazad et al. used micro-driving behavior as a measure of driver performance on combined curves and optimized the safety conditions of existing road curves by implementing warning signs [11]. Wang et al. analyzed the geometric design parameters that affect speed variations on four types of combined curves [12]. However, there were two problems: (1) Different types of combined curves have not been compared in terms of micro-driving behavior. (2) The priority of geometric design parameters for different types of combined curves has not been determined, i.e., when conducting road designs, road designers prioritize the sequence in which design parameters are met when terrain or economic conditions are constrained.
This study addresses these concerns by replicating a mountainous freeway in Hunan province on a driving simulator and collecting continuous micro-driving behavior data. The study will analyze the speed and lane departure behaviors of four types of combined curves, including downslope, upslope, crest, and sag curves. A comparison will be made to assess the coefficient of variation of these behaviors. To determine the relationship between micro-driving behaviors and combined curve geometric design, random forest (RF) models will be employed. SHAP values for each geometric design parameter will be calculated to determine the priority of geometric design parameters for different types of combined curves.
2. Literature Review
The previous research has examined the impact of combined curves in geometric design on vehicle safety and operation. This section will critically evaluate and integrate the previous related studies.
2.1. Geometric Design and Safety
Haghighi and NIMA [13] investigated the impact of different geometric design parameters of rural two-lane highways on the severity of traffic accidents. They suggested utilizing a multi-level model which successfully identified the indirect effects of geometric design characteristics on collision severity. The model also analyzed the hierarchy of collision data. The results of the analysis indicated significant variations in the severity of cross-sectional collisions. Joseph et al. [14] quantified the effects of geometric design characteristics on frontal curve collisions and developed a model to assess the safety performance of multiple horizontal curves on two-lane non-urban roads. The findings of the study provide crucial insights into enhancing road safety measures.
Fu et al. [15] examined the fundamental correlation between geometric design parameters and lateral safety incidents. They employed the one-way ANOVA method and maximum lane departure as an analysis variable to determine the statistical outcomes of the maximum lane departure for novice and experienced drivers in various geometric design parameter curve sections. The study indicated a positive correlation between the maximum lane departure and the spatial curvature mutation when it exceeds a certain critical value. The direction of curves with sudden deflection plays a significant role in lane departure accidents. Experienced drivers have demonstrated lower maximum lane departure than novice drivers.
2.2. Combined Curves’ Geometric Design and Micro-Driving Behaviors
Bella [7] compared the speed difference between a crest curve and non-combined curve and found that the speed difference of the non-combined curve was lower than that of the crest curve. Bella [16] used an interactive driving simulator, and the simulation results were used to evaluate the impact of concave combined and non-combined curves with different configurations on the driver’s speed behavior. The study found that these curves have the same characteristics as the horizontal curves of concave combination. Among geometric design characteristics, how complex alignment and its adjacent sections affect deceleration and acceleration was the most important.
Wang et al. [17] classified combined curves into four types: upslope curves, downslope curves, sag curves, and crest curves. They used multiple linear regression models to estimate the impact of combined curves on lateral acceleration. They found that the inverse of the horizontal curve radius and slope severity affect all types of lateral stability, whereas length only impacts crest curves. Wang et al. [12] examined speed changes on four combined curves: downslope, upslope, sag curves, and crest curves. The study found that the frequency of speed change behavior varied with the four combined curves. Additionally, the study revealed that different types of combined curves were impacted differently by the geometric design characteristics, resulting in varying degrees of significance of their influence on speed change. Finally, the impact of the neighboring section’s geometric design parameters on speed change was considerable and variable. As a result, it is necessary to investigate the combined curves independently and consider their adjacent segments while designing the combined curves.
Peng et al. [18] analyzed the relationship between single-lane road departure crashes and roadside features using a negative binomial model for collision frequency and a multinomial logit model for collision severity. The results indicated that shoulder width, lateral clearance, and side slope conditions significantly influence road departure collisions. Roque and Jalayer [19] found that evasive maneuvers and a lack of concentration or fatigue may lead to drivers leaving their travel lane. Geometric design features of roads and road edges, such as lane width and clear zone, play a significant role in whether human operational errors result in collision accidents. Chen [1] analyzed the longitudinal acceleration distribution curve, including parameters like slope and curvature. Based on frequent isometric longitudinal acceleration measurements, he proposed a novel modeling method. The study found a positive correlation between the slope difference and the average curvature difference in the upslope and downslope with longitudinal acceleration. However, the average curvature exhibited a negative correlation with longitudinal acceleration.
Previous research has not compared the distinguishing characteristics of various micro-driving behaviors comprehensively. This study compares speed change behavior and lane departure behavior, with a focus on the geometric design characteristics that influence them.
3. Data Preparation
3.1. Geometric Data
The Yongji test road is a 24 km long mountainous freeway with two lanes in each direction and numerous small-radius curves. A cross-sectional view of the road is illustrated in Figure 1. The road’s blueprinted longitudinal grade varies from −6.0% to +4.0%, and it has a cross-section width of 10.50 m (including a 0.5 m wide curb, 3.75 m wide lanes, and 2.50 m wide shoulders).
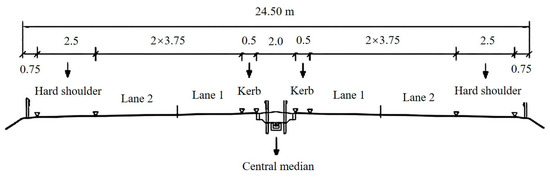
Figure 1.
Details of simulated road cross-section.
The vertical curves’ grades are represented by downslope and upslope lines, with sag and crest curves appearing when the grade direction changes within the horizontal curve. The test freeway has 70 combined curves, including 23 downslope, 21 upslope, 14 crest, and 12 sag curves. The statistical description of geometric design parameters for combined curves is presented in Table 1. Each horizontal curve was divided into individual segments, including approach transition, circular section, and departure transition. Table 2 presents the variations in geometric design parameters of the preceding 300 m segment of the combined curve relative to the combined curve, as well as the variations in geometric design parameters of the following 300 m segment of the combined curve relative to the combined curve. Figure 2 illustrates the layout of each type of combined curve.

Table 1.
Geometric design parameters of combined curves.

Table 2.
Geometric design changes of combined curve and adjacent segments.
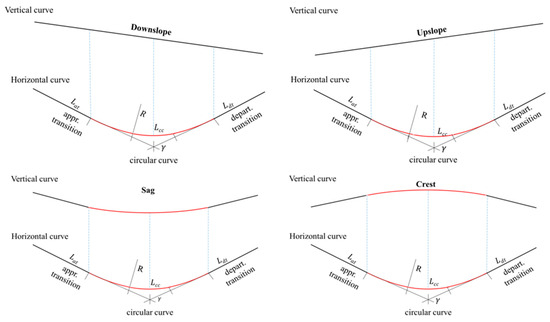
Figure 2.
Configuration of the four types of combined curves.
3.2. Micro-Driving Behavior Data Collection
The micro-driving behavior data was collected using the Tongji University driving simulator, as illustrated in Figure 3 and previously discussed in [20]. A summary is provided here. The simulator dome contains a fully equipped Renault Megane III vehicle cab installed on an eight-degree-of-freedom motion system with an X-Y motion range of 20 × 5 m. An immersive five-projector system delivers a front image view of 250° × 40° at 1400 × 1050 resolution refreshed at 60 Hz. The motion system can provide acceleration in all directions within the range of −6.5 m/s2 to +6.5 m/s2.

Figure 3.
Tongji University driving simulator.
The result of a sickness test from previous studies on the motion system of the same road exceeded the commonly used standard of 75% [17,21]. The simulated roadway environment is displayed using SCANeRTM studio software, and a force feedback system acquires data from the steering wheel, pedals, and gear shift lever to control the simulation.
The researchers selected 30 drivers based on the population distribution of gender and age among drivers in Hunan province. Of the participants, 22 were male and 8 were female, representing 26.7% of the sample. The age range of participants was between 23 and 59 years, with a mean of 36.5 years (SD = 10.4). There is a significant population of novice drivers in China. In Hunan province in 2013, the number of car drivers with cumulative driving experience of one year or less was 781,900, accounting for approximately 12.6% of all drivers in Hunan province [22]. Driving experience was also taken into consideration.
According to the “Provisions on the Issuance and Use of Motor Vehicle Driving Licenses” promulgated by the Ministry of Public Security of China, drivers have a one-year probationary period after their initial application for a driving license or the addition of the driving category. After the practice period and gaining certain driving experience, drivers are allowed to drive alone on freeways [23]. Consequently, in the driving simulator experiment all participants were required to have driven at least 10,000 total kilometers and to have averaged at least 3000 km annually.
The experimental procedure is detailed in [24], and hence, this paper provides only a brief introduction. To minimize the influence of variables beyond the study’s scope, the daytime, dry pavement, and freeway driving scenarios were selected. To avoid the influence of vehicle interactions on driving behavior, the experimental scenarios were conducted in a free-flowing state. The experimental conditions, such as visibility, road conditions, and vehicle interactions, were controlled to better analyze the effect of geometric design parameters on driving behavior.
The experiment comprises three phases: preparation, warm-up, and testing. The experimental procedure is depicted in Figure 4. During the preparation phase, the participants first answered a questionnaire about their demographic and driving experience. Participants were briefed on the study’s purpose, the simulated driving task’s nature, and potential risks. During the warm-up phase, they drove for approximately ten minutes on a typical freeway without mountains to familiarize themselves with the simulator. Following a five-minute break, they proceeded to the test phase, where each participant drove on the fully simulated Yongji Freeway. After finishing, each participant took a 5 min break and filled out the simulated dizziness questionnaire. Following that, they proceeded to drive in the opposite direction.

Figure 4.
Experimental procedure.
4. Micro-Driving Behavior
4.1. Speed Change Behavior
The discrepancy between the maximum and minimum speed values serves as an indicator of speed consistency. This study examines both acceleration and deceleration behaviors. The maximum and minimum speeds attained by each driver on each combined curve were extracted from the continuous speed data. If drivers reached their maximum speed on a curve before reaching their minimum speed, the difference in speed was calculated and plotted as a negative speed change. Conversely, if drivers reached their minimum speed prior to reaching their maximum speed, the difference in speed was regarded as a positive speed change.
where is the travel distance, is the speed preceding the curve, and is the speed following the curve. < 0 if = , = . > 0 if = , = . The distributions of speed difference for each type of combined curve are listed in Table 3.

Table 3.
Distribution characteristics of speed differences in combined curves (km/h).
Table 3 displays that the minimum speed difference value ranges between −41.88 km/h and −32.32 km/h, with the maximum value being between 29.57 km/h and 42.53 km/h. Figure 5 illustrates the speed difference distributions for each type of combined curve.
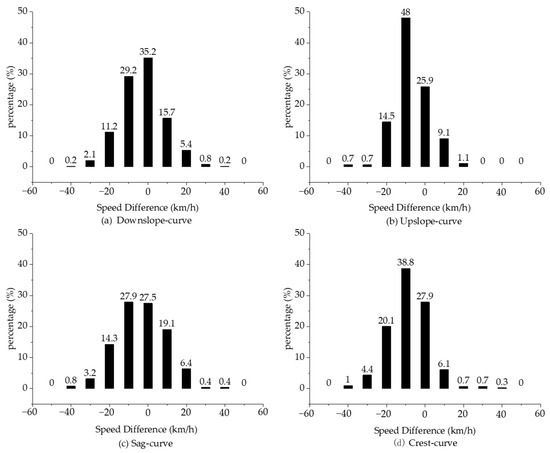
Figure 5.
The distribution of speed differences on the combined curve.
Figure 5 shows the distribution of speed differences across four different types of combined curves. The speeds for all four curves are mostly distributed between −25 km/h and 15 km/h, and the peak distributions occur between −15 km/h and 5 km/h. The speed differences on the upslope curve are more concentrated, with 48% falling between −15 km/h and −5 km/h. Conversely, the sag curve exhibits the most dispersed distribution of speed differences.
4.2. Lane Departure Behavior
The lane departure incidents on the four combined curve types were categorized into two types of departures: those in the direction of centrifugal force (IDCF) and those against it (ADCF). Figure 6 depicts a vehicle exhibiting lane departure behavior in both IDCF and ADCF.
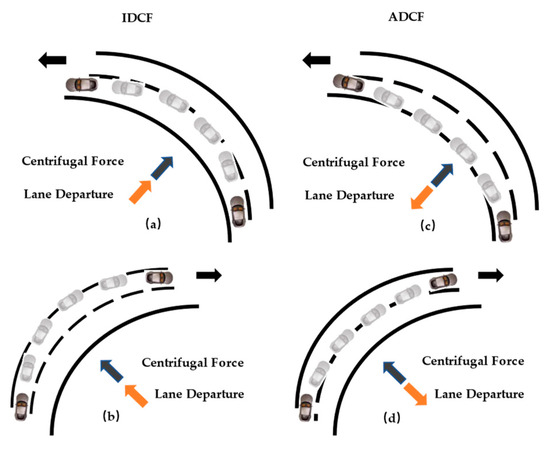
Figure 6.
IDCF and ADCF categorization diagrams: (a) IDCF departure occurs during vehicle left turn; (b) IDCF departure occurs during vehicle right turn; (c) ADCF departure occurs during vehicle left turn; (d) ADCF departure occurs during vehicle right turn.
Of all lane departure behaviors, IDCF lane departure (52.2%) has a greater percentage than ADCF lane departure (47.8%). IDCF lane departure is more likely to occur while driving. Table 4 displays the extracted lateral departure value and departure persistence distance value for the two different centripetal force directions.

Table 4.
Statistical description of the two types of lane departure.
From the data presented in Table 4, it is evident that there exist significant differences in the persistence distance between the two types of lane departure behavior. Specifically, the mean lateral departure of ADCF was 0.36 m, while that of IDCF was 0.81 m. Additionally, the average persistence distance for ADCF lane departure was 60.64 m, whereas for IDCF lane departure, it was 72.75 m. These data suggest that the IDCF behavior is more severe than ADCF.
4.3. Micro-Behavior Comparison of Four Combined Curves
Previous studies have shown that it is necessary to study the different types of combined curves separately [17]. In addition, the micro-driving behavior may vary according to the type of combined curve. To determine which behavior requires more attention in the development of AVs and ADASs, it is advisable to compare the variation of speed changes and lane departure behavior changes for each type of curve. The Shapiro–Wilk and Kolmogorov–Smirnov methods were applied to conduct normality tests on the original data. They found that the speed change data and the lane departure data rejected the assumption of a normal distribution for data at a 0.05 significance level.
Taking into account the non-normal distribution of the data, the article uses the coefficient of variation to measure the variability of the data instead of using the variance. The coefficient of variation is a statistical measure used to measure the relative variability of data. The formula is as follows:
If the coefficient of variation of the speed change exceeds that of the lane departure, it indicates that the vehicle’s speed is changing frequently during operation, and the magnitude and frequency of these speed changes are greater than the lane departure changes. AVs and ADASs should pay more attention to speed changes during the curve.
If the coefficient of variation of lane departure is larger, it suggests that the driver has inadequate lateral stability and is more susceptible to lane departure while driving. Priority should be given to lane departure with AVs and ADASs.
Due to the differing units of measurement with speed change in km/h and lane departure in m, the Z-score standardized method was used to standardize the differences in speed and lane departure.
Considering that the calculation of the coefficient of variation includes the mean and that the Z-score standardized method gives a mean of zero and that the data are not normally distributed, the use of the median as a substitute for the mean provides a better description of the basic characteristics of the data. Therefore, the method of calculating the coefficient of variation has been optimized using the median instead of the mean.
The vehicle operation data of 30 drivers were used for each combined curve. The results are shown in Table 5.

Table 5.
Coefficient of variation of combined curves with micro-driving behavior.
Table 5 shows the results of the coefficient of variation of the micro-driving behavior on four combined curve types. The speed change behavior requires more attention than the lane departure behavior for the sag curve, as the former experiences a higher coefficient of variation. Conversely, for upslope curves and crest curves more attention should be paid to the lane departure behavior, where the lane departure variation exceeds that of the speed change. On the downslope curve, both speed change and lane departure have the highest coefficient of variation. Referring to previous research, significant speed increases are more likely to occur on downslope curves [17], so speed change requires more attention.
Table 5 shows that the downslope curve has the highest coefficient of variation of speed change (15.884) of the four combined curve types, indicating the worst speed change. In contrast, the upslope curve has the highest consistency of vehicle speed (4.436). The downslope curve results in the highest coefficient of variation of lane departure (41.114).
5. Shapley Explanation for the Relationship between Micro-Behavior and Geometric Design
The RF model was utilized to examine the quantitative correlation between micro-behavior and geometric design parameters. The importance of the variables was ranked and filtered using the shapely explanation. Based on a comparison of the coefficient of variations, the influences of geometric design parameters such as downslope curves and sag curves on speed change behavior were analyzed, while the influences of upslope curves and crest curves on lane departure behavior were investigated.
5.1. Methodology
5.1.1. Random Forest
There are many methods suitable for the analysis, such as traditional linear regression models, generalized linear regression models, and newer algorithms such as XGBoost, support vector machines, random forests, and so on.
The random forest model (RF) is used in this study. RF is a widely implemented machine learning technique capable of addressing both classification and regression problems [25]. RF is a flexible and powerful machine learning algorithm suitable for various types of data, including continuous numerical data, data with classification labels, and mixed-type data.
RF involves multiple decision trees that are combined through a majority voting mechanism to generate a final decision [26].
It can be understood as assuming the input features are and in the RF model, where represents the road geometric design parameters. The meaning of varies across different combined curves: on downslope curves, it represents both speed variation and lane departure values; on upslope and crest curves, it represents lane departure values; and on sag curves, it represents speed variation. is the number of features. The process is (1) select a random sample set from the training dataset ; (2) generate a decision tree on ; (3) repeat steps (1) and (2) for n times to obtain decision trees ; (4) summarize the predictions for each random sample , providing the function of the RF [27].
RF not only captures complex relationships, but also evaluates the importance of features, allowing interpretation of how features affect the response variable. In addition, RF was able to retain all features, largely due to the use of the bagging learning mechanism, which constructs a large collection of decorrelated trees, thereby reducing overfitting. In addition, each tree in RF is constructed using a randomly selected subset of features from the sample data.
In previous studies, RF has been applied to traffic safety research. RF has been established as an effective approach for accident prediction [26,28,29], with an increased level of prediction accuracy [30]. Gatera [31] developed two models using training and validation datasets to predict traffic accidents using RF. Su et al. [32] used an RF model to study and evaluate the importance of five continuous variables (average speed, queue length, cumulative number of vehicles in queue, cumulative duration, and cumulative number of vehicles) on traffic flow variables. Yan and Shen [33] used RF as their basic prediction model, and tuned its parameters using Bayesian Optimization (BO), and analyzed the severity of traffic accidents with 15 factors related to traffic, time, and weather. BO-RF provides interpretable results through relative importance and partial dependence plots, allowing the identification of factors with significant impacts on the severity of traffic accidents.
The RF model was implemented by calling the RandomForestRegressor from the sklearn library, version 1.0.2, in Python. To ensure the model’s generalizability and to prevent overfitting, the code defines the search range for hyperparameters during the construction of the RF model. Each hyperparameter has three possible values, and grid search is employed to automatically find the best combination of hyperparameters.
To mitigate the impact of outliers and better reflect the overall performance of the model, the paper employs the mean absolute error (MAE) metric to evaluate the performance of the RF model. This metric is calculated using the following formula:
5.1.2. SHAP
SHAP (Shapley Additive Explanations) is a novel model interpretation method that combines optimal credit allocation with local explanations using Shapley values from game theory [34]. Unlike statistical models, machine learning methods struggle to quantify the marginal and interaction effects of influencing factors, making it difficult to formulate more targeted security strategies [35].
SHAP is used to characterize the performance of machine learning methods [36]. For a subset of risk factors (where represents the set of all risk factors), two models are trained to extract the influence of factor . The first model is trained with factor , and the other model is trained without factor , where and are the values of input risk factors. For each possible subset , the difference in the model output is computed. The Shapley values for the risk factor are then calculated using Formula (5).
Predictive SHAP values refer to the impact of risk factors calculated based on a single observation, while dataset-level SHAP values refer to the importance of risk factors and the interaction effects between them calculated based on all observations. For example, SHAP interaction scores can be calculated as the difference between the Shapley scores of a factor with and without another factor.
SHAP values were computed to rank factors contributing significantly to micro-behavior based on the RF models. MAE was used to evaluate the RF models because of its intuitiveness and robustness. MAE measures the average absolute difference between predicted and actual values, making it easier to evaluate performance. Its robustness to outliers is due to its use of absolute values, which mitigates the impact of individual outliers. This makes it suitable for datasets with outliers. The model was trained using Python software (version 3.10) with the ‘RandomForestRegressor’ and ‘shap’ packages.
5.2. RF-SHAP Analysis of Mirco-Behavior on Combined Curves
The correlation among the geometric design parameters was analyzed via heat maps prior to executing RF and SHAP. Figure 7 displays the heat map.
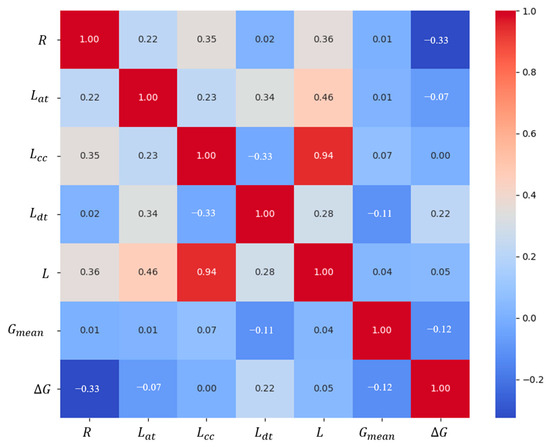
Figure 7.
The heat map of combined curves’ geometric design parameters.
Figure 7 illustrates a high correlation between and , with a correlation coefficient of 0.94. Additionally, is correlated with , with a correlation coefficient of 0.46. Consequently, when performing random effects modeling, did not enter the model. RF-SHAP results are shown in Section 5.2.1 and Section 5.2.2. Section 5.2.1 sorts geometric design parameters in descending order based on their mean absolute SHAP values. A higher SHAP value represents a more significant contribution to micro-driving behavior estimation.
5.2.1. Speed Change Behavior on Downslope and Sag Curve
In this study, speed differences below the 7.5th percentile are defined as the threshold for substantial speed reduction behavior, while those exceeding the 92.5th percentile are considered as the threshold for substantial speed increase behavior. The RF model utilizes all values representing substantial speed reduction and increase as the dependent variable data, with ten geometric design parameters serving as independent variables.
- (1)
- Downslope Curve
The MAE of the RF model is 5.861. Figure 8 displays the SHAP values of the downslope curves’ geometric design parameters.
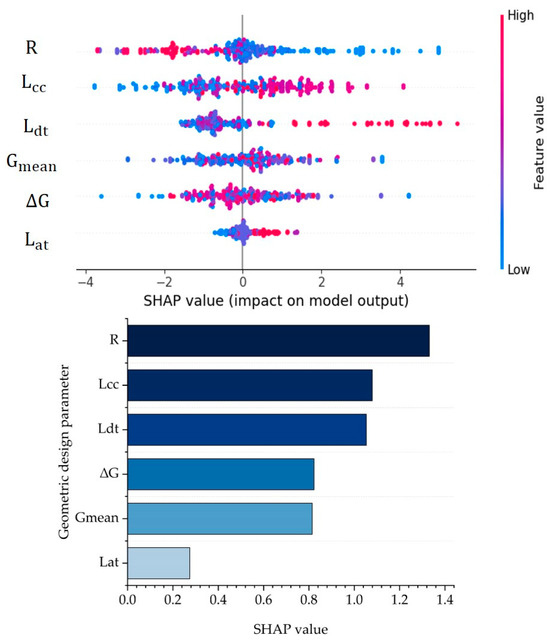
Figure 8.
The SHAP values for geometric design parameters of downslope curves.
Furthermore, Figure 8 demonstrates that among all geometric design parameters included in downslope curves, the SHAP value of is the highest, indicating that has the greatest impact on the speed variation behavior of vehicles on downslope curves. Following this, other influential factors include , , and . The smallest SHAP value for is observed upon entering a downslope curve.
A prior study demonstrated that speed was impacted by adjacent alignments [17]. The study also considered the geometric design parameters of the preceding 300 m segment and the following 300 m segment of the combined curve. The RF model exhibited a MAE of 5.55, and Figure 9 displays the SHAP values of the geometric design parameters for the adjacent alignment of the downslope curve.
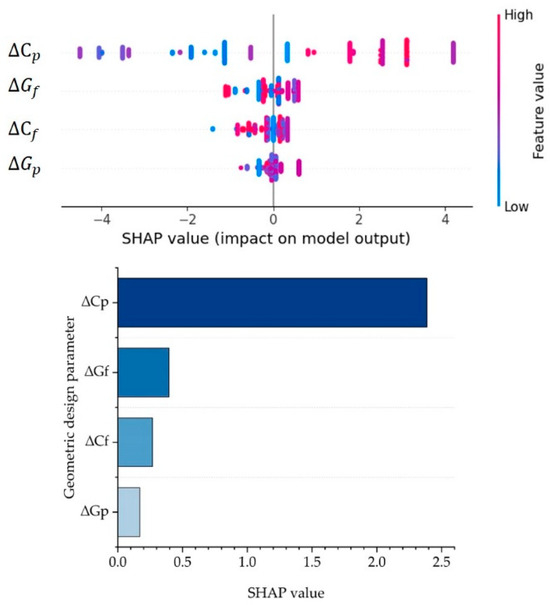
Figure 9.
The SHAP values for adjacent alignment geometric design parameters of downslope curves.
Figure 9 shows that the SHAP values for in the downslope curve are the highest, at 2.38, indicating a significant influence on the speed change behavior of downslope curves. This is followed by for the downslope curve, with an SHAP value of 0.3951, which may be due to the following slope change affecting driver visibility. and have smaller impacts on the speed behavior of downslope curves.
- (2)
- Sag Curve
The MAE of the RF model is 5.68. Figure 10 displays the SHAP values of geometric design parameters for sag curves.
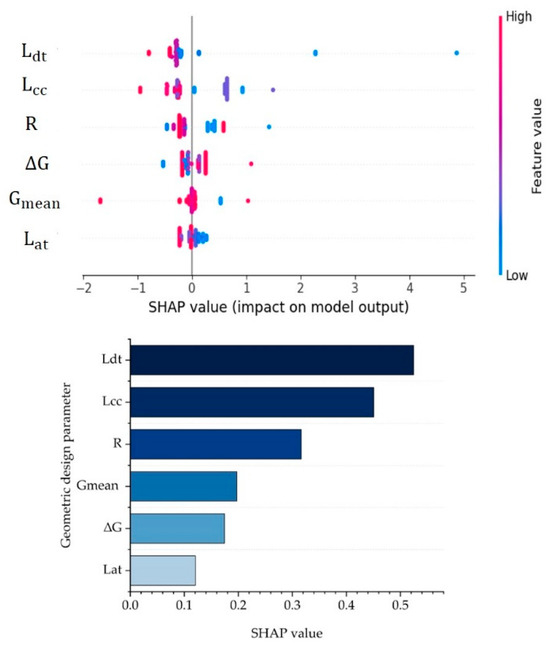
Figure 10.
The SHAP values for the geometric design parameters of sag curves.
According to Figure 10, the SHAP values for are the highest for sag curves, indicating that it has the most significant impact on speed change behavior in terms of geometric design parameters. After , the next most influential factors are , R, and . The SHAP value for is the smallest.
As demonstrated in Figure 11, which showcases the SHAP values of geometric design parameters adjacent to sag curves in alignment, the RF model’s MAE is 5.74.
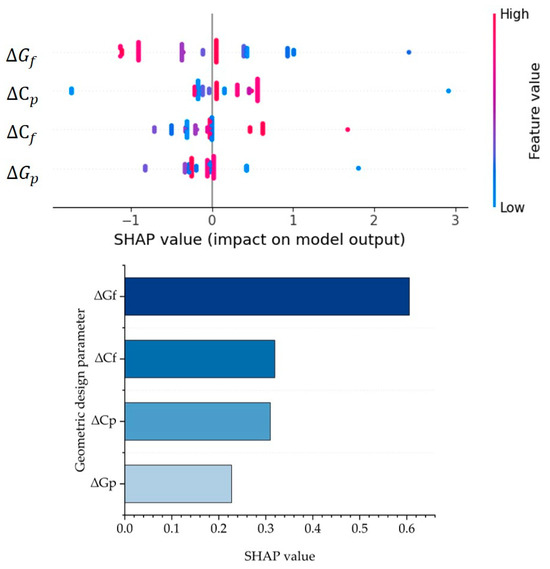
Figure 11.
The SHAP values for adjacent alignment geometric design parameters of sag curves.
Figure 11 reveals that on sag curves, the SHAP values for have the highest impact on the speed change behavior of sag curves, with a value of 0.61. The following curvature change () has an SHAP value of 0.32, meaning it also has an impact on speed behavior, but to a lesser extent. Additionally, and exhibit an impact on sag curve speed behavior, but their effect is not as pronounced.
5.2.2. Lane Departure Behavior on Downslope, Upslope, and Crest Curves
Three types of lane departure behavior were modeled separately: the direction of centrifugal force (IDCF) and against the direction of centrifugal force (ADCF) were modeled separately.
- (1)
- Downslope Curve
The MAE for the RF model on IDCF lane departure behavior in the downslope curve is 0.2108. Figure 12 shows the SHAP values for the geometric design parameters of the downslope curve.
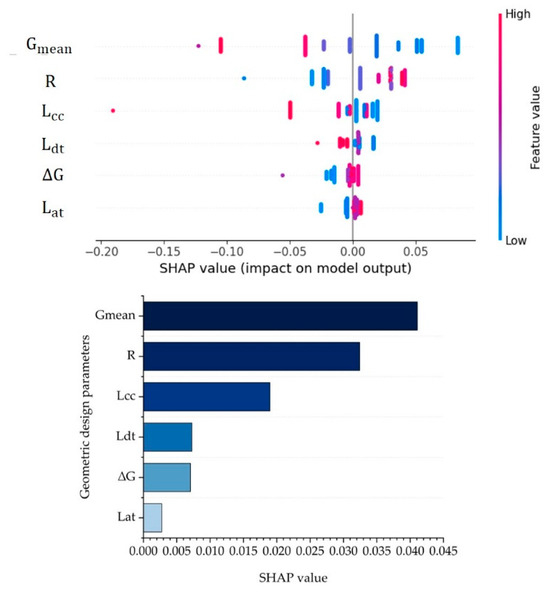
Figure 12.
The SHAP values for the geometric design parameters of IDCF lane departure behavior on downslope curve.
From Figure 12, the design parameter that has the greatest impact on the IDCF for the downslope curve is . The SHAP values of and are next to . Other geometric design parameters have a relatively low impact compared to the .
The MAE of the RF model of ADCF lane departure behavior in the downslope curve is 0.2468. Figure 13 displays the SHAP values for the geometric design parameters of the downslope curve.
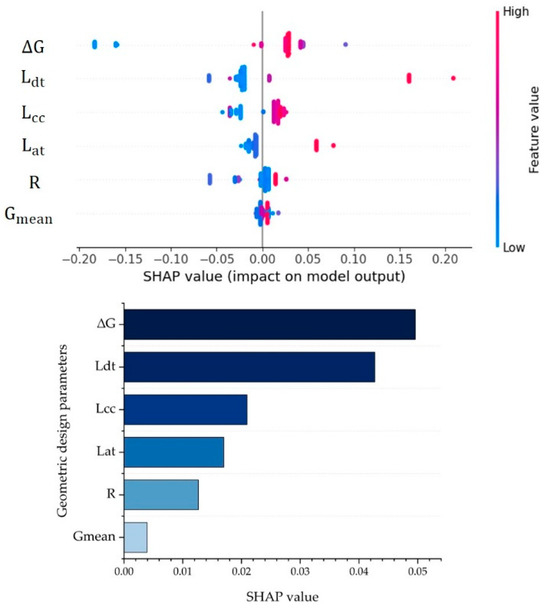
Figure 13.
The SHAP values for the geometric design parameters of ADCF lane departure behavior in downslope curve.
According to Figure 13, the of the SHAP value for slope difference is the largest at 0.050. The SHAP values of and are next to . The , and have less effect on the ADCF lane departures on downslope curves.
- (2)
- Upslope Curve
The MAE for the RF model on IDCF lane departure behavior in the upslope curve is 0.2363. Figure 14 shows the SHAP values for the geometric design parameters of the upslope curve.
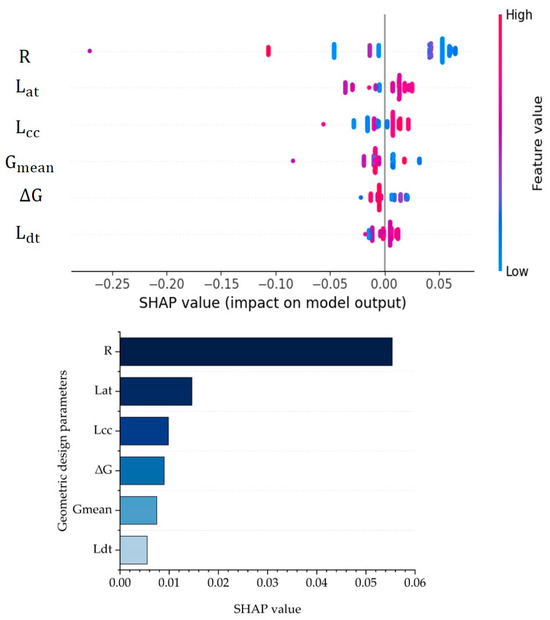
Figure 14.
The SHAP values for the geometric design parameters of IDCF lane departure behavior on upslope curve.
From Figure 14, the design parameter that has the greatest impact on the IDCF lane departure behavior of the upslope curve is . Other geometric design parameters have a relatively lower impact compared to the radius.
The MAE of the RF model of ADCF lane departure behavior in the upslope curve is 0.2747. Figure 15 displays the SHAP values for the geometric design parameters of the upslope curve.
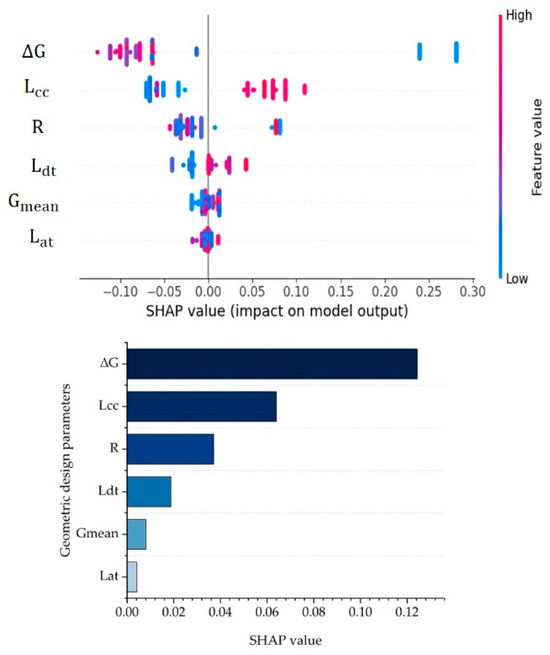
Figure 15.
The SHAP values for the geometric design parameters of ADCF lane departure behavior on upslope curve.
According to the Figure 15, the of SHAP value for slope difference is the largest at 0.1243. The SHAP values of and R are next to . The and have less effect on the ADCF lane departures in upslope-curves.
- (3)
- Crest Curve
The MAE for the RF model of IDCF lane departure behavior in crest curves is 0.2619. Figure 16 shows the SHAP values for the geometric design parameters of crest curves for IDCF lane departure behavior.
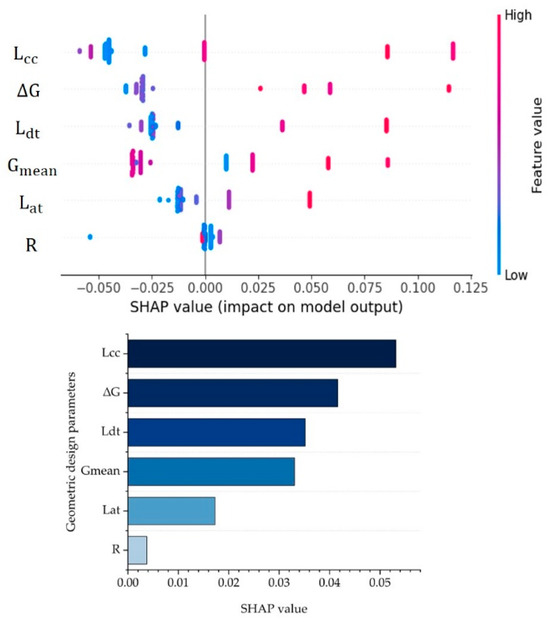
Figure 16.
The SHAP values for the geometric design parameters of IDCF lane departure behavior on crest curve.
From Figure 16, it is evident that , and have the greatest influence on the IDCF lane departure of the crest curve.
The MAE for the RF model of ADCF lane departure behavior in crest curve is 0.2146. Figure 17 shows the SHAP values for the geometric design parameters of crest curves for ADCF lane departure behavior.
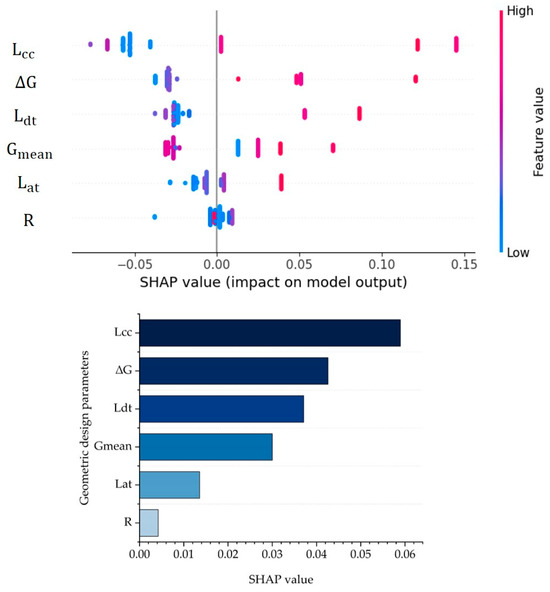
Figure 17.
The SHAP values for the geometric design parameters of ADCF lane departure behavior on crest curve.
From Figure 17, the parameters that have the most influence on the ADCF lane departure of the crest curve are , , and .
6. Discussion
Most previous road safety research has focused on established motorways. Accident data, real-world vehicle testing, and naturalistic driving are typically used in these studies. However, driving simulation technology offers opportunities to improve the safety of newly built roads and complex motorways. Continuous vehicle operating data, driver control data, etc., are collected in a controlled experimental environment [37].
Moreover, mountainous freeways pose additional challenges for autonomous driving and driver assistance systems due to the complexity of horizontal and vertical curves. Safety designs for combined curves need be approached from multiple dimensions. Recent research has highlighted the importance of analyzing combined curves [38]. Prior studies have developed statistical models to investigate the correlation between the geometric design of highway and vehicle operation such as speed differential, lateral acceleration, and vehicle trajectory [39,40].
To better understand the driver’s performance when driving in a combined curve, this study converts the speed difference into the speed change behavior and converts the vehicle trajectory data into the lane departure behavior. It can reflect the driver’s adaptability to the road alignment intuitively. From the data distribution characteristics of the micro-driving behavior on the four types of combined curves, we can also intuitively see that the micro-driving behavior of the four types of combined curves is different. By comparing the coefficient of variation, we confirm this point that for different combined curves, different driving behavior should be paid more attention.
It can also provide new ideas for the safety evaluation of combined curves. In the case of sag curves, the coefficient of variation of the driver‘s speed difference is larger than the lane departure, and the speed is discrete, indicating that the speed change behavior of sag curves needs more attention. Some scholars have used stratified negative binomial analysis to analyze the collision frequency of sag curves, and the results also indicate that speed, horizontal curvature, and slope all have a significant impact on the collision frequency of sag curves [38]. The curve speed warning, adaptive cruise control, etc., and the speed-related driver assistance systems need to be concerned with these two types of combined curves. For downslope curves, upslope curves and crest curves, the lane departure warning, lane centering control, and lane departure prevention, etc., should be concerned with these three types of combined curves. The coefficient of variation of the driver‘s speed difference in downslope driving is larger than in other types of combined curves.
The order of importance of geometric design parameters generally remained consistent between the RF and RF-SHAP models, but there were instances where the order of importance of individual variables varied significantly. For example, there were notable discrepancies in the IDCF departure models for upslope curves (), crest curves (, R), and the ADCF departure model for crest curves (). In addition, there were cases where the design parameter importance rankings differed significantly between the RF and RF-SHAP results, such as the speed variation models for downslope and sag curves.
The discrepancies in design parameter importance rankings between RF and RF-SHAP models primarily stem from differences in how they calculate feature importance. The RF model typically employs impurity-based metrics like Gini impurity or information gain to assess feature importance, based on the effectiveness of feature splits at decision tree nodes, thereby measuring the contribution of features to the model’s predictive accuracy. In contrast, the RF-SHAP model integrates the SHAP method, which considers the impact of each feature on each sample and the contribution of different feature values to the model output. Feature importance in the RF-SHAP model is derived from statistical computations of SHAP values for each feature, providing the average contribution of each feature to the model output.
Unlike the RF model, the SHAP values in the RF-SHAP model not only indicate the contribution of each feature to the overall model output but also illustrate the influence of each feature value on the model output for each sample. This allows for a more detailed analysis of the impact of individual feature values on model predictions, leading to a comprehensive understanding of model behavior. Additionally, RF-SHAP yields more robust results by considering the contribution of each sample’s features rather than relying solely on aggregate dataset statistics, making it more resilient to data with imbalanced distributions or outliers. Consequently, the feature importance results from the RF-SHAP model were deemed more reliable for subsequent analysis in the study.
From the results of the RF model and the SHAP values, we can see that the geometric design parameters that affect micro-driving behavior are different for different combinations of line shapes. For example, for sag curves, the top four geometric design parameters affecting speed change behavior are the length of the departure transition, the length of the circular curve, the radius, and the slope change of the following section. For the upslope curve, the top three geometric design parameters affecting the ADCF lane departure are , ,. For the crest curve, the top three geometric design parameters affecting the IDCF and ADCF lane departure are , and . This is consistent with existing research, as studies have indicated that the length of overlap between horizontal curves and sag curves () has a significant impact on lateral acceleration [17]. Lateral acceleration also directly influences lane departure values.
From another perspective in this study, when improving the design of the combined curves, we can gather which design parameters should be prioritized and which design parameter will be the focus for optimization. In fact, the process of optimizing the design of combined curves could be summarized based on the research:
- Selecting key safety evaluation measures.
Speed change and lane departure behavior are selected as the safety evaluation measures of combined curves.
- Ranking of geometric design parameters of combined curves.
The quantitative relationships between geometric design parameters of combined curves and safety evaluation measures should be established. Significant geometric design parameters could be obtained. The priority of each design parameters could be determined using the SHAP value.
- Optimizing design based on safety evaluation measures.
Priority must be given to the geometric design parameters with the largest SHAP value for design optimization.
Previous studies have demonstrated that drivers have different micro-driving behaviors when driving on different types of combination curves, while identifying geometric design parameters that have a significant effect on micro-driving behavior [12]. In this study, the RF-SHAP model was used to quantify the importance of roadway geometric design parameters on speed change and lane departure on different combination curves. However, due to the limitations of the sample data, which was not combined with accident data and natural driving data, the causal relationship between the independent and dependent variables needs to be better validated.
7. Conclusions
The purpose of this paper is to analyze the speed change and lane departure behaviors of combined curves considering downslope curves, upslope curves, sag curves, and crest curves. In this study, a mountainous freeway in Hunan province was reproduced in a driving simulator and micro-driving behavior data were continuously collected. The coefficients of variation of speed change and lane departure were compared for four types of combined curves.
The RF model and SHAP value were calculated, and the priority of each significant design parameter was determined.
Such a study is necessary and important because poorly designed roads with combined curves can increase driving risk. Much of new construction is in the mountainous areas of western China, where the terrain requires engineers to design roads with combined horizontal and vertical curves. However, automated driving and driver assistance systems do not consider the micro-behavior of different types of combined alignments, and quantitative design guidelines for combined curves are currently unavailable [41].
In future studies, the sample size will be expanded, and we will also validate the findings by combining them with accident data and natural driving data. Other more advanced machine learning methods will also be used to further enhance the validity of the research results.
Author Contributions
X.W. (Xiaomeng Wang): conceptualization, methodology, software, validation, investigation, formal analysis, data curation. X.W. (Xiaomeng Wang) and X.W. (Xuanzong Wei): writing—original draft preparation, writing—review and editing, visualization. X.W. (Xuesong Wang): resources, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was approved by the ethics committee of Tongji Hospital (Approval Date: 11 November 2010).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to a confidentiality agreement signed during the experiment.
Acknowledgments
This study was supported by the Research on Freight Road Operational Risk Identification and Intervention Methods Based on Holographic Traffic Data, Qinghai Provincial Transportation Construction Management Co., Ltd., Qinghai Provincial Transportation Holdings Group Co., Ltd., and the Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, Z.; Wang, X.; Guo, Q. Effect of Combined Horizontal and Vertical Curve on Vehicle Longitudinal Acceleration of Mountainous Freeway. In Proceedings of the 19th COTA International Conference of Transportation Professionals, Nanjing, China, 6–8 July 2019. [Google Scholar]
- Chen, Z.; Wang, X.; Guo, Q.; Tarko, A. Towards Human-like Speed Control in Autonomous Vehicles: A Mountainous Freeway Case. Accid. Anal. Prev. 2022, 166, 106566. [Google Scholar] [CrossRef] [PubMed]
- American Association of State Highway and Transportation Officials (AASHTO). A Policy on Geometric Design of Highways and Streets; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2018. [Google Scholar]
- Hanno, D. Effect of the Combination of Horizontal and Vertical Alignments on Road Safety. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 2004. [Google Scholar]
- Misaghi, P.; Hassan, Y. Modeling operating speed and speed differential on two-lane rural roads. J. Transp. Eng. 2005, 131, 408–418. [Google Scholar] [CrossRef]
- Nie, B.; Hassan, Y. Modeling driver speed behavior on horizontal curves of different road classifications. In Proceedings of the 84th Transportation Research Board Annual Meeting, Washington, DC, USA, 21–25 January 2007. [Google Scholar]
- Bella, F. Driving simulator for speed research on two-lane rural roads. Accid. Anal. Prev. 2008, 40, 1078–1087. [Google Scholar] [CrossRef] [PubMed]
- Sawtelle, A.; Shirazi, M.; Garder, P.E.; Rubin, J. Exploring the impact of seasonal weather factors on frequency of lane-departure crashes in Maine. J. Transp. Saf. Secur. 2022, 15, 445–466. [Google Scholar] [CrossRef]
- Destination Zero Deaths: Louisiana Strategic Highway Safety Plan. 2018. Available online: https://destinationzerodeaths.com/Images/Site%20Images/ActionPlans/SHSP.pdf (accessed on 7 November 2023).
- Zhou, X. Approach and Application of Steering on Freeway Curve Based on Visual Information; Wuhan University of Technology: Wuhan, China, 2010. [Google Scholar]
- Kazemzadehazad, S.; Monajjem, S.; Larue, G.S.; King, M.J. Evaluating new treatments for improving driver performance on combined horizontal and crest vertical curves on two-lane rural roads: A driving simulator study. Transp. Res. Part F Traffic Psychol. Behav. 2019, 62, 727–739. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X. Speed Change Behavior on Combined Horizontal and Vertical Curves: Driving Simulator-based Analysis. Accid. Anal. Prev. 2018, 119, 215–224. [Google Scholar] [CrossRef]
- Haghighi, N.; Liu, X.C.; Zhang, G.; Porter, R.J. Impact of roadway geometric features on crash severity on rural two-lane highways. Accid. Anal. Prev. 2018, 11, 34–42. [Google Scholar] [CrossRef]
- Joseph, N.M.; Harikrishna, M.; Anjaneyulu, M.V.L.R. Safety Evaluation of Multiple Horizontal Curves Using Statistical Models. Int. J. Veh. Saf. 2021, 12, 81–97. [Google Scholar] [CrossRef]
- Fu, X.; He, S.; Du, J.; Ge, T. Effects of Spatial Geometric Mutation of Highway Alignments on Lane Departure at Curved Sections. Zhongguo Gonglu Xuebao/China J. Highw. Transp. 2019, 32, 106–114. [Google Scholar]
- Bella, F. Effects of Combined Curves on Driver’s Speed Behavior: Driving Simulator 40 Study. Transp. Res. Procedia 2014, 3, 100–108. [Google Scholar] [CrossRef]
- Wang, X.; Wang, T.; Tarko, A.; Tremont, P.J. The influence of combined alignments on lateral acceleration on mountainous freeways: A driving simulator study. Accid. Anal. Prev. 2015, 76, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Geedipally, S.R.; Lord, D. Effect of Roadside Features on Single-Vehicle Roadway Departure Crashes on Rural Two-Lane Roads. Transp. Res. Rec. 2012, 2309, 21–29. [Google Scholar] [CrossRef]
- Roque, C.; Jalayer, M. Improving roadside design policies for safety enhancement using hazard-based duration modeling. Accid. Anal. Prev. 2018, 120, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Wang, X.; Lin, H.; He, Y.; Yang, L. Evaluating Alignment Consistency for Mountainous Freeway in Design Stage: Driving Simulator-Based Approach. In Proceedings of the 92th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Kennedy, R.S.; Lane, N.E.; Berbaum, K.S.; Lilienthal, M.G. Simulator sickness questionnaire: An enhanced method for quantifying simulator sickness. Int. J. Aviat. Psychol. 1993, 3, 203–220. [Google Scholar] [CrossRef]
- Hunan Bureau of Statistics. Available online: https://tjj.hunan.gov.cn/hntj/tjfx/jmxx/2014jmxx/201507/t20150717_3785983.html (accessed on 24 January 2024).
- The Central People’s Government of the People’s Republic of China. Available online: https://www.gov.cn/gongbao/content/2022/content_5679696.htm?eqid=b59297960001ed3600000003645a02a2 (accessed on 24 January 2024).
- Wang, X.; Wang, X.; Cai, B.; Liu, J. Combined alignment effects on deceleration and acceleration: A driving simulator study. Transp. Res. Part C Emerg. Technol. 2019, 104, 172–183. [Google Scholar] [CrossRef]
- Dogru, N.; Subasi, A. Traffic accident detection using random forest classifier. In Proceedings of the 2018 15th Learning and Technology Conference (L & T), Jeddah, Saudi Arabia, 25–26 February 2018. [Google Scholar]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2017, 40, 2681–2693. [Google Scholar] [CrossRef]
- Zhu, C.; Brown, C.T.; Dadashova, B.; Ye, X.; Sohrabi, S.; Potts, I. Investigation on the driver-victim pairs in pedestrian and bicyclist crashes by latent class clustering and random forest algorithm. Accid. Anal. Prev. 2023, 182, 106964. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, D.; Arvin, R.; Khattak, A.J.; Han, L.D. Predicting intersection crash frequency using connected vehicle data: A framework for geographical random forest. Accid. Anal. Prev. 2023, 179, 106880. [Google Scholar] [CrossRef]
- Kang, K.; Ryu, H. Predicting types of occupational accidents at construction sites in Korea using random forest model. Saf. Sci. 2019, 120, 226–236. [Google Scholar] [CrossRef]
- Choi, J.; Gu, B.; Chin, S.; Lee, J.-S. Machine learning predictive model based on national data for fatal accidents of construction workers. Autom. Constr. 2020, 110, 102974. [Google Scholar] [CrossRef]
- Gatera, A.; Kuradusenge, M.; Bajpai, G.; Mikeka, C.; Shrivastava, S. Comparison of random forest and support vector machine regression models for forecasting road accidents. Sci. Afr. 2023, 21, e01739. [Google Scholar] [CrossRef]
- Su, Z.; Liu, Q.; Zhao, C.; Sun, F.A. Traffic Event Detection Method Based on Random Forest and Permutation Importance. Mathematics 2022, 10, 873. [Google Scholar] [CrossRef]
- Yan, M.; Shen, Y. Traffic Accident Severity Prediction Based on Random Forest. Sustainability 2022, 14, 1729. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wen, X.; Xie, Y.; Jiang, L.S.; Pu, Z.; Ge, T. Applications of machine learning methods in traffic crash severity modelling: Current status and future directions. Transp. Rev. 2021, 41, 855–879. [Google Scholar] [CrossRef]
- Tamim Kashifi, M.; Jamal, A.; Samim Kashefi, M.; Almoshaogeh, M.; Masiur Rahman, S. Predicting the travel mode choice with interpretable machine learning techniques: A comparative study. Travel Behav. Soc. 2022, 29, 279–296. [Google Scholar] [CrossRef]
- Sarwar, M.T.; Anastasopoulos, P.C.; Golshani, N.; Hulme, K.F. Grouped random parameters bivariate probit analysis of perceived and observed aggressive driving behavior: A driving simulation study. Anal. Methods Accid. Res. 2017, 13, 52–64. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Li, X.; Wang, Y.; Zeng, Q. Effects of geometric attributes of horizontal and sag vertical curve combinations on freeway crash frequency. Accid. Anal. Prev. 2023, 186, 107056. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Guo, Z.; Li, Y. Driver operational level identification of driving risk and graded time-based alarm under near-crash conditions: A driving simulator study. Accid. Anal. Prev. 2022, 166, 106544. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, F.; Chen, S.; Xing, G.; Xie, Z.; Wang, F. A dynamic method to predict driving risk on sharp curves using multi-source data. Accid. Anal. Prev. 2023, 191, 107228. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Design Specification for Highway Alignment; China Communications Press: Beijing, China, 2017.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).