Blasting Vibration Control and Signal Analysis of Adjacent Existing Deterioration Tunnels
Abstract
1. Introduction
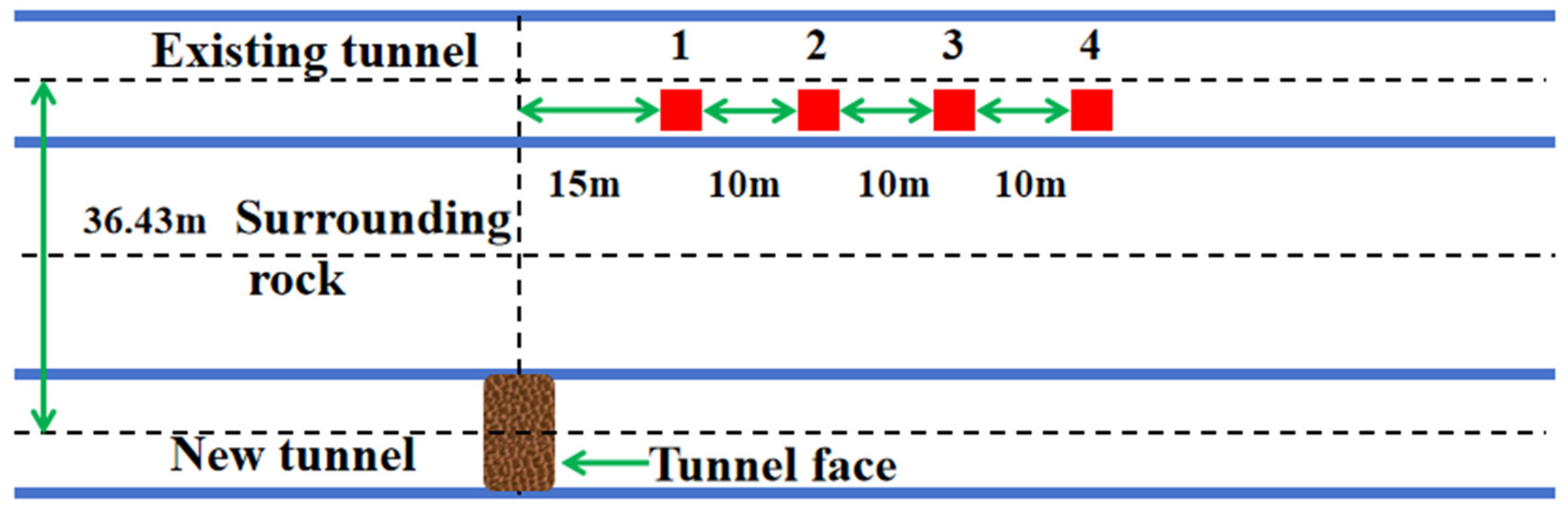
2. General Situation of Deterioration Tunnel
3. Numerical Simulation of Blasting Vibration Control
3.1. Model Overview
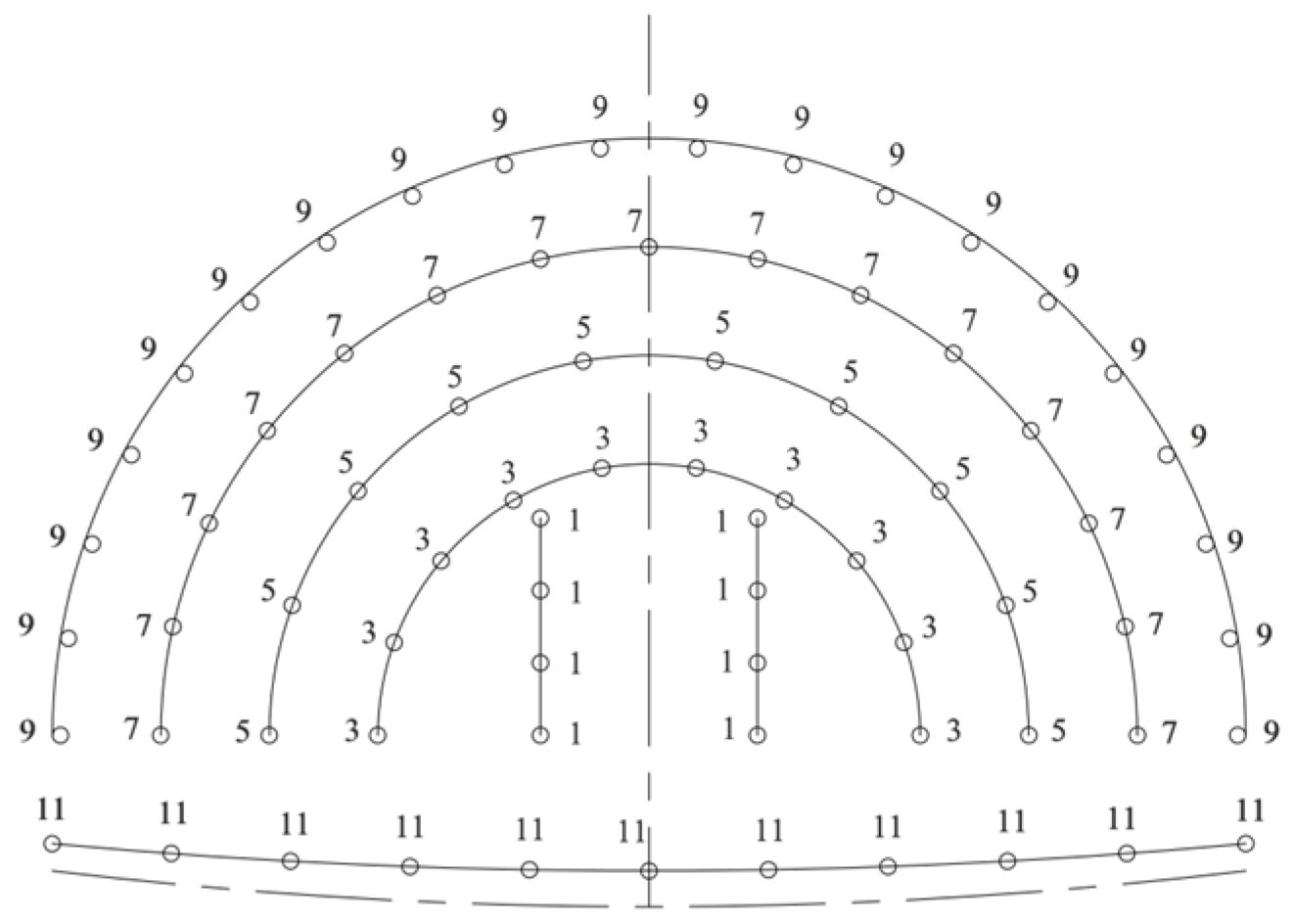
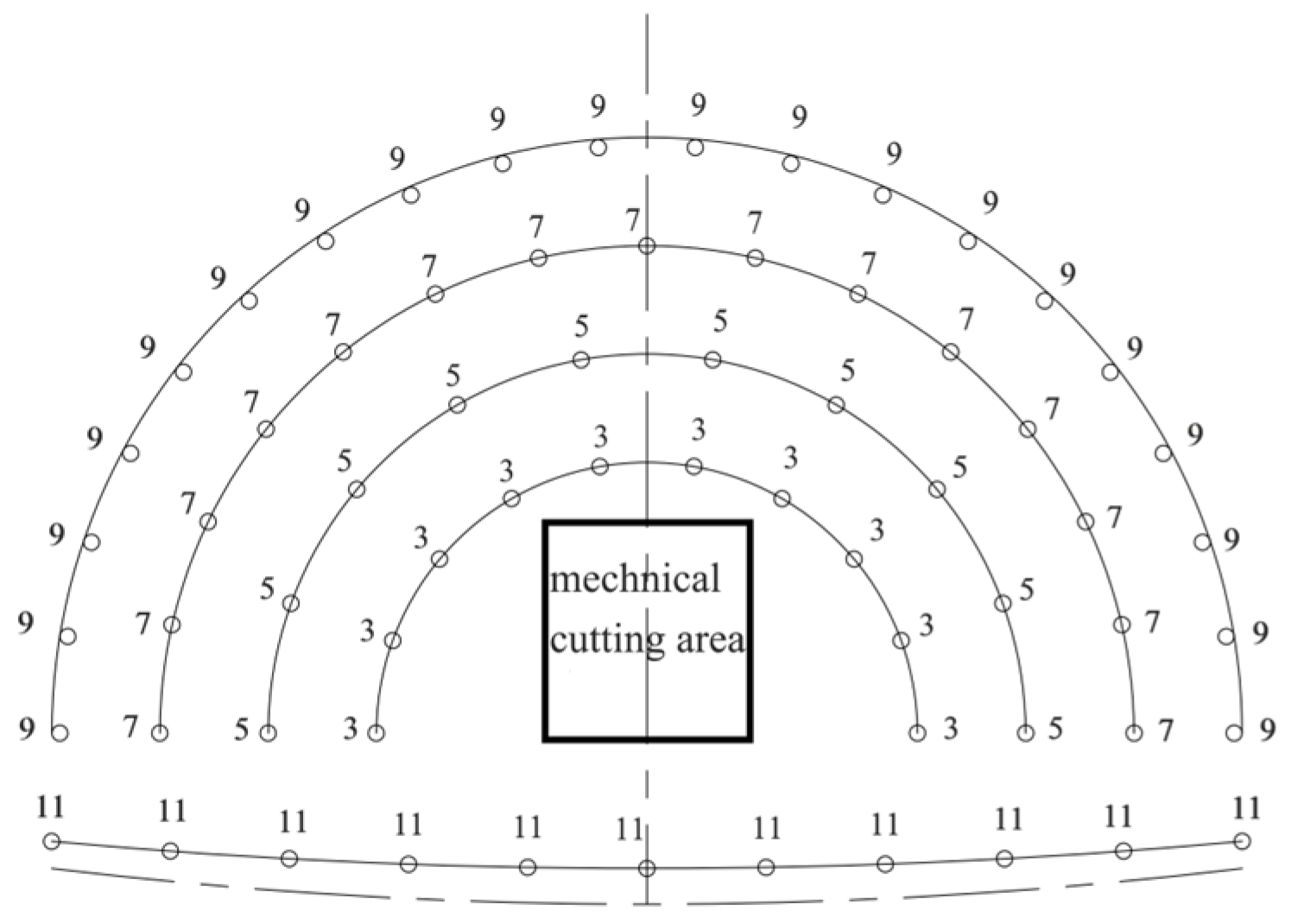
3.2. Arrangement of Measuring Points
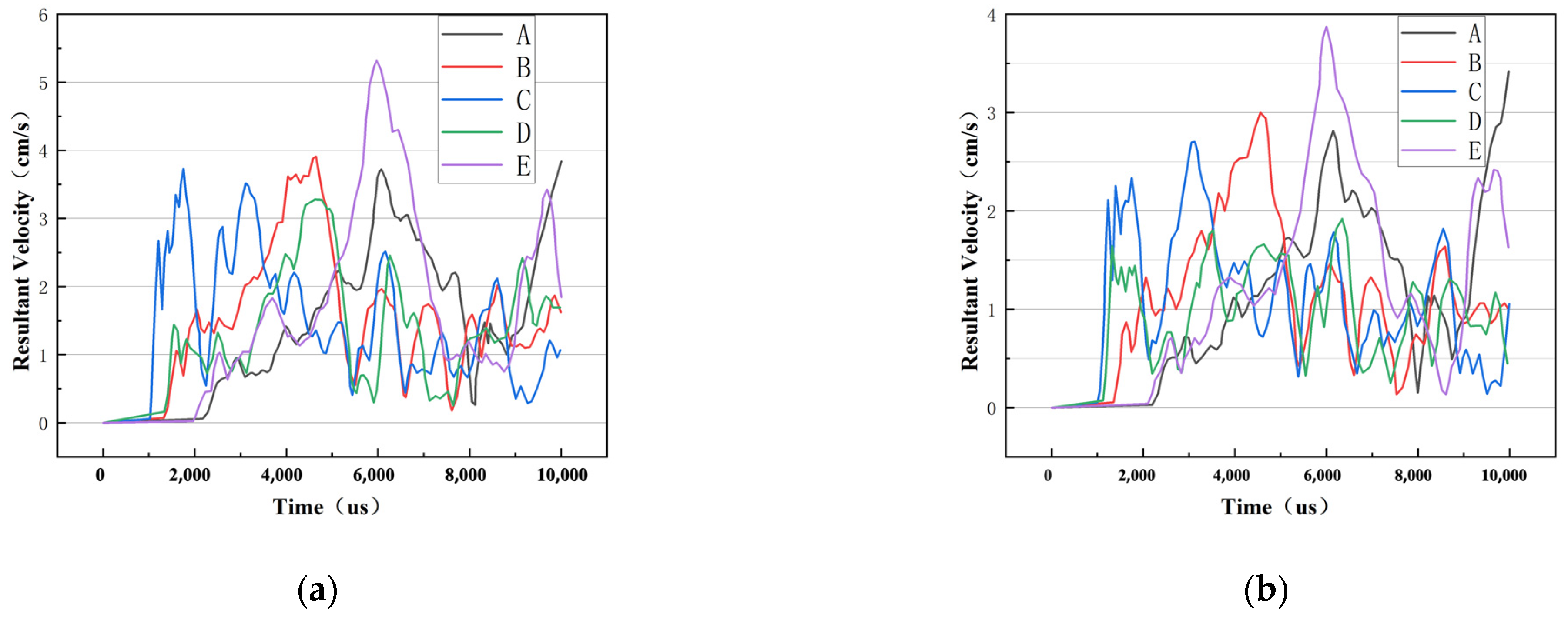
3.3. Comparison of Numerical Simulation Results
3.3.1. Stress Propagation Comparison
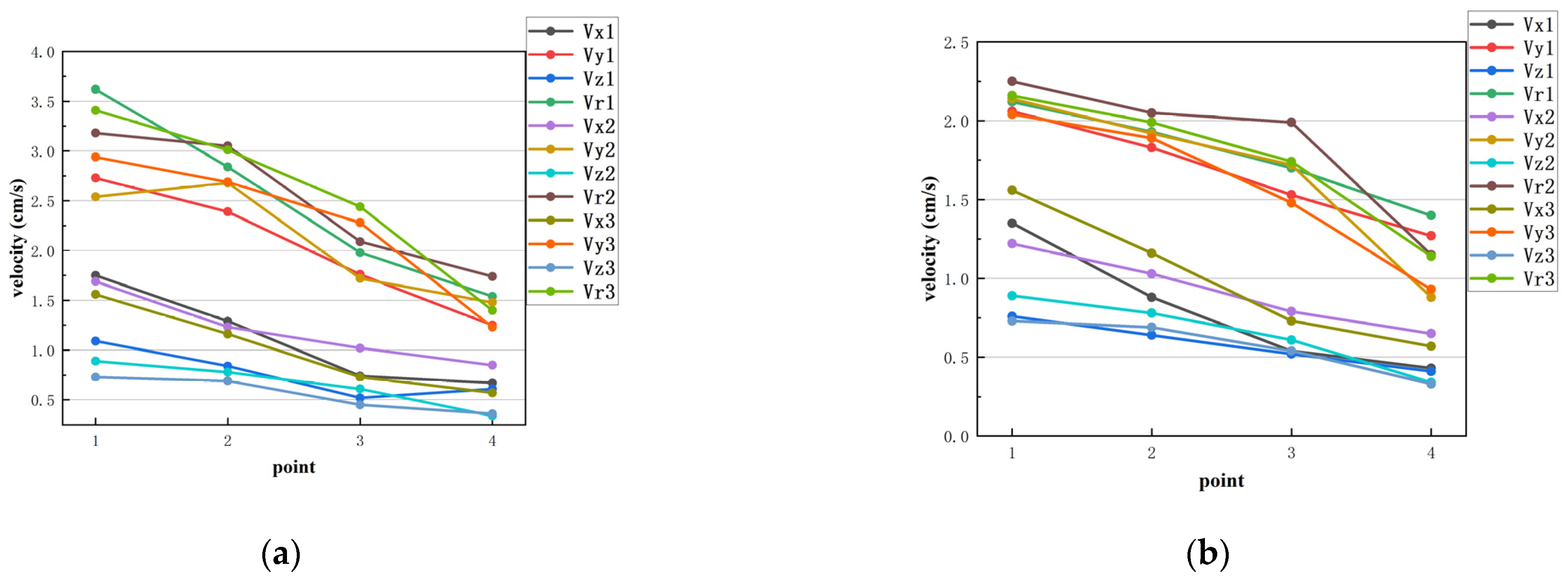
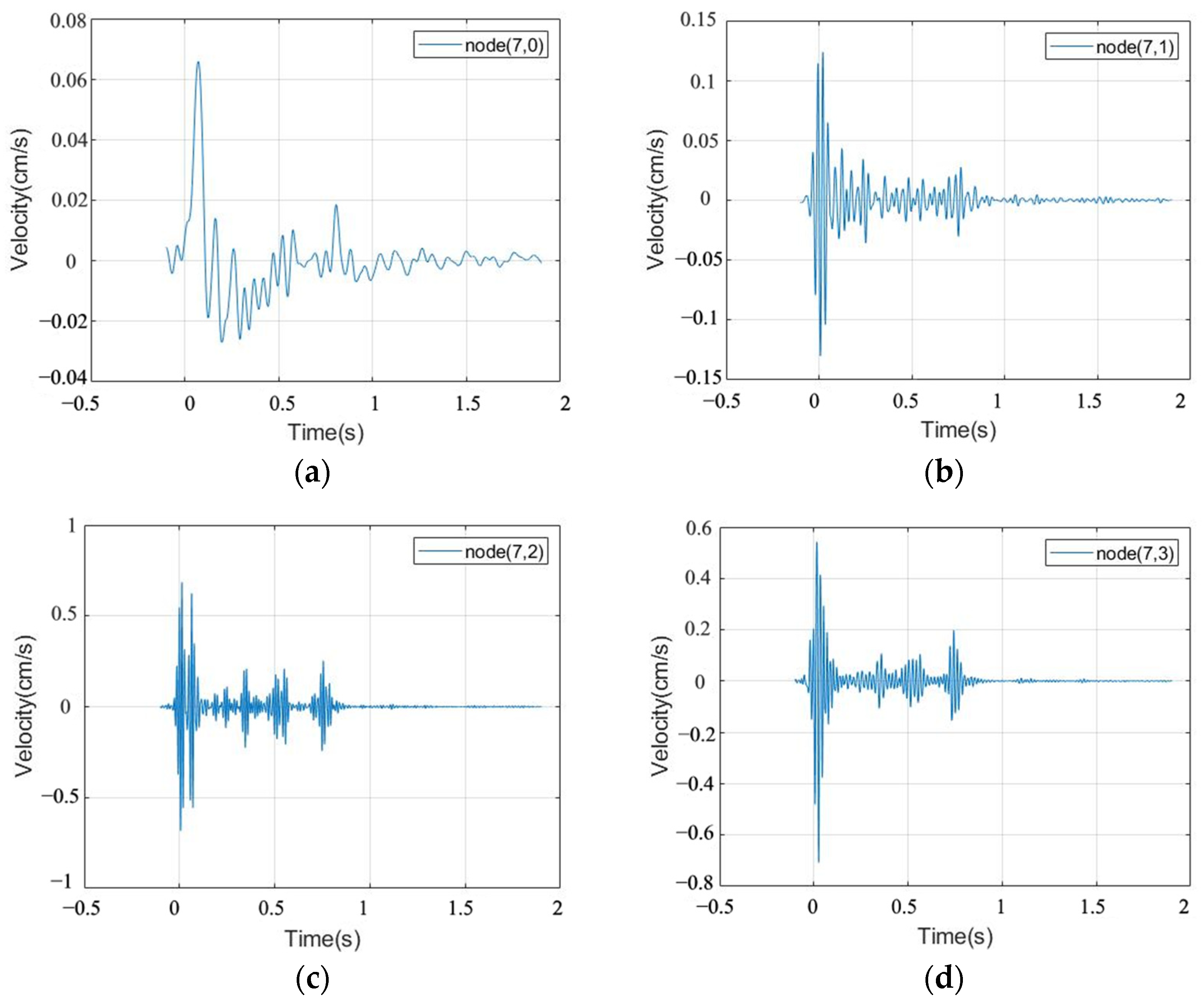
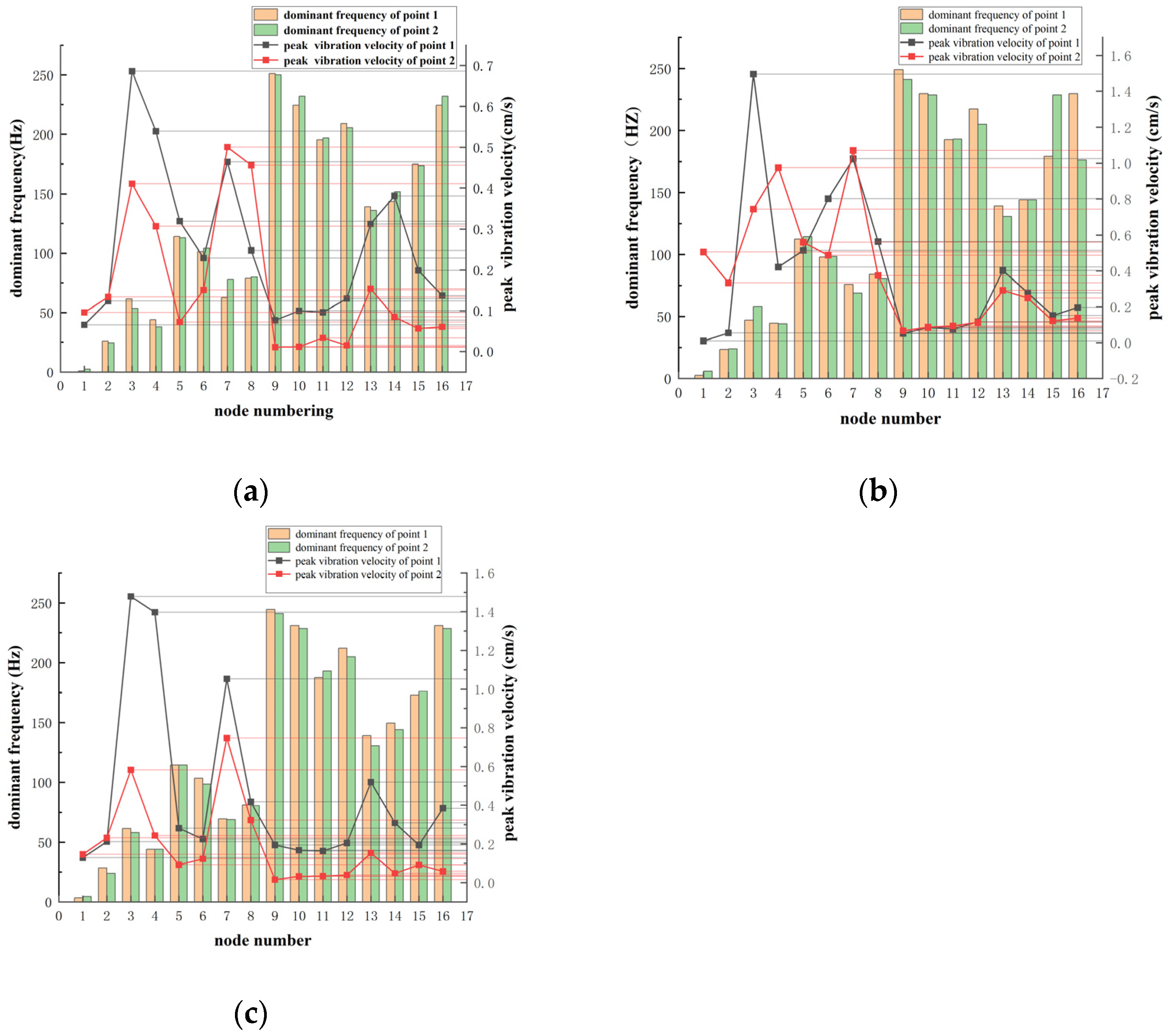
3.3.2. Comparison of Vibration Velocity
4. Field Experiment of Blasting Vibration Control
4.1. Arrangement of Existing Tunnel Measuring Points
4.2. Blasting Scheme
4.2.1. Normal Detonator Blasting
4.2.2. Mechanical Cutting Blasting
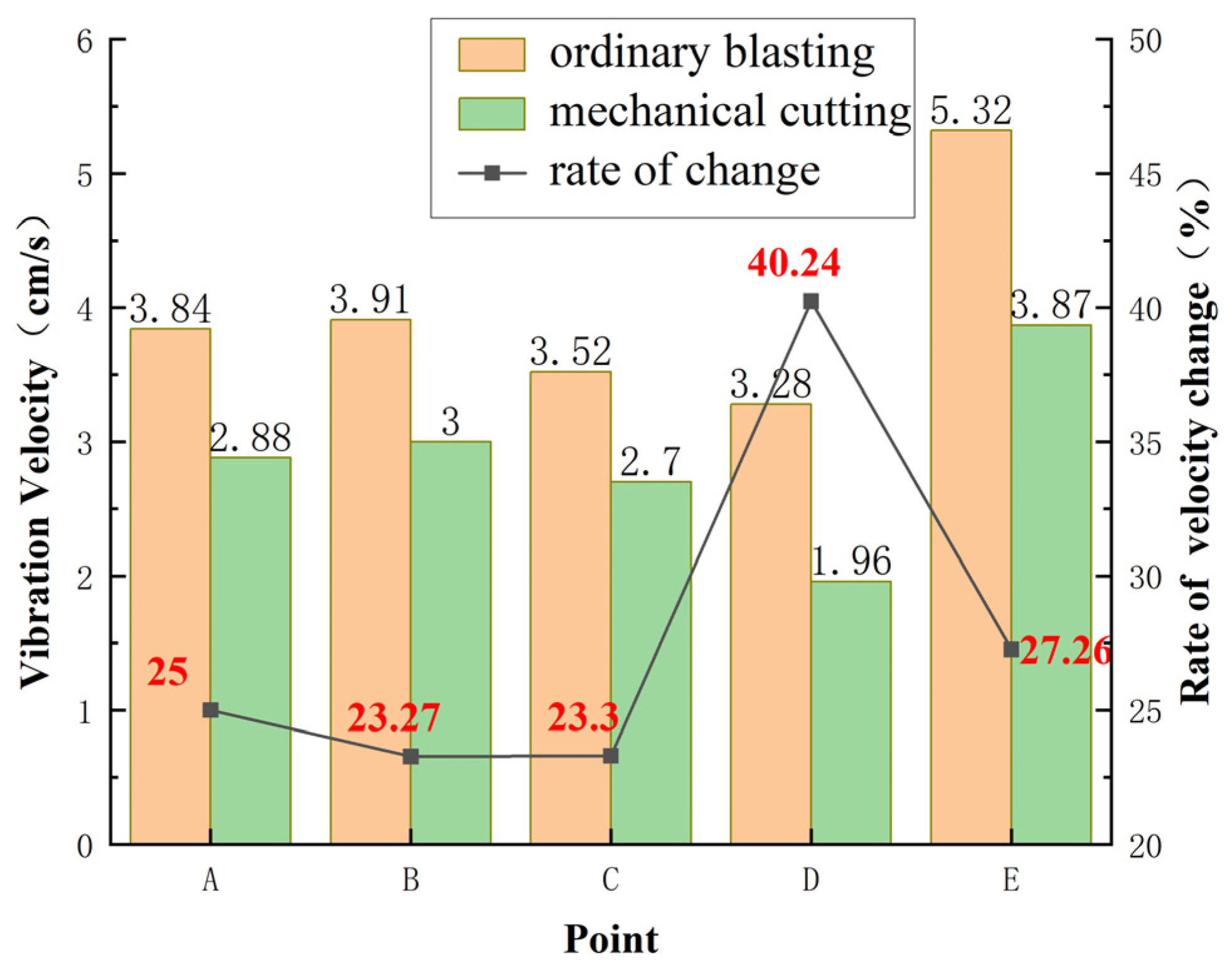
4.3. Comparison of Vibration Velocity
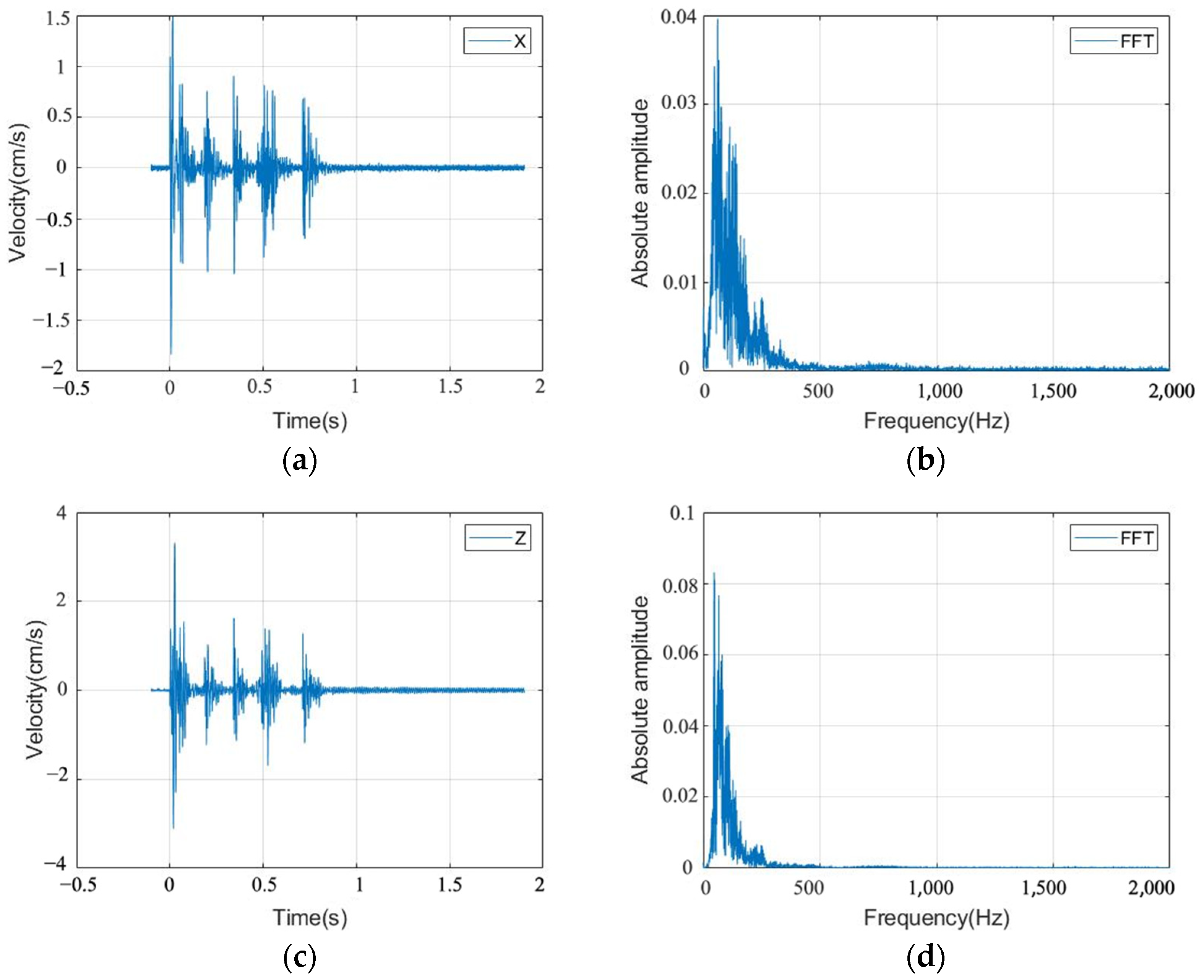
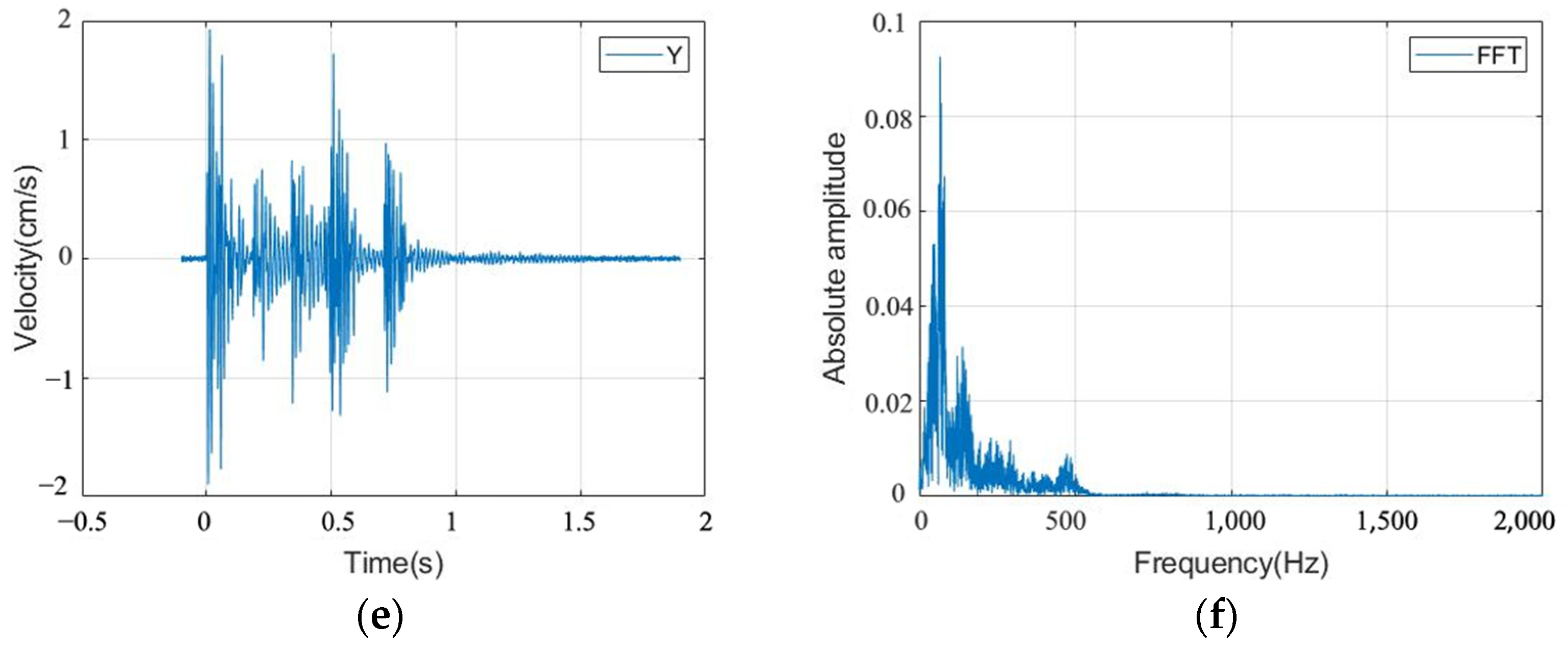
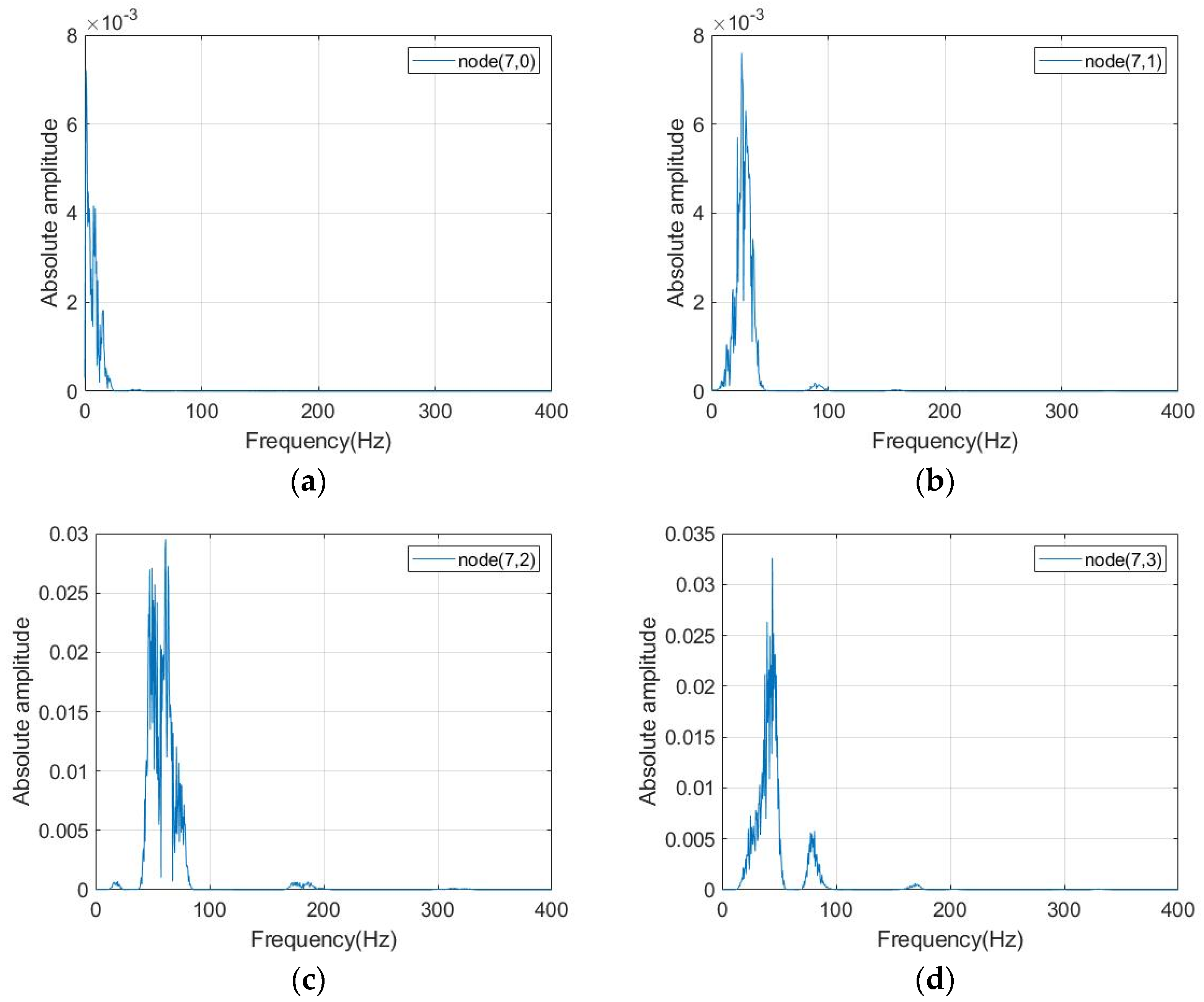
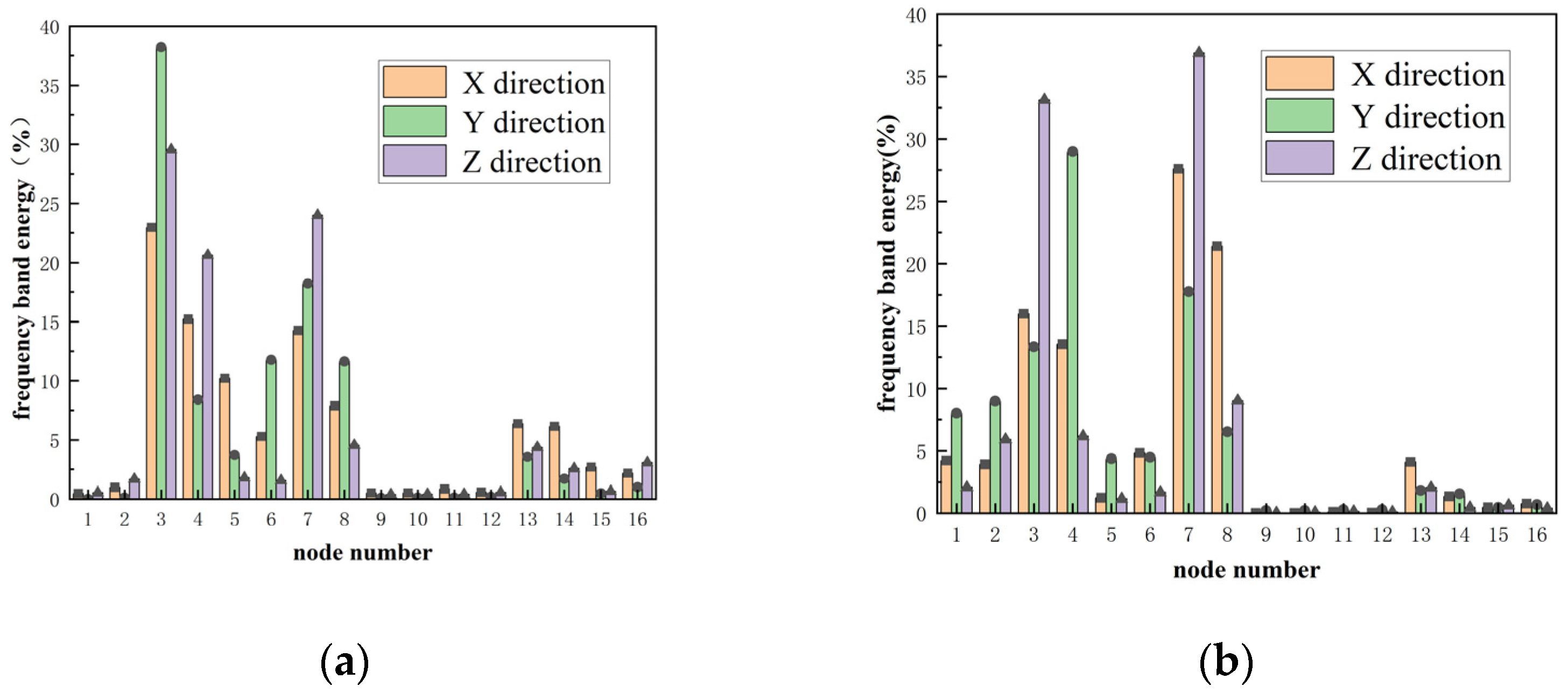
5. Wavelet Packet Analysis of Measured Data
6. Conclusions
- (1)
- When the full section detonator explodes, the stress wave spreads in an arc shape and has a large range. In the blasting of the mechanical cutting method, the second layer hole is connected with the mechanical cutting area, and the blasting stress wave propagates along the four directions of the cut hole to form a petal-shaped stress ring, and the diffusion range is obviously reduced.
- (2)
- The use of mechanical cutting instead of traditional cutting hole blasting can effectively reduce the blasting vibration. The vibration velocity of the existing deterioration tunnel is reduced by 38% maximum, and the vibration velocity of the other points is reduced by 20~30%. Mechanical cutting provides several free surfaces for the blasting of the surrounding holes of the tunnel, which can realize the vibration control of the blasting adjacent existing deterioration tunnel.
- (3)
- The energy of the blasting vibration signal is mainly concentrated near the frequency band where the main frequency of the original signal is located. The main excitation frequency range of the existing deterioration tunnel is 31.25~46.875 Hz, and the energy of the blasting vibration signal is not evenly distributed in the frequency band but is mainly concentrated in the low frequency band. The damage degree of surrounding rock decreases with the increase of distance. When the blasting seismic wave passes through the surrounding rock, the damping of the rock mass will filter out the vibration signal of higher frequency, which plays an effect similar to the low-pass filter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.G. Vibration safety impact assessment and technical measures for vibration reduction in blasting engineering. Water Resour. Plan. Des. 2015, 5, 95–97. [Google Scholar]
- Xia, C.C.; Liu, Z.F.; Shan, G.Y.; Shen, S.W. Explosive dosage calculation based on blasting vibration velocity and control value. Mod. Tunn. Technol. 2018, 4, 163–170. [Google Scholar]
- Jiang, H. Study on evaluation of shock-absorbing blasting scheme for urban underground tunnel driving. Bull. Sci. Technol. 2017, 33, 254–257. [Google Scholar]
- Li, G. Shock absorption control during underground excavation, drilling and explosion in subway engineering. Urban Roads Bridges Flood Control 2018, 5, 240–242. [Google Scholar]
- Li, Z.; He, C.; Wang, B.; Yang, S.Z.; Guo, X.X. Reasonable differential time interval of urban tunnel crossing composite strata. Pao Cha Yu Ch’ung Chi. Explos. Shock. Waves 2016, 1, 93–100. [Google Scholar]
- Tang, Y.; Cao, Y.; Luo, M.R.; Wu, Y.L. Application of high precision digital detonator in vibration reduction of blasting construction. Blasting 2011, 28, 107–109. [Google Scholar]
- Yang, Y. Interference vibration reduction technique of ultra-short delay step blasting between holes. Eng. Blasting 2019, 25, 53–59. [Google Scholar]
- Ma, J.; Li, X.L.; Wang, J.G.; Tao, Z.H.; Zuo, T.; Li, Q.; Zhang, X.H. Experimental Study on Vibration Reduction Technology of Hole-by-Hole Presplitting Blasting. Geofluids 2021, 2021, 5403969. [Google Scholar] [CrossRef]
- Ren, D.F.; Jian, Z.F.; Meng, X.D.; Zhang, X.M.; Zheng, W.C.; Meng, L.T. Application of digital detonator staggered shock absorption blasting technology in subway tunnel construction. Blasting 2020, 2, 53–59. [Google Scholar]
- Wu, X.D.; Gong, M.; Wu, H.J.; Hu, G.F.; Wang, S.J. Vibration reduction technology and the mechanisms of surrounding rock damage from blasting in neighborhood tunnels with small clearance. Int. J. Min. Sci. Technol. 2023, 33, 625–637. [Google Scholar] [CrossRef]
- Sun, Z.; Xie, S.Z.; Zhang, X.T.; Zhou, H.M.; Wang, H.L.; Wang, C. Vibration reduction effect of damping hole in blasting excavation of small distance tunnel. J. Shandong Univ. Sci. Technol. 2019, 1, 25–31. [Google Scholar]
- Yang, J.S. Study on staggered peak vibration reduction by triangular cut blasting in urban shallow buried tunnels. Eng. Blasting 2019, 20, 20–26. [Google Scholar]
- Ke, M.; Zhifei, S. Wavelet packet analysis on blasting vibration signal under different cutting method. J. Vibroeng. 2022, 24, 116–127. [Google Scholar]
- Zhou, Z.L.; Zhang, J.K.; Cheng, R.S.; Rui, Y.C.; Cai, X.; Chen, L. Improving purity of blasting vibration signals using advanced Empirical Mode Decomposition and Wavelet packet technique. Appl. Acoust. 2022, 201, 109097. [Google Scholar] [CrossRef]
- Wang, H.L.; Bai, H.B.; Zhao, Y.; Wang, B.; Wang, H.J. Denoising algorithm of blasting signal based on Fourier decomposition and wavelet packet analysis. Blasting 2021, 38, 37–44. [Google Scholar]
- Wang, W.; Li, X.H.; Chen, Z.B.; Fan, L.; Sun, F. Characteristic analysis of energy entropy of blasting vibration signal based on wavelet packet transformation. Explos. Mater. 2019, 6, 19–23. [Google Scholar]
- Chen, G.; Li, Q.Y.; Li, D.Q.; Wu, Z.-Y.; Liu, Y. Main frequency band of blast vibration signal based on wavelet packet transform. Appl. Math. Model. 2019, 74, 569–585. [Google Scholar] [CrossRef]
- Huang, D.; Cui, S.; Li, X. Wavelet packet analysis of blasting vibration signal of mountain tunnel. Soil. Dyn. Earthq. Eng. 2019, 117, 72–80. [Google Scholar] [CrossRef]
- Li, C.X.; Yang, R.S.; Wang, Y.B.; Kang, Y.Q.; Zhang, Y.T.; Xie, P. Theoretical and numerical simulation investigation of deep hole dispersed charge cut blasting. Int. J. Coal Sci. Technol. 2023, 10, 15. [Google Scholar] [CrossRef]
- Wu, H.J.; Gong, M.; Zhao, Q.; Wu, X.D.; Liu, X.Y. Vibration Energy Comparison Helps Identify Formation Time of New Free Surface in Urban Tunnel Blasting. Appl. Sci. 2022, 19, 10061. [Google Scholar] [CrossRef]
- Lou, Q.X.; Tao, T.J.; Tian, X.C.; Xie, C.J. Research on numerical simulation method of limestone impact failure based on HJC constitutive model. Blasting 2022, 39, 71–79. [Google Scholar]
- Li, F.; Wang, X.B. Wavelet packet analysis of controlled excavation blasting signals in a nclear power plant. Min. Eng. Res. 2016, 31, 1–5. [Google Scholar] [CrossRef]
- Fei, H.; Zeng, X.Y.; Yang, Z.G. Wavelet packet analysis of tunneling blasting vibration on earth surface. Explos. Shock Waves 2017, 37, 77–83. [Google Scholar]
- Shan, R.L.; Song, Y.W.; Bai, Y. Study on energy attenuation characteristics of blasting signals based on wavelet packet transform. J. Min. Sci. 2018, 3, 119–128. [Google Scholar] [CrossRef]
- Tang, F.Y.; Wang, J.Z.; Cui, Z.R. Application of energy criterion in blasting vibration safety. Blasting 2009, 4, 85–88. [Google Scholar]
- Han, L.; Xin, C.W.; Liang, S.F. Experimental study on vibration characteristics of deep-hole step blasting in near and far regions. J. Vib. Shock 2017, 36, 65–70. [Google Scholar] [CrossRef]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Chen, J.H.; Qiu, W.G.; Zhao, X.W.; Wang, H.L. Vibration characteristics analysis of the metro tunnel subarea blasting based on wavelet packet technology. J. Vib. Shock 2022, 6, 222–228+255. [Google Scholar] [CrossRef]
- Zhu, Q.J.; Jiang, F.X.; Yu, Z.X. Study on energy distribution characteristics of blasting vibration and microseismic signal of rock failure. Chin. J. Rock Mech. Eng. 2012, 4, 723–730. [Google Scholar]
- Shan, R.L.; Bai, Y.; Song, Y.W. Wavelet packet analysis of blasting vibration signal of frozen vertical shaft model. J. China Coal Soc. 2016, 8, 1923–1932. [Google Scholar]
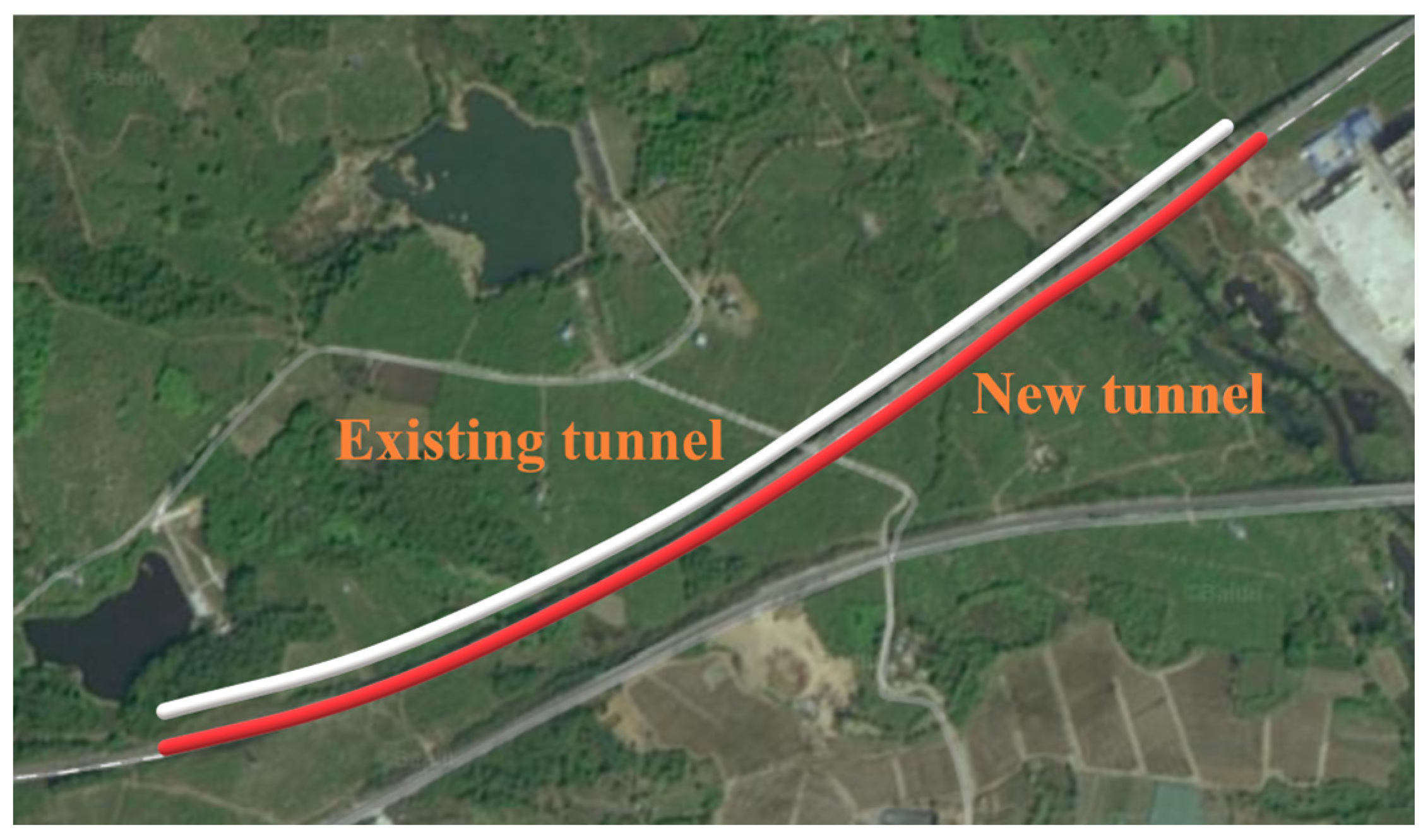

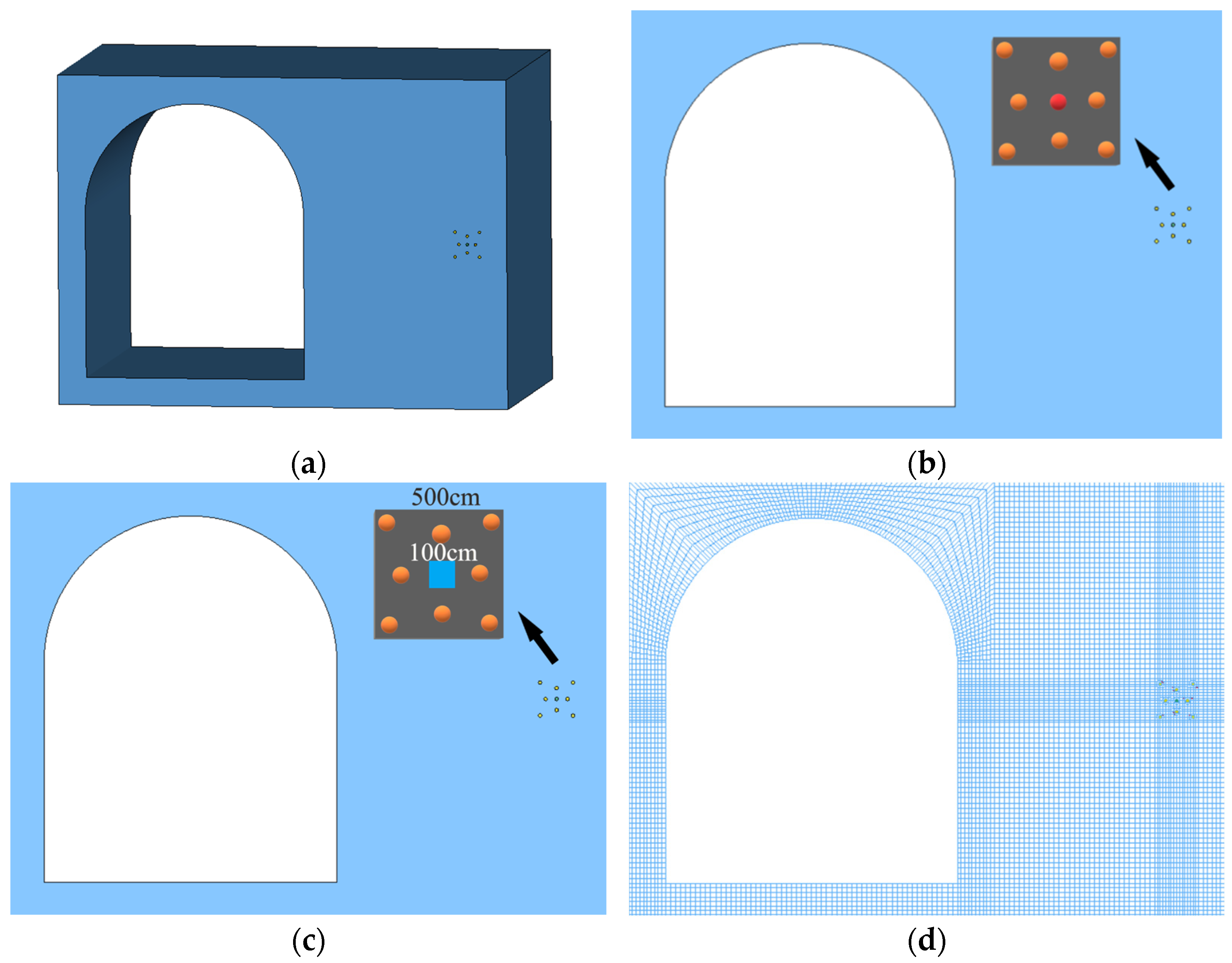
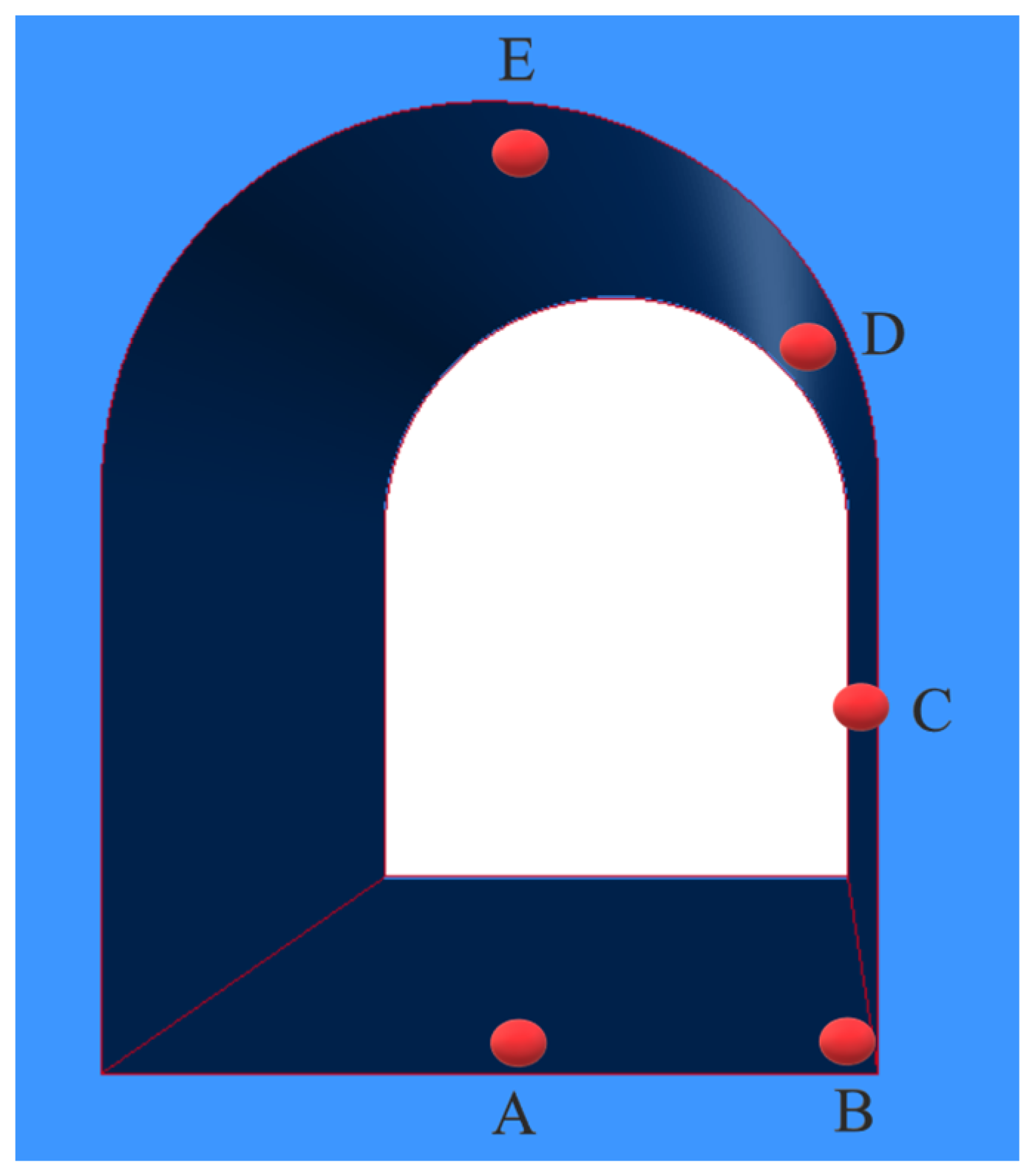

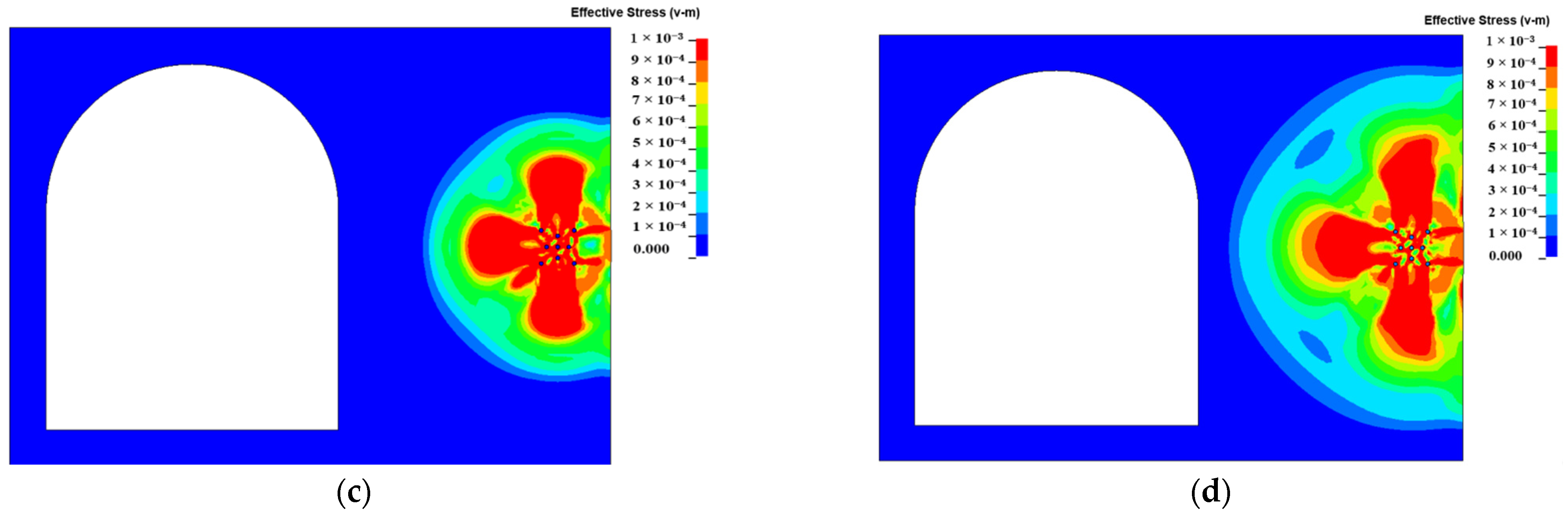



| Mileage | Relative Altitude (m) | Relative Relation | Structure |
|---|---|---|---|
| DK346 + 880~DK347 + 285 | 32.987~36.430 | parallel | existing tunnel |
| DK346 + 880~DK347 + 285 | 32.987~36.430 | parallel | kerosene pipe |
| DK347 + 140 | 35.197 | above | power tower |
| EOSID | A | B | OMEG | ||||
|---|---|---|---|---|---|---|---|
| 3 | 2.762 | 0.0844 | 5.2 | 2.1 | 0.5 | 0.0387 | 1.0 |
| 2400 | 13 | 0.275 | 24 | 1.1 | 1.12 | 44.5 | 0.0015 | 1.2 × 10−6 | 1 × 10−7 | 0.11 |
| 5.0 | 1.46 | 3.5 × 10−4 | 0.01 | 0.1 | 0.04 | 1.0 | 0.12 | 0.25 | 0.42 | 0 |
| Hole Class | Number | Hole Diameter (mm) | Segment | Hole Depth (m) | Charge in a Single Hole (kg) | Cumulative Charge (kg) |
|---|---|---|---|---|---|---|
| Cutting hole | 8 | 42 | 1 | 1.6 | 0.9 | 7.2 |
| Auxiliary hole | 10 | 42 | 3 | 1.3 | 0.3 | 3.0 |
| 10 | 42 | 5 | 1.3 | 0.3 | 3.0 | |
| Peripheral hole | 15 | 42 | 7 | 1.3 | 0.3 | 4.5 |
| 20 | 42 | 9 | 1.3 | 0.3 | 6.0 | |
| Bottom hole | 11 | 42 | 11 | 1.3 | 0.3 | 3.3 |
| Total | 74 | 27.0 |
| Hole Class | Number | Hole Diameter (mm) | Segment | Hole Depth (m) | Charge in a Single Hole (kg) | Cumulative Charge (kg) |
|---|---|---|---|---|---|---|
| Auxiliary hole | 10 | 42 | 3 | 1.3 | 0.3 | 3.0 |
| 10 | 42 | 5 | 1.3 | 0.3 | 3.0 | |
| Peripheral hole | 15 | 42 | 7 | 1.3 | 0.3 | 4.5 |
| 20 | 42 | 9 | 1.3 | 0.3 | 6.0 | |
| Bottom hole | 11 | 42 | 11 | 1.3 | 0.3 | 3.3 |
| Total | 66 | 19.8 |
| Layer | Si,0 | Si,1 | … | Si,j−1 | Si,j |
|---|---|---|---|---|---|
| 1 | 0~1000 | data | … | 1000~2000 | |
| 2 | 0~500 | 500~1000 | … | 1000~1500 | 1500~2000 |
| 3 | 0~250 | 250~500 | … | 1500~1750 | 1750~2000 |
| 4 | 0~125 | 125~250 | … | 1750~1875 | 1875~2000 |
| 5 | 0~62.5 | 62.5~125 | … | 1875~1937.5 | 1937.5~2000 |
| 6 | 0~31.25 | 31.25~62.5 | … | 1937.5~1968.75 | 1968.75~2000 |
| 7 | 0~15.625 | 15.625~31.25 | … | 1968.75~1984.375 | 1984.375~2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Shi, J.; Zhang, H. Blasting Vibration Control and Signal Analysis of Adjacent Existing Deterioration Tunnels. Appl. Sci. 2024, 14, 2212. https://doi.org/10.3390/app14052212
Xu W, Shi J, Zhang H. Blasting Vibration Control and Signal Analysis of Adjacent Existing Deterioration Tunnels. Applied Sciences. 2024; 14(5):2212. https://doi.org/10.3390/app14052212
Chicago/Turabian StyleXu, Wenxiang, Jianjun Shi, and Hao Zhang. 2024. "Blasting Vibration Control and Signal Analysis of Adjacent Existing Deterioration Tunnels" Applied Sciences 14, no. 5: 2212. https://doi.org/10.3390/app14052212
APA StyleXu, W., Shi, J., & Zhang, H. (2024). Blasting Vibration Control and Signal Analysis of Adjacent Existing Deterioration Tunnels. Applied Sciences, 14(5), 2212. https://doi.org/10.3390/app14052212





