Abstract
Workpiece placement plays a crucial role when performing complex surface machining task robotically. If the feasibility of a robotic task needs to be guaranteed, the maximum available capabilities should be higher than the joint capabilities required for task execution. This can be challenging, especially when performing a complex surface machining task with a collaborative robot, which tend to have lower motion capabilities than conventional industrial robots. Therefore, the kinematic and dynamic capabilities within the robot workspace should be evaluated prior to task execution and optimized considering specific task requirements. In order to estimate maximum directional kinematic capabilities considering the requirements of the surface machining task in a physically consistent and accurate way, the Decomposed Twist Feasibility (DTF) method will be used in this paper. Estimation of the total kinematic performance capabilities can be determined accurately and simply using this method, adjusted specifically for robotic surface machining purposes. In this study, we present the numerical results that prove the effectiveness of the DTF method in identifying the optimal placement of predetermined machining tasks within the robot’s workspace that requires lowest possible joint velocities for task execution. These findings highlight the practicality of the DTF method in enhancing the feasibility of complex robotic surface machining operations.
1. Introduction
The complexity of production processes and the variety of products in small and medium-sized businesses with high-mix, low-volume production require relatively high investment costs in the case of conventional industrial robotization [1]. This has resulted in a shortage of robotic work processes within small-scale production companies. Thus, most production processes are still performed manually, which often cannot ensure optimal and competitive production. The development of collaborative robotic systems in combination with other technologies offers more and more [2] opportunities for the automation of jobs, even in companies with custom production such as the toolmaking industry.
A collaborative robotic system aims to achieve more flexible execution of even highly complex tasks. It can also help to increase the adaptability of robotic systems by incorporating humans into the work process [3,4] when full automation is not viable or financially justifiable. Collaborative robots assist humans to achieve a more efficient work process by relieving them of monotonous and physically demanding tasks, while the humans use their abilities of flexibility, adaptability, and intelligence. As a result, improved productivity and market competitiveness could be achieved by this approach. To attain greater flexibility and adaptability of collaborative robotic systems, and thus shorten the time required to implement a specific robotic task solution, some algorithms have recently been developed to enable more autonomous trajectory planning [5]. To make such robotic tasks feasible, a thorough understanding of the robot’s moving abilities within its working space is essential for planning and executing more complex robotic tasks, such as robotic surface machining [6].
In the case of complex robotic tasks, where simultaneous tracking of the tool tip along the surface of the workpiece at a constant tool speed is required, such as milling [7,8], welding [9], composite laying [10,11] or hammer peening, it is not always necessary that such a task will be feasible with the required technological parameters for arbitrary workpiece placement in the robot’s workspace. The available motion capabilities are reduced significantly if we compare collaborative robots to traditional industrial robots, due to the size of the integrated actuators [6]. The predefined robot’s surface machining path will be executable successfully according to the required technological parameters only if we determine the appropriate placement of the workpiece. To ensure that the collaborative robot’s capabilities will not be exceeded during the execution of the robotic task, it is necessary to determine the workpiece placement for which the robot’s movement capabilities are the best possible. Moreover, this ensures the robotic task can be accomplished with increased tool speed, which results in significant time savings during the usually time-consuming surface machining process.
In the past, researchers have searched for the optimal position of the workpiece based on different kinematic criteria. Due to the reduced stiffness of robots compared to conventional CNC machines, optimal workpiece placement was determined to optimize the stiffness of the robot along a trajectory, and thereby increase the accuracy of robotic machining, such as robotic milling [8,12,13]. By optimizing workpiece placement, the improved accuracy of robot-based additive manufacturing can be achieved, particularly for applications such as robotic 3D printing [14]. The primary goal of determining the optimal placement of the workpiece for other authors has been to minimize energy consumption [15,16]. In the case of collaborative robots, authors often search for the kinematically optimal placement of the workpiece in order to ensure the feasibility of the robotic task [11,17], to perform the task as quickly as possible without exceeding the robot’s maximum kinematic capabilities [18], or to identify optimal workpiece placement that results in the maximum possible manipulability and consequently requires the lowest possible joint torques [19].
Different objective functions can be chosen in order to determine the optimal placement of the workpiece. For kinematically optimal placement of the workpiece, most authors use well-accepted and widely used methods, such as the Yoshikawa manipulability index [20], the minimum singular value, or the condition number. These quantitative measures represent approximation of the general motion ability, which are not sufficiently reliable if we have to improve the directional motion capabilities along the required task direction. In this case, the manipulator velocity ratio is usually used to estimate the ability to move in the desired direction. Some other authors also include additional criteria in the optimization process, such as constraints related to joint limits, singularities, collisions with the environment [21], etc.
To determine the optimal placement of a known robotic path composed of a set of waypoints, it is necessary to evaluate the motion capabilities of each waypoint on the robotic path and formulate an appropriate objective function that characterizes the placement of the entire path in the form of a single scalar value. Some authors maximize the mean value of the velocity performance measure to find the optimal path placement [22,23,24]. The mean value is simple to calculate and understand. However, sometimes the mean result can be misleading if the spread of results is uneven. Since the average is computed considering all the data values in a data set, it is influenced highly by the outliers, especially if they are located on only one side of the data set. In the case of workpiece placement, a high average value may indicate a workpiece placement where the selected kinematic index is extremely high, while, for other waypoints, the movement capabilities may be considerably worse, and vice versa. In [22,24], the minimum value of kinematic performance measures is selected, which characterizes the worst kinematic abilities throughout a path to determine the best worst-case performance along the path.
In this paper, we will optimize workpiece placement by maximizing the motion capabilities along the entire path, whereby the evaluation of the maximum achievable tool velocity will be based on the DTF (Decomposed Task Feasibility) method presented in [25]. Unlike other methods, the DTF method offers a simple and accurate solution for the determination of the total directional kinematic capabilities of each waypoint on the path, and it is specifically designed for robotic surface machining purposes as we show in this paper via a short analysis, which incorporates differential geometric properties of the machining path on the workpiece surface. The optimization results will determine the workpiece placement that requires the lowest possible joint velocities for task execution. The numerical results will confirm the effectiveness of the DTF method in the case of the optimal placement of a predefined machining task within the robot’s workspace. Thereby, the feasibility and increased flexibility of the robotic machining task can be achieved in combination with intuitive collaboration between human and robot.
The remainder of this paper is structured as follows. In Section 2, the intuitive human–robot collaboration is presented in the case of the definition of the robotic machining task. The related methods for evaluation of the feasible kinematic directional capabilities are also outlined. In the same section, a DTF method is described to evaluate the achievable linear and angular velocities when synchronized motion is required, such as in the case of the robotic surface machining applications, and geometric analysis of the DTF method is also given. An optimization problem for optimal workpiece placement is also formulated in this section, and the case studies are described by six different robot paths. In Section 3, the numerical results of the described optimization problem in the case of the UR5e robot are shown, and their validation is given based on the comparison of four different placements of each analyzed workpiece. Finally, Section 4 provides a discussion along with a corresponding conclusion.
2. Materials and Methods
2.1. Human–Robot Collaboration
In industry, we often encounter workpiece finishing technologies, where the tool must accurately follow the path along the surface of a geometrically complex surface. This is one of the most complex tasks for robotization. As a result, in the traditional approach, the use of expensive CAD/CAM software, which requires highly skilled and experienced professionals, is inevitable. Furthermore, preparation of a robot program might be a very time-consuming process with numerous iterations with a simulation phase in the loop. In addition, the setup of the robotic cell (which must be designed to fulfill safety requirements related to ISO 10218 [26]) with an industrial robot and a workpiece on the worktable can also be very demanding. Such an approach presents quite a challenge in custom-based low-volume, high-mix industry. An alternative approach can employ an open cell with a collaborative robot complying with ISO/TS 15066 [27], which provides harmless physical contact with a human worker, and is easy to use. Then, we can usefully exploit these good features of collaborative robots to design a fast and intuitive robot-teaching process. Thus, robot machining may be significantly simplified and such a process, in which we could employ less skilled human operators. In this paper, we briefly present possible solution in part one. The process workflow can be divided into a number of major phases: (i) setting the workpiece on the worktable; (ii) clamping the workpiece; (iii) determining workpiece placement; (iv) setting the workpiece area for surface finishing; (v) generating a machining path within the selected area; (vi) setting up the technological parameters; (vii) verification of the machining path; (viii) execution of the robot task; and (ix) visual inspection of the finished workpiece. In this paper, we highlight the definition of the robot task, which can be performed intuitively in the collaborative mode. The definition of the machining area on the workpiece can be performed in collaborative mode by kinesthetic guidance of the robot in such a way that the operator determines all the boundary points of the processing surface by touching the surface of the workpiece with the tip of the robot tool. The activation of the kinesthetic guidance of the robot is initiated by pressing a control button on the user ring mounted on the robot flange. Thus, the robot switches to the so-called free-drive mode. The boundary position points of the area can be determined manually by the operator and saved point-by-point. The holographic interface enables direct graphic representation of the defined surface, according to the tapped points. It may also enable set up of most of the important technological parameters to support easy and intuitive use of the flexible robot cell, as can be seen from Figure 1.
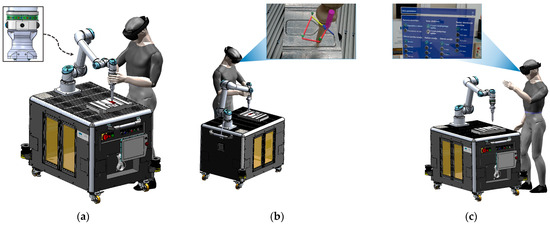
Figure 1.
Intuitive definition of the robotic surface machining area through human–robot collaboration: (a) the kinesthetic guidance of the robot, (b) the definition of the machining area through a holographic interface, (c) setting up the technological parameters through a holographic interface.
The described workflow above can become stuck in the verification phase, i.e., it can show that the robot task is not feasible for a variety of reasons, among which we emphasize kinematic feasibility due to the speed limits of the robot’s joints, which are typically rather low in case of collaborative robots. Then, it is necessary to break the workflow, and then to repeat the sequence and reposition the workpiece, clamp it again, determine its placement, set the workpiece machining area (optionally), etc., and if the verification fails again, it should be repeated again. This may be quite a cumbersome process and it may take numerous iterations before it ultimately results in the feasible position of the workpiece. In order to simplify it, it is necessary to insert an additional subprocess into the workflow, which will provide optimization of the workpiece position by taking into account the feasibility issue.
2.2. Feasible Kinematic Directional Capabilities
To ensure the feasibility of the predefined machining task, workpiece placement should be such that all waypoints on the surface are reachable by the robot, and the tool tip can move between them with the desired tool speed. To find such placement of a robotic machining trajectory, motion capabilities have to be analyzed for each segment of the desired path. Some existing kinematic performance indices are typically used for this purpose [28]. A detailed review of the related studies has found that most of them overlook the exact task requirements, suffer from physical inconsistency, do not include the maximum kinematic limits in the consideration, or are computationally intensive.
When evaluating a robot’s ability to move its end-effector toward an arbitrary direction, a qualitative measure based on analyzing the manipulability ellipsoid is most often used, which was first introduced by Yoshikawa [20]. It is shown in Figure 2 and defined as:
where is a Jacobian matrix of the robot mechanism, with elements of and i = 1…m, j = 1…n. Yoshikawa’s manipulability index aims to provide information regarding the proximity to a singular configuration. Additionally, the condition number, or minimum singular value [29], can also be used to estimate the proximity to a singular configuration. These indices offer a general evaluation of a robot’s capabilities, which can be useful for optimizing the design [30] or other general characteristics of a robot. But it is important to note that these performance measures are often of limited practical usefulness, particularly when the focus is on improving the directional kinematic capabilities within a predefined robotic task.
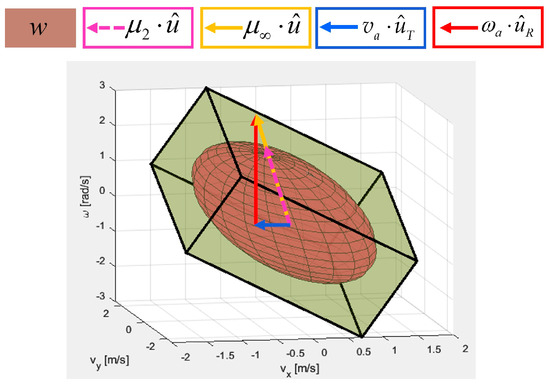
Figure 2.
Graphical representation of the Yoshikawa manipulability index ; maximum feasible tool velocity (ellipsoid approach); maximum feasible tool velocity (polytope approach); maximum linear velocity (DTF method); and maximum angular velocity (DTF method) in the case of a 3-DOF planar robotic mechanism.
For evaluation of the directional kinematic capabilities of the robot’s end-effector, researchers have proposed various performance metrics. One such metric, presented in [31], involves calculating the distance from the center to the surface of the manipulability ellipsoid along the desired directional vector. This metric is also named the manipulator velocity ratio, which was first presented in [32], and defined as:
where denotes the direction of the end-effector velocity vector, and is the scalar, which represents the velocity transmission ratio in direction , as is shown in Figure 2. By utilizing the Euclidian norm, this approach provides estimation of a robot’s motion capabilities in the task space relative to the robot effort required in the joint space. Another approach, outlined in [32], suggests using the manipulability polytope as an alternative metric, which is obtained considering the exact joint velocity limits. The magnitude of the maximum feasible tool velocity along under the velocity constraints, as can be seen from Figure 2, can be expressed as:
where is the minimum infinity norm solution of . In comparison to the manipulability ellipsoid, the manipulability polytope seems to be more appropriate for the calculation of the robot’s feasible task-space capabilities, while it considers the exact joint velocity limits. However, both methods could lead to a performance measure that combines linear and angular movement capabilities into a single scalar value, which makes the calculation physically inconsistent [33]. Different methods have been proposed to address this issue and overcome the problem of physical inconsistency. Some authors have introduced new performance measures [34,35], which consider only translational directional capabilities. Another method, proposed in [36], involves power manipulability as a fully homogeneous and physically consistent performance measure. Unfortunately, establishing a direct relationship between the power vector and particular task requirements could be challenging in this case.
Since elements of the twist vector space do not share the same physical unit, the linear and angular velocity capabilities should be addressed independently. Therefore, Yoshikawa [37] separated the total manipulability measure into translational and rotational manipulability measures. He introduced the translational and rotational manipulability measures in both weak and strong senses. Similarly, the separated translational and rotational capabilities can be defined based on the manipulability polytope approach [38]. In this case, two different types of weak-sense manipulability polytope can be obtained, i.e., the velocity polytope and the velocity polytope, respectively. The weak-sense manipulability polytope can be used only in the case where the angular velocity is irrelevant to the task execution [38,39,40], which is not suitable in the case of robot machining applications. The set of all linear (angular) velocities that are feasible under the constraints that the tool orientation is kept constant form the translational (rotational) manipulability polytope in the strong sense [37,41,42]. However, robot surface machining applications with purely translational (rotational) motion exist rarely in actual industrial cases.
To avoid the shortcomings of the described methods in the case of simultaneous linear and angular motion analysis, a method called Decomposed Twist Feasibility (DTF) was presented in [25], to evaluate accurate and physically meaningful information about a feasible linear and angular velocity in a specific task direction for robotic machining purposes. The kinematic capabilities of the tool in a task space are limited by the joint velocity limit. To determine the maximal velocity capabilities in the task space, we also need take the desired motion synchronization into consideration. Therefore, the maximum linear and angular velocity can be derived from the condition:
and as a result, it can be calculated based on the DTF method as:
where denotes a 3xn translational Jacobian submatrix, denotes a 3xn rotational Jacobian submatrix, is the unit vector in the desired linear velocity direction and is the unit vector in the desired angular velocity direction. Here, we considered and , where and represent the linear velocity vector and the angular velocity vector, respectively, as can be seen from Figure 2; whereas, and stand for the linear speed and the angular speed, respectively.
In contrast to the existing methods, where the desired motion synchronization is not considered, the relative importance of the synchronized linear and angular motion is, in the case of the DTF method, considered by a task-dependent velocity ratio factor that represents synchronization between linear and angular velocity; it is independent of velocity profile scaling. It can be computed from the kinematic parameters as ; however, in robotic machining, it can be considered as a parameter that exclusively depends on the geometry of the workpiece surface and the machining path.
2.3. Geometric Analysis of the DTF Method for 5-Axis Robotic Machining
In the following, we provide a geometric analysis of the DTF method under the assumption that we consider the robotic motion problem to be a 5-axis robotic machining process in which the tool tip is required to follow the path embedded on the workpiece surface while maintaining normal orientation to the surface with zero tool rotation about its own axis. In this case, the angular velocity of the robot end-effector can be determined as:
where is the unit normal vector on the surface at a path point, is its time derivative, and stands for vector cross product. In addition, we can introduce the Darboux frame along the curve on the surface [43], which is associated with the path point and constructed on the surface as a moving frame along the path curve such that it consists of triple-unit orthogonal vectors , where stands for the unit curve tangent vector and can be called a unit bitangent vector; vectors and span the tangent plane that is perpendicular to the normal vector and is attached to the surface at the path point. The triple evolves along the path curve such that its differential can be described by the following formula:
where , , and are the point-specific curve-on-surface characteristic properties, i.e., the normal curvature, the geodesic curvature, and the geodesic torsion of the path curve at that point, respectively; whereas, denotes a differential and stands for the differential path length. These functions determine important properties for surface curves. The normal curvature is related to the measure of the curve curvature that is due to the curvature of the underlying surface—it is projected onto the plane, which is spanned by the vectors, and can be used to tell us the extent to which the surface itself is curving along the curve. The geodesic curvature is the curvature of the curve projected onto the surface tangent plane spanned by vectors and . And the geodesic torsion is the relative torsion that measures the rate of change in the surface normal around the curve’s tangent—it is related to the rate of rotation of the tangent plane around the tangent of the curve.
From (8) one can deduce the time derivative of the unit normal vector as:
where represents the linear speed of a virtual particle, which travels along the path curve. Through the combination of (7) and (9) we can now derive the angular velocity vector as:
The latter result shows that the angular velocity depends on the surface and path curve characteristics since it is embedded on the workpiece surface. If we consider and then the angular speed can be further derived as:
Finally, the task-dependent parameter can be expressed from (11) as:
It is clearly shown that parameter is determined only by the curve-on-surface geometry characteristics expressed via the normal curvature and the geodesic torsion.
Furthermore, the angular velocity direction can be computed as follows:
One should note that, in our case, the unit tangent vector is fully aligned with the linear velocity vector such that and the latter result can be rewritten as:
If we introduce the skew-symmetric matrix such that the cross product in (14) can be replaced by the matrix product as , then it yields:
where is a diagonal matrix of proper dimension. We can clearly see the dependance of the angular velocity direction on the curve-on-surface characteristics (expressed via the curve normal curvature, the curve geodesic torsion, and the surface normal) that is related to the geometry of the surface workpiece and the machining path. However, the direction of angular velocity is also determined by the linear velocity direction, i.e., by the path’s curve tangent direction vector; the angular velocity is synchronized with the linear velocity via the curve-on-surface characteristics.
We can conclude that, in the case of 5-axis robotic machining, the parameter of maximum linear (angular) speed () from Equation (5) (Equation (6)) depends not only on the robot kinematics but also on the workpiece surface characteristics and the machining path curve embedded on the surface as is shown analytically by (7)–(15).
2.4. Optimal Workpiece Placement
Finding the optimal placement of the workpiece can often be crucial for completing a complex manufacturing task successfully. In order to reach all the waypoints on the workpiece surface and move between them at the required tool speed, the robot has to operate below its maximum kinematic capabilities. Therefore, the goal of the optimization process is to find the workpiece placement relative to the robot’s base position that maximizes the robot’s ability to move along the specified path on the surface, which results in the completion of the robotic task with the lowest joint velocities.
Each workpiece has its own local coordinate system {O}, which is positioned at one of the corners of the workpiece, and determines the workpiece’s placement relative to the robot’s base frame {B}, as can be seen from Figure 3. The placement of the local coordinate system of the workpiece {O} can be determined by three variables (X,Y,φ). By moving the workpiece in the X-Y plane, the position of the workpiece can be determined relative to the robot’s base frame {B} on the mobile platform. The orientation of the workpiece can be adjusted by rotating it around the z-axis, represented by the angle φ. The z-axis position of the workpiece remains fixed, and is determined by the height of the mobile platform, while the rotations are also fixed around the X and Y axes.
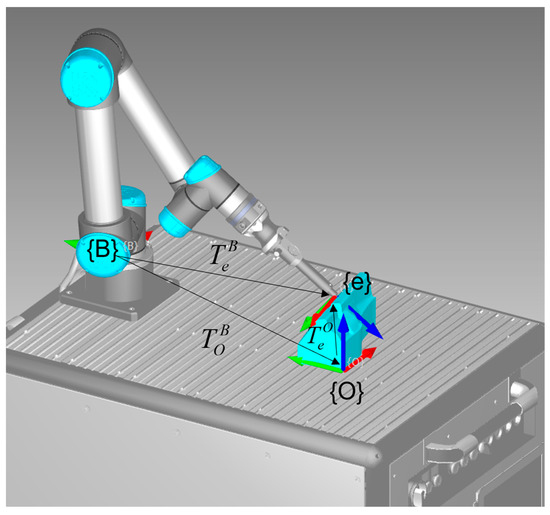
Figure 3.
UR5e collaborative robot on a mobile platform and presentation of the coordinate system (red-green-blue arrows refer to x-y-z Cartesian coordinate system axes).
The prescribed robot path on the workpiece surface consists of a set of waypoints through which the robot needs to move with a constant linear speed while keeping the tool orientation perpendicular to the curved surface. Based on the DTF method, the maximum achievable tool velocity can be obtained at each waypoint along the path, considering the required motion on the surface. To evaluate the optimality of any given workpiece placement, it is necessary to propose an appropriate objective function based on the calculated maximum achievable tool velocities at each waypoint. Since the most challenging waypoint for the robot is the one where the value of the maximum achievable linear velocity is the lowest, the minimum value along the path will be calculated as a criterion, which is defined as:
2.5. Optimization Criterion
Only the directional kinematic capabilities of the robot will be considered in this study. In the case of surface machining, the machining path consists of a set of waypoints, which the robot has to follow, and are known a priori. To find the optimum placement of the workpiece with regard to the proposed machining requirements, the following optimization criterion will be expressed as:
To determine the kinematically optimal placement of the workpiece, the optimization problem can be formulated as maximizing the objective function F(x, y, φ):
subject to:
- -
- The joint angles of the robot should be bounded between its positional joint limits:
- -
- The workpiece should be located within a working area, which is defined relative to the robot’s base frame {B} within the range:
- -
- The rotation of the workpiece should be limited between:
All waypoints on the robot’s path should be reachable, which means that an inverse kinematics (IK) solution exists for all waypoints on the robot’s path.
3. Results and Discussion
3.1. Experimental Setup
Validation of the proposed method for optimizing the workpiece placement will be demonstrated on a Universal Robots UR5e collaborative robot for six different machining paths. The maximum feasible linear velocity will be determined at each waypoint of the robot’s path, based on the maximum kinematic capabilities of the UR5e robot considering the required machining direction. The maximum allowed joint velocities for the UR5e robot are limited between +/− 180 for all six joints. The optimal placement of the workpiece will be searched using the “surrogate” optimization algorithm [44], which was developed for solving complex and computationally demanding optimization problems.
The results will be presented based on three different workpieces, as is shown in Figure 4a–c. For each workpiece, two different machining paths are determined, as shown in Figure 4d–i, where the black lines define the machining paths across the workpiece surface.
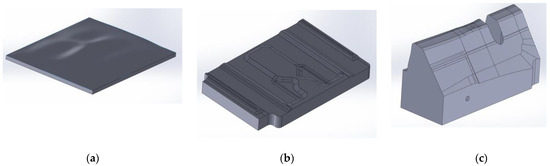
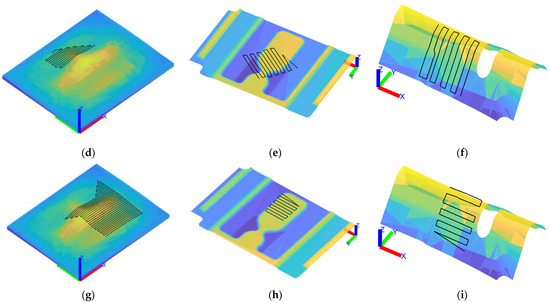
Figure 4.
Three-dimensional model of a workpiece: (a) Workpiece 1, (b) Workpiece 2, (c) Workpiece 3, and the machining paths across the surface of the workpiece: (d) 1A, (e) 2A, (f) 3A, (g) 1B, (h) 2B, (i) 3B; surface color is coded by the surface point height (blue—low value, yellow—high value).
3.2. Optimization Results
The optimal workpiece placement was determined based on the optimization problem described in (8) and optimisation constraints listed in Table 1. For optimisation purposes, only UP, RIGHT, and NON-FLIP robot`s configuration will be considered.

Table 1.
Optimization constraints.
The optimal placement is named as “Optim”, it is represented by the green-colored workpiece shown in Figure 5a–f. The optimal workpiece placement of each machining path is described by the transformation matrix , as is shown in Table 2. For comparison, three other placements of the workpiece will be evaluated, named: “Init”, “1”, and “2”. Additional workpiece placements will be added to the analysis in order to verify the effectiveness of the proposed objective function and thus demonstrate the relationship between the value of the objective function and the maximum measured joint velocities required for executing the predefined machining trajectory.
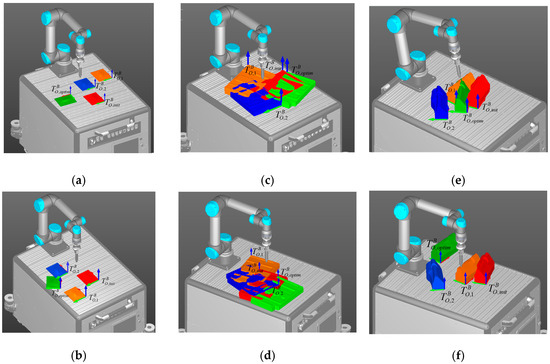
Figure 5.
Workpiece placement on the mobile platform for the machining paths: (a) 1A, (b) 1B, (c) 2A, (d) 2B, (e) 3A, (f) 3B. Red-colored workpiece shows its initial placement “Init”, blue- and orange-colored workpieces show its intermediate placements, respectively, and green -colored workpiece shows its optimal position “Optim”.

Table 2.
Optimal workpiece placement, described by the transformation matrix for the machining paths: (a) 1A, (b) 1B, (c) 2A, (d) 2B, (e) 3A, (f) 3B.
The workpiece placement “Init”, shown as a red-colored workpiece, represents the initial placement of the workpiece defined by , while workpiece placements “1” and “2”, shown as blue- and orange-colored workpieces, represent random workpiece placements on the mobile platform, defined by and , respectively. Each placement is represented by the workpiece reference frame, where the red arrow represents the x-axis, the green arrow represents the y-axis, and the blue arrow the z-axis, respectively.
For each analyzed workpiece placement, we calculated and displayed the maximum achievable linear velocity Vmax at each waypoint on the robot’s path, calculated by the DTF method (4). The results are presented in Figure 6 in the form of a swarm scatter chart for each machining path. From Figure 6, it can clearly be seen that the highest worst-case maximum achievable linear velocity is calculated for the optimal placement of the workpiece in all six cases.
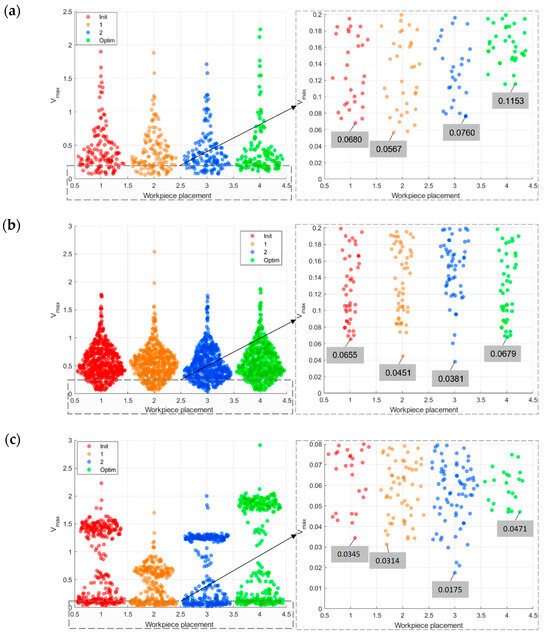
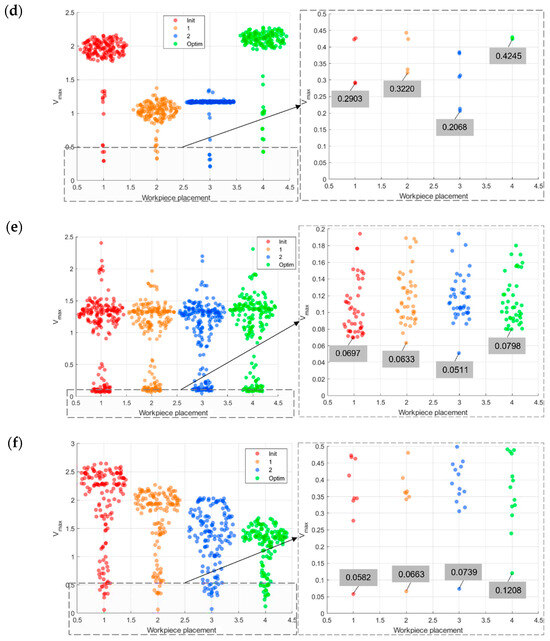
Figure 6.
Representation of the calculated maximum achievable tool velocity Vmax at each waypoint on the robot’s path, and minimum value of Vmax for four placements of the workpiece in the case of the machining paths: (a) 1A, (b) 1B, (c) 2A, (d) 2B, (e) 3A, (f) 3B. Red, blue, orange, and green colors refer to initial workpiece placement “Init”, intermediate workpiece placements “1” and ”2” and optimal workpiece placement “Optim”, respectively.
3.3. Simulation Results
In order to validate the optimal workpiece placement method, the joint velocities along the entire trajectory were measured by the offline simulation tool URSim. The data were captured using the Real-Time Data Exchange (RTDE) protocol, which is based on the TCP/P communication, and allows reading data at a frequency of 500 Hz. Only the measured joint velocities were analyzed, since our goal was to find the kinematically optimal position of the workpiece. The joint velocities were measured for all four placements of the workpiece: “Init”, “1”, “2”, “Optim”, and all the robotic trajectories were executed with the same machining parameters displayed in Table 3, where the path was followed at a constant TCP speed.

Table 3.
Machining parameters.
The infinity norm of the joint velocities, which represents the maximum value of the joint velocity vector, were calculated at each time step for all four placements of the workpiece. These values are shown by the swam chart plot in Figure 7. The maximum value of the entire trajectory is displayed for each placement. It can be seen that the lowest infinity norm of joint velocities was required for the optimal workpiece placement compared to the other workpiece placements, considering the same machining parameters.
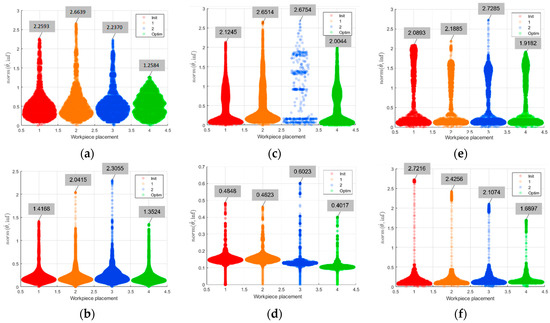
Figure 7.
Representation of the joint velocity infinity norm for four different placements of the workpiece in the case of the machining paths: (a) 1A, (b) 1B, (c) 2A, (d) 2B, (e) 3A, (f) 3B. Red, blue, orange, and green colors refer to initial workpiece placement “Init”, intermediate workpiece placements “1” and ”2” and optimal workpiece placement “Optim”, respectively.
The percentage of joint velocity reduction was calculated by comparing the considered workpiece placement to its optimal placement in the form of the parameter of improvement imp:
In the case of machining path 1A, the lowest value of the maximum achievable linear velocity along the entire path was calculated for the orange-colored workpiece placement. As a result, the highest measured values of the maximum joint velocities were measured for the same workpiece placement (2.66). A 52.8% reduction in maximum joint velocities was achieved in comparison to the optimal workpiece placement. Similar findings were found in the case of all the other machining paths as well. For machining path 1B, the lowest values of the maximum achievable linear velocity along the path were measured for the blue-colored workpiece placement (2.31). In this case, we reduced the maximum joint velocities by 41.3% for the optimal workpiece placement. In the case of machining path 2A, the lowest value of the maximum achievable linear velocity along the path was calculated for the blue-colored workpiece placement, as is shown in Figure 6c. The highest joint velocities were achieved for this workpiece placement as well (2.67), as can be seen from Figure 7c. For the optimal workpiece placement, the maximum joint velocities were reduced by 25.1%.
As depicted in Figure 6d, the lowest value of the maximum achievable linear velocity along the path for machining path 2B was calculated for the placement of the workpiece shown in blue. As shown in Figure 7d, the maximum joint velocities were observed for this workpiece placement (0.60). For optimal placement of machining path 2B, the maximum joint velocities were reduced by 33.3%. Similar improvement can also be seen for machining paths 3A and 3B, where the maximum joint velocities were reduced by 29.7% in the case of machining path 3A and 37.9% for machining path 3B. Based on the results, we can confirm that the maximum achievable linear velocity along a path is linked directly to the maximum joint velocities, and, consequently, to the evaluation of feasibility of the robotic task.
4. Conclusions
When planning a feasible robotic task, it is crucial to ensure that the required joint capabilities are below the maximum capabilities available. This can be challenging, especially in the case of more complex robotic tasks, such as robotic surface machining. To calculate the maximum kinematic end-effector capabilities of each waypoint on the predefined robotic path, an approach called the Decomposed Twist Feasibility (DTF) method was used in this study, which can provide precise, dimensionally homogeneous and physically consistent information about the maximum robot tool speed considering maximum joint velocities while fulfilling the surface machining requirements.
The optimal placement of the workpiece can be determined based on the optimization criterion presented in this study. The optimization criterion is based on the idea of evaluating the robot’s motion performance capabilities at the most critical waypoint on the robot’s path to determine the best worst-case performance along the entire path. The experiment was shown and verified on the 6-axis collaborative robot UR5e for robotic machining purposes. The optimization results confirm the effectiveness of the described method, as we achieved the lowest values of maximum joint velocities for all the machining paths in the case of optimal workpiece placement. Therefore, it can be concluded that maximizing the achievable linear velocity along the machining path, calculated based on the DTF method, is linked directly to the measured maximum joint velocities along the machining path. By optimizing the workpiece placement based on the proposed method, we can ensure a feasible robotic machining task, or perform the machining task at a higher linear speed. Since the DTF method is designed to analyze only pure kinematic properties, the dynamic capabilities according to the specified task parameters should also be taken into account in order to identify a feasible workpiece placement.
Author Contributions
The presented work was carried out with significant contributions of both authors. S.S.: conceptualization, derivation of the proposed method, software, validation, analysis, and writing—original draft preparation; A.H.: methodology, derivation of the proposed method, formal analysis, writing—review and editing, and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Slovenian Research Agency (ARRS) under a Grant for the Research Program P2–0028, and in part by a project of the Republic of Slovenia and the European Union from the European Regional Development Fund, ROBOTOOL-1, Grant number OP20.03540.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gajšek, B.; Stradovnik, S.; Hace, A. Sustainable Move towards Flexible, Robotic, Human-Involving Workplace. Sustainability 2020, 12, 6590. [Google Scholar] [CrossRef]
- Costa, G.D.; Petry, M.R.; Moreira, A.P. Augmented Reality for Human-Robot Collaboration and Cooperation in Industrial Applications: A Systematic Literature Review. Sensors 2022, 22, 2725. [Google Scholar] [CrossRef]
- Hwang, P.-J.; Hsu, C.-C.; Chou, P.-Y.; Wang, W.-Y.; Lin, C.-H. Vision-Based Learning from Demonstration System for Robot Arms. Sensors 2022, 22, 2678. [Google Scholar] [CrossRef]
- Khawaja, F.I.; Kanazawa, A.; Kinugawa, J.; Kosuge, K. A Human-Following Motion Planning and Control Scheme for Collaborative Robots Based on Human Motion Prediction. Sensors 2021, 21, 8229. [Google Scholar] [CrossRef]
- Kanazawa, A.; Kinugawa, J.; Kosuge, K. Adaptive Motion Planning for a Collaborative Robot Based on Prediction Uncertainty to Enhance Human Safety and Work Efficiency. IEEE Trans. Robot. 2019, 35, 817–832. [Google Scholar] [CrossRef]
- Hähnel, S.; Pini, F.; Leali, F.; Dambon, O.; Bergs, T.; Bletek, T. Reconfigurable Robotic Solution for Effective Finishing of Complex Surfaces. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation 2018, Turin, Italy, 4–7 September 2018; pp. 1285–1290. [Google Scholar]
- Ye, C.; Yang, J.; Zhao, H.; Ding, H. Task-dependent workpiece placement optimization for minimizing contour errors induced by the low posture-dependent stiffness of robotic milling. Int. J. Mech. Sci. 2021, 205, 106601. [Google Scholar] [CrossRef]
- Vosniakos, G.-C.; Matsas, E. Improving feasibility of robotic milling through robot placement optimisation. Robot. Comput.-Integr. Manuf. 2010, 26, 517–525. [Google Scholar] [CrossRef]
- Henao, J.C.R.; Garzón, J.A.J.; Muñoz, L.D. Manipulability index study on the KUKA robot KR5 ARC HW. In Proceedings of the 2012 XVII Symposium of Image, Signal Processing, and Artificial Vision (STSIVA), Medellin, Colombia, 12–14 September 2012; pp. 72–77. [Google Scholar]
- Malhan, R.K.; Shembekar, A.V.; Kabir, A.M.; Bhatt, P.M.; Shah, B.; Zanio, S.; Nutt, S.; Gupta, S.K. Automated planning for robotic layup of composite prepreg. Robot. Comput.-Integr. Manuf. 2021, 67, 102020. [Google Scholar] [CrossRef]
- Malhan, R.K.; Kabir, A.M.; Shah, B.; Gupta, S.K. Identifying Feasible Workpiece Placement with Respect to Redundant Manipulator for Complex Manufacturing Tasks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5585–5591. [Google Scholar]
- Gotlih, J.; Brezocnik, M.; Balic, J.; Karner, T.; Razborsek, B.; Gotlih, K. Determination of accuracy contour and optimization of workpiece positioning for robot milling. Adv. Prod. Eng. Manag. 2017, 12, 233–244. [Google Scholar] [CrossRef][Green Version]
- Xue, Y.; Sun, Z.; Liu, S.; Gao, D.; Xu, Z. Stiffness-Oriented Placement Optimization of Machining Robots for Large Component Flexible Manufacturing System. Machines 2022, 10, 389. [Google Scholar] [CrossRef]
- Bhatt, P.M.; Kulkarni, A.; Malhan, R.K.; Gupta, S.K. Optimizing Part Placement for Improving Accuracy of Robot-Based Additive Manufacturing. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 859–865. [Google Scholar]
- Ur-Rehman, R.; Caro, S.; Chablat, D.; Wenger, P. Multi-objective path placement optimization of parallel kinematics machines based on energy consumption, shaking forces and maximum actuator torques: Application to the Orthoglide. Mech. Mach. Theory 2010, 45, 1125–1141. [Google Scholar] [CrossRef]
- Santos, R.; Steffen, J.V.; Saramago, S. Optimal Task Placement of a Serial Robot Manipulator for Manipulability and Mechanical Power Optimization. Intell. Inf. Manag. 2010, 2, 512–525. [Google Scholar] [CrossRef]
- Malhan, R.; Kabir, A.; Shah, B.; Centea, T.; Gupta, S. Determining Feasible Robot Placements in Robotic Cells for Composite Prepreg Sheet Layup. Presented at the 14th International Manufacturing Science and Engineering Conference, Erie, PA, USA, 10–14 June 2019. [Google Scholar]
- Lu, L.; Zhang, J.; Fuh, J.Y.H.; Han, J.; Wang, H. Time-optimal tool motion planning with tool-tip kinematic constraints for robotic machining of sculptured surfaces. Robot. Comput.-Integr. Manuf. 2020, 65, 101969. [Google Scholar] [CrossRef]
- Balci, B.; Donovan, J.; Roberts, J.; Corke, P. Optimal Workpiece Placement Based on Robot Reach, Manipulability and Joint Torques. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 12302–12308. [Google Scholar]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Doan, N.; Lin, W. Optimal robot placement with consideration of redundancy problem for wrist-partitioned 6R articulated robots. Robot. Comput.-Integr. Manuf. 2017, 48, 233–242. [Google Scholar] [CrossRef]
- Aspragathos, N.A.; Foussias, S. Optimal location of a robot path when considering velocity performance. Robotica 2002, 20, 139–147. [Google Scholar] [CrossRef]
- Valsamos, H.; Nektarios, T.; Aspragathos, N.A. Optimal Placement of Path Following Robot Task Using Genetic Algorithms. IFAC Proc. Vol. 2006, 39, 132–137. [Google Scholar] [CrossRef]
- Nektarios, A.; Aspragathos, N.A. Optimal location of a general position and orientation end-effector’s path relative to manipulator’s base, considering velocity performance. Robot. Comput.-Integr. Manuf. 2010, 26, 162–173. [Google Scholar] [CrossRef]
- Stradovnik, S.; Hace, A. Task-Oriented Evaluation of the Feasible Kinematic Directional Capabilities for Robot Machining. Sensors 2022, 22, 4267. [Google Scholar] [CrossRef]
- ISO 10218-1/2:2011; Robots and Robotic Devices Safety Requirements for Industrial Robots Part 1: Robots/Part 2: Robot Systems and Integration. ISO: Genewa, Switzerland, 2011.
- ISO/TS 15066:2016; Robots and Robotic Devices Collaborative Robots. ISO: Genewa, Switzerland, 2016.
- Morishige, K.; Sato, Y. Optimization of Workpiece Placement in Sealing Operation Using Industrial Robot Considering Manipulability. Presented at the International Symposium on Flexible Automation, Kanazawa Japan, 15–19 July 2018. [Google Scholar]
- Zhang, L.; Guo, S.; Huang, Y.; Xiong, X. Kinematic Singularity Analysis and Simulation for 7DOF Anthropomorphic Manipulator. Int. J. Mechatron. Appl. Mech. 2019, 1, 157–164. [Google Scholar]
- Feng, Y.; Fang, L.; Bu, W.; Kang, J. Multi-objective Optimization for Design of Redundant Serial Robots. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 4987–4991. [Google Scholar]
- Chiu, S.L. Task Compatibility of Manipulator Postures. Int. J. Robot. Res. 1988, 7, 13–21. [Google Scholar] [CrossRef]
- Bicchi, A.; Melchiorri, C.; Balluchi, D. On the mobility and manipulability of general multiple limb robots. IEEE Trans. Robot. Autom. 1995, 11, 215–228. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Manipulator Performance Measures—A Comprehensive Literature Survey. J. Intell. Robot Syst. 2014, 77, 1–24. [Google Scholar] [CrossRef]
- Boschetti, G. A Novel Kinematic Directional Index for Industrial Serial Manipulators. Appl. Sci. 2020, 10, 5953. [Google Scholar] [CrossRef]
- Boschetti, G.; Rosa, R.; Trevisani, A. Parallel Robot Translational Performance Evaluation through Direction-Selective Index (DSI). J. Robot. 2011, 2011, 129506. [Google Scholar] [CrossRef][Green Version]
- Mansouri, I.; Ouali, M. The power manipulability—A new homogeneous performance index of robot manipulators. Robot. Comput.-Integr. Manuf. 2011, 27, 434–449. [Google Scholar] [CrossRef]
- Yoshikawa, T. Translational and rotational manipulability of robotic manipulators. In Proceedings of the IECON ‘91: 1991 International Conference on Industrial Electronics, Control and Instrumentation, Kobe, Japan, 28 October–1 November 1991; Volume 2, pp. 1170–1175. [Google Scholar]
- Finotello, R.; Grasso, T.; Rossi, G.; Terribile, A. Computation of kinetostatic performances of robot manipulators with polytopes. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998; Volume 4, pp. 3241–3246. [Google Scholar]
- Jihong, L.; Won, K.T. Inverse kinematic solution based on decomposed manipulability. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 2, pp. 1514–1519. [Google Scholar]
- Long, P.; Padir, T. Constrained Manipulability for Humanoid Robots Using Velocity Polytopes. Int. J. Humanoid Robot. 2020, 17, 1950037. [Google Scholar] [CrossRef]
- Moulianitis, V.; Katrantzis, E.; Stravopodis, N.; Aspragathos, N. A Comparative Study of Three Manipulator Performance Measures. In Proceedings of the 26th International Conference on Robotics in Alpe-Adria-Danube Region, RAAD 2017, Turin, Italy, 21–23 July 2017; pp. 19–27. [Google Scholar]
- Mansfeld, N.; Keppler, M.; Haddadin, S. Speed Gain in Elastic Joint Robots: An Energy Conversion-Based Approach. IEEE Robot. Autom. Lett. 2021, 6, 4600–4607. [Google Scholar] [CrossRef]
- Banchoff, T.F.; Lovett, S. Differential Geometry of Curves and Surfaces; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Wang, Y.; Shoemaker, C. A General Stochastic Algorithmic Framework for Minimizing Expensive Black Box Objective Functions Based on Surrogate Models and Sensitivity Analysis. arXiv 2014, arXiv:1410.6271. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).