A Tolerance Specification Automatic Design Method for Screening Geometric Tolerance Types
Abstract
1. Introduction
2. Related Work
2.1. Application of Ontology in the Field of Product Design Tolerance Design
2.2. Screening of Automatically Generating AT-Types
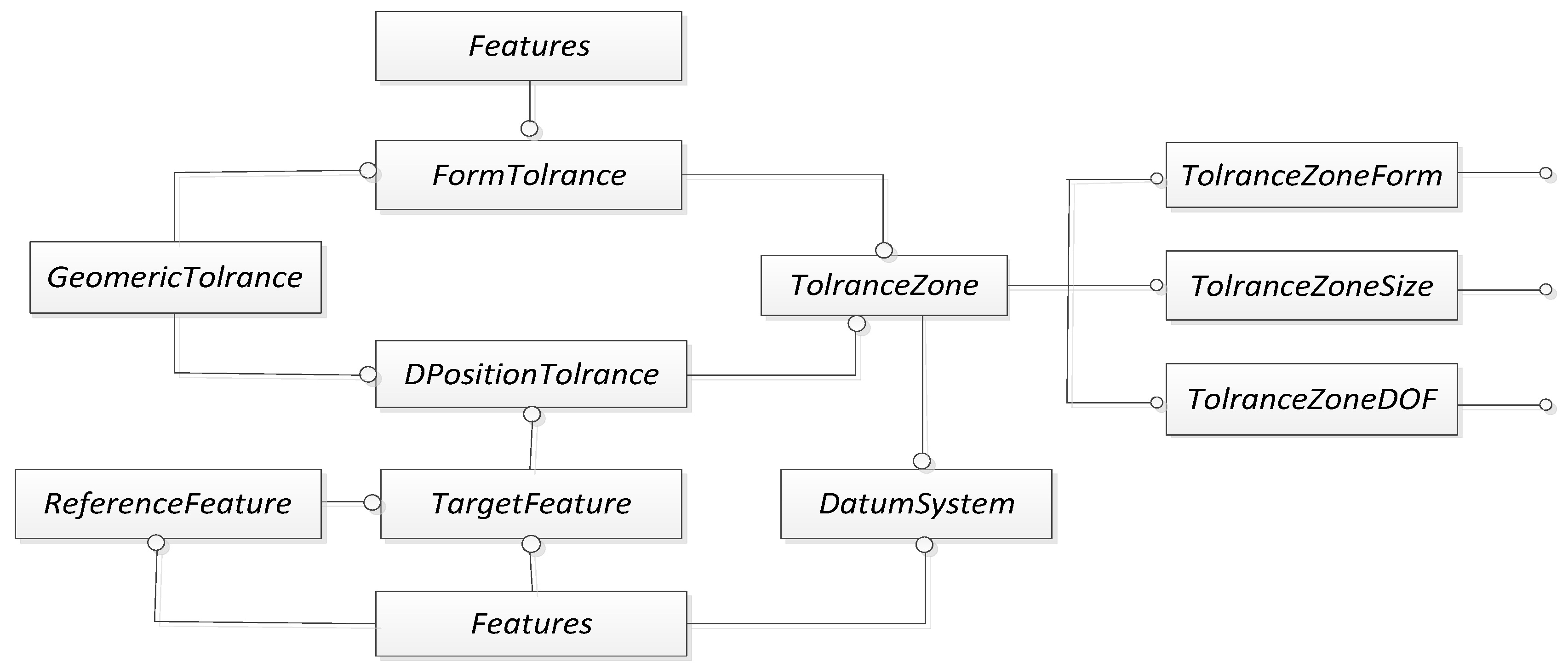
3. Constructing an AT Representation Model Containing Tolerance-Zone DOF Layers
3.1. Tolerance-Zone Layer
3.2. Tolerance-Zone DOF Layer
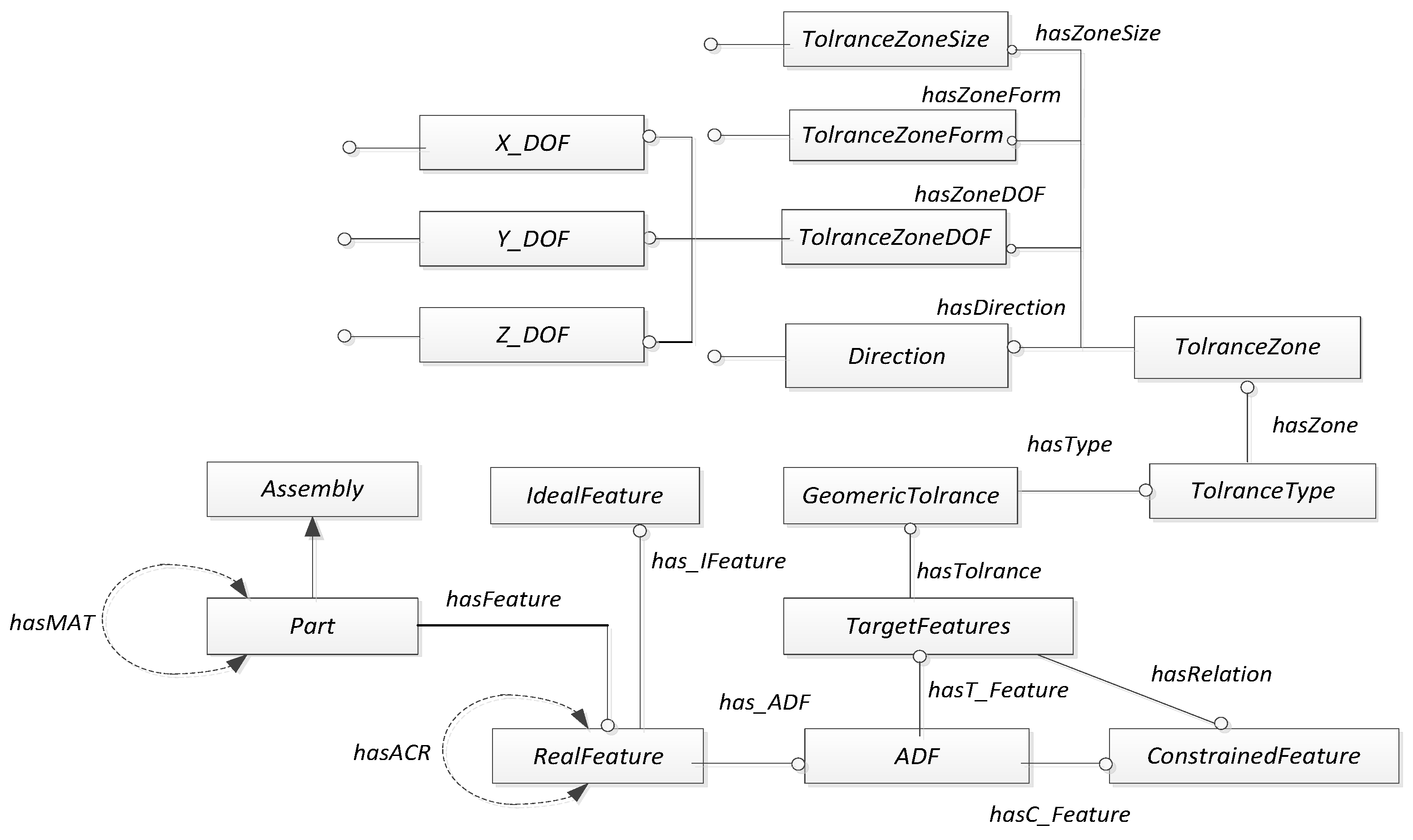
4. Construction of an Ontology Framework for Assembly Tolerance Domain Oriented to Tolerance-Zone DOFs
4.1. Semantic Modelling of Geometric Tolerance Information with Tolerance-Zone DOFs
4.2. Construction of an AT Information Meta-Ontology Model Based on Tolerance-Zone DOFs
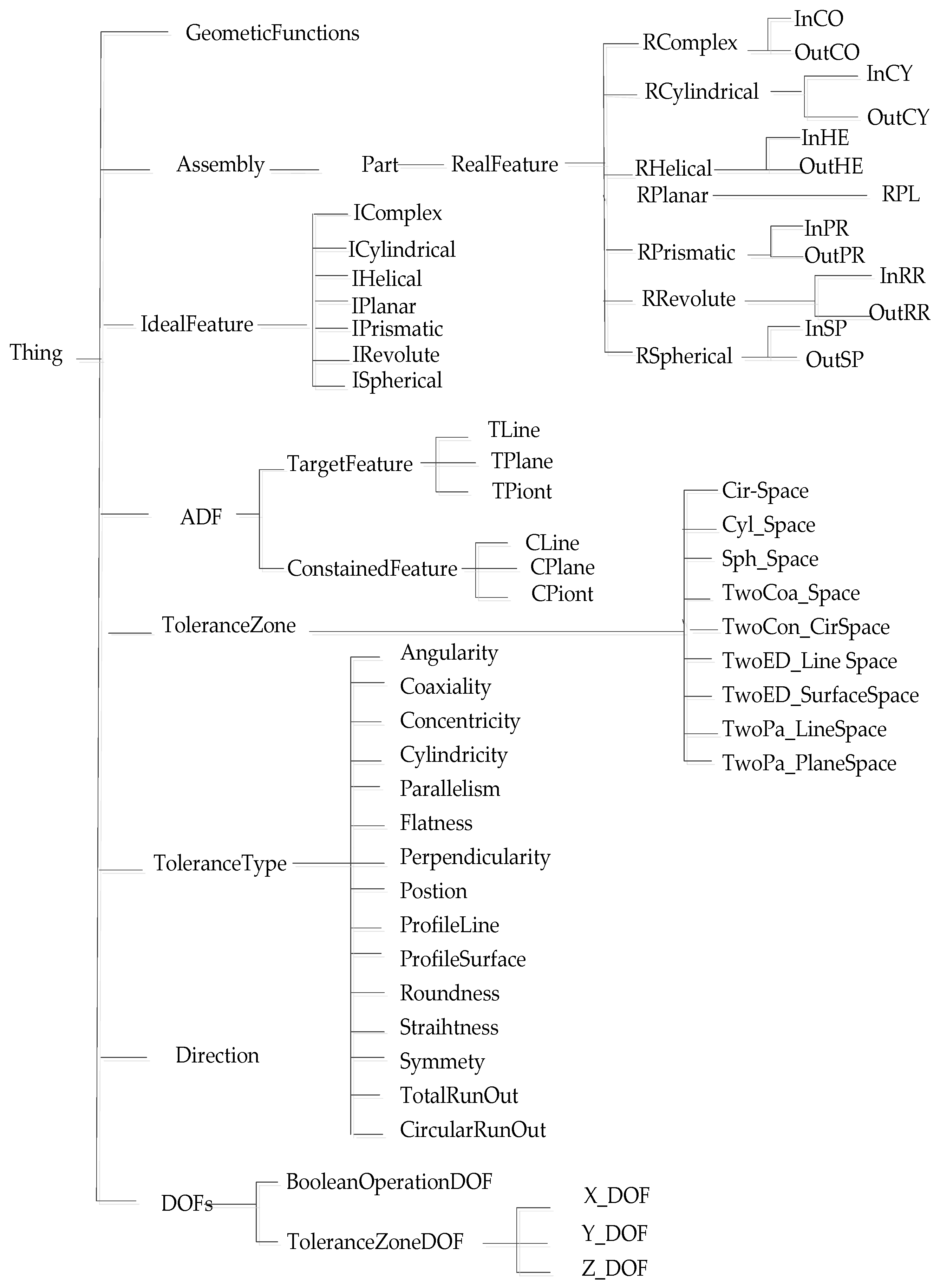
4.3. Constructing the Class of AT Information Ontology Knowledge Base
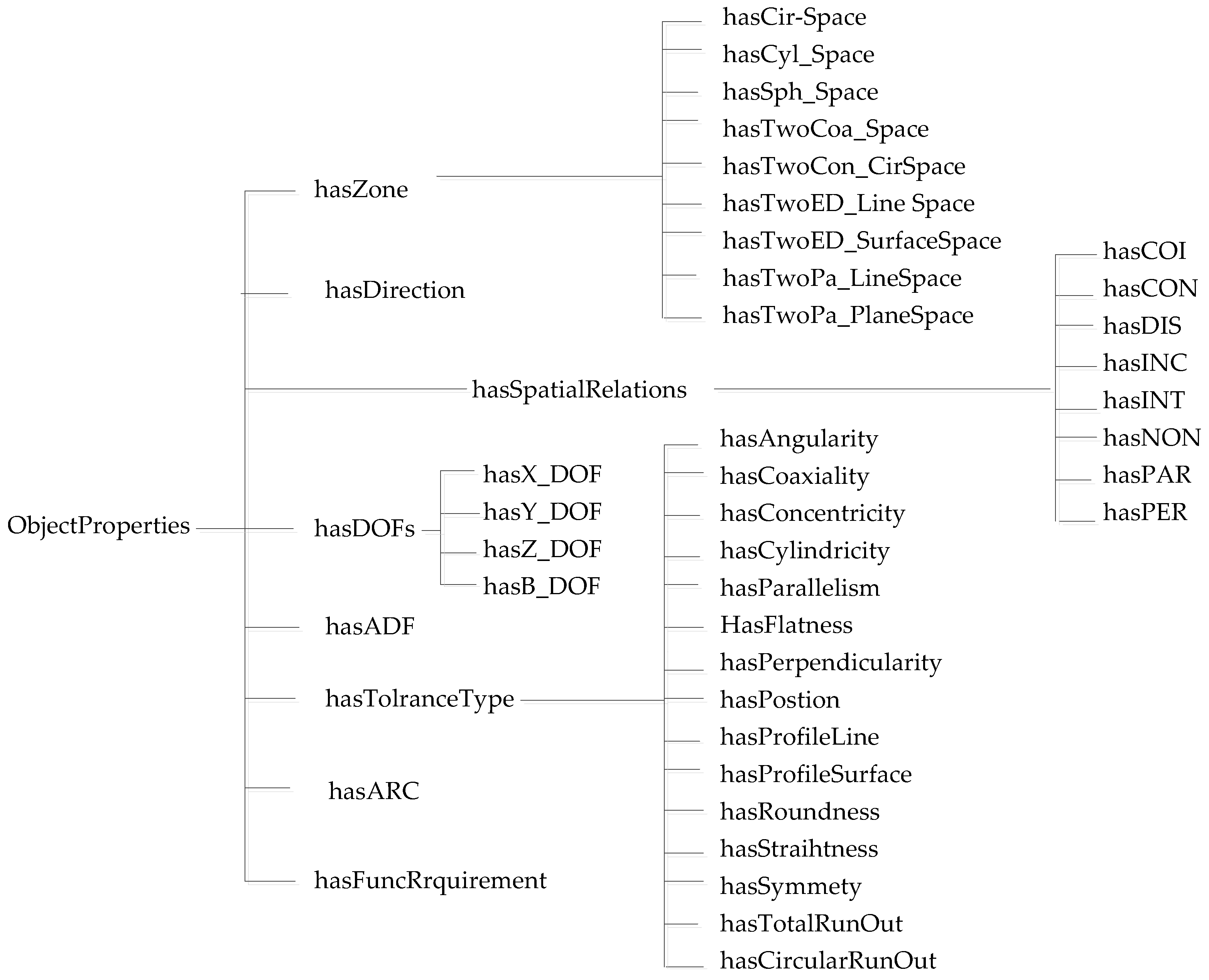
4.4. Defining Class Properties
4.5. OWL/SWRL Representation for AT Information Based on Tolerance-Zone DOFs
4.5.1. SWRL Representation of Generation Rules for AT Specifications
- SWRL representation of rules for generating shape tolerance types. The form tolerance type is related to the target feature element type. SWRL rules are constructed according to the correspondence between the type of the target feature element and the form tolerance [3], and the automatically generated SWRL rule base for form tolerance items can be obtained [5,23,31]. For example, the commonly used shape tolerance types for cylinders are cylindricity, centre element axis straightness, cross-section roundness and rotation bus straightness; the inference rules are as follows: RCyindrical(?x) ∧ ICyindrical(?y) ∧ hasNON(?x,?y) → hasCylindricity(?x,?y) ∧ HasRoundness(?x,?y) ∧ hasStraihtness(?x,?y).
- SWRL representation of rules for generating orientation–position tolerance types. The orientation–position tolerance type of the target feature element is closely related to the orientation and position of the constrained feature element. The mapping relationship between the assembly tolerance type and the spatial relationship is expressed as the corresponding SWRL inference rule, and the SWRL rule base for the automatic generation of the orientation–position tolerance type can be established. For example, if the target feature plane and the constraint feature plane are perpendicular to each other, the tolerance types that can be selected for the target feature elements are positional and perpendicular. The inference rules are expressed as follows: TPlane(?x) ∧ CPlane(?y) ∧ hasPER(?x,?y)→ hasPerpendicularity(?x,?y) ∧ hasPostion(?x,?y).
4.5.2. SWRL Representation of Inference Rules for Screening Tolerance Types
- Reasoning rules for common DOF vector Vc. In the coordinate system, if the normal direction of the target feature element is the Y-axis direction, the vector Vt is an instance of the class Y_DOF. The measurement reference feature DOF vector Vf is an instance of class DOFs. Then, the values of the elements in the vector VC are the Boolean values between Vt and Vf. Based on the adjacency matrix Mvi,3×6, which represents the tolerance-zone DOF vectors, the inference rule for finding the values of the six data attributes of the vector Vc is constructed. For example, the SWRL of the inference rule for finding the value of translational DOFs in the Y-axis direction for the vector Vc is expressed as: hasDOF_Y(Vt,?x) ∧ hasDOF_Y(Vf,?y) ∧ swrlb:notEqual(?x, ?y) -> hasDOF_Y(Vc, false); hasDOF_Y(Vt,?x) ∧ hasDOF_Y(Vf,?y) ∧ swrlb:Equal(?x, ?y) -> hasDOF_Y(Vc, ture).Similarly, the inference rules can be constructed for the other five data attribute values in the common DOF vector Vc.
- Reasoning rules for the control parameter DOF vector V0. If Vp is the auxiliary DOF vector, the control parameter DOF vector V0 is the result of the Boolean of the auxiliary DOF vector VP and the common DOF vector VC. With reference to the method of determining the inference rule for the common DOF vector, the inference rule for determining the six data values in the control parameter DOF vector V0 is constructed. As an example, the SWRL of the inference rule for finding the rotational DOF value of the DOF vector V0 around the Y axis is expressed as follows: hasDOF_aroundY(Vc,?x) ∧ hasDOF_aroundY(Vp,?y) ∧ swrlb:notEqual(?x, ?y) -> hasDOF_aroundY(V0, false); hasDOF_aroundY(Vc,?x) ∧ hasDOF_aroundY(Vp,?y) ∧ swrlb:Equal(?x, ?y) -> hasDOF_aroundY(V0, true).Similarly, the inference rules can be constructed for the other five data values in the vector of control parameter DOFs V0.
- Inference rules for determining the comparative DOFs V’ij_k. If Vij_k is a vector of DOFs for the different tolerance types of an AFE (subscript i is the part number, j is the contact surface number, and k is the tolerance mark sequence number) and V0 is a vector of control parameter DOFs, then the comparative DOFs vector V’ij_k is the result of a Boolean operation between Vij_k and V0. With reference to the method of determining the inference rule for the common DOF vector, the inference rule for determining the values of the six data attributes in the comparative DOF vector V’ij_k is constructed. As an example, the SWRL of the inference rule for determining the value of the translational DOF in the Y axis of the comparative DOF vector V’ij_k is expressed as follows: hasDOF_Y(Vij_k,?x) ∧ hasDOF_Y(V0,?y) ∧ swrlb:notEqual(?x, ?y) -> hasDOF_Y(V’ij_k, false); hasDOF_Y(Vij_k,?x) ∧ hasDOF_Y(V0,?y) ∧ swrlb:Equal(?x, ?y) -> hasDOF_Y(V’ij_k, true).
- Reasoning rules for screening tolerance types. If the comparison DOF vector V’ij_k and the control parameter DOF vector V0 are equal, then V’ij_k is the comparison DOF for the preferred tolerance type. For this purpose, the SWRL rule for filtering the tolerance type is obtained and described as follows: hasDOF_X(V’ij_k,?b) ∧ hasDOF_X(V0,?c) ∧ swrlb:Equal(?b, ?c) ∧ hasDOF_Y(V’ij_k,?d) ∧ hasDOF_Y(V0,?e) ∧ swrlb:Equal(?d, ?e) ∧ hasDOF_Z (V’ij_k,?f)∧ hasDOF_Y(V0,?g) ∧ swrlb:Equal(?f, ?g) ∧ hasDOF_aroundX(V’ij_k,?k) ∧ hasDOF_aroundX(V0,?l) ∧ swrlb:Equal(?k,?l) ∧ hasDOF_aroundY(V’ij_k,?m) ∧ hasDOF_aroundY(V0,?n) ∧ swrlb:Equal(?m,?n) ∧ hasDOF_aroundZ(V’ij_k,?j) ∧ hasDOF_aroundZ(V0,?k) ∧ swrlb:Equal(?j, ?k)->Select_of_effectiveness(V’ij_k,ture).
5. Implementation and Examples
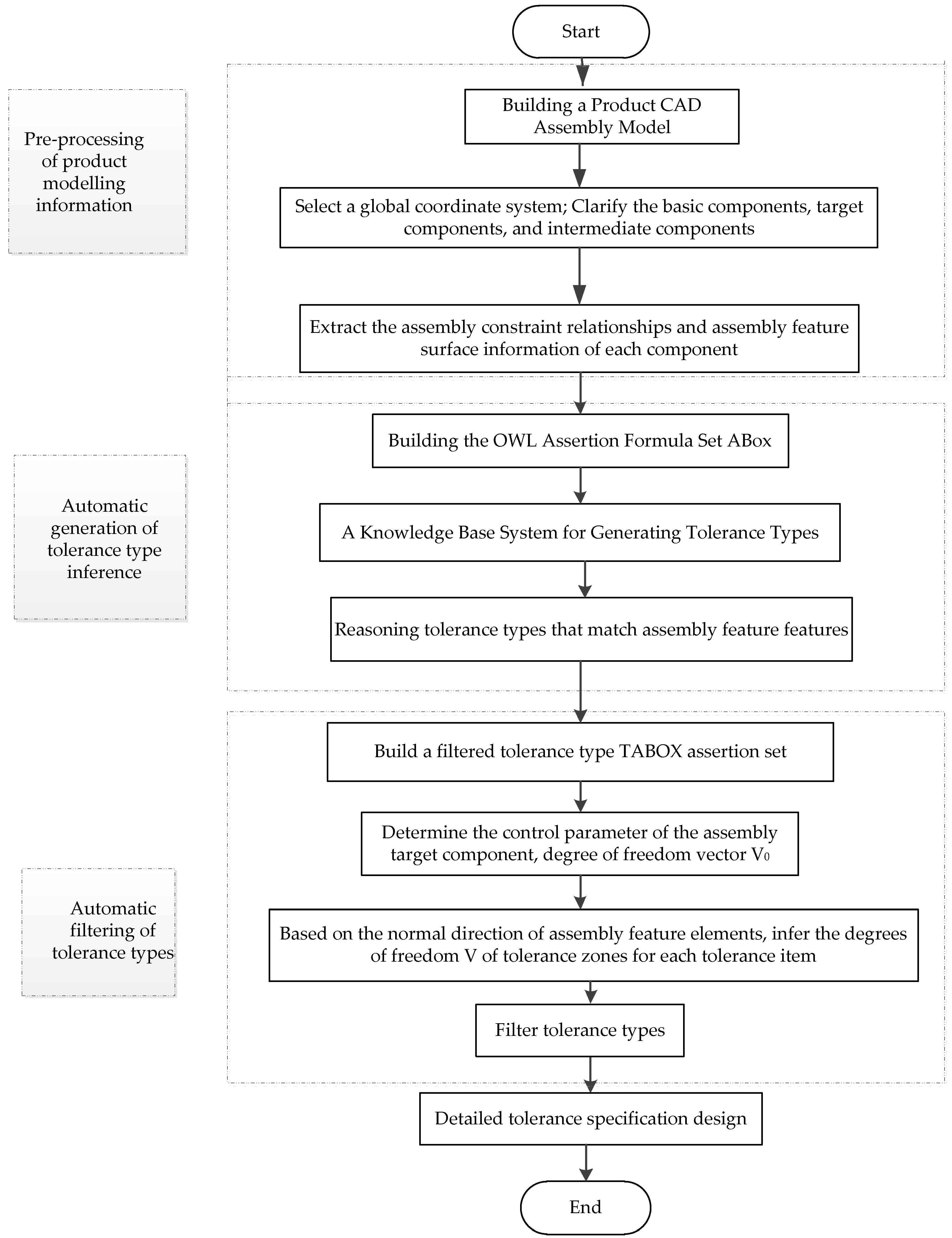
5.1. Constructing an Automatic Generation Algorithm for Screening AT Types Based on Tolerance-Zone DOF Ontology
5.2. Example Verification
5.2.1. Pre-Processing of Product Modelling Information
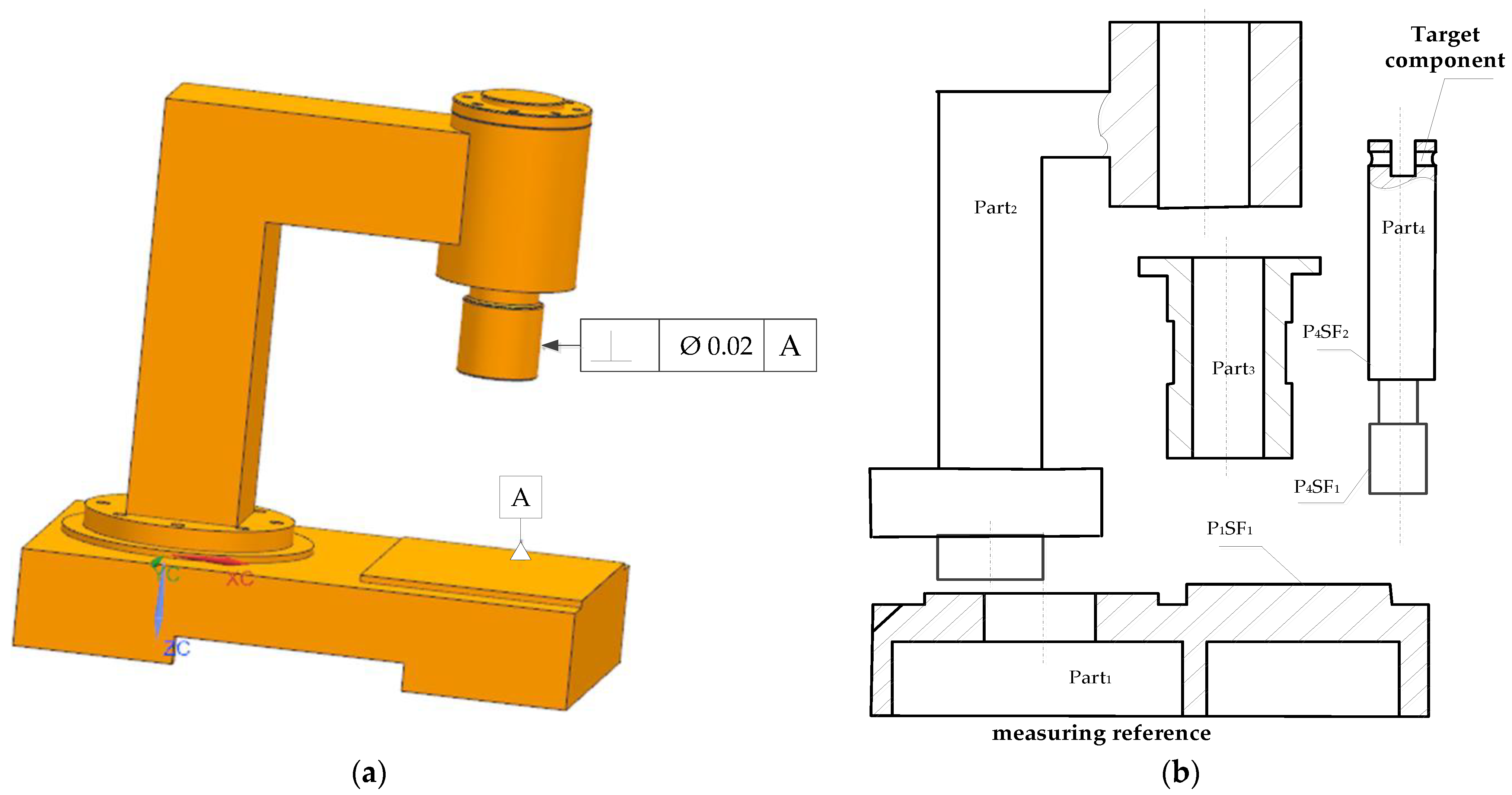
- Acquisition of 3D models of products. The CAD 3D assembly model of the product was constructed, as shown in Figure 9a.
- The measurement target and reference object of the assembly and the global coordinate system were defined. The geometric functional requirement of the assembly was perpendicularity, as shown in Figure 9a. Then, the part Part4 was defined as the target part of the assembly, and Part1 was defined the measurement datum part. According to the measurement elements and datum elements, the global coordinate system was established, as shown in Figure 9b.
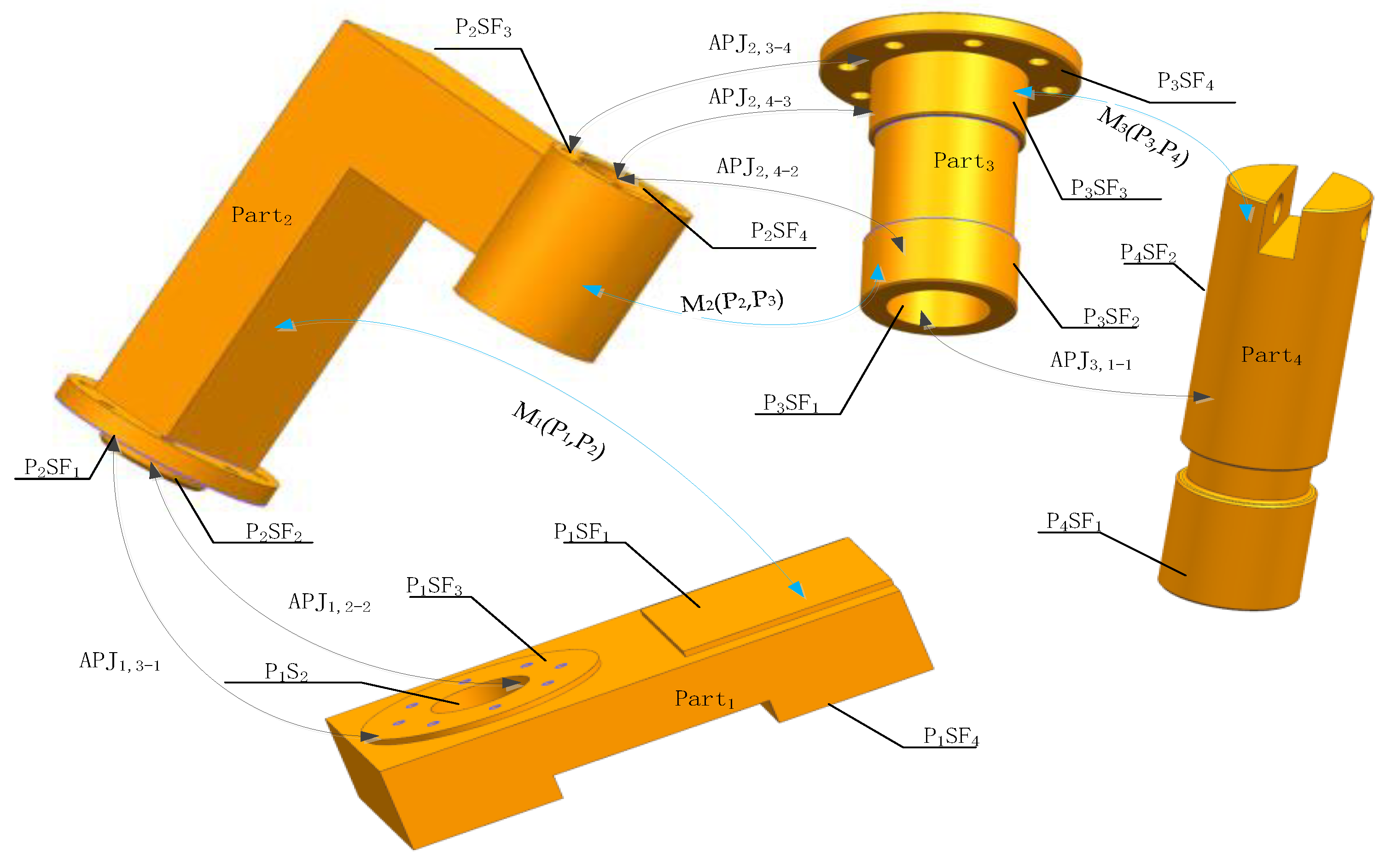
- According to the method introduced in reference [27], we extracted the assembly constraint information of the simple stamping model from the product assembly design data structure in the CAD system, such as the assembly constraint relationship between parts shown in Figure 10. In the figure, Mi(Pu,Pv) indicates the assembly relationship between the assembled workpieces, subscript i indicates the assembly number, Pu,Pv indicates the assembled part number, respectively, and u is not equal to v. APJk,l-n indicates the localisation constraint connection between the assembled feature surfaces of the parts, subscript k indicates the assembly number of the parts and l,m indicates the feature surface number of the different parts, respectively; we extracted the assembly feature surfaces (AFSs) information of each part, such as the geometric and coordinate feature information of these AFSs and the geometric spatial relationship between each AFE of the part.
5.2.2. Automatically Generate Tolerance Items for Parts of the Assembly
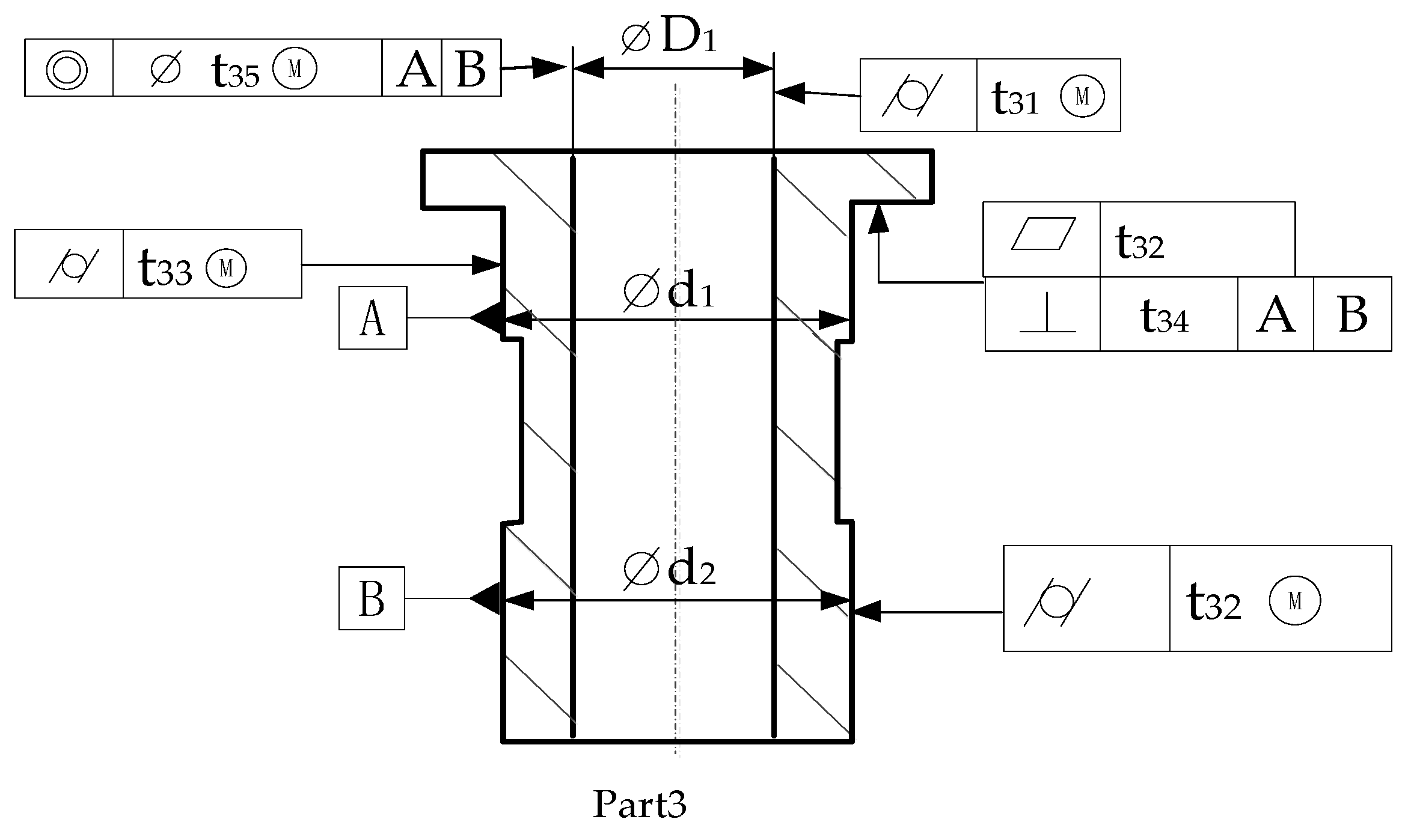
- Building the axiom set of the OWL assertions ABox. The OWL assertion axiom set ABox was established, which represents the assembly constraint relationships between the geometric product components based on these AFSs of each component and these constraint relationships between features. Taking Part3 in Figure 10 as an example, the constraint relationship assertion AP between the parts was obtained, and AP can be expressed as per Equation (5).
- 2.
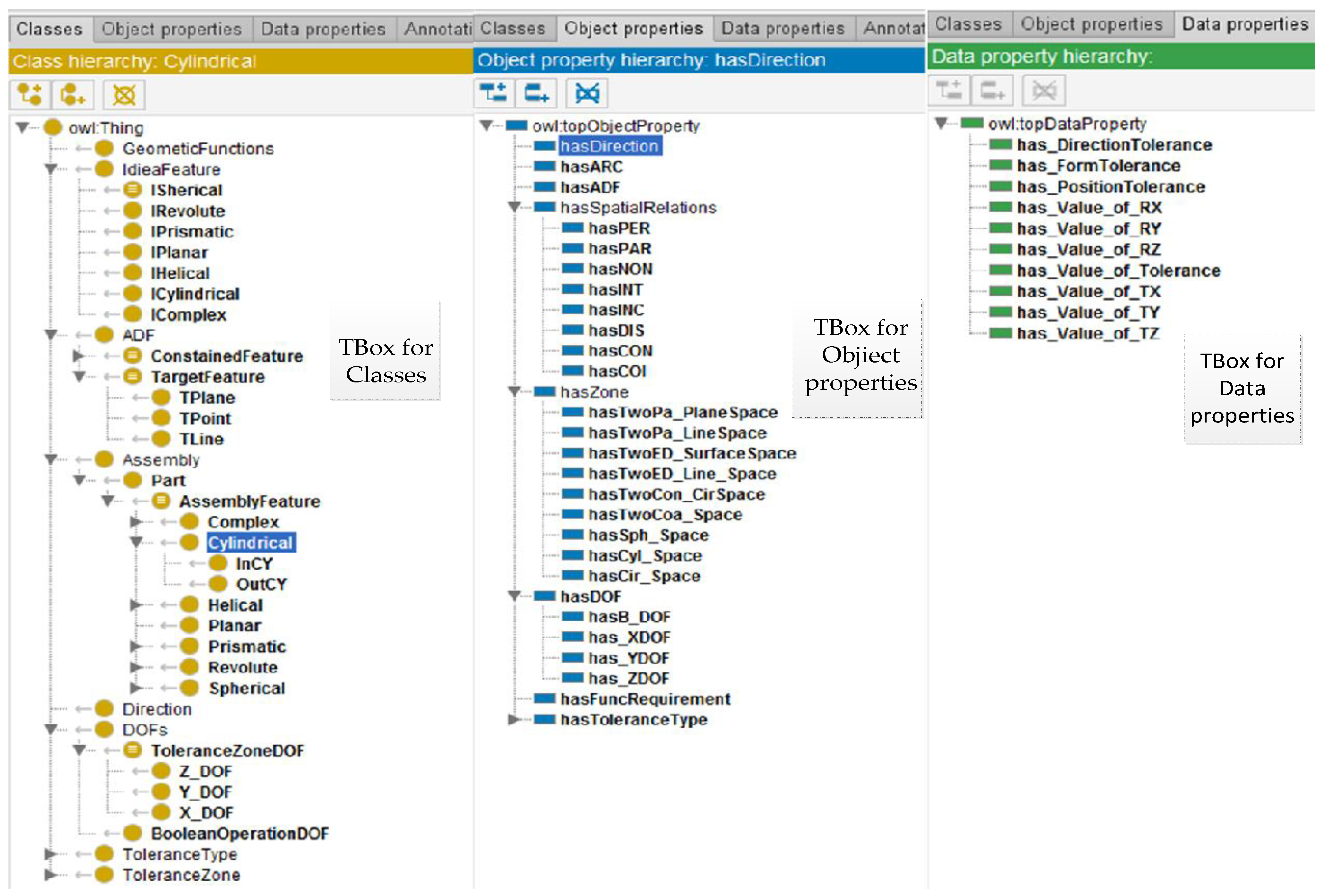
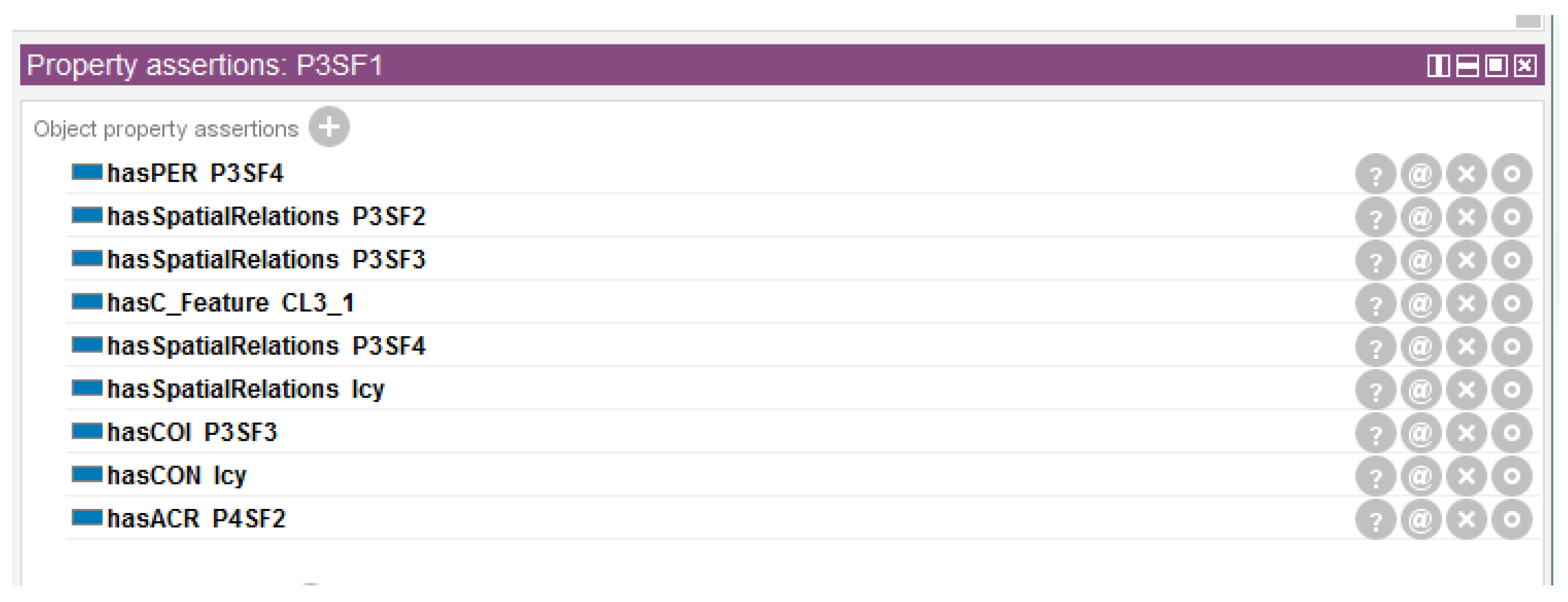
- A knowledge ontology library for the automatic generation of tolerance types was built. Following 4.5.3 and 4.5.4, the input of TBox, a set of terms for the tolerance specification design concepts, was realised using the protege5.5 ontology editor application, as shown in Figure 11. Taking part Part3 as an example, the AP AF and AFR assertion sets were input into the ontology editing tool software Protege 5.5 to realise the establishment of the OWL assertion axiom set ABox, and the tolerance type auto-generation knowledge base was finally obtained. The object property assertion of the assembly feature face P3SF1 of part P3 is shown in Figure 12.
- 3.
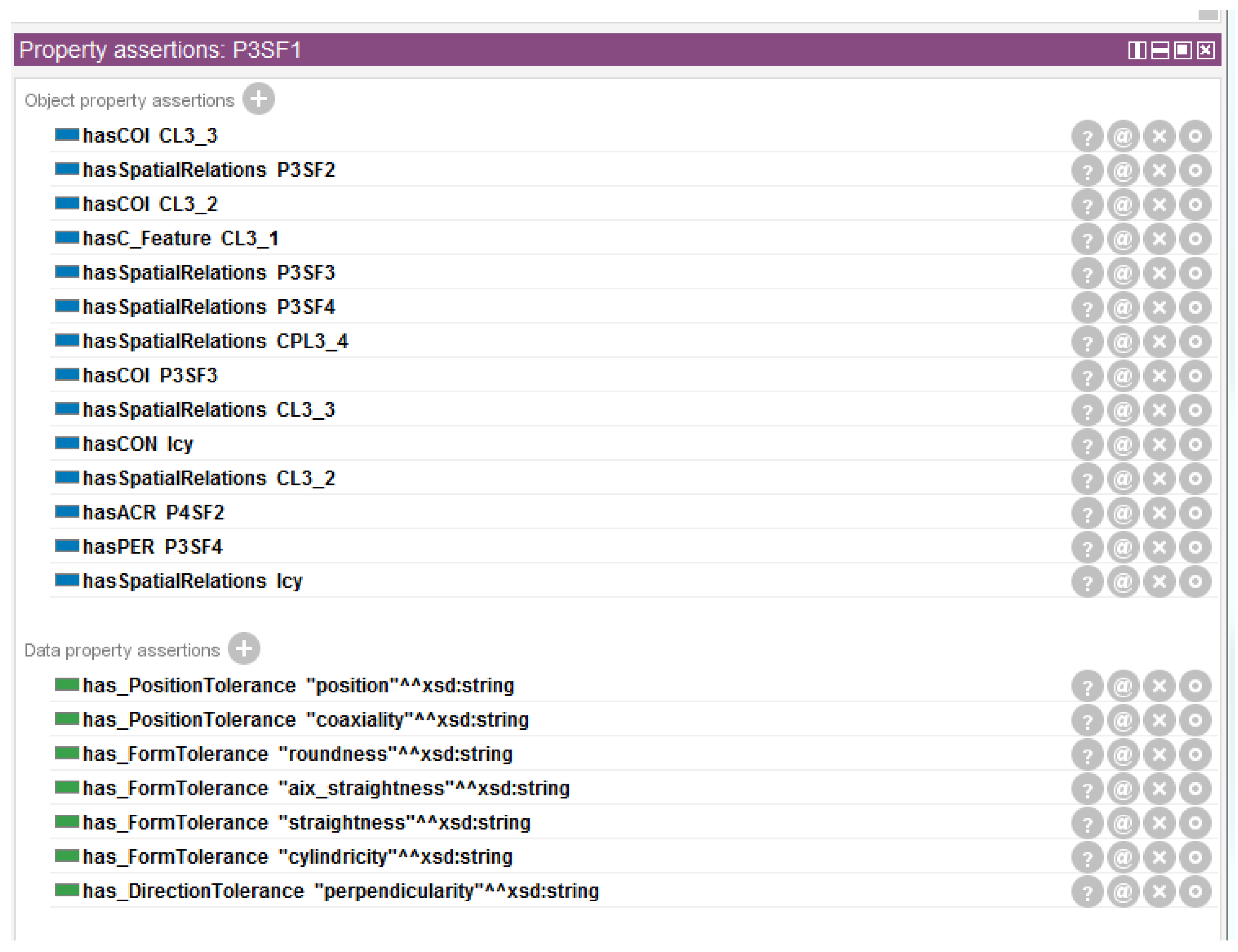
- Inference generation for tolerance types. The SWRL inference rules [35] were input to automatically recommend tolerance items for each part of the assembly. Taking part Part3 as an example, the inference result of feature surface P3SF1 was obtained, as shown in Figure 13. The tolerance types for other assembly feature surfaces are shown in Table 4.
5.2.3. Automatic Screening of AT Types
- Constructing the set of tolerance type assertions TABOX for each assembly face of Part3. According to the reasoning in Section 5.2.2, the tolerance types of each AFS P3SF1, P3SF2, P3SF3, and P3SF4 of part Part3 were obtained. The selection tolerance type assertion set As was constructed, as represented by Equation (8).
- 2.
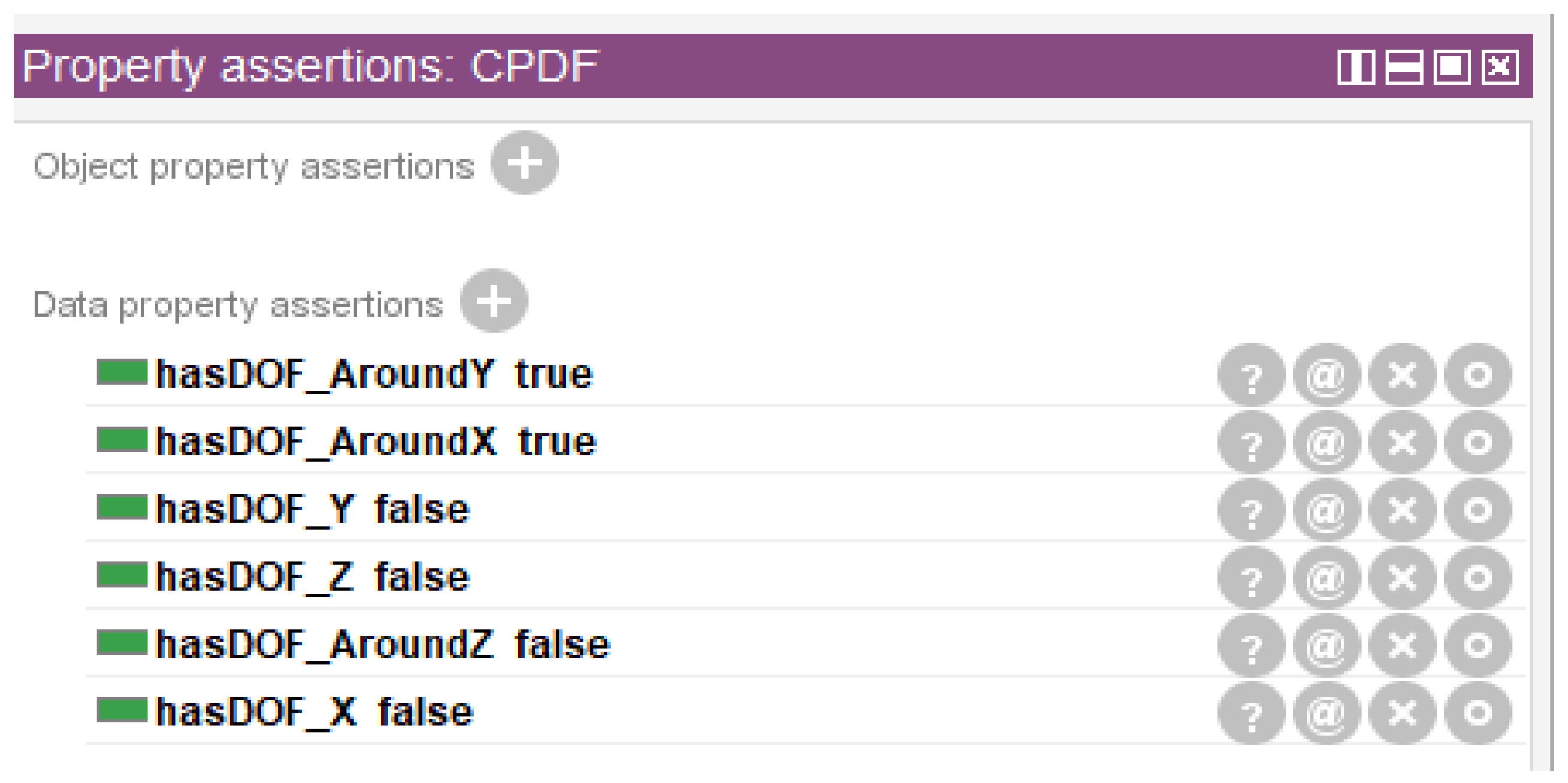
- Setting of the control parameters DOF vector V0. Based on the geometric functional requirements of the assembly and the coordinate system determined in step 2 of Section 5.2.1, we instantiated tolerance-zone DOFs under the DOF class in the tolerance specification design knowledge ontology library. Based on this, the common parameter DOF determination rule and the control parameter DOF determination rule proposed in Section 4.5.2 were combined to infer the control parameter DOF vector V0 (the instantiation name is represented by CPDF). The data properties of instance CPDF are shown in Figure 14. The control parameter DOF vector V0 = (0 0 0 1 1 0) can be obtained from the data attributes of CPDF.
- 3.
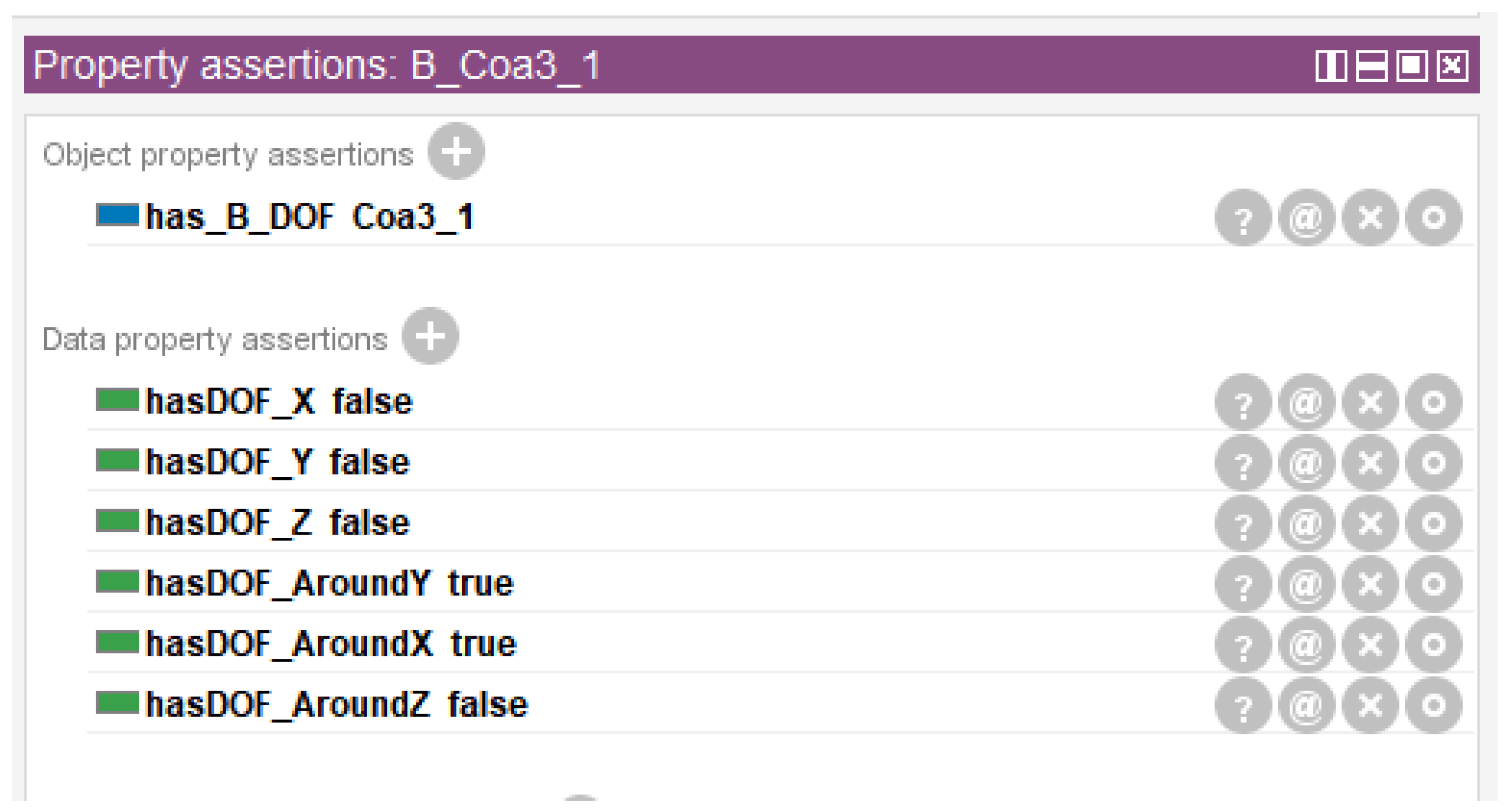
- Determination of comparative DOFs for different tolerance types. Using the comparative DOF calculation inference rule proposed in Section 4.5.2, the comparative DOFs for the different tolerance types on the AFSs of the work piece Part3 were inferred. The AFS P3S1 of the work piece Part3 had multiple recommended tolerance types, and coaxiality tolerance was one of them. Example B_ Coa3 is the comparative DOF for instance Coa3. After reasoning through the SWRL rule for comparing DOFs, the attribute values of the B_Coa3_1 instance were obtained, as shown in Figure 15.
- 4.
- Screening of tolerance types. Using the screening rules proposed in Section 4.5.2, the screening of inferred tolerances for all the feature faces of part Part3 was completed, and the results are shown in Table 5.
5.2.4. Detailed Design of Tolerance Specifications
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Armillotta, A. A method for computer-aided specification of geometric tolerances. Comput. Des. 2013, 45, 1604–1616. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, T.; Cao, Y.; Yang, J.; Jiang, X. A computer-aided tolerance specification method based on multiple attributes decision-making. Int. J. Adv. Manuf. Technol. 2020, 111, 1735–1750. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Gao, J.; Hong, J. New reasoning algorithm for assembly tolerance specifications and corresponding tolerance zone types. Comput. Des. 2011, 43, 1606–1628. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Wang, J. Hierarchical Reasoning Model of Tolerance Information and Its Using in Reasoning Technique of Geometric Tolerance Types. In Intelligent Robotics and Applications: First International Conference, ICIRA 2008 Wuhan, China, 15–17 October 2008 Proceedings, Part II, Wuhan, China, 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 858–868. [Google Scholar]
- Qie, Y.; Qiao, L.; Cui, Y.; Anwer, N. A Doman Ontology for Assembly Tolerance Design. In Proceedings of the 2017 ASME International Mechanical Engineering Conference and Exhibition, Tampa, FL, USA, 3–9 November 2017; Volume 2. [Google Scholar]
- Luo, C.; Franciosa, P.; Mo, Z.; Ceglarek, D. A Framework for Tolerance Modeling based on Parametric Space Envelope. J. Manuf. Sci. Eng. 2020, 142, 061007. [Google Scholar] [CrossRef]
- Johannesson, H.; Söderberg, R. Structure and Matrix Models for Tolerance Analysis from Configuration to Detail Design. Res. Eng. Des. 2000, 12, 112–125. [Google Scholar] [CrossRef]
- Hong, Y.S.; Chang, T.C. A comprehensive review of tolerancing research. Int. J. Prod. Res. 2002, 40, 2425–2459. [Google Scholar] [CrossRef]
- Mao, J.; Zong, Y. Assembly Tolerance Modeling Based on Generalized Directed Graph. Procedia CIRP 2015, 27, 318–323. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, G.; Lin, Z.; Van den Bussche, J. Inconsistency-tolerant reasoning with OWL DL. Int. J. Approx. Reason 2014, 55, 557–584. [Google Scholar] [CrossRef]
- Moguillansky, M.O. Ontology reasoning and evolution with inconsistency tolerance. AI Commun. 2016, 29, 405–407. [Google Scholar] [CrossRef]
- Zhong, Y.; Qin, Y.; Huang, M.; Lu, W.; Gao, W.; Du, Y. Automatically generating assembly tolerance types with an ontology-based approach. Comput. Des. 2013, 45, 1253–1275. [Google Scholar] [CrossRef]
- Shi, X.; Tian, X.; Wang, G. Screening Product Tolerances Considering Semantic Variation Propagation and Fusion for Assembly Precision Analysis. Int. J. Precis. Eng. Man. 2020, 21, 1259–1278. [Google Scholar] [CrossRef]
- Liu, G.; Huang, M.; Chen, L. Optimization Method of Assembly Tolerance Types Based on Degree of Freedom. Appl. Sci. 2023, 13, 9774. [Google Scholar] [CrossRef]
- Khodaygan, S.; Movahhedy, M.R.; Saadat Fomani, M. Tolerance analysis of mechanical assemblies based on modal interval and small degrees of freedom (MI-SDOF) concepts. Int. J. Adv. Manuf. Technol. 2010, 50, 1041–1061. [Google Scholar] [CrossRef]
- Yang, L.; Cormican, K.; Yu, M. Ontology Learning for Systems Engineering Body of Knowledge. IEEE Trans. Ind. Informatics 2021, 17, 1039–1047. [Google Scholar] [CrossRef]
- Gupta, R.K.; Gurumoorthy, B. Feature-based ontological framework for semantic interoperability in product development. Adv. Eng. Inform. 2021, 48, 101260. [Google Scholar] [CrossRef]
- Chhim, P.; Chinnam, R.B.; Sadawi, N. Product design and manufacturing process based ontology for manufacturing knowledge reuse. J. Intell. Manuf. 2019, 30, 905–916. [Google Scholar] [CrossRef]
- Anjum, N.; Harding, J.A.; Young, R.I.; Case, K. Manufacturability verification through feature-based ontological product models. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1086–1098. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Lu, W.; Liu, X.; Scott, P.J.; Jiang, X. A review of representation models of tolerance information. Int. J. Adv. Manuf. Technol. 2018, 95, 2193–2206. [Google Scholar] [CrossRef]
- Hagedorn, T.J.; Smith, B.; Krishnamurty, S.; Grosse, I. Interoperability of disparate engineering domain ontologies using basic formal ontology. J. Eng. Des. 2019, 30, 625–654. [Google Scholar] [CrossRef]
- Su, S.; Wang, Y.; Chen, C.; Li, P.; Zhang, D.; Chen, G. Research on the knowledge representation and retrieval for mechanical product design based on ontology. Int. J. Wirel. Mob. Comput. 2019, 16, 340–349. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, Z.; Shi, L.; Qian, J.; Qimuge, S.; Song, D. A hierarchical assembly knowledge representation framework and microdevice assembly ontology. Adv. Eng. Inform. 2022, 53, 101705. [Google Scholar] [CrossRef]
- Li, Z.; Huang, M.; Zhong, Y.; Qin, Y. A Description Logic Based Ontology for Knowledge Representation in Process Planning for Laser Powder Bed Fusion. Appl. Sci. 2022, 12, 4612. [Google Scholar] [CrossRef]
- Roh, B.; Kumara, S.R.T.; Witherell, P.; Simpson, T.W. Ontology-based Process Map for Metal Additive Manufacturing. J. Mater. Eng. Perform. 2021, 30, 8784–8797. [Google Scholar] [CrossRef]
- Chen, R.; Lu, Y.; Witherell, P.; Simpson, T.W.; Kumara, S.; Yang, H. Ontology-Driven Learning of Bayesian Network for Causal Inference and Quality Assurance in Additive Manufacturing. IEEE Robot. Autom. Lett. 2021, 6, 6032–6038. [Google Scholar] [CrossRef]
- Zhong, Y.; Qin, Y.; Huang, M.; Lu, W.; Chang, L. Constructing a meta-model for assembly tolerance types with a description logic based approach. Comput. Des. 2014, 48, 1–16. [Google Scholar] [CrossRef]
- Peng, Z.; Huang, M.; Zhong, Y.; Tang, Z. Construction of ontology for auto-interpretable tolerance semantics in skin model. J. Amb. Intel. Hum. Comp. 2020, 11, 3545–3558. [Google Scholar] [CrossRef]
- Sarigecili, M.I.; Roy, U.; Rachuri, S. Interpreting the semantics of GD&T specifications of a product for tolerance analysis. Comput. Des. 2014, 47, 72–84. [Google Scholar] [CrossRef]
- Shah, J.J.; Yan, Y.; Zhang, B. Dimension and tolerance modeling and transformations in feature based design and manufacturing. J. Intell. Manuf. 1998, 9, 475–488. [Google Scholar] [CrossRef]
- Desrochers, A.; Clément, A. A dimensioning and tolerancing assistance model for CAD/CAM systems. Int. J. Adv. Manuf. Technol. 1994, 9, 352–361. [Google Scholar] [CrossRef]
- Anselmetti, B. Generation of functional tolerancing based on positioning features. Comput. Des. 2006, 38, 902–919. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, B.; Wu, Z.; Yang, J. Study on functional specification scheme on interface based on positioning features. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 745–753. [Google Scholar] [CrossRef]
- Ma, N.; Yang, B.; Li, J.; Liu, Y.; Wang, D.; Gao, C. Transfer method of geometric tolerance items based on assembly joints. Int. J. Adv. Manuf. Technol. 2021, 117, 1689–1708. [Google Scholar] [CrossRef]
- Qin, Y.; Zhong, Y.; Huang, M.; Liu, F. An assembly tolerance representation model based on spatial relations for generating assembly tolerance types. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 228, 1005–1020. [Google Scholar] [CrossRef]
- ISO 1101:2012; Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out. International Organization for Standardization: Geneva, Switzerland, 2012.



| Tolerance Code | TS1 | TS2 | TS3 | TS4 | TS5 | TS6 | TS7 | TS8 | TS9 |
|---|---|---|---|---|---|---|---|---|---|
| TZ form |  |  |  |  |  | 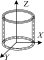 | 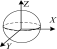 |  |  |
| DOI 1 | TZ | TX, TY | TX, TY | TZ | TZ | TZ | TY | ||
| RX, RY, RZ | RX, RZ | RZ | RX, RY, RZ | RZ | RZ | RX, RY, RZ | RX, RZ | ||
| DOFs | TX, TY | TZ, | TZ, | TX, TY, | TX, TY, | TX, TY | TX, TY, TZ | TX, TZ | TX, TY, TZ |
| RY | RX, RY | RX, RY, | RX, RY | RY, | RX, RY, RZ | ||||
| Representation | Ti (1,1,0) | Ti (0,0,1) | Ti (0,0,1) | Ti (1,1,0) | Ti (1,1,0) | Ti (1,1,0) | Ti (1,1,1) | Ti (1,1,1) | Ti (1,1,1) |
| Ri (0,0,0) | Ri (0,1,0) | Ri (1,1,0) | Ri (0,0,0) | Ri (1,1,0) | Ri (1,1,0) | Ri (0,0,0) | Ri (0,1,0) | Ri (1,1,1) |
| Tolerance Number | Tolerance Type | Common Typical Assembly Feature Features (Exported Features) | |||||
|---|---|---|---|---|---|---|---|
| Cylindrical Surface (Line) | Plane (Plane) | Free-form Surface (Point, Line, Surface) | Sphere (Point) | Circular Countertop (Point, Line) | Prismatic Surface (Line, Surface) | ||
| TT01 |  | TS4 | TS4 | TS4 | |||
| TT02 | Single direction  | TS2 | TS2 | TS2 | TS2 | ||
| TT03 | In any direction  | TS5 | |||||
| TT04 |  | TS3 | |||||
| TT05 |  | TS6 | |||||
| TT06 |  | TS8 | TS8 | ||||
| TT07 |  | TS9 | TS9 | ||||
| TT08 | Single direction 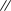 | TS3 | |||||
| TT09 | In any direction 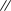 | TS5 | TS3 | ||||
| TT10 | Single direction  | TS3 | |||||
| TT11 | In any direction  | TS5 | TS3 | ||||
| TT12 | In any direction  | TS5 | TS3 | ||||
| TT13 | Single directional  | TS3 | TS2 | ||||
| TT14 |  | TS3 | |||||
| TT15 |  | TS3 | |||||
| TT16 |  | TS1 | TS1 | ||||
| TT17 | In any direction 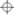 | TS5 | TS3 | TS7 | |||
| TT18 | Radial circular  | TS4 | |||||
| TT19 | Axial circular  | TS2 | |||||
| TT20 | Total radial  | TS6 | |||||
| TT21 | Total axial  | TS3 | |||||
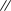 indicates parallelism, symbol
indicates parallelism, symbol  indicates perpendicularity, symbol
indicates perpendicularity, symbol  indicates coaxiality, t, symbol
indicates coaxiality, t, symbol  indicates straightness, symbol
indicates straightness, symbol 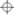 indicates positionality, symbol
indicates positionality, symbol 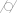 indicates cylindricity, symbol
indicates cylindricity, symbol  indicates roundness, symbol
indicates roundness, symbol  indicates flatness, symbol
indicates flatness, symbol 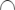 indicates line profile, symbol
indicates line profile, symbol  indicates surface profile, symbol
indicates surface profile, symbol  indicates symmetry, symbol
indicates symmetry, symbol  indicates run-out, symbol
indicates run-out, symbol  indicates inclination and symbol
indicates inclination and symbol  indicates total run-out.
indicates total run-out.| Serial Number | Object Properties | Domain | Range |
|---|---|---|---|
| 1 | hasZone | RealFeature | ToleranceZone |
| 2 | hasSpatialRelations | ConstainedFeature/RealFeature | TargetFeature/RealFeature |
| 3 | hasDOFs | ToleranceType | DOFs |
| 4 | hasToleranceType | TargetFeature/RealFeature | TolerranceType |
| 5 | hasADF | ConstainedFeature | TargetFeature |
| 6 | HasACR | RealFeature | RealFeature |
| 7 | hasFuncRequirement | Assembly | FuncRequirement |
| Data Properties | Domain | Data Types | |
| 8 | hasDOF_AroundX | DOFs | Boolean |
| 9 | hasDOF_AroundY | DOFs | Boolean |
| 10 | hasDOF_AroundZ | DOFs | Boolean |
| 11 | hasDOF_X | DOFs | Boolean |
| 12 | hasDOF_Y | DOFs | Boolean |
| 13 | hasDOF_Z | DOFs | Boolean |
| 14 | hasDirection | ToleranceZone | String |
| 15 | Select_of_effectiveness | TolerranceType | Boolean |
| ASF 1 |  |  |  | 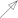 |  | 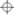 |  | 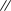 |  |  | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In the Plan | In Any Direction | |||||||||||
| Recommended tolerances | P3S1 | √ | √ | √ | √ | √ | √ | √ | ||||
| P3S2 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| P3S3 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| P3S4 | √ | √ | √ | √ | √ | √ | ||||||
| ASF 1 |  |  | 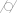 | 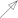 |  | 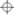 |  | 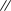 |  |  | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In the Plan | In Any Direction | |||||||||||
| Selected tolerances | P3S1 | √ | √ | √ | √ | √ | √ | |||||
| P3S2 | √ | √ | √ | √ | √ | √ | ||||||
| P3S3 | √ | √ | √ | √ | √ | √ | ||||||
| P3S4 | √ | √ | √ | √ | ||||||||
| ASF 1 |  |  | 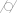 | 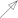 |  | 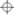 |  | 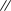 |  |  | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In the Plan | In Any Direction | |||||||||||
| Qin [35] method | P3S1 | √ | √ | √ | √ | √ | √ | √ | ||||
| P3S2 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| P3S3 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| P3S4 | √ | √ | √ | √ | √ | √ | ||||||
| Our method | P3S1 | √ | √ | √ | √ | √ | √ | |||||
| P3S2 | √ | √ | √ | √ | √ | √ | ||||||
| P3S3 | √ | √ | √ | √ | √ | √ | ||||||
| P3S4 | √ | √ | √ | √ | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Huang, M.; Su, W. A Tolerance Specification Automatic Design Method for Screening Geometric Tolerance Types. Appl. Sci. 2024, 14, 1302. https://doi.org/10.3390/app14031302
Liu G, Huang M, Su W. A Tolerance Specification Automatic Design Method for Screening Geometric Tolerance Types. Applied Sciences. 2024; 14(3):1302. https://doi.org/10.3390/app14031302
Chicago/Turabian StyleLiu, Guanghao, Meifa Huang, and Wenbo Su. 2024. "A Tolerance Specification Automatic Design Method for Screening Geometric Tolerance Types" Applied Sciences 14, no. 3: 1302. https://doi.org/10.3390/app14031302
APA StyleLiu, G., Huang, M., & Su, W. (2024). A Tolerance Specification Automatic Design Method for Screening Geometric Tolerance Types. Applied Sciences, 14(3), 1302. https://doi.org/10.3390/app14031302






