Strength Analysis of Cylindrical Shells with Tangential Nozzles under Internal Pressure
Abstract
1. Introduction
2. Establishment of Finite Element Models
2.1. Geometric Model
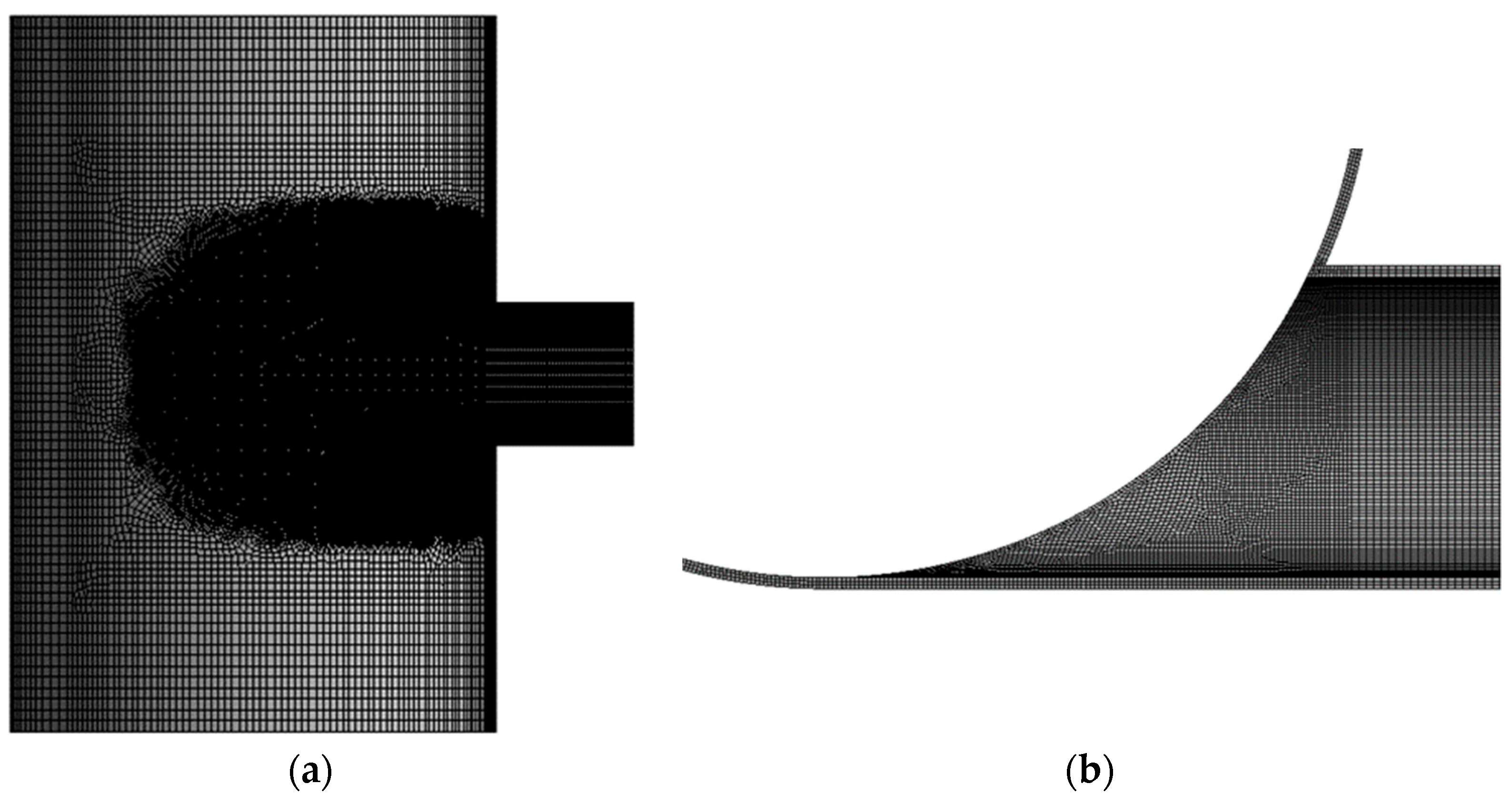
2.2. Mesh Model
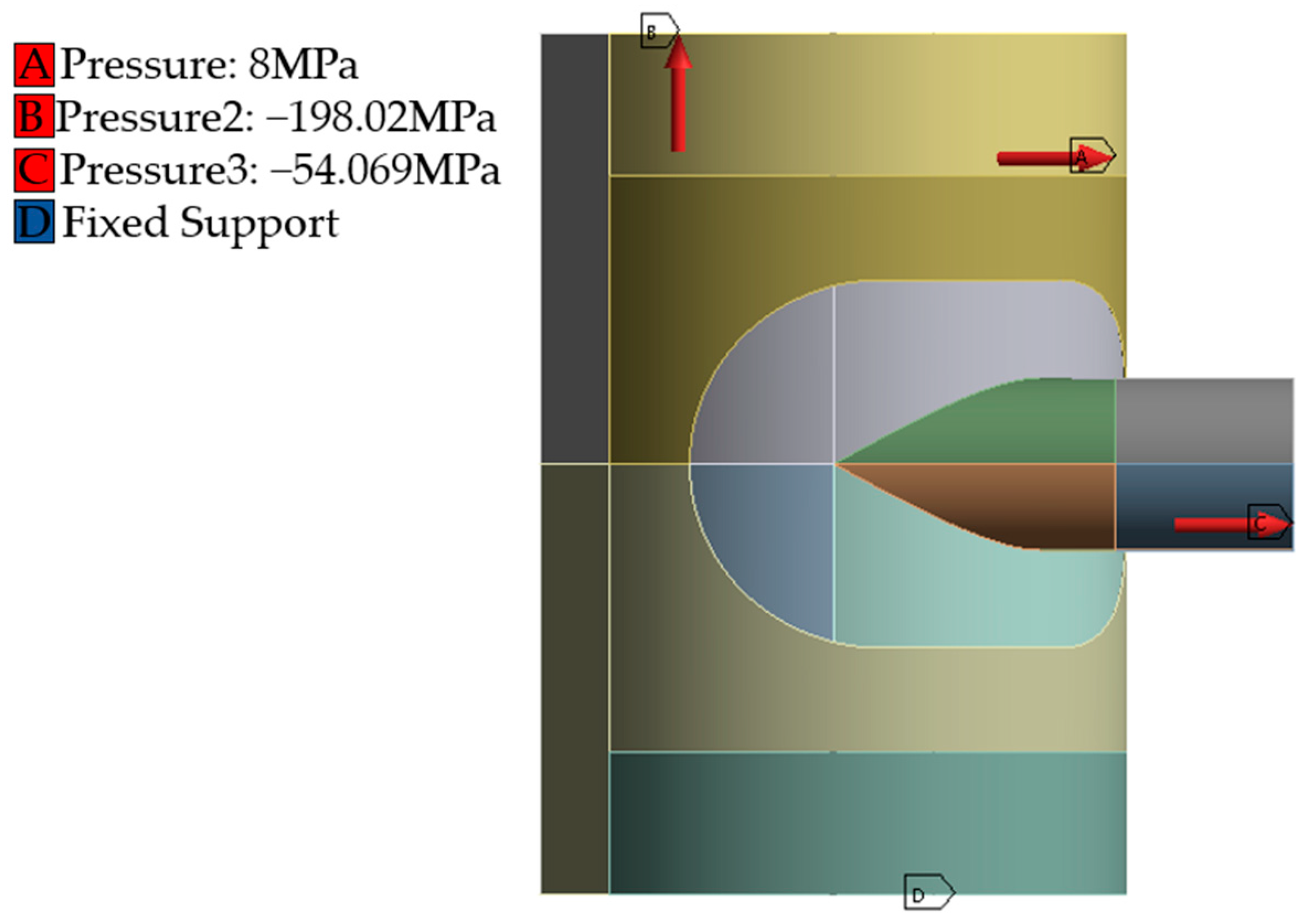
2.3. Loads and Constraints
3. Limit–Load Analysis
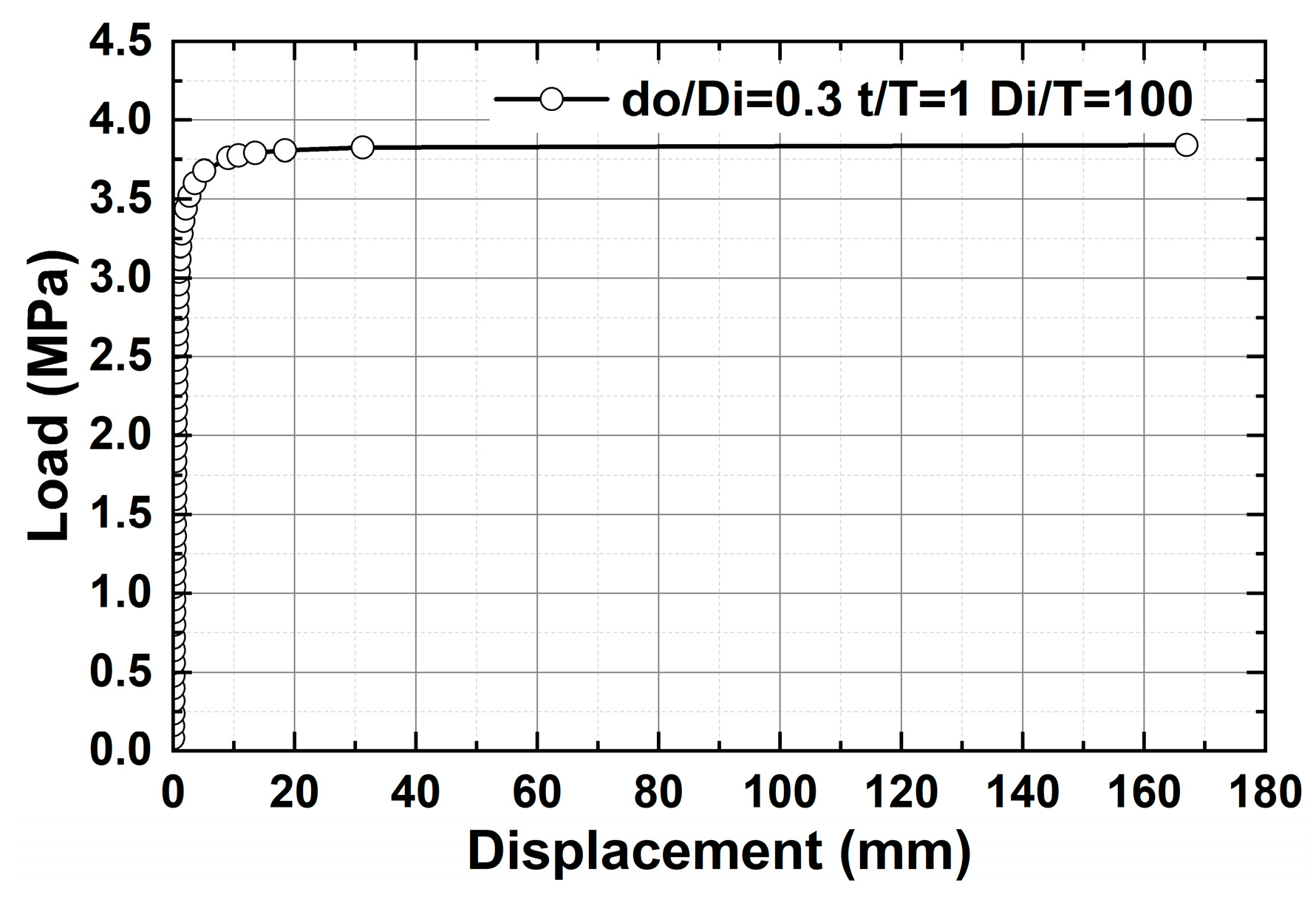
3.1. Limit–Load Analysis Method
3.2. Results of Limit–Load Analysis
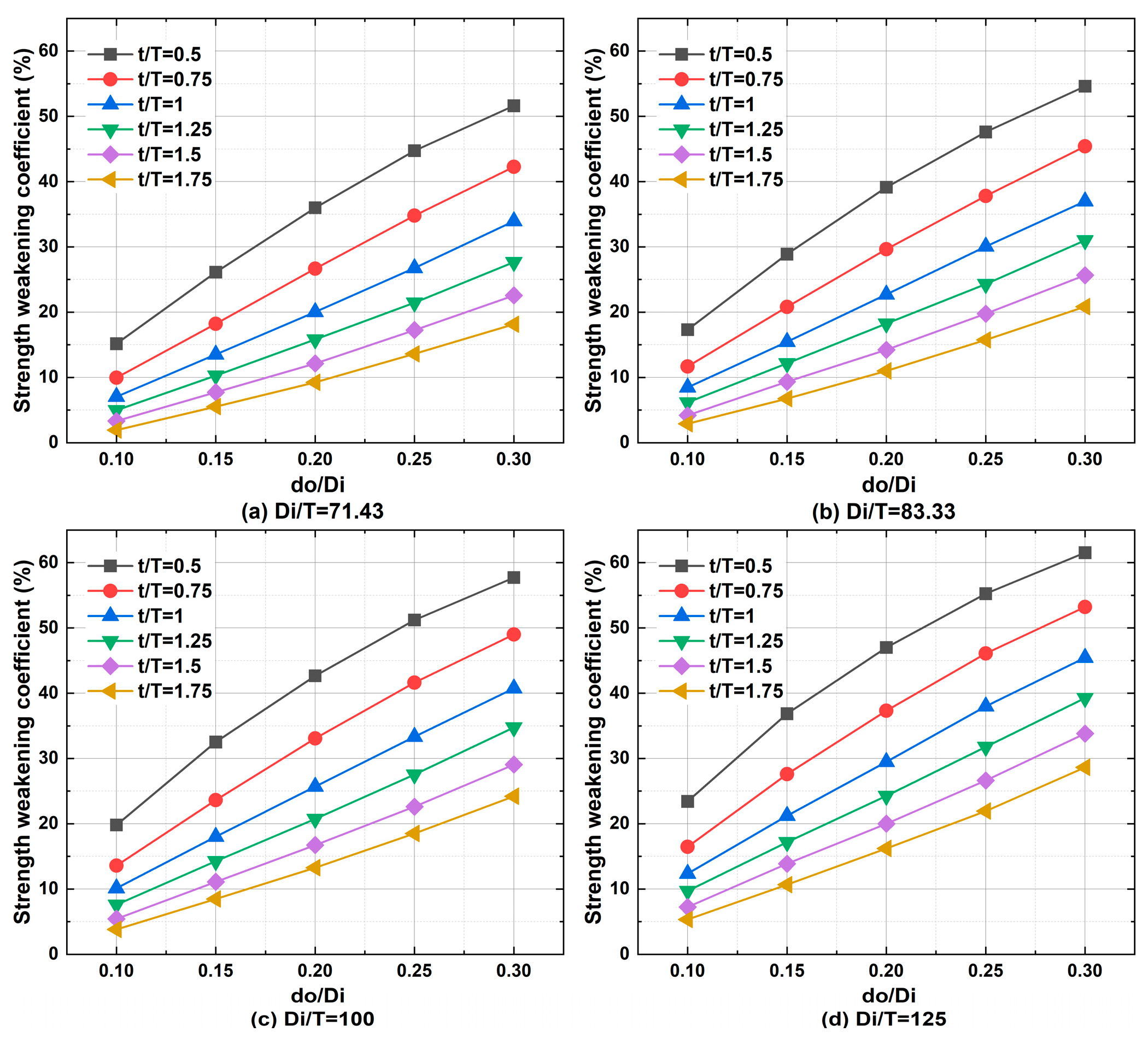
3.3. Strength–Weakening Coefficient and Its Influence Factors
4. Regression of the Strength–Weakening Coefficient
4.1. Regression of the Strength–Weakening Coefficient
4.2. Numerical Verification of Regression Equations of the Strength–Weakening Coefficient
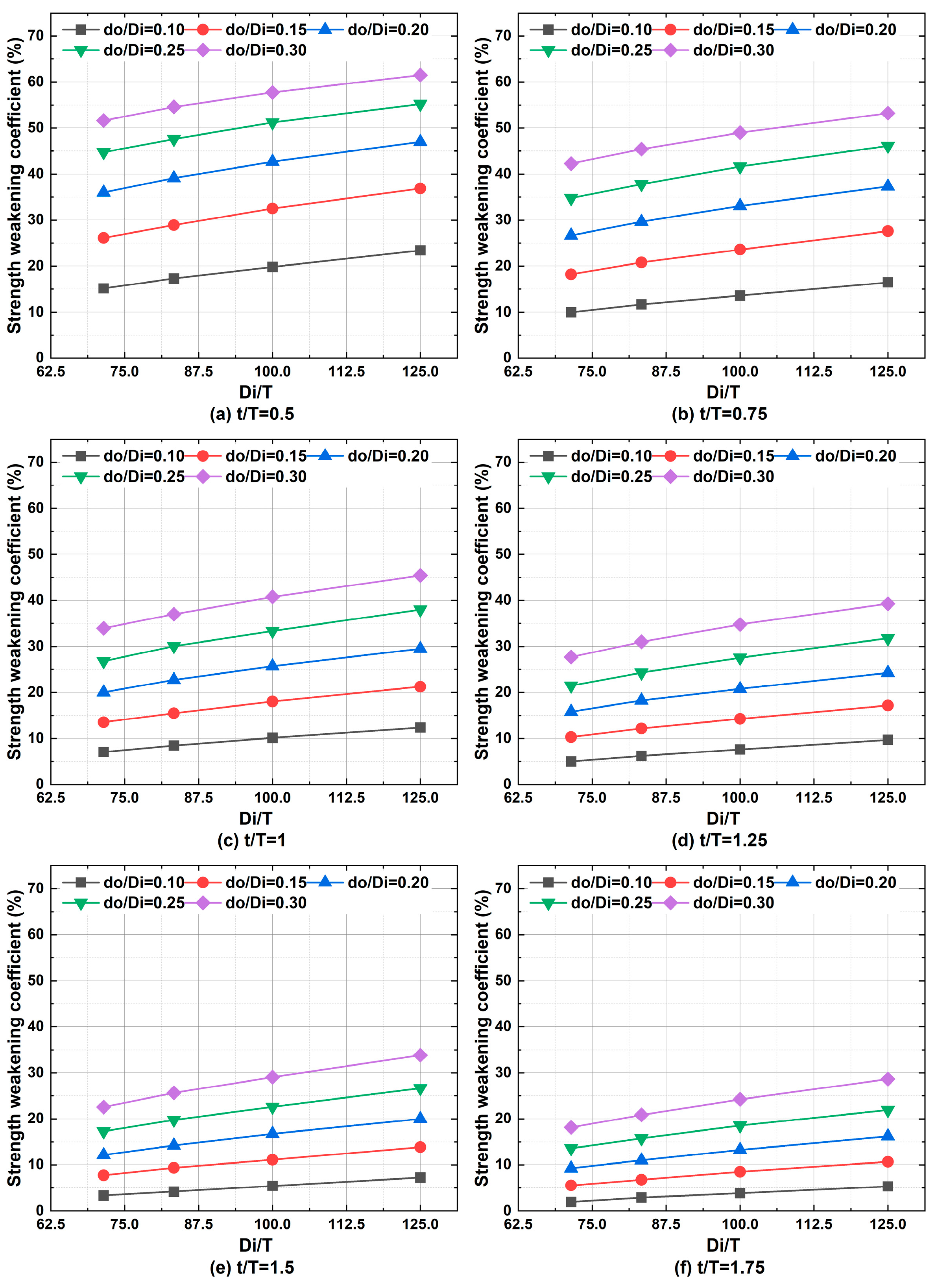
4.3. Applicability of the Regression Equations of the Strength–Weakening Coefficient for Different Shell Diameters
5. Conclusions
- (1)
- For the strength design of cylindrical shell structure with tangential nozzles, in view of the fact that there is no accurate strength design method, this paper proposes a limit–load analysis approach based on a finite element method.
- (2)
- The weakening degree of the ultimate load-bearing capacity of cylindrical shells with tangential nozzles was defined as the strength–weakening coefficient and the influence of do/Di, t/T and Di/T was studied. It was found that with increasing do/Di and Di/T and decreasing t/T, the strength–weakening coefficient increases or, in other words, the ultimate load-bearing capacity of the cylindrical shell decreases.
- (3)
- With sufficient numerical calculation of the ultimate load-bearing capacity of the cylindrical shell with tangential nozzles under internal pressure, the regression equation of the strength–weakening coefficient was obtained which was numerically verified for accuracy. Clearly, by providing the formulas for strength evaluation, this work delves deeper into the subject compared to other similar studies in the literature and yields more practical outcomes.
- (4)
- Due to the use of dimensionless parameters, the regression equation is suitable for different shell diameters with a tangential nozzle structure. The regression equations of the strength–weakening coefficient provide a reference way for the strength design of cylindrical shell structures with tangential nozzles under internal pressure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.B.; Wei, X.L.; Xiang, S.; Guo, C.X.; Liu, H. Stress analysis for tangential bonded structure of pressure vessel and pipe based on finite element method. J. Hunan Inst. Eng. 2005, 29–33. [Google Scholar] [CrossRef]
- Johnson, W.R.; Zhu, X.-K.; Sindelar, R.; Wiersma, B. A parametric finite element study for determining burst strength of thin and thick-walled pressure vessels. Int. J. Press. Vessel. Pip. 2023, 204, 104968. [Google Scholar] [CrossRef]
- Wang, H.F.; Sang, Z.F.; Xue, L.P.; Widera, G.E.O. Burst Pressure of Pressurized Cylinders With Hillside Nozzle. J. Press. Vessel Technol. 2009, 131, 041204. [Google Scholar] [CrossRef]
- Skopinskii, V.N.; Berkov, N.A.; Stolyarova, N.A. Elasto-Plastic Deformation of a Pressure Vessel with a Nonradial Branch Pipe and Determination of the Limit Load. J. Mach. Manuf. Reliab. 2018, 47, 507–515. [Google Scholar] [CrossRef]
- Prakash, A.; Raval, H.K.; Gandhi, A.; Pawar, D.B. Plastic Limit Load Analysis of Cylindrical Pressure Vessels with Different Nozzle Inclination. J. Inst. Eng. Ser. C 2016, 97, 163–174. [Google Scholar] [CrossRef]
- Tang, Q.H.; Liu, K.; Sang, Z.F.; Li, C. Parametric analysis for limit load of cylindrical shell with radial nozzle under combined loadings. Chem. Eng. Mach. 2020, 47, 192–200. [Google Scholar]
- Xu, X.Y. The Research on Strength Analysis for Cylindrical Shell with Hillside Nozzle Structure under Internal Pressure. Master’s Thesis, Nanjing Tech University, Nanjing, China, 2014. [Google Scholar]
- Xue, L.; Widera, G.E.O.; Sang, Z. Parametric FEA Study of Burst Pressure of Cylindrical Shell Intersections. J. Press. Vessel Technol. 2010, 132, 031203. [Google Scholar] [CrossRef]
- Zhang, S.L.; He, X.H. Research on elastic buckling critical pressure of cylindrical shell with nozzle structure. Mach. Des. Manuf. 2017, 21–24. [Google Scholar] [CrossRef]
- Zhang, J.W.; He, X.H. Research on critical buckling pressure of orthotropic titanium cylindrical shell with nozzle structure. Press. Vessel Technol. 2020, 37, 20–26+35. [Google Scholar]
- Fan, H.C.; Hu, L.N. Pressure vessel nozzle local stress prediction software based on ABAQUS- machine learning. SoftwareX 2023, 24, 101550. [Google Scholar] [CrossRef]
- Wang, X.M.; Yan, D.S.; Xia, S.Q.; Guo, X.H. Application of limiting load method in stress analysis—Six important issues about stress analysis design for pressure vessels (Ⅳ). Petro-Chem. Equip. Technol. 2016, 37, 1–5+7. [Google Scholar]
- Majid, M.R. A Review of Elasto-Plastic Shakedown Analysis with Limited Plastic Deformations and Displacements. Period. Polytech. Civ. Eng. 2018, 62, 812–817. [Google Scholar]
- Zuo, A.D. Discussion of evaluation method for limit load analysis by using ANSYS. Process Equip. Pip. 2020, 57, 1–7. [Google Scholar]
- GB/T 150.2-2011; Pressure vessels—Part 2: Materials. Standards Press of China: Beijing, China, 2012.
- Bai, H.Y.; Fang, Y.L. ANSYS limit load analysis method in pressure vessel design. Press. Vessel Technol. 2014, 31, 47–50. [Google Scholar]
- Nadarajah, C.; Mackenzie, D.; Boyle, J.T. Limit and shakedown analysis of nozzle/cylinder intersections under internal pressure and in-plane moment loading. Int. J. Press. Vessel. Pip. 1996, 68, 261–272. [Google Scholar] [CrossRef]
- Wen, H.B.; Fu, L.; Yang, H.L.; Liu, Y. Stability analysis for the pressure vessel with special tangential nozzle. J. Sichuan Univ. Sci. Eng. (Nat. Sci. Ed. ) 2013, 26, 54–57. [Google Scholar]
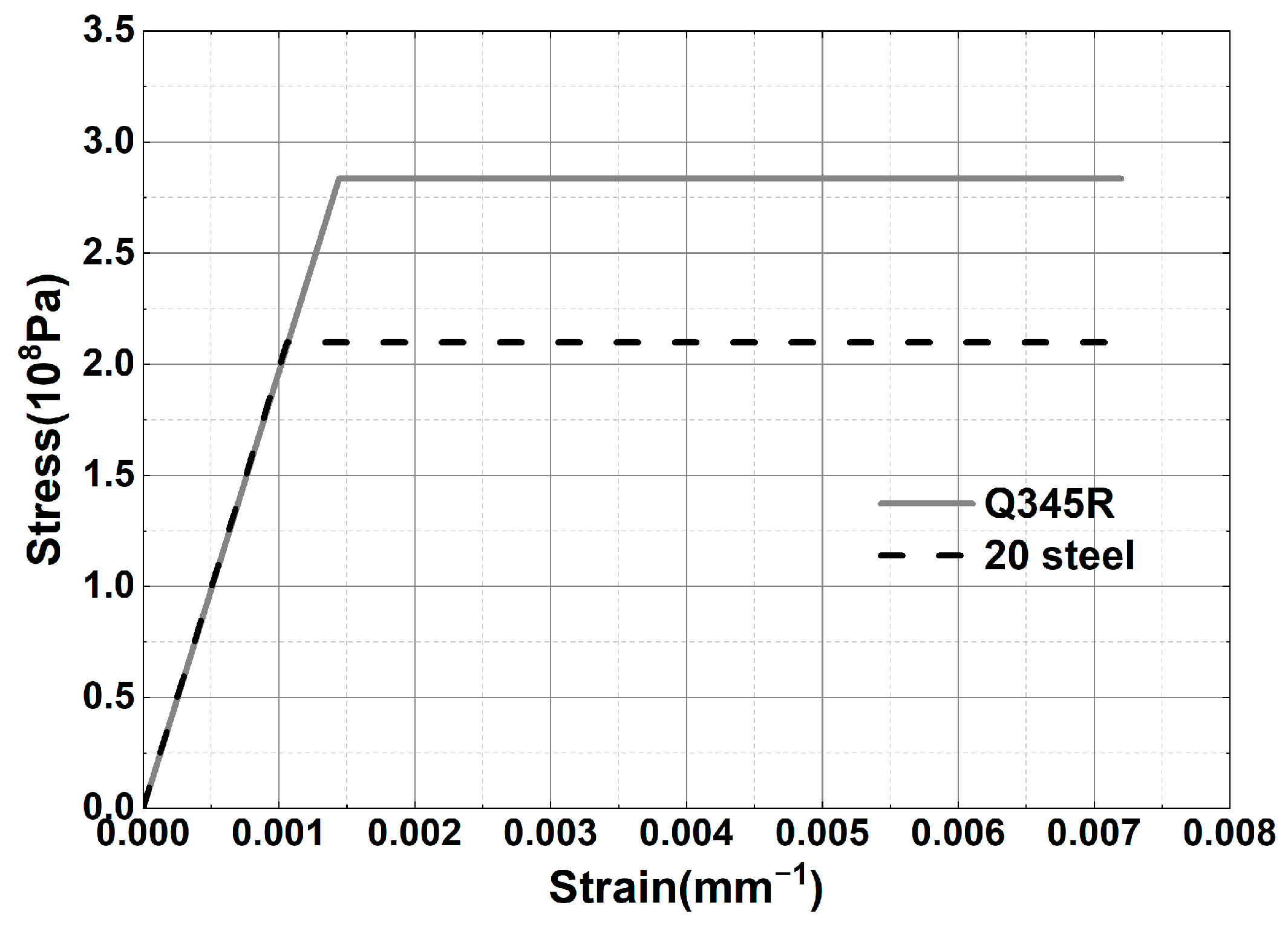




| Material | Thickness/mm | Design Temperature/°C | Allowable Stress/MPa | Yield Strength/MPa | Tangential Modulus/MPa | Elastic Modulus/MPa | Poisson’s Specific | Density /kg·m−3 |
|---|---|---|---|---|---|---|---|---|
| Q345R | 3~16 | 100 | 189 | 283.5 | 0 | 197,000 | 0.3 | 7850 |
| 20 | >16~40 | 100 | 140 | 210 | 0 | 197,000 | 0.3 | 7850 |
| do/Di | t/T | Di/T |
|---|---|---|
| 0.10 | 0.5 | 71.43 |
| 0.15 | 0.75 | 83.33 |
| 0.20 | 1 | 100 |
| 0.25 | 1.25 | 125 |
| 0.30 | 1.5 | |
| 1.75 |
| Di/T | Limit Load/MPa | von Mises Stress/MPa |
|---|---|---|
| 71.43 | 9.040 | 287.47 |
| 83.33 | 7.765 | 286.94 |
| 100 | 6.480 | 286.22 |
| 125 | 5.190 | 285.42 |
| do/Di | t/T | Di/T | Limit Load P/MPa | The Finite Element Solution of Strength–Weakening Coefficient K/% | The Formula Solution of Strength–Weakening Coefficient K/% | Relative Difference/% |
|---|---|---|---|---|---|---|
| 0.13 | 0.8 | 90.91 | 5.90 | 17.18 | 17.10 | 0.50 |
| 0.27 | 0.8 | 111.11 | 3.21 | 45.01 | 44.44 | 1.28 |
| 0.18 | 1.4 | 90.91 | 6.09 | 14.49 | 14.41 | 0.56 |
| 0.22 | 1.4 | 111.11 | 4.52 | 22.54 | 22.30 | 1.05 |
| do/Di | t/T | Di/T | Di/mm | T/mm | Limit Load of Cylinder with Tangential Nozzle P/MPa | Limit Load of a Cylinder P0/MPa | The Finite Element Solution of Strength–Weakening Coefficient K/% | The Formula Solution of Strength–Weakening Coefficient K/% | Relative Difference/% |
|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 0.75 | 100 | 500 | 5 | 5.6000 | 6.48 | 13.58 | 13.88 | 2.23 |
| 1000 | 10 | 5.6000 | 6.48 | 13.58 | 13.88 | 2.23 | |||
| 2000 | 20 | 5.6080 | 6.48 | 13.46 | 13.88 | 3.17 | |||
| 0.25 | 0.50 | 100 | 500 | 5 | 3.1589 | 6.48 | 51.25 | 50.13 | 2.19 |
| 1000 | 10 | 3.1618 | 6.48 | 51.21 | 50.13 | 2.10 | |||
| 2000 | 20 | 3.1694 | 6.48 | 51.09 | 50.13 | 1.88 | |||
| 0.15 | 1.25 | 100 | 500 | 5 | 5.5531 | 6.48 | 14.30 | 13.98 | 2.25 |
| 1000 | 10 | 5.5549 | 6.48 | 14.28 | 13.98 | 2.07 | |||
| 2000 | 20 | 5.5402 | 6.48 | 14.50 | 13.98 | 3.59 | |||
| 0.30 | 1.5 | 100 | 500 | 5 | 4.5802 | 6.48 | 29.32 | 28.68 | 2.17 |
| 1000 | 10 | 4.5962 | 6.48 | 29.07 | 28.68 | 1.34 | |||
| 2000 | 20 | 4.5962 | 6.48 | 29.07 | 28.68 | 1.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Qian, C.; Wu, Z. Strength Analysis of Cylindrical Shells with Tangential Nozzles under Internal Pressure. Appl. Sci. 2024, 14, 2363. https://doi.org/10.3390/app14062363
Zhao X, Qian C, Wu Z. Strength Analysis of Cylindrical Shells with Tangential Nozzles under Internal Pressure. Applied Sciences. 2024; 14(6):2363. https://doi.org/10.3390/app14062363
Chicago/Turabian StyleZhao, Xiaofeng, Caifu Qian, and Zhiwei Wu. 2024. "Strength Analysis of Cylindrical Shells with Tangential Nozzles under Internal Pressure" Applied Sciences 14, no. 6: 2363. https://doi.org/10.3390/app14062363
APA StyleZhao, X., Qian, C., & Wu, Z. (2024). Strength Analysis of Cylindrical Shells with Tangential Nozzles under Internal Pressure. Applied Sciences, 14(6), 2363. https://doi.org/10.3390/app14062363





