Abstract
This paper presents two methods of shaping the mesh topology of lightweight structures as spherical domes. The two given methods of dividing the initial face of the polyhedra determine the obtained structures, which differ in the way of connecting the nodal points. These points were obtained by applying the algorithm for calculating spherical coordinates presented in the paper, which were then converted to the Cartesian system using transformation formulas. Two models of dome structures are presented, based on a 4608-hedron according to the first division method, and on a 4704-hedron, using the second proposed method with numerical analysis. Thus, the novelty of this paper is an implementation of the formulas and algorithms from geodesic domes based on the regular dodecahedron to the regular octahedron, which has not been presented so far. The choice of the shape of the structure has impacts on sustainable development, dictated by structural and visual considerations, leading to the design of a light structure with low consumption of construction material (steel), which can undoubtedly be helpful when making the final structure shape. In addition, according to this research, it can be concluded that using the first method to create a geodesic dome mesh is more straightforward, safer, and requires less design experience.
1. Introduction
The popularization of the geodesic dome, first designed by Walther Bauersfeld, gave rise to new structures characterized by enclosing the largest volume in the smallest space, using the smallest possible amount of material. The process of popularizing coverings in the form of domes is attributed to Buckminster Fuller, who in June 1954 obtained a patent for a “geodesic, hemispherical structure for enclosing space” [1]. It is worth emphasizing that these domes, thanks to their lightness and great design, can be designed in accordance with current trends in economic design and the so-called sustainable development.
The process of the most regular division of the sphere, leading to obtaining a covering structure in the form of a geodesic dome, is undoubtedly challenging and intriguing. Many architects, engineers, and designers have developed various methods of dividing the initial regular polyhedra following Fuller’s patent [1]. Dividing each initial face of the polyhedron into smaller parts (tessellation) generates a three-way mesh. The vertices of the resulting mesh, projected centrally onto the sphere, create a polyhedron approximating the sphere, in which only the nodes lie on the sphere’s surface. This process can be found in the works of J. Clinton [2,3], T. Tarnai [4,5,6], P. Huybers [7,8,9,10,11,12], G. N. Pavlov [13,14], C. Kitrick [15,16], H. Lalvani [17,18,19,20], M. Wenninger [21,22], J. Rębielak [23], H.S.M. Coxeter [24], J. Fuliński [25], and many others.
The use of appropriate methods of shaping structural forms has become a challenge for aesthetic reception while taking into account the visual considerations of society.
Preliminary determination of the shape of the structure, as well as an indication of the relationships between the elements that constitute it, are the initial stages of shaping spatial structural forms. The following sets of the process of shaping geodesic dome structures include, among other things, optimization of the obtained structures. Thanks to this process, we receive a covering in the form of a geodesic dome, highlighting the advantages of this type of spatial form of structure. This is primarily about economic considerations, determined by the use of a small amount of construction material, which in turn leads to an increasing interest in this type of construction solution among architects and builders.
Many scientific studies are focusing on the optimization of geodesic domes. The use of optimization algorithms concerning the shaped dome structures makes it possible to obtain covers with optimal cross-sections, sizes, and shapes, which consequently reduces the weight of the analyzed structure. Gradient-based optimization methods were applied in the paper of Gythiel and Schevenels [26]. The optimal design of reticulated shell structures using metaheuristic algorithms was studied by Saka [27,28], Kaveh and Talatahari [29], and Çarbas and Saka [30]. The development of a metaheuristic algorithm was presented by Dede et al. [31] as Rao’s algorithm. Dede et al. [32] also presented another approach known as the Jaya algorithm. Many other papers aimed at optimizing structures in the form of domains, including Ye and Lu [33], as well as Grzywinski et al. [34].
Creating the structural form of a geodesic dome involves dividing its initial regular polyhedron into smaller faces by approximating each of its edges. The polyhedron that was the source of Fuller’s patent [1] was the icosahedron, and it is on its basis (as well as on the dodecahedron) that most studies on spherical coverings in the form of geodesic domes are based. The feature distinguishing these two polyhedra from other Platonic solids is the higher symmetry and repeatability of elements that can be achieved compared to meshes based on other polyhedra. However, it should be emphasized here that the remaining polyhedra, including the regular octahedron, are also the basis for shaping the topology of geodesic dome grids.
The aspect of sustainable development is becoming more important over the years. In this case, the structures must be designed with due care and knowledge. Therefore, lightweight structures [35,36,37,38,39,40] perfectly fit into the idea of sustainable development. Additionally, research on the shaping and optimization of structures through the use of cross-section has a positive impact on the aspect of sustainable development [41,42,43]. Moreover, thanks to the use of advanced software, it allows the implementation of spectacular structures that become the showcase of a city or even a country. The available software allows you to design lightweight structures with maximum use and respect for materials, in line with the idea of sustainable development.
This paper aims to present the mesh topology of shaping structural solutions in the form of geodesic domes while considering two different methods of creating. The base polyhedron for generating the analyzed domes is a regular octahedron, i.e., that is not commonly used when creating geodesic domes. Generally, the regular octahedron is more complicated in the process of creating domes but the shape is more effective than in the case of the dodecahedron, which is the biggest advantage of this structure. Until now, the octahedron was analyzed only by Pilarska [44,45,46] and Bysiec [47]. Based on this research, the paper presents in detail the process of creating the mesh topology of geodesic dome grids, using the example of two structures, a 4608-hedron and a 4704-hedron. Thus, the novelty of this paper is an implementation of the formulas and algorithms from geodesic domes based on the regular dodecahedron to the regular octahedron, which has not been presented so far. It should be emphasized that the dome shaped according to the first method is an easier solution due to the mesh topology of their forms. Moreover, the results obtained from the comparative static and strength analysis also indicate the advantage of this dome over the other construction solutions used. In addition, this research also shows that exciting structures can be made in the spirit of sustainable development.
2. Shaping Geodesic Dome Mesh
The paper presents the topology of mesh creation of two selected geodesic domes obtained by regular octahedron transformations. The indicated topology includes a mutual, strictly defined arrangement of nodes and the method of their connection. The paper did not involve typical optimization of the structure, as was the case in [26,27,28,29,30,31,32,33,34], and research was carried out on which methods of creating a topology mesh result in lower steel consumption and, therefore, more sustainable use of the construction material.
The two geodesic domes, which are the subject of the paper, are structures derived from two different divisions of the initial triangular meshes of a regular octahedron (Figure 1). The division methods used meet the conditions given by J. Fuliński [25].
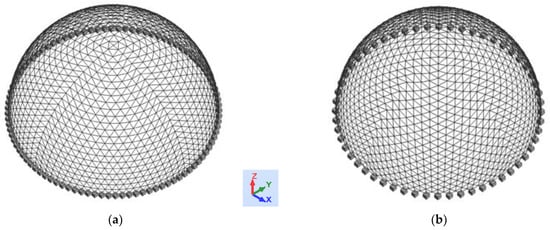
Figure 1.
Meshes of geodesic domes generated from a regular octahedron using (a) the first division method and (b) the second division method.
2.1. The First Method of Dividing a Regular Octahedron
The first method of dividing the initial regular octahedron triangle involves dividing its edges into n-parts and then generating three groups of lines parallel to its edges. Figure 2 shows the division of the initial triangle.
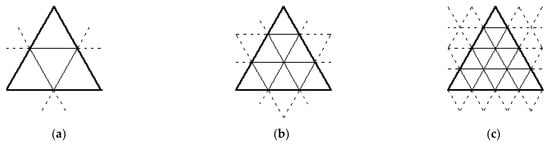
Figure 2.
Division of the triangular face of the initial regular octahedron according to the first method: (a) n = 2, (b) n = 3, and (c) n = 4.
According to the assumptions of the presented method, the n value for the 4608-hedron was calculated using the following formula [25]:
where:
N is the number of faces obtained by dividing a regular octahedron;
n is the number of the division points of the initial triangular octahedron face.
Dividing each edge of the initial triangular mesh of the regular octahedron into 24 parts and connecting the division points according to the rules consistent with the first method leads to creating a 4608-hedron geodesic dome grid.
2.1.1. Determining the Nodal Points of a Dome Shaped according to the First Method
First, the initial triangle of the regular octahedron was described on the first quarter of the hemisphere in the polar coordinate system. The range of analyzed meridian angles is ϕ ∈ <0;90°>, as well as λ ∈ <0;90°> for the latitudinal angles. Taking into account the assumptions of the first method, the division into meridian angles was made by dividing the edges into equal sections, determining the angle between subsequent points using the following formula:
where:
n is the number of the division points of the initial triangular octahedron face.
Then, the formula for the angular ordinate of subsequent layers of nodal points was determined:
where:
is the number of point layers, ∈.

Table 1.
Values of meridional angular ordinates.
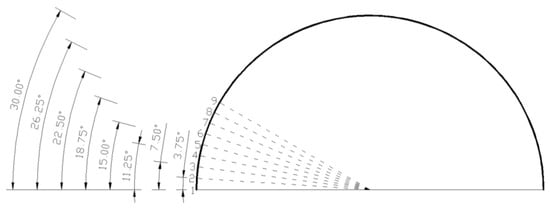
Figure 3.
Meridian angular coordinates for the first 9 layers of points.
In the case of latitudinal coordinates λ, based on the analysis of Figure 2, the formula for the angle between subsequent points on the same layer was derived:
Then, a general formula was determined for the latitudinal angular ordinate of the point for individual layers.
where:
is the number of points in the layer .
According to the above formula, the latitudinal angular coordinate was determined for all dome layers except for the top, where there is only one point with Cartesian coordinates P(0;0;R), as shown in Figure 1.

Table 2.
Latitudinal coordinates for the exemplary first and fifth layers (Figure 3).
The angular ordinates obtained in this way were grouped in pairs to create the angular coordinates of each node in one quarter of the analyzed dome (Figure 3). Therefore, each point received three factors describing its position in space according to the scheme . For example, the location of the point described as fifth on layer five was given the format .
The coordinates obtained in this way create a cloud of points describing the nodes of the dome. To enter them into the numerical program, each point was converted to a Cartesian coordinate system. To move from the spherical coordinate system to the Cartesian coordinate system P(x,y,z), the transformation formulas were used:
In the case of point using the above transformation rules, a point with coordinates in the Cartesian system was obtained:
The above procedure was applied to all points, making it possible to generate a mesh of the computational model in the numerical program.
2.2. The Second Method of Dividing a Regular Octahedron
The second method of dividing the triangular face of the initial regular octahedron consists in dividing the edges of the triangle into n parts and then drawing three groups of lines parallel to the height lines of each edge.
By the assumptions of the presented method, the value of n was calculated for the 4704-hedron according to the following formula [25]:
where:
is the number of faces obtained by dividing a regular octahedron;
is the number of the division points of the initial triangular octahedron face.
By dividing the edges of the initial triangular mesh of the regular octahedron into 28 parts and connecting the division points according to the rules consistent with the second method used, a 4704-hedron geodesic dome mesh was obtained.
Determining the Nodal Points of a Dome Shaped according to the Second Method
The procedure for determining nodal points for a dome shaped according to the presented second method of dividing the initial triangle of a regular octahedron is similar to the first method. You should determine the division points for the first quarter in a spherical system, and then convert the results to the Cartesian system, as shown in Figure 1.
The angular distance between meridian ordinates was determined based on the following formula:
where:
is the number of the division points of the initial triangular octahedron face.
Then, the angular ordinate of the subsequent layers of points was determined based on the following formula:
where:
is the number of point layers, .
The values obtained from formula 12 for all n layers are listed in Table 3.

Table 3.
Values of meridional angular ordinates.
Taking into account the division of the initial triangular mesh of the regular octahedron in accordance with the assumptions of the second method (Figure 4), the formula for the latitudinal ordinate of points on individual layers was used. In this case, the layers were divided into three repeating groups.
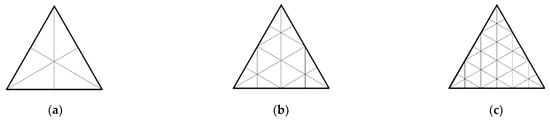
Figure 4.
Division of the triangular face of the initial regular octahedron according to the second method: (a) n = 2, (b) n = 4, (c) n = 6.
- group 1—for layers .
is the consecutive layer number from the group;
is the number of the division points of the initial triangular octahedron face.
Then, a formula was derived for the angular ordinate of the k element in a given layer:
where:
is the number of points in the layer, .
Table 4 presents the results obtained for the exemplary first (a = 1) and seventh (a = 3) layers belonging to group 1.

Table 4.
Latitudinal coordinates for the first and seventh layers from group 1.
- group 2—for layers . As in the case of group 1, first, the formula for the latitudinal ordinate was determined, followed by the formula for the angular ordinate of the k element in a given layer.
is the consecutive layer number from the group;
is the number of the division points of the initial triangular octahedron face.
where:
is the number of points in the layer, .
Table 5 shows the values of the angle for the exemplary second layer (a = 1) and eighth layer (a = 3) belonging to group 2.

Table 5.
Latitudinal coordinates for the second and eighth layers from group 2.
- group 3—for layers In this case, the formula was also determined first for the latitudinal ordinate and then for the angular ordinate of the k element in a given layer.
is the consecutive layer number from the group;
is the number of the division points of the initial triangular octahedron face.
where:
is the number of points in the layer, .
Table 6 shows the values of the angle for the exemplary third (a = 1) and ninth (a = 3) layers belonging to group 3.

Table 6.
Latitudinal coordinates for the third and ninth layers from group 3.
From the obtained results, a point cloud with Cartesian coordinates was created in a similar case for the dome generated according to the first division method, presented in Section 2.1.1 of the paper.
3. Combination of Loads
3.1. Variable Loads
The domes modeled in the numerical program were loaded with snow for zone 2 and wind, following guidelines from Eurocode 1 [48].
When loading the domes with snow, the roof shape coefficient was taken for analysis based on cylindrical roofs due to their similar cross-sectional shape. Covers were considered for both even and uneven snow distribution on the slope, as shown in Figure 5 and Figure 6.
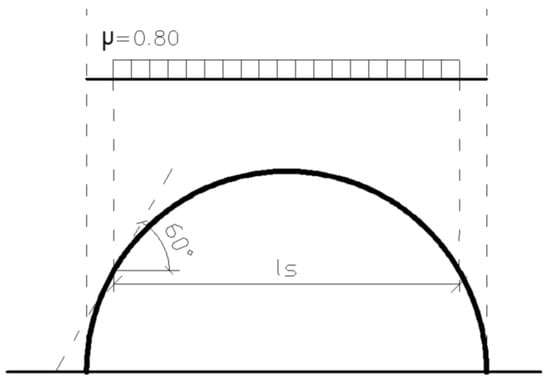
Figure 5.
Roof shape coefficient for even snow load [48].
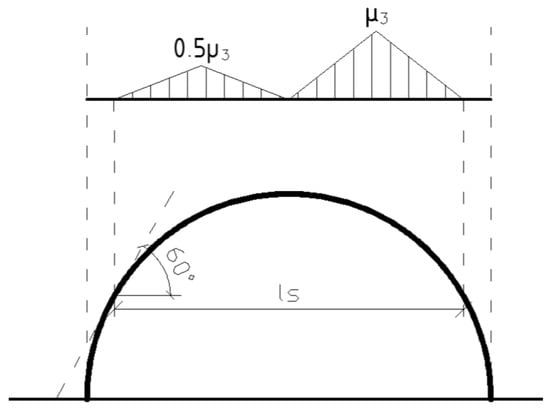
Figure 6.
Roof shape coefficient for uneven snow load [48].
Based on the calculations, the value of the roof shape coefficient was:
while, in accordance with the recommendations of Eurocode 1 [48], the maximum value of the coefficient μ3 = 2.00 was assumed.
The selection of the coefficients of the external pressure value for domes on a circular projection was made based on Figure 7.12 of Eurocode 1 [48], and the coefficients for individual curves were read. The coefficient values are listed in Table 7.

Table 7.
Values of external pressure coefficients [39].
The internal pressure coefficients were assumed by note 2 in Section 7.2.9 of Eurocode 1 [48] with the values +0.20 and −0.30.
3.2. Additional Dead Load of Geodesic Dome
The roof covering was made of LSG glass (Laminated Safety Glass) with resistance class P6B, mounted at points in the nodes of the steel structure with a nominal thickness of 23.04 mm, with a characteristic weight gk = 0.58 [kN/m2].
4. Numerical Analysis Parameters
4.1. General Remarks
The studied domes, thanks to their structure, constitute an exciting research field, which is supported by numerous works, e.g., Pilarska [44,45,46], Bysiec [47], Pilarska and Maleska [49], Bysiec et al. [50], and Bysiec and Maleska [51]. The problem in this type of structure is optimizing these facilities in terms of steel consumption, which in turn affects the carbon footprint. Static and strength analysis software comes to the rescue for this type of problem and, therefore, also for the optimization of these objects. Experimental results are desired in scientific research, but due to the size of the presented structures and their complexity, experimenting is impossible. Therefore, Robot Structural software from Autodesk was used, which enabled the static and strength analysis of these objects, thanks to the adopted principles of building mechanics and Eurocode 1 [48] as well as Eurocode 3 [52] design standards.
4.2. Material Properties
All elements (steel struts) of the generated geodesic domes were assigned a tubular cross-section “R” made of S235 steel (yield strength of 235 MPa), which has the following properties: (i) volumetric weight (γ) 7850 kg/m3, (ii) Young’s modulus (E) 210 GPa, (iii) Poisson’s ratio (ν) 0.3, (iv) Kirchhoff module (G) 80.76 GPa, (v) partial safety factor (γM) 1.0, and (vi) thermal expansion coefficient (α) 1.2 × 10−5. Supports were given as restraints, and nodes were assumed to be articulated (Figure 1).
4.3. Numerical Models
Calculations and dimensions of the modeled two geodesic domes were performed in a numerical program considering the finite element method and using the currently applicable Eurocode 3 design standards for steel structures [52]. The geodesic domes were 49.97 m wide and 25.0 m high, but they had different mesh topologies depending on the method of dividing. In the numerical model, the maximal shape of finite elements did not exceed 0.5 m, as in the studies in [46,47,49].
Using the first method of dividing the initial triangular face of a regular octahedron, a geodesic dome was obtained, the base of which was 4608-hedron, consisting of 3404 rods, 1200 nodes, and 2304 claddings. The second analyzed method allowed for shaping a dome with a 4704-hedron base, composed of 3500 bars, 1205 nodes, and 2352 claddings (Figure 1).
The created structures were loaded with eight load cases, taking into account the self-weight of the dome (case 1) and the laminated tempered glass covering (case 2), evenly distributed snow (case 3) and unevenly distributed snow (case 4), as well as the effect of wind outside and inside the domes (cases 5–8). Based on Eurocode 1 [48], 16 load combinations were developed in the ultimate and serviceability limit states.
5. Result from Numerical Analysis
5.1. Internal Forces
Based on the results of internal forces obtained in the numerical program, the distribution of strut forces in the considered domes was developed.
Figure 7 shows maps of axial forces in the dome struts modeled according to the first method.
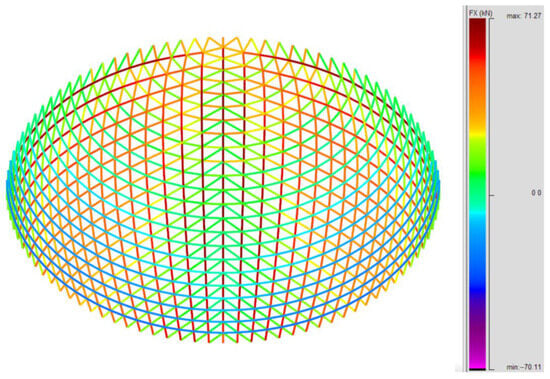
Figure 7.
Maps of axial internal forces in the struts of a dome created according to the first method from a 4608-hedron.
In the case of dividing the initial triangle of a regular octahedron according to the first method, the maximum internal compressive and tensile forces of the struts are similar in value. The struts, forming the first eight layers described at the nodes nw ∈ <2;8>, form tensioned rings; in the higher layers with nw ∈ <9;14>, alternating compression and tension of the struts occurs, depending on the place on the ring. In the upper parts with nw > 14, only compressive forces occur. The struts resulting from the displacement of the side arms of the initial triangle along their entire length are compressed, obtaining maximum values of internal forces at the edges of the regular octahedron forming the dome.
Maps of axial internal forces determined for the dome created according to the second method are shown in Figure 8.
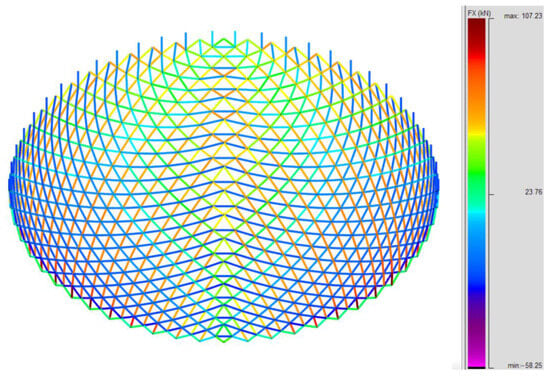
Figure 8.
Maps of axial internal forces in the struts of a dome created according to the second method from a 4704-hedron.
In the second dome analyzed, the maximum internal forces occur in the support zone. Most of the compressive forces are transferred by the struts generated on the straight line perpendicular to the base of the triangle forming the face of the regular octahedron, the struts generated on the straight lines perpendicular to the side walls of the triangle. Depending on their position relative to the base of the dome, they transfer compressive forces in the upper zone and tensile forces at the base, except for the ring forming the last layer of diagonal struts due to the transfer of compressive forces from struts perpendicular to the base of the starting triangle.
5.2. Strut Dimensioning
Considering the values of axial internal forces (Table 8) occurring in the struts (negative values for tension and positive values for compression), first of all, both structures were divided into four groups of struts (Figure 9 and Figure 10).

Table 8.
Division of struts into groups.
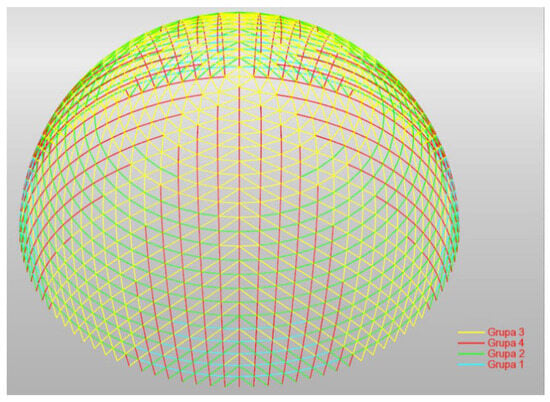
Figure 9.
Division of struts into groups in a dome created according to the first method (4608-hedron).
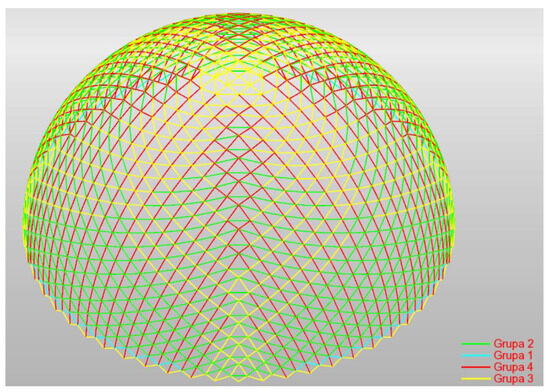
Figure 10.
Division of struts into groups in a dome created according to the second method (4704-hedron).
Then, for individual groups of struts, cross-sections were selected from round tubular sections, considering the maximum use of the load-bearing capacity in the range from 0.80 to 1.00, as shown in Table 9.

Table 9.
Assumed cross-sections for individual groups of struts.
6. Comparative Analysis of the Obtained Results
6.1. Geometric Parameters
First, the number of elements of the analyzed structures was summarized, including panels, nodes, struts, and supports (Figure 11).
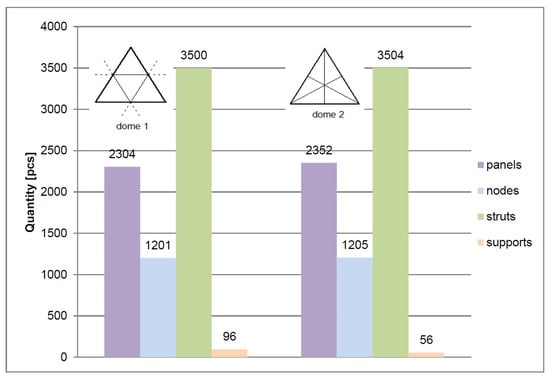
Figure 11.
Geometric parameters of the modeled domes generated from 4608-hedron and 4704-hedron.
The developed domes are characterized by a similar number of nodes, struts and panels. The difference in the number of struts and nodes does not exceed 1%. For panels, the difference does not exceed 5%. However, a significant difference was obtained in the number of support nodes, which is approximately 70% larger in the dome created according to the first method than in the case of the dome generated according to the second method.
6.2. Internal Forces
The maximum values of compressive forces in the struts of the dome generated according to the first method are 34% lower than in the dome created according to the second method (Figure 12), i.e., 71.27 kN for the dome made with 4608-hedron and 107.23 kN for the dome designed with 4704-hedron. Tensile forces, on the other hand, show 20% higher values in the case of the dome created according to the first method, i.e., −70.11 kN for the dome made of 4608-hedron and −58.25 kN for the dome made of 4704-hedron.
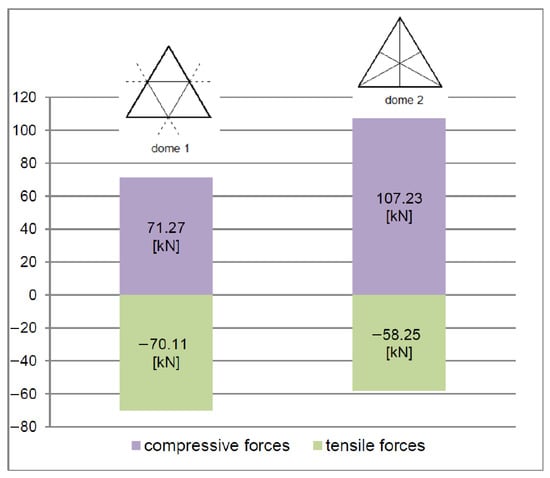
Figure 12.
Maximal values of axial forces in the struts of modeled domes generated from 4608-hedron and 4704-hedron.
6.3. Support Reactions
The values of the obtained support reactions for the dome made according to the second method are approximately 100% higher than in the case of the first method (Figure 13). This is due to fewer supports for a similar structure weight.
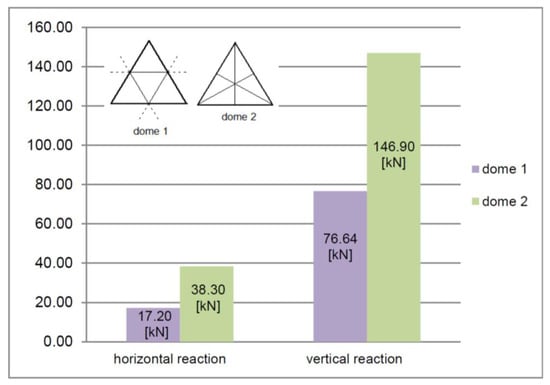
Figure 13.
Maximal values of support reactions of modeled domes generated from 4608-hedron and 4704-hedron.
6.4. The Weight of the Domes
Taking into account the adopted cross-sections of the struts divided into four groups, the weight of individual groups was compared, as well as the total weight of the analyzed domes (Figure 14). The weights of the analyzed structures are very similar. They differ from each other by approximately one tone. The weight of individual groups of struts for the first dome increases with the magnitude of the forces these struts transfer. The first and second groups carrying tensile forces constitute less than one-quarter of the total weight of the structure. The fourth group dominates in terms of weight in both domes. This is influenced by compressive forces, which require stiff and, therefore, heavier cross-sections. Group one, in the case of the dome created using the first method, is almost four times heavier than in the dome shaped according to the second method. This is related to the adopted cross-section and the number of elements in this group. The second and third groups in the first dome follow the trend of increasing weight due to the compressive forces. In the second dome, the weight of these groups is similar. In the second dome, the weight of the fourth group, despite the occurrence of higher compressive forces, is lower than in the first dome, which is due to the smaller total length of the struts in this group.
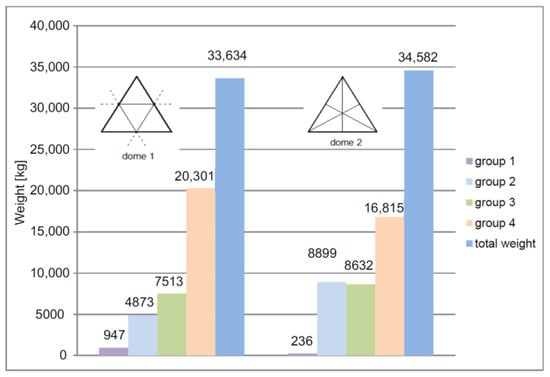
Figure 14.
Weight of individual groups of struts and entire domes generated from 4608-hedron and 4704-hedron.
6.5. Nodal Displacements
Based on calculations in the serviceability limit state, Figure 15 presents the values of nodal displacements in the analyzed domes. Vertical and horizontal displacements are caused by gravitational forces. The value of vertical displacements indicates lower stiffness along the vertical axis of the dome made according to the second method.
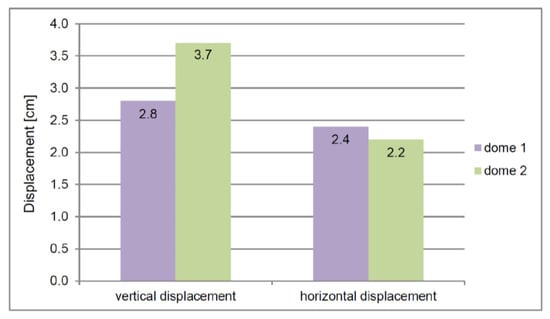
Figure 15.
Vertical and horizontal displacements of nodes of domes generated from 4608-hedron and 4704-hedron.
7. Discussion
Creating the mesh of a geodesic dome structure is a process based on various methods of generating its mesh topology, considering appropriate connections of the resulting nodes using strut elements. The designed lightweight covering structure is efficient and economical and allows for covering large areas without using internal supports. To further emphasize the advantages of this type of structure, it is worth paying attention to its optimization process, aimed at obtaining the lowest possible weight of the designed geodesic dome. Dome optimization has been the subject of many scientific considerations for years. The various optimization algorithms developed are constantly analyzed, improved, and used to reduce the weight of the domes and thus enhance the value of lightweight structures. Taking into account various design variables during the optimization process reduces the weight of the structure to varying degrees. For example, treating the number of rings as well as the number of nodes as design variables determines the number of structure elements (Kaveh and Talatahari [53]). In turn, the height of the dome changes the length of its elements (Saka [28]). However, adapting the cross-section of strut elements directly affects the weight of the covering, which is presented in this paper and in the paper by Bysiec [47].
The results presented in the paper will be used for further analysis, considering other aspects apart from geometry, mesh topology, statics, and the aspect of sustainable development. We are talking here primarily about an extended analysis of the behavior of geodesic domes shaped based on a regular octahedron under a given dynamic load, considering various methods of creating their topology. Initial research on this topic has already been carried out in the papers of Pilarska and Maleska [49], Bysiec et al. [50], as well as Bysiec and Maleska [51]. It should be added that this research used numerical software (Robot Structural Analysis 2023 and Dlubal RFEM 6) based on finite element methods, and it is planned to continue using this type of software in the future
8. Conclusions
The mesh topology of creating geodesic domes is a process that requires using an appropriate method of connecting nodes, creating a mesh of struts of the modeled structure. In this paper, two methods were used to create meshes of geodesic domes based on the division of the initial triangle, which is one of the faces of a regular octahedron. The design examples include a 4608-hedron geodesic dome modeled according to the first method and a 4704-hedron dome reflecting the second division method.
Based on the preceding results and discussion, some concluding remarks can be drawn as follows:
- The mesh of struts obtained in the structure shaped according to the first subdivision method allows us to work on the computational model in computer programs efficiently. Also, it facilitates the possibility of grouping struts during assembly. The mesh obtained according to the second method may cause problems during the task implementation and may also result in difficulties with modeling the structure.
- To create the computational model of the first analyzed dome, it was necessary to divide it into nw groups based on the same division rules. In the case of the second dome, this division had to consider the shifting of the nodes, which resulted in the need to divide it into three additional groups of struts. Such difficulties may cause mistakes and complicate the generation of the computational model. Creating the dome according to the first subdivision method is, therefore, much more straightforward and minimizes the possibility of making mistakes.
- The model obtained according to the first method gives the impression of continuity of the mesh of struts at the connections of the initial faces of the regular octahedron, while these connections in the dome shaped according to the second method cause the illusion of discontinuity of the mesh of struts, which may make assembly difficult and create a feeling of lack of aesthetics.
- In the first dome, a more even distribution of axial forces can be observed over the entire surface, and the values of extreme compressive forces are comparable to the maximum value of tensile forces.
- Another argument for using the first method of creating a mesh topology is the number of supports and, therefore, the value of the support reactions. Due to the more distributed weight of the dome on the ground, the foundations can be designed more economically. The second division method has completely different characteristics of transferring forces from external impacts on the foundations. The accumulation of extreme axial forces is located within the vertical struts extending from the foundation, and their values are due to the smaller number of supports. After minor changes in the static scheme by adding vertical struts in the support zone and thus increasing the number of supports almost twice, this would reduce the values of the maximum compressive forces and lead to a reduction in the cross-section in the fourth group of struts and, consequently, a reduction in the weight of the structure.
- In terms of usability, the first dome is less susceptible to vertical deflections, which indicates its greater stiffness in this direction.
Using the first method of dividing the edges of the initial triangular face of a regular octahedron to create a geodesic dome mesh is more straightforward, safer, and requires less design experience. However, the division according to the second method should not be abandoned, because taking into account the specificity of the analyzed structure’s operation and introducing minor changes to the static scheme, we can obtain a structure with similar, and possibly better, parameters. Therefore, further considerations in this area and further detailed analysis are necessary, taking into account not only the structure’s weight but also the dynamic load. In addition, we also plan to research the impact of the dome-shaping method on the structure’s life cycle, as was the case with bridges [54,55,56].
Author Contributions
Conceptualization, D.B. and T.M.; methodology, D.B. and S.J.; software, S.J.; validation, D.B. and S.J.; formal analysis, S.J. and D.B.; investigation, D.B., S.J. and T.M.; writing—original draft preparation, D.B. and T.M.; writing—review and editing, D.B. and T.M.; visualization, D.B., S.J. and T.M.; supervision, T.M.; project administration, D.B. and T.M.; funding acquisition, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fuller, B.R. Geodesic Dome. U.S. Patent 2,682,235, 29 June 1954. [Google Scholar]
- Clinton, J.D. Advanced Structural Geometry Studies. Part I, Polyhedral Subdivision Concept for Structural Application; NASA Contractor Report, NASA CR-1734; NASA: Washington, DC, USA, 1971.
- Clinton, J.D. Lowest common frequency: b2 + bc + c2. Int. J. Space Struct. 1990, 7, 213–222. [Google Scholar] [CrossRef]
- Tarnai, T. Spherical Grid Structures: Geometric Essays on Geodesic Domes; Hungarian Institute for Building Science: Budapest, Hungary, 1987. [Google Scholar]
- Tarnai, T. Geodesic domes: Natural and man-made. Int. J. Space Struct. 1996, 11, 13–25. [Google Scholar] [CrossRef]
- Tarnai, T.; Lengyel, A.; Gaspar, Z. The roundest polyhedral with symmetry constraints. Symmetry 2017, 9, 41. [Google Scholar]
- Huybers, P. The use of polyhedral for building structures. Struct. Topol. 1982, 6, 33–42. [Google Scholar]
- Huybers, P. The Polyhedral World. Beyond the Cube. The Architecture of Space Frames and Polyhedra; Gabriel, J.F., Ed.; John Wiley & Sons, Inc.: Chichester, UK, 1997; pp. 243–279. [Google Scholar]
- Huybers, P. Dome-type space structures of ellipsoidal form. Int. J. Space Struct. 1990, 7, 299–310. [Google Scholar] [CrossRef]
- Huybers, P. The chiral polyhedra. J. Int. Assoc. Shell Spat. Struct. 1999, 40, 133–143. [Google Scholar]
- Huybers, P.; van der Ende, G. Polyhedral patterns. In Proceedings of the International Symposium on Theory, Design and Realization of Shell and Spatial Structures, Nagoya, Japan, 9–13 October 2001; Kunieda, H., Ed.; IASS & Architectural Institute of Japan: Nagoya, Japan, 2001. [Google Scholar]
- Huybers, P. The Morphology of Building Structures. In ICCS’02: Proceedings of the International Conference on Computational Science—Part III, Amsterdam, The Netherlands, 21–24 April 2002; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Pavlov, G.N. Determination of parameters of crystal latticed surfaces composed of hexagonal plane faces. Int. J. Space Struct. 1990, 7, 169–187. [Google Scholar] [CrossRef]
- Pavlov, G.N. Calculation of geometrical parameters and projection of geodesic domes and shells based on the network subdivision of the system D. In Space Structures 4; Thomas Telford Ltd.: London, UK, 1993. [Google Scholar]
- Kitrick, C.J. Tensegrity Module Structure and Method of Inter-Connecting the Modules. U.S. Patent 4,207,715, 17 June 1980. [Google Scholar]
- Kitrick, C.J. A unified approach to class I, II & III geodesic forms. Int. J. Space Struct. 1990, 7, 223–248. [Google Scholar]
- Lalvani, H. Structures on hyper-structures. Struct. Topol. 1982, 6, 13–16. [Google Scholar]
- Lalvani, H. Continuous transformations of subdivided periodic surfaces. Int. J. Space Struct. 1990, 5, 255–279. [Google Scholar] [CrossRef]
- Lalvani, H.; Katz, N. Computer-generated transformations of geodesic spheres. In Space Structures 4; Thomas Telford: London, UK, 1993. [Google Scholar]
- Lalvani, H. Higher dimension periodic table of regular and semi-regular polytopes. Int. J. Space Struct. 1996, 11, 27–57. [Google Scholar] [CrossRef]
- Wenniger, M.J. Artistic tessellation patterns on spherical surface. Int. J. Space Struct. 1990, 7, 249–256. [Google Scholar]
- Wenniger, M.J.; Messer, P.W. Patterns of the spherical surface. Int. J. Space Struct. 1996, 11, 221–232. [Google Scholar]
- Rębielak, J. Shaping of Space Structures. Examples of Applications of Formian in the Design of Tension-Strut Systems; Oficyna Wydawnicza Politechniki Wrocławskiej: Wroclaw, Poland, 2005. [Google Scholar]
- Coxeter, H.S.M. Regular Polytopes, 3rd ed.; Dover Publications: New York, NY, USA, 1973. [Google Scholar]
- Fuliński, J. Geometria Kratownic Powierzchniowych; The Work of Wrocław Scientific Society; Państwowe Wydawnictwo Naukowe: Wroclaw, Poland, 1973. [Google Scholar]
- Gythiel, W.; Schevenels, M. Gradient-based size, shape, and topology optimization of single-layer reticulated shells subject to distributed loads. Struc. Multidiscip. Opti. 2022, 65, 144. [Google Scholar] [CrossRef]
- Saka, M. Optimum geometry design of geodesic domes using harmony search algorithm. Comput. Struct. 2007, 10, 595–606. [Google Scholar] [CrossRef]
- Saka, M. Optimum topological design of geometrically nonlinear single layer latticed domes using coupled genetic algorithm. Comput. Struct. 2007, 85, 1635–1646. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Geometry and topology optimization of geodesic domes using charged system search. Struct. Multidiscip. Optim. 2011, 43, 215–229. [Google Scholar] [CrossRef]
- Çarbas, S.; Saka, M.P. Optimum topology design of various geometrically nonlinear latticed domes using improved harmony search method. Struct. Multidiscip. Optim. 2012, 45, 377–399. [Google Scholar] [CrossRef]
- Dede, T.; Atmaca, B.; Grzywinski, M.; Rao, R.V. Optimal design of dome structures with recently developed algorithm: Rao series. Structures 2022, 42, 65–79. [Google Scholar] [CrossRef]
- Dede, T.; Grzywinski, M.; Selejdak, J. Continuous size optimization of large-scale dome structures with dynamic constraints. Struct. Eng. Mech. 2020, 73, 397–405. [Google Scholar] [CrossRef]
- Ye, J.; Lu, M. Optimizations of domes against instability. Steel Compos. Struct. 2018, 28, 427–438. [Google Scholar] [CrossRef]
- Grzywinski, M.; Dede, T.; Ozdemir, Y.I. Optimization of the braced dome structures by using Jaya algorithm with frequency constraints. Steel Compos. Struct. 2019, 30, 47–55. [Google Scholar] [CrossRef]
- Rosso, M.M.; Cucuzza, R.; Aloisio, A.; Marano, G.C. Enhanced Multi-Strategy Particle Swarm Optimization for Constrained Problems with an Evolutionary-Strategies-Based Unfeasible Local Search Operator. Appl. Sci. 2022, 12, 2285. [Google Scholar] [CrossRef]
- Rad, M.M.; Habashneh, M.; Lógó, J. Reliability based bi-directional evolutionary topology optimization of geometric and material nonlinear analysis with imperfections. Comput. Struct. 2023, 287, 107120. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. Optimal design of skeletal structures via the charged system search algorithm. Struct. Multidiscip. Optim. 2010, 41, 893–911. [Google Scholar] [CrossRef]
- Cucuzza, R.; Rosso, M.M.; Aloisio, A.; Melchiorre, J.; Giudice, M.L.; Marano, G.C. Size and Shape Optimization of a Guyed Mast Structure under Wind, Ice and Seismic Loading. Appl. Sci. 2022, 12, 4875. [Google Scholar] [CrossRef]
- Yan, X.; Hiong, Y.; Bao, D.W.; Xie, Y.M.; Peng, X. A Multi-volume constraint approach to diverse form designs from topology optimization. Eng. Strcut. 2023, 279, 115525. [Google Scholar] [CrossRef]
- Fraternali, F.; Carpentieri, G.; Modano, M.; Fabbrocino, F.; Skelton, R.E. A tensegrity approach to the optimal reinforcement of masonry domes and vaults through fiber-reinforced composite materials. Compos. Struc. 2015, 134, 247–254. [Google Scholar] [CrossRef]
- Cucuzza, F.; Bertetto, A.M.; Domaneshi, M.; Tarantini, R.; Cardoni, A.; Cimellaro, G.P. Numerical and Experimental Dynamic Analysis of 3D-Printed Pierced Vault. In Italian Workshop on Shell and Spatial Structures. In Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2023; pp. 269–278. [Google Scholar]
- Cucuzza, R.; Domaneschi, M.; Rosso, M.M.; Martinelli, L.; Marano, G.C. Structural Optimization Through Cutting Stock Problem. In Italian Workshop on Shell and Spatial Structures. 2023. In Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2023; pp. 210–220. [Google Scholar]
- Cucuzza, R.; Cardoni, A.; Manuello, A.; Domaneschi, M.; Cimellaro, G.; Marano, G. Experimental Investigation of the Static and Dynamic behaviors of 3D-Printed Shell Structures. In Proceedings of the 15th World Congress on Computational Mechanics (WCCM-APCOM2022), Yokohama, Japan, 31 July–5 August 2022. [Google Scholar]
- Pilarska, D. Octahedron—Based spatial bar structures–the form of large areas covers. In Proceedings of the Third Scientific Conference Environmental Challenges in Civil Engineering, Opole, Poland, 23–25 April 2018. [Google Scholar]
- Pilarska, D. Comparative analysis of various design solutions of octahedron—Based spatial bar structures. In Proceedings of the XXIV Conference of Lightweight Structures in Civil Engineering, Lodz, Poland, 7 December 2018. [Google Scholar]
- Pilarska, D. Two subdivision methods based on the regular octahedron for single-and double-layer spherical geodesic domes. Int. J. Space Struct. 2020, 35, 160–173. [Google Scholar] [CrossRef]
- Bysiec, D. Sustainable Shaping of Lightweight Structures Created According to Different Methods. Sustainability 2023, 15, 3236. [Google Scholar] [CrossRef]
- EC 1991; Eurocode 1; Actions on Structures. European Committee for Standardization: Brussels, Belgium, 2005.
- Pilarska, D.; Maleska, T. Numerical Analysis of Steel Geodesic Dome under Seismic Excitations. Materials 2021, 14, 4493. [Google Scholar] [CrossRef] [PubMed]
- Bysiec, D.; Maleska, T.; Janda, A. Dynamic characteristic of geodesic domes with different location of mass. In Proceedings of the Eighth International Symposium on Life-Cycle Civil Engineering, Milan, Italy, 2–6 July 2023. [Google Scholar] [CrossRef]
- Bysiec, D.; Maleska, T. Influence of the mesh structure of geodesic domes on their seismic response in applied directions. Arch. Civ. Eng. 2023, LXIX, 65–78. [Google Scholar] [CrossRef]
- EC 1993; Eurocode 3; Design of Steel Structures. European Committee for Standardization: Brussels, Belgium, 2005.
- Kaveh, A.; Talatahari, S. Size optimization of space trusses using Big Bang−Big Crunch algorithm. Comput. Struct. 2009, 87, 1129–1140. [Google Scholar] [CrossRef]
- Messore, M.M.; Capacci, L.; Bionini, F. Life-cycle cost-based risk assessment of aging bridge networks. Struct. Infrastruct. Eng. 2020, 17, 515–533. [Google Scholar] [CrossRef]
- Capacci, L.; Bionini, F.; Titi, A. Lifetime seismic resilience of aging bridges and road networks. Struct. Infrastruct. Eng. 2020, 16, 266–286. [Google Scholar] [CrossRef]
- Kosić, M.; Millen, M.; Viana da Fonseca, A.; Logar, J.; Dolsek, M. Estimation of Scenario-based Liquefaction Probability with Consideration of Ground-motion Randomness. J. Earthq. Eng. 2021, 26, 7933–7955. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).