Abstract
Here, we employ natural time analysis of seismicity together with non-extensive statistical mechanics aiming at shortening the occurrence time window of the Kahramanmaraş-Gazientep M7.8 earthquake. The results obtained are in the positive direction pointing to the fact that after 3 February 2023 at 11:05:58 UTC, a strong earthquake was imminent. Natural time analysis also reveals a minimum fluctuation of the order parameter of seismicity almost three and a half months before the M7.8 earthquake, pointing to the initiation of seismic electrical activity. Moreover, before this earthquake occurrence, the detrended fluctuation analysis of the earthquake magnitude time-series reveals random behavior. Finally, when applying earthquake nowcasting, we find average earthquake potential score values which are compatible with those previously observed before strong () earthquakes. The results obtained may improve our understanding of the physics of crustal phenomena that lead to strong earthquakes.
1. Introduction
The Kahramanmaraş-Gaziantep 7.8 Pazarcik earthquake (EQ) [1] took place on 6 February 2023 at 01:17:35 UTC and was followed within 9 h by the 7.5 Elbistan EQ [2] at 10:24:48 UTC, giving rise to the 2023 Kahramanmaraş, Turkey, EQ doublet [3]; see Figure 1. According to the International Blue Crescent Relief and Development Foundation [4] situation report, the Turkish Ministry of Interior had announced that the fatal casualties in the Kahramanmaraş EQs doublet totaled more than 50,399 lives. Moreover, 8476 people lost their lives in Syria, which was also affected by these EQs. It was one of the deadliest disasters in Turkey and Syria during the last millennium [3]. In total, 16 percent of Turkey’s population, that is 14 million people, were affected by these catastrophic events [4].
Almost two weeks before the Kahramanmaraş EQ doublet, i.e., on 25 January 2023, a paper was submitted [5] in which a novel procedure for estimating the time of occurrence of an impending strong EQ was presented. This new procedure was based on the combination of the results obtained from natural time analysis (NTA), see below, and non-extensive statistical mechanics (NESM) pioneered by Tsallis [6]. Tsallis [6] introduced a new functional form for the entropy, which is now generally called Tsallis entropy [7,8,9,10,11,12,13,14,15,16]
where is the entropic index, are the probabilities for each microstate i and is the Boltzmann constant. In the case , Equation (1) recovers the Boltzmann entropy
Using a fragment–asperity model [17], Posadas and Sotolongo-Costa [18] have recently estimated the Tsallis entropy for the case of EQs; for further details, see Section 2.4. It is the combination of the latter quantity with the entropy change under time reversal in NTA that allows the estimation of the occurrence time of the impending EQ [5].
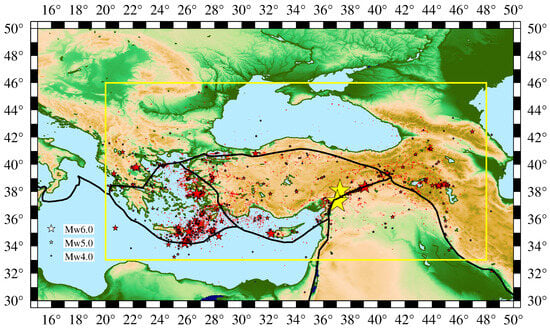
Figure 1.
The epicenters (red stars) of all EQs reported by AFAD with magnitude during the period 1 January 2020 to 31 December 2022 (see Section 2.1). The yellow stars depict the epicenters of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ [1] and the 7.5 Elbistan EQ [2] that occurred on 6 February 2023 at 01:17:34 UTC and 10:24:48 UTC, respectively. The black thick lines depict the tectonic plate boundaries [19].
NTA, which is based on a new concept of time termed natural time, was introduced in 2001 [20] and has found useful applications that range from EQ preparatory processes to heart dynamics [21,22,23,24,25,26,27,28,29,30,31,32] and from atmospheric sciences [33,34,35,36] to finance [37]; for a recent review, see [38]. It was originally focused on the discrimination of the low-frequency ( Hz) electric signals that are observed before EQs, which are called Seismic Electric Signals (SES) [23,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53], from similar-looking signals of man-made origin [54]. The physical properties of SES [23,42] provide information on the magnitude M of the impending EQ, on the probable epicentral area, and an estimation of its occurrence time. In the first publications by Varotsos et al. [20,54], it was shown that NTA may reveal that SES exhibited critical dynamics, while it has been also used for the identification of criticality in the seismicity inside the probable epicentral area. As will be further elaborated in Section 2.3, NTA there may provide a first estimate of the occurrence time of the impending EQ [20,44,55,56] (see also Chapter 7 of [23] and Chapters 5 and 9 of [38]). Additionally, NTA provides means to identify temporal correlations between EQ magnitudes (see Section 6.3 of [23] and references therein), which is a very hot topic, see, e.g., the recent meta-analysis by Petrillo and Zhuang [57]. Within the NTA framework, an entropy S has been introduced [20,54]; see Section 2.3 for its detailed properties. Most importantly, S has found useful applications in seismicity as well as in a variety of other physical systems, see, e.g., Chapters 7, 8, 9, and 13 of [38]. Earthquake nowcasting [58,59,60,61,62,63,64,65,66], which enables seismic hazard estimation, is also based on natural time; see Section 2.6. As Rundle et al. [58] state, natural time when applied to EQ seismicity has the advantage that it is not necessary to decluster the aftershocks.
It is important to note, however, that the study of the time-occurrence series of EQs may provide additional information to that obtained by NTA. The fractal and multifractal character of such time-series has been studied by Telesca et al. [67] and Telesca and Lapenna [68], revealing new properties of seismicity. Recently, the fractal characteristics of seismicity identified by the interevent times have found useful applications to cases of induced seismicity [69], see also [70], as well as in the case of the Anatolian region with implications for seismic hazards before and during the 2023 Kahramanmaraş seismic sequence [71]. Additionally, in forecasting fractal studies, see, e.g., [72,73], declustered catalogs are used. To date, NTA has not been applied to such catalogs. Such an application, however, may lead to interesting results and is within the future plans of our group.
So far, the new procedure introduced by Varotsos et al. [5] has been applied to the case of the super-giant 2011 M9 Tohoku EQ in Japan as well as in three strong EQs in the western part of northern America [74], which included the 2017 M8.2 Chiapas Mexico EQ, the deadly 19 September 2017 M7.1 Mexican flatslab EQ, and the 2019 Ridgecrest EQ in California. It is the purpose of the present paper to examine whether this procedure could have been applied before the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ in order to provide an improved estimate of the EQ occurrence compared to that previously found solely by means of NTA [20,51,75,76,77]. The paper is organized as follows. In Section 2, the EQ catalog and the methods used are presented, the results are shown and discussed in Section 3, and our conclusions are summarized in Section 4.
2. Materials and Methods
2.1. The Seismic Data Used
The seismic data used come from the Turkish Disaster and Emergency Management Authority (AFAD) and are publicly available at the site https://deprem.afad.gov.tr/event-catalog (last accessed on 7 May 2023). We considered all EQs within the region (see the yellow rectangle in Figure 1).
The frequency–magnitude distribution (FMD) for the EQs during the period 1 January 2002 to 31 December 2022 is shown in Figure 2a, the reported magnitude in 93% of these cases is the local magnitude ML; otherwise, moment magnitude was reported; see https://deprem.afad.gov.tr/event-catalog (last accessed on 7 May 2023). For AFAD, it is reported that ML and scales are almost equivalent for a wide range of magnitude values (see [78] and references therein); thus, this catalog could be considered homogeneous with respect to magnitude (cf. a unified EQ catalog is necessary for this kind of analysis, see, e.g., [79]). There, beyond the cumulative FMD depicted by open squares, the non-cumulative FMD [80] is also shown with open triangles. According to the Gutenberg–Richter (GR) law [81] for EQs, the number of EQs of magnitude (M) greater than m follows an exponential decay
where a reflects the total rate of sesmicity in the region and the b-value (which is usually close to unity, see, e.g., [23]) is related to the level of seismicity in the region (c.f. for a possible correlation between these two parameters see [82]). As shown in Figure 2a (obtained by the standard code ZMAP [83] using maximum likelihood estimation, see, e.g., [84]), the GR law of Equation (3) is valid for , where the magnitude of completeness equals 3.5. We also examined that setting to the latter value, , secures temporal completeness since 1 January 2002; see Section 3 below. For the readers’ better information, we note that new methods for the estimation of the magnitude distribution parameters have been recently proposed in the literature [85,86]. Moreover, further details on the seismicity of Turkey and its monitoring can be found in [71] and references therein. Since it will be needed later for the analyses presented in Section 3, we also investigated in Figure 2b the completeness of the catalog obtained from AFAD during the period from 1 January 2020 to 1 January 2023 within a 3° × 3° area centered at the actual epicenter of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ.
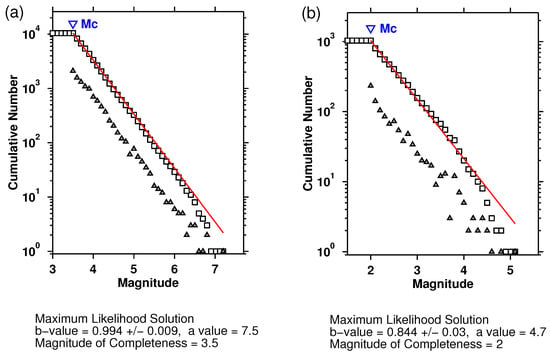
Figure 2.
Cumulative (squares) and non-cumulative (triangles) FMD for the EQs (a) within the region during the period 1 January 2002 to 31 December 2022 and (b) within a 3° × 3° area centered at the actual epicenter of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ during the period from 1 January 2020 to 1 January 2023, as estimated by ZMAP [83]. The b-value and have been calculated by applying the maximum curvature method (see, e.g., [87] and references therein) in the automatic selection of ZMAP. The red lines represent the GR relation.
2.2. Seismotectonic Background
The epicenter of the 7.8 EQ is located at the East Anatolian Fault (EAF) zone; see Figure 3. The EAF structure is considered to be a left-lateral strike–slip fault, of ∼700 km length [88], bounding the northeast Arabian plate movement with respect to the Anatolian plate. For the fault segments at the eastern end of the fault zone, this movement occurs at ∼10 mm/yr [88]. At the northeastern part, the left-lateral EAF intersects with the right-lateral North Anatolian Fault (NAF), which are considered to be the main structures in the tectonics of the eastern Mediterranean [89]. The Anatolian microplate is located between EAF and NAF and moves westward under the influence of internal deformation due to the collision of the Arabian and African plates with the Eurasian plate [90]. It is still debated, however, up to what point the EAF is extended to the west [88]. According to Medvedeva et al. [89], the southwestern end of the EAF zone transfers into the Cyprus Island Arc and the Dead Sea Fault zone. The focal mechanism solution for the 7.8 EQ indicates a left-lateral strike–slip with a length of the ruptured fault zone ∼300 km (see Ref. [89] and references therein).
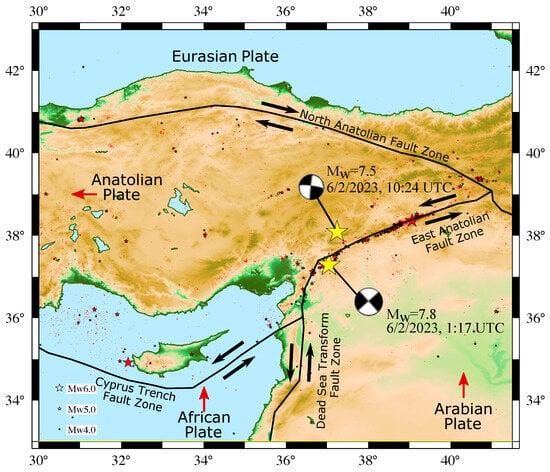
Figure 3.
The tectonic settings of the Anatolian region along with the epicenters (yellow stars) and the focal mechanisms of the two catastrophic EQs of at 01:17:34 UTC and at 10:24:48 UTC on 6 February 2023. The red arrows indicate the movement of the tectonic plates, and the black arrows indicate the direction of movement along the major fault zones; see [89] and references therein (cf. for a review of the historical seismicity in the region, see [91]).
2.3. Natural Time Analysis: Background
In a series comprising N EQ events (which can be considered as a temporal point pattern [5,92]), natural time corresponding to the k-th EQ of magnitude is defined [20] as . Thus, we abandon the notion of conventional time but maintain the EQ energy , see, e.g., [93] and Chapter 6 of [23]) together with the order of occurrence k. In NTA, the pair , where is the normalized energy, is attributed to each event k, and we consider the normalized power spectrum , where . The quantities can be considered (see, e.g., Appendix A.3 of [38] and references therein) as probabilities, and hence with corresponds to the characteristic function [94] for . This characteristic function provides information for the distribution: for example, the moments that are equal to the derivatives () at . In a similar sense, when considering in the region of close to 0, a quantity was obtained from the Maclaurin series
where
For the case of SES activities, mentioned in the Introduction, that exhibit critical dynamics [54], it has been shown [20,23] that the corresponding takes the form:
Moreover, it has been shown that
at criticality for various dynamical systems [20,23,38,95] that include SES activities; see, e.g., Table 8.1 on page 343 of [23]. In general, is suitable for identifying the approach to a critical point. Especially, in NTA of EQs, can be thought of [23,38] as an order parameter (OP) for seismicity because its value diminishes abruptly when a strong EQ takes place, while the statistics of its fluctuations share properties observed in well-known critical systems [96].
One of the advantages of NTA is that it allows for monitoring the fluctuations of the OP of seismicity within an EQ catalog. For this purpose, we consider an excerpt of this catalog consisting of W successive events. We then deduce the totality of values resulting from subexcerpts of the successive 6 to W EQs. For this set of values, we calculate the mean value and the standard deviation , leading to the variability of :
that quantifies the fluctuations within this EQ catalog excerpt. The quantity of Equation (8) is interrelated with the square root of the Ginzburg criterion (cf. Equation (6.25) of [97]) whose usefulness in the physics of EQs has been explained by Holliday et al. [98]. Finally, how varies in conventional time can be pursued by sliding event by event the window of W consecutive EQs in the EQ catalog; the occurrence time of the EQ that followed the last one of the window studied is attributed to each obtained. It has been experimentally observed that appropriately selected minima of labeled in regional EQ catalogs [51,99] coincide with the initiation of the emission of SES activities signaling that a strong EQ is going to occur within a maximum lead time of 5 months [23].
The entropy S in natural time [20,54] is given by
In the case of a “uniform” distribution [54], are considered independent and identically distributed (IID) positive random variables and S becomes . The application [23,38] of time-reversal , i.e., , in Equation (9) leads to
The quantity differs from S, leading to an entropy change
upon time reversal. Thus, S is time-reversal asymmetric [23]. Moreover, S is a dynamic entropy, different from static ones, e.g., Shannon entropy, that is positive, concave, and experimentally (Lesche) stable [100,101] (see Chapter 3 of [23]).
The entropy change under time reversal is also crucial for the identification of the approach of the system to a dynamic phase transition [5,38,74]. For this purpose, S and are calculated for a natural time window of length i (=number of consecutive events) sliding event by event through the whole time-series. Equation (11) is then used for estimating , thus resulting in a time-series of consecutive values.
NTA can provide an estimate of the occurrence time of the impending EQ when analyzing seismicity in the area candidate to suffer the strong EQ after the initiation of an SES activity or after the observation of . Such examples for Greece can be found in Chapter 7 of [23] while for Japan, Mexico, and California, they can be found in Chapter 5 of [38]. Usually [20,22,44,55,56], the strong EQ occurs a few days up to one week or so after a true coincidence of of the evolving seismicity to that of the critical state, of Equation (6). The following criteria have been used (see, e.g., [23,38]) to assure such a coincidence:
- The “average” distance between the curves of and for should be . Details on this calculation can be found in [20,23].
- The final approach of the evolving to must be from below, see, e.g., Figure 5 of [77], which alternatively means that gradually decreases with time before reaching the critical value of Equation (7).
- At the coincidence, both entropies S and in natural time must be smaller than .
- Since this process (critical dynamics) is considered to be self-similar, the occurrence time of the true coincidence should not markedly vary upon changing the magnitude threshold which is used for NTA of seismicity.
- The final approach described by the second criterion starts to be obeyed after an EQ for which of seismicity in the candidate epicentral area under time reversal exhibits a local minimum. In simple words, after exceeds S by a large amount, starts decreasing to finally approach 0.070.
2.4. Non-Extensive Statistical Mechanics Model for EQs
Sotolongo-Costa and Posadas [17] introduced a fragment–asperity model for EQs which is based on NESM. They considered two rough surfaces, the movement of which is hindered by fragments. The latter are generated during EQ occurrence by breakage of the plates simulating the fault. The magnitude of an EQ is related to distribution of the fragment sizes which effectively determine the value of the stress needed to overcome asperities and allow motion of the plates. Hence, the EQ energy is related to the size of the fragments, the distribution of which is determined by maximizing the Tsallis entropy of Equation (1). The model was later revisited by Silva et al. [10] by employing a more realistic relation between EQ energy and the size of the fragments. Most interestingly, the NESM model of EQs provided a generalization of the GR law for the distribution of EQ magnitudes, which relates [12,14] the aforementioned (see Section 2.1) b-value with the non-extensitivity parameter q according to the formula
2.5. Detrended Fluctuation Analysis of EQ Magnitudes
Detrendred fluctuation analysis (DFA) was firstly introduced by Peng et al. [102] as a method for the quantification of long-range correlations in non-stationary time-series. A comparison of DFA with power spectral methods and wavelet-based estimators of scaling behavior can be found in [103,104], respectively. DFA has found useful applications in a wide variety of fields ranging from the study of DNA [102,105,106] and biological signals [107,108,109,110,111] to EQs [112], meteorology [113,114] and atmospheric physics [115]. DFA has been generalized into a multifractal method by Kantelhardt et al. [116] which has also found widespread applications, see, e.g., [117,118,119], including seismicity.
In the case of DFA of EQ magnitudes, we first sum the time-series of consecutive EQ magnitudes to obtain the profile after removing the average value . Then, we divide the W values of the profile into l equal non-overlapping segments and find the polynomial of order n trend in each segment. The root mean square fluctuation is defined as the DFA measure
at scale . We repeat this procedure for various values of l and examine the validity of the scaling relation , where the exponent a is called the DFA exponent. This exponent characterizes the correlation properties of the EQ magnitude time-series: when , is anti-correlated, if , the time-series is not correlated (white noise), while indicates the presence of long-range correlations. In the present application, we used a window of consecutive EQ magnitudes moving by one EQ each time along the AFAD EQ magnitude time-series to obtain a new time-series of . For the calculation of the DFA exponents , we employed the DFA [102,120] computer program dfa.c of Physionet [121] (it is freely available at https://www.physionet.org/content/dfa/1.0.0/dfa.c, last accessed on 19 May 2023).
2.6. Earthquake Nowcasting
Using the concept of natural time, Rundle et al. [58] introduced EQ nowcasting to estimate seismic hazards [29,32,59,65,66,122,123,124,125,126,127,128,129,130]. Many applications of EQ nowcasting have been published in various fields of Earth Sciences including induced seismicity [60,62], the temporal clustering of EQs [61], and theoretical EQ models [131], while recently the method has been applied [132] for nowcasting volcanic eruptions.
Our group in a series of publications [124,125,129] has employed EQ nowcasting to obtain epicentral information for a future EQ. To this end, the EQ potential score (EPS) of EQ nowcasting is calculated [58] using the cumulative distribution function for the number of ‘small’ EQs (of magnitude ) that take place in the time interval between two ’large’ EQs (of magnitude ) within a large region, e.g., for the eastern Mediterranean [124]. Using a self-consistency radius R, Varotsos et al. [124] introduced average EPS maps by calculating within a circle of radius R centered at a point of a square lattice—denoted by —and averaged the resulting EPS values within the same radius R to obtain at a point the value
where the summation is restricted to the lattice points whose distance from the observation point is smaller than or equal to R, and N stands for the number of these points. The study of the eastern Mediterranean which is relevant to our case of the Kahramanmaraş, Turkey, EQ doublet [3] resulted in an optimum value of km when using , leading to
when using the United States National Earthquake Information Center Preliminary Determination of Epicenter (US-NEIC PDE) catalog available from the United States Geological Survey https://earthquake.usgs.gov/earthquakes/search/ (last accessed on 19 May 2023); for more details, see [124].
3. Results and Discussion
The results shown in Figure 2a, together with the fact that the variability of the OP of seismicity when using local EQ catalogs in various regions of the world [74,77,133] has been made for with , led us to select for such an analysis in natural time only the EQs with . Upon this selection, we have that the average rate of EQs (of ) within is around 50 EQs per month. By employing the method of analysis presented in Section 2.3, we found for with W = 300, 250, 200, 150, and 100, which correspond to time periods of six to two months practically covering the aforementioned lead time of SES activities, the results shown in Figure 4.
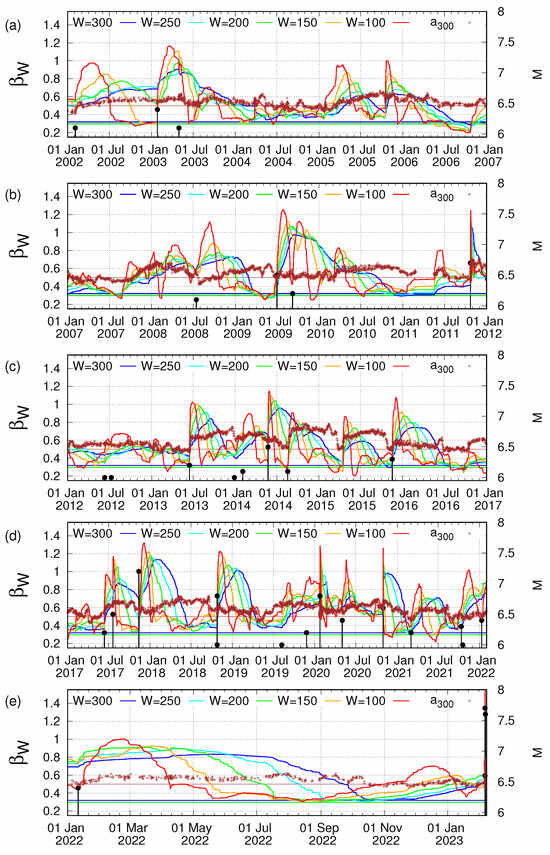
Figure 4.
The variabilities (left scale) for (blue), 250 (cyan), 200 (green), 150 (orange), and 100 (red), versus the conventional time since 1 January 2002 until the Kahramanmaraş, Turkey, EQ doublet. Panels (a–e) correspond to consecutive time periods. The brown plus symbols depict the values of the DFA exponent (left scale) estimated within a moving window of 300 consecutive EQs; see Section 2.5. The brown horizontal line corresponds to . The blue and green horizontal lines correspond to and , respectively, that border the for W = 300, 250, 200, 150, and 100 observed during the period 14 August 2022 to 18 October 2022 before the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ; see panel (e). The EQs reported by AFAD are shown with the black candlesticks ending at circles, the magnitude M of which can be read using the right scale.
In this figure, we present during the almost 20-year period 1 January 2002 to the time of occurrence of the Kahramanmaraş, Turkey, EQ doublet on 6 February 2023. In Figure 4e, we present in an expanded time scale the results during the final period from 1 January 2022 to 6 February 2023. Although for different values of W exhibit different dynamics, we observe that all values studied exhibit local minima during the period from 14 August 2022 to 18 October 2022 whose values lie between and . The ratio falls within the limits found [133] in Japan for the variability minima that preceded all EQs of magnitude since 1984 (cf. this criterion was also found valid; see, e.g., Section 1.5.1 of [38], for the case of the 2015 7.9 Ogasawara EQ, which is the single EQ in Japan after the M9 Tohoku EQ studied in [133]).
As stated in the Appendix of [134], for a variability minimum to be of precursory nature, the EQs that lead to the minima and should belong to the same critical process before the strong EQ. This fact was secured [134] by inspecting whether 90% of the EQs that led to are included in the EQs that led to . Turning now to the present case, we examine whether such a critical process is also observed in the present case. For this reason, we inspect from the EQ catalog whether the EQs that lead to a minimum, e.g., , are included in the EQs leading to or or or . We found that in all combinations , the EQs that lead to of Figure 4e are included in the EQs that lead to with percentages that exceed 98%. Hence, according to [134], the variability minima of Figure 4e belong to the same critical process that preceded by almost three and a half months (when considering the time lag since ) the Kahramanmaraş, Turkey, EQ doublet.
An inspection of Figure 4 reveals that such a critical process leading to simultaneous (within almost two months, i.e., 14 August to 18 October 2022) minima of within the aforementioned limits is unique during the almost 20-year period of our study that consists of 241 months. Hence, the probability of observing by chance such a phenomenon could be approximated by %, which points to the statistical significance of the critical process identified in Figure 4e.
Here, we note that NTA focuses on the identification of precursory behavior before strong EQs. An inspection of Figure 4 reveals that during the study period from 1 January 2002 to the time of occurrence of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ, the only EQ with that occured in the region is the 7.3 Halabaya EQ on 12 November 2017 [135]; see Figure 4d. This EQ has been shown to result in a variability minimum when studying the seismicity in a wider area, i.e., that of the eastern Mediterranean [136], in conjunction with EQ networks based on similar activity patterns [137]. The exact details of the corresponding variability minimum can be found in Table 3 and Figure 4b of [136]. The statistical significance and the predictive ability of the precursory minima have been discussed in detail in Sections 1.5.2, 12.13.1 and 12.13.2 of [38] by employing receiver operating characteristics [138] as well as event coincidence analysis [139,140]. For EQs of magnitude , NTA has to be combined with the preseismic information carried by SES, see, e.g., [23,44,55,56], in order to provide an improved estimation of the occurrence time of the impending EQ.
The fact that this critical process is of a truly precursory nature is also strengthened because the behavior of the DFA exponent is compatible with that previously found in Japan [134] (see their Figures 3–8), Mexico [75] (see their Figure 3), and California [76] (see their Figure 3). In Figure 4e, we observe that during the period when the minimum was observed, values of well above 0.5 appear, pointing to long-range correlations (cf. on 15 September 2022 ), while later and just before the Kahramanmaraş, Turkey, EQ doublet, fluctuates around 0.5, indicating a breakdown of the correlations to a random behavior (cf. on 19 January 2022 ).
The observation of a precursory variability minimum is expected [48,51,75,76,99] to be accompanied by the initiation of an SES activity. The occurrence time of the impending EQ can be estimated by analyzing the seismicity in the area probable to suffering from strong EQs in order to identify the fulfillment of the five criteria mentioned in Section 2.3. In the present case of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ, however, no SES data were available, since a Varotsos–Alexopoulos–Nomicos (VAN) telemetric network [23,40,41,42,43] does not operate in Turkey [53]. Thus, such an estimation of the area to suffer from strong EQs by means of SES is missing. To overcome this difficulty and in order to examine whether seismicity has reached criticality in the epicentral region, we decided—in this a posteriori study—to investigate the seismicity after 18 October 2022 within a 3° × 3° area centered at the actual epicenter of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ. An NTA of seismicity was made for various magnitude thresholds , 2.1, …3.2 and the five criteria of Section 2.3 were found to be obeyed in all the 13 cases examined, while for eight of them, the date of true coincidence was observed from 17 to 21 January 2023, i.e., almost two weeks before the Kahramanmaraş, Turkey, EQ doublet. Indicative results of such a study are shown in Figure 5. This two-week time lag would have been the estimation of the occurrence time of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ by means of NTA if we did not proceed to the combination of NTA with NESM in [5,74].
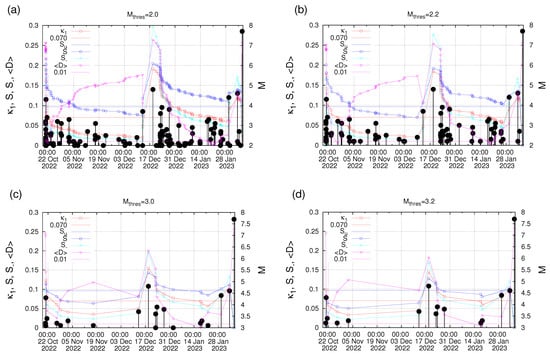
Figure 5.
The values of , S, , and (left scale) as they evolve event after event for the seismicity inside the 3° × 3° area around the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ epicenter. The EQs reported by AFAD are shown with the black candlesticks ending at circles, the magnitude M of which can be read in the right scale. Panels (a–d) correspond to = 2.0, 2.2, 3.0, and 3.2, respectively.
Varotsos et al. [5,74] suggested that in order to improve the estimate of the occurrence time of an impending EQ, one should also study the time-series of and of seismicity within the area to suffer the strong EQ, at comparable scales of i consecutive events, in order to identify similar transient changes. The necessity of such a similarity has been discussed in detail in Section 5 of [74] and mainly stems from the fact that as we approach the strong EQ, fluctuations increase, making their presence evident in both NTA and NESM. The time-series of the Tsallis entropy together with the entropy change in natural time under time reversal are shown in Figure 6 for the time period after the true coincidence (17 to 21 January 2023) until the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ. An inspection of Figure 6 reveals a similar transient behavior indicated by the red arrows that lasts from 29 January to 3 February 2023, i.e., almost three days before the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ.
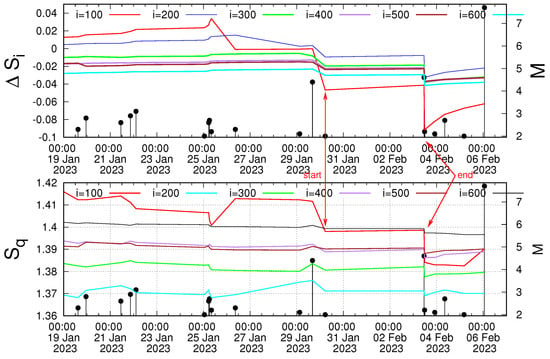
Figure 6.
The quantities (upper panel) in NTA and (lower panel) Tsallis entropy of NESM versus the conventional time (UTC) inside the 3° × 3° area around the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ epicenter. The red arrows indicate the simultaneous transient changes of and after the validity of the criticality condition . They start and end upon the occurrence of two EQs of magnitudes 4.4 and 4.6, respectively. These two EQs occurred on 29 January 2023 at 16:12:39 UTC and on 3 February 2023 at 11:05:08 UTC with epicenters at 35.88° N 35.78° E and 37.21° N 36.40° E, respectively. The EQs reported by AFAD are shown with the black candlesticks ending at circles, the magnitude M of which can be read in the right scale.
We observe that the combination of NTA with NESM may provide an improved estimate of the occurrence time of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ by a significant factor, i.e., from almost two weeks to almost three days. This, i.e., the improvement of the estimate of the occurrence time of an impending strong EQ, is compatible with the results found for the 2011 M9 Tohoku, Japan, EQ [5], the 2017 M8.2 Chiapas, Mexico, EQ [74], and the 2019 M7.1 Ridgecrest EQ [74]. In our view, it is this point that stresses the importance of fluctuations before strong EQs, which should be also studied in the future for other catastrophic EQs.
As already mentioned, there were no SES data before the Kahramanmaraş, Turkey, EQ doublet. In such cases, NTA may provide an estimate of the epicentral area of the impending EQ by means of a spatiotemporal study, see, e.g., Chapter 3 of [38] and references therein. However, such an analysis is possible when the local EQ catalog used fully covers the study area, which is rarely possible when national boundaries exist in this area. In these cases, our group has suggested [124,125,129] that the average EPS maps based on Equation (15) may provide an estimate of the epicentral location of the impending EQ. The calculation of the map should be made on the date of the variability minimum identified before the strong EQ. Following Varotsos et al. [124] and Section 2.6, we depict in Figure 7a the map calculated on 18 October 2022. The value of at the grid point closer to the epicenter of the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ is 54%. In Figure 7b, we depict the map estimated after the last EQ just (12 min) before the 7.5 Elbistan EQ. Although the 7.8 took place only 9 h before, EQ nowacasting methodology leads to an at the grid point closer to the new epicenter of 49%. Interestingly, the two values 54% and 49% compare favorably with the of 50% that was observed at the grid point closest to the epicenter 38.72° N 43.51° E of the 2011 7.1 Van, Turkey, EQ [141] on the date of the corresponding variability minimum; see Table 1 and Section 4 of [124]. The two new values confirm the original observation [124] that EQs usually occur in regions where is mediocre; see also Figure 6a of [125].
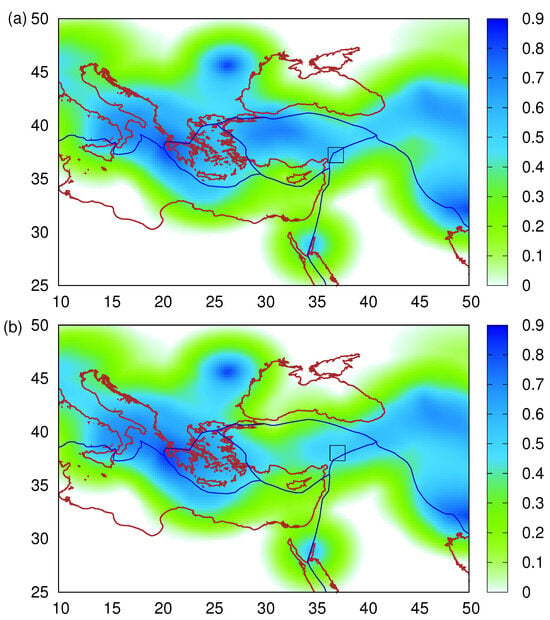
Figure 7.
Average EPS maps, depicted by the color scale, according to Equation (15) (see Section 2.6 and [124]) estimated (a) on 18 October 2022 for the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ and (b) on 6 February 2023 at 10:12:17 UTC, i.e., approximately 12 min, before the 7.5 Elbistan EQ occurrence. The EQ epicenters are shown by the open squares, and the blue thick lines depict the tectonic plate boundaries [19].
4. Summary and Conclusions
We performed NTA of the seismicity preceding the Kahramanmaraş, Turkey, EQ doublet. The following results have been obtained:
- The study of the fluctuations of the OP of seismicity during an almost 20-year period has revealed a unique minimum that ended at 18 October 2022, i.e., almost three and a half months before the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ occurrence.
- The simultaneous study of the DFA exponent has also shown a breakdown of the long-range correlations between EQ magnitudes before the 7.8 EQ in a way compatible with previous observations in Japan, Mexico, and California.
- When studying the seismicity after inside a 3° × 3° area around the 7.8 EQ epicenter, we found that the power spectrum coincidence of the evolving seismicity to that corresponding to critical behavior occurs around 19 January 2023, i.e., almost two weeks before the 7.8 EQ occurrence.
- The above estimation of the occurrence time of the impending strong EQ can be improved when employing NTA and NESM through the comparison of the time-series of the Tsallis entropy and the entropy change under time reversal. Such an analysis reveals that after 3 February 2023 at 11:05:58 UTC, the 7.8 EQ was imminent. This result is compatible with those found in Japan, Mexico, and California.
- By employing the modern method of earthquake nowcasting, we showed how may provide precursory information on the epicenter location of both the Kahramanmaraş-Gaziantep 7.8 Pazarcik EQ and the 7.5 Elbistan EQ. The values were 54% and 49%, respectively, being compatible with previous observations [124,125] that strong EQs occur at locations where is mediocre.
Interestingly, the first four results are similar to those observed before strong EQs in Japan, Mexico and California, which were mainly subduction or strike–slip EQs. Although every EQ is a different case history, we hope that the present a posteriori results trigger a better understanding of the crustal phenomena as well as shed light in a unified manner on the EQ preparatory processes before strong EQs. Such an approach may become also useful for improving EQ prediction efforts based on NTA and NESM in the future.
Author Contributions
Conceptualization, N.V.S. and E.S.S.; methodology, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; software, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; validation, E.S.S., S.-R.G.C. and P.K.V.; formal analysis, N.V.S., E.S.S. and P.K.V.; investigation, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; resources, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; data curation, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; writing—original draft preparation, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; writing—review and editing, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; visualization, N.V.S., E.S.S., S.-R.G.C. and P.K.V.; supervision, N.V.S. and E.S.S.; project administration, N.V.S. and E.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are publicly available as mentioned in Section 2.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AFAD | Turkish Disaster and Emergency Management Authority |
| DFA | Detrended Fluctuation Analysis |
| DNA | Deoxyribonucleic Acid |
| EAF | East Anatolian Fault |
| EPS | Earthquake Potential Score |
| EQ | Earthquake |
| GR | Gutenberg–Richter |
| NAF | North Anatolian fault |
| NESM | Non-Extensive Statistical Mechanics |
| NTA | Natural Time Analysis |
| OP | Order Parameter |
| SES | Seismic Electric Signals |
| USGS | United States Geological Survey |
| UTC | Universal Time Code |
| VAN | Varotsos–Alexopoulos–Nomicos |
References
- United States Geological Survey, Earthquake Hazards Program. M 7.8-Pazarcik Earthquake, Kahramanmaras Earthquake Sequence. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us6000jllz/executive (accessed on 23 November 2023).
- United States Geological Survey, Earthquake Hazards Program. M 7.5-Elbistan Earthquake, Kahramanmaras Earthquake Sequence. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us6000jlqa/executive (accessed on 23 November 2023).
- Jia, Z.; Jin, Z.; Marchandon, M.; Ulrich, T.; Gabriel, A.A.; Fan, W.; Shearer, P.; Zou, X.; Rekoske, J.; Bulut, F.; et al. The complex dynamics of the 2023 Kahramanmaraş, Turkey, Mw 7.8-7.7 earthquake doublet. Science 2023, 381, 985–990. [Google Scholar] [CrossRef]
- International Blue Crescent Relief and Development Foundation. Devastating Earthquakes in Southern Türkiye and Northern Syria, April 6th 2023, Situation Report 20. Available online: https://reliefweb.int/report/turkiye/devastating-earthquakes-southern-turkiye-and-northern-syria-april-6th-2023-situation-report-20-entr (accessed on 23 November 2023).
- Varotsos, P.; Sarlis, N.; Skordas, E.; Nagao, T.; Kamogawa, M. Natural time analysis together with non-extensive statistical mechanics shorten the time window of the impending 2011 Tohoku M9 earthquake in Japan. Commun. Nonlinear Sci. Numer. Simul. 2023, 125, 107370. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. A Stat. Mech. Its Appl. 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy: Interdisciplinary Applications; Santa Fe Institute Studies in the Sciences of Complexity; Oxford University Press, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Abe, S. Stability of Tsallis entropy and instabilities of Rényi and normalized Tsallis entropies: A basis for q-exponential distributions. Phys. Rev. E 2002, 66, 046134. [Google Scholar] [CrossRef]
- Silva, R.; França, G.S.; Vilar, C.S.; Alcaniz, J.S. Nonextensive models for earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L. A non-extensive approach in investigating the seismicity of L’Aquila area (central Italy), struck by the 6 April 2009 earthquake (ML = 5.8). Terra Nova 2010, 22, 87–93. [Google Scholar] [CrossRef]
- Telesca, L. Analysis of Italian seismicity by using a non-extensive approach. Tectonophysics 2010, 494, 155–162. [Google Scholar] [CrossRef]
- Telesca, L. Nonextensive analysis of seismic sequences. Phys. A Stat. Mech. Its Appl. 2010, 389, 1911–1914. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-extensive and natural time analysis of seismicity before the Mw6.4, October 12, 2013 earthquake in the South West segment of the Hellenic Arc. Phys. A Stat. Mech. Its Appl. 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Posadas, A. Fragment-Asperity Interaction Model for Earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef] [PubMed]
- Posadas, A.; Sotolongo-Costa, O. Non-extensive entropy and fragment–asperity interaction model for earthquakes. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106906. [Google Scholar] [CrossRef]
- Bird, P. An updated digital model of plate boundaries. Geochem. Geophys. Geosyst. 2003, 4, 1027. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Spatio-Temporal complexity aspects on the interrelation between Seismic Electric Signals and Seismicity. Pract. Athens Acad. 2001, 76, 294–321. [Google Scholar]
- Papasimakis, N.; Pallikari, F. Correlated and uncorrelated heart rate fluctuations during relaxing visualization. Europhys. Lett. 2010, 90, 48003. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Uyeda, S.; Kamogawa, M. Natural-time analysis of critical phenomena: The case of Seismicity. Europhys. Lett. 2010, 92, 29002. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time; Precursory Seismic Electric Signals, Earthquakes and other Complex Time-Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Benson, P.; Sammonds, P. Natural time analysis of critical phenomena: The case of acoustic emissions in triaxially deformed Etna basalt. Phys. A Stat. Mech. Its Appl. 2013, 392, 5172–5178. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Karadimitrakis, A.; Eftaxias, K. Natural time analysis of critical phenomena: The case of pre-fracture electromagnetic emissions. Chaos 2013, 23, 023117. [Google Scholar] [CrossRef]
- Vallianatos, F.; Karakostas, V.; Papadimitriou, E. A Non-Extensive Statistical Physics View in the Spatiotemporal Properties of the 2003 (Mw6.2) Lefkada, Ionian Island Greece, Aftershock Sequence. Pure Appl. Geophys. 2014, 171, 1343–1354. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Hloupis, G. Multiresolution wavelets and natural time analysis before the January-February 2014 Cephalonia (Mw6.1-6.0) sequence of strong earthquake events. Phys. Chem. Earth Parts A/B/C 2015, 85–86, 201–209. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Potirakis, S.; Eftaxias, K. Criticality features in ULF magnetic fields prior to the 2011 Tohoku earthquake. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2015, 91, 25–30. [Google Scholar] [CrossRef]
- Pasari, S. Nowcasting Earthquakes in the Bay of Bengal Region. Pure Appl. Geophys. 2019, 176, 1417–1432. [Google Scholar] [CrossRef]
- Yang, S.S.; Potirakis, S.M.; Sasmal, S.; Hayakawa, M. Natural Time Analysis of Global Navigation Satellite System Surface Deformation: The Case of the 2016 Kumamoto Earthquakes. Entropy 2020, 22, 674. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Hloupis, G.; Chatzopoulos, G. The Evolution of Preseismic Patterns Related to the Central Crete (Mw6.0) Strong Earthquake on 27 September 2021 Revealed by Multiresolution Wavelets and Natural Time Analysis. Geosciences 2022, 12, 33. [Google Scholar] [CrossRef]
- Pasari, S.; Verma, H.; Sharma, Y.; Choudhary, N. Spatial distribution of seismic cycle progression in northeast India and Bangladesh regions inferred from natural time analysis. Acta Geophys. 2023, 71, 89–100. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C. A new tool for the study of the ozone hole dynamics over Antarctica. Atmos. Environ. 2012, 47, 428–434. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C.; Cracknell, A.P. Precursory signals of the major El Niño Southern Oscillation events. Theor. Appl. Climatol. 2016, 124, 903–912. [Google Scholar] [CrossRef]
- Varotsos, C.; Efstathiou, M.; Christodoulakis, J. The lesson learned from the unprecedented ozone hole in the Arctic in 2020; A novel nowcasting tool for such extreme events. J. Atmos.-Sol.-Terr. Phys. 2020, 207, 105330. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Mazei, Y.; Saldaev, D.; Efstathiou, M.; Voronova, T.; Xue, Y. Nowcasting of air pollution episodes in megacities: A case study for Athens, Greece. Atmos. Pollut. Res. 2021, 12, 101099. [Google Scholar] [CrossRef]
- Mintzelas, A.; Kiriakopoulos, K. Natural time analysis in financial markets. Algorithmic Financ. 2016, 5, 37–46. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time, Part II. Advances in Disaster Prediction Using Complex Systems; Springer Nature Switzerland AG: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K.; Lazaridou, M. Earthquake prediction and electric signals. Nature 1986, 322, 120. [Google Scholar] [CrossRef]
- Varotsos, P.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals. Tectonophysics 1991, 188, 321–347. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals, II. Tectonophysics 1993, 224, 1–37. [Google Scholar] [CrossRef]
- Varotsos, P. The Physics of Seismic Electric Signals; TERRAPUB: Tokyo, Japan, 2005; p. 338. [Google Scholar]
- Lazaridou-Varotsos, M.S. Earthquake Prediction by Seismic Electric Signals. The Success of the VAN Method over Thirty Years; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M. The Prediction of Two Large Earthquakes in Greece. Eos Trans. AGU 2008, 89, 363. [Google Scholar] [CrossRef]
- Huang, Q. Rethinking earthquake-related DC-ULF electromagnetic phenomena: Towards a physics-based approach. Nat. Hazards Earth Syst. Sci. 2011, 11, 2941–2949. [Google Scholar] [CrossRef]
- Huang, Q. Retrospective investigation of geophysical data possibly associated with the Ms8.0 Wenchuan earthquake in Sichuan, China. J. Asian Earth Sci. 2011, 41, 421–427. [Google Scholar] [CrossRef]
- Xu, G.; Han, P.; Huang, Q.; Hattori, K.; Febriani, F.; Yamaguchi, H. Anomalous behaviors of geomagnetic diurnal variations prior to the 2011 off the Pacific coast of Tohoku earthquake (Mw9.0). J. Asian Earth Sci. 2013, 77, 59–65. [Google Scholar] [CrossRef]
- Skordas, E.; Sarlis, N. On the anomalous changes of seismicity and geomagnetic field prior to the 2011 9.0 Tohoku earthquake. J. Asian Earth Sci. 2014, 80, 161–164. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Xu, G.; Ashida, R.; Chen, C.H.; Febriani, F.; Yamaguchi, H. Further investigations of geomagnetic diurnal variations associated with the 2011 off the Pacific coast of Tohoku earthquake (Mw 9.0). J. Asian Earth Sci. 2015, 114, 321–326. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Huang, Q.; Hirooka, S.; Yoshino, C. Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J. Asian Earth Sci. 2016, 129, 13–21. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Identifying the occurrence time of an impending major earthquake: A review. Earthq. Sci. 2017, 30, 209–218. [Google Scholar] [CrossRef]
- Xue, J.; Huang, Q.; Wu, S.; Nagao, T. LSTM-Autoencoder Network for the Detection of Seismic Electric Signals. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5917012. [Google Scholar] [CrossRef]
- Sindirgi, P. A Closed-Form Alternative for the Frequency Distribution of Stably Distributed Random Components in Daily-Mean Self-Potential (SP) Time Series: Example from Urla Station, Turkey. Pure Appl. Geophys. 2023, 180, 2827–2840. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Attempt to distinguish electric signals of a dichotomous nature. Phys. Rev. E 2003, 68, 031106. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M.; Tanaka, H. Analysis of electrical activity and seismicity in the natural time domain for the volcanic-seismic swarm activity in 2000 in the Izu Island region, Japan. J. Geophys. Res. 2009, 114, B02310. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M. Reply to Comment on “The Prediction of Two Large Earthquakes in Greece”. Eos Trans. AGU 2010, 91, 163. [Google Scholar] [CrossRef]
- Petrillo, G.; Zhuang, J. The debate on the earthquake magnitude correlations: A meta-analysis. Sci. Rep. 2022, 12, 20683. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Donnellan, A.; Grant Ludwig, L.; Luginbuhl, M.; Gong, G. Nowcasting earthquakes. Earth Space Sci. 2016, 3, 480–486. [Google Scholar] [CrossRef]
- Rundle, J.B.; Luginbuhl, M.; Giguere, A.; Turcotte, D.L. Natural Time, Nowcasting and the Physics of Earthquakes: Estimation of Seismic Risk to Global Megacities. Pure Appl. Geophys. 2018, 175, 647–660. [Google Scholar] [CrossRef]
- Luginbuhl, M.; Rundle, J.B.; Hawkins, A.; Turcotte, D.L. Nowcasting Earthquakes: A Comparison of Induced Earthquakes in Oklahoma and at the Geysers, California. Pure Appl. Geophys. 2018, 175, 49–65. [Google Scholar] [CrossRef]
- Luginbuhl, M.; Rundle, J.B.; Turcotte, D.L. Natural Time and Nowcasting Earthquakes: Are Large Global Earthquakes Temporally Clustered? Pure Appl. Geophys. 2018, 175, 661–670. [Google Scholar] [CrossRef]
- Luginbuhl, M.; Rundle, J.B.; Turcotte, D.L. Statistical physics models for aftershocks and induced seismicity. Phil. Trans. R. Soc. A 2018, 377, 20170397. [Google Scholar] [CrossRef]
- Rundle, J.; Stein, S.; Donnellan, A.; Turcotte, D.L.; Klein, W.; Saylor, C. The Complex Dynamics of Earthquake Fault Systems: New Approaches to Forecasting and Nowcasting of Earthquakes. Rep. Prog. Phys. 2021, 84, 076801. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P. Nowcasting Earthquakes by Visualizing the Earthquake Cycle with Machine Learning: A Comparison of Two Methods. Surv. Geophys. 2022, 43, 483–501. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A.; Fox, G.; Crutchfield, J.P.; Granat, R. Nowcasting Earthquakes:Imaging the Earthquake Cycle in California with Machine Learning. Earth Space Sci. 2021, 8, e2021EA001757. [Google Scholar] [CrossRef]
- Rundle, J.; Donnellan, A.; Fox, G.; Ludwig, L.; Crutchfield, J. Does the Catalog of California Earthquakes, with Aftershocks Included, Contain Information about Future Large Earthquakes? Earth Space Sci. 2023, 10, e2022EA002521. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Macchiato, M. Mono- and multi-fractal investigation of scaling properties in temporal patterns of seismic sequences. Chaos Solitons Fractals 2004, 19, 1–15. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V. Measuring multifractality in seismic sequences. Tectonophysics 2006, 423, 115–123. [Google Scholar] [CrossRef]
- Telesca, L.; Thai, A.T.; Cao, D.T.; Cao, D.T.; Dinh, Q.V.; Mai, X.B. Fractal and Spectral Analysis of Seismicity in the Lai Chau Area (Vietnam). Fractal Fract. 2023, 7, 776. [Google Scholar] [CrossRef]
- Telesca, L.; Thai, A.T.; Lovallo, M.; Cao, D.T.; Nguyen, L.M. Shannon Entropy Analysis of Reservoir-Triggered Seismicity at Song Tranh 2 Hydropower Plant, Vietnam. Appl. Sci. 2022, 12, 8873. [Google Scholar] [CrossRef]
- Zaccagnino, D.; Telesca, L.; Tan, O.; Doglioni, C. Clustering Analysis of Seismicity in the Anatolian Region with Implications for Seismic Hazard. Entropy 2023, 25, 835. [Google Scholar] [CrossRef]
- Hamdache, M.; Peláez, J.A.; Gospodinov, D.; Henares, J.; Galindo-Zaldívar, J.; Sanz de Galdeano, C.; Ranguelov, B. Stochastic Modeling of the Al Hoceima (Morocco) Aftershock Sequences of 1994, 2004 and 2016. Appl. Sci. 2022, 12, 8744. [Google Scholar] [CrossRef]
- Hamdache, M.; Henares, J.; Peláez, J.A.; Damerji, Y. Fractal Analysis of Earthquake Sequences in the Ibero-Maghrebian Region. Pure Appl. Geophys. 2019, 176, 1397–1416. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Nagao, T.; Kamogawa, M.; Flores-Márquez, E.L.; Ramírez-Rojas, A.; Perez-Oregon, J. Improving the Estimation of the Occurrence Time of an Impending Major Earthquake Using the Entropy Change of Seismicity in Natural Time Analysis. Geosciences 2023, 13, 222. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Ramírez-Rojas, A.; Flores-Márquez, E.L. Identifying the Occurrence Time of the Deadly Mexico M8.2 Earthquake on 7 September 2017. Entropy 2019, 21, 301. [Google Scholar] [CrossRef]
- Skordas, E.S.; Christopoulos, S.R.G.; Sarlis, N.V. Detrended fluctuation analysis of seismicity and order parameter fluctuations before the M7.1 Ridgecrest earthquake. Nat. Hazards 2020, 100, 697–711. [Google Scholar] [CrossRef]
- Flores-Márquez, E.L.; Ramírez-Rojas, A.; Perez-Oregon, J.; Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Natural Time Analysis of Seismicity within the Mexican Flat Slab before the M7.1 Earthquake on 19 September 2017. Entropy 2020, 22, 730. [Google Scholar] [CrossRef]
- Çıvgın, B.; Scordilis, E.M. Investigating the consistency of online earthquake catalogs of Turkey and surroundings. J. Seismol. 2019, 23, 1255–1278. [Google Scholar] [CrossRef]
- Merdasse, M.; Hamdache, M.; Peláez, J.A.; Henares, J.; Medkour, T. Earthquake Magnitude and Frequency Forecasting in Northeastern Algeria using Time Series Analysis. Appl. Sci. 2023, 13, 1566. [Google Scholar] [CrossRef]
- Mignan, A. Functional shape of the earthquake frequency-magnitude distribution and completeness magnitude. J. Geophys. Res. Solid Earth 2012, 117, B08302. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Perez-Oregon, J.; Muñoz-Diosdado, A.; Rudolf-Navarro, A.; Guzmán-Sáenz, A.; Angulo-Brown, F. On the possible correlation between the Gutenberg-Richter parameters of the frequency-magnitude relationship. J. Seismol. 2018, 22, 1025–1035. [Google Scholar] [CrossRef]
- Wiemer, S. A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Marzocchi, W.; Sandri, L. A review and new insights on the estimation of the b-value and its uncertainty. Ann. Geophys. 2003, 46, 1271–1282. [Google Scholar] [CrossRef]
- Godano, C.; Petrillo, G.; Lippiello, E. Evaluating the incompleteness magnitude using an unbiased estimate of the b value. Geophys. J. Int. 2023, 236, 994–1001. [Google Scholar] [CrossRef]
- van der Elst, N.J. B-Positive: A Robust Estimator of Aftershock Magnitude Distribution in Transiently Incomplete Catalogs. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021027. [Google Scholar] [CrossRef]
- Godano, C.; Petrillo, G. Estimating the Completeness Magnitude mc and the b-Values in a Snap. Earth Space Sci. 2023, 10, e2022EA002540. [Google Scholar] [CrossRef]
- Güvercin, S.E.; Karabulut, H.; Konca, A.O.; Doğan, U.; Ergintav, S. Active seismotectonics of the East Anatolian Fault. Geophys. J. Int. 2022, 230, 50–69. [Google Scholar] [CrossRef]
- Medvedeva, A.; Vydrin, D.; Krylov, A.; Shiryborova, A.; Smirnova, D.; Tsukanova, E.; Kânoğlu, U.; Medvedev, I. The Turkish Tsunami of 6 February 2023 in the Northeastern Mediterranean. Pure Appl. Geophys. 2023, 180, 3177–3193. [Google Scholar] [CrossRef]
- Emre, O.; Duman, T.Y.; Özalp, S.; Šaroĝlu, F.; Olgun, S.; Elmacl, H.; Čan, T. Active fault database of Turkey. Bull. Earthq. Eng. 2018, 16, 3229–3275. [Google Scholar] [CrossRef]
- Şeşetyan, K.; Stucchi, M.; Castelli, V.; Capera, A.A.G. Kahramanmaraş-Gaziantep Türkiye M7.7 Earthquake, 6 February 2023 (04:17 GMT+03:00) Large Historical Earthquakes of the Earthquake-Affected Region: A Preliminary Report. Boğaziçi University, Kandilli Observatory and Earthquake Research Institute, Department of Earthquake Engineering: Istanbul, Turkey, 2023. Available online: https://eqe.boun.edu.tr/sites/eqe.boun.edu.tr/files/kahramanmaras-gaziantep_earthquake_06-02-2023_large_hist_eqs_v1.pdf (accessed on 5 December 2023).
- Brillinger, D.R. Time series, point processes, and hybrids. Can. J. Stat. 1994, 22, 177–206. [Google Scholar] [CrossRef]
- Kanamori, H. Quantification of Earthquakes. Nature 1978, 271, 411–414. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications, Volume II; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Sarlis, N.V.; Varotsos, P.A.; Skordas, E.S. Flux avalanches in YBa2Cu3O7−x films and rice piles: Natural time domain analysis. Phys. Rev. B 2006, 73, 054504. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Similarity of fluctuations in systems exhibiting Self-Organized Criticality. Europhys. Lett. 2011, 96, 28006. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Holliday, J.R.; Rundle, J.B.; Turcotte, D.L.; Klein, W.; Tiampo, K.F.; Donnellan, A. Space-Time Clustering and Correlations of Major Earthquakes. Phys. Rev. Lett. 2006, 97, 238501. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
- Lesche, B. Instabilities of Renyi entropies. J. Stat. Phys. 1982, 27, 419. [Google Scholar] [CrossRef]
- Lesche, B. Renyi entropies and observables. Phys. Rev. E 2004, 70, 017102. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Talkner, P.; Weber, R.O. Power spectrum and detrended fluctuation analysis: Application to daily temperatures. Phys. Rev. E 2000, 62, 150–160. [Google Scholar] [CrossRef]
- Audit, B.; Becry, E.; Muzy, G.; Arneodo, A. Wavelet-based estimators of scaling behavior. IEEE Trans. Inf. Theory 2002, 48, 2938. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Peng, C.K.; Simons, M.; Stanley, H.E. Linguistic Features of Noncoding DNA Sequences. Phys. Rev. Lett. 1994, 73, 3169–3172. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Mantegna, R.N.; Matsa, M.E.; Peng, C.K.; Simons, M.; Stanley, H.E. Long-range correlation properties of coding and noncoding DNA sequences: GenBank analysis. Phys. Rev. E 1995, 51, 5084–5091. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.C.; Rosenblum, M.G.; Peng, C.K.; Mietus, J.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461. [Google Scholar] [CrossRef]
- Havlin, S.; Buldyrev, S.V.; Bunde, A.; Goldberger, A.L.; Ivanov, P.C.; Peng, C.K.; Stanley, H.E. Scaling in nature: From DNA through heartbeats to weather. Phys. A Stat. Mech. Its Appl. 1999, 273, 46–69. [Google Scholar] [CrossRef]
- Stanley, H.E.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Peng, C.K.; Simons, M. Scaling features of noncoding DNA. Phys. A Stat. Mech. Its Appl. 1999, 273, 1–18. [Google Scholar] [CrossRef]
- Hardstone, R.; Poil, S.S.; Schiavone, G.; Jansen, R.; Nikulin, V.; Mansvelder, H.; Linkenkaer-Hansen, K. Detrended Fluctuation Analysis: A Scale-Free View on Neuronal Oscillations. Front. Physiol. 2012, 3, 450. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S.; Kantelhardt, J.W.; Penzel, T.; Peter, J.H.; Voigt, K. Correlated and Uncorrelated Regions in Heart-Rate Fluctuations during Sleep. Phys. Rev. Lett. 2000, 85, 3736–3739. [Google Scholar] [CrossRef]
- Lennartz, S.; Livina, V.N.; Bunde, A.; Havlin, S. Long-term memory in earthquakes and the distribution of interoccurrence times. Europhys. Lett. 2008, 81, 69001. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Nunes Amaral, L.A.; Goldberger, A.L.; Stanley, H.E. Stochastic feedback and the regulation of biological rhythms. Europhys. Lett. 1998, 43, 363. [Google Scholar] [CrossRef]
- Ivanova, K.; Ackerman, T.P.; Clothiaux, E.E.; Ivanov, P.C.; Stanley, H.E.; Ausloos, M. Time correlations and 1/f behavior in backscattering radar reflectivity measurements from cirrus cloud ice fluctuations. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Varotsos, C.; Kirk-Davidoff, D. Long-memory processes in ozone and temperature variations at the region 60° S-60° N. Atmos. Chem. Phys. 2006, 6, 4093–4100. [Google Scholar] [CrossRef]
- Kantelhardt, J.; Zschiegner, S.A.; Koscienly-Bunde, E.; Bunde, A.; Havlin, S.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Oświȩcimka, P.; Kwapień, J.; Drożdż, S. Wavelet versus detrended fluctuation analysis of multifractal structures. Phys. Rev. E 2006, 74, 016103. [Google Scholar] [CrossRef]
- Ihlen, E. Introduction to Multifractal Detrended Fluctuation Analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Mintzelas, A.; Papadopoulou, K.A. Micro-scale, mid-scale, and macro-scale in global seismicity identified by empirical mode decomposition and their multifractal characteristics. Sci. Rep. 2018, 8, 9206. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Mantegna, R.N.; Simons, M.; Stanley, H.E. Statistical properties of DNA sequences. Phys. A Stat. Mech. Its Appl. 1995, 221, 180–192. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mictus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet - Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215. [Google Scholar] [CrossRef]
- Pasari, S.; Sharma, Y. Contemporary Earthquake Hazards in the West-Northwest Himalaya: A Statistical Perspective through Natural Times. Seismol. Res. Lett. 2020, 91, 3358–3369. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A. Nowcasting Earthquakes in Southern California With Machine Learning: Bursts, Swarms, and Aftershocks May Be Related to Levels of Regional Tectonic Stress. Earth Space Sci. 2020, 7, e2020EA001097. [Google Scholar] [CrossRef]
- Varotsos, P.K.; Perez-Oregon, J.; Skordas, E.S.; Sarlis, N.V. Estimating the epicenter of an impending strong earthquake by combining the seismicity order parameter variability analysis with earthquake networks and nowcasting: Application in Eastern Mediterranean. Appl. Sci. 2021, 11, 10093. [Google Scholar] [CrossRef]
- Perez-Oregon, J.; Varotsos, P.K.; Skordas, E.S.; Sarlis, N.V. Estimating the Epicenter of a Future Strong Earthquake in Southern California, Mexico, and Central America by Means of Natural Time Analysis and Earthquake Nowcasting. Entropy 2021, 23, 1658. [Google Scholar] [CrossRef] [PubMed]
- Pasari, S.; Simanjuntak, A.V.H.; Neha; Sharma, Y. Nowcasting earthquakes in Sulawesi Island, Indonesia. Geosci. Lett. 2021, 8, 27. [Google Scholar] [CrossRef]
- Pasari, S.; Simanjuntak, A.V.H.; Mehta, A.; Neha; Sharma, Y. A synoptic view of the natural time distribution and contemporary earthquake hazards in Sumatra, Indonesia. Nat. Hazards 2021, 108, 309–321. [Google Scholar] [CrossRef]
- Pasari, S.; Simanjuntak, A.V.H.; Mehta, A.; Neha; Sharma, Y. The Current State of Earthquake Potential on Java Island, Indonesia. Pure Appl. Geophys. 2021, 178, 2789–2806. [Google Scholar] [CrossRef]
- Christopoulos, S.R.G.; Varotsos, P.K.; Perez-Oregon, J.; Papadopoulou, K.A.; Skordas, E.S.; Sarlis, N.V. Natural Time Analysis of Global Seismicity. Appl. Sci. 2022, 12, 7496. [Google Scholar] [CrossRef]
- Pasari, S. Nowcasting earthquakes in Iran: A quantitative analysis of earthquake hazards through natural times. J. Afr. Earth Sci. 2023, 198, 104821. [Google Scholar] [CrossRef]
- Perez-Oregon, J.; Angulo-Brown, F.; Sarlis, N.V. Nowcasting Avalanches as Earthquakes and the Predictability of Strong Avalanches in the Olami-Feder-Christensen Model. Entropy 2020, 22, 1228. [Google Scholar] [CrossRef]
- Fildes, R.A.; Turcotte, D.L.; Rundle, J.B. Natural time analysis and nowcasting of quasi-periodic collapse events during the 2018 Kīlauea volcano eruptive sequence. Earth Space Sci. 2022, 9, e2022EA002266. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Tanaka, H.; Uyeda, S. Minimum of the order parameter fluctuations of seismicity before major earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2013, 110, 13734–13738. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. Space Phys. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. M 7.3-29 km S of Halabja, Iraq. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us2000bmcg/executive (accessed on 5 December 2023).
- Mintzelas, A.; Sarlis, N. Minima of the fluctuations of the order parameter of seismicity and earthquake networks based on similar activity patterns. Phys. A Stat. Mech. Its Appl. 2019, 527, 121293. [Google Scholar] [CrossRef]
- Tenenbaum, J.N.; Havlin, S.; Stanley, H.E. Earthquake networks based on similar activity patterns. Phys. Rev. E 2012, 86, 046107. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Donges, J.; Schleussner, C.F.; Siegmund, J.; Donner, R. Event coincidence analysis for quantifying statistical interrelationships between event time series. Eur. Phys. J. Spec. Top. 2016, 225, 471–487. [Google Scholar] [CrossRef]
- Siegmund, J.F.; Siegmund, N.; Donner, R.V. CoinCalc—A new R package for quantifying simultaneities of event series. Comput. Geosci. 2017, 98, 64–72. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. M 7.1-27 km NNE of Van, Turkey. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/usp000j9rr/executive (accessed on 4 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).