Critical Review of Techniques for Food Emulsion Characterization
Abstract
1. Introduction
2. Emulsion Formation and Stability
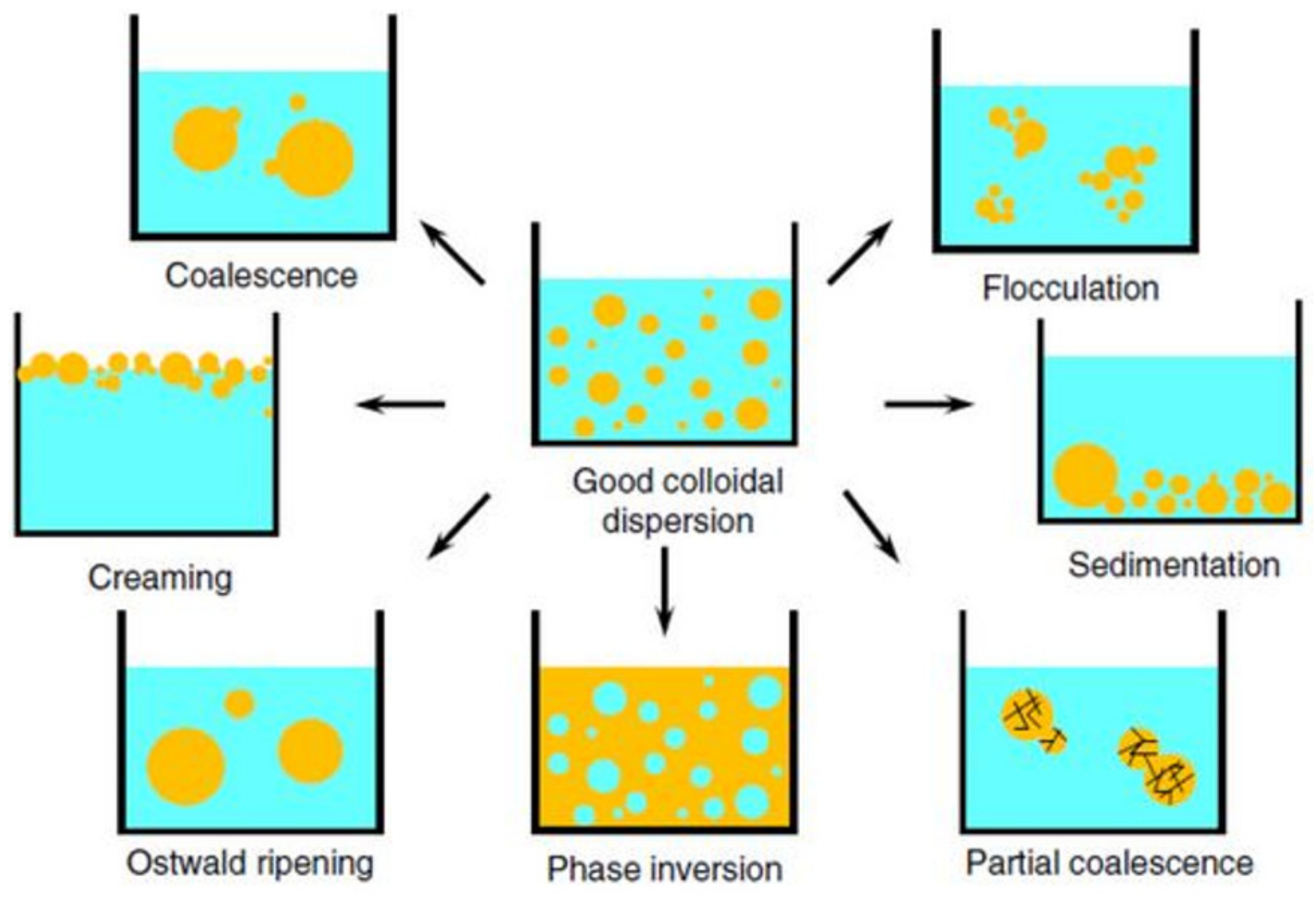
3. Techniques for Emulsion Characterization
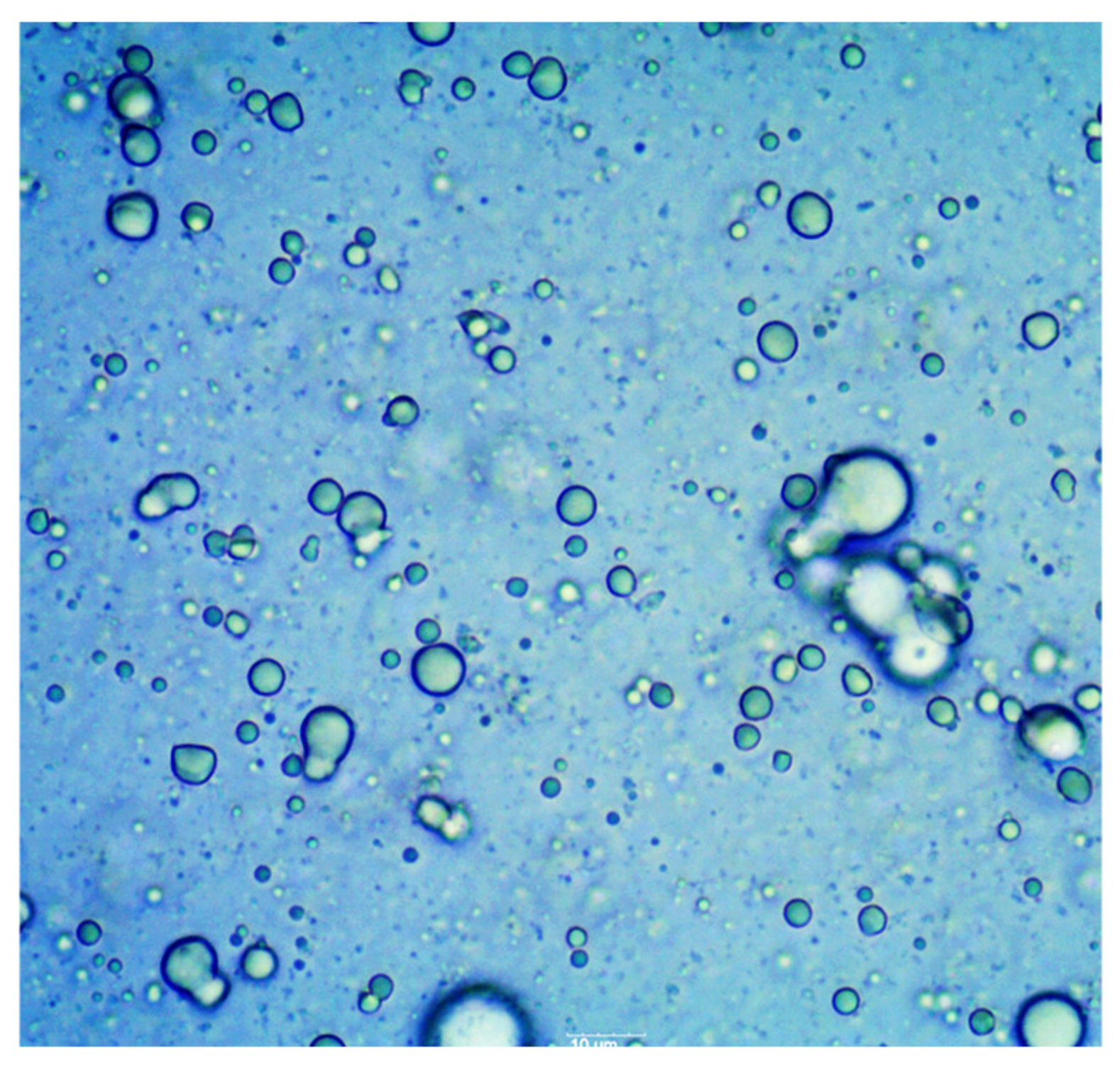
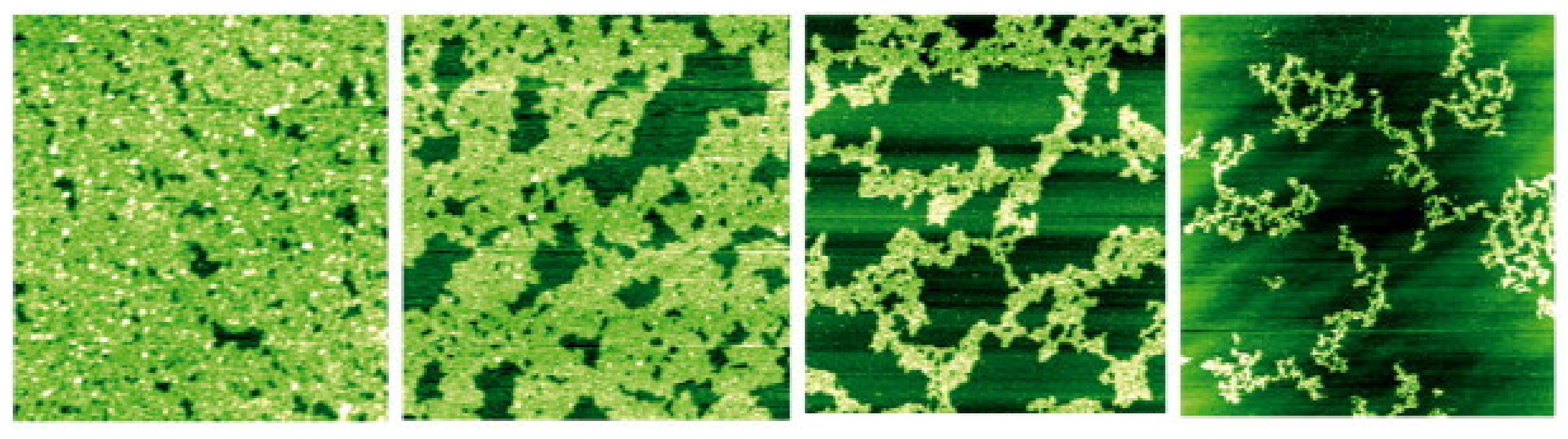
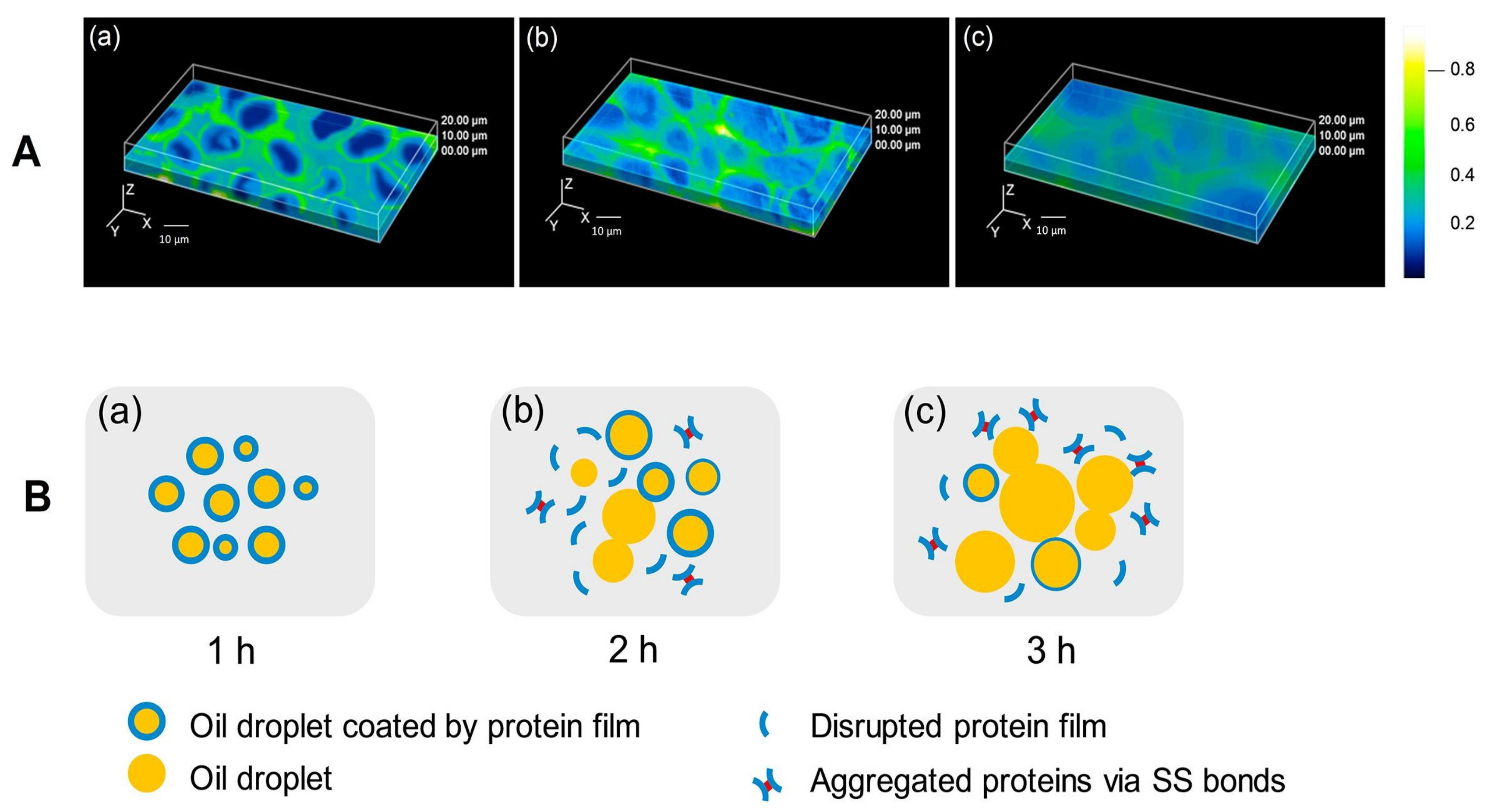
3.1. Microscopic Analysis
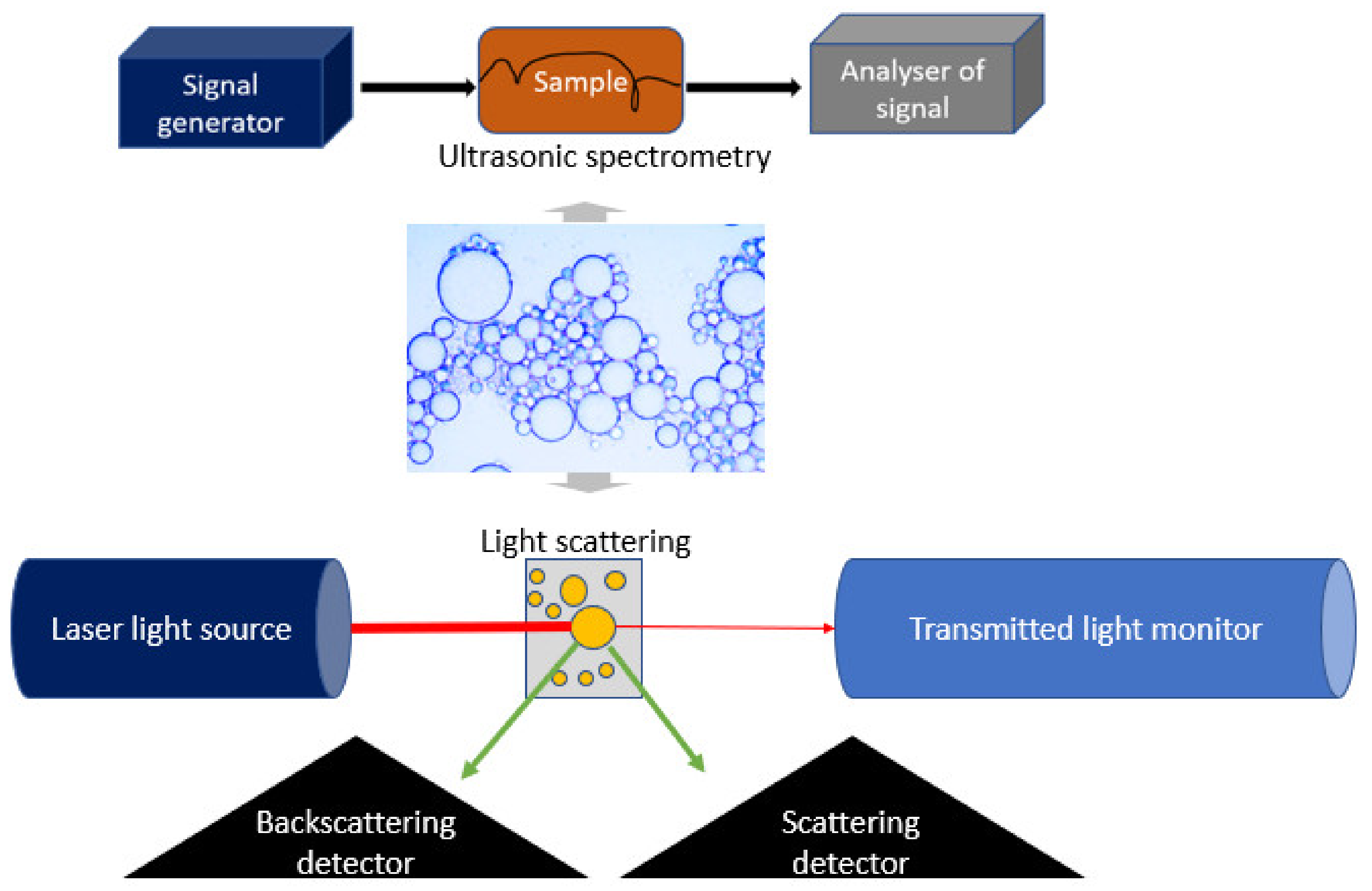
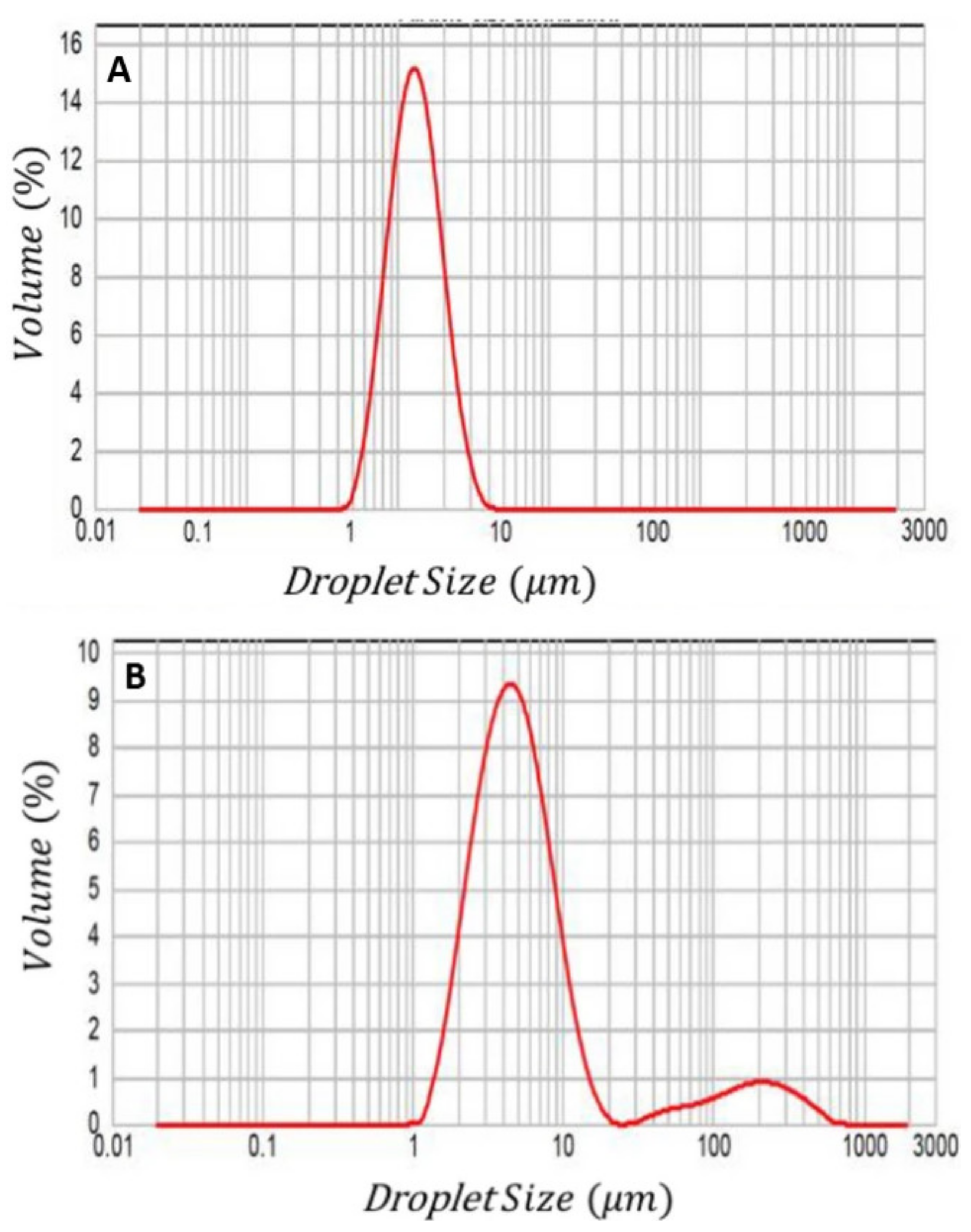
3.2. Droplet Size Analysis
3.3. Determination of Emulsion Optical Properties
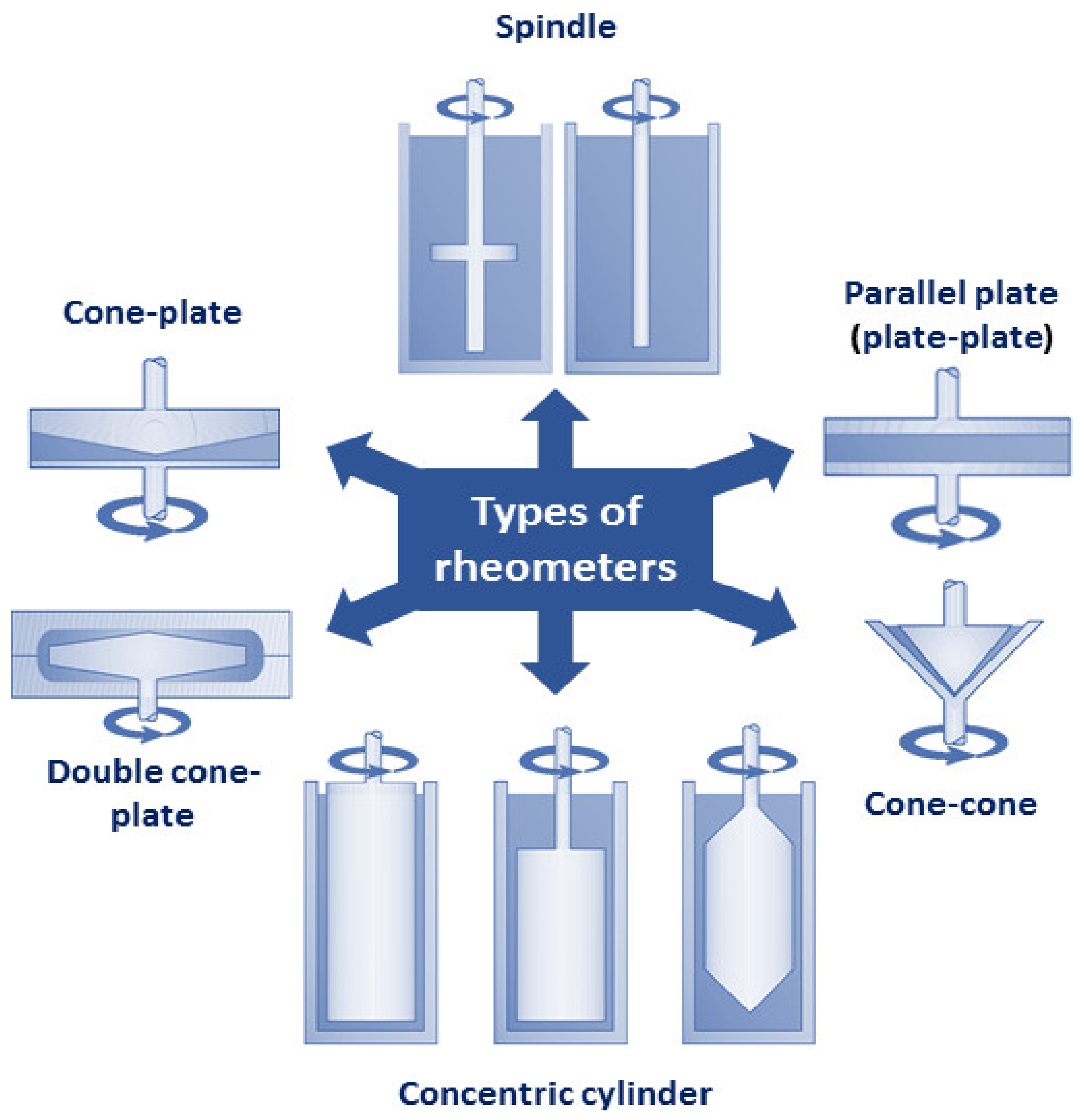
3.4. Rheological Analysis of Emulsions
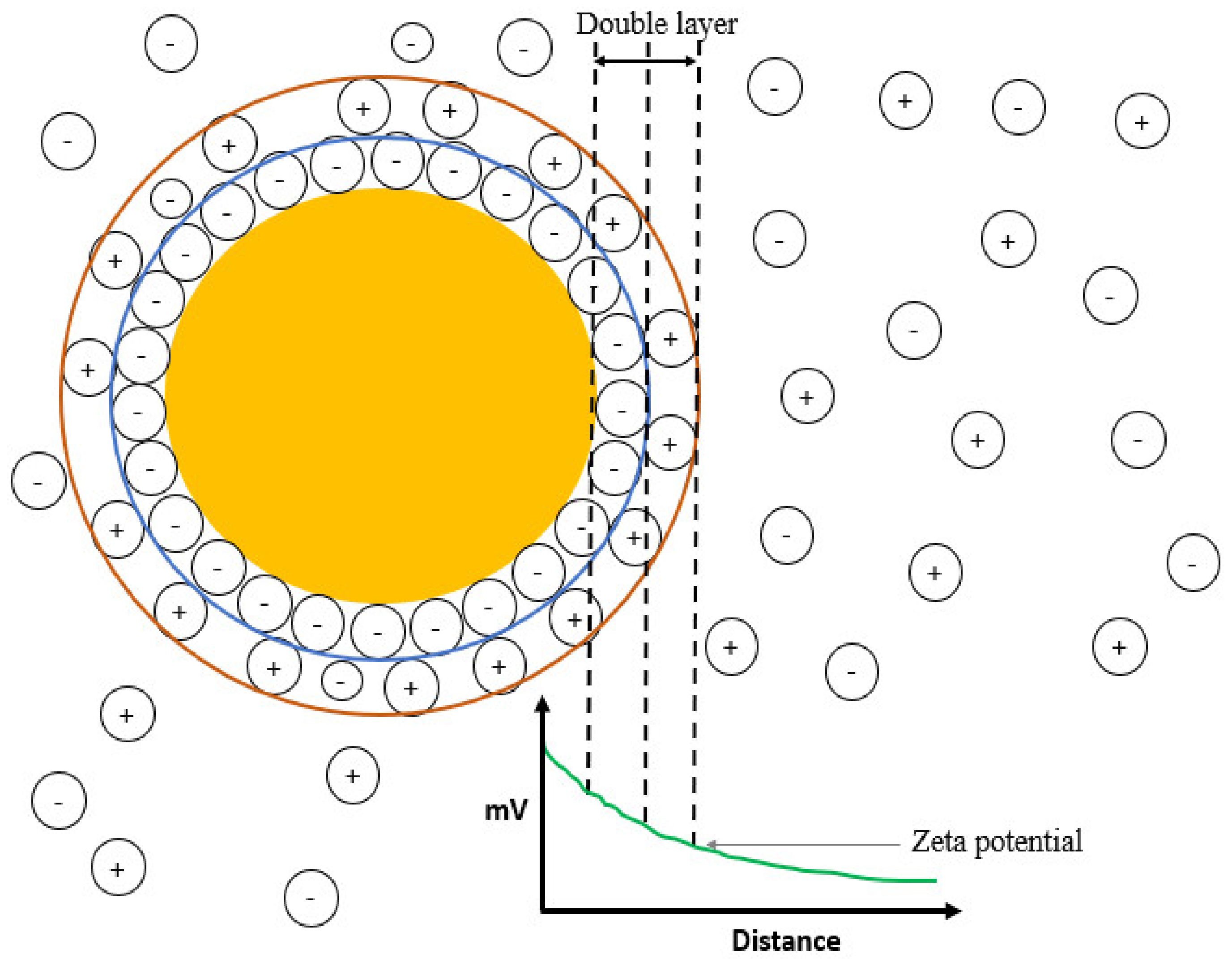
3.5. Determination of Zeta Potential
3.6. Determination of pH Value
3.7. Determination of Electrical Conductivity
3.8. Thermal Properties Analysis
3.9. Accelerated Stability Testing
3.10. Fourier–Transform Infrared Spectroscopy (FTIR) Analysis
3.11. Raman Spectroscopy
3.12. Photon Density Wave (PDW) Spectroscopy
3.13. Texture Analysis
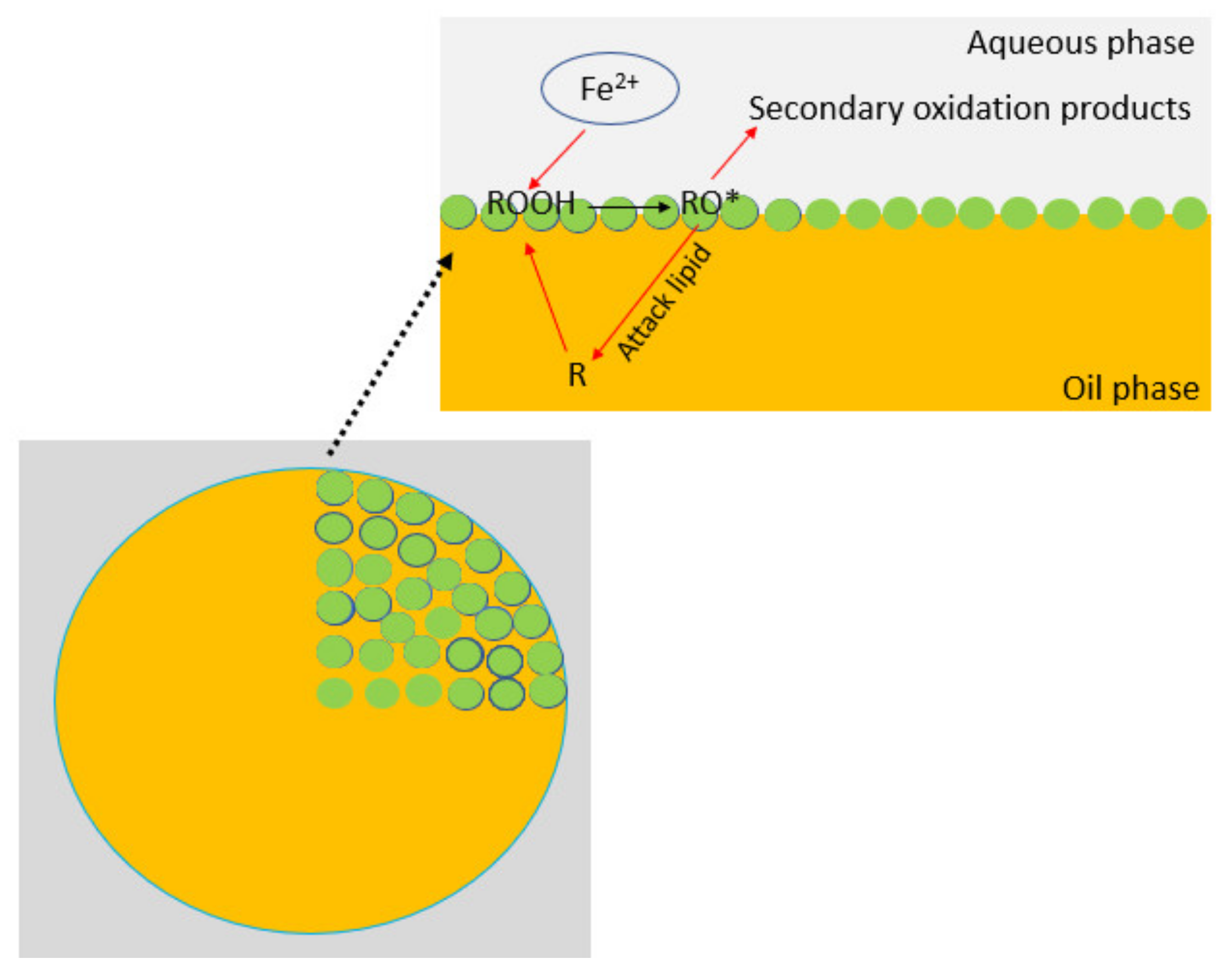
3.14. Oxidation
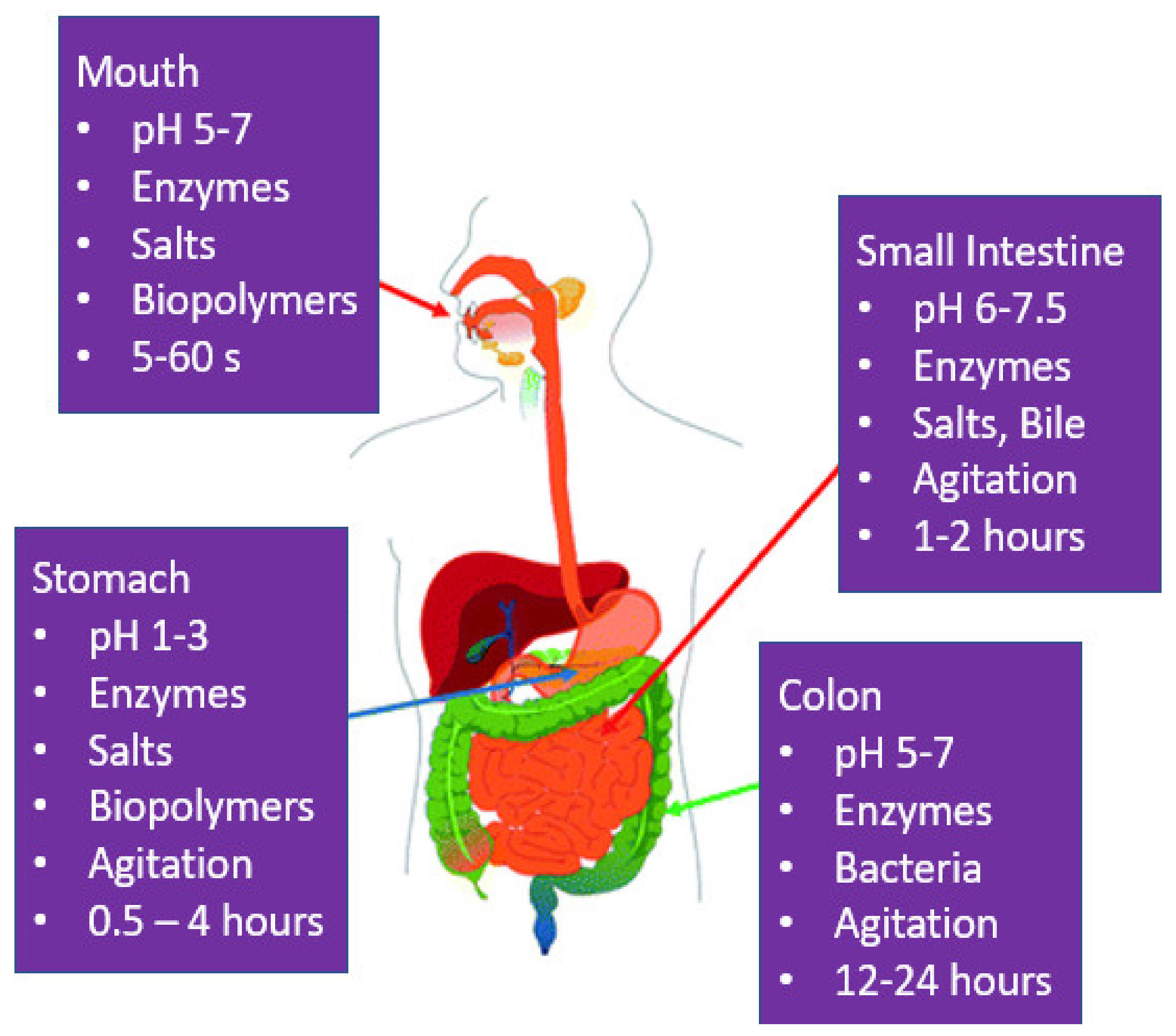
3.15. In Vitro Digestion
4. Emulsion Fractionation and Characterization Methods
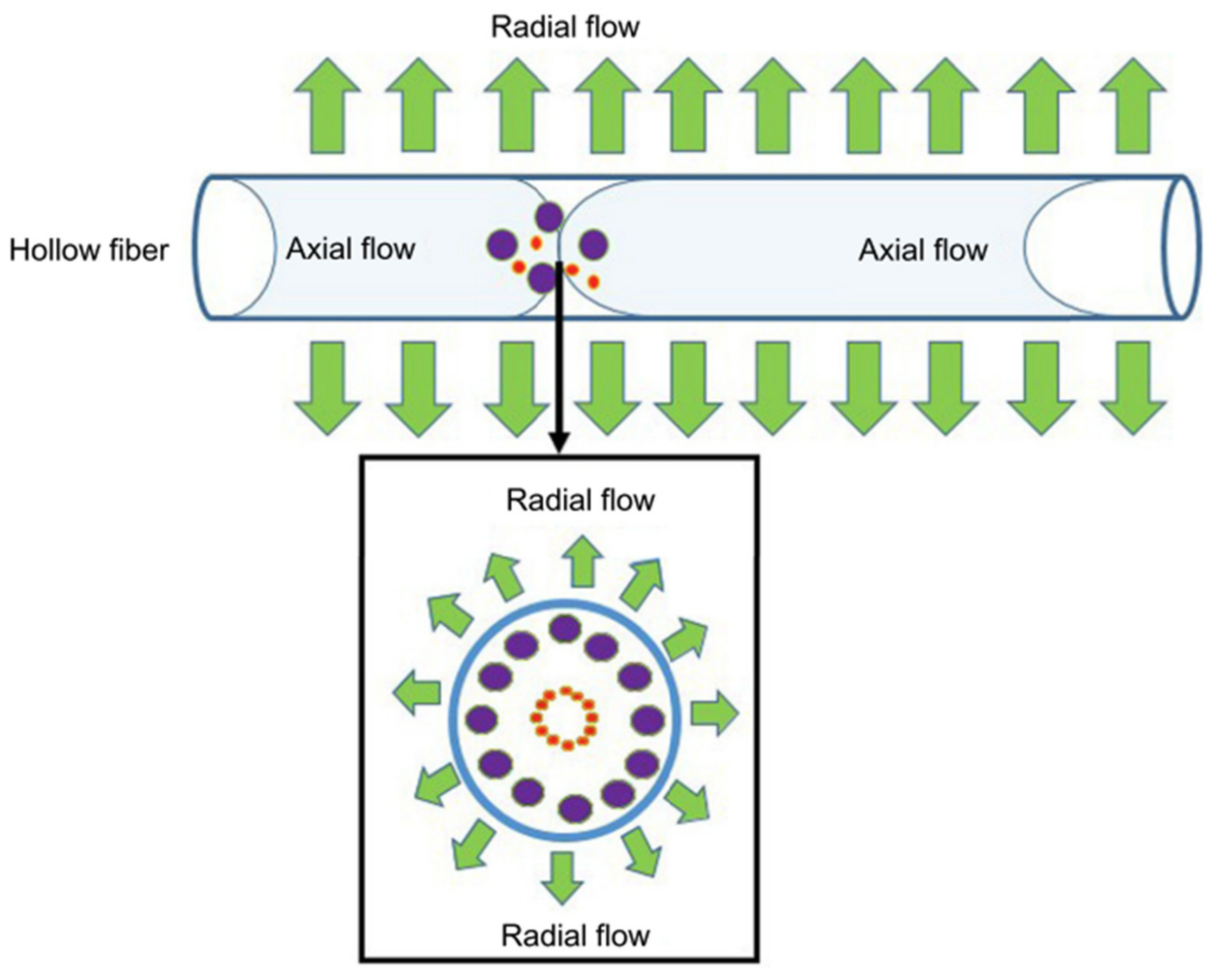
4.1. Field-Flow Fractionation (FFF)
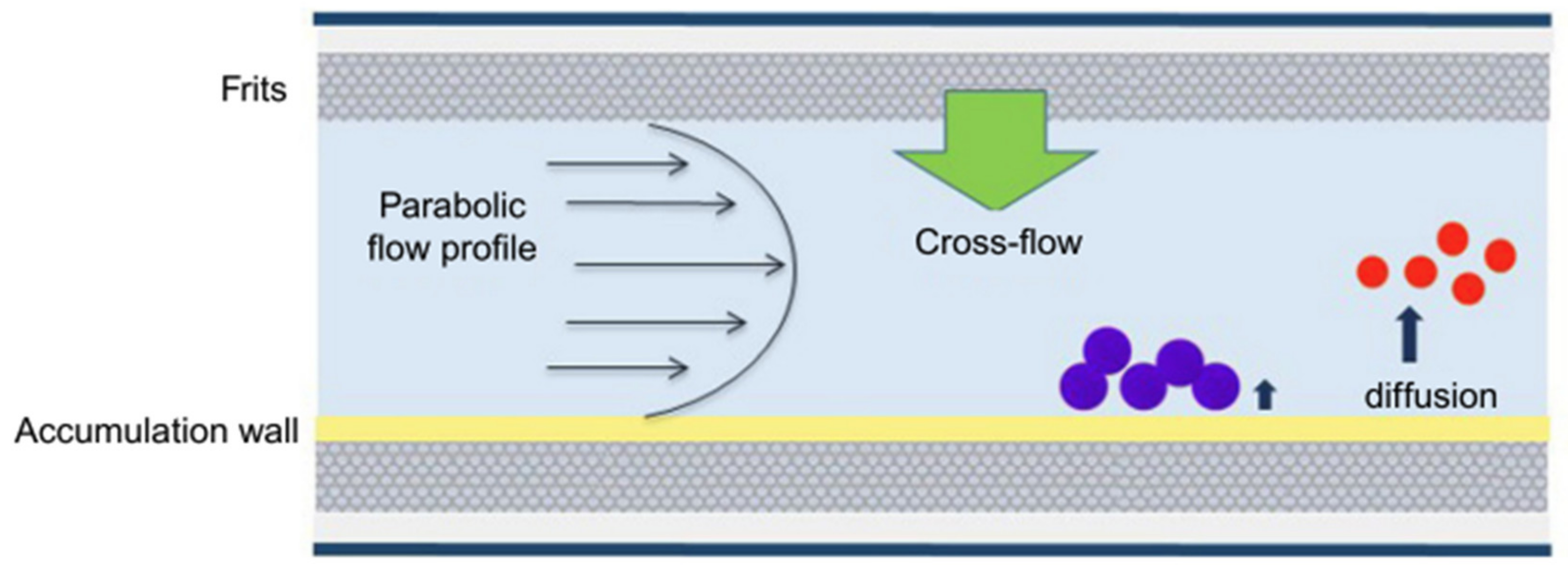
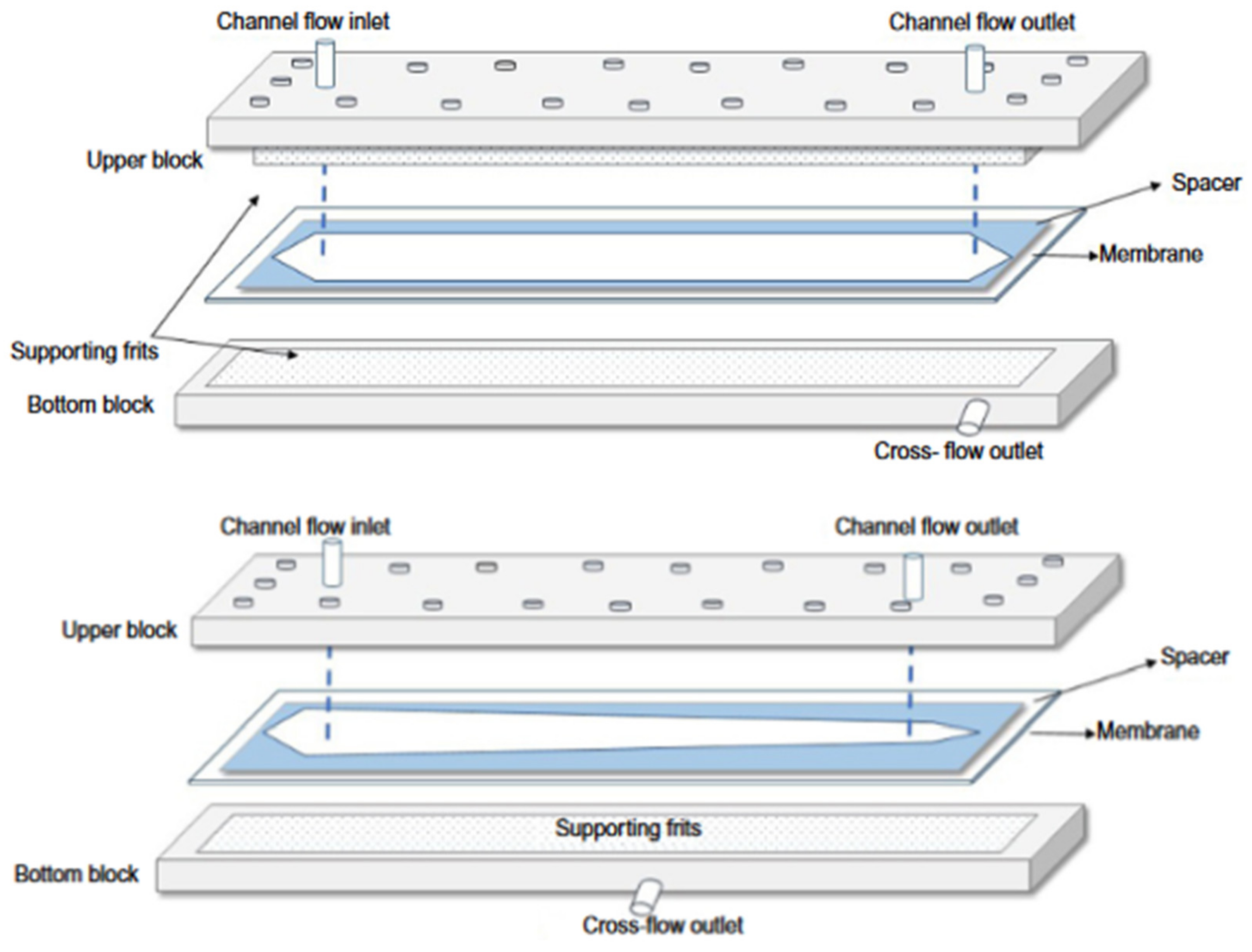
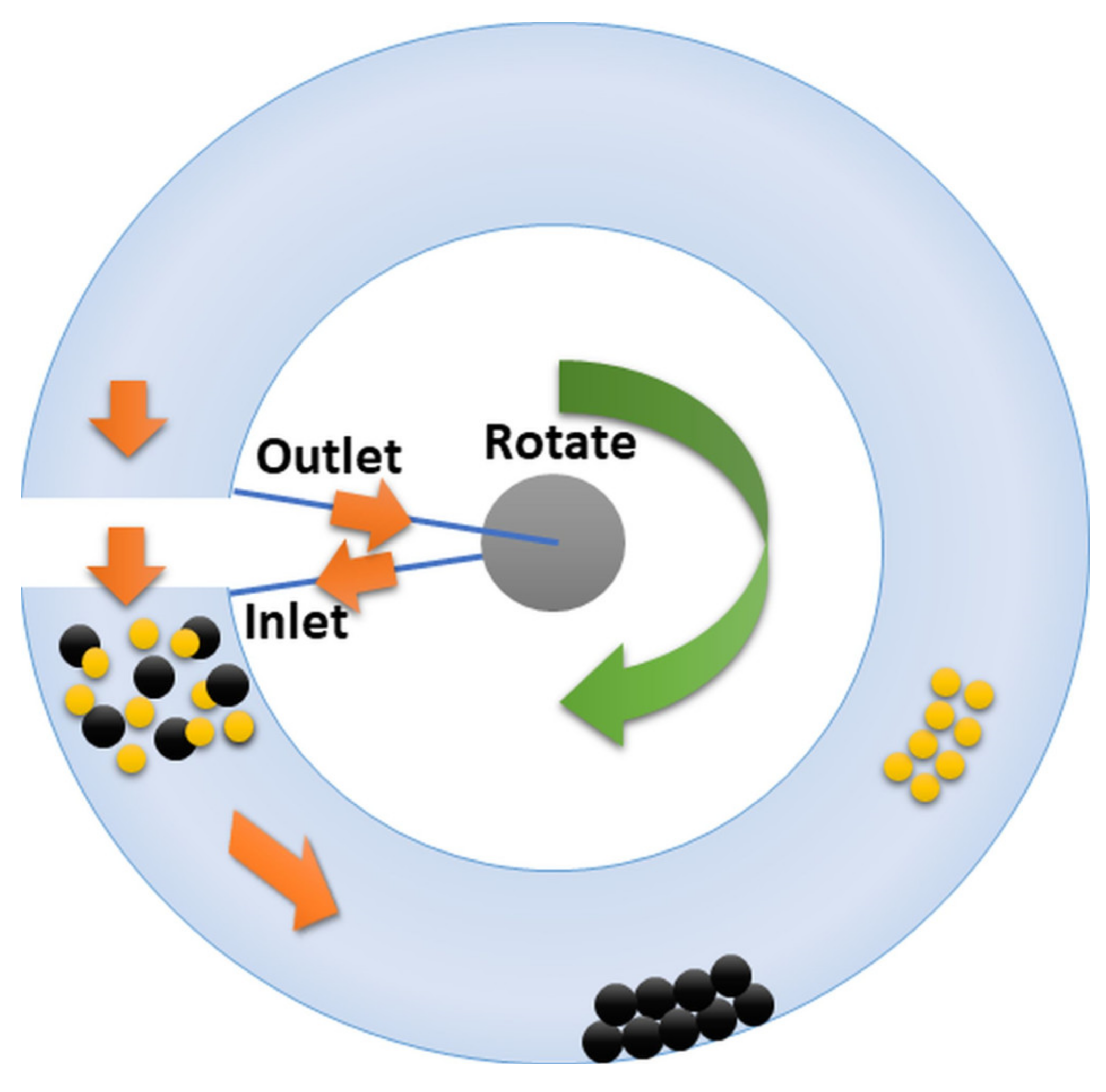
4.2. Capillary Hydrodynamic Fractionation (CHDF)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kupikowska-Stobba, B.; Grzeczkowicz, M.; Lewińska, D. A one-step in vitro continuous flow assessment of protein release from core-shell polymer microcapsules designed for therapeutic protein delivery. Biocybern. Biomed. Eng. 2021, 41, 1347–1364. [Google Scholar] [CrossRef]
- McClements, D.J. Food Emulsions: Principles, Practices, and Techniques, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 1–676. [Google Scholar] [CrossRef]
- Kasprzak, M.M.; Macnaughtan, W.; Harding, S.; Wilde, P.; Wolf, B. Stabilisation of oil-in-water emulsions with non-chemical modified gelatinised starch. Food Hydrocoll. 2018, 81, 409–418. [Google Scholar] [CrossRef]
- Hu, X.; McClements, D.J. Construction of plant-based adipose tissue using high internal phase emulsions and emulsion gels. Innov. Food Sci. Emerg. Technol. 2022, 78, 103016. [Google Scholar] [CrossRef]
- Ataeian, P.; Aroyan, L.; Parwez, W.; Tam, K.C. Emulsions undergoing phase transition: Effect of emulsifier type and concentration. J. Colloid Interface Sci. 2022, 617, 214–223. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Lee, P.W.; Martens, T.D.; McClements, D.J. Comparison of Emulsifying Properties of Plant and Animal Proteins in Oil-in-Water Emulsions: Whey, Soy, and RuBisCo Proteins. Food Biophys. 2022, 17, 409–421. [Google Scholar] [CrossRef]
- Lee, J.; Wi, G.; Choi, M.J. The rheological properties and stability of gelled emulsions applying to κ-carrageenan and methyl cellulose as an animal fat replacement. Food Hydrocoll. 2023, 136, 108243. [Google Scholar] [CrossRef]
- Yang, F.S.; Caldwell, K.D.; Myers, M.N.; Giddings, J.C. Colloid characterization by sedimentation field-flow fractionation. III. Emulsions. J. Colloid Interface Sci. 1983, 93, 115–125. [Google Scholar] [CrossRef]
- Sanka, I.; Bartkova, S.; Pata, P.; Smolander, O.P.; Scheler, O. Investigation of Different Free Image Analysis Software for High-Throughput Droplet Detection. ACS Omega 2021, 6, 22625–22634. [Google Scholar] [CrossRef] [PubMed]
- Kasprzak, M.M.; Sady, M.; Kruk, J.; Bartkova, S.; Sanka, I.; Scheler, O.; Jamróz, E.; Berski, W.; Onacik-Gür, S.; Szram, R.; et al. Replacement of milk fat by rapeseed oil stabilised emulsion in commercial yogurt. PeerJ 2023, 11, e16441. [Google Scholar] [CrossRef]
- Sanka, I.; Bartkova, S.; Pata, P.; Ernits, M.; Meinberg, M.M.; Agu, N.; Aruoja, V.; Smolander, O.-P.; Scheler, O. User-friendly analysis of droplet array images. Anal. Chim. Acta 2023, 1272, 341397. [Google Scholar] [CrossRef]
- Qiu, L.; Zhang, Y.; Long, X.; Ye, Z.; Qu, Z.; Yang, X.; Wang, C. Scanning Electron Microscopy Investigation for Monitoring the Emulsion Deteriorative Process and Its Applications in Site-Directed Reaction with Paper Fabric. Molecules 2021, 26, 6471. [Google Scholar] [CrossRef] [PubMed]
- Fischer, P.; Windhab, E.J. Rheology of food materials. Curr. Opin. Colloid Interface Sci. 2011, 16, 36–40. [Google Scholar] [CrossRef]
- Zhou, B.; Drusch, S.; Hogan, S.A. Confined flow behavior under high shear rates and stability of oil/water high internal phase emulsions (HIPEs) stabilized by whey protein isolate: Role of protein concentration and pH. Food Res. Int. 2022, 160, 111674. [Google Scholar] [CrossRef] [PubMed]
- Alade, O.S.; Mahmoud, M.; Al Shehri, D.A.; Sultan, A.S. Rapid Determination of Emulsion Stability Using Turbidity Measurement Incorporating Artificial Neural Network (ANN): Experimental Validation Using Video/Optical Microscopy and Kinetic Modeling. ACS Omega 2021, 6, 5910–5920. [Google Scholar] [CrossRef] [PubMed]
- Ravindran, S.; Williams, M.A.K.; Ward, R.L.; Gillies, G. Understanding how the properties of whey protein stabilized emulsions depend on pH, ionic strength and calcium concentration, by mapping environmental conditions to zeta potential. Food Hydrocoll. 2018, 79, 572–578. [Google Scholar] [CrossRef]
- Gerzhova, A.; Mondor, M.; Benali, M.; Aider, M. Study of total dry matter and protein extraction from canola meal as affected by the pH, salt addition and use of zeta-potential/turbidimetry analysis to optimize the extraction conditions. Food Chem. 2016, 201, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Dalmazzone, C.; Noïk, C.; Clausse, D. Application of DSC for Emulsified System Characterization. Oil Gas Sci. Technol.—Rev. D’ifp Energ. Nouv. 2009, 64, 543–555. [Google Scholar] [CrossRef]
- Reiner, J.; Ly, T.T.; Liu, L.; Karbstein, H.P. Melt Emulsions: Influence of the Cooling Procedure on Crystallization and Recrystallization of Emulsion Droplets and their Influence on Dispersion Viscosity upon Storage. Chem. Ing. Tech. 2022, 94, 356–364. [Google Scholar] [CrossRef]
- Nickolov, Z.S.; Paruchuri, V.; Shah, D.O.; Miller, J.D. FTIR–ATR studies of water structure in reverse micelles during the synthesis of oxalate precursor nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2004, 232, 93–99. [Google Scholar] [CrossRef]
- Hou, F.; Yang, S.; Ma, X.; Gong, Z.; Wang, Y.; Wang, W. Characterization of Physicochemical Properties of Oil-in-Water Emulsions Stabilized by Tremella fuciformis Polysaccharides. Foods 2022, 11, 3020. [Google Scholar] [CrossRef]
- Zhou, H.; Tan, Y.; McClements, D.J. Applications of the INFOGEST In Vitro Digestion Model to Foods: A Review. Annu. Rev. Food Sci. Technol. 2023, 14, 135–156. [Google Scholar] [CrossRef]
- Chuesiang, P.; Kim, J.T.; Shin, G.H. Observation of curcumin-encapsulated Pickering emulsion stabilized by cellulose nanocrystals-whey protein isolate (CNCs-WPI) complex under in vitro lipid digestion through INFOGEST model. Int. J. Biol. Macromol. 2023, 234, 123679. [Google Scholar] [CrossRef] [PubMed]
- Menard, O.; Lesmes, U.; Shani-Levi, C.S.; Calahorra, A.A.; Lavoisier, A.; Morzel, M.; Rieder, A.; Feron, G.; Nebbia, S.; Mashiah, L.; et al. Static in vitro digestion model adapted to the general older adult population: An INFOGEST international consensus. Food Funct. 2023, 14, 4569–4582. [Google Scholar] [CrossRef]
- Tadros, T.F. Emulsion Formation, Stability, and Rheology. In Emulsion Formation and Stability; Wiley: Hoboken, NJ, USA, 2013; pp. 1–75. [Google Scholar] [CrossRef]
- Janssen, P.H.; Noik, C.; Dalmazzone, C. Emulsion Formation in a Model Choke-Valve. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001. [Google Scholar] [CrossRef]
- Anton, N.; Vandamme, T.F. Nano-emulsions and micro-emulsions: Clarifications of the critical differences. Pharm. Res. 2011, 28, 978–985. [Google Scholar] [CrossRef] [PubMed]
- McClements, D.J. Food Emulsions: Principles, Practices, and Techniques, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar] [CrossRef]
- Tadros, T.; Izquierdo, P.; Esquena, J.; Solans, C. Formation and stability of nano-emulsions. Adv. Colloid Interface Sci. 2004, 108–109, 303–318. [Google Scholar] [CrossRef] [PubMed]
- Delmas, T.; Piraux, H.; Couffin, A.-C.; Texier, I.; Vinet, F.; Poulin, P.; Cates, M.E.; Bibette, J. How to prepare and stabilize very small nanoemulsions. Langmuir 2011, 27, 1683–1692. [Google Scholar] [CrossRef] [PubMed]
- Salem, M.A.; Ezzat, S.M.; Salem, M.A.; Ezzat, S.M. Nanoemulsions in Food Industry. In Some New Aspects of Colloidal Systems in Foods; BoD–Books: Norderstedt, Germany, 2018. [Google Scholar] [CrossRef]
- Posocco, P.; Perazzo, A.; Preziosi, V.; Laurini, E.; Pricl, S.; Guido, S. Interfacial tension of oil/water emulsions with mixed non-ionic surfactants: Comparison between experiments and molecular simulations. RSC Adv. 2016, 6, 4723–4729. [Google Scholar] [CrossRef]
- Tadros, T.F. An Introduction to Surfactants; Walter de Gruyter: Berlin, Germany, 2014. [Google Scholar] [CrossRef]
- Wollenweber, C.; Makievski, A.V.; Miller, R.; Daniels, R. Adsorption of hydroxypropyl methylcellulose at the liquid/liquid interface and the effect on emulsion stability. Colloids Surf. A Physicochem. Eng. Asp. 2000, 172, 91–101. [Google Scholar] [CrossRef]
- Jian, C.; Poopari, M.R.; Liu, Q.; Zerpa, N.; Zeng, H.; Tang, T. Reduction of Water/Oil Interfacial Tension by Model Asphaltenes: The Governing Role of Surface Concentration. J. Phys. Chem. B 2016, 120, 5646–5654. [Google Scholar] [CrossRef]
- Kupikowska-Stobba, B.; Kasprzak, M. Fabrication of nanoparticles for bone regeneration: New insight into applications of nanoemulsion technology. J. Mater. Chem. B 2021, 9, 5221–5244. [Google Scholar] [CrossRef]
- Hu, Y.T.; Ting, Y.; Hu, J.Y.; Hsieh, S.C. Techniques and methods to study functional characteristics of emulsion systems. J. Food Drug Anal. 2017, 25, 16–26. [Google Scholar] [CrossRef]
- Kilpatrick, P.K. Water-in-Crude Oil Emulsion Stabilization: Review and Unanswered Questions. Energy Fuels 2012, 26, 4017–4026. [Google Scholar] [CrossRef]
- Marrucci, G. A theory of coalescence. Chem. Eng. Sci. 1969, 24, 975–985. [Google Scholar] [CrossRef]
- Dickinson, E. Flocculation of protein-stabilized oil-in-water emulsions. Colloids Surf. B Biointerfaces 2010, 81, 130–140. [Google Scholar] [CrossRef] [PubMed]
- Rahn-Chique, K.; Puertas, A.M.; Romero-Cano, M.S.; Rojas, C.; Urbina-Villalba, G. Nanoemulsion stability: Experimental evaluation of the flocculation rate from turbidity measurements. Adv. Colloid Interface Sci. 2012, 178, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Tayeb, H.H.; Sainsbury, F. Nanoemulsions in drug delivery: Formulation to medical application. Nanomedicine 2018, 13, 2507–2525. [Google Scholar] [CrossRef]
- Gupta, A.; Eral, H.B.; Hatton, T.A.; Doyle, P.S. Nanoemulsions: Formation, properties and applications. Soft Matter 2016, 12, 2826–2841. [Google Scholar] [CrossRef] [PubMed]
- Tadros, T.F. Emulsion Formation and Stability; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013. [Google Scholar] [CrossRef]
- Chanamai, R.; McClements, D.J. Dependence of creaming and rheology of monodisperse oil-in-water emulsions on droplet size and concentration. Colloids Surf. A Physicochem. Eng. Asp. 2000, 172, 79–86. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Yuan, T.; Wang, C.; Gao, R.; Hu, G.; Xu, J.; Zhao, J. Synthesis and properties of zwitterionic gemini surfactants for enhancing oil recovery. J. Mol. Liq. 2020, 311, 113179. [Google Scholar] [CrossRef]
- Koroleva, M.; Nagovitsina, T.; Yurtov, E. Nanoemulsions stabilized by non-ionic surfactants: Stability and degradation mechanisms. Phys. Chem. Chem. Phys. 2018, 20, 10369–10377. [Google Scholar] [CrossRef]
- Kralova, I.; Sjöblom, J. Surfactants Used in Food Industry: A Review. J. Dispers. Sci. Technol. 2009, 30, 1363–1383. [Google Scholar] [CrossRef]
- Ng, N.; Rogers, M.A. Surfactants. In Encyclopedia of Food Chemistry; Elsevier: Amsterdam, The Netherlands, 2019; pp. 276–282. [Google Scholar] [CrossRef]
- Witthayapanyanon, A.; Harwell, J.H.; Sabatini, D.A. Hydrophilic–lipophilic deviation (HLD) method for characterizing conventional and extended surfactants. J. Colloid Interface Sci. 2008, 325, 259–266. [Google Scholar] [CrossRef]
- Salager, J.-L.; Marquez, R.; Bullon, J.; Forgiarini, A. Formulation in Surfactant Systems: From-Winsor-to-HLDN. Encyclopedia 2022, 2, 778–842. [Google Scholar] [CrossRef]
- Acosta, E.J.; Yuan, J.S.; Bhakta, A.S. The characteristic curvature of ionic surfactants. J. Surfactants Deterg. 2008, 11, 145–158. [Google Scholar] [CrossRef]
- Tan, C.; McClements, D.J. Application of Advanced Emulsion Technology in the Food Industry: A Review and Critical Evaluation. Foods 2021, 10, 812. [Google Scholar] [CrossRef]
- de Carvalho-Guimarães, F.B.; Correa, K.L.; de Souza, T.P.; Rodríguez Amado, J.R.; Ribeiro-Costa, R.M.; Silva-Júnior, J.O.C. A Review of Pickering Emulsions: Perspectives and Applications. Pharmaceuticals 2022, 15, 1413. [Google Scholar] [CrossRef]
- Yang, Y.; Fang, Z.; Chen, X.; Zhang, W.; Xie, Y.; Chen, Y.; Liu, Z.; Yuan, W. An overview of pickering emulsions: Solid-particle materials, classification, morphology, and applications. Front. Pharmacol. 2017, 8, 235054. [Google Scholar] [CrossRef] [PubMed]
- Muhamad, I.I.; Quin, C.H.; Selvakumaran, S. Preparation and evaluation of water-in-soybean oil–in-water emulsions by repeated premix membrane emulsification method using cellulose acetate membrane. J. Food Sci. Technol. 2016, 53, 1845–1855. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo, P.; Esquena, J.; Tadros, T.F.; Dederen, C.; Garcia, M.J.; Azemar, N.; Solans, C. Formation and Stability of Nano-Emulsions Prepared Using the Phase Inversion Temperature Method. Langmuir 2001, 18, 26–30. [Google Scholar] [CrossRef]
- Guzey, D.; McClements, D.J. Formation, stability and properties of multilayer emulsions for application in the food industry. Adv. Colloid Interface Sci. 2006, 128–130, 227–248. [Google Scholar] [CrossRef]
- Salvia-Trujillo, L.; Soliva-Fortuny, R.; Rojas-Graü, M.A.; McClements, D.J.; Martín-Belloso, O. Edible Nanoemulsions as Carriers of Active Ingredients: A Review. Annu. Rev. Food Sci. Technol. 2017, 8, 439–466. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Surface Forces. In The Handbook of Surface Imaging and Visualization; CRC Press: Boca Raton, FL, USA, 2022; pp. 793–816. [Google Scholar] [CrossRef]
- pH-Controlled Macromolecule Encapsulation in and Release from Polyelectrolyte Multilayer Nanocapsules—Sukhorukov—2001—Macromolecular Rapid Communications—Wiley Online Library n.d. Available online: https://onlinelibrary.wiley.com/doi/10.1002/1521-3927(20010101)22:1%3C44::AID-MARC44%3E3.0.CO;2-U (accessed on 10 January 2024).
- Guzey, D.; Kim, H.J.; McClements, D.J. Factors influencing the production of O/W emulsions stabilized by β-lactoglobulin–pectin membranes. Food Hydrocoll. 2004, 18, 967–975. [Google Scholar] [CrossRef]
- Chen, G.; Tao, D. An experimental study of stability of oil–water emulsion. Fuel Process. Technol. 2005, 86, 499–508. [Google Scholar] [CrossRef]
- Foundations of Colloid Science—Robert, J. Hunter—Oxford University Press n.d. Available online: https://global.oup.com/academic/product/foundations-of-colloid-science-9780198505020?cc=pl&lang=en& (accessed on 10 December 2023).
- Dapčević Hadnadev, T.; Dokić, P.; Krstonošić, V.; Hadnadev, M. Influence of oil phase concentration on droplet size distribution and stability of oil-in-water emulsions. Eur. J. Lipid Sci. Technol. 2013, 115, 313–321. [Google Scholar] [CrossRef]
- Ghasemi, H.; Darjani, S.; Mazloomi, H.; Mozaffari, S. Preparation of stable multiple emulsions using food-grade emulsifiers: Evaluating the effects of emulsifier concentration, W/O phase ratio, and emulsification process. SN Appl. Sci. 2020, 2, 1–9. [Google Scholar] [CrossRef]
- Akhter, S.; Jain, G.K.; Ahmad, F.J.; Khar, R.K.; Jain, N.; Khan, Z.I.; Talegaonkar, S. Investigation of Nanoemulsion System for Transdermal Delivery of Domperidone: Ex-vivo and in vivo Studies. Curr. Nanosci. 2008, 4, 381–390. [Google Scholar] [CrossRef]
- Medina, S.C.; Anjum, D.H.; Behzad, A.R.; Vilagines, R.D.; Tabatabai, A.; Leiknes, T.O. Microscopy techniques applied to submicron characterization of oilfield produced water. J. Pet. Sci. Eng. 2021, 206, 108930. [Google Scholar] [CrossRef]
- Bellalta, P.; Troncoso, E.; Zúñiga, R.N.; Aguilera, J.M. Rheological and microstructural characterization of WPI-stabilized O/W emulsions exhibiting time-dependent flow behavior. LWT-Food Sci. Technol. 2012, 46, 375–381. [Google Scholar] [CrossRef]
- Bartkova, S.; Vendelin, M.; Sanka, I.; Pata, P.; Scheler, O. Droplet image analysis with user-friendly freeware CellProfiler. Anal. Methods 2020, 12, 2287–2294. [Google Scholar] [CrossRef]
- Binks, B.P.; Dong, J. Emulsions and equilibrium phase behaviour in silicone oil + water + nonionic surfactant mixtures. Colloids Surf. A Physicochem. Eng. Asp. 1998, 132, 289–301. [Google Scholar] [CrossRef]
- Ishibashi, C.; Hondoh, H.; Ueno, S. Influence of morphology and polymorphic transformation of fat crystals on the freeze-thaw stability of mayonnaise-type oil-in-water emulsions. Food Res. Int. 2016, 89, 604–613. [Google Scholar] [CrossRef] [PubMed]
- Binks, B.P.; Olusanya, S.O. Pickering emulsions stabilized by coloured organic pigment particles. Chem. Sci. 2016, 8, 708–723. [Google Scholar] [CrossRef]
- Saffarionpour, S.; Diosady, L.L. Delivery of Ferric Sodium EDTA by Water-in-Oil-in-Water (W1/O/W2) Double Emulsions: Influence of Carrier Oil on its In Vitro Bioaccessibility. Food Bioprocess Technol. 2022, 15, 421–439. [Google Scholar] [CrossRef]
- Sikorska, E.; Khmelinskii, I.; Sikorski, M. Fluorescence spectroscopy and imaging instruments for food quality evaluation. In Evaluation Technologies for Food Quality; Woodhead Publishing: Cambridge, UK, 2019; pp. 491–533. [Google Scholar] [CrossRef]
- Klymchenko, A.S.; Roger, E.; Anton, N.; Anton, H.; Shulov, I.; Vermot, J.; Mely, Y.; Vandamme, T.F. Highly lipophilic fluorescent dyes in nano-emulsions: Towards bright non-leaking nano-droplets. RSC Adv. 2012, 2, 11876–11886. [Google Scholar] [CrossRef]
- Thijssen, J.H.J.; Schofield, A.B.; Clegg, P.S. How do (fluorescent) surfactants affect particle-stabilized emulsions? Soft Matter 2011, 7, 7965–7968. [Google Scholar] [CrossRef]
- Yu, D.; Li, G.; Liu, W.; Li, Y.; Song, Z.; Wang, H.; Guan, F.; Chen, X. A fluorescent pickering-emulsion stabilizer prepared using carbon nitride quantum dots and laponite nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2019, 563, 310–317. [Google Scholar] [CrossRef]
- Klang, V.; Matsko, N.B.; Valenta, C.; Hofer, F. Electron microscopy of nanoemulsions: An essential tool for characterisation and stability assessment. Micron 2012, 43, 85–103. [Google Scholar] [CrossRef]
- Saupe, A.; Gordon, K.C.; Rades, T. Structural investigations on nanoemulsions, solid lipid nanoparticles and nanostructured lipid carriers by cryo-field emission scanning electron microscopy and Raman spectroscopy. Int. J. Pharm. 2006, 314, 56–62. [Google Scholar] [CrossRef]
- Dudkiewicz, A.; Tiede, K.; Loeschner, K.; Jensen, L.H.S.; Jensen, E.; Wierzbicki, R.; Boxall, A.B.; Molhave, K. Characterization of nanomaterials in food by electron microscopy. TrAC Trends Anal. Chem. 2011, 30, 28–43. [Google Scholar] [CrossRef]
- Rosso, A.; Lollo, G.; Chevalier, Y.; Troung, N.; Bordes, C.; Bourgeois, S.; Maniti, O.; Granjon, T.; Dugas, P.-Y.; Urbaniak, S.; et al. Development and structural characterization of a novel nanoemulsion for oral drug delivery. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 593, 124614. [Google Scholar] [CrossRef]
- Review of Nanoemulsion Formulation and Characterization Techniques: EBSCOhost n.d. Available online: https://web.s.ebscohost.com/ehost/detail/detail?vid=0&sid=e1eaf248-dc1e-4691-9a8b-06cc757ccad8%40redis&bdata=Jmxhbmc9cGwmc2l0ZT1laG9zdC1saXZl#AN=136112967&db=asn (accessed on 10 December 2023).
- Franken, L.E.; Boekema, E.J.; Stuart, M.C.A. Transmission Electron Microscopy as a Tool for the Characterization of Soft Materials: Application and Interpretation. Adv. Sci. 2017, 4, 1600476. [Google Scholar] [CrossRef]
- Helene Søgaard, L. General Rights Ultrastructure of Emulsions—A Comparative Electron Microscopy Study; Technical University of Denmark: Lyngby, Denmark, 2013. [Google Scholar]
- Hurbain, I.; Sachse, M. The future is cold: Cryo-preparation methods for transmission electron microscopy of cells. Biol. Cell 2011, 103, 405–420. [Google Scholar] [CrossRef]
- Kanno, H.; Speedy, R.J.; Angell, C.A. Brief Introduction to High-Pressure Freezing. Science 2013, 189, 880–881. [Google Scholar] [CrossRef]
- Niu, H.; Wang, W.; Dou, Z.; Chen, X.; Chen, X.; Chen, H.; Fu, X. Multiscale combined techniques for evaluating emulsion stability: A critical review. Adv. Colloid Interface Sci. 2023, 311, 102813. [Google Scholar] [CrossRef] [PubMed]
- Mackie, A.R.; Gunning, A.P.; Wilde, P.J.; Morris, V.J. Orogenic Displacement of Protein from the Oil/Water Interface. Langmuir 1999, 16, 2242–2247. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Breen, P.; Xu, Z.; Masliyah, J.H. Asphaltene Films at a Toluene/Water Interface. Energy Fuels 2006, 21, 274–285. [Google Scholar] [CrossRef]
- Ho, T.M.; Abik, F.; Mikkonen, K.S. An overview of nanoemulsion characterization via atomic force microscopy. Crit. Rev. Food Sci. Nutr. 2022, 62, 4908–4928. [Google Scholar] [CrossRef]
- Morris, V.J. Probing molecular interactions in foods. Trends Food Sci. Technol. 2004, 15, 291–297. [Google Scholar] [CrossRef]
- Li, G.; Xu, X.; Zuo, Y.Y. Langmuir-Blodgett transfer from the oil-water interface. J. Colloid Interface Sci. 2023, 630, 21–27. [Google Scholar] [CrossRef]
- Jin, H.; Lu, Q.; Chen, X.; Ding, H.; Gao, H.; Jin, S. The use of Raman spectroscopy in food processes: A review. Appl. Spectrosc. Rev. 2016, 51, 12–22. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Zheng, H.; Yuan, D.; Mao, L. Physical properties and salt release of potato starch-based emulsion gels with OSA starch-stabilized oil droplets. LWT 2021, 141, 110929. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Q.; Shang, J.; Mao, Z.S.; Yang, C. Measurement methods of particle size distribution in emulsion polymerization. Chin. J. Chem. Eng. 2021, 39, 1–5. [Google Scholar] [CrossRef]
- Carvalho, P.M.; Felício, M.R.; Santos, N.C.; Gonçalves, S.; Domingues, M.M. Application of light scattering techniques to nanoparticle characterization and development. Front. Chem. 2018, 6, 386753. [Google Scholar] [CrossRef]
- Fischer, K.; Schmidt, M. Pitfalls and novel applications of particle sizing by dynamic light scattering. Biomaterials 2016, 98, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, S. DLS and zeta potential—What they are and what they are not? J. Control. Release 2016, 235, 337–351. [Google Scholar] [CrossRef] [PubMed]
- Anderson, W.; Kozak, D.; Coleman, V.A.; Jämting, Å.K.; Trau, M. A comparative study of submicron particle sizing platforms: Accuracy, precision and resolution analysis of polydisperse particle size distributions. J. Colloid Interface Sci. 2013, 405, 322–330. [Google Scholar] [CrossRef] [PubMed]
- Klein, M.; Menta, M.; Dacoba, T.G.; Crecente-Campo, J.; Alonso, M.J.; Dupin, D.; Loinaz, I.; Grassl, B.; Séby, F. Advanced nanomedicine characterization by DLS and AF4-UV-MALS: Application to a HIV nanovaccine. J. Pharm. Biomed. Anal. 2020, 179, 113017. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.; Smith, M.C.; Crist, R.M.; Clogston, J.D.; McNeil, S.E. Analyzing the influence of PEG molecular weight on the separation of PEGylated gold nanoparticles by asymmetric-flow field-flow fractionation. Anal. Bioanal. Chem. 2015, 407, 8661–8672. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Li, G.; Zhang, B. Opposite results of emulsion stability evaluated by the TSI and the phase separation proportion. Colloids Surf. A Physicochem. Eng. Asp. 2018, 558, 402–409. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, B.K.; Lee, M.H. Effect of small molecular surfactants on physical, turbidimetric, and rheological properties of Pickering nanoemulsions stabilized with whey protein isolate. Food Biosci. 2023, 51, 102214. [Google Scholar] [CrossRef]
- Perrin, L.; Desobry-Banon, S.; Gillet, G.; Desobry, S. Study and optimization of oil-in-water emulsions formulated by low- and high-frequency ultrasounds. Int. J. Cosmet. Sci. 2023, 45, 198–213. [Google Scholar] [CrossRef]
- Mengual, O.; Meunier, G.; Cayré, I.; Puech, K.; Snabre, P. TURBISCAN MA 2000: Multiple light scattering measurement for concentrated emulsion and suspension instability analysis. Talanta 1999, 50, 445–456. [Google Scholar] [CrossRef]
- Preetz, C.; Hauser, A.; Hause, G.; Kramer, A.; Mäder, K. Application of atomic force microscopy and ultrasonic resonator technology on nanoscale: Distinction of nanoemulsions from nanocapsules. Eur. J. Pharm. Sci. 2010, 39, 141–151. [Google Scholar] [CrossRef]
- Benita, S.; Levy, M.Y. Submicron Emulsions as Colloidal Drug Carriers for Intravenous Administration: Comprehensive Physicochemical Characterization. J. Pharm. Sci. 1993, 82, 1069–1079. [Google Scholar] [CrossRef]
- Nordén, T.P.; Siekmann, B.; Lundquist, S.; Malmsten, M. Physicochemical characterisation of a drug-containing phospholipid-stabilised o/w emulsion for intravenous administration. Eur. J. Pharm. Sci. 2001, 13, 393–401. [Google Scholar] [CrossRef]
- Whittinghill, J.M.; Norton, J.; Proctor, A. A fourier transform infrared spectroscopy study of the effect of temperature on soy lecithin-stabilized emulsions. J. Am. Oil Chem. Soc. 1999, 76, 1393–1398. [Google Scholar] [CrossRef]
- Chantrapornchai, W.; Clydesdale, F.; McClements, D.J. Influence of Droplet Size and Concentration on the Color of Oil-in-Water Emulsions. J. Agric. Food Chem. 1998, 46, 2914–2920. [Google Scholar] [CrossRef]
- Silva, C.A.; Saraiva, S.V.; Bonetti, D.; Higuti, R.T.; Cunha, R.L.; Pereira, L.O.; Silva, F.V.; Fileti, A.M. Measurements of bimodal droplet size distribution of emulsions using ultrasonic spectroscopy in the long and intermediate wavelength regimes. Chem. Eng. Sci. 2022, 252, 117274. [Google Scholar] [CrossRef]
- Baboota, S.; Shakeel, F.; Ahuja, A.; Ali, J.; Shafiq, S. Design, development and evaluation of novel nanoemulsion formulations for transdermal potential of celecoxib. Acta Pharm. 2007, 57, 315–332. [Google Scholar] [CrossRef]
- Mirhosseini, H.; Tan, C.P. Discrimination of orange beverage emulsions with different formulations using multivariate analysis. J. Sci. Food Agric. 2010, 90, 1308–1316. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wei, Z.-C.; Deng, Y.-Y.; Dong, H.; Zhang, Y.; Tang, X.-J.; Li, P.; Liu, G.; Zhang, M.-W. Comparison of the Effects of Different Food-Grade Emulsifiers on the Properties and Stability of a Casein-Maltodextrin-Soybean Oil Compound Emulsion. Molecules 2020, 25, 458. [Google Scholar] [CrossRef] [PubMed]
- Velandia, S.F.; Marchal, P.; Lemaitre, C.; Sadtler, V.; Roques-Carmes, T. Evaluation of the repartition of the particles in Pickering emulsions in relation with their rheological properties. J. Colloid Interface Sci. 2021, 589, 286–297. [Google Scholar] [CrossRef]
- Li, G.; Zhao, Y.; Zhang, J.; Hao, J.; Xu, D.; Cao, Y. CaCO3 loaded lipid microspheres prepared by the solid-in-oil-in-water emulsions technique with propylene glycol alginate and xanthan gum. Front. Nutr. 2022, 9, 961326. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, H.; Liu, W.; Zou, L.; McClements, D.J. A review of the rheological properties of dilute and concentrated food emulsions. J. Texture Stud. 2020, 51, 45–55. [Google Scholar] [CrossRef]
- Barnes, H.A. Rheology of emulsions—A review. Colloids Surf. A Physicochem. Eng. Asp. 1994, 91, 89–95. [Google Scholar] [CrossRef]
- Kasprzak, M.M.; Berski, W.; Krystyjan, M.; Jamróz, E.; Florczuk, A.; Tkaczewska, J.; Zając, M.; Domagała, J.; Lett, A.M.; Ptasznik, S. Effects of fibre addition and processing on the stability, rheology and in vitro gastric digestion of whey protein-xanthan gum stabilised emulsions with high oil phase. LWT 2023, 178, 114465. [Google Scholar] [CrossRef]
- Ozturk, B.; McClements, D.J. Progress in natural emulsifiers for utilization in food emulsions. Curr. Opin. Food Sci. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Evans, M.; Ratcliffe, I.; Williams, P.A. Emulsion stabilisation using polysaccharide–protein complexes. Curr. Opin. Colloid Interface Sci. 2013, 18, 272–282. [Google Scholar] [CrossRef]
- Dickinson, E. Hydrocolloids as emulsifiers and emulsion stabilizers. Food Hydrocoll. 2009, 23, 1473–1482. [Google Scholar] [CrossRef]
- Geremias-Andrade, I.M.; Souki, N.P.D.B.G.; Moraes, I.C.F.; Pinho, S.C. Rheological and mechanical characterization of curcumin-loaded emulsion-filled gels produced with whey protein isolate and xanthan gum. LWT 2017, 86, 166–173. [Google Scholar] [CrossRef]
- Howarth, R.W. A bridge to nowhere: Methane emissions and the greenhouse gas footprint of natural gas. Energy Sci. Eng. 2014, 2, 47–60. [Google Scholar] [CrossRef]
- Samavati, V.; Emam-Djomeh, Z.; Mohammadifar, M.A.; Omid, M.; Mehdinia, A.L.I. Stability and Rheology of Dispersions Containing Polysaccharide, Oleic Acid and Whey Protein Isolate. J. Texture Stud. 2012, 43, 63–76. [Google Scholar] [CrossRef]
- Sivapratha, S.; Sarkar, P. Multiple layers and conjugate materials for food emulsion stabilization. Crit. Rev. Food Sci. Nutr. 2018, 58, 877–892. [Google Scholar] [CrossRef]
- Yang, S.; Qin, W.; Zhao, X.; He, F.; Gong, H.; Liu, Y.; Feng, Y.; Zhou, Y.; Yu, G.; Li, J. Interfacial self-assembled behavior of pH/light-responsive host-guest alginate-based supra-amphiphiles for controlling emulsifying property. Carbohydr. Polym. 2021, 266, 118121. [Google Scholar] [CrossRef]
- Liao, W.; Gharsallaoui, A.; Dumas, E.; Elaissari, A. Understanding of the key factors influencing the properties of emulsions stabilized by sodium caseinate. Compr. Rev. Food Sci. Food Saf. 2022, 21, 5291–5317. [Google Scholar] [CrossRef] [PubMed]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Yin, H.; Pu, J.; Wan, Y.; Xiang, B.; Bechtel, P.J.; Sathivel, S. Rheological and Functional Properties of Catfish Skin Protein Hydrolysates. J. Food Sci. 2010, 75, E11–E17. [Google Scholar] [CrossRef]
- Hesarinejad, M.A.; Koocheki, A.; Razavi, S.M.A. Dynamic rheological properties of Lepidium perfoliatum seed gum: Effect of concentration, temperature and heating/cooling rate. Food Hydrocoll. 2014, 35, 583–589. [Google Scholar] [CrossRef]
- Karatay, G.G.B.; Galvão, A.M.M.T.; Hubinger, M.D. Storage Stability of Conventional and High Internal Phase Emulsions Stabilized Solely by Chickpea Aquafaba. Foods 2022, 11, 1588. [Google Scholar] [CrossRef]
- Sridharan, S.; Meinders, M.B.J.; Sagis, L.M.C.; Bitter, J.H.; Nikiforidis, C.V. Starch controls brittleness in emulsion-gels stabilized by pea flour. Food Hydrocoll. 2022, 131, 107708. [Google Scholar] [CrossRef]
- Domian, E.; Mańko-Jurkowska, D. The effect of homogenization and heat treatment on gelation of whey proteins in emulsions. J. Food Eng. 2022, 319, 110915. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R. Boundary Layers and Related Topics. Fluid. Mech. 2016, 469–532. [Google Scholar] [CrossRef]
- Castilla, R.; Peña, M. Jupyter Notebooks for the study of advanced topics in Fluid Mechanics. Comput. Appl. Eng. Educ. 2023, 31, 1001–1013. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Masalova, I. Shear and normal stresses in flow of highly concentrated emulsions. J. Nonnewton Fluid. Mech. 2007, 147, 65–68. [Google Scholar] [CrossRef]
- Avranas, A.; Stalidis, G.; Ritzoulis, G. Demulsification rate and zeta potential of O/W emulsions. Colloid Polym. Sci. 1988, 266, 937–940. [Google Scholar] [CrossRef]
- Gurpret, K.; Singh, S.K. Review of Nanoemulsion Formulation and Characterization Techniques. Indian J. Pharm. Sci. 2018, 80, 781–789. [Google Scholar] [CrossRef]
- Pinto, I.; Buss, A. ζ Potential as a Measure of Asphalt Emulsion Stability. Energy Fuels 2020, 34, 2143–2151. [Google Scholar] [CrossRef]
- Yilmaz, E.; Borchert, H.H. Design of a phytosphingosine-containing, positively-charged nanoemulsion as a colloidal carrier system for dermal application of ceramides. Eur. J. Pharm. Biopharm. 2005, 60, 91–98. [Google Scholar] [CrossRef] [PubMed]
- Đorđević, S.M.; Cekić, N.D.; Savić, M.M.; Isailović, T.M.; Ranđelović, D.V.; Marković, B.D.; Savić, S.R.; Stamenić, T.T.; Daniels, R.; Savić, S.D. Parenteral nanoemulsions as promising carriers for brain delivery of risperidone: Design, characterization and in vivo pharmacokinetic evaluation. Int. J. Pharm. 2015, 493, 40–54. [Google Scholar] [CrossRef] [PubMed]
- Schmelz, T.; Lesmes, U.; Weiss, J.; McClements, D.J. Modulation of physicochemical properties of lipid droplets using β-lactoglobulin and/or lactoferrin interfacial coatings. Food Hydrocoll. 2011, 25, 1181–1189. [Google Scholar] [CrossRef]
- Madivoli, E.S.; Kareru, P.G.; Gachanja, A.N.; Mugo, S.M.; Makhanu, D.S. Phytofabrication of iron nanoparticles and their catalytic activity. SN Appl. Sci. 2019, 1, 879. [Google Scholar] [CrossRef]
- Moreira, J.B.; Goularte, P.G.; de Morais, M.G.; Costa, J.A.V. Preparation of beta-carotene nanoemulsion and evaluation of stability at a long storage period. Food Sci. Technol. 2019, 39, 599–604. [Google Scholar] [CrossRef]
- Dickinson, E. Structure formation in casein-based gels, foams, and emulsions. Colloids Surf. A Physicochem. Eng. Asp. 2006, 288, 3–11. [Google Scholar] [CrossRef]
- Li, D.; Zhao, Y.; Wang, X.; Tang, H.; Wu, N.; Wu, F.; Yu, D.; Elfalleh, W. Effects of (+)-catechin on a rice bran protein oil-in-water emulsion: Droplet size, zeta-potential, emulsifying properties, and rheological behavior. Food Hydrocoll. 2020, 98, 105306. [Google Scholar] [CrossRef]
- Kulmyrzaev, A.A.; Schubert, H. Influence of KCl on the physicochemical properties of whey protein stabilized emulsions. Food Hydrocoll. 2004, 18, 13–19. [Google Scholar] [CrossRef]
- Zhang, Z.; Dalgleish, D.G.; Goff, H.D. Effect of pH and ionic strength on competitive protein adsorption to air/water interfaces in aqueous foams made with mixed milk proteins. Colloids Surf. B Biointerfaces 2004, 34, 113–121. [Google Scholar] [CrossRef] [PubMed]
- McLean, J.D.; Kilpatrick, P.K. Effects of Asphaltene Aggregation in Model Heptane–Toluene Mixtures on Stability of Water-in-Oil Emulsions. J. Colloid Interface Sci. 1997, 196, 23–34. [Google Scholar] [CrossRef]
- McClements, D.J.; Lu, J.; Grossmann, L. Proposed Methods for Testing and Comparing the Emulsifying Properties of Proteins from Animal, Plant, and Alternative Sources. Colloids Interfaces 2022, 6, 19. [Google Scholar] [CrossRef]
- Anema, S.G.; Lowe, E.K.; Li, Y. Effect of pH on the viscosity of heated reconstituted skim milk. Int. Dairy J. 2004, 14, 541–548. [Google Scholar] [CrossRef]
- Siau, C.L.; Karim, A.A.; Norziah, M.H.; Wan Rosli, W.D. Effects of cationization on DSC thermal profiles, pasting and emulsifying properties of sago starch. J. Sci. Food Agric. 2004, 84, 1722–1730. [Google Scholar] [CrossRef]
- Eicke, H.F.; Borkovec, M.; Das-Gupta, B. Conductivity of water-in-oil microemulsions: A quantitative charge fluctuation model. J. Phys. Chem. 1989, 93, 314–317. [Google Scholar] [CrossRef]
- Briggs, N.; Raman, A.K.Y.; Barrett, L.; Brown, C.; Li, B.; Leavitt, D.; Aichele, C.P.; Crossley, S. Stable pickering emulsions using multi-walled carbon nanotubes of varying wettability. Colloids Surf. A Physicochem. Eng. Asp. 2018, 537, 227–235. [Google Scholar] [CrossRef]
- Kawanami, T.; Togashi, K.; Fumoto, K.; Hirano, S.; Zhang, P.; Shirai, K.; Hirasawa, S. Thermophysical properties and thermal characteristics of phase change emulsion for thermal energy storage media. Energy 2016, 117, 562–568. [Google Scholar] [CrossRef]
- Chiesa, M.; Garg, J.; Kang, Y.T.; Chen, G. Thermal conductivity and viscosity of water-in-oil nanoemulsions. Colloids Surf. A Physicochem. Eng. Asp. 2008, 326, 67–72. [Google Scholar] [CrossRef]
- Wilson, O.M.; Hu, X.; Cahill, D.G.; Braun, P.V. Colloidal metal particles as probes of nanoscale thermal transport in fluids. Phys. Rev. B 2002, 66, 224301. [Google Scholar] [CrossRef]
- D’alessandro, G.; Potenza, M.; Corasaniti, S.; Sfarra, S.; Coppa, P.; Bovesecchi, G.; de Monte, F. Modeling and Measuring Thermodynamic and Transport Thermophysical Properties: A Review. Energies 2022, 15, 8807. [Google Scholar] [CrossRef]
- Zhang, W.P.; Li, L.Y.; Jia, B.; Ou, W.H.; Song, L.L.; Zhang, Q.J. Preparation and characteristics of multiple emulsions containing liquid crystals. Liq. Cryst. 2018, 45, 1186–1195. [Google Scholar] [CrossRef]
- Gill, P.; Moghadam, T.T.; Ranjbar, B. Differential Scanning Calorimetry Techniques: Applications in Biology and Nanoscience. J. Biomol. Tech. 2010, 21, 167. [Google Scholar]
- Garti, N.; Aserin, A.; Tiunova, I.; Fanun, M. A DSC study of water behavior in water-in-oil microemulsions stabilized by sucrose esters and butanol. Colloids Surf. A Physicochem. Eng. Asp. 2000, 170, 1–18. [Google Scholar] [CrossRef]
- Niizawa, I.; Sihufe, G.A.; Zorrilla, S.E. Design of whey protein aggregates towards microgel-stabilized emulsion generation. LWT 2021, 152, 112324. [Google Scholar] [CrossRef]
- Abdolmaleki, K.; Alizadeh, L.; Hosseini, S.M.; Nayebzadeh, K. Concentrated O/W emulsions formulated by binary and ternary mixtures of sodium caseinate, xanthan and guar gums: Rheological properties, microstructure, and stability. Food Sci. Biotechnol. 2020, 29, 1685–1693. [Google Scholar] [CrossRef]
- Kasprzak, M.; Jamróz, E.; Nowak, N.; Grzebieniarz, W.; Tkaczewska, J. Design of triple-layer films with blackseed protein as dispersion or emulsion. Food Chem. 2024, 435, 137533. [Google Scholar] [CrossRef]
- Zografi, G. Physical stability assessment of emulsions and related disperse systems: A critical review. J. Soc. Cosmet. Chem. 1982, 33, 345–358. [Google Scholar]
- Estanqueiro, M.; Conceição, J.; Amaral, M.H.; Santos, D.; Silva, J.B.; Lobo, J.M.S. Characterization and stability studies of emulsion systems containing pumice. Braz. J. Pharm. Sci. 2014, 50, 361–369. [Google Scholar] [CrossRef]
- Cannell, J.S. Fundamentals of stability testing. Int. J. Cosmet. Sci. 1985, 7, 291–303. [Google Scholar] [CrossRef]
- Navarro-Pérez, Y.M.; Cedeño-Linares, E.; Norman-Montenegro, O.; Ruz-Sanjuan, V.; Mondeja-Rivera, Y.; Hernández-Monzón, A.M.; González-Bedia, M.M. Prediction of the physical stability and quality of O/W cosmetic emulsions using full factorial design [Predicción de la estabilidad física y calidad de emulsiones cosméticas O/W mediante diseño factorial completo]. J. Pharm. Pharmacogn. Res. 2021, 9, 98–112. [Google Scholar] [CrossRef]
- Dinache, A.; Tozar, T.; Smarandache, A.; Andrei, I.R.; Nistorescu, S.; Nastasa, V.; Staicu, A.; Pascu, M.L.; Romanitan, M.O. Spectroscopic Characterization of Emulsions Generated with a New Laser-Assisted Device. Molecules 2020, 25, 1729. [Google Scholar] [CrossRef]
- Schestkowa, H.; Drusch, S.; Wagemans, A.M. FTIR analysis of β-lactoglobulin at the oil/water-interface. Food Chem. 2020, 302, 125349. [Google Scholar] [CrossRef]
- Hayati, I.N.; Man, Y.B.C.; Tan, C.P.; Aini, I.N. Monitoring peroxide value in oxidized emulsions by Fourier transform infrared spectroscopy. Eur. J. Lipid Sci. Technol. 2005, 107, 886–895. [Google Scholar] [CrossRef]
- Jorgensen, L.; Van De Weert, M.; Vermehren, C.; Bjerregaard, S.; Frokjaer, S. Probing structural changes of proteins incorporated into water-in-oil emulsions. J. Pharm. Sci. 2004, 93, 1847–1859. [Google Scholar] [CrossRef]
- Zhou, G.W.; Li, G.Z.; Chen, W.J. Fourier Transform Infrared Investigation on Water States and the Conformations of Aerosol-OT in Reverse Microemulsions. Langmuir 2002, 18, 4566–4571. [Google Scholar] [CrossRef]
- Sechler, T.D.; DelSole, E.M.; Deák, J.C. Measuring properties of interfacial and bulk water regions in a reverse micelle with IR spectroscopy: A volumetric analysis of the inhomogeneously broadened OH band. J. Colloid Interface Sci. 2010, 346, 391–397. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, J.; Frank, K.; Schuchmann, H.P. Attenuated total reflection infrared (ATR-IR) spectroscopy of a water-in-oil emulsion. Appl. Spectrosc. 2011, 65, 1024–1028. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, J.; Frank, K.; Zehentbauer, F.M.; Schuchmann, H.P. Infrared Spectroscopy of Bilberry Extract Water-in-Oil Emulsions: Sensing the Water-Oil Interface. Biosensors 2016, 6, 13. [Google Scholar] [CrossRef] [PubMed]
- Daoud, S.; Bou-maroun, E.; Dujourdy, L.; Waschatko, G.; Billecke, N.; Cayot, P. Fast and direct analysis of oxidation levels of oil-in-water emulsions using ATR-FTIR. Food Chem. 2019, 293, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Ying, Y. Applications of Raman Spectroscopy in Agricultural Products and Food Analysis: A Review. Appl. Spectrosc. Rev. 2011, 46, 539–560. [Google Scholar] [CrossRef]
- Huang, W.E.; Li, M.; Jarvis, R.M.; Goodacre, R.; Banwart, S.A. Shining light on the microbial world the application of Raman microspectroscopy. Adv. Appl. Microbiol. 2010, 70, 153–186. [Google Scholar] [CrossRef]
- Jin, H.; Ma, Q.; Dou, T.; Jin, S.; Jiang, L. Raman Spectroscopy of Emulsions and Emulsion Chemistry. Crit. Rev. Anal. Chem. 2023. [Google Scholar] [CrossRef]
- Wei, Z.; Cheng, J.; Huang, Q. Food-grade Pickering emulsions stabilized by ovotransferrin fibrils. Food Hydrocoll. 2019, 94, 592–602. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Y.; Jamali, M.A.; Peng, Z. Manipulating interfacial behaviour and emulsifying properties of myofibrillar proteins by L-Arginine at low and high salt concentration. Int. J. Food Sci. Technol. 2021, 56, 999–1012. [Google Scholar] [CrossRef]
- Wu, L.; Wang, L.; Qi, B.; Zhang, X.; Chen, F.; Li, Y.; Sui, X.; Jiang, L. 3D confocal Raman imaging of oil-rich emulsion from enzyme-assisted aqueous extraction of extruded soybean powder. Food Chem. 2018, 249, 16–21. [Google Scholar] [CrossRef]
- Elizalde, O.; Azpeitia, M.; Reis, M.M.; Asua, J.M.; Leiza, J.R. Monitoring Emulsion Polymerization Reactors: Calorimetry Versus Raman Spectroscopy. Ind. Eng. Chem. Res. 2005, 44, 7200–7207. [Google Scholar] [CrossRef]
- Dropsit, E.; Hoppe, S.; Chapron, D.; Durand, A.; Bourson, P. In situ conversion monitoring of styrene emulsion polymerization by deconvolution of a single reference band near 1000 cm−1. J. Raman Spectrosc. 2019, 50, 1938–1948. [Google Scholar] [CrossRef]
- Schlappa, S.; Bressel, L.; Reich, O.; Münzberg, M. Advanced Particle Size Analysis in High-Solid-Content Polymer Dispersions Using Photon Density Wave Spectroscopy. Polymers 2023, 15, 3181. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, S.; Reich, O.; Bressel, L. Exploitation of inline photon density wave spectroscopy for titania particle syntheses. J. Am. Ceram. Soc. 2023, 106, 671–680. [Google Scholar] [CrossRef]
- Sandmann, M.; Münzberg, M.; Bressel, L.; Reich, O.; Hass, R. Inline monitoring of high cell density cultivation of Scenedesmus rubescens in a mesh ultra-thin layer photobioreactor by photon density wave spectroscopy. BMC Res. Notes 2022, 15, 54. [Google Scholar] [CrossRef]
- Hass, R.; Mnzberg, M.; Bressel, L.; Reich, O. Industrial applications of Photon Density Wave spectroscopy for in-line particle sizing [Invited]. Appl. Opt. 2013, 52, 1423–1431. [Google Scholar] [CrossRef]
- Bressel, L.; Münzberg, M.; Hass, R.; Reich, O. Fiber-optical particle sizing by photon density wave spectroscopy. 23rd Int. Conf. Opt. Fibre Sens. 2014, 915756, 733–736. [Google Scholar] [CrossRef]
- Bressel, K.; Müller, W.; Leser, M.E.; Reich, O.; Hass, R.; Wooster, T.J. Depletion-Induced Flocculation of Concentrated Emulsions Probed by Photon Density Wave Spectroscopy. Langmuir 2020, 36, 3504–3513. [Google Scholar] [CrossRef] [PubMed]
- Kazemeini, S.M.; Campos, D.P.; Rosenthal, A.J. Muscle activity during oral processing of sticky-cohesive foods. Physiol. Behav. 2021, 242, 113580. [Google Scholar] [CrossRef]
- Rosenthal, A.J.; Thompson, P. What is cohesiveness?—A linguistic exploration of the food texture testing literature. J. Texture Stud. 2021, 52, 294–302. [Google Scholar] [CrossRef]
- Rosenthal, A.J. Instrumental characterisation of textural properties of solid and semi-solid food. In Modifying Food Texture: Volume 2: Sensory Analysis, Consumer Requirements and Preferences; Woodhead Publishing: Sawston, UK, 2015; pp. 89–105. [Google Scholar] [CrossRef]
- McMullen, R.L.; Gorcea, M.; Chen, S. Emulsions and their Characterization by Texture Profile Analysis. In Handbook of Formulating Dermal Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA; Scrivener Publishing LLC: Beverly, MA, USA, 2016; pp. 129–153. [Google Scholar] [CrossRef]
- Yang, X.; Gong, T.; Li, D.; Li, A.; Sun, L.; Guo, Y. Preparation of high viscoelastic emulsion gels based on the synergistic gelation mechanism of xanthan and konjac glucomannan. Carbohydr. Polym. 2019, 226, 115278. [Google Scholar] [CrossRef] [PubMed]
- Ingrassia, R.; Busti, P.A.; Boeris, V. Physicochemical and mechanical properties of a new cold-set emulsion gel system and the effect of quinoa protein fortification. LWT 2022, 156, 113048. [Google Scholar] [CrossRef]
- Ahn, N.; Park, J.H.; Chai, C.; Imm, J.Y. The interaction of milk sphingomyelin and proteins on stability and microstructure of dairy emulsions. J. Dairy Sci. 2022, 105, 3832–3845. [Google Scholar] [CrossRef] [PubMed]
- Tkaczewska, J.; Jamróz, E.; Guzik, P.; Kopeć, M. Attempt to Extend the Shelf-Life of Fish Products by Means of Innovative Double-Layer Active Biodegradable Films. Polymers 2022, 14, 1717. [Google Scholar] [CrossRef] [PubMed]
- Riesz, P.; Kondo, T. Free radical formation induced by ultrasound and its biological implications. Free Radic. Biol. Med. 1992, 13, 247–270. [Google Scholar] [CrossRef]
- Fereidoon, S.; Ying, Z. Lipid oxidation and improving the oxidative stability. Chem. Soc. Rev. 2010, 39, 4067–4079. [Google Scholar] [CrossRef]
- Ghelichi, S.; Hajfathalian, M.; Yesiltas, B.; Sørensen, A.-D.M.; García-Moreno, P.J.; Jacobsen, C. Oxidation and oxidative stability in emulsions. Compr. Rev. Food Sci. Food Saf. 2023, 22, 1864–1901. [Google Scholar] [CrossRef] [PubMed]
- Laguerre, M.; Bily, A.; Roller, M.; Birti’c, S.B. Mass Transport Phenomena in Lipid Oxidation and Antioxidation. Annu. Rev. Food Sci. Technol. 2017, 8, 391–411. [Google Scholar] [CrossRef]
- Nielsen, N.S.; Timm-Heinrich, M.; Jacobsen, C. Comparison of Wet-Chemical Methods for Determination of Lipid Hydroperoxides. J. Food Lipids 2003, 10, 35–50. [Google Scholar] [CrossRef]
- Guillén-Sans, R.; Guzmán-Chozas, M. The thiobarbituric acid (TBA) reaction in foods: A review. Crit. Rev. Food Sci. Nutr. 1998, 38, 315–350. [Google Scholar] [CrossRef]
- Thomsen, B.R.; Yesiltas, B.; Sørensen, A.D.M.; Hermund, D.B.; Glastrup, J.; Jacobsen, C. Comparison of Three Methods for Extraction of Volatile Lipid Oxidation Products from Food Matrices for GC–MS Analysis. JAOCS J. Am. Oil Chem. Soc. 2016, 93, 929–942. [Google Scholar] [CrossRef]
- Merkx, D.W.H.; Hong, G.T.S.; Ermacora, A.; Van Duynhoven, J.P.M. Rapid Quantitative Profiling of Lipid Oxidation Products in a Food Emulsion by 1H NMR. Anal. Chem. 2018, 90, 4863–4870. [Google Scholar] [CrossRef] [PubMed]
- Beysseriat, M.; Decker, E.A.; McClements, D.J. Preliminary study of the influence of dietary fiber on the properties of oil-in-water emulsions passing through an in vitro human digestion model. Food Hydrocoll. 2006, 20, 800–809. [Google Scholar] [CrossRef]
- McClements, D.J.; Li, Y. Review of in vitro digestion models for rapid screening of emulsion-based systems. Food Funct. 2010, 1, 32–59. [Google Scholar] [CrossRef]
- Scheuble, N.; Schaffner, J.; Schumacher, M.; Windhab, E.J.; Liu, D.; Parker, H.; Steingoetter, A.; Fischer, P. Tailoring Emulsions for Controlled Lipid Release: Establishing in vitro-in Vivo Correlation for Digestion of Lipids. ACS Appl. Mater. Interfaces 2018, 10, 17571–17581. [Google Scholar] [CrossRef]
- Bai, L.; Lv, S.; Xiang, W.; Huan, S.; McClements, D.J.; Rojas, O.J. Oil-in-water Pickering emulsions via microfluidization with cellulose nanocrystals: 2. In vitro lipid digestion. Food Hydrocoll. 2019, 96, 709–716. [Google Scholar] [CrossRef]
- Mat, D.J.L.; Souchon, I.; Michon, C.; Le Feunteun, S. Gastro-intestinal in vitro digestions of protein emulsions monitored by pH-stat: Influence of structural properties and interplay between proteolysis and lipolysis. Food Chem. 2020, 311, 125946. [Google Scholar] [CrossRef]
- Grundy, M.M.; Abrahamse, E.; Almgren, A.; Alminger, M.; Andres, A.; Ariëns, R.M.; Bastiaan-Net, S.; Bourlieu-Lacanal, C.; Brodkorb, A.; Bronze, M.R.; et al. INFOGEST inter-laboratory recommendations for assaying gastric and pancreatic lipases activities prior to in vitro digestion studies. J. Funct. Foods 2021, 82, 104497. [Google Scholar] [CrossRef]
- Mulet-Cabero, A.-I.; Egger, L.; Portmann, R.; Ménard, O.; Marze, S.; Minekus, M.; Le Feunteun, S.; Sarkar, A.; Grundy, M.M.-L.; Carrière, F.; et al. A standardised semi-dynamic in vitro digestion method suitable for food—An international consensus. Food Funct. 2020, 11, 1702–1720. [Google Scholar] [CrossRef] [PubMed]
- Armand, M.; Pasquier, B.; André, M.; Borel, P.; Senft, M.; Peyrot, J.; Salducci, J.; Portugal, H.; Jaussan, V.; Lairon, D. Digestion and absorption of 2 fat emulsions with different droplet sizes in the human digestive tract. Am. J. Clin. Nutr. 1999, 70, 1096–1106. [Google Scholar] [CrossRef]
- Guo, Q.; Bellissimo, N.; Rousseau, D. Role of gel structure in controlling in vitro intestinal lipid digestion in whey protein emulsion gels. Food Hydrocoll. 2017, 69, 264–272. [Google Scholar] [CrossRef]
- Ye, A.; Wang, X.; Lin, Q.; Han, J.; Singh, H. Dynamic gastric stability and in vitro lipid digestion of whey-protein-stabilised emulsions: Effect of heat treatment. Food Chem. 2020, 318, 126463. [Google Scholar] [CrossRef]
- Kenta, S.; Raikos, V.; Kapolos, J.; Koliadima, A.; Karaiskakis, G. Sedimentation Field-Flow Fractionation as a Tool for the Study of Milk Protein-Stabilized Model Oil-in-Water Emulsions: Effect of Protein Concentration and Homogenization Pressure. J. Liq. Chromatogr. Relat. Technol. 2013, 36, 288–303. [Google Scholar] [CrossRef]
- Qu, H.; Wang, J.; Wu, Y.; Zheng, J.; Krishnaiah, Y.S.; Absar, M.; Choi, S.; Ashraf, M.; Cruz, C.N.; Xu, X. Asymmetric flow field flow fractionation for the characterization of globule size distribution in complex formulations: A cyclosporine ophthalmic emulsion case. Int. J. Pharm. 2018, 538, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, K.D.; Li, J. Emulsion characterization by the combined sedimentation field—Flow fractionation—Photon correlation spectroscopy methods. J. Colloid Interface Sci. 1989, 132, 256–268. [Google Scholar] [CrossRef]
- Miller, C.M.; Venkatesan, J.; Silebi, C.A.; Sudol, E.D.; El-Aasser, M.S. Characterization of Miniemulsion Droplet Size and Stability Using Capillary Hydrodynamic Fractionation. J. Colloid Interface Sci. 1994, 162, 11–18. [Google Scholar] [CrossRef]
- Giordani, S.; Marassi, V.; Placci, A.; Zattoni, A.; Roda, B.; Reschiglian, P. Field-Flow Fractionation in Molecular Biology and Biotechnology. Molecules 2023, 28, 6201. [Google Scholar] [CrossRef]
- Venkatesh, S.; Li, J.; Caldwell, K.D.; Anderson, B.D. Compositional heterogeneity in parenteral lipid emulsions after sedimentation field flow fractionation. J. Pharm. Sci. 1998, 87, 859–866. [Google Scholar] [CrossRef]
- Chmelik, J. Applications of field-flow fractionation in proteomics: Presence and future. Proteomics 2007, 7, 2719–2728. [Google Scholar] [CrossRef]
- Yohannes, G.; Jussila, M.; Hartonen, K.; Riekkola, M.L. Asymmetrical flow field-flow fractionation technique for separation and characterization of biopolymers and bioparticles. J. Chromatogr. A 2011, 1218, 4104–4116. [Google Scholar] [CrossRef] [PubMed]
- Reschiglian, P.; Zattoni, A.; Roda, B.; Michelini, E.; Roda, A. Field-flow fractionation and biotechnology. Trends Biotechnol. 2005, 23, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Janča, J.; Sobota, J. Trends in Polymer and Particle Characterization by Microfluidic Field-Flow Fractionation Methods: Science or Business? Int. J. Polym. Anal. Charact. 2014, 19, 296–308. [Google Scholar] [CrossRef]
- Saenmuangchin, R.; Techarang, T.; Mekprayoon, S.; Zulfah, N.L.; Siripinyanond, A. Field-flow fractionation. In Sample Introduction Systems in ICPMS and ICPOES; Elsevier: Amsterdam, The Netherlands, 2020; pp. 357–380. [Google Scholar] [CrossRef]
- Wahlund, K.G. Flow field-flow fractionation: Critical overview. J. Chromatogr. A 2013, 1287, 97–112. [Google Scholar] [CrossRef]
- Zattoni, A.; Roda, B.; Borghi, F.; Marassi, V.; Reschiglian, P. Flow field-flow fractionation for the analysis of nanoparticles used in drug delivery. J. Pharm. Biomed. Anal. 2014, 87, 53–61. [Google Scholar] [CrossRef]
- Shin, S.Y.; Seo, J.W.; Kim, J.Y.; Williams, P.S.; Moon, M.H. Flow Field-Flow Fractionation with a Thickness-Tapered Channel. Anal. Chem. 2022, 94, 14460–14466. [Google Scholar] [CrossRef] [PubMed]
- Marassi, V.; Roda, B.; Casolari, S.; Ortelli, S.; Blosi, M.; Zattoni, A.; Costa, A.L.; Reschiglian, P. Hollow-fiber flow field-flow fractionation and multi-angle light scattering as a new analytical solution for quality control in pharmaceutical nanotechnology. Microchem. J. 2018, 136, 149–156. [Google Scholar] [CrossRef]
- Rambaldi, D.C.; Zattoni, A.; Casolari, S.; Reschiglian, P.; Roessner, D.; Johann, C. An Analytical Method for Size and Shape Characterization of Blood Lipoproteins. Clin. Chem. 2007, 53, 2026–2029. [Google Scholar] [CrossRef][Green Version]
- Marassi, V.; Beretti, F.; Roda, B.; Alessandrini, A.; Facci, P.; Maraldi, T.; Zattoni, A.; Reschiglian, P.; Portolani, M. A new approach for the separation, characterization and testing of potential prionoid protein aggregates through hollow-fiber flow field-flow fractionation and multi-angle light scattering. Anal. Chim. Acta 2019, 1087, 121–130. [Google Scholar] [CrossRef]
- Lee, J.Y.; Byeon, S.K.; Moon, M.H. Profiling of oxidized phospholipids in lipoproteins from patients with coronary artery disease by hollow fiber flow field-flow fractionation and nanoflow liquid chromatography-tandem mass spectrometry. Anal. Chem. 2015, 87, 1266–1273. [Google Scholar] [CrossRef]
- Carlshaf, A.; Jonsson, J.A. Perturbations of the Retention Parameter Due to Sample Overloading in Hollow-Fiber Flow Field-Flow Fractionation. Sep. Sci. Technol. 1993, 28, 1191–1201. [Google Scholar] [CrossRef]
- Litzén, A. Separation Speed, Retention, and Dispersion in Asymmetrical Flow Field-Flow Fractionation as Functions of Channel Dimensions and Flow Rates. Anal. Chem. 1993, 65, 461–470. [Google Scholar] [CrossRef]
- Gale, B.K.; Caldwell, K.D.; Bruno Frazier, A. A micromachined electrical field-flow fractionation (μ-EFFF) system. IEEE Trans. Biomed. Eng. 1998, 45, 1459–1469. [Google Scholar] [CrossRef]
- Tri, N.; Caldwell, K.; Beckett, R. Development of Electrical Field-Flow Fractionation. Anal. Chem. 2000, 72, 1823–1829. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, Y.; Shen, S.; Lee, S.; Dou, H. Field-flow fractionation: A gentle separation and characterization technique in biomedicine. TrAC Trends Anal. Chem. 2018, 108, 231–238. [Google Scholar] [CrossRef]
- Makan, A.C.; Williams, R.P.; Pasch, H. Field Flow Fractionation for the Size, Molar Mass, and Gel Content Analysis of Emulsion Polymers for Water-Based Coatings. Macromol. Chem. Phys. 2016, 217, 2027–2040. [Google Scholar] [CrossRef]
- Choi, J.; Fuentes, C.; Fransson, J.; Wahlgren, M.; Nilsson, L. Separation and zeta-potential determination of proteins and their oligomers using electrical asymmetrical flow field-flow fractionation (EAF4). J. Chromatogr. A 2020, 1633, 461625. [Google Scholar] [CrossRef] [PubMed]
- Erdem, B.; Sully, Y.; Sudol, E.D.; Dimonie, V.L.; El-Aasser, M.S. Determination of Miniemulsion Droplet Size via Soap Titration. Langmuir 2000, 16, 4890–4895. [Google Scholar] [CrossRef]
- Silebi, C.A.; Dosramos, J.G. Separation of submicrometer particles by capillary hydrodynamic fractionation (CHDF). J. Colloid Interface Sci. 1989, 130, 14–24. [Google Scholar] [CrossRef]
- Texter, J. Capillary Hydrodynamic Fractionation of Organic Nanopigment Dispersions. In Particle Sizing and Characterization; ACS: Singapore, 2004; pp. 151–173. [Google Scholar] [CrossRef]
- Clementi, L.A.; Artetxe, Z.; Aguirreurreta, Z.; Agirre, A.; Leiza, J.R.; Gugliotta, L.M.; Vega, J.R. Capillary hydrodynamic fractionation of hydrophobic colloids: Errors in the estimated particle size distribution. Particuology 2014, 17, 97–105. [Google Scholar] [CrossRef]
- DosRamos, J.G.; Silebi, C.A. The determination of particle size distribution of submicrometer particles by capillary hydrodynamic fractionation (CHDF). J. Colloid Interface Sci. 1990, 135, 165–177. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kupikowska-Stobba, B.; Domagała, J.; Kasprzak, M.M. Critical Review of Techniques for Food Emulsion Characterization. Appl. Sci. 2024, 14, 1069. https://doi.org/10.3390/app14031069
Kupikowska-Stobba B, Domagała J, Kasprzak MM. Critical Review of Techniques for Food Emulsion Characterization. Applied Sciences. 2024; 14(3):1069. https://doi.org/10.3390/app14031069
Chicago/Turabian StyleKupikowska-Stobba, Barbara, Jacek Domagała, and Mirosław M. Kasprzak. 2024. "Critical Review of Techniques for Food Emulsion Characterization" Applied Sciences 14, no. 3: 1069. https://doi.org/10.3390/app14031069
APA StyleKupikowska-Stobba, B., Domagała, J., & Kasprzak, M. M. (2024). Critical Review of Techniques for Food Emulsion Characterization. Applied Sciences, 14(3), 1069. https://doi.org/10.3390/app14031069




