SocialJGCF: Social Recommendation with Jacobi Polynomial-Based Graph Collaborative Filtering
Abstract
1. Introduction
2. Problem and Related Work
2.1. Problem Statement
2.2. Related Work
3. Method
3.1. Overall Architecture
3.1.1. Embedding Layer
3.1.2. Propagation Layer
3.1.3. Prediction Layer
3.2. Complexity Analysis
| Algorithm 1 SocialJGCF |
| 1: Procedure SocialJGCF () Input: —adjacency matrix of social graph —adjacency matrix of user-item interaction graph 2: Initialize: initial embeddings for users and iterms 3: 4: 5: 6: 7: 8: return 9: end procedure |
| Algorithm 2 JGCF |
| 1: Procedure JGCF () 2: Initialize:I 3: Initialize: 4: for to K do 5: 6: end for 7: 8: 9: 10: return 11: end procedure |
3.2.1. Time Complexity
3.2.2. Space Complexity
4. Experiments
4.1. Experimental Setup
4.2. Performance Evaluation
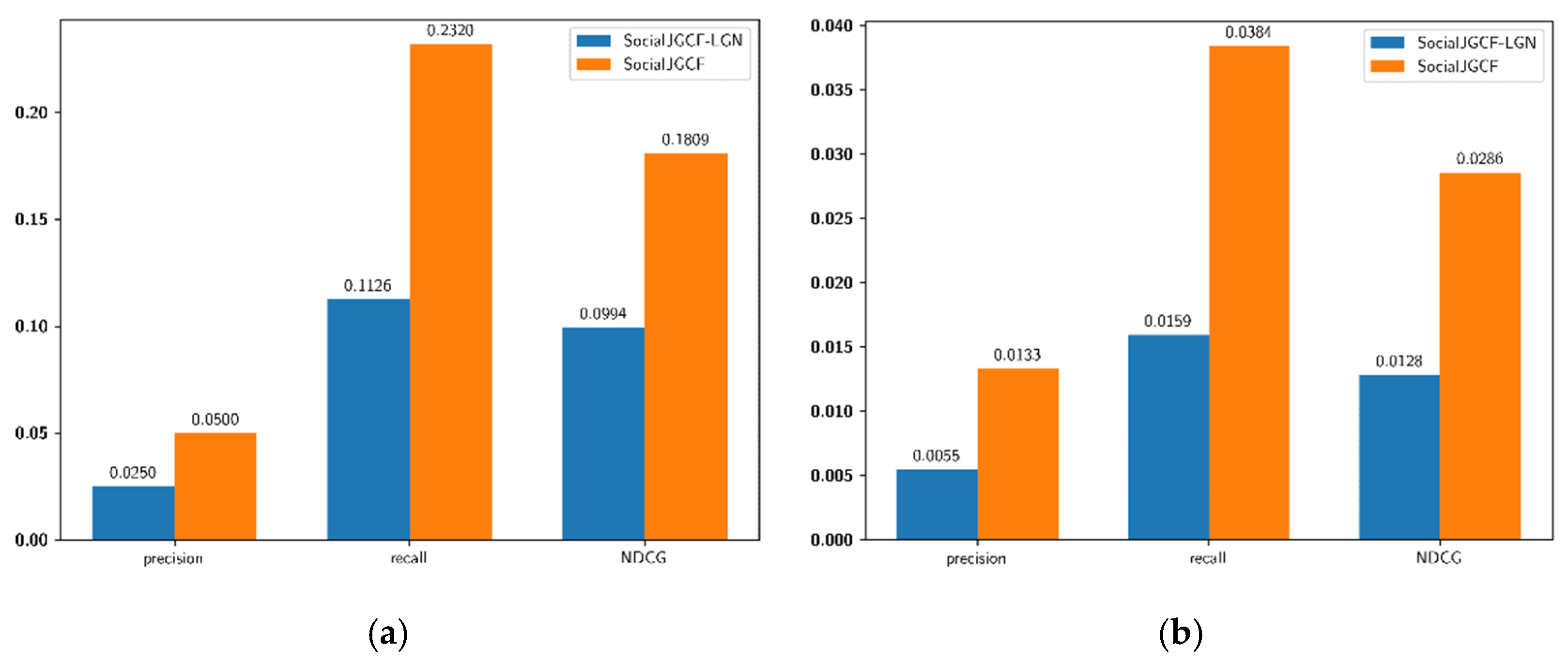
4.3. Comparisons of Graph Fusion Methods
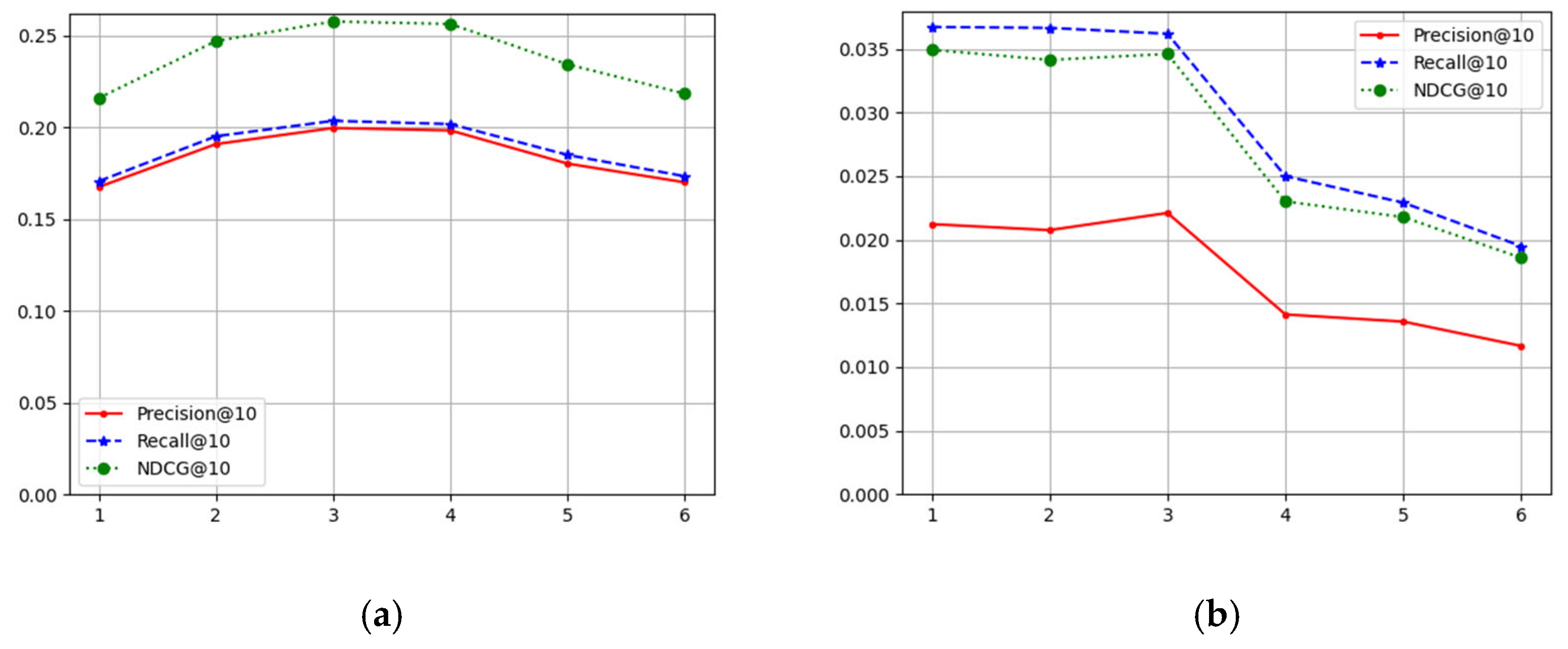
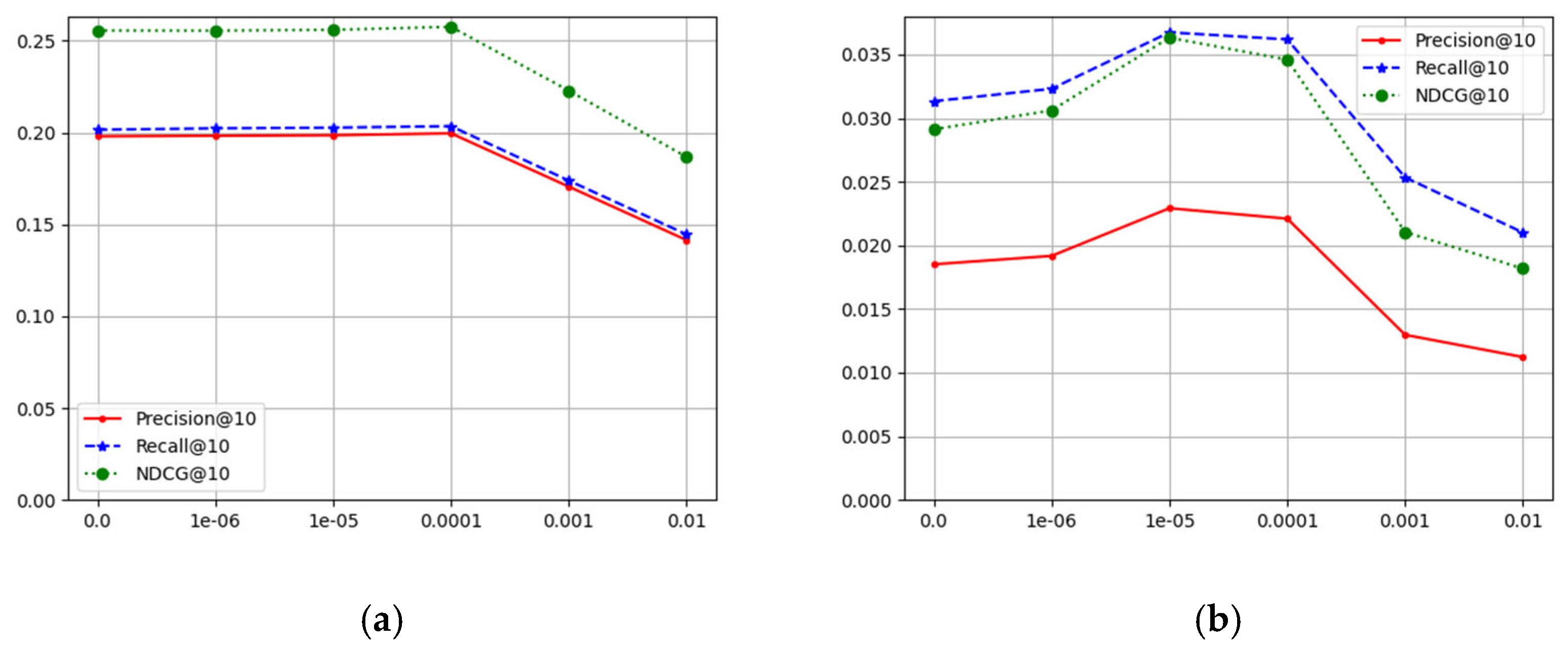
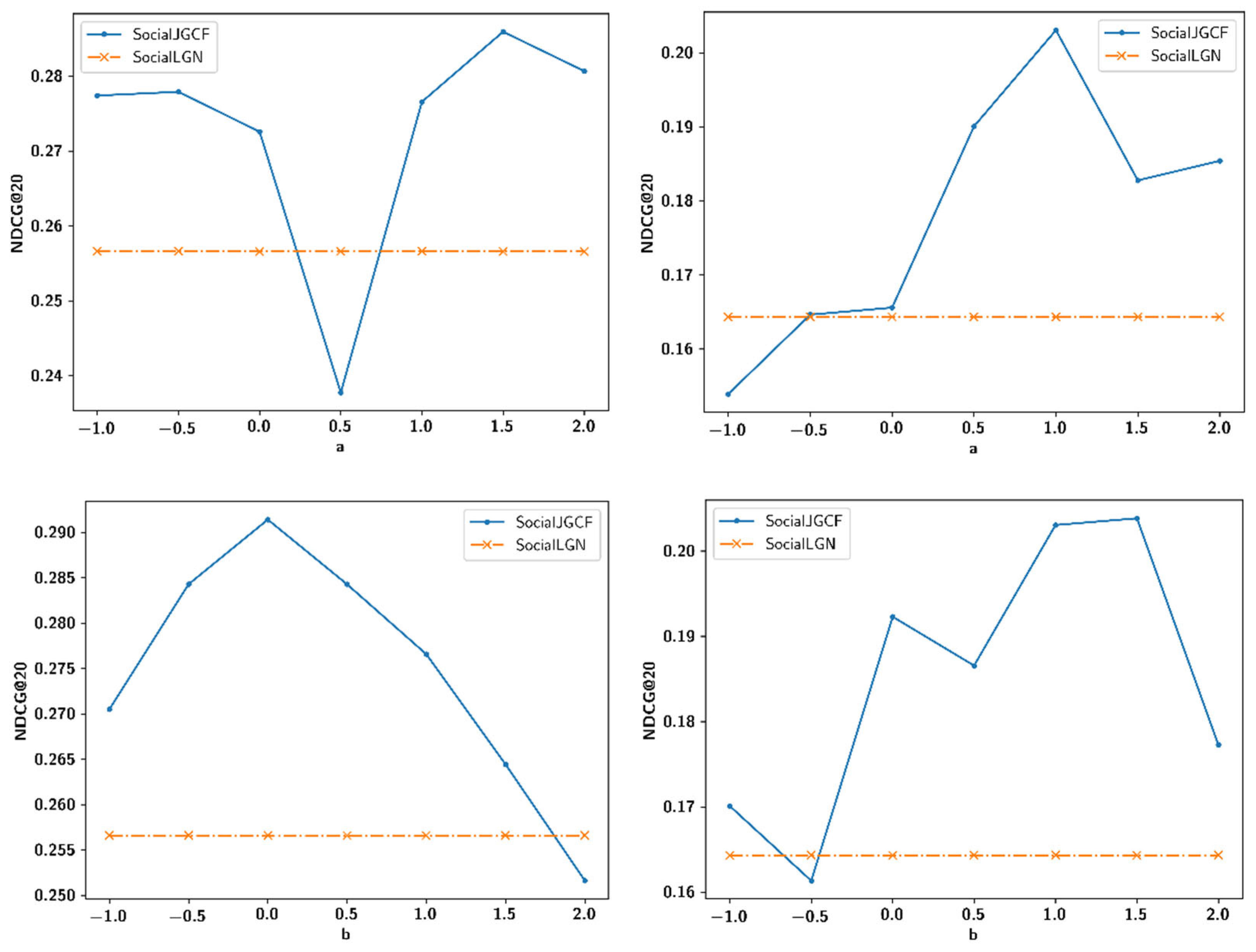
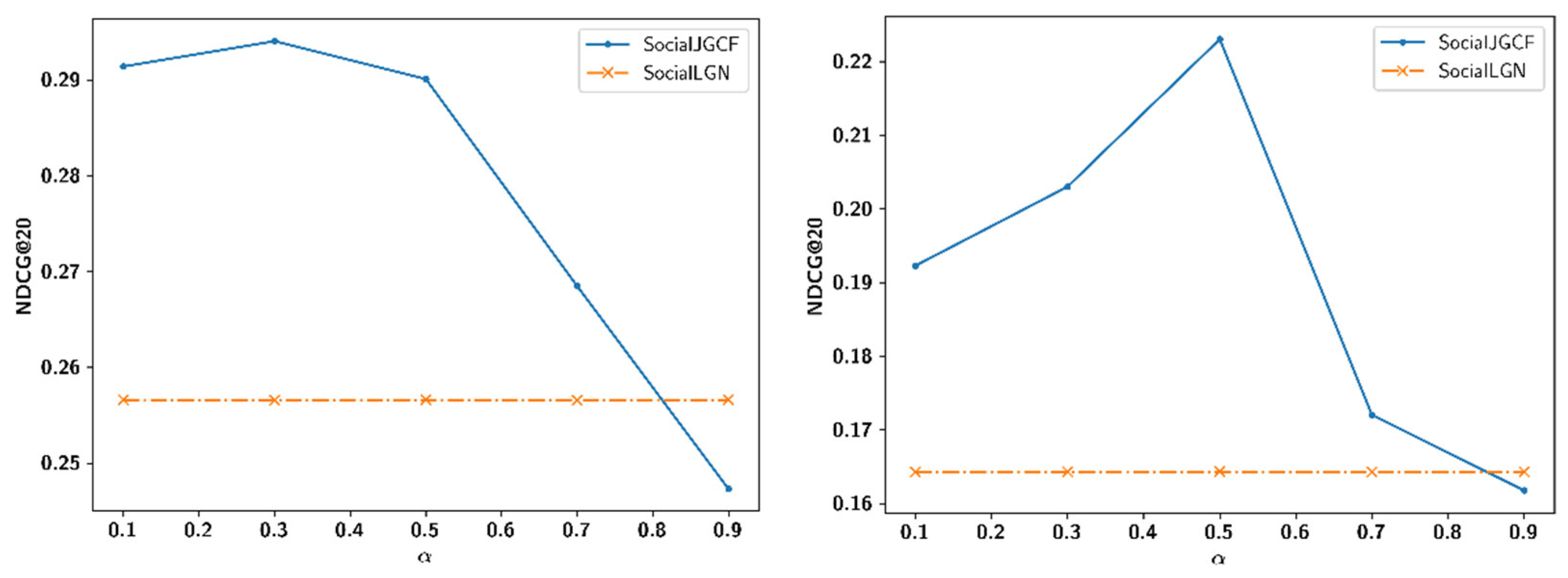
4.4. Sensitivity Analysis for Hyperparameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koren, Y.; Bell, R.; Volinsky, C. Matrix Factorization Techniques for Recommender Systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Covington, P.; Adams, J.; Sargin, E. Deep Neural Networks for YouTube Recommendations. In Proceedings of the 10th ACM Conference on Recommender Systems (RecSys ’16), Boston, MA, USA, 15–19 September 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 191–198. [Google Scholar]
- Gao, C.; Wang, X.; He, X.; Li, Y. Graph Neural Networks for Recommender System. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining (WSDM ’22), Tempe, AZ, USA, 21–25 February 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1623–1625. [Google Scholar] [CrossRef]
- Cialdini, R.B.; Goldstein, N.J. Social influence: Compliance and conformity. Annu. Rev. Psychol. 2004, 55, 591–621. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Yin, H.; Li, J.; Gao, M.; Huang, Z.; Cui, L. Enhance social recommendation with adversarial graph convolutional networks. IEEE Trans. Knowl. Data Eng. 2020, 34, 3727–3739. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, D.; Liu, C.; Lyu, M.R.; King, I. Recommender systems with social regularization. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining (WSDM ’11), Hong Kong, China, 9–12 February 2011; Associationfor Computing Machinery: New York, NY, USA, 2011; pp. 287–296. [Google Scholar]
- Wu, L.; Sun, P.; Fu, Y.; Hong, R.; Wang, X.; Wang, M. A Neural Influence Diffusion Model for Social Recommendation. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR’19), Paris, France, 21–25 July 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 235–244. [Google Scholar]
- Guo, G.; Zhang, J.; Yorke-Smith, N. TrustSVD: Collaborative filtering with both the explicit and implicit influence of user trust and of item ratings. In Proceedings of the AAAI, Austin, TX, USA, 25–30 January 2015; pp. 123–129. [Google Scholar]
- Wu, S.; Sun, F.; Zhang, W.; Xie, X.; Cui, B. Graph Neural Networks in Recommender Systems: A Survey. ACM Comput. Surv. 2022, 55, 97. [Google Scholar] [CrossRef]
- Sharma, K.; Lee, Y.C.; Nambi, S.; Salian, A.; Shah, S.; Kim, S.W.; Kumar, S. A survey of graph neural networks for social recommender systems. ACM Comput. Surv. 2024, 56, 265. [Google Scholar] [CrossRef]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph Neural Networks for Social Recommendation. In Proceedings of the The World Wide Web Conference (WWW ’19), San Francisco, CA, USA, 13–17 May 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 417–426. [Google Scholar]
- Wu, Q.; Zhang, H.; Gao, X.; He, P.; Weng, P.; Gao, H.; Chen, G. Dual graph attention networks for deep latent representation of multifaceted social effects in recommender systems. In Proceedings of the WWW Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2091–2102. [Google Scholar]
- Wu, L.; Li, J.; Sun, P.; Hong, R.; Ge, Y.; Wang, M. Diffnet++: A neural influence and interest diffusion network for social recommendation. IEEE Trans. Knowl. Data Eng. 2020, 34, 4753–4766. [Google Scholar] [CrossRef]
- Chen, T.; Wong, R.C.-W. An efficient and effective framework for session-based social recommendation. In Proceedings of the WSDM Conference, Virtual, 8–12 March 2021; pp. 400–408. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Wang, S.; Hu, L.; Wang, Y.; He, X.; Sheng, Q.Z.; Orgun, M.A.; Cao, L.; Ricci, F.; Yu, P.S. Graph learning based recommender systems: A review. In Proceedings of the 30th International Joint Conference on Artificial Intelligence, IJCAI 2021, Montreal, QC, Canada, 19–27 August 2021. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations—ICLR 2017 Conference Track, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, NY, USA, 4–9 December 2017; Curran Associates Inc.: New York, NY, USA, 2017. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’20), Virtual, 25–30 July 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 639–648. [Google Scholar]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.-S. Neural graph collaborative filtering. In Proceedings of the SIGIR Conference, Paris, France, 21–25 July 2019; pp. 165–174. [Google Scholar]
- Tan, Q.; Liu, N.; Zhao, X.; Yang, H.; Zhou, J.; Hu, X. Learning to hash with graph neural networks for recommender systems. In Proceedings of the WWW Conference, Taiwan, 20–24 April 2020; pp. 1988–1998. [Google Scholar]
- Mu, N.; Zha, D.; He, Y.; Tang, Z. Graph Attention Networks for Neural Social Recommendation. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 1320–1327. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Li, X.; Yu, Z.; Guo, B.; Chen, L.; Zhou, X. Exploring Multi-Dimension User-Item Interactions with Attentional Knowledge Graph Neural Networks for Recommendation. IEEE Trans. Big Data 2023, 9, 212–226. [Google Scholar] [CrossRef]
- Wu, B.; Zhong, L.; Yao, L.; Ye, Y. EAGCN: An Efficient Adaptive Graph Convolutional Network for Item Recommendation in Social Internet of Things. IEEE Internet Things J. 2022, 9, 16386–16401. [Google Scholar] [CrossRef]
- Qian, T.; Liang, Y.; Li, Q.; Xiong, H. Attribute Graph Neural Networks for Strict Cold Start Recommendation. IEEE Trans. Knowl. Data Eng. 2022, 34, 3597–3610. [Google Scholar] [CrossRef]
- Yu, J.; Yin, H.; Xia, X.; Chen, T.; Cui, L.; Nguyen, Q.V.H. Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for Recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’22), Madrid, Spain, 11–15 July 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1294–1303. [Google Scholar]
- Guo, J.; Du, L.; Chen, X.; Ma, X.; Fu, Q.; Han, S.; Zhang, D.; Zhang, Y. On Manipulating Signals of User-Item Graph: A Jacobi Polynomial-based Graph Collaborative Filtering. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ’23), Long Beach, CA, USA, 6–10 August 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 602–613. [Google Scholar]
- Chen, L.; Wu, L.; Hong, R.; Zhang, K.; Wang, M. Revisiting graph based collaborative filtering: A linear residual graph convolutional network approach. In Proceedings of the AAAI Conference, Vancouver, BC, Canada, 20–27 February 2020; pp. 27–34. [Google Scholar]
- Li, C.; Jia, K.; Shen, D.; Shi, C.J.; Yang, H. Hierarchical representation learning for bipartite graphs. In Proceedings of the IJCAI Conference, Macao, China, 10–16 August 2019; pp. 2873–2879. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph Convolutional Neural Networks for Web-Scale Recommender Systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD ’18), London, UK, 19–23 August 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 974–983. [Google Scholar] [CrossRef]
- Chang, J.; Gao, C.; He, X.; Jin, D.; Li, Y. Bundle Recommendation with Graph Convolutional Networks. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’20), Virtual, 25–30 July 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1673–1676. [Google Scholar] [CrossRef]
- Ma, H.; King, I.; Lyu, M.R. Learning to recommend with social trust ensemble. In Proceedings of the SIGIR Conference, Boston, MA, USA, 19–23 July 2009; pp. 203–210. [Google Scholar]
- Li, X.; Sun, L.; Ling, M.; Peng, Y. A survey of graph neural network based recommendation in social networks. Neurocomputing 2023, 549, 126441. [Google Scholar] [CrossRef]
- Jamali, M.; Ester, M. A matrix factorization technique with trust propagation for recommendation in social networks. In Proceedings of the Fourth ACM Conference on Recommender Systems (RecSys ’10), Barcelona, Spain, 26–30 September 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 135–142. [Google Scholar]
- Mandal, S.; Maiti, A. Graph Neural Networks for Heterogeneous Trust based Social Recommendation. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Lin, W.; Gao, Z.; Li, B. Guardian: Evaluating Trust in Online Social Networks with Graph Convolutional Networks. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications, Toronto, ON, Canada, 6–9 July 2020; pp. 914–923. [Google Scholar] [CrossRef]
- Salamat, A.; Luo, X.; Jafari, A. HeteroGraphRec: A heterogeneous graph-based neural networks for social recommendations. Knowl.-Based Syst. 2021, 217, 106817. [Google Scholar] [CrossRef]
- Song, W.; Xiao, Z.; Wang, Y.; Charlin, L.; Zhang, M.; Tang, J. Session-Based Social Recommendation via Dynamic Graph Attention Networks. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining (WSDM ’19), Melbourne, Australia, 11–15 February 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 555–563. [Google Scholar] [CrossRef]
- Han, H.; Zhang, M.; Hou, M.; Zhang, F.; Wang, Z.; Chen, E.; Wang, H.; Ma, J.; Liu, Q. STGCN: A spatial-temporal aware graph learning method for POI recommendation. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 1052–1057. [Google Scholar]
- Liao, J.; Zhou, W.; Luo, F.; Wen, J.; Gao, M.; Li, X.; Zeng, J. SocialLGN: Light graph convolution network for social recommendation. Inf. Sci. 2022, 589, 595–607. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, H. A Deep Graph Neural Network-Based Mechanism for Social Recommendations. IEEE Trans. Ind. Inform. 2021, 17, 2776–2783. [Google Scholar] [CrossRef]
- Xu, H.; Huang, C.; Xu, Y.; Xia, L.; Xing, H.; Yin, D. Global Context Enhanced Social Recommendation with Hierarchical Graph Neural Networks. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 701–710. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence (UAI ’09), Montreal, Canada, 18–21 June 2009; AUAI Press: Arlington, VA, USA, 2019; pp. 452–461. [Google Scholar]

| Unified Graph | Dual Graphs | ||
|---|---|---|---|
| Non-Frequency Based | Frequency Based | ||
| Trust-based recommendation | [7,13,37] | [11,38,39,42] | [41] |
| Cold-start recommendation | [24] | [40] | this paper |
| Dataset | LastFM | Epinions |
|---|---|---|
| User # | 1892 | 22,164 |
| Item # | 17,632 | 296,277 |
| Interaction # | 92,834 | 922,267 |
| Interaction Density | 0.278% | 0.140% |
| Relation # | 25,434 | 355,494 |
| Relation Density | 0.711% | 0.072% |
| Dataset | Metric | BPR | LightGCN | SocialLGN | SocialJGCF | Improvement |
|---|---|---|---|---|---|---|
| LastFM | Precision@10 | 0.1449 | 0.1960 | 0.1972 | 0.1997 | 1.2677% |
| Precision@20 | 0.1062 | 0.1359 | 0.1368 | 0.1380 | 0.8772% | |
| Recall@10 | 0.1480 | 0.2003 | 0.2026 | 0.2036 | 0.4936% | |
| Recall@20 | 0.2177 | 0.2771 | 0.2794 | 0.2815 | 0.7516% | |
| NDCG@10 | 0.1835 | 0.2536 | 0.2566 | 0.2575 | 0.3507% | |
| NDCG@20 | 0.2095 | 0.2789 | 0.2822 | 0.2832 | 0.3543% | |
| Epinions | Precision@10 | 0.0184 | 0.0228 | 0.0215 | 0.0221 | 2.7907% |
| Precision@20 | 0.0149 | 0.0184 | 0.0175 | 0.0183 | 4.5714% | |
| Recall@10 | 0.0325 | 0.0379 | 0.0351 | 0.0362 | 3.1339% | |
| Recall@20 | 0.0515 | 0.0604 | 0.0567 | 0.0583 | 2.8219% | |
| NDCG@10 | 0.0303 | 0.0354 | 0.0332 | 0.0346 | 4.2169% | |
| NDCG@20 | 0.0364 | 0.0426 | 0.0399 | 0.0418 | 4.7619% |
| Dataset | Metric | BPR | LightGCN | SocialLGN | SocialJGCF | Improvement |
|---|---|---|---|---|---|---|
| LastFM | Precision@10 | 0.0333 | 0.0417 | 0.0458 | 0.0583 | 27.2926% |
| Precision@20 | 0.0188 | 0.0312 | 0.0333 | 0.0375 | 12.6126% | |
| Recall@10 | 0.1858 | 0.1727 | 0.1974 | 0.2297 | 16.3627% | |
| Recall@20 | 0.1910 | 0.2416 | 0.2663 | 0.2811 | 5.5576% | |
| NDCG@10 | 0.1212 | 0.1374 | 0.1419 | 0.1728 | 21.7759% | |
| NDCG@20 | 0.1240 | 0.1596 | 0.1643 | 0.1902 | 15.7638% | |
| Epinions | Precision@10 | 0.0127 | 0.0139 | 0.0127 | 0.0133 | 4.7244% |
| Precision@20 | 0.0097 | 0.0109 | 0.0102 | 0.0107 | 4.9020% | |
| Recall@10 | 0.0369 | 0.0403 | 0.0371 | 0.0384 | 3.5040% | |
| Recall@20 | 0.0571 | 0.0643 | 0.0603 | 0.0620 | 2.8192% | |
| NDCG@10 | 0.0273 | 0.0292 | 0.0266 | 0.0286 | 7.5188% | |
| NDCG@20 | 0.0345 | 0.0378 | 0.0348 | 0.0370 | 6.3218% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Chen, Z. SocialJGCF: Social Recommendation with Jacobi Polynomial-Based Graph Collaborative Filtering. Appl. Sci. 2024, 14, 12070. https://doi.org/10.3390/app142412070
Lu H, Chen Z. SocialJGCF: Social Recommendation with Jacobi Polynomial-Based Graph Collaborative Filtering. Applied Sciences. 2024; 14(24):12070. https://doi.org/10.3390/app142412070
Chicago/Turabian StyleLu, Heng, and Ziwei Chen. 2024. "SocialJGCF: Social Recommendation with Jacobi Polynomial-Based Graph Collaborative Filtering" Applied Sciences 14, no. 24: 12070. https://doi.org/10.3390/app142412070
APA StyleLu, H., & Chen, Z. (2024). SocialJGCF: Social Recommendation with Jacobi Polynomial-Based Graph Collaborative Filtering. Applied Sciences, 14(24), 12070. https://doi.org/10.3390/app142412070






