Unified Elasto-Plastic Solution for High-Speed Railway Tunnel in Cold Regions Considering Dual Transverse Isotropic Model of Frozen Rock Mass
Abstract
1. Introduction
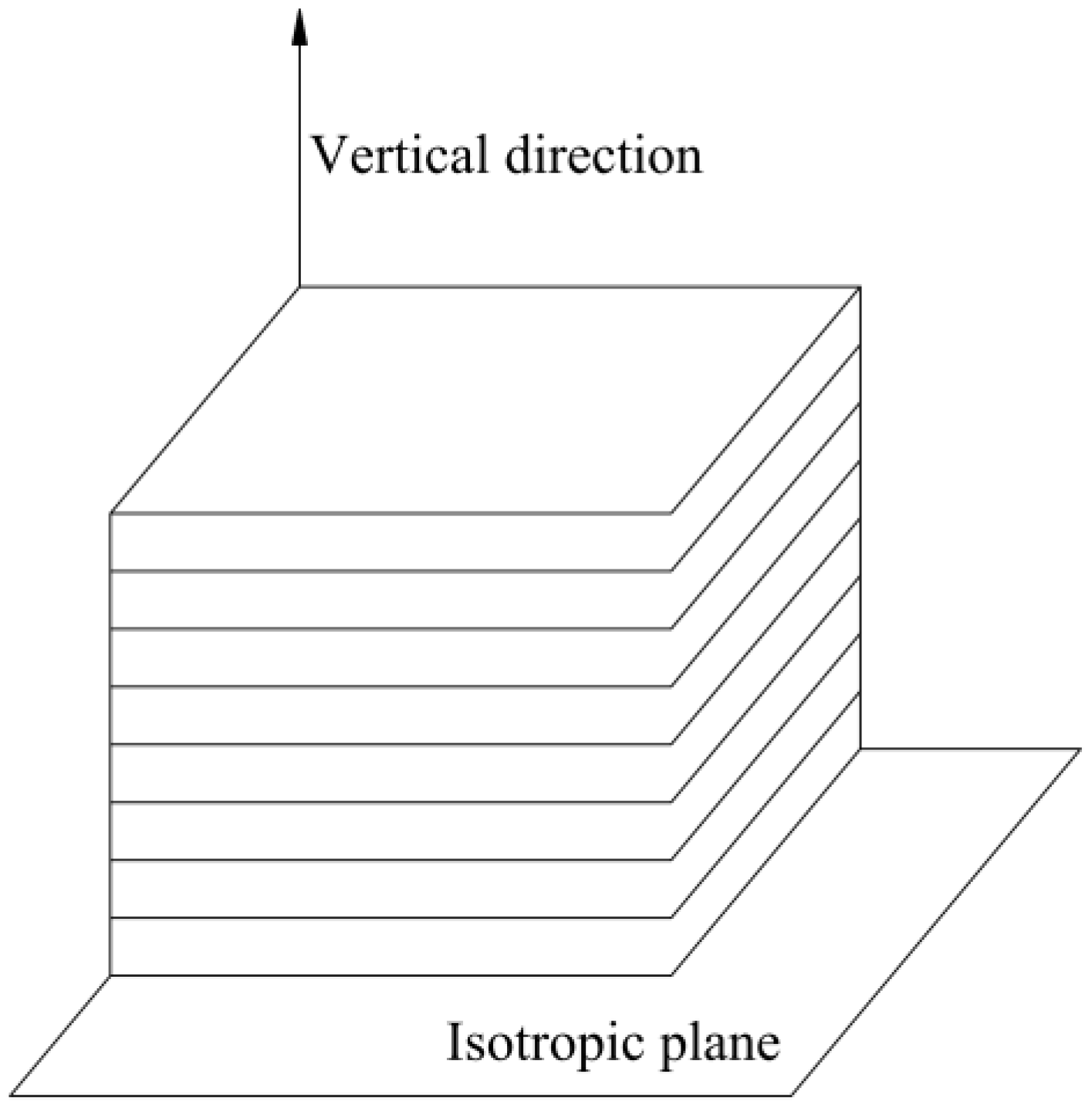
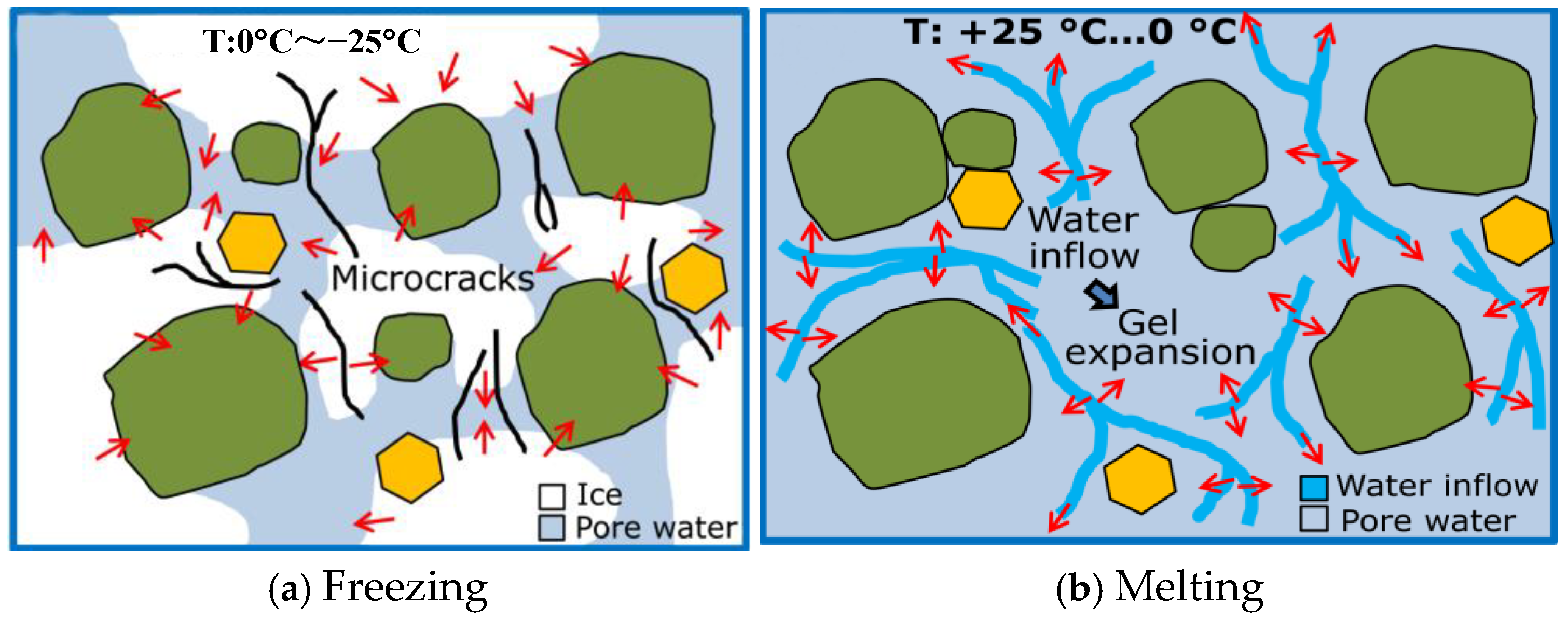
2. Dual Transverse Isotropic Model of Frozen Rock Mass
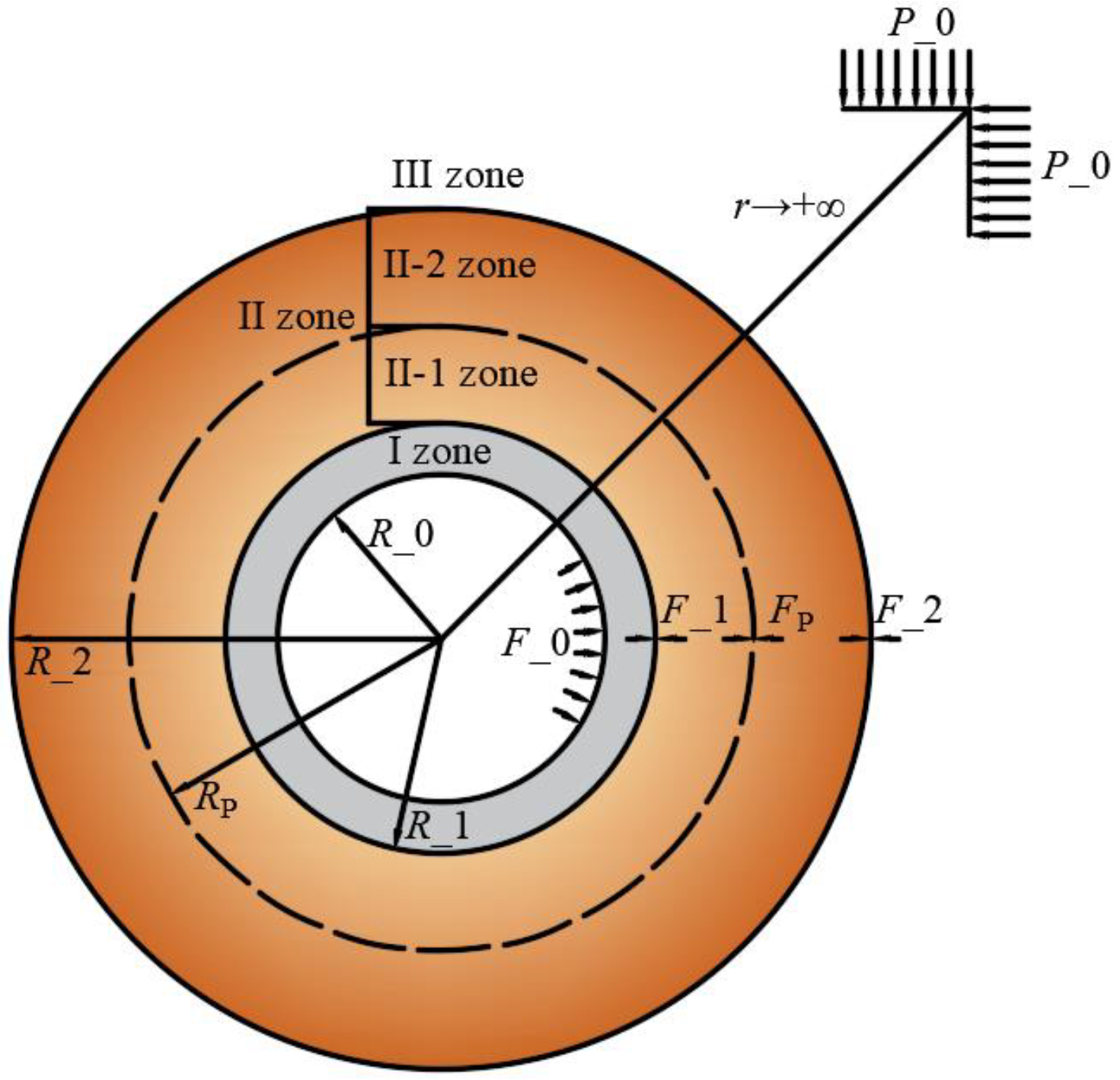
3. Establishing of Mechanical Model
4. Solution of Mechanical Model
4.1. Mechanical Analysis of Zone I
4.2. Mechanical Analysis of Zone II-1
4.3. Mechanical Analysis of Zone II-2
4.4. Mechanical Analysis of Zone III
4.5. Solution of Stress and Displacement
5. Verification of Model Solution
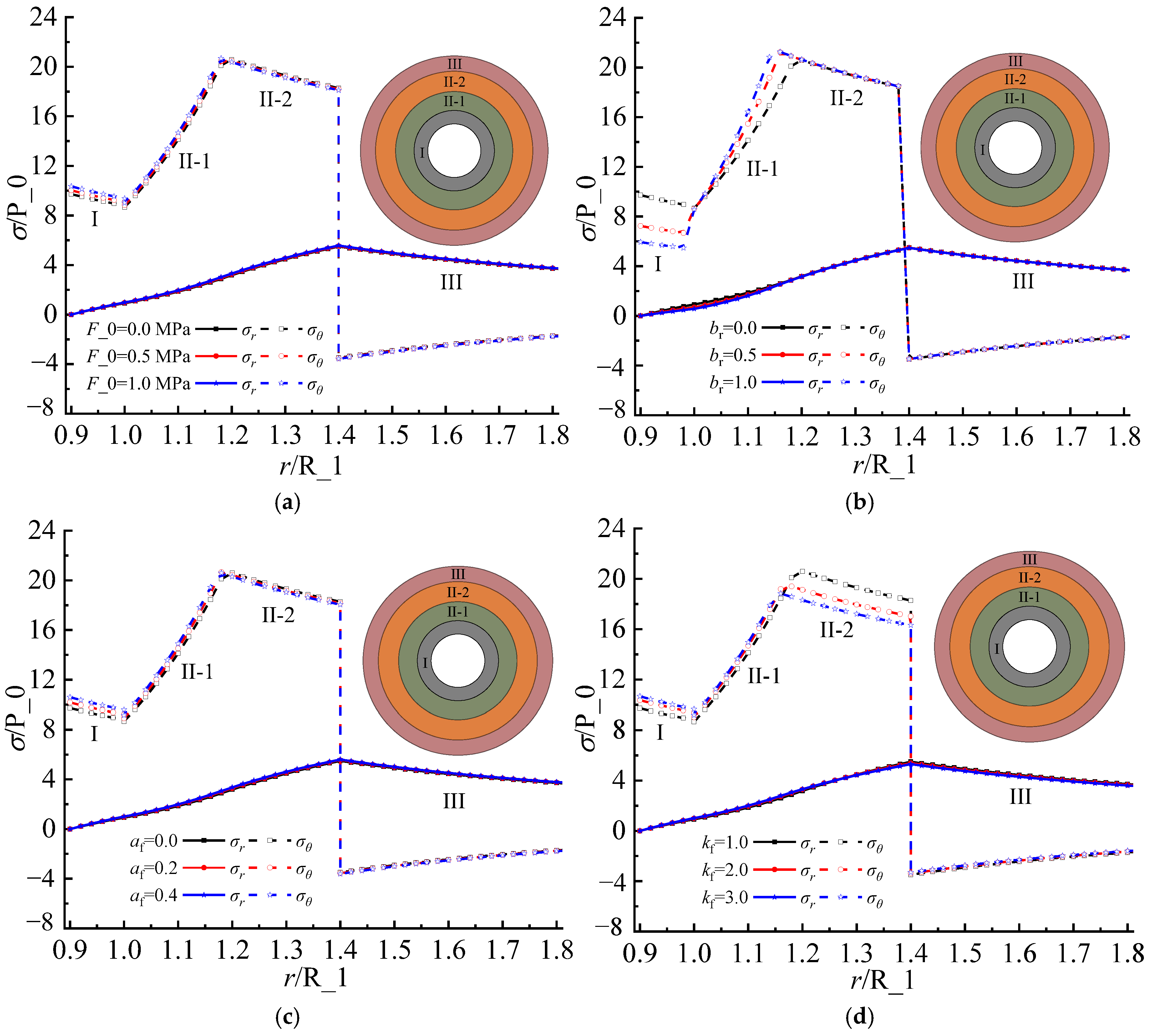
5.1. Analysis of Model Solution
5.2. Comparison with Existing Models
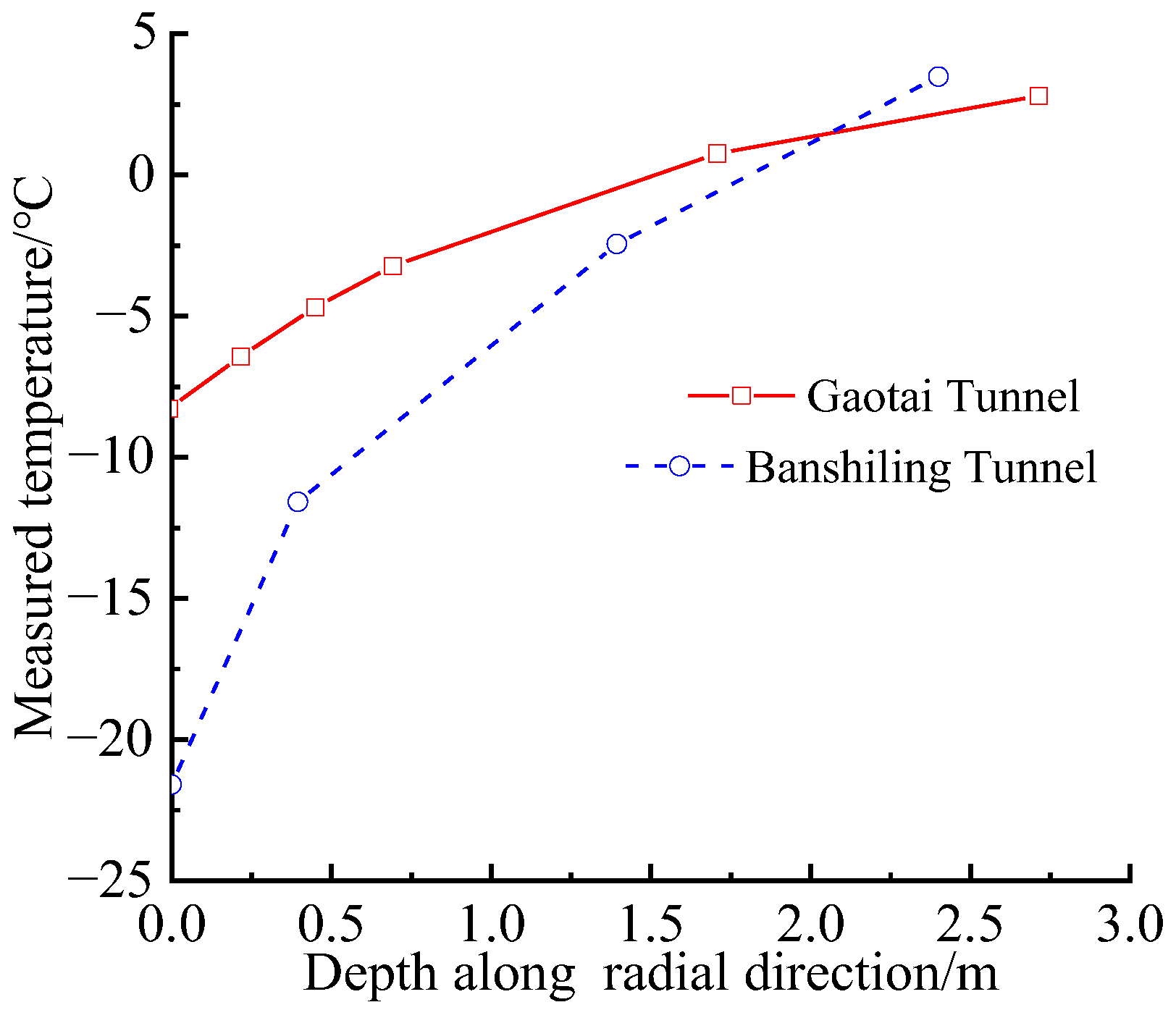
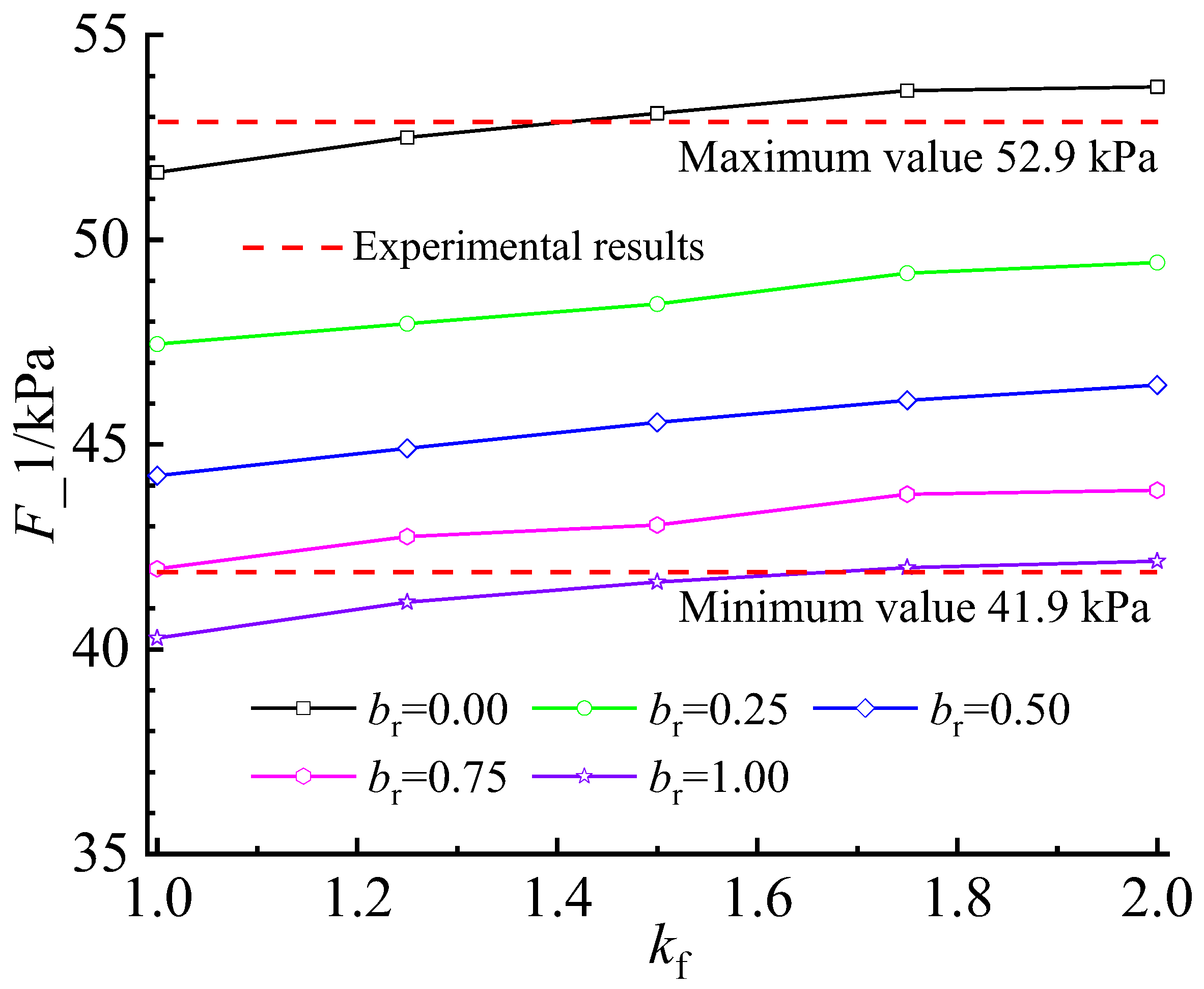
5.3. Comparison with Experimental Results
6. Analysis of Model Parameters
7. Conclusions
- (1)
- A dual transverse isotropic model of frozen rock mass is proposed based on strain and elastic modulus. If the values of these parameters are reasonable, the dual transverse isotropic model can be simplified as the isotropy case.
- (2)
- By combining unified strength theory and the non-associated flow rule, an elasto-plastic mechanical model for a high-speed railway tunnel in cold regions is established and solved by considering the dual transverse isotropy of frozen rock mass. The accuracy of the mechanical model proposed by the authors is verified by comparing it with that of existing models and the test results based on the same model parameters.
- (3)
- A significant negative correlation exists between RP and F_0, br, αf, and kf, as well as between F_1 and parameter br. Further, a positive correlation exists between F_1 and F_0, αf, and kf. During the design of tunnel structures in cold regions, parameters F_0, αf, and kf should be reasonably considered, whereas parameter br should be carefully considered.
- (4)
- The increase in elastic modulus with depth along the radial direction is assumed to be a power-law function. Other functional forms should be further explored based on on-site monitoring and experimental results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| σ | Stress |
| ε | Strain |
| k | Anisotropic frost heave coefficients |
| εv | Volumetric strain |
| E | Elastic modulus |
| r | Distance from the tunnel center in the radial direction |
| Ruf | Depth of the frozen rock mass |
| αf | Radial gradient influence coefficient of the frozen rock mass |
| R_0 | Inner radius of zone I |
| R_1 | Outer radius of zone I or the inner radius of zone II |
| R_2 | Outer radius of zone II or the inner radius of zone III |
| RP | Plastic radius of the frozen rock mass zone II |
| F_0 | Pressure acting on the inner surface of the support structure |
| F_1 | Pressure acting on the outer surface of the support structure or the frost-heaving force |
| FP | Pressure acting on the contact surface between zone II-1 and zone II-2 |
| F_2 | Pressure acting on the contact surface between zone II-2 and zone III |
| P_0 | Initial ground stress in the tunnel situ |
| u | Displacement |
| μ | Poisson’s ratio |
| A B | Unified strength theory parameters |
| br | Influence coefficient of intermediate principal stress |
| c | Cohesion |
| φ | Internal friction angle |
| D | An integral constant related to the boundary conditions |
| β | Characteristic parameters related to shear expansion |
| Q | An integral constant related to the boundary conditions |
| subscripts r, θ, and l | Radial, circumferential, and longitudinal directions, respectively |
| subscripts f and uf | Frozen and unfrozen rock mass, respectively |
References
- Lai, Y.M.; Wu, H.; Wu, Z.W.; Liu, S.Y.; Den, X.J. Analytical viscoelastic solution for frost force in cold-region tunnels. Cold Reg. Sci. Technol. 2000, 31, 227–234. [Google Scholar] [CrossRef]
- Zhao, P.Y.; Chen, J.X.; Luo, Y.B.; Li, Y.; Chen, L.J.; Wang, C.W.; Hu, T.T. Field measurement of air temperature in a cold region tunnel in northeast China. Cold Reg. Sci. Technol. 2020, 171, 102957. [Google Scholar] [CrossRef]
- Gao, G.Y.; Chen, Q.S.; Zhang, Q.S.; Chen, G.Q. Analytical elasto-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels. Cold Reg. Sci. Technol. 2012, 72, 50–57. [Google Scholar] [CrossRef]
- Feng, Q.; Jiang, B.S.; Zhang, Q.; Wang, L.P. Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels. Cold Reg. Sci. Technol. 2014, 108, 59–68. [Google Scholar] [CrossRef]
- Liu, W.W.; Feng, Q.; Fu, S.G.; Wang, C.X. Elasto-plastic solution for cold-regional tunnels considering the compound effect of non-uniform frost heave, supporting strength and supporting time. Tunn. Undergr. Space Technol. 2018, 82, 293–302. [Google Scholar] [CrossRef]
- Xia, C.C.; Lv, Z.T.; Li, Q.; Huang, J.H.; Bai, X.Y. Transversely isotropic frost heave of saturated rock under unidirectional freezing condition and induced frost heaving force in cold region tunnels. Cold Reg. Sci. Technol. 2018, 152, 48–58. [Google Scholar] [CrossRef]
- Feng, Q.; Fu, S.G.; Wang, C.X.; Liu, W.W.; Wang, Y.; Qiao, W.G. Analytical elasto-plastic solution for frost force of cold-region tunnels considering anisotropic frost heave in the surrounding rock. KSCE J. Civ. Eng. 2019, 23, 3831–3842. [Google Scholar] [CrossRef]
- Du, J.M.; Fang, Q.; Wang, G.; Zhang, D.L.; Chen, T.L. Fatigue damage and residual life of secondary lining of high-speed railway tunnel under aerodynamic pressure wave. Tunn. Undergr. Space Technol. 2021, 111, 103851. [Google Scholar] [CrossRef]
- Lv, Z.T.; Yuan, S.Q.; Lin, H. Analytical stress solution for cold region tunnels with unequal ground stress and support delay under different frost heave conditions of surrounding rock. Cold Reg. Sci. Technol. 2023, 206, 103742. [Google Scholar] [CrossRef]
- Lv, Z.T.; Xia, C.C.; Wang, Y.S.; Luo, J. Analytical elasto-plastic solution of frost heaving force in cold region tunnels considering transversely isotropic frost heave of surrounding rock. Cold Reg. Sci. Technol. 2019, 163, 87–97. [Google Scholar] [CrossRef]
- Li, H.W.; Lai, Y.M.; Zhang, H.Y.; Chen, Y.Y.; Jiang, W.T.; Tian, Y.; Ran, J.C. Composite lining-ground interaction behavior in a cold-region circular tunnel under isotropic frost heave action. Cold Reg. Sci. Technol. 2023, 207, 103771. [Google Scholar] [CrossRef]
- Cao, S.P.; Xia, C.C.; Zhou, S.W.; Zhang, Y. Unified strength-based elastoplastic solution for frost heaving force of cold-region tunnels considering dual non-uniform frost heaving of surrounding rock. Cold Reg. Sci. Technol. 2024, 217, 104054. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, W.W.; Jiang, B.S. Analytical solution for the stress and deformation of rock surrounding a cold-regional tunnel under unequal compression. Cold Reg. Sci. Technol. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Yu, Y.; Ling, X.Z.; Tang, L.; Han, X.; Geng, L.; Wei, S.W. Analytical solution for the soil-lining interaction in cold region deep tunnel considering the delayed installation of the lining. Cold Reg. Sci. Technol. 2021, 189, 103329. [Google Scholar] [CrossRef]
- Huang, S.B.; Liu, Q.S.; Liu, Y.Z.; Ye, Z.Y.; Cheng, A.P. Freezing strain model for estimating the unfrozen water content of saturated rock under low temperature. Int. J. Geomech. 2018, 18, 04017137. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Xu, F.; Zhang, B.; Xu, H.B.; Gao, Y. Model test on frost heaving pressure induced by frozen partial ponding behind tunnel lining in cold region. Tunn. Undergr. Space Technol. 2024, 145, 105607. [Google Scholar] [CrossRef]
- Tan, X.J.; Chen, W.Z.; Yang, J.P.; Cao, J.J. Laboratory investigations on the mechanical properties degradation of granite under freeze–thaw cycles. Cold Reg. Sci. Technol. 2011, 68, 130–138. [Google Scholar] [CrossRef]
- Zhang, H.M.; Meng, X.Z.; Yang, G.S. A study on mechanical properties and damage model of rock subjected to freeze-thaw cycles and confining pressure. Cold Reg. Sci. Technol. 2020, 174, 103056. [Google Scholar] [CrossRef]
- Gu, J.F.; Li, K.; Su, L. Modified nonlinear Mohr–Coulomb fracture criteria for isotropic materials and transversely isotropic UD composites. Mech. Mater. 2020, 151, 103649. [Google Scholar] [CrossRef]
- Yang, W.Y.; Bai, P.P.; Fang, J.B.; Li, Y.T.; Shi, Z.Q.; Zhou, Q.H. Contact responses of transversely isotropic layered material with imperfect interface. Int. J. Mech. Sci. 2024, 272, 109145. [Google Scholar] [CrossRef]
- Jiang, H.Q.; Niu, F.J.; Ma, Q.G.; Jiang, W.T.; Hu, H.; Wang, E.L.; Jiao, C.L.; Li, Z.G. Thermal characteristics investigation of a high-speed railway tunnel by field monitoring in Northeast of China. Transp. Geotech. 2021, 30, 100615. [Google Scholar] [CrossRef]
- Du, J.M.; Fang, Q.; Wang, G.; Wang, J. Analytical solution of a circular lined tunnel with alterable mechanical property under hydrostatic stress and internal pressure. J. Cent. South Univ. 2022, 29, 2757–2770. [Google Scholar] [CrossRef]
- Galan, I.; Baldermann, A.; Kusterle, W.; Dietzel, M.; Mittermayr, F. Durability of shotcrete for underground support– Review and update. Constr. Build. Mater. 2019, 202, 465–493. [Google Scholar] [CrossRef]
- Yu, M.H. Twin shear stress yield criterion Author links open overlay panel. Int. J. Mech. Sci. 1983, 25, 71–74. [Google Scholar] [CrossRef]
- Wang, C.W.; Liu, X.L.; Song, D.Q.; Wang, E.Z.; Zhang, J.M. Elasto-plastic analysis of the surrounding rock mass in circular tunnel using a new numerical model based on generalized nonlinear unified strength theory. Comput. Geotech. 2023, 154, 105163. [Google Scholar] [CrossRef]
- Liu, X.Y.; Liu, E.L. Application of new twin-shear unified strength criterion to frozen soil Author links open overlay panel. Cold Reg. Sci. Technol. 2019, 167, 102857. [Google Scholar] [CrossRef]
- Hou, Y.; Min, J.Y.; Lin, J.P.; Lee, M.G. Modeling stress anisotropy, strength differential, and anisotropic hardening by coupling quadratic and stress-invariant-based yield functions under non-associated flow rule. Mech. Mater. 2022, 174, 104458. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Han, X.H. Parameter identification for the non-associated flow rules representing corner effects through the equivalent tangential shear modulus reduction after abrupt strain-path change. Int. J. Plast. 2023, 169, 103726. [Google Scholar] [CrossRef]
- Wang, S.C.; Shang, H.C.; Han, M.; Zhou, C.; Chen, Q.; Lou, Y.S. Lode-dependent Yld91 function for anisotropic-asymmetric hardening modeling of metals under non-associated flow rule. J. Mater. Process. Technol. 2024, 325, 118298. [Google Scholar] [CrossRef]
- Du, J.M.; Zhang, X.; Wang, H.L. Elasto-plastic solution for a circular lined tunnel considering yield criteria for surrounding rock and functionally graded lining in cold-region tunnels. Sustainability 2023, 15, 11577. [Google Scholar] [CrossRef]
- Sun, B. Model test study of frost heaving pressures in tunnels excavated in fractured rock mass in cold regions. Sci. Cold Arid Reg. 2010, 2, 405–410. [Google Scholar]
- Bomarito, G.F.; Leser, P.E.; Warner, J.E.; Leser, W.P. On the optimization of approximate control variates with parametrically defined estimators. J. Comput. Phys. 2022, 451, 110882. [Google Scholar] [CrossRef]
- Belomestny, D.; Goldman, A.; Naumov, A.; Samsonov, S. Theoretical guarantees for neural control variates in MCMC. Math. Comput. Simul. 2024, 220, 382–405. [Google Scholar] [CrossRef]

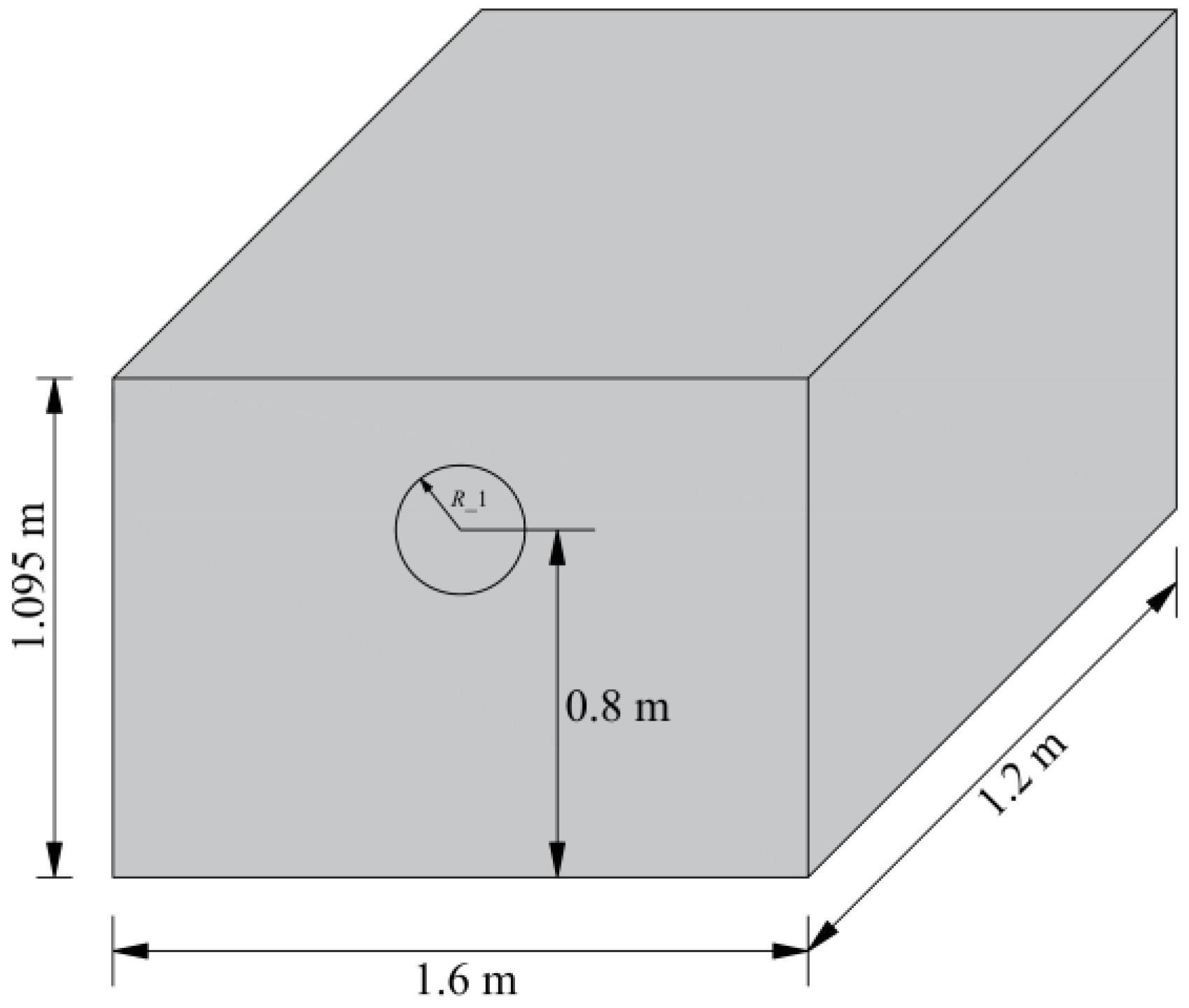
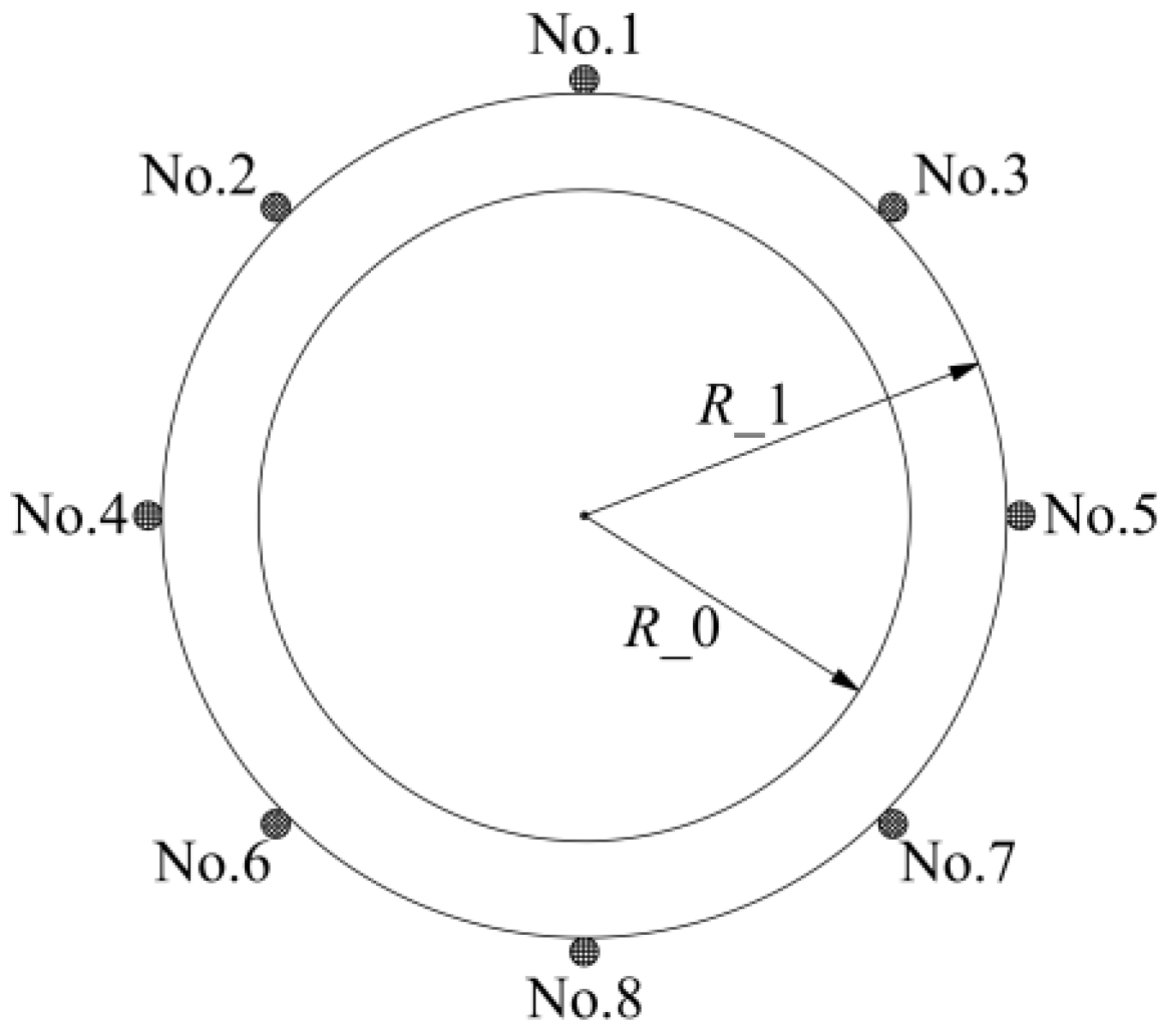

| Zone | Elastic Modulus/GPa | Poisson’s Ratio | Cohesion/MPa | Internal Friction Angle/° |
|---|---|---|---|---|
| Support zone | 28.0 | 0.16 | / | / |
| Frozen rock mass zone | 7.8 | 0.35 | 1.7 | 45 |
| Unfrozen rock mass zone | 4.6 | 0.33 | / | / |
| Zone | Elastic Modulus/MPa | Poisson’s Ratio | Cohesion/kPa | Internal Friction Angle/° |
|---|---|---|---|---|
| Support zone | 615.0 | 0.205 | / | / |
| Frozen rock mass zone | 74.0 | 0.41 | 4.5 | 31.2 |
| Unfrozen rock mass zone | 37.0 | 0.41 | 3.0 | 24.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Ma, W.; Fang, Q. Unified Elasto-Plastic Solution for High-Speed Railway Tunnel in Cold Regions Considering Dual Transverse Isotropic Model of Frozen Rock Mass. Appl. Sci. 2024, 14, 11796. https://doi.org/10.3390/app142411796
Zhao P, Ma W, Fang Q. Unified Elasto-Plastic Solution for High-Speed Railway Tunnel in Cold Regions Considering Dual Transverse Isotropic Model of Frozen Rock Mass. Applied Sciences. 2024; 14(24):11796. https://doi.org/10.3390/app142411796
Chicago/Turabian StyleZhao, Peng, Weibin Ma, and Qian Fang. 2024. "Unified Elasto-Plastic Solution for High-Speed Railway Tunnel in Cold Regions Considering Dual Transverse Isotropic Model of Frozen Rock Mass" Applied Sciences 14, no. 24: 11796. https://doi.org/10.3390/app142411796
APA StyleZhao, P., Ma, W., & Fang, Q. (2024). Unified Elasto-Plastic Solution for High-Speed Railway Tunnel in Cold Regions Considering Dual Transverse Isotropic Model of Frozen Rock Mass. Applied Sciences, 14(24), 11796. https://doi.org/10.3390/app142411796







