Exploration of Machine Learning Models for Prediction of Gene Electrotransfer Treatment Outcomes
Abstract
1. Introduction
2. Materials and Methods
2.1. Paper Selection and Data Curation
- conducted GET experiments with PEFs and plasmid DNA;
- did not use additional therapeutic techniques to achieve success;
- used a pulse configuration with a maximum of two separate voltage levels;
- provided results in terms of significant difference from the control;
- conducted experiments either in vitro or in vivo.
2.2. Determination of the Most Important Features
2.3. Training of the Machine Learning Models
2.4. Assessing the Accuracy of the Models
3. Results
3.1. Dataset Summary
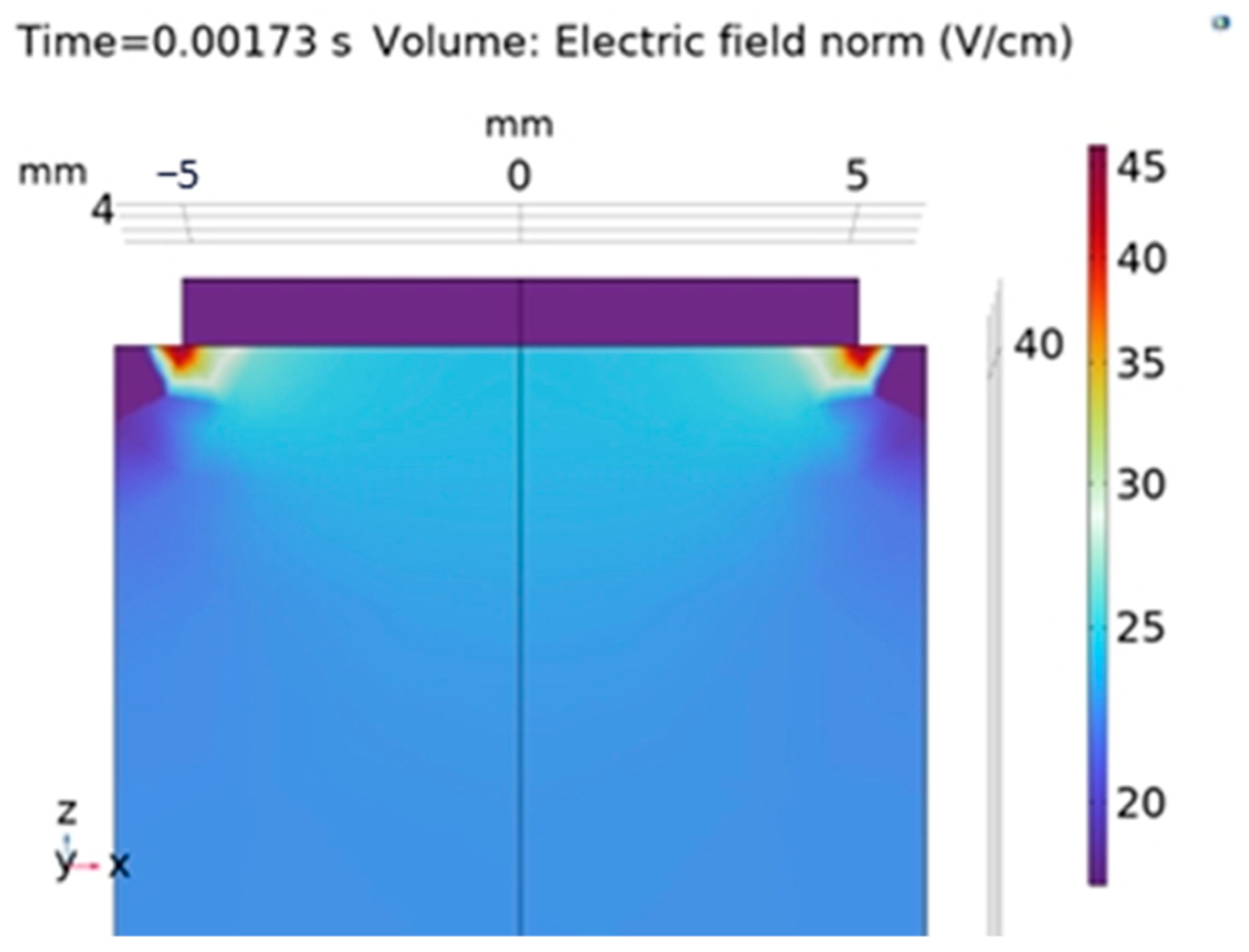
3.2. FEM Simulation of Monopolar Electrode
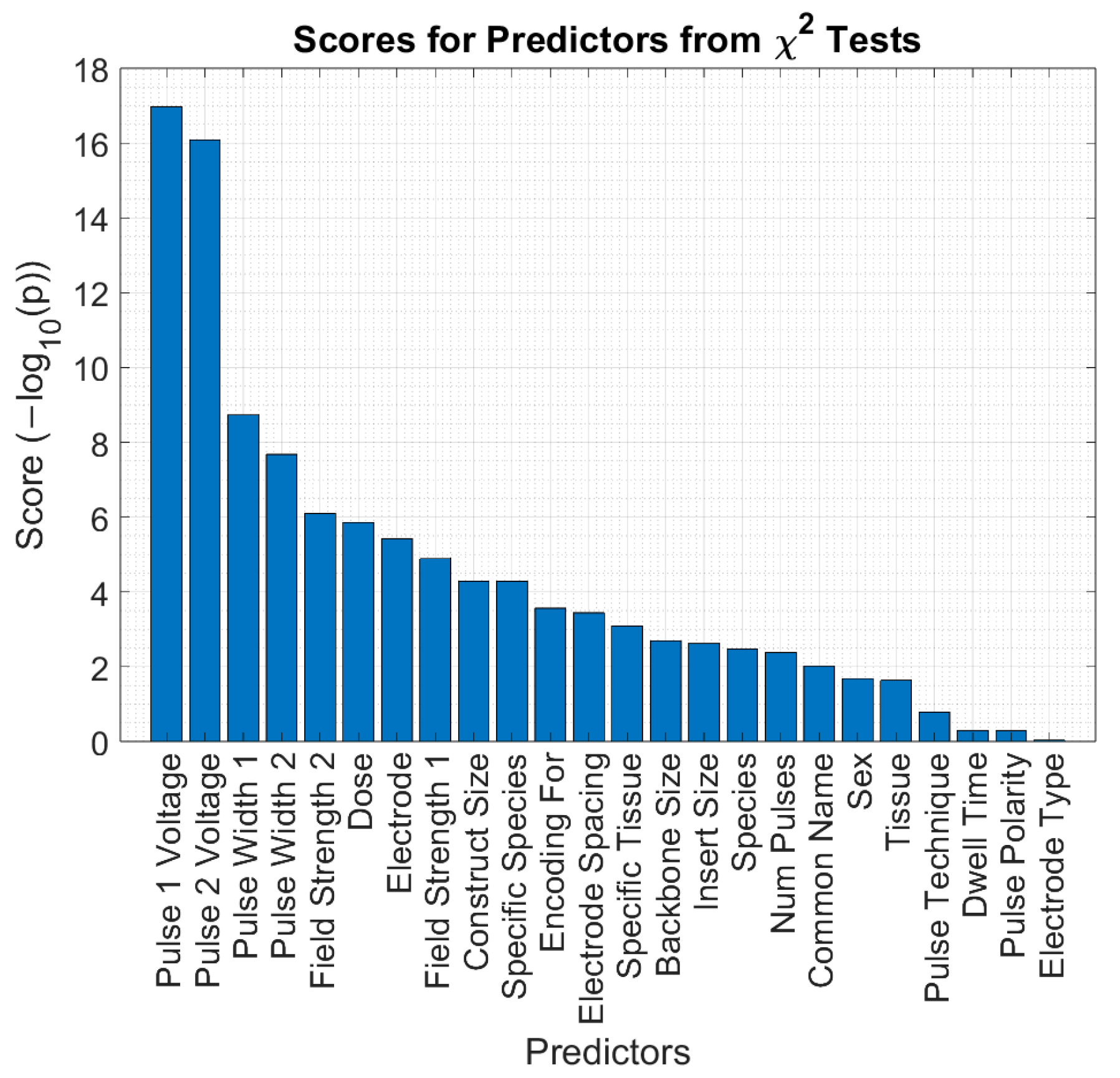
3.3. Results for Feature Selection
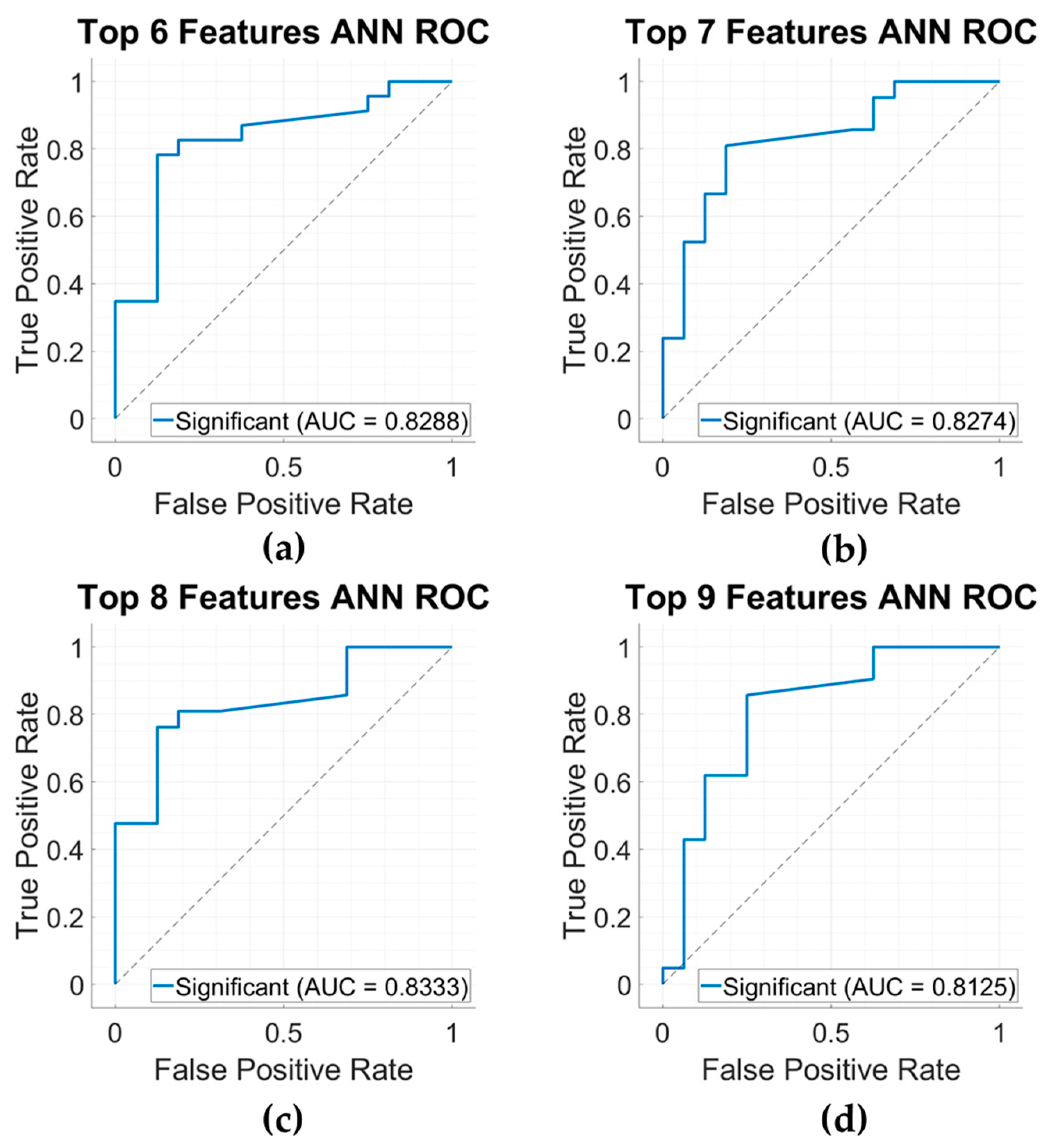
3.4. Model Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anguela, X.M.; High, K.A. Entering the modern era of gene therapy. Annu. Rev. Med. 2019, 70, 273–288. [Google Scholar] [CrossRef] [PubMed]
- Potter, H.; Heller, R. Transfection by electroporation. Curr. Protoc. Mol. Biol. 2018, 121, 9.3. 1–9.3. 13. [Google Scholar] [CrossRef] [PubMed]
- Nishi, T.; Yoshizato, K.; Yamashiro, S.; Takeshima, H.; Sato, K.; Hamada, K.; Kitamura, I.; Yoshimura, T.; Saya, H.; Kuratsu, J.-i. High-efficiency in vivo gene transfer using intraarterial plasmid DNA injection following in vivo electroporation. Cancer Res. 1996, 56, 1050–1055. [Google Scholar] [PubMed]
- Jaroszeski, M.J.; Gilbert, R.; Nicolau, C.; Heller, R. In vivo gene delivery by electroporation. Adv. Drug Deliv. Rev. 1999, 35, 131–137. [Google Scholar] [CrossRef]
- Boye, C.; Arpag, S.; Francis, M.; DeClemente, S.; West, A.; Heller, R.; Bulysheva, A. Reduction of plasmid vector backbone length enhances reporter gene expression. Bioelectrochemistry 2022, 144, 107981. [Google Scholar] [CrossRef]
- Miklavcic, D.; Semrov, D.; Mekid, H.; Mir, L. In vivo electroporation threshold determination. In Proceedings of the 22nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (cat. No. 00CH37143), Chicago, IL, USA, 23–28 July 2000; pp. 2815–2818. [Google Scholar]
- Meglič, S.H.; Pavlin, M. The impact of impaired DNA mobility on gene electrotransfer efficiency: Analysis in 3D model. BioMed. Eng. OnLine 2021, 20, 85. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, X.; Zang, L.; Yan, S.; Wu, X. Process Analysis and Parameter Selection of Cardiomyocyte Electroporation Based on the Finite Element Method. Cardiovasc. Eng. Technol. 2024, 15, 22–38. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Yan, Z.; Liu, K. Response characteristics and optimization of electroporation: Simulation based on finite element method. Electromagn. Biol. Med. 2021, 40, 321–337. [Google Scholar] [CrossRef]
- Langus, J.; Kranjc, M.; Kos, B.; Šuštar, T.; Miklavčič, D. Dynamic finite-element model for efficient modelling of electric currents in electroporated tissue. Sci. Rep. 2016, 6, 26409. [Google Scholar] [CrossRef]
- Ferreira, E.; Potier, E.; Logeart-Avramoglou, D.; Salomskaite-Davalgiene, S.; Mir, L.M.; Petite, H. Optimization of a gene electrotransfer method for mesenchymal stem cell transfection. Gene Ther. 2008, 15, 537–544. [Google Scholar] [CrossRef]
- Heller, R.; Lundberg, C.M.; Burcus, N.; Edelblute, C.; Guo, S. Gene electrotransfer of plasmids encoding cytokines as an effective immunotherapy approach for melanoma. J. Immunol. 2016, 196, 213.16. [Google Scholar] [CrossRef]
- Peng, W.; Polajžer, T.; Yao, C.; Miklavčič, D. Dynamics of cell death due to electroporation using different pulse parameters as revealed by different viability assays. Ann. Biomed. Eng. 2024, 52, 22–35. [Google Scholar] [CrossRef] [PubMed]
- Saulis, G.; Saulė, R. Comparison of electroporation threshold for different cell lines in vitro. Acta Phys. Pol. A 2009, 115, 1056–1058. [Google Scholar] [CrossRef]
- Forjanič, T.; Markelc, B.; Marčan, M.; Bellard, E.; Couillaud, F.; Golzio, M.; Miklavčič, D. Electroporation-induced stress response and its effect on gene electrotransfer efficacy: In vivo imaging and numerical modeling. IEEE Trans. Biomed. Eng. 2019, 66, 2671–2683. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271. [Google Scholar] [CrossRef]
- Davalos, R.V.; Rubinsky, B.; Otten, D.M. A feasibility study for electrical impedance tomography as a means to monitor tissue electroporation for molecular medicine. IEEE Trans. Biomed. Eng. 2002, 49, 400–403. [Google Scholar] [CrossRef]
- Davalos, R.V.; Otten, D.M.; Mir, L.M.; Rubinsky, B. Electrical impedance tomography for imaging tissue electroporation. IEEE Trans. Biomed. Eng. 2004, 51, 761–767. [Google Scholar] [CrossRef]
- Ivorra, A.; Rubinsky, B. In vivo electrical impedance measurements during and after electroporation of rat liver. Bioelectrochemistry 2007, 70, 287–295. [Google Scholar] [CrossRef]
- Atkins, R.M.; Fawcett, T.J.; Gilbert, R.; Hoff, A.M.; Connolly, R.; Brown, D.W.; Llewellyn, A.J.; Jaroszeski, M.J. Impedance spectroscopy as an indicator for successful in vivo electric field mediated gene delivery in a murine model. Bioelectrochemistry 2017, 115, 33–40. [Google Scholar] [CrossRef]
- Moisescu, M.G.; Radu, M.; Kovacs, E.; Mir, L.M.; Savopol, T. Changes of cell electrical parameters induced by electroporation. A dielectrophoresis study. Biochim. Et Biophys. Acta (BBA)-Biomembr. 2013, 1828, 365–372. [Google Scholar] [CrossRef]
- Daud, A.I.; DeConti, R.C.; Andrews, S.; Urbas, P.; Riker, A.I.; Sondak, V.K.; Munster, P.N.; Sullivan, D.M.; Ugen, K.E.; Messina, J.L. Phase I trial of interleukin-12 plasmid electroporation in patients with metastatic melanoma. J. Clin. Oncol. 2008, 26, 5896–5903. [Google Scholar] [CrossRef] [PubMed]
- Daud, A.; Algazi, A.P.; Ashworth, M.T.; Fong, L.; Lewis, J.; Chan, S.E.; Buljan, M.; Molina, M.A.; Takamura, K.T.; Diep, T.T. Systemic antitumor effect and clinical response in a phase 2 trial of intratumoral electroporation of plasmid interleukin-12 in patients with advanced melanoma. J. Clin. Oncol. 2014, 32, 15. [Google Scholar] [CrossRef]
- Lucas, M.L.; Jaroszeski, M.J.; Gilbert, R.; Heller, R. In vivo electroporation using an exponentially enhanced pulse: A new waveform. DNA Cell Biol. 2001, 20, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Pavšelj, N.; Préat, V. DNA electrotransfer into the skin using a combination of one high-and one low-voltage pulse. J. Control. Release 2005, 106, 407–415. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Jackson, D.L.; Burcus, N.I.; Chen, Y.-J.; Xiao, S.; Heller, R. Gene electrotransfer enhanced by nanosecond pulsed electric fields. Mol. Ther.-Methods Clin. Dev. 2014, 1-8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Donate, A.; Bulysheva, A.; Edelblute, C.; Jung, D.; Malik, M.A.; Guo, S.; Burcus, N.; Schoenbach, K.; Heller, R. Thermal assisted in vivo gene electrotransfer. Curr. Gene Ther. 2016, 16, 83–89. [Google Scholar] [CrossRef][Green Version]
- Bulysheva, A.; Hornef, J.; Edelblute, C.; Jiang, C.; Schoenbach, K.; Lundberg, C.; Malik, M.A.; Heller, R. Coalesced thermal and electrotransfer mediated delivery of plasmid DNA to the skin. Bioelectrochemistry 2019, 125, 127–133. [Google Scholar] [CrossRef]
- López-Alonso, B.; Sarnago, H.; Lucía, Ó.; Briz, P.; Burdío, J.M. Real-time impedance monitoring during electroporation processes in vegetal tissue using a high-performance generator. Sensors 2020, 20, 3158. [Google Scholar] [CrossRef]
- Atkins, R.M.; Fawcett, T.J.; Gilbert, R.; Hoff, A.M.; Connolly, R.; Brown, D.W.; Jaroszeski, M.J. Real-time impedance feedback to enhance cutaneous gene electrotransfer in a murine skin model. Bioelectrochemistry 2021, 142, 107885. [Google Scholar] [CrossRef]
- Barnes, H.; Humphries, S.M.; George, P.M.; Assayag, D.; Glaspole, I.; Mackintosh, J.A.; Corte, T.J.; Glassberg, M.; Johannson, K.A.; Calandriello, L. Machine learning in radiology: The new frontier in interstitial lung diseases. Lancet Digit. Health 2023, 5, e41–e50. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.K.; Saxena, S.; Lakshmanan, K.; Sangaiah, A.K.; Chauhan, H.; Shrivastava, S.; Singh, R.K. Deep feature learning for histopathological image classification of canine mammary tumors and human breast cancer. Inf. Sci. 2020, 508, 405–421. [Google Scholar] [CrossRef]
- Huttunen, R.; Leppänen, T.; Duce, B.; Arnardottir, E.S.; Nikkonen, S.; Myllymaa, S.; Töyräs, J.; Korkalainen, H. A Comparison of Signal Combinations for Deep Learning-Based Simultaneous Sleep Staging and Respiratory Event Detection. IEEE Trans. Biomed. Eng. 2022, 70, 1704–1714. [Google Scholar] [CrossRef] [PubMed]
- Zappatore, M.; Cerfeda, G.; Merla, C.; Tarricone, L. Machine learning for H-FIRE protocols: Tuning parameters for high-frequency irreversible electroporation by machine learning. IEEE Microw. Mag. 2021, 22, 42–59. [Google Scholar] [CrossRef]
- De Cillis, A.; Merla, C.; Tarricone, L.; Zappatore, M. Machine-Learning for Optimization of Electrodes and Waveforms for Electroporation. In Proceedings of the 2022 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cape Town, South Africa, 5–9 September 2022; pp. 031–034. [Google Scholar]
- Eresen, A.; Zhou, K.; Sun, C.; Shangguan, J.; Wang, B.; Pan, L.; Hu, S.; Pang, Y.; Zhang, Z.; Tran, R.M.N. Early assessment of irreversible electroporation ablation outcomes by analyzing MRI texture: Preclinical study in an animal model of liver tumor. Am. J. Transl. Res. 2022, 14, 5541. [Google Scholar]
- Briz, P.; López-Alonso, B.; Sarnago, H.; Burdío, J.; Lucía, O. Tumor location on electroporation therapies by means of multi-electrode structures and machine learning. Bioelectrochemistry 2023, 154, 108510. [Google Scholar] [CrossRef]
- Patino, C.A.; Mukherjee, P.; Lemaitre, V.; Pathak, N.; Espinosa, H.D. Deep learning and computer vision strategies for automated gene editing with a single-cell electroporation platform. SLAS Technol. Transl. Life Sci. Innov. 2021, 26, 26–36. [Google Scholar] [CrossRef]
- Vitale, J.; Sassi, M.; Pecchia, L. A Machine Learning Approach for Predicting Electrophysiological Responses in Genetically Modified HEK Cells. In Proceedings of the European Medical and Biological Engineering Conference, Portoroz, Slovenia, 9–13 June 2024; pp. 1–14. [Google Scholar]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; Wiley: New York, NY, USA, 1973; Volume 3. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Heller, R.; Jaroszeski, M.; Atkin, A.; Moradpour, D.; Gilbert, R.; Wands, J.; Nicolau, C. In vivo gene electroinjection and expression in rat liver. FEBS Lett. 1996, 389, 225–228. [Google Scholar] [CrossRef] [PubMed]
- Heller, L.; Jaroszeski, M.; Coppola, D.; Pottinger, C.; Gilbert, R.; Heller, R. Electrically mediated plasmid DNA delivery to hepatocellular carcinomas in vivo. Gene Ther. 2000, 7, 826–829. [Google Scholar] [CrossRef]
- Pasquet, L.; Chabot, S.; Bellard, E.; Markelc, B.; Rols, M.-P.; Reynes, J.-P.; Tiraby, G.; Couillaud, F.; Teissie, J.; Golzio, M. Safe and efficient novel approach for non-invasive gene electrotransfer to skin. Sci. Rep. 2018, 8, 16833. [Google Scholar] [CrossRef]
- Boye, C.; Arpag, S.; Burcus, N.; Lundberg, C.; DeClemente, S.; Heller, R.; Francis, M.; Bulysheva, A. Cardioporation enhances myocardial gene expression in rat heart. Bioelectrochemistry 2021, 142, 107892. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, J.N. Receiver operating characteristic curve in diagnostic test assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef] [PubMed]
- Rols, M.-P.; Delteil, C.; Golzio, M.; Dumond, P.; Cros, S.; Teissie, J. In vivo electrically mediated protein and gene transfer in murine melanoma. Nat. Biotechnol. 1998, 16, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Heller, L.; Pottinger, C.; Jaroszeski, M.J.; Gilbert, R.; Heller, R. In vivo electroporation of plasmids encoding GM-CSF or interleukin-2 into existing B16 melanomas combined with electrochemotherapy induces long-term antitumour immunity. Melanoma Res. 2000, 10, 577–583. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Nolan, E.; Kreitschitz, S.; Rabussay, D.P. Enhanced delivery of naked DNA to the skin by non-invasive in vivo electroporation. Biochim. Et Biophys. Acta (BBA)-Gen. Subj. 2002, 1572, 1–9. [Google Scholar] [CrossRef]
- Ferraro, B.; Cruz, Y.L.; Coppola, D.; Heller, R. Intradermal delivery of plasmid VEGF165 by electroporation promotes wound healing. Mol. Ther. 2009, 17, 651–657. [Google Scholar] [CrossRef]
- Heller, R.; Cruz, Y.; Heller, L.C.; Gilbert, R.A.; Jaroszeski, M.J. Electrically mediated delivery of plasmid DNA to the skin, using a multielectrode array. Hum. Gene Ther. 2010, 21, 357–362. [Google Scholar] [CrossRef]
- Reberšek, M.; Faurie, C.; Kandušer, M.; Čorović, S.; Teissié, J.; Rols, M.-P.; Miklavčič, D. Electroporator with automatic change of electric field direction improves gene electrotransfer in-vitro. Biomed. Eng. Online 2007, 6, 25. [Google Scholar] [CrossRef]
- Hojman, P.; Zibert, J.R.; Gissel, H.; Eriksen, J.; Gehl, J. Gene expression profiles in skeletal muscle after gene electrotransfer. BMC Mol. Biol. 2007, 8, 56. [Google Scholar] [CrossRef]
- Kos, S.; Vanvarenberg, K.; Dolinsek, T.; Cemazar, M.; Jelenc, J.; Préat, V.; Sersa, G.; Vandermeulen, G. Gene electrotransfer into skin using noninvasive multi-electrode array for vaccination and wound healing. Bioelectrochemistry 2017, 114, 33–41. [Google Scholar] [CrossRef]
- Bulysheva, A.A.; Hargrave, B.; Burcus, N.; Lundberg, C.G.; Murray, L.; Heller, R. Vascular endothelial growth factor-A gene electrotransfer promotes angiogenesis in a porcine model of cardiac ischemia. Gene Ther. 2016, 23, 649–656. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, P.E.; Nikulin, M.S. A Guide to Chi-Squared Testing; John Wiley & Sons: Hoboken, NJ, USA, 1996; Volume 280. [Google Scholar]


| Feature | Description |
|---|---|
| Common Name | Common name of plasmid used in study |
| Dose | Dose of plasmid in μg |
| Electrode | Electrode configuration |
| Electrode Type | Penetrating or non-penetrating electrode |
| Backbone Name | Name of backbone in plasmid |
| Promoter Name | Name of promoter in plasmid |
| Construct Size | Size of entire plasmid in kb |
| Backbone Size | Size of backbone of plasmid in kb |
| Insert Size | Size of insert of plasmid in kb |
| Encoding For | Name of protein encoded for |
| Pulse Technique | Straight pulsing between 2 electrodes or multielectrode array pulsing |
| Pulse Polarity | Same or alternating polarity when different pulse parameters are used |
| Pulse V1/V2 | Pulse amplitude of the first/second pulse in volts |
| Field Strength 1/2 | Field strength of the first/second pulse in volts/cm |
| Pulse Width 1/2 | Pulse width of the first/second pulse in μs |
| Number of Pulses | Number of pulses/pulse trains |
| Dwell Time | Time between pulses/pulse trains in s |
| Electrode Spacing | Distance between electrodes in cm |
| General/Specific Tissue | Target tissue for the study |
| Sex | Sex of the animal/source cells |
| General/Specific Species | Species of the animal/source cells |
| Expression Location | Location(s) of expression determined via histology of the target tissue(s) |
| Outcome | Success or failure of the treatment based on source author(s) significance criteria |
| Source | Plasmid Common Name | Species/Cell Line | Electrode | Pulse Polarity | Experiments |
|---|---|---|---|---|---|
| [42] | pRc/CMV-Luc | Sprague Dawley Rat | 6-Needle Circle | Positive | 7 |
| [48] | pUT531 | B6D2F1 Mouse | 2-Plate | Positive | 10 |
| [43] | pCMV-Luc+ | Sprague Dawley Rat | 7-Needle | Positive | 11 |
| [49] | pCMV-Luc+ | BC57B1/6 Mouse | 7-Needle | Positive | 1 |
| [49] | pCMV-Luc+ | BC57B1/6 Mouse | 7-Needle | Positive | 4 |
| [50] | pLuc | SKH1 Mouse | Caliper | Alternating | 12 |
| [25] | pCMVLuc | Wistar Rat | Caliper | Positive | 7 |
| [51] | pVEGF | Sprague Dawley Rat | 4-Plate | Positive | 2 |
| [52] | gWiz-Luc | C57B1/6 Mouse | Caliper + 6-Needle | Positive | 8 |
| [22] | pUMVC3-hIL-12-NGVL3 | Human | 6-Needle Circle | Positive | 24 |
| [53] | pEGFP-C1 | Chinese Hamster Ovarian Cells | 4-Pin Circle | Positive + Alternating | 4 |
| [54] | phGFP-S655T | C57Black/C Mouse | 2-Plate | Alternating | 1 |
| [54] | phGFP-S655T | Wistar Rat | 2-Plate | Alternating | 1 |
| [26] | gWiz-Luc | HaCaT Cells | Cuvette | Positive | 2 |
| [44] | pCMV-tdTomato | C57Bl/6 Mouse | Contact Wire | Positive | 9 |
| [11] | pDRIVE2-CMV | Mesenchymal Stem Cells | Cuvette | Positive | 7 |
| [55] | pVAX2-LUC | C57BL/6 Mouse | Plate + 7-Pin Hex | Positive | 3 |
| [56] | pVax1-hVEGF165(pVEGF-A) | Yorkshire Pig | 4-Pin | Positive | 1 |
| [3] | pCH110 | Wistar Rat | 2-Pin | Positive | 4 |
| [45] | gWiz-Luc and NTC9385R-Luc | Sprague Dawley Rat | Monopolar + 4-Pin | Positive + Alternating | 4 |
| [5] | gWiz-Luc and NTC9385R-Luc | Sprague Dawley Rat | Caliper | Alternating | 10 |
| Model | Accuracy | Sensitivity | Specificity | F1-Score | MCC | ROC AUC |
|---|---|---|---|---|---|---|
| Basic ANN | 59.0% | 0% | 100.0% | 0.0 | −1.0 | 0.6036 |
| Optimized ANN | 66.7% | 56.3% | 73.9% | 0.5806 | 0.3050 | 0.6536 |
| Hyperparameter Optimized ANN | 59.0% | 43.8% | 69.6% | 0.4667 | 0.1365 | 0.4875 |
| Top 5 Features ANN | 71.8% | 43.8% | 91.3% | 0.5600 | 0.4092 | 0.4679 |
| Top 6 Features ANN | 64.1% | 25.0% | 91.3% | 0.3636 | 0.2223 | 0.8478 |
| Top 7 Features ANN | 69.2% | 43.8% | 87.0% | 0.5385 | 0.3459 | 0.8288 |
| Top 8 Features ANN | 66.7% | 31.3% | 91.3% | 0.4348 | 0.2891 | 0.8274 |
| Top 9 Features ANN | 69.2% | 37.5% | 91.3% | 0.5000 | 0.3509 | 0.8333 |
| Basic SVM | 53.9% | 31.3% | 69.6% | 0.3571 | 0.0087 | 0.8125 |
| Top 5 Features SVM | 59.0% | 0% | 100.0% | 0.0 | −1.0 | 0.4214 |
| Top 6 Features SVM | 59.0% | 0% | 100.0% | 0.0 | −1.0 | 0.3234 |
| Top 7 Features SVM | 64.1% | 31.3% | 87.0% | 0.4167 | 0.2218 | 0.6012 |
| Top 8 Features SVM | 64.1% | 31.3% | 87.0% | 0.4167 | 0.2218 | 0.6012 |
| Top 9 Features SVM | 64.1% | 31.3% | 87.0% | 0.4167 | 0.2218 | 0.5744 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otten, A.; Francis, M.; Bulysheva, A. Exploration of Machine Learning Models for Prediction of Gene Electrotransfer Treatment Outcomes. Appl. Sci. 2024, 14, 11601. https://doi.org/10.3390/app142411601
Otten A, Francis M, Bulysheva A. Exploration of Machine Learning Models for Prediction of Gene Electrotransfer Treatment Outcomes. Applied Sciences. 2024; 14(24):11601. https://doi.org/10.3390/app142411601
Chicago/Turabian StyleOtten, Alex, Michael Francis, and Anna Bulysheva. 2024. "Exploration of Machine Learning Models for Prediction of Gene Electrotransfer Treatment Outcomes" Applied Sciences 14, no. 24: 11601. https://doi.org/10.3390/app142411601
APA StyleOtten, A., Francis, M., & Bulysheva, A. (2024). Exploration of Machine Learning Models for Prediction of Gene Electrotransfer Treatment Outcomes. Applied Sciences, 14(24), 11601. https://doi.org/10.3390/app142411601






