An Enhanced Deep Q Network Algorithm for Localized Obstacle Avoidance in Indoor Robot Path Planning
Abstract
1. Introduction
- (1)
- The PER mechanism is introduced to optimize the sample selection strategy, prioritize the use of key experiences, and accelerate the learning process;
- (2)
- Adopting the Duel DQN structure to improve strategy stability and learning efficiency by decomposing the value function and advantage function;
- (3)
- Drawing on Munchausen’s idea of reinforcement learning, a regularized “logarithmic strategy” is added to enhance the robustness of the reward signal and further improve the performance and stability of the algorithm.
2. Related Work
3. Implementation Based on PER-D2MQN Algorithm
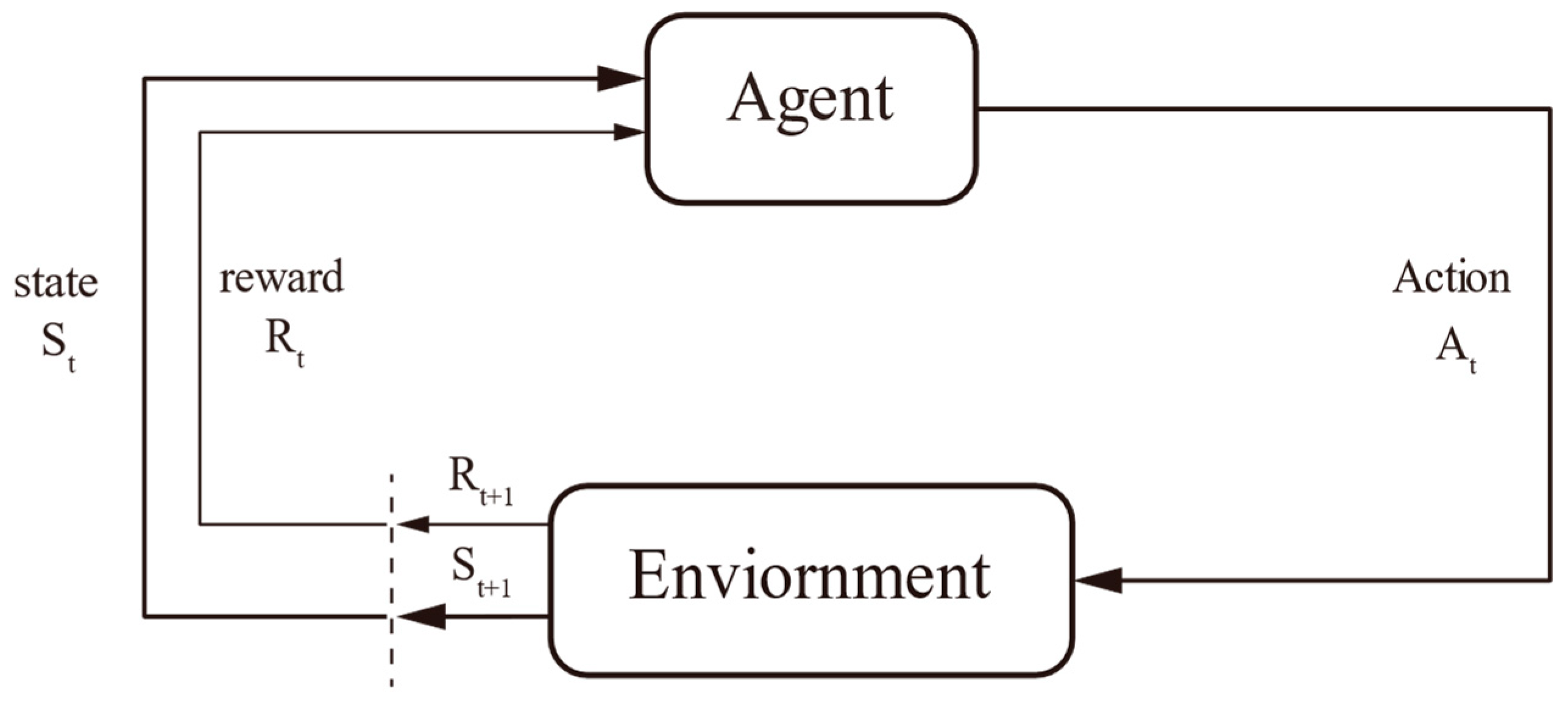
3.1. Theoretical Foundation
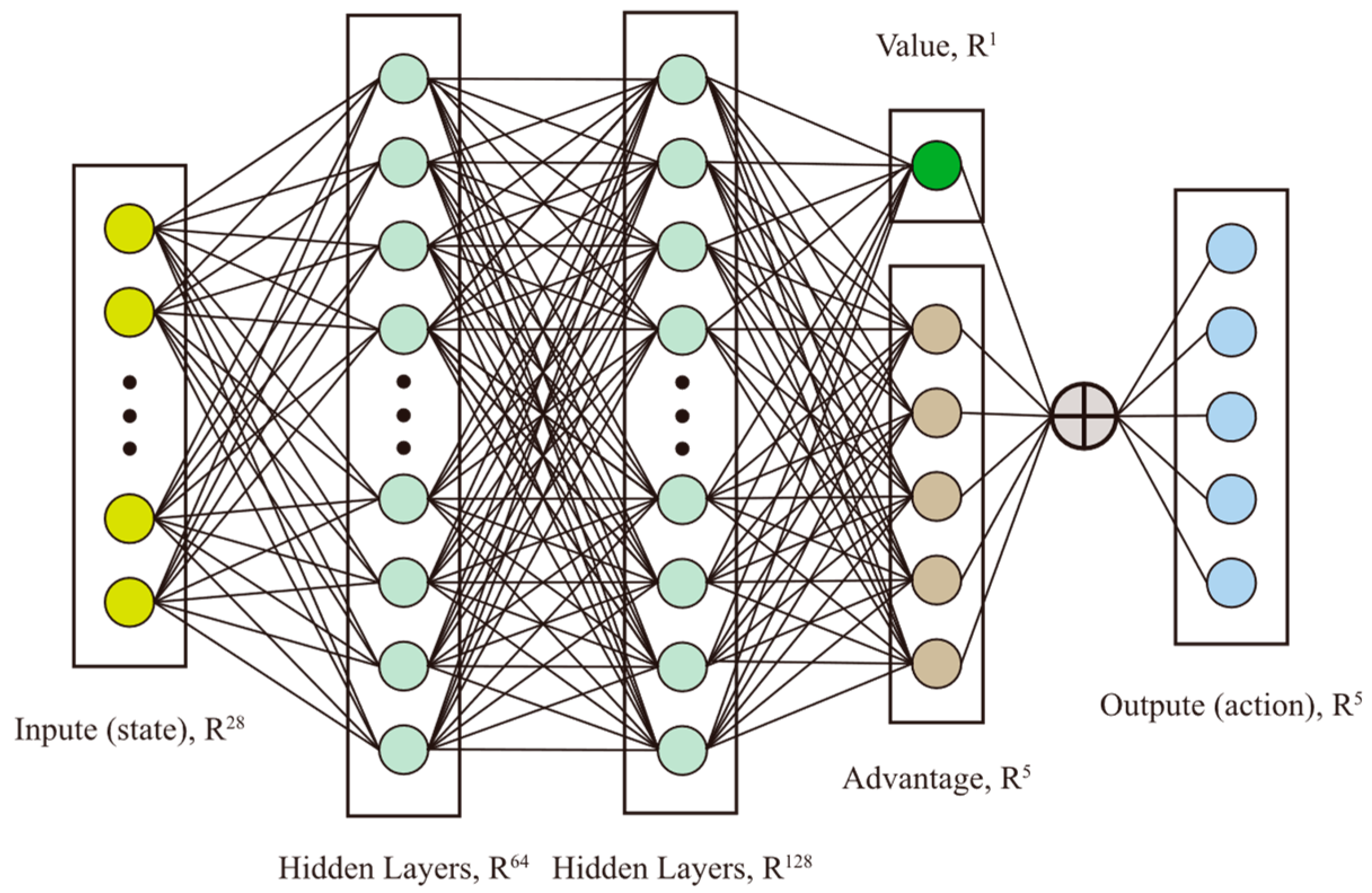
3.2. Duel DQN Structure Model
3.3. Prioritized Experience Replay Buffer
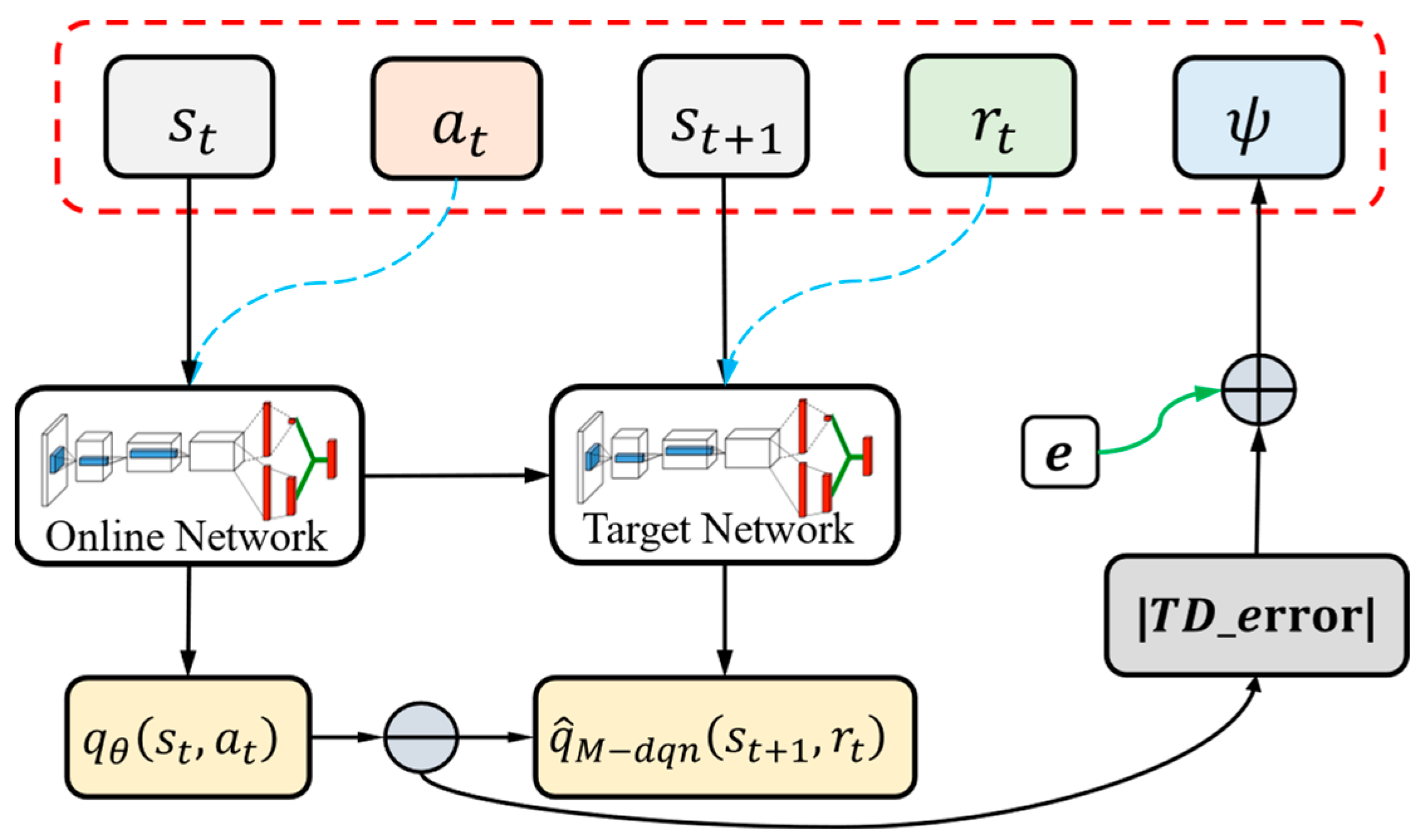
3.4. PER-D2MQN
| Algorithm 1: PER-D2MQN Algorithm |
| Input: Output: 1 Initialize 2 Initialize online network and target network with random weights and biases 3 for episode 1 to E do 4 Initialize state (Reset Environment) 5 for t 1 to episode_step do 6 Observe state and input state into online network 7 Select action using 8 Execute action in the environment, get , , and flag 9 Store experience () into with maximum priority of 10 if size of batch _size then 11 Sample batch from based on priority weights 12 for each () in batch do 13 Compute ; 14 Compute Munchausen log policy term: 15 Compute Munchausen reward: 16 Compute target: 17 Compute target: 18 Compute loss: 19 Update priorities in 20 Gradient descent on loss 21 if global_step % target update 0 then 22 Update target network 23 if done then 24 Break 25 Increment global_step 26 if then 27 |
4. Environment Design
4.1. Action Design of Turtlebot3 Robot
4.2. State Design of Turtlebot3 Robot
4.3. Reward Function
4.4. Exploration Strategy
4.5. Assumptions
5. Experimental Analysis
5.1. Experimental Platform and Parameter Setting
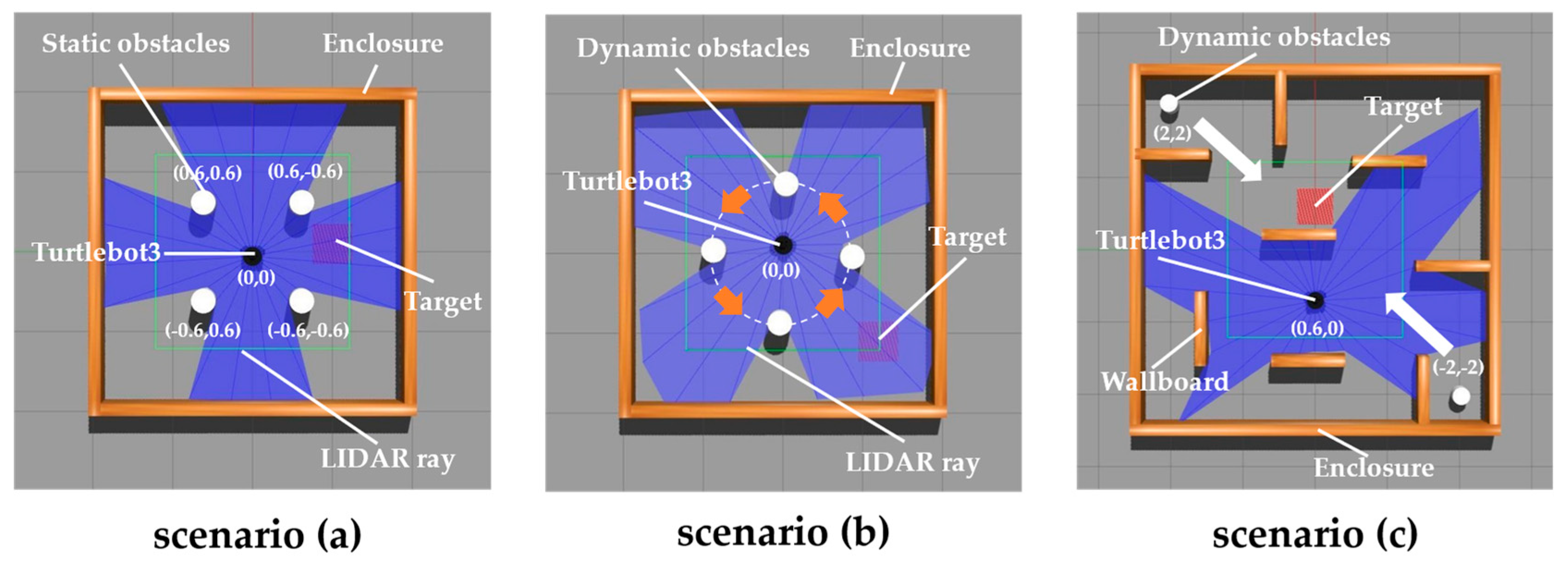
5.2. Experimental Simulation Environment
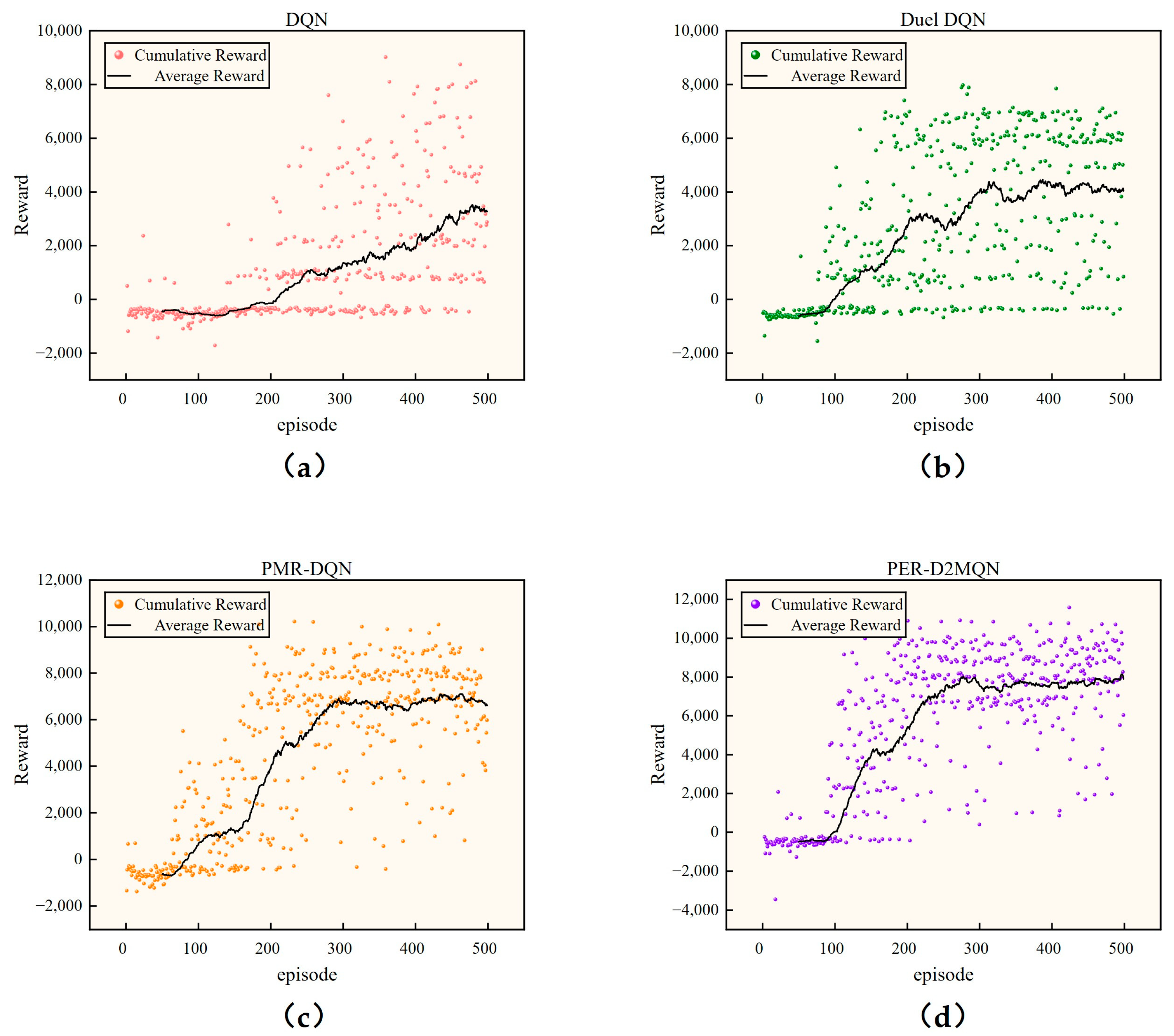
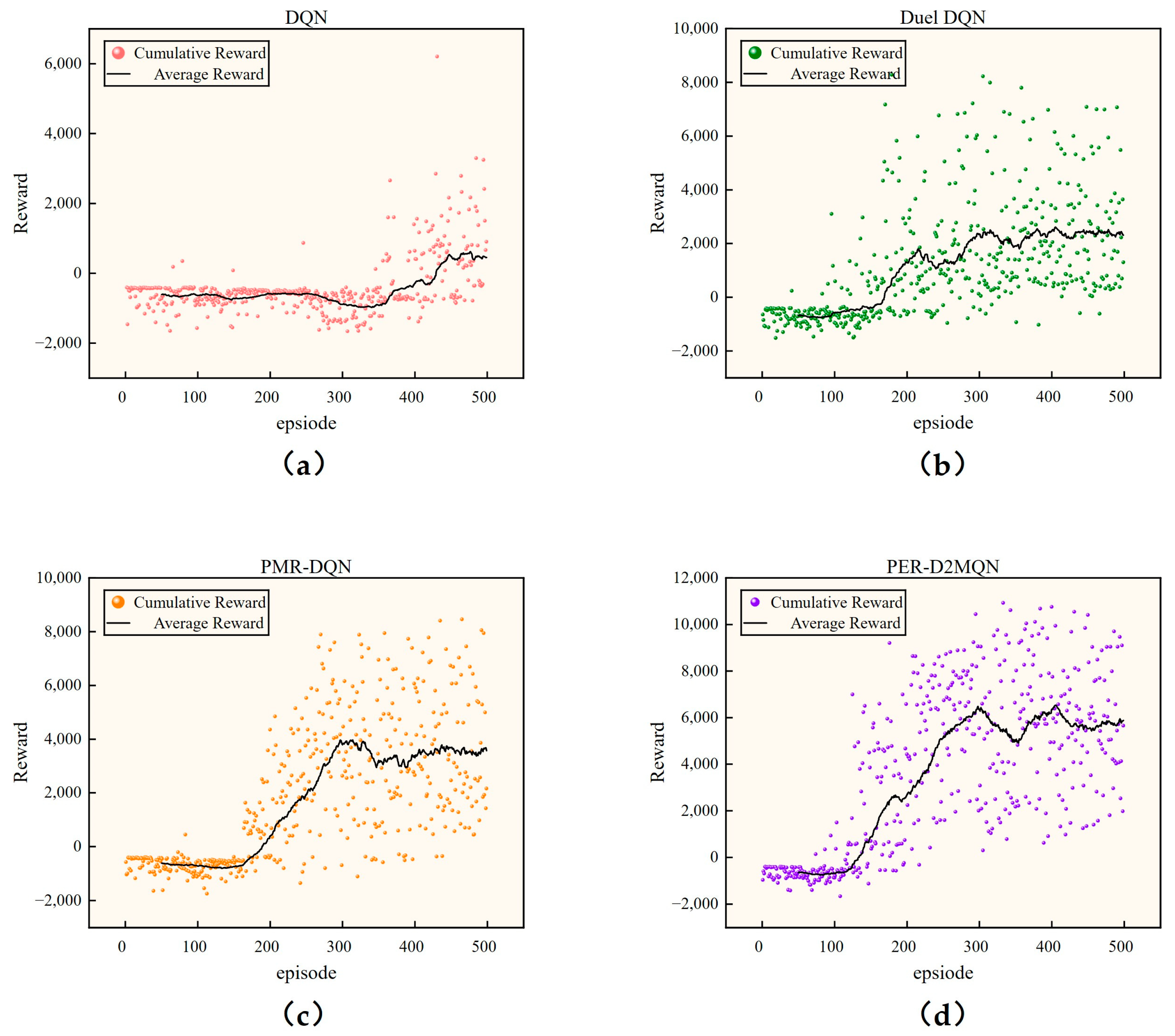
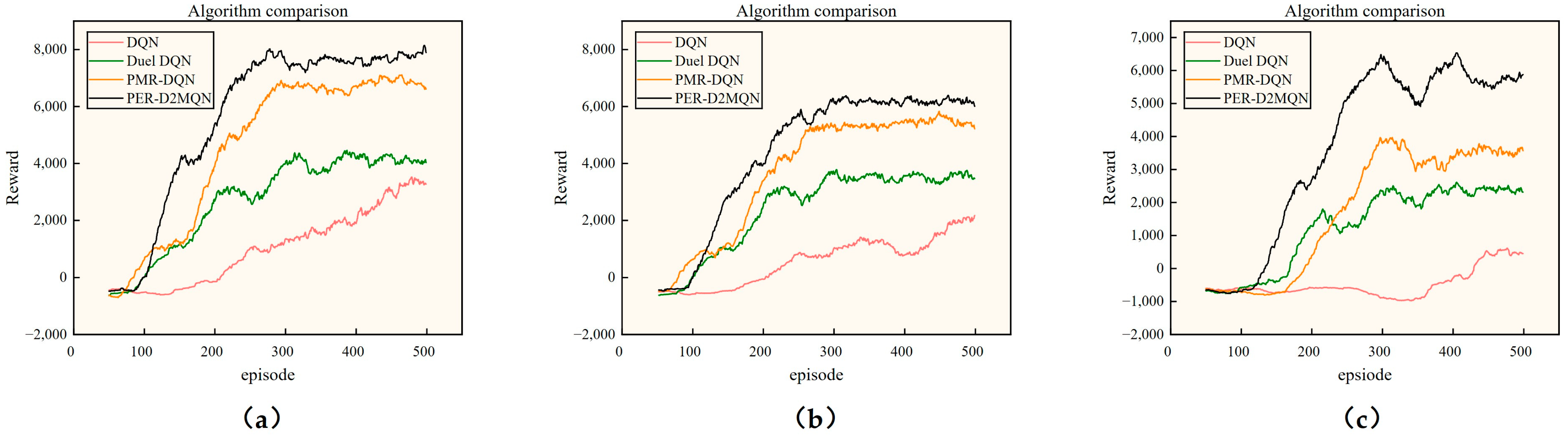
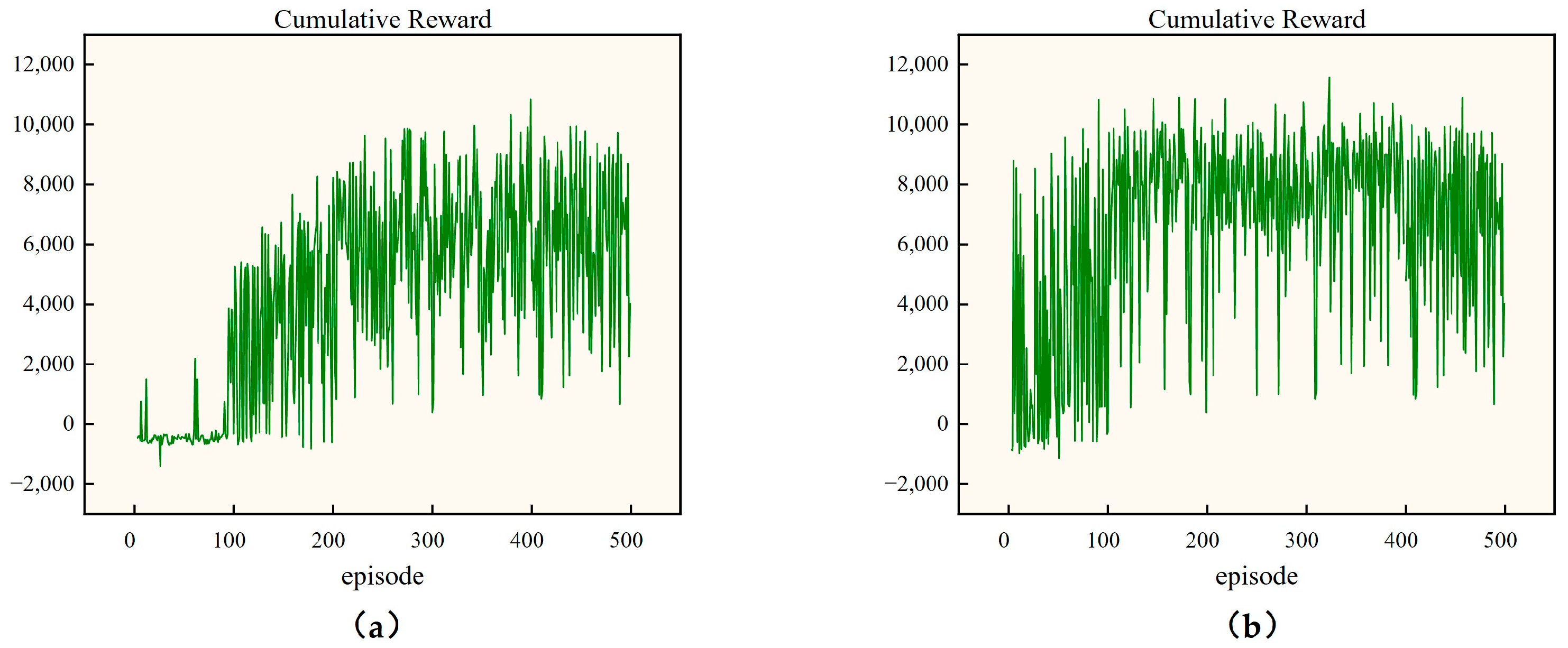
5.3. Simulation Comparison Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Panigrahi, P.K.; Bisoy, S.K. Localization strategies for autonomous mobile robots: A review. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6019–6039. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del-Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Gök, M. Dynamic path planning via Dueling Double Deep Q-Network (D3QN) with prioritized experience replay. Appl. Soft Comput. 2024, 158, 111503. [Google Scholar] [CrossRef]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of Autonomous Path Planning Algorithms for Mobile Robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Song, J.; Zhao, M.; Liu, Y.; Liu, H.; Guo, X. Multi-Rotor UAVs Path Planning Method based on Improved Artificial Potential Field Method. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8242–8247. [Google Scholar]
- Lee, M.-F.R.; Yusuf, S.H. Mobile Robot Navigation Using Deep Reinforcement Learning. Processes 2022, 10, 2748. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Wei, Y.; Zheng, R. A Reinforcement Learning Framework for Efficient Informative Sensing. IEEE Trans. Mob. Comput. 2020, 27, 2306–2317. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar] [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning. arXiv 2016, arXiv:1511.06581. Available online: https://arxiv.org/abs/1511.06581 (accessed on 14 July 2024).
- Kim, H.; Lee, W. Dynamic Obstacle Avoidance of Mobile Robots Using Real-Time Q Learning. In Proceedings of the 2022 International Conference on Electronics, Information, and Communication (ICEIC), Jeju, Republic of Korea, 6–9 February 2022; IEEE: New York, NY, USA, 2022; pp. 1–2. [Google Scholar]
- Wang, C.; Yang, X.; Li, H. Improved Q Learning Applied to Dynamic Obstacle Avoidance and Path Planning. IEEE Access 2022, 10, 92879–92888. [Google Scholar] [CrossRef]
- Zhou, Q.; Lian, Y.; Wu, J.; Zhu, M.; Wang, H.; Cao, J. An optimized Q Learning algorithm for mobile robot local path planning. Knowl.-Based Syst. 2024, 286, 111400. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Picos, K.; Pantrigo, J.J.; Montemayor, A.S.; Cuesta-Infante, A. Mobile Robot Path Planning Using a QAPF Learning Algorithm for Known and Unknown Environments. IEEE Access 2022, 10, 84648–84663. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2016, arXiv:1511.05952. Available online: https://arxiv.org/abs/1511.05952 (accessed on 15 July 2024).
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In International Conference on Machine Learning, Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 June 2018; Dy, J., Krause, A., Eds.; JMLR-Journal Machine Learning Research: San Diego, CA, USA, 2018; Volume 80, Available online: https://webofscience.clarivate.cn/wos/alldb/full-record/WOS:000683379201099 (accessed on 15 July 2024).
- Vieillard, N.; Pietquin, O.; Geist, M. Munchausen Reinforcement Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 4235–4246. [Google Scholar]
- Liu, S.; Zheng, C.; Huang, Y.; Quek, T.Q. Distributed Reinforcement Learning for Privacy-Preserving Dynamic Edge Caching. IEEE J. Sel. Areas Commun. 2022, 40, 749–760. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Kuang, L.; Han, X.; Xue, H. Improved Robot Path Planning Method Based on Deep Reinforcement Learning. Sensors 2023, 23, 5622. [Google Scholar] [CrossRef]
- Zhang, F.; Gu, C.; Yang, F. An Improved Algorithm of Robot Path Planning in Complex Environment Based on Double DQN. arXiv 2021, arXiv:2107.11245. [Google Scholar]
- Yang, Y.; Wang, J.; Zhang, H.; Dai, S. Path planning of mobile robot based on improved DDQN. J. Phys. Conf. Ser. 2024, 2021, 012029. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, Z.; Lv, J.; Shi, L.; Hou, Z.; Xu, S. DM-DQN: Dueling Munchausen deep Q network for robot path planning. Complex Intell. Syst. 2023, 9, 4287–4300. [Google Scholar] [CrossRef]
- Kong, F.; Wang, Q.; Gao, S.; Yu, H. B-APFDQN: A UAV Path Planning Algorithm Based on Deep Q-Network and Artificial Potential Field. IEEE Access 2023, 11, 44051–44064. [Google Scholar] [CrossRef]
- Li, J.; Shen, D.; Yu, F.; Zhang, R. Air Channel Planning Based on Improved Deep Q Learning and Artificial Potential Fields. Aerospace 2023, 10, 758. [Google Scholar] [CrossRef]
- Li, W.; Yue, M.; Shangguan, J.; Jin, Y. Navigation of Mobile Robots Based on Deep Reinforcement Learning: Reward Function Optimization and Knowledge Transfer. Int. J. Control. Autom. Syst. 2023, 21, 563–574. [Google Scholar] [CrossRef]
- Sivaranjani, A.; Vinod, B. Artificial Potential Field Incorporated Deep-Q-Network Algorithm for Mobile Robot Path Prediction. Intell. Autom. Soft Comput. 2023, 35, 1135–1150. [Google Scholar] [CrossRef]
- Han, Q.; Feng, S.; Wu, X.; Qi, J.; Yu, S. Retrospective-Based Deep Q Learning Method for Autonomous Pathfinding in Three-Dimensional Curved Surface Terrain. Appl. Sci. 2023, 13, 6030. [Google Scholar] [CrossRef]
- Tu, G.-T.; Juang, J.-G. UAV Path Planning and Obstacle Avoidance Based on Reinforcement Learning in 3D Environments. Actuators 2023, 12, 57. [Google Scholar] [CrossRef]
- Xie, R.; Meng, Z.; Zhou, Y.; Ma, Y.; Wu, Z. Heuristic Q Learning based on experience replay for three-dimensional path planning of the unmanned aerial vehicle. Sci. Prog. 2020, 103, 003685041987902. [Google Scholar] [CrossRef]
- Yao, J.; Li, X.; Zhang, Y.; Ji, J.; Wang, Y.; Zhang, D.; Liu, Y. Three-Dimensional Path Planning for Unmanned Helicopter Using Memory-Enhanced Dueling Deep Q Network. Aerospace 2022, 9, 417. [Google Scholar] [CrossRef]
- Lin, C.-J.; Jhang, J.-Y.; Lin, H.-Y.; Lee, C.-L.; Young, K.-Y. Using a Reinforcement Q Learning-Based Deep Neural Network for Playing Video Games. Electronics 2019, 8, 1128. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, P.; Zeng, Z.; Xiao, J.; Lu, H.; Zhou, Z. Robot navigation in a crowd by integrating deep reinforcement learning and online planning. Appl. Intell. 2022, 52, 15600–15616. [Google Scholar] [CrossRef]
- Almazrouei, K.; Kamel, I.; Rabie, T. Dynamic Obstacle Avoidance and Path Planning through Reinforcement Learning. Appl. Sci. 2023, 13, 8174. [Google Scholar] [CrossRef]
- Kamalova, A.; Lee, S.G.; Kwon, S.H. Occupancy Reward-Driven Exploration with Deep Reinforcement Learning for Mobile Robot System. Appl. Sci. 2022, 12, 9249. [Google Scholar] [CrossRef]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Singapore, 2017; pp. 3389–3396. [Google Scholar]
- Gao, J.; Ye, W.; Guo, J.; Li, Z. Deep reinforcement learning for indoor mobile robot path planning. Sensors 2020, 20, 5493. [Google Scholar] [CrossRef] [PubMed]
- Matej, D.; Skocaj, D. Deep reinforcement learning for map-less goal-driven robot navigation. Int. J. Adv. Robot. Syst. 2021, 18, 1–13. [Google Scholar] [CrossRef]

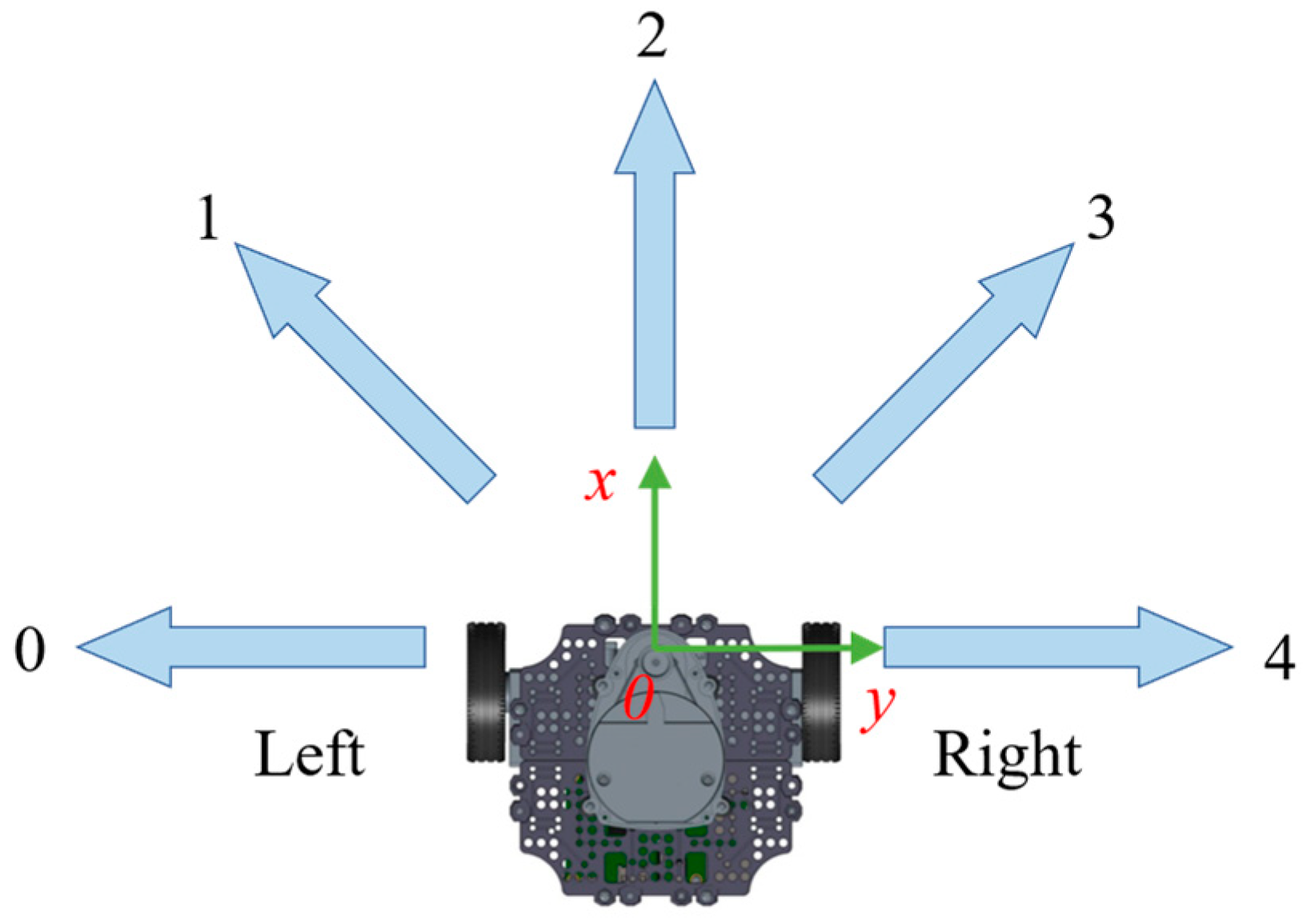


| Action | 0 | 1 | 2 | 3 | 4 |
| Angular Velocity | −1.5 | −0.75 | 0 | 0.75 | 1.5 |
| Hyperparameter | Value | Description |
|---|---|---|
| 0.99 | Discount factor | |
| 0.03 | Temperature factor | |
| 0.99 | Exploration rate of action | |
| 0.00025 | Neural network learning rate | |
| 1.0 | Exploration rate of action | |
| 0.01 | Minimum exploration rate | |
| episode_step | 6000 | One episode time step |
| target_update | 2000 | Update rate of the target network |
| Min_batch size | 64 | The size of a set of experience extracted |
| 0.6 | Constants that determine a specific priority | |
| PERB | 1,000,000 | Experience Replay Buffer Maximum Capacity |
| Algorithm | Success Rate | Convergence Average Steps | Convergence Average Time/s |
|---|---|---|---|
| DQN | 13.6% | 161 | 78 |
| Duel DQN | 36.2% | 94 | 45 |
| PMR-DQN | 57.6% | 74 | 38 |
| PER-D2MQN | 65.8% | 64 | 31 |
| Algorithm | Success Rate | Convergence Average Steps | Convergence Average Time/s |
|---|---|---|---|
| DQN | 9.5% | 357 | 174 |
| Duel DQN | 27.7% | 144 | 70 |
| PMR-DQN | 46.3% | 88 | 43 |
| PER-D2MQN | 52.7% | 77 | 38 |
| Algorithm | Success Rate | Convergence Average Steps | Convergence Average Time/s |
|---|---|---|---|
| DQN | 0.2% | — | — |
| Duel DQN | 12.2% | 238 | 116 |
| PMR-DQN | 23.8% | 167 | 81 |
| PER-D2MQN | 44.6% | 91 | 44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Yu, J.; Qian, S. An Enhanced Deep Q Network Algorithm for Localized Obstacle Avoidance in Indoor Robot Path Planning. Appl. Sci. 2024, 14, 11195. https://doi.org/10.3390/app142311195
Chen C, Yu J, Qian S. An Enhanced Deep Q Network Algorithm for Localized Obstacle Avoidance in Indoor Robot Path Planning. Applied Sciences. 2024; 14(23):11195. https://doi.org/10.3390/app142311195
Chicago/Turabian StyleChen, Cheng, Jiantao Yu, and Songrong Qian. 2024. "An Enhanced Deep Q Network Algorithm for Localized Obstacle Avoidance in Indoor Robot Path Planning" Applied Sciences 14, no. 23: 11195. https://doi.org/10.3390/app142311195
APA StyleChen, C., Yu, J., & Qian, S. (2024). An Enhanced Deep Q Network Algorithm for Localized Obstacle Avoidance in Indoor Robot Path Planning. Applied Sciences, 14(23), 11195. https://doi.org/10.3390/app142311195






