A New Method for 3D Dental Records Related to Orthopedic Treatments: The Hemimaxillary Plane Reference System and Its Clinical Implications
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
- The use of a new stable three-dimensional intra-hemimaxillary reference system (represented by the plane perpendicular to the plane Ans-Pns-N and passing through the line Ans-Pns) makes it possible to minimize measurement errors caused by three-dimensional maxillary bone movements during treatment.
- For clinical improvements to be achieved in the expansion phase, it is necessary that the molar rotation angle (γ) and the intermolar angle (β) at the end of expansion are less than the difference between the respective pre-treatment angle and the orthopedic expansion angle.
- It is possible to calculate expansion angles (α and δ) by a reliable and reproducible method, respecting radiation protection principles, without requiring post-expansion CBCT scans, with the following formulas:
- By offering a practical and minimally invasive approach for assessing RME outcomes, this study contributes to advancing safer and more effective orthodontic practices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Angell, D.H. Treatment of irregularity of the permanent or adult teeth. Dent. Cosm. 1860, 1, 540–544. [Google Scholar]
- Haas, A.J. Palatal expansion: Just the beginning of dentofacial orthopedics. Am. J. Orthod. 1970, 57, 219–255. [Google Scholar] [CrossRef] [PubMed]
- Ugolini, A.; Cerruto, C.; Di Vece, L.; Ghislanzoni, L.H.; Sforza, C.; Doldo, T.; Silvestrini-Biavati, A.; Caprioglio, A. Dental arch response to Haas-type rapid maxillary expansion anchored to deciduous vs permanent molars: A multicentric randomized controlled trial. Angle Orthod. 2015, 85, 570–576. [Google Scholar] [CrossRef] [PubMed]
- Angelieri, F.; Cevidanes, L.H.; Franchi, L.; Gonçalves, J.R.; Benavides, E.; McNamara, J.A., Jr. Midpalatal suture maturation: Classification method for individual assessment before rapid maxillary expansion. Am. J. Orthod. Dentofac. Orthop. 2013, 144, 759–769. [Google Scholar] [CrossRef] [PubMed]
- Proffit, W.R.; Fields, H.W. Biomeccanica e meccanica. In Ortodonzia Moderna; Masson Publisher: Milano, Italy, 2001; pp. 313–382. [Google Scholar]
- Capozzi, F. (Ed.) Considerazioni sul significato clinico e biologico della disgiunzione rapida del palato. In La Disgiunzione Rapida del Palato in Ortognatodonzia; Piccin Nuova Libraia Publisher: Padova, Italy, 2008; pp. 1–52. [Google Scholar]
- Franchi, L.; Baccetti, T.; Lione, R.; Fanucci, E.; Cozza, P. Modifications of midpalatal sutural density induced by rapid maxillary expansion: A low-dose computed-tomography evaluation. Am. J. Orthod. Dentofac. Orthop. 2010, 137, 486–488. [Google Scholar] [CrossRef] [PubMed]
- Wertz, R.A. Skeletal and dental changes accompanying rapid midpalatal suture opening. Am. J. Orthod. 1970, 58, 41–66. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Xu, T.; Zou, W. Effects of rapid maxillary expansion on the midpalatal suture: A systematic review. Eur. J. Orthod. 2015, 37, 651–655. [Google Scholar] [CrossRef] [PubMed]
- Sayar, G.; Kılınç, D.D. Rapid maxillary expansion outcomes according to midpalatal suture maturation levels. Prog. Orthod. 2019, 20, 27. [Google Scholar] [CrossRef] [PubMed]
- Podesser, B.; Williams, S.; Crismani, A.G.; Bantleon, H.P. Evaluation of the effects of rapid maxillary expansion in growing children using computer tomography scanning: A pilot study. Eur. J. Orthod. 2007, 29, 37–44. [Google Scholar] [CrossRef]
- McNamara, J.A., Jr.; Baccetti, T.; Franchi, L.; Herberger, T.A. Rapid maxillary expansion followed by fixed appliances: A long-term evaluation of changes in arch dimensions. Angle Orthod. 2003, 73, 344–353. [Google Scholar]
- De Baets, J. The role of the upper first molar in lower incisor crowding. J. Clin. Orthod. 1995, 29, 146–157. [Google Scholar] [PubMed]
- Ladner, P.T.; Muhl, Z.F. Changes concurrent with orthodontic treatment when maxillary expansion is a primary goal. Am. J. Orthod. Dentofac. Orthop. 1995, 108, 184–193. [Google Scholar] [CrossRef]
- Chung, C.H.; Font, B. Skeletal and dental changes in the sagittal, vertical, and transverse dimensions after rapid palatal expansion. Am. J. Orthod. Dentofac. Orthop. 2004, 126, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Cerruto, C.; Ugolini, A.; Di Vece, L.; Doldo, T.; Caprioglio, A.; Silvestrini-Biavati, A. Cephalometric and dental arch changes to Haas-type rapid maxillary expander anchored to deciduous vs permanent molars: A multicenter, randomized controlled trial. J. Orofac. Orthop. 2017, 78, 385–393. [Google Scholar] [CrossRef]
- Ciambotti, C.; Ngan, P.; Durkee, M.; Kohli, K.; Kim, H. A comparison of dental and dentoalveolar changes between rapid palatal expansion and nickel-titanium palatal expansion appliances. Am. J. Orthod. Dentofac. Orthop. 2001, 119, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Sandikçioğlu, M.; Hazar, S. Skeletal and dental changes after maxillary expansion in the mixed dentition. Am. J. Orthod. Dentofac. Orthop. 1997, 111, 321–327. [Google Scholar] [CrossRef] [PubMed]
- Pangrazio-Kulbersh, V.; Wine, P.; Haughey, M.; Pajtas, B.; Kaczynski, R. Cone beam computed tomography evaluation of changes in the naso-maxillary complex associated with two types of maxillary expanders. Angle Orthod. 2012, 82, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, L.; Albertini, E.; Arreghini, A.; D’Alessandro, A.; Siciliani, G. Rapid maxillary expansion on the permanent teeth versus the deciduous teeth: Comparison of skeletal and dentoalveolar effects by volumetric tomography. J. World Fed. Orthod. 2015, 4, 2–7. [Google Scholar]
- Kartalian, A.; Gohl, E.; Adamina, M.; Enciso, R. Cone-beam computer tomography evaluation of the maxillary dentoskeletal complex after rapid palatal expansion. Am. J. Orthod. Dentofac. Orthop. 2010, 138, 486–492. [Google Scholar] [CrossRef] [PubMed]
- Ok, U.P.D.; Kaya, T.U. Fractal Perspective on the Rapid Maxillary Expansion Treatment; Evaluation of the Relationship Between Midpalatal Suture Opening and Dental Effects. J. Stomatol. Oral Maxillofac. Surg. 2022, 123, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Pereira, J.D.S.; Jacob, H.B.; Locks, A.; Brunetto, M.; Ribeiro, G.L.U. Evaluation of the rapid and slow maxillary expansion using cone-beam computed tomography: A randomized clinical trial. Dent. Press J. Orthod. 2017, 22, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Christie, K.F.; Boucher, N.; Chung, C.H. Effects of bonded rapid palatal expansion on the transverse dimensions of the maxilla: A cone-beam computed tomography study. Am. J. Orthod. Dentofac. Orthop. 2010, 137, S79–S85. [Google Scholar] [CrossRef] [PubMed]
- Rosa, M.; Lucchi, P.; Manti, G.; Caprioglio, A. Rapid Palatal Expansion in the absence of posterior cross-bite to intercept maxillary incisor crowding in the mixed dentition: A CBCT evaluation of spontaneous changes of untouched permanent molars. Eur. J. Paediatr. Dent. 2016, 17, 286–294. [Google Scholar]
- Serafin, M.; Fastuca, R.; Zecca, P.A.; Lagravère, M.; Caprioglio, A. 3D occlusal changes of upper first molars after rapid maxillary expansion on permanent versus deciduous teeth: A retrospective multicenter CBCT study. Prog. Orthod. 2023, 24, 24. [Google Scholar] [CrossRef] [PubMed]
- Angle, E.H. Classification of malocclusion. Dent. Cosmos. 1899, 41, 248–264. [Google Scholar]
- Minich, C.M.; Araújo, E.A.; Behrents, R.G.; Buschang, P.H.; Tanaka, O.M.; Kim, K.B. Evaluation of skeletal and dental asymmetries in Angle Class II subdivision malocclusions with cone-beam computed tomography. Am. J. Orthod. Dentofac. Orthop. 2013, 144, 57–66. [Google Scholar] [CrossRef]
- Alavi, D.G.; BeGole, E.A.; Schneider, B.J. Facial and dental arch asymmetries in Class II subdivision malocclusion. Am. J. Orthod. Dentofac. Orthop. 1988, 93, 38–46. [Google Scholar] [CrossRef]
- Janson, G.R.; Metaxas, A.; Woodside, D.G.; de Freitas, M.R.; Pinzan, A. Three-dimensional evaluation of skeletal and dental asymmetries in Class II subdivision malocclusions. Am. J. Orthod. Dentofac. Orthop. 2001, 119, 406–418. [Google Scholar] [CrossRef] [PubMed]
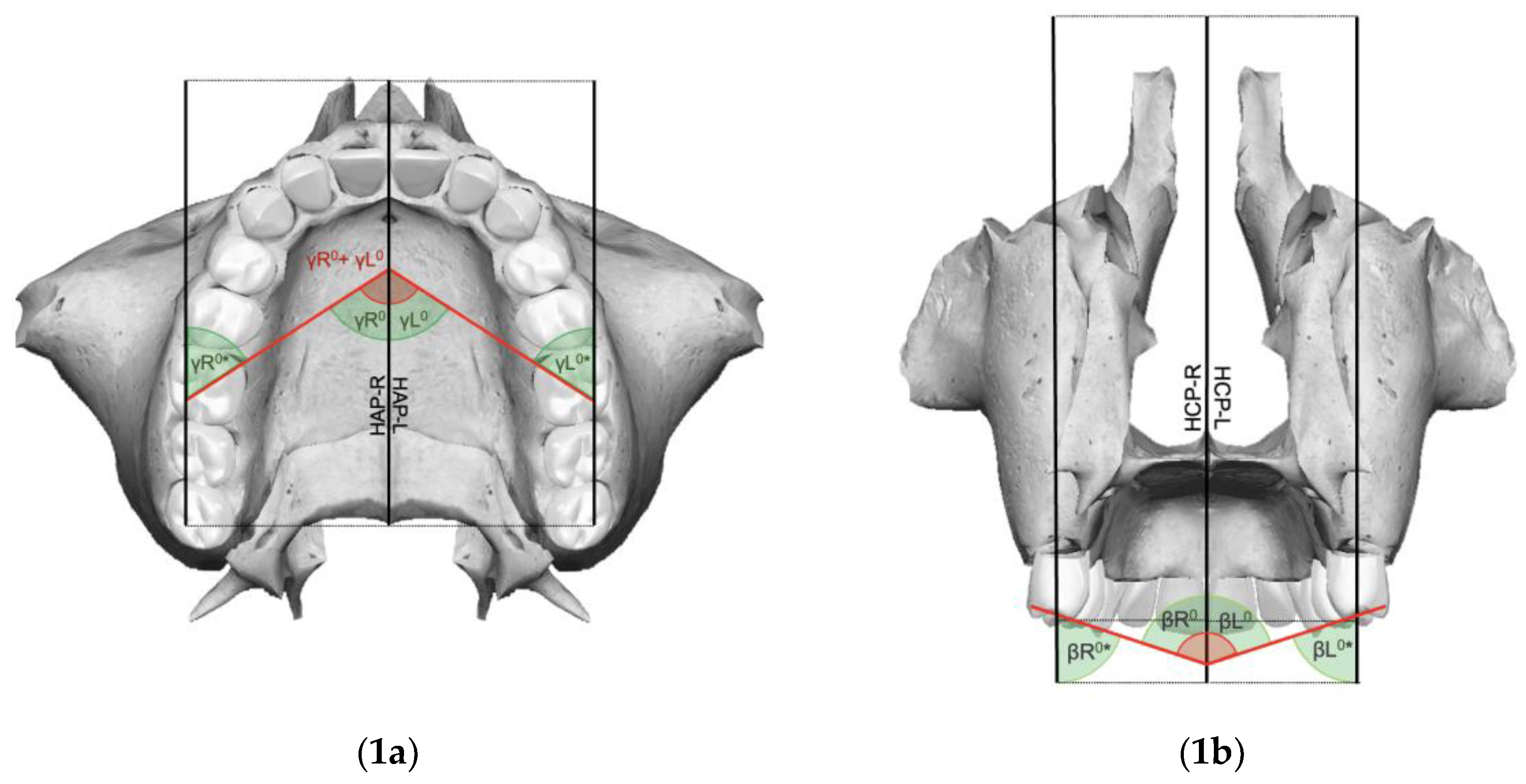
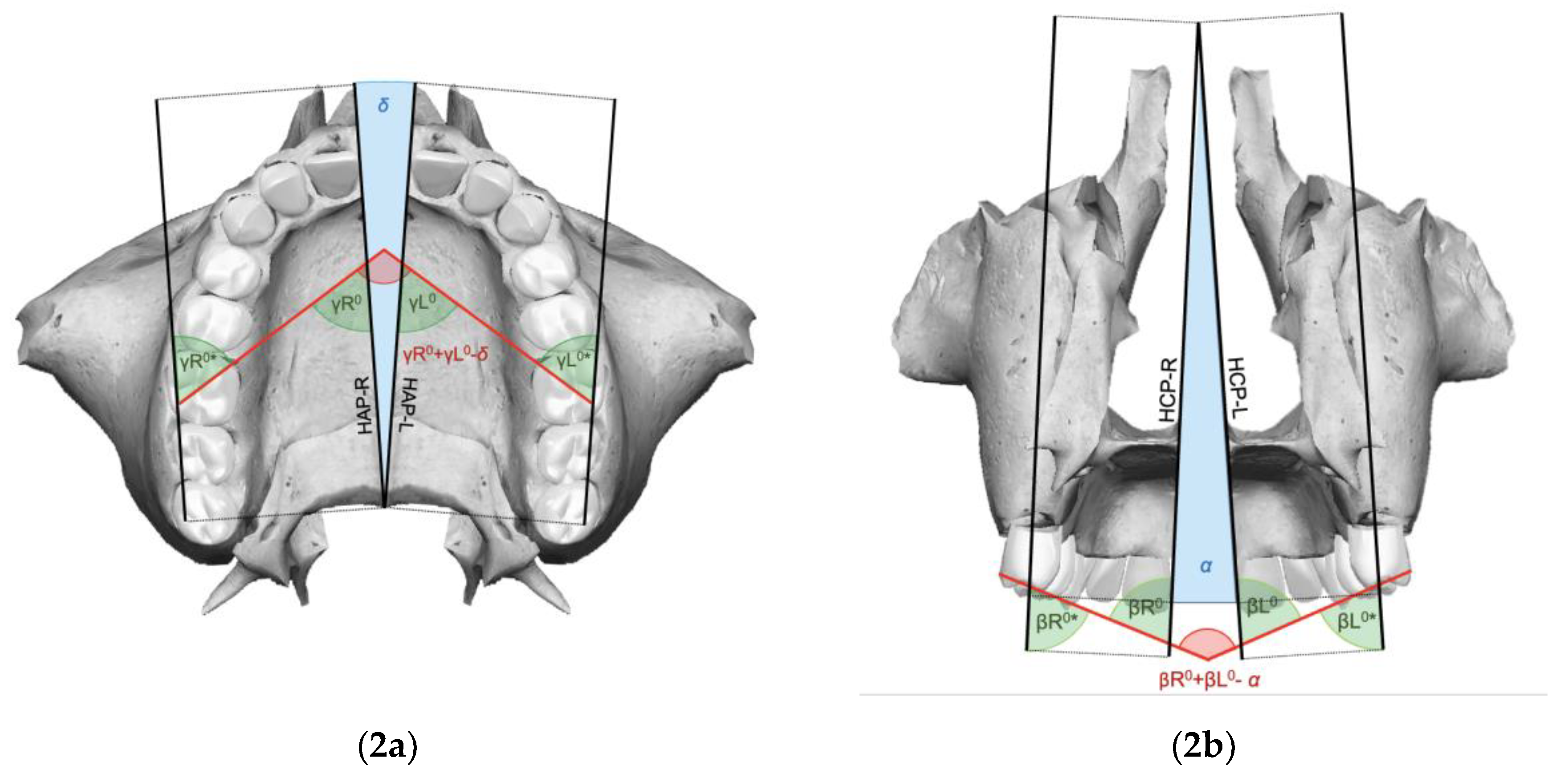
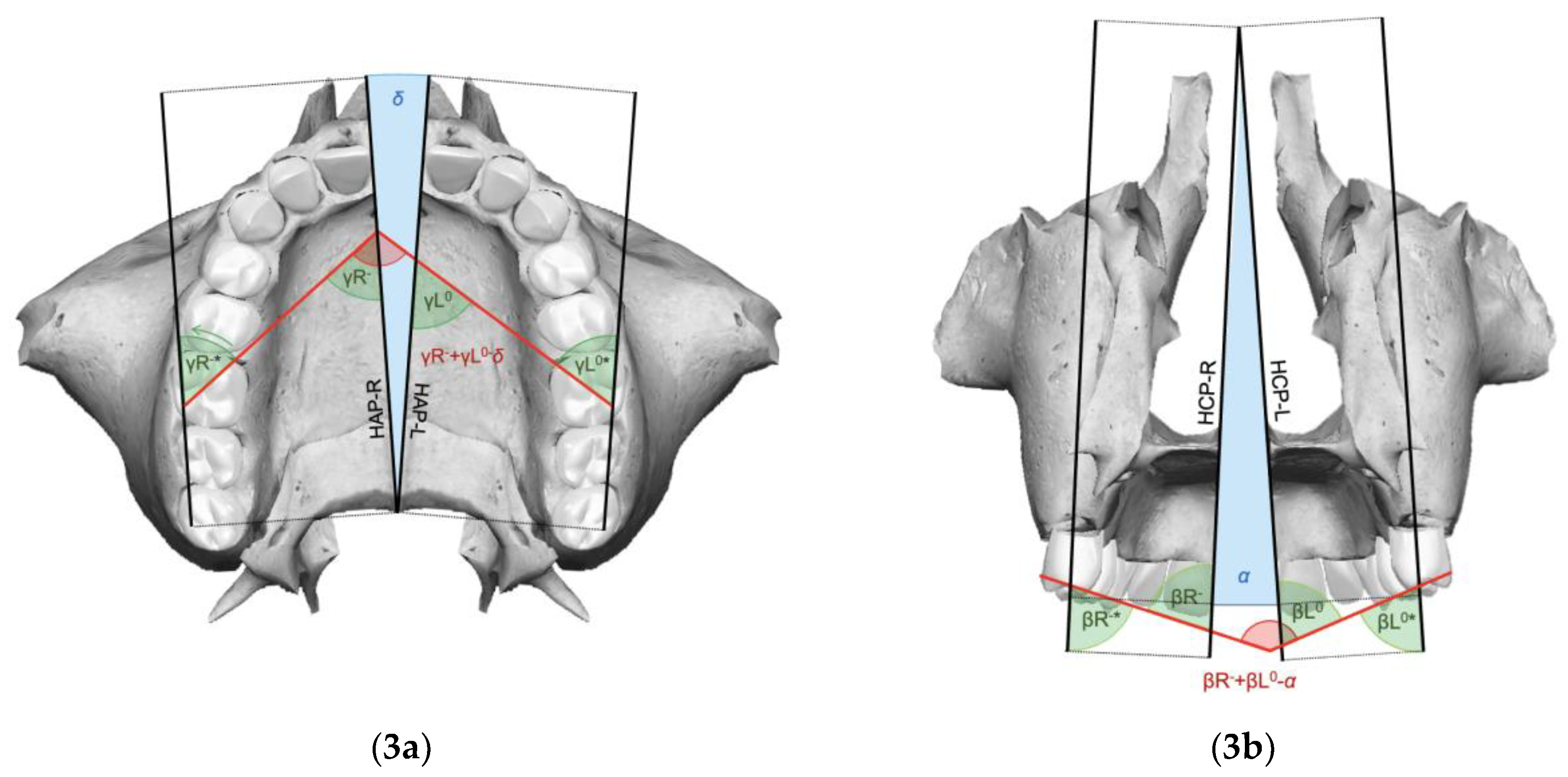


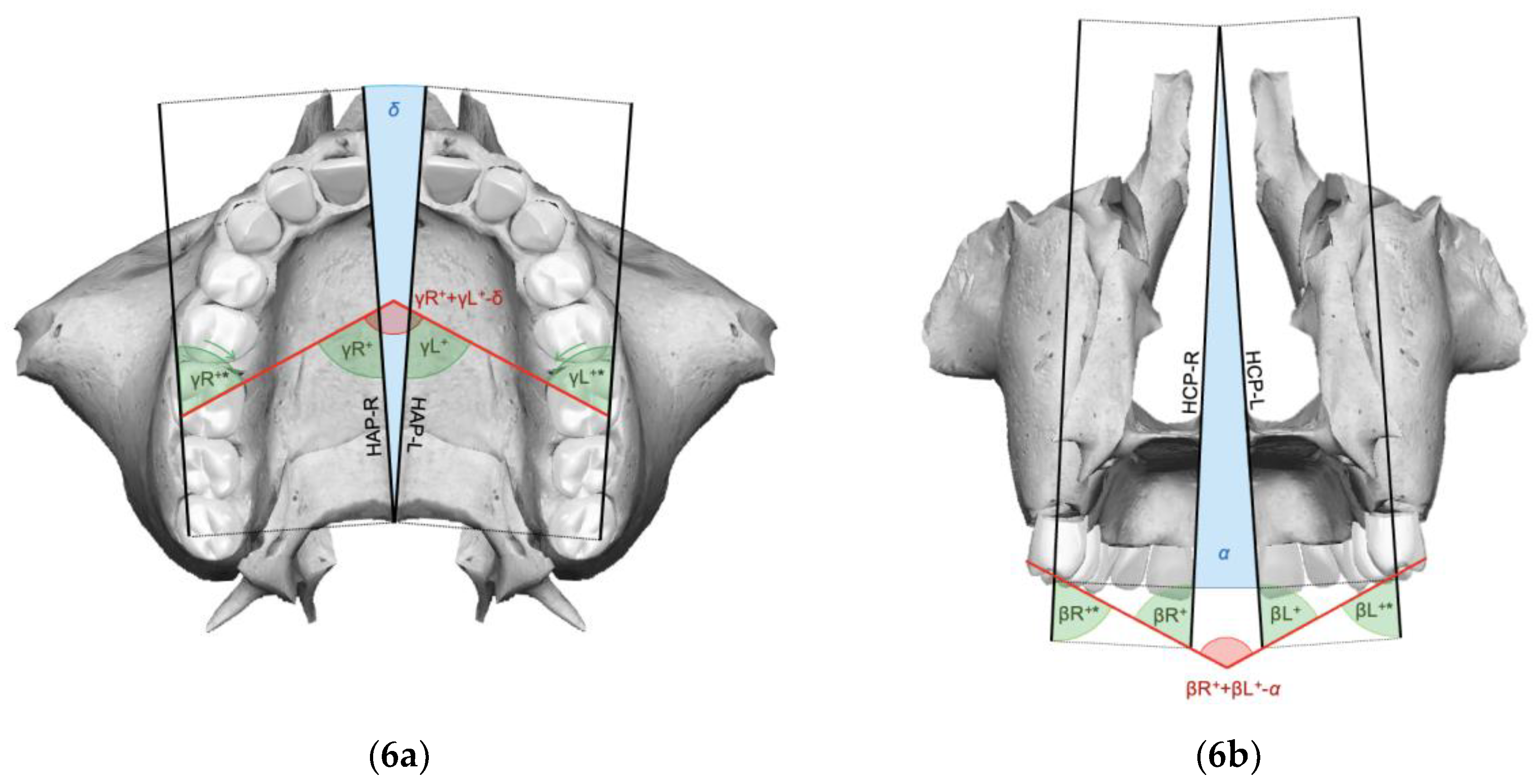


| Landmarks | |
|---|---|
| Anterior Nasal Spine (Ans) | Most anterior point of the Ans (right and left) |
| Posterior Nasal Spine (Pns) | Most posterior point of the Pns |
| Nasion (N) | Most anterior point of the fronto-nasal suture |
| Mesio-Vestibular Cusp (MVC) | Apex of the MV cusp of the upper first molar (right and left) |
| Mesio-Palatal Cusp (MPC) | Apex of the MP cusp of the upper first molar (right and left) |
| Disto-Buccal Cusp (DBC) | Apex of the DB cusp of the upper first molar (right and left) |
| Planes | |
|---|---|
| Hemi Sagittal Plane (HSP) | Plane passing through the Ans (right and left), Pns, and N |
| Hemi Coronal Plane (HCP) | Plane perpendicular to the HSP (right and left) and HAP, passing through the Pns |
| Hemi Axial Plane (HAP) | Plane perpendicular to the HSP (right and left) and HCP, passing through the Pns |
| Angles | |
|---|---|
| Intermolar angle (β) | Angle between the MVC and the MPC of the maxillary first molar line of the right and left sides |
| Right molar angle (βR) | Angle generated by the intersection of the maxillary midline with the line joining the MVC and the MPC of the maxillary right first molar |
| Left molar angle (βL) | Angle generated by the intersection of the maxillary midline with the line joining the MVC and the MPC of the maxillary left first molar |
| Molar angle of rotation (γ) | Angle formed by the intersection of the lines passing over the tips of the MPC and the DBC of the right and left maxillary upper first molars |
| Right molar angle of rotation (γR) | Angle formed by the intersection of the line passing over the MPC and the DBC tips of the right maxillary upper first molar and the Ans-Pns segment |
| Left molar angle of rotation (γL) | Angle formed by the intersection of the line passing over the MPC and the DBC tips of the left maxillary upper first molar and the Ans-Pns segment |
| Orthopedic expansion angle on frontal view (α) | Angle corresponding to the pyramid-like splaying pattern of the post-expansion maxillary components, projected on the frontal view |
| Orthopedic expansion angle on axial view (δ) | Angle corresponding to the pyramid-like splaying pattern of the post-expansion maxillary components, projected on the axial view |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iannotti, L.; Serafin, M.; Caprioglio, A. A New Method for 3D Dental Records Related to Orthopedic Treatments: The Hemimaxillary Plane Reference System and Its Clinical Implications. Appl. Sci. 2024, 14, 11132. https://doi.org/10.3390/app142311132
Iannotti L, Serafin M, Caprioglio A. A New Method for 3D Dental Records Related to Orthopedic Treatments: The Hemimaxillary Plane Reference System and Its Clinical Implications. Applied Sciences. 2024; 14(23):11132. https://doi.org/10.3390/app142311132
Chicago/Turabian StyleIannotti, Lara, Marco Serafin, and Alberto Caprioglio. 2024. "A New Method for 3D Dental Records Related to Orthopedic Treatments: The Hemimaxillary Plane Reference System and Its Clinical Implications" Applied Sciences 14, no. 23: 11132. https://doi.org/10.3390/app142311132
APA StyleIannotti, L., Serafin, M., & Caprioglio, A. (2024). A New Method for 3D Dental Records Related to Orthopedic Treatments: The Hemimaxillary Plane Reference System and Its Clinical Implications. Applied Sciences, 14(23), 11132. https://doi.org/10.3390/app142311132








