Walking Back the Data Quantity Assumption to Improve Time Series Prediction in Deep Learning
Abstract
1. Introduction
- -
- Identification of a nonlinear relationship between dataset size and predictive performance, with significant variations in metrics such as RMSE (up to 66%) and MAPE (up to 44%) across different models and time series.
- -
- Proposal of a methodology that optimizes data usage, illustrating how strategic selection of observations can enhance computational efficiency without compromising model accuracy.
- -
- Demonstration that, in certain cases, smaller datasets can outperform larger ones in terms of overall model performance, depending on the time series structure and the model employed.
2. Related Works
2.1. Neural Networks for Time Series Forecasting
2.2. Impact of Data Quantity in Time Series Forecasting
2.3. Transfer Learning and Multi-Task Learning
2.4. Rolling Window Validation
3. Methodology
3.1. Multilayer Perceptron (MLP) Networks
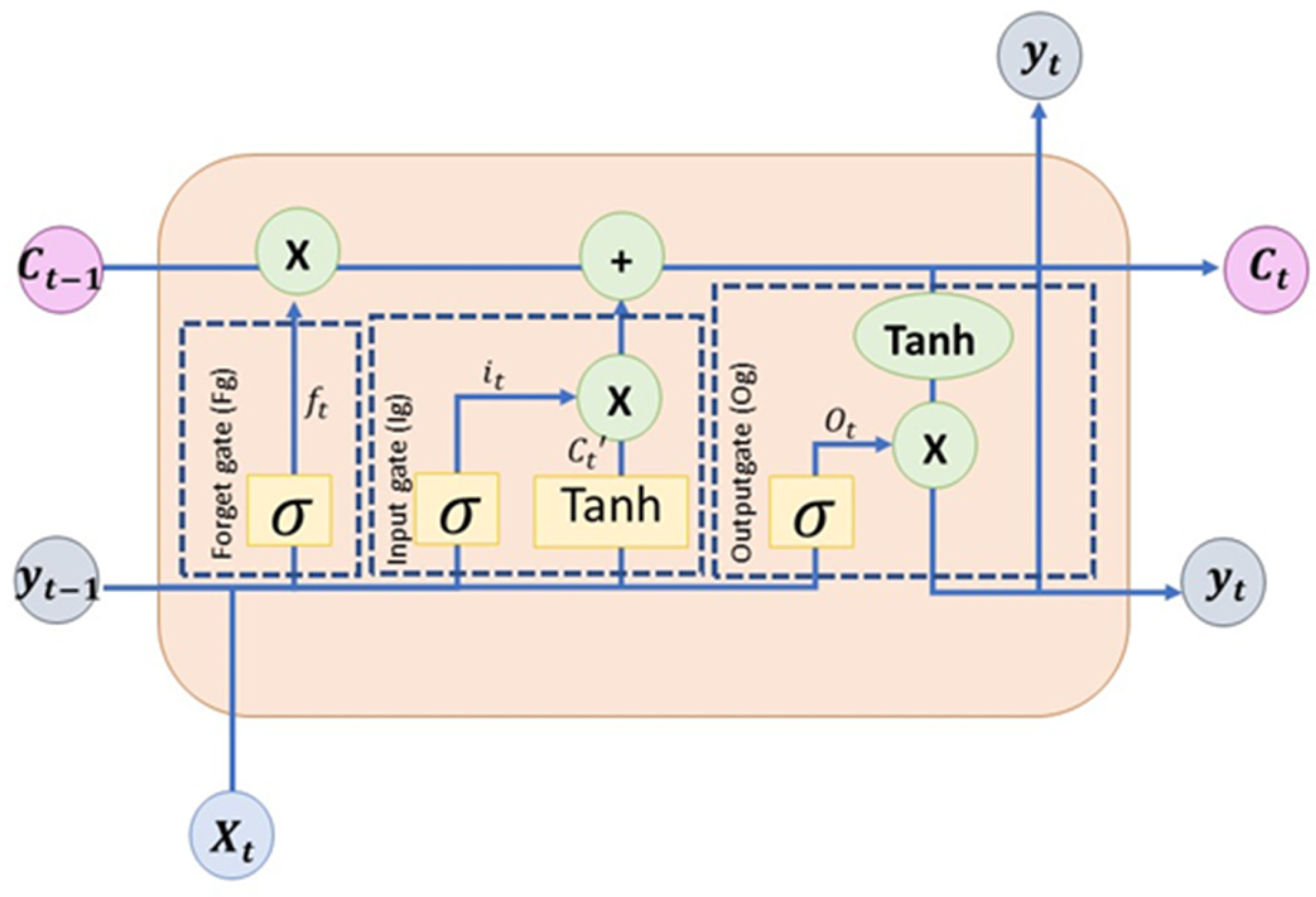
3.2. Long Short-Term Memory (LSTM) Networks
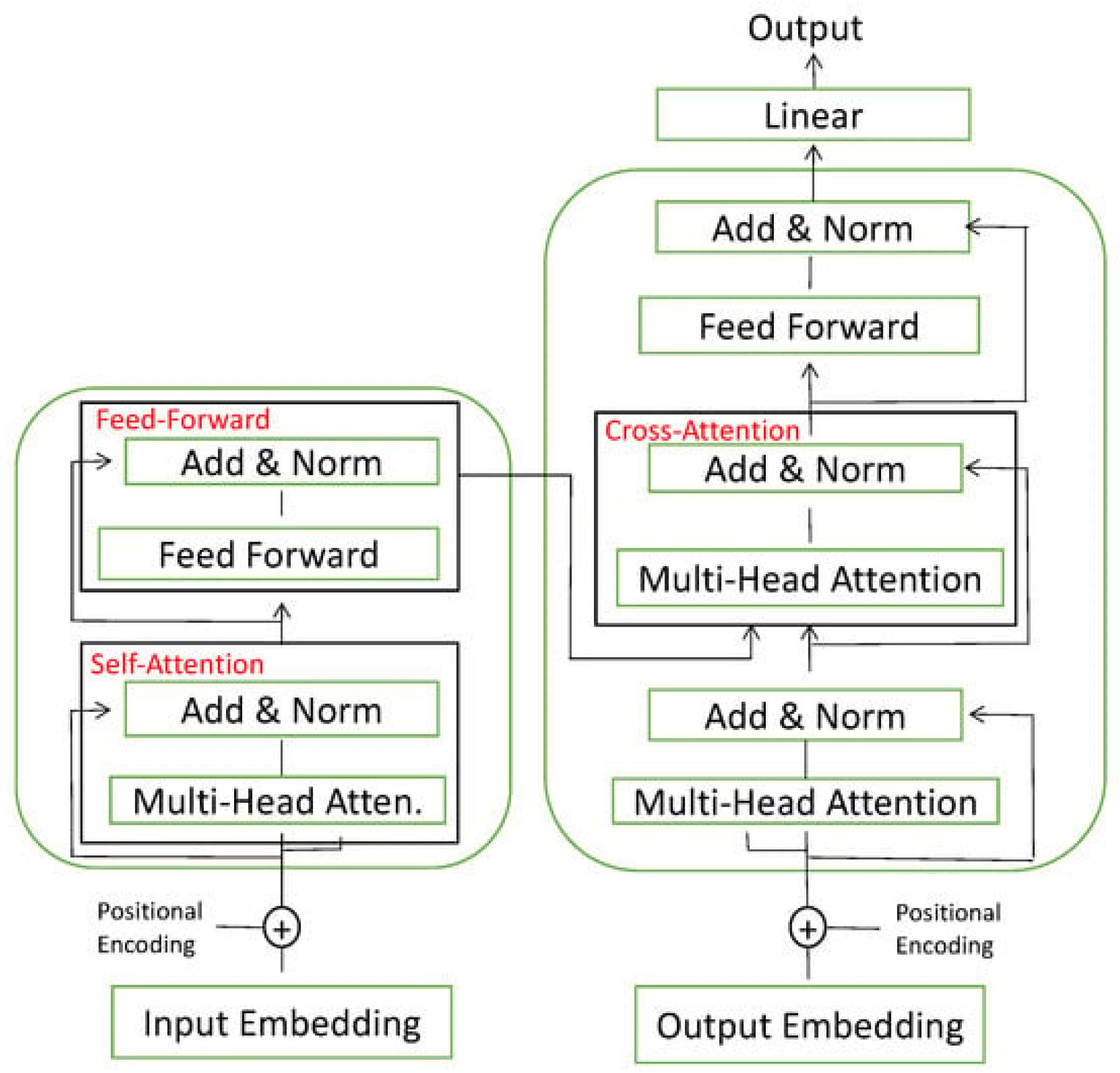
3.3. Transformer Networks
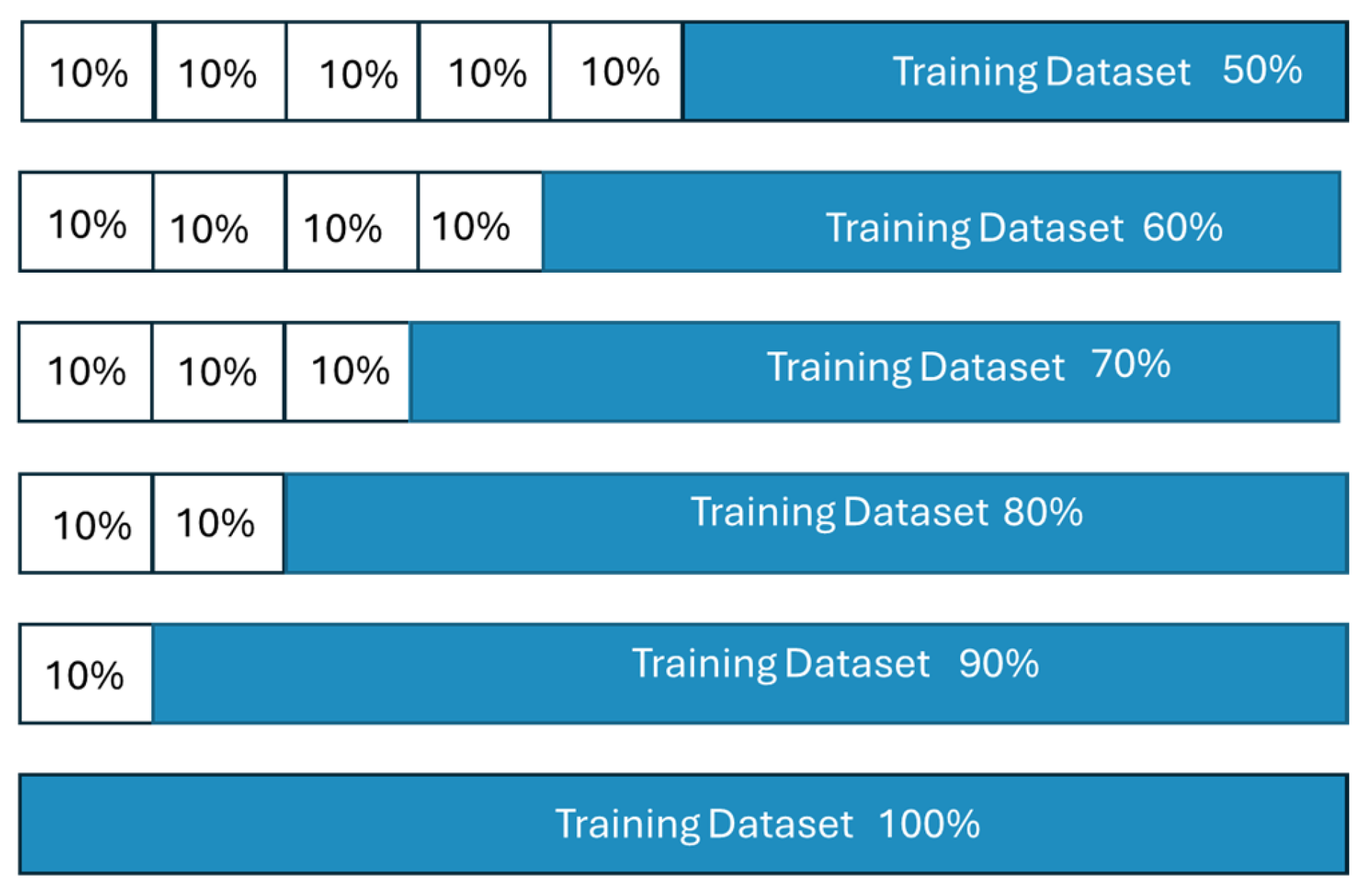
3.4. Walking Back
4. Dataset Details and Performance Metrics
4.1. Dataset
4.2. Error Metrics
4.3. Parameters
- -
- Learning rate: This parameter dictates the rate at which weights are adjusted throughout the learning process. A smaller learning rate results in a more precise but slower algorithm, whereas a larger value accelerates the process at the cost of accuracy. Thus, it is vital to identify a balanced value.
- -
- Batch size: This indicates the number of samples processed before the network’s weights are updated.
- -
- Epoch: This term refers to the total number of times the model will process the entire dataset during training.
- -
- Optimization algorithm: This specifies the learning algorithm employed to train the neural model. The Adam algorithm, commonly used for training LSTMs, merges the benefits of RMSProp—akin to gradient descent—with momentum [69]. In this study, the Adam algorithm has been utilized in all ANNs.
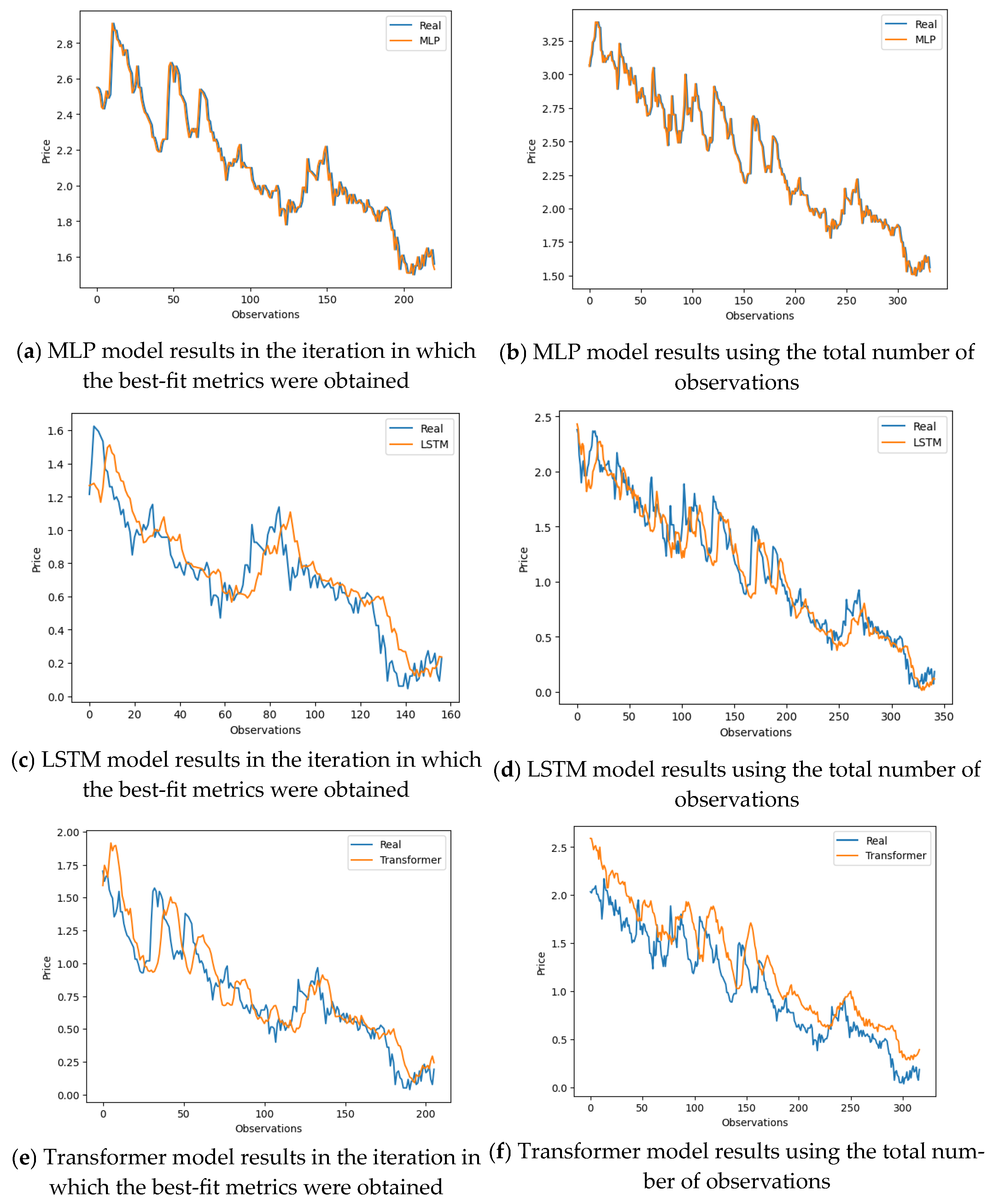
5. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shiblee, M.; Kalra, P.K.; Chandra, B. Time Series Prediction with Multilayer Perceptron (MLP): A New Generalized Error Based Approach. In Advances in Neuro-Information Processing; Köppen, M., Kasabov, N., Coghill, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 37–44. [Google Scholar]
- Yulita, I.N.; Abdullah, A.S.; Helen, A.; Hadi, S.; Sholahuddin, A.; Rejito, J. Comparison multi-layer perceptron and linear regression for time series prediction of novel coronavirus COVID-19 data in West Java. J. Phys. Conf. Ser. 2021, 1722, 012021. [Google Scholar] [CrossRef]
- Borghi, P.H.; Zakordonets, O.; Teixeira, J.P. A COVID-19 time series forecasting model based on MLP ANN. Procedia Comput. Sci. 2021, 181, 940–947. [Google Scholar] [CrossRef] [PubMed]
- Khashei, M.; Hajirahimi, Z. A comparative study of series arima/mlp hybrid models for stock price forecasting. Commun. Stat. Simul. Comput. 2019, 48, 2625–2640. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Li, J.; Sun, Q.; Wang, H. NGCU: A New RNN Model for Time-Series Data Prediction. Big Data Res. 2022, 27, 100296. [Google Scholar] [CrossRef]
- Amalou, I.; Mouhni, N.; Abdali, A. Multivariate time series prediction by RNN architectures for energy consumption forecasting. Energy Rep. 2022, 8, 1084–1091. [Google Scholar] [CrossRef]
- De Rojas, A.L.; Jaramillo-Morán, M.A.; Sandubete, J.E. EMDFormer model for time series forecasting. AIMS Math. 2024, 9, 9419–9434. [Google Scholar] [CrossRef]
- Tuli, S.; Casale, G.; Jennings, N.R. TranAD: Deep transformer networks for anomaly detection in multivariate time series data. Proc. VLDB Endow. 2022, 15, 1201–1214. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 1877–1901. [Google Scholar]
- Valiant, L.G. A theory of the learnable. Commun. ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef]
- Rivasplata, O.; Parrado-Hernandez, E.; Shawe-Taylor, J.S.; Sun, S.; Szepesvari, C. PAC-Bayes bounds for stable algorithms with instance-dependent priors. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Xu, P.; Kumar, D.; Yang, W.; Zi, W.; Tang, K.; Huang, C.; Cheung, J.C.K.; Prince, S.J.D.; Cao, Y. Optimizing Deeper Transformers on Small Datasets. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, Online, 1–6 August 2021; Zong, C., Xia, F., Li, W., Navigli, R., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 2089–2102. [Google Scholar] [CrossRef]
- Clark, T.E.; McCracken, M.W. Improving Forecast Accuracy by Combining Recursive and Rolling Forecasts. Int. Econ. Rev. 2009, 50, 363–395. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. An Empirical Comparison of Methods for Forecasting Using Many Predictors; Princeton University: Princeton, NJ, USA, 2005; Volume 46. [Google Scholar]
- Kaveh, M.; Mesgari, M.S. Application of Meta-Heuristic Algorithms for Training Neural Networks and Deep Learning Architectures: A Comprehensive Review. Neural Process. Lett. 2023, 55, 4519–4622. [Google Scholar] [CrossRef]
- Zito, F.; Cutello, V.; Pavone, M. Deep Learning and Metaheuristic for Multivariate Time-Series Forecasting. In Proceedings of the 18th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2023), Salamanca, Spain, 5–7 September 2023; García Bringas, P., Pérez García, H., Martínez de Pisón, F.J., Martínez Álvarez, F., Troncoso Lora, A., Herrero, Á., Calvo Rolle, J.L., Quintián, H., et al., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 249–258. [Google Scholar]
- Mizdrakovic, V.; Kljajic, M.; Zivkovic, M.; Bacanin, N.; Jovanovic, L.; Deveci, M.; Pedrycz, W. Forecasting bitcoin: Decomposition aided long short-term memory based time series modeling and its explanation with Shapley values. Knowl. Based Syst. 2024, 299, 112026. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mirboluki, A.; Mehraein, M.; Malik, A.; Heddam, S.; Kisi, O. Improved prediction of monthly streamflow in a mountainous region by Metaheuristic-Enhanced deep learning and machine learning models using hydroclimatic data. Theor. Appl. Climatol. 2024, 155, 205–228. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long short term memory networks for anomaly detection in time series. In Proceedings of the 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, ESANN, Bruges, Belgium, 4–6 October 2015; Volume 2015, p. 89. [Google Scholar]
- Guo, T.; Lin, T.; Lu, Y. An interpretable LSTM neural network for autoregressive exogenous model. arXiv 2018, arXiv:1804.05251. [Google Scholar]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar]
- Zhang, T.; Zhang, Y.; Cao, W.; Bian, J.; Yi, X.; Zheng, S.; Li, J. Less Is More: Fast Multivariate Time Series Forecasting with Light Sampling-oriented MLP Structures. arXiv 2022. [Google Scholar] [CrossRef]
- Yi, K.; Zhang, Q.; Fan, W.; Wang, S.; Wang, P.; He, H.; An, N.; Lian, D.; Cao, L.; Niu, Z. Frequency-domain MLPs are More Effective Learners in Time Series Forecasting. Adv. Neural Inf. Process. Syst. 2023, 36, 76656–76679. [Google Scholar]
- Madhusudhanan, K.; Jawed, S.; Schmidt-Thieme, L. Hyperparameter Tuning MLPs for Probabilistic Time Series Forecasting. arXiv 2024. [Google Scholar] [CrossRef]
- Lazcano, A.; Jaramillo-Morán, M.A.; Sandubete, J.E. Back to Basics: The Power of the Multilayer Perceptron in Financial Time Series Forecasting. Mathematics 2024, 12, 1920. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.-C.; Yang, Y.; Liu, H. Modeling Long-and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the 41st International ACM SIGIR Conference on Research and Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Cheng, B.; Titterington, D.M. Neural Networks: A Review from a Statistical Perspective. Stat. Sci. 1994, 9, 2–30. [Google Scholar]
- Kim, K.; Han, I. Genetic algorithms approach to feature discretization in artificial neural networks for the prediction of stock price index. Expert Syst. Appl. 2000, 19, 125–132. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Dridi, A.; Afifi, H.; Moungla, H.; Boucetta, C. Transfer Learning for Classification and Prediction of Time Series for Next Generation Networks. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–18 June 2021; pp. 1–6. [Google Scholar]
- Oreshkin, B.; Carpo, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Ruder, S. An Overview of Multi-Task Learning in Deep Neural Networks. arXiv 2017, arXiv:1706.05098. [Google Scholar]
- Mahmoud, R.A.; Hajj, H.; Karameh, F.N. A systematic approach to multi-task learning from time-series data. Appl. Soft Comput. 2020, 96, 106586. [Google Scholar] [CrossRef]
- Abolghasemi, M.; Hyndman, R.; Spiliotis, E.; Bergmeir, C. Model selection in reconciling hierarchical time series. Mach. Learn. 2022, 111, 739–789. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Cerqueira, V.; Torgo, L.; Smailović, J.; Mozetič, I. A Comparative Study of Performance Estimation Methods for Time Series Forecasting. In Proceedings of the 2017 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Tokyo, Japan, 19–21 October 2017; pp. 529–538. [Google Scholar]
- Inoue, A.; Jin, L.; Rossi, B. Rolling window selection for out-of-sample forecasting with time-varying parameters. J. Econom. 2017, 196, 55–67. [Google Scholar] [CrossRef]
- Casolaro, A.; Capone, V.; Iannuzzo, G.; Camastra, F. Deep Learning for Time Series Forecasting: Advances and Open Problems. Information 2023, 14, 598. [Google Scholar] [CrossRef]
- Zivot, E.; Wang, J. Rolling Analysis of Time Series. In Modeling Financial Time Series with S-Plus®; Zivot, E., Wang, J., Eds.; Springer: New York, NY, USA, 2003; pp. 299–346. ISBN 978-0-387-21763-5. [Google Scholar]
- Moghaddam, A.H.; Moghaddam, M.H.; Esfandyari, M. Stock market index prediction using artificial neural network. J. Econ. Finance Adm. Sci. 2016, 21, 89–93. [Google Scholar] [CrossRef]
- Göçken, M.; Özçalıcı, M.; Boru, A.; Dosdoğru, A.T. Integrating metaheuristics and Artificial Neural Networks for improved stock price prediction. Expert Syst. Appl. 2016, 44, 320–331. [Google Scholar] [CrossRef]
- Keles, D.; Scelle, J.; Paraschiv, F.; Fichtner, W. Extended forecast methods for day-ahead electricity spot prices applying artificial neural networks. Appl. Energy 2016, 162, 218–230. [Google Scholar] [CrossRef]
- Fan, X.; Li, S.; Tian, L. Chaotic characteristic identification for carbon price and an multi-layer perceptron network prediction model. Expert Syst. Appl. 2015, 42, 3945–3952. [Google Scholar] [CrossRef]
- Han, M.; Ding, L.; Zhao, X.; Kang, W. Forecasting carbon prices in the Shenzhen market, China: The role of mixed-frequency factors. Energy 2019, 171, 69–76. [Google Scholar] [CrossRef]
- Li, W. Analysis on the Weight initialization Problem in Fully-Connected Multi-layer Perceptron Neural Network. In Proceedings of the 2020 International Conference on Artificial Intelligence and Computer Engineering (ICAICE), Beijing, China, 6–8 November 2020; pp. 150–153. [Google Scholar]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning. arXiv 2021, arXiv:2106.11342. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2019. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021. [Google Scholar] [CrossRef]
- Cholakov, R.; Kolev, T. Transformers predicting the future. Applying attention in next-frame and time series forecasting. arXiv 2021. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 22419–22430. [Google Scholar]
- Zeyer, A.; Bahar, P.; Irie, K.; Schlüter, R.; Ney, H. A Comparison of Transformer and LSTM Encoder Decoder Models for ASR. In Proceedings of the 2019 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Singapore, 4–18 December 2019; pp. 8–15. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Dauphin, Y.N.; Bengio, Y. Big Neural Networks Waste Capacity. arXiv 2013. [Google Scholar] [CrossRef]
- Botchkarev, A. Performance Metrics (Error Measures) in Machine Learning Regression, Forecasting and Prognostics: Properties and Typology. arXiv 2018, arXiv:1809.03006. [Google Scholar]
- Olawoyin, A.; Chen, Y. Predicting the Future with Artificial Neural Network. Procedia Comput. Sci. 2018, 140, 383–392. [Google Scholar] [CrossRef]
- Li, J. Assessing the accuracy of predictive models for numerical data: Not r nor r2, why not? Then what? PLoS ONE 2017, 12, e0183250. [Google Scholar] [CrossRef]
- Botchkarev, A. A new typology design of performance metrics to measure errors in machine learning regression algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 45–76. [Google Scholar] [CrossRef]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Naser, M.Z.; Alavi, A.H. Error Metrics and Performance Fitness Indicators for Artificial Intelligence and Machine Learning in Engineering and Sciences. Archit. Struct. Constr. 2023, 3, 499–517. [Google Scholar] [CrossRef]
- Lin, T.; Guo, T.; Aberer, K. Hybrid Neural Networks for Learning the Trend in Time Series. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2273–2279. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Cheruyot, R.; Wachera, A.N. Rainfall and runoff time-series trend analysis using LSTM recurrent neural network and wavelet neural network with satellite-based meteorological data: Case study of Nzoia hydrologic basin. Complex Intell. Syst. 2022, 8, 213–236. [Google Scholar] [CrossRef]
- Zhang, G.P.; Kline, D.M. Quarterly Time-Series Forecasting with Neural Networks. IEEE Trans. Neural Netw. 2007, 18, 1800–1814. [Google Scholar] [CrossRef]
- Sun, R. Optimization for deep learning: Theory and algorithms. arXiv 2019. [Google Scholar] [CrossRef]
- Hanifi, S.; Cammarono, A.; Zare-Behtash, H. Advanced hyperparameter optimization of deep learning models for wind power prediction. Renew. Energy 2024, 221, 119700. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Beck, J.V.; Arnold, K.J. Parameter Estimation in Engineering and Science; John and Wiley and Sons: Hoboken, NJ, USA, 1977; ISBN 978-0-471-06118-2. [Google Scholar]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Bandara, K.; Hewamalage, H.; Liu, Y.-H.; Kang, Y.; Bergmeir, C. Improving the accuracy of global forecasting models using time series data augmentation. Pattern Recognit. 2021, 120, 108148. [Google Scholar] [CrossRef]
- Iglesias, G.; Talavera, E.; González-Prieto, Á.; Mozo, A.; Gómez-Canaval, S. Data Augmentation techniques in time series domain: A survey and taxonomy. Neural Comput. Appl. 2023, 35, 10123–10145. [Google Scholar] [CrossRef]
- Haussler, D. Decision theoretic generalizations of the PAC model for neural net and other learning applications. Inf. Comput. 1992, 100, 78–150. [Google Scholar] [CrossRef]
- Meade, N. Evidence for the selection of forecasting methods. J. Forecast. 2000, 19, 515–535. [Google Scholar] [CrossRef]
- Shi, J.; Ma, Q.; Ma, H.; Li, L. Scaling Law for Time Series Forecasting. arXiv 2024. [Google Scholar] [CrossRef]
- Guo, Z.X.; Wong, W.K.; Li, M. Sparsely connected neural network-based time series forecasting. Inf. Sci. 2012, 193, 54–71. [Google Scholar] [CrossRef]
- Linjordet, T.; Balog, K. Impact of Training Dataset Size on Neural Answer Selection Models. In Advances in Information Retrieval; Azzopardi, L., Stein, B., Fuhr, N., Mayr, P., Hauff, C., Hiemstra, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 828–835. [Google Scholar]
- Zhou, J.; Shi, J.; Li, G. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]

| Time Serie | 1st Iteration | 2nd Iteration | 3rd Iteration | 4th Iteration | 5th Iteration | 6th Iteration | Total Observations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||
| GOLD | 740 | 186 | 888 | 223 | 1036 | 260 | 1184 | 297 | 1332 | 334 | 1480 | 371 | 1851 |
| WTI | 4115 | 1029 | 4938 | 1235 | 5761 | 1441 | 6584 | 1647 | 7408 | 1852 | 8230 | 2058 | 10,288 |
| Apple | 2088 | 522 | 2505 | 627 | 2923 | 731 | 3340 | 836 | 3758 | 940 | 4175 | 1044 | 5219 |
| OMIE | 16,612 | 4153 | 19,380 | 4846 | 22,149 | 5538 | 24,918 | 6230 | 27,686 | 6922 | 27,686 | 6922 | 34,608 |
| Model | Learning Rate | Batch | Epoch | Hidden Layers | Optimizer | Ff_dim | Num_heads |
|---|---|---|---|---|---|---|---|
| Transformer | 0.001 | 150 | 150 | 1 | Adam | 75 | 6 |
| LSTM | 0.001 | 25 | 100 | 2 | Adam | - | - |
| MLP | 0.001 | 25 | 75 | 2 | Adam | - | - |
| Metrics GOLD | ||||||
|---|---|---|---|---|---|---|
| Time Serie | ANN | RMSE | MSE | MAPE | R2 | Time |
| MLP | 1° | 0.08 | 0.01 | 15.47 | 0.95 | 6.37 |
| 2° | 0.06 | 0.00 | 18.36 | 0.97 | 6.86 | |
| 3° | 0.07 | 0.01 | 20.09 | 0.96 | 6.27 | |
| 4° | 0.07 | 0.00 | 21.67 | 0.97 | 7.86 | |
| 5° | 0.07 | 0.00 | 24.14 | 0.97 | 7.09 | |
| 6° | 0.10 | 0.01 | 26.47 | 0.96 | 8.96 | |
| LSTM | 1° | 0.15 | 0.02 | 32.74 | 0.80 | 26.07 |
| 2° | 0.16 | 0.02 | 34.13 | 0.79 | 32.11 | |
| 3° | 0.18 | 0.03 | 27.21 | 0.84 | 30.14 | |
| 4° | 0.18 | 0.03 | 25.06 | 0.85 | 32.36 | |
| 5° | 0.18 | 0.03 | 26.00 | 0.87 | 34.34 | |
| 6° | 0.18 | 0.03 | 17.82 | 0.91 | 40.57 | |
| TRANS | 1° | 3.69 | 13.64 | 1101.49 | −169.90 | 31.65 |
| 2° | 0.23 | 0.05 | 59.72 | 0.48 | 34.93 | |
| 3° | 0.19 | 0.03 | 31.23 | 0.76 | 40.77 | |
| 4° | 0.30 | 0.09 | 31.93 | 0.59 | 54.46 | |
| 5° | 0.24 | 0.05 | 32.90 | 0.75 | 60.89 | |
| 6° | 0.29 | 0.08 | 47.88 | 0.70 | 61.07 | |
| Metrics WTI | ||||||
|---|---|---|---|---|---|---|
| Time Serie | ANN | RMSE | MSE | MAPE | R2 | Time |
| MLP | 1° | 2.49 | 6.20 | 41.58 | 0.97 | 16.62 |
| 2° | 2.34 | 5.45 | 37.21 | 0.97 | 16.47 | |
| 3° | 2.30 | 5.28 | 35.03 | 0.98 | 17.66 | |
| 4° | 2.17 | 4.72 | 34.63 | 0.98 | 20.33 | |
| 5° | 2.02 | 4.07 | 35.06 | 0.98 | 29.40 | |
| 6° | 2.01 | 4.02 | 35.63 | 0.98 | 31.85 | |
| LSTM | 1° | 5.35 | 28.69 | 43.11 | 0.95 | 70.63 |
| 2° | 4.56 | 20.81 | 8.89 | 0.94 | 72.87 | |
| 3° | 4.37 | 19.17 | 8.47 | 0.94 | 110.60 | |
| 4° | 4.04 | 16.33 | 7.51 | 0.95 | 118.62 | |
| 5° | 4.03 | 16.29 | 7.88 | 0.95 | 131.19 | |
| 6° | 4.15 | 17.29 | 8.05 | 0.94 | 151.46 | |
| TRANS | 1° | 6.87 | 47.32 | 45.97 | 0.92 | 138.38 |
| 2° | 5.19 | 27.02 | 9.80 | 0.93 | 217.77 | |
| 3° | 5.16 | 26.69 | 9.87 | 0.92 | 216.02 | |
| 4° | 4.78 | 22.90 | 9.16 | 0.93 | 223.83 | |
| 5° | 5.00 | 25.00 | 9.51 | 0.92 | 264.62 | |
| 6° | 4.60 | 21.19 | 8.61 | 0.93 | 300.67 | |
| Metrics Apple | ||||||
|---|---|---|---|---|---|---|
| Time Serie | ANN | RMSE | MSE | MAPE | R2 | Time |
| MLP | 1° | 2.75 | 7.55 | 13.41 | 0.98 | 9.22 |
| 2° | 3.08 | 9.51 | 12.34 | 0.97 | 10.49 | |
| 3° | 3.87 | 14.97 | 12.31 | 0.97 | 11.34 | |
| 4° | 2.82 | 7.97 | 14.72 | 0.98 | 13.45 | |
| 5° | 3.55 | 12.60 | 16.64 | 0.98 | 15.65 | |
| 6° | 2.72 | 7.40 | 22.22 | 0.99 | 15.34 | |
| LSTM | 1° | 11.08 | 122.89 | 5.20 | 0.71 | 42.09 |
| 2° | 17.81 | 317.18 | 9.15 | 0.00 | 44.47 | |
| 3° | 27.19 | 739.29 | 13.75 | −1.44 | 61.23 | |
| 4° | 28.99 | 840.89 | 14.47 | −1.31 | 70.45 | |
| 5° | 36.04 | 1299.15 | 19.15 | −1.90 | 67.74 | |
| 6° | 75.27 | 5666.90 | 45.01 | −8.00 | 80.35 | |
| TRANS | 1° | 38.86 | 1510.48 | 18.79 | −2.36 | 113.49 |
| 2° | 48.00 | 2304.44 | 27.09 | −5.96 | 121.31 | |
| 3° | 86.16 | 7424.24 | 50.37 | −23.44 | 146.48 | |
| 4° | 108.10 | 11,685.85 | 64.97 | −32.37 | 142.26 | |
| 5° | 104.38 | 10,896.09 | 63.74 | −24.72 | 194.40 | |
| 6° | 111.03 | 12,329.70 | 69.36 | −21.07 | 207.48 | |
| Metrics OMIE | |||||
|---|---|---|---|---|---|
| Time Serie | ANN | RMSE | MSE | R2 | Time |
| MLP | 1° | 10.71 | 114.73 | 0.84 | 35.81 |
| 2° | 11.02 | 121.55 | 0.86 | 64.83 | |
| 3° | 12.02 | 144.36 | 0.85 | 61.99 | |
| 4° | 12.95 | 167.58 | 0.85 | 59.95 | |
| 5° | 12.71 | 161.47 | 0.87 | 70.77 | |
| 6° | 12.91 | 166.65 | 0.88 | 71.21 | |
| LSTM | 1° | 16.54 | 273.87 | 0.63 | 254.31 |
| 2° | 16.85 | 284.11 | 0.67 | 267.75 | |
| 3° | 18.62 | 346.75 | 0.64 | 308.86 | |
| 4° | 19.78 | 391.53 | 0.66 | 413.56 | |
| 5° | 19.02 | 361.81 | 0.71 | 422.07 | |
| 6° | 20.35 | 414.43 | 0.71 | 436.84 | |
| TRANS | 1° | 16.71 | 279.28 | 0.63 | 686.82 |
| 2° | 17.19 | 295.69 | 0.65 | 829.67 | |
| 3° | 18.52 | 343.01 | 0.64 | 880.48 | |
| 4° | 19.64 | 385.83 | 0.66 | 997.92 | |
| 5° | 18.73 | 351.08 | 0.72 | 1130.10 | |
| 6° | 21.47 | 461.04 | 0.67 | 1150.56 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazcano, A.; Hidalgo, P.; Sandubete, J.E. Walking Back the Data Quantity Assumption to Improve Time Series Prediction in Deep Learning. Appl. Sci. 2024, 14, 11081. https://doi.org/10.3390/app142311081
Lazcano A, Hidalgo P, Sandubete JE. Walking Back the Data Quantity Assumption to Improve Time Series Prediction in Deep Learning. Applied Sciences. 2024; 14(23):11081. https://doi.org/10.3390/app142311081
Chicago/Turabian StyleLazcano, Ana, Pablo Hidalgo, and Julio E. Sandubete. 2024. "Walking Back the Data Quantity Assumption to Improve Time Series Prediction in Deep Learning" Applied Sciences 14, no. 23: 11081. https://doi.org/10.3390/app142311081
APA StyleLazcano, A., Hidalgo, P., & Sandubete, J. E. (2024). Walking Back the Data Quantity Assumption to Improve Time Series Prediction in Deep Learning. Applied Sciences, 14(23), 11081. https://doi.org/10.3390/app142311081






