Net Primary Production Simulation and Influencing Factors Analysis of Forest Ecosystem Based on a Process-Based Model
Abstract
1. Introduction
2. Materials and Methods
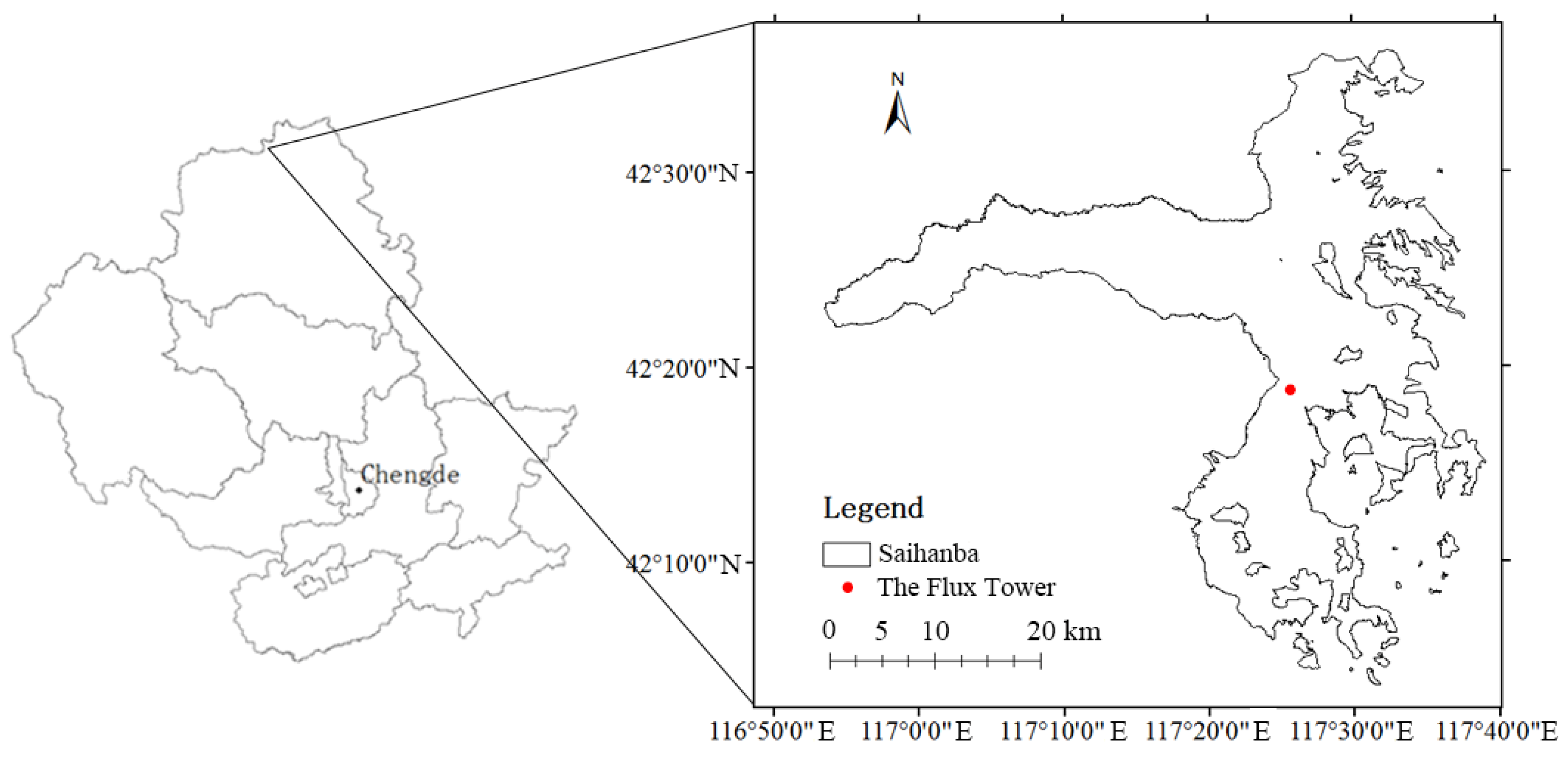
2.1. Study Area
2.2. The Flux Tower
2.3. Data and Preprocessing
2.3.1. Meteorological Data
2.3.2. Land Cover Type Data
2.3.3. Leaf Area Index (LAI) Data
2.3.4. ALOS Remote Sensing Image
2.3.5. MODIS NPP Data
2.4. Analysis of Influencing Factors
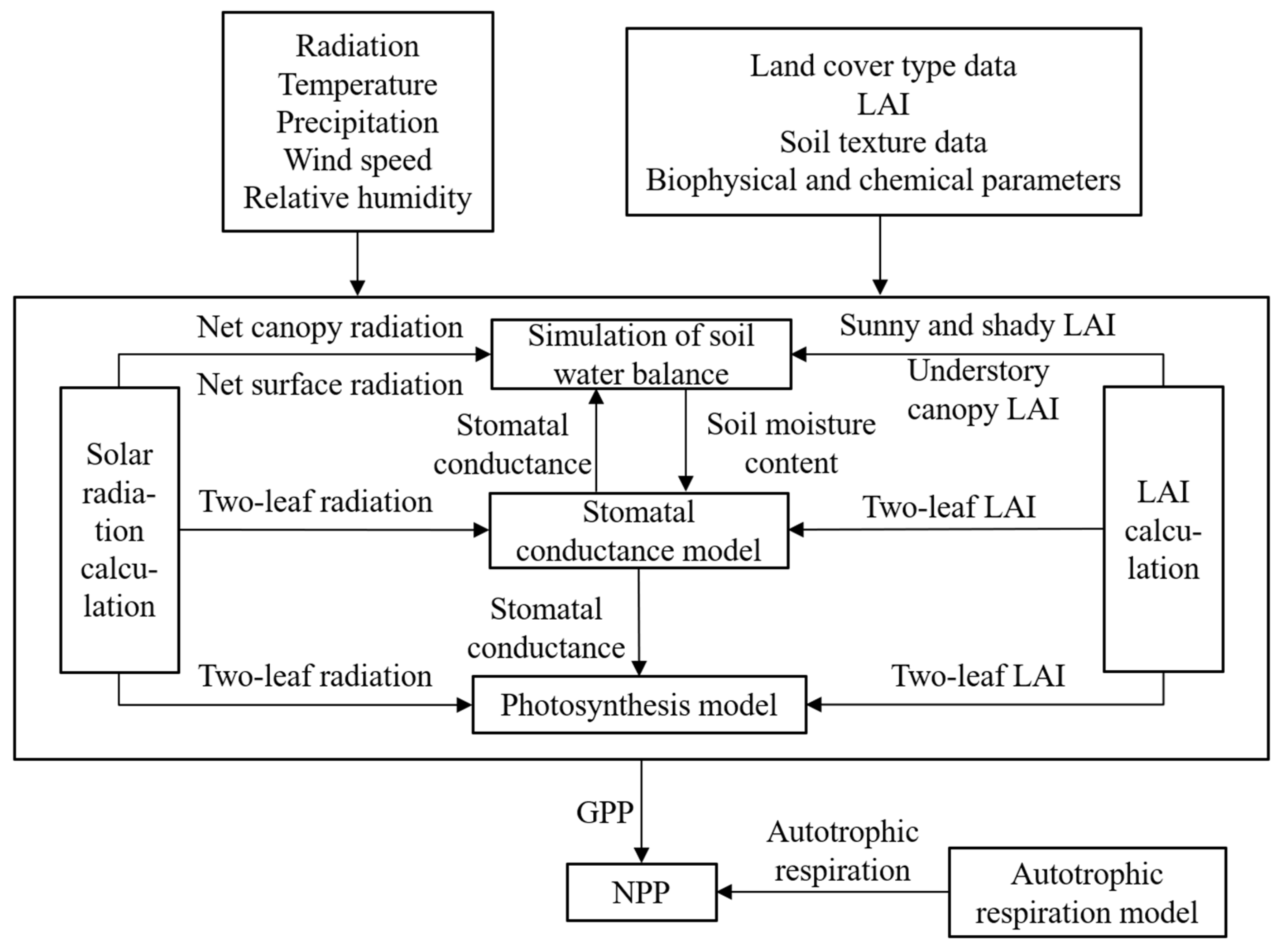
2.5. Model Description
2.5.1. Photosynthesis–Stomatal Conductance Model
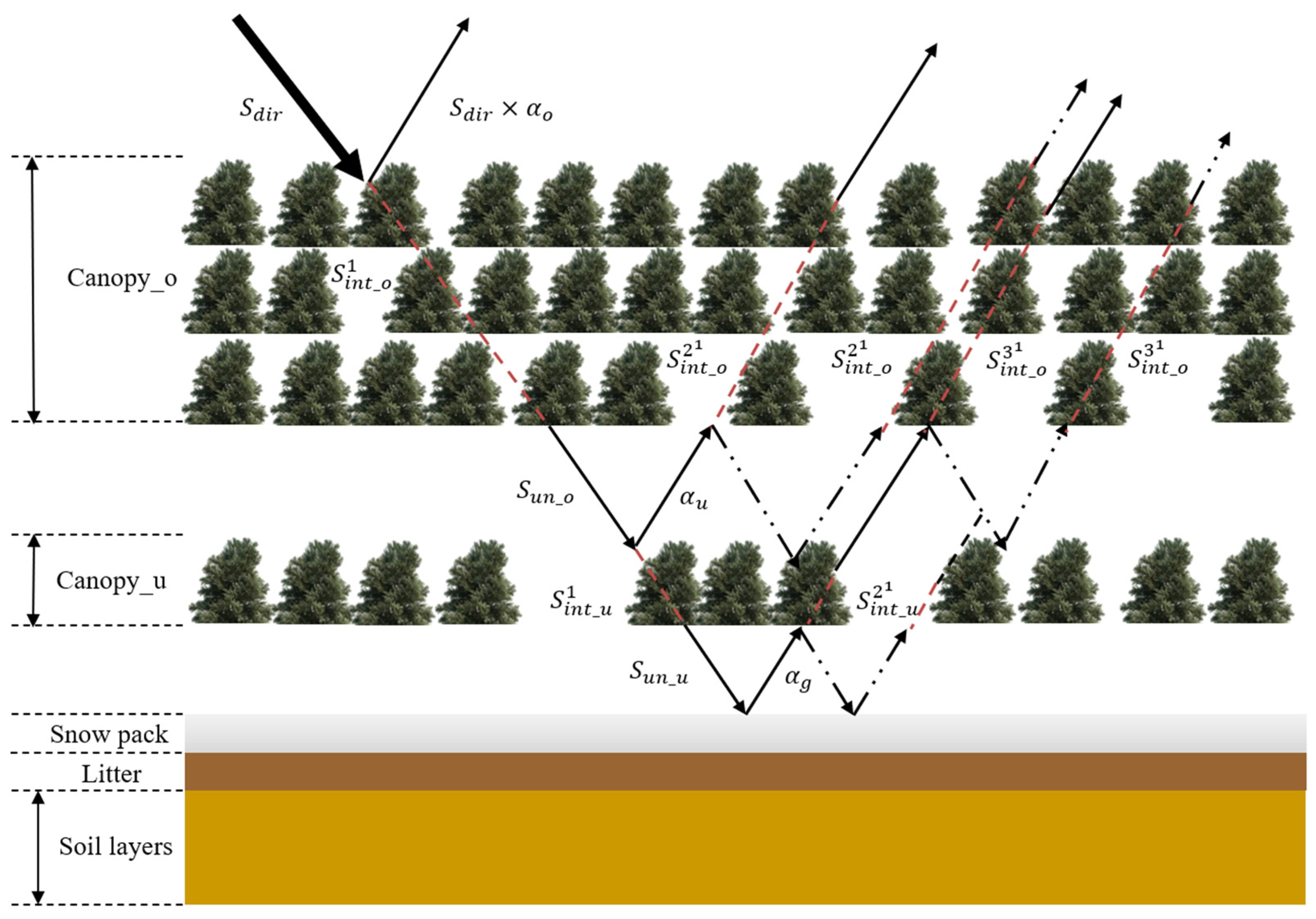
2.5.2. Radiative Transfer Model
2.5.3. Vegetation Autotrophic Respiration Model
2.5.4. Soil Moisture Balance Model
2.5.5. Canopy Temperature Model
3. Results
3.1. Flux Tower Scale Simulation
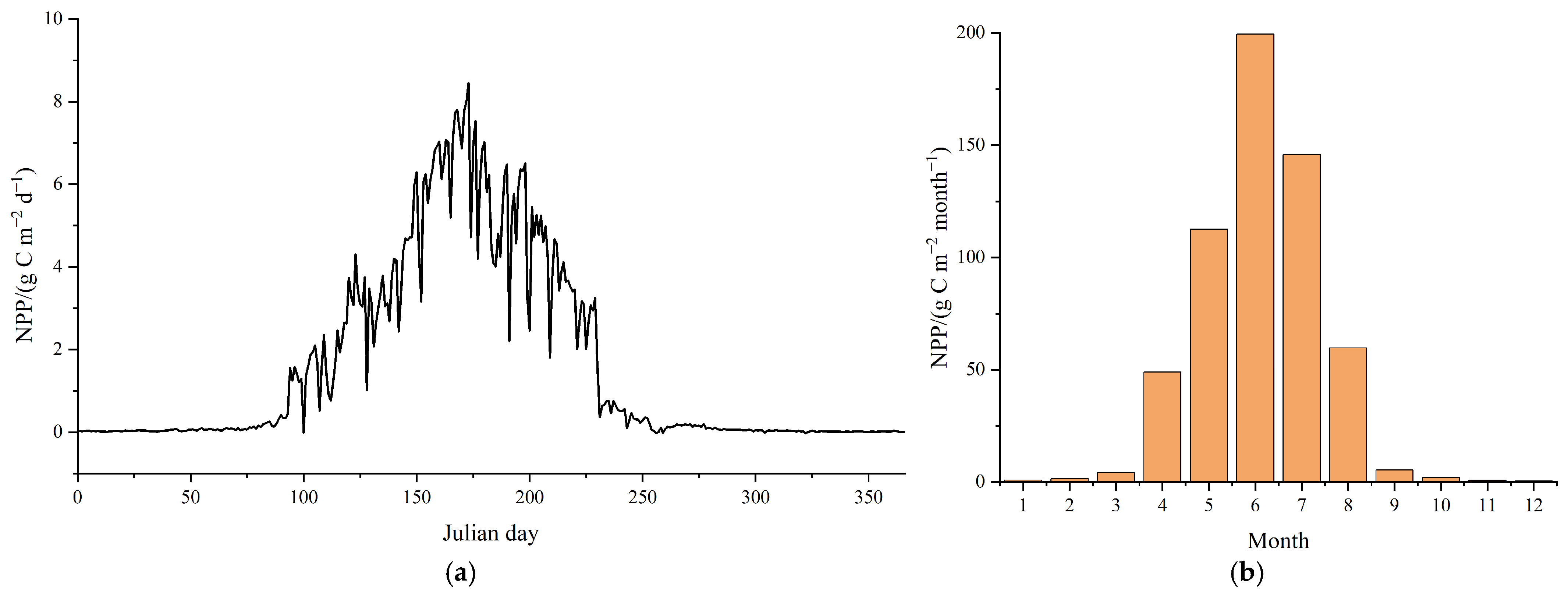
3.1.1. NPP Simulation
3.1.2. NPP Influencing Factors Analysis
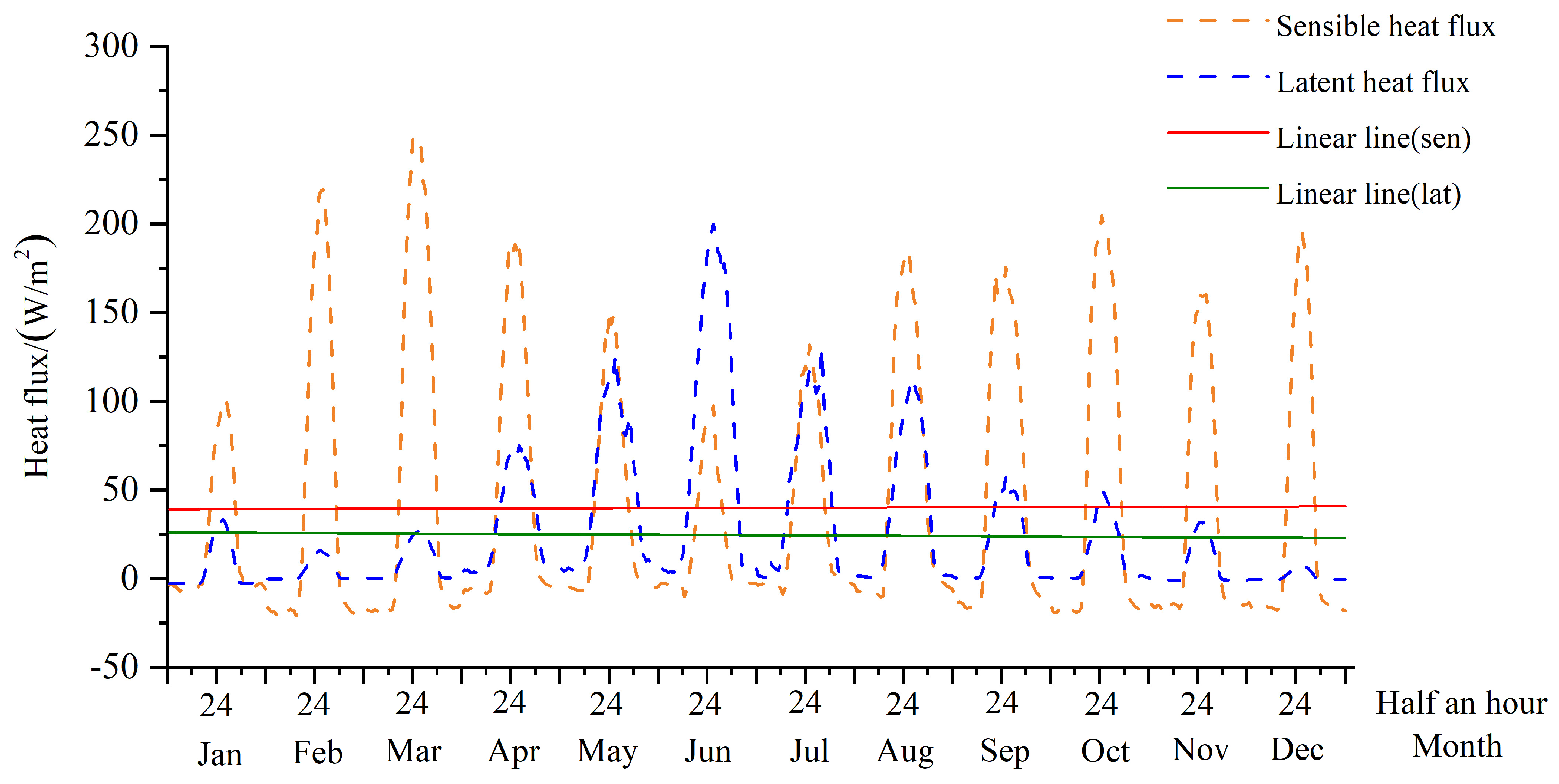
3.1.3. Simulation of Latent and Sensible Heat Fluxes
3.1.4. Canopy Temperature Simulation
3.2. Regional Scale Simulation
3.2.1. Simulation Results
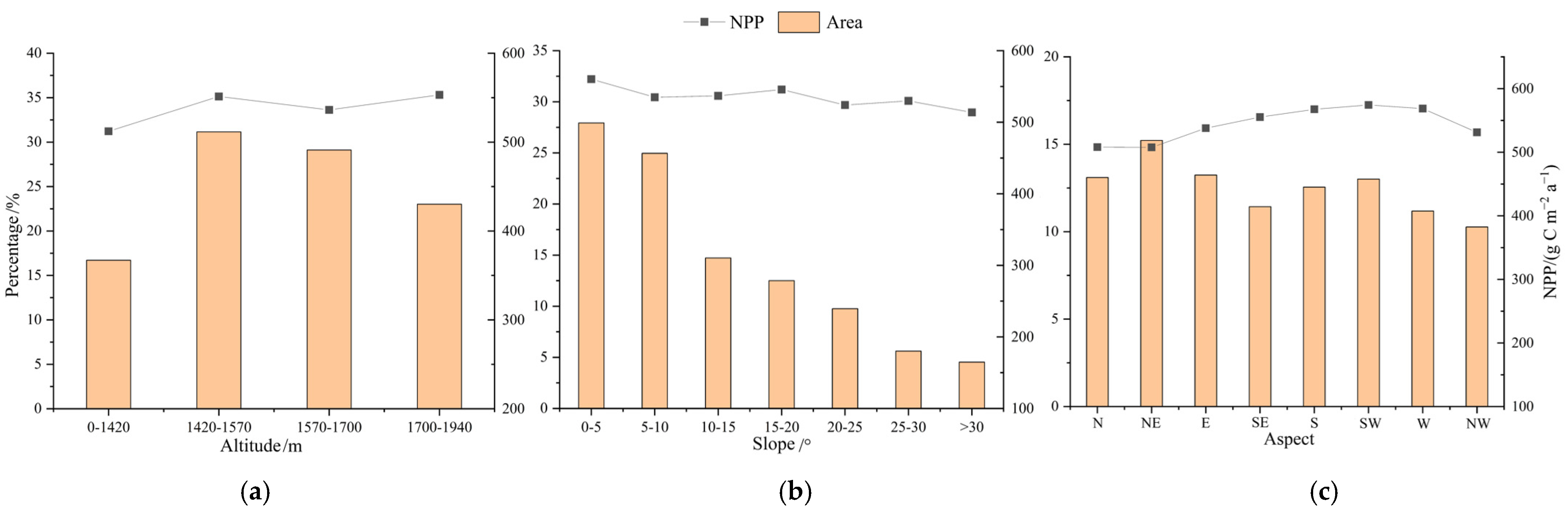
3.2.2. Analysis of the Impact of Topographic Factors on NPP
- Altitude
- 2.
- Slope
- 3.
- Aspect
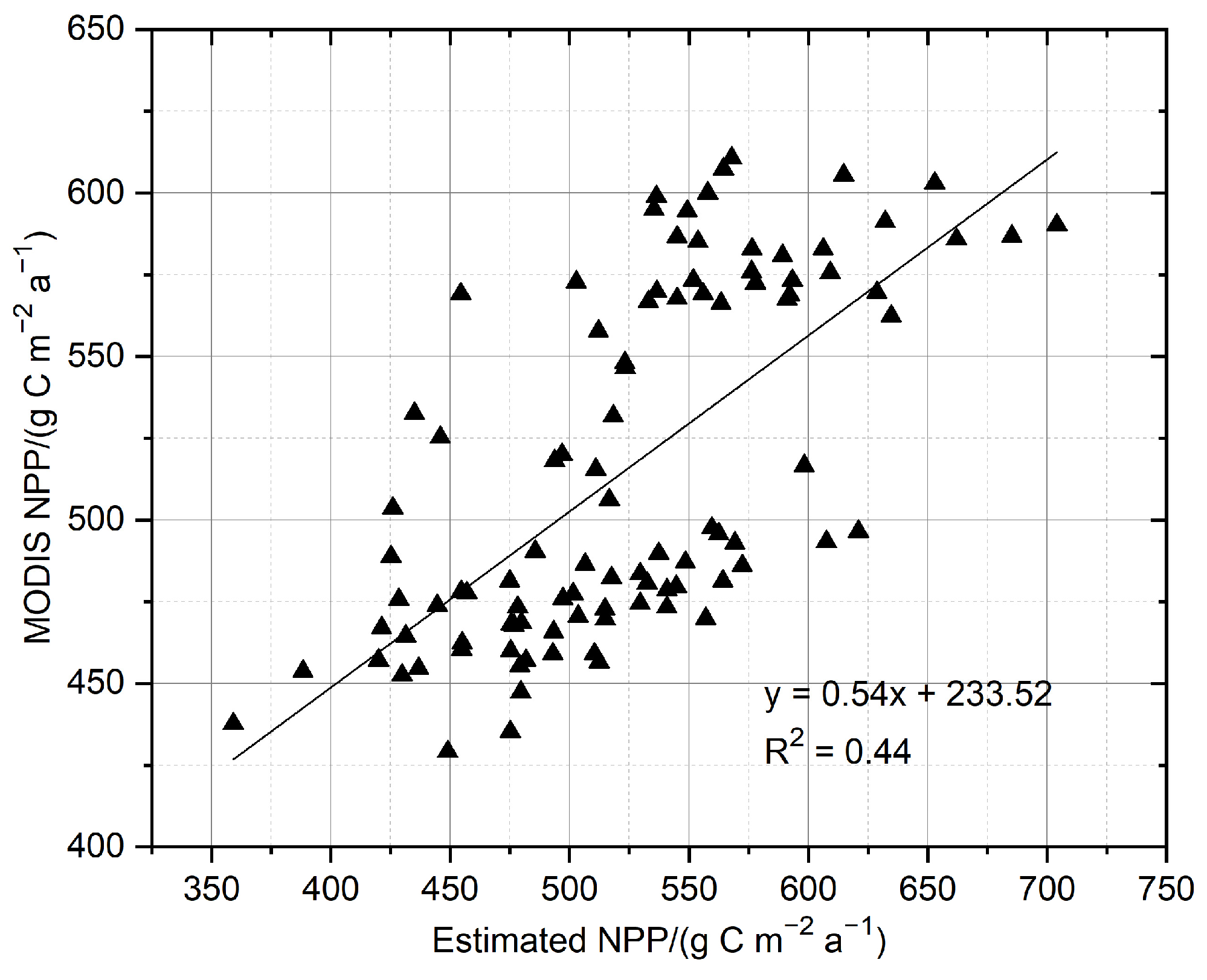
3.2.3. Validation of Estimated NPP
4. Discussion
4.1. Diurnal and Seasonal Variations of Latent and Sensible Heat Fluxes
4.2. The Influence of Slope Aspect on Forest Growth
4.3. Simulation of Forest NPP
4.4. Limitations and Direction of Improvements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, X.; Liu, G.; Chen, J.; Chen, M.; Liu, J.; Ju, W.; Sun, R.; Zhou, W. Net primary productivity of China’s terrestrial ecosystems from a process model driven by remote sensing. J. Environ. Manag. 2007, 85, 563–573. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Han, N.; Xu, X.; Liu, Y.; Zhu, D.; Zheng, J.; Dong, L.; et al. Assimilating spatiotemporal MODIS LAI data with a particle filter algorithm for improving carbon cycle simulations for bamboo forest ecosystems. Sci. Total Environ. 2019, 694, 133803.1–133803.14. [Google Scholar] [CrossRef]
- Pelt, R.; Sillett, S.; Kruse, W.; Freund, J.; Kramer, R. Emergent crowns and light-use complementarity lead to global maximum biomass and leaf area in Sequoia sempervirens forests. For. Ecol. Manag. 2016, 375, 279–308. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Xue, M.; Chen, Y.; Jia, L.; Wang, X.; Yan, M.; Tian, X. Estimation of net primary productivity by beps model-a case study in fujian province. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 6213–6216. [Google Scholar] [CrossRef]
- Running, S.; Coughlan, J. A general model of forest ecosystem processes for regional applications I. Hydrologic balance, canopy gas exchange and primary production processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Lieth, H. Primary Productivity of the Biosphere; Whittaker, R., Ed.; Spring: New York, NY, USA, 1975. [Google Scholar]
- Wang, Z.; Zhou, Y.; Sun, X.; Xu, Y. Estimation of NPP in Huangshan district based on deep learning and CASA model. Forests 2024, 15, 1467. [Google Scholar] [CrossRef]
- Sallaba, F.; Lehsten, D.; Seaquist, J.; Sykes, M. A rapid NPP meta-model for current and future climate and CO2 scenarios in Europe. Ecol. Model. 2015, 302, 29–41. [Google Scholar] [CrossRef]
- Canadell, J.; Mooney, H.; Baldocchi, D.; Berry, J.; Ehleringer, J.; Field, C.; Gower, S.; Hollinger, D.; Hunt, J.; Jackson, R.; et al. Carbon metabolism of the terrestrial biosphere: A multi-technique appraoch for improved understanding. Ecosystems 2000, 3, 115–130. [Google Scholar] [CrossRef]
- Wang, B.; Li, M.; Fan, W.; Zhang, F. Quantitative simulation of C budgets in a forest in Heilongjiang province, China. iForest—Biogeosci. For. 2016, 10, 128–135. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Cihlar, J.; Chen, W. Net Primary Productivity Mapped for Canada at 1-km Resolution. Glob. Ecol. Biogeogr. 2002, 11, 115–129. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Bai, Y.; Kojo, U.; Igbawua, T.; Chang, Q.; Zhang, D.; Yao, F. Evaluation and improvement of the daily boreal ecosystem productivity simulator in simulating gross primary productivity at 41 flux sites across Europe. Ecol. Model. 2018, 368, 205–232. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Cihlar, J.; Park, W. A process-based boreal ecosystem productivity simulator using remote sensing inputs. Remote Sens. Environ. 1997, 62, 158–175. [Google Scholar] [CrossRef]
- Kojo, U.; Zhang, J.; Maharjan, S.; Bai, Y.; Zhang, S.; Yao, F. Analysis of spatiotemporal dynamics of forest Net Primary Productivity of Nepal during 2000–2015. Int. J. Remote Sens. 2020, 41, 4336–4364. [Google Scholar] [CrossRef]
- Guan, D.; Nie, J.; Zhou, L.; Chang, Q.; Cao, J. How to simulate carbon sequestration potential of forest vegetation? A forest carbon sequestration model across a typical mountain city in China. Remote Sens. 2023, 15, 5096. [Google Scholar] [CrossRef]
- Holdridge, L. Determination of world plant formations from simple climatic data. Science 1947, 105, 367–368. [Google Scholar] [CrossRef]
- Woodward, F.; Williams, B. Climate and plant distribution at global and local scales. Vegetatio 1987, 69, 189–197. [Google Scholar] [CrossRef]
- Neilson, R. A Model for Predicting Continental-Scale Vegetation Distribution and Water Balance. Ecol. Appl. 1995, 5, 362–385. [Google Scholar] [CrossRef]
- Delire, C.; Foley, J.; Thompson, S. Evaluating the carbon cycle of a coupled atmosphere-biosphere model. Glob. Biogeochem. Cycles 2003, 17, 1012. [Google Scholar] [CrossRef]
- Kucharik, C.; Barford, C.; Maayar, M.; Wofsy, S.; Monson, R.; Baldocchi, D. A multiyear evaluation of a Dynamic Global Vegetation Model at three AmeriFlux forest sites: Vegetation structure, phenology, soil temperature, and CO2 and H2O vapor exchange. Ecol. Model. 2006, 196, 1–31. [Google Scholar] [CrossRef]
- Xie, X.; Li, A.; Jin, H. The simulation models of the forest carbon cycle on a large scale: A review. Acta Ecol. Sin. 2018, 38, 41–54. [Google Scholar] [CrossRef]
- Kucharik, C.; Foley, J.; Delire, C.; Fisher, V.; Coe, M.; Lenters, J.; Young-Molling, C.; Ramankutty, N.; Norman, J.; Gower, S. Testing the performance of a dynamic global ecosystem model: Water balance, carbon balance, and vegetation structure. Glob. Biogeochem. Cycles 2000, 105, 795–825. [Google Scholar] [CrossRef]
- Potter, C.; Randerson, J.; Field, C.; Matson, P.; Vitousek, P.; Mooney, H.; Klooster, S. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Parton, W.; Stewart, J.; Cole, C. Dynamics of C, N, P and S in grassland soils: A model. Biogeochemistry 1988, 5, 109–131. [Google Scholar] [CrossRef]
- Farquhar, G.; Caemmerer, S.; Berry, J. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef]
- Matsushita, B.; Chen, J.; Kameyama, S.; Tamura, M. Estimation of net primary productivity using Boreal Ecosystem Productivity Simulator—A case study for Hokkaido Island, Japan. In Proceedings of the IEEE Transactions on International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 2346–2348. [Google Scholar] [CrossRef]
- Higuchi, K.; Shashkov, A.; Chan, D.; Saigusa, N.; Murayama, S.; Yamamoto, S.; Kondo, H.; Chen, J.; Liu, J.; Chen, B. Simulations of seasonal and inter-annual variability of gross primary productivity at Takayama with BEPS ecosystem model. Agric. For. Meteorol. 2005, 134, 143–150. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, Q.; Chen, J.; Wang, Y.; Liu, J.; Sun, R.; Tang, S. Observation and simulation of net primary productivity in Qilian Mountain, western China. J. Environ. Manag. 2007, 85, 574–584. [Google Scholar] [CrossRef]
- Fu, Y.; Tian, D.; Hou, Z.; Wang, M.; Zhang, N. Review on the evaluation of global forest carbon sink function. J. Beijing For. Univ. 2022, 44, 1–10. [Google Scholar] [CrossRef]
- Tan, W.; Zhou, L.; Liu, K. Soil aggregate fraction-based 14C analysis and its application in the study of soil organic carbon turnover under forests of differents ages. Chin. Sci. Bull. 2013, 58, 1936–1947. [Google Scholar] [CrossRef]
- Yang, H. Assessment on Plantation Forest Visual Resource of Saihanba Mechanical Plantation. Ph.D. Thesis, Hebei Agricultural University, Baoding, China, 2017. [Google Scholar]
- Xiao, F.; Zhang, Q.; Fan, S. Progress of research on carbon fixation and storage of forest ecosystems in China. World For. Res. 2006, 19, 53–57. [Google Scholar] [CrossRef]
- Lu, W. Research on Parameter Optimization and Application of Forest Carbon Cycle Model(BEPS) at Hourly Time Steps. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2016. [Google Scholar]
- Mao, X. Study on the Model of Northeast Forest Carbon Cycle at Daily Step and the Integrated Application of Remote Sensing. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2011. [Google Scholar]
- Zhou, M. Research on the Hydrological Process and Laws of Larix Gmelini Ecosystem at the Greater Xingan Mountains. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2003. [Google Scholar]
- Zhang, Y. Energy and Water Budget of a Poplar Plantation in Suburban Beijing. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2010. [Google Scholar]
- Qi, Y. Estimates of Forest Above Ground Carbon Storage Using Remote Sensing in Daxing’an Mountains. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2014. [Google Scholar]
- Xiong, H.; YU, F.; Gu, X.; Wu, X. Biomass, net production, carbon storage and spatial distribution features of different forest vegetation in Fanjing Mountains. Ecol. Environ. Sci. 2021, 30, 264–273. [Google Scholar] [CrossRef]
- Yang, H.; Peng, B.; Fan, H.; Gu, J.; Li, R.; Li, W. Study on relationship of topographic factors and leaf area index in different forest type. J. Hebei For. Sci. Technol. 2018, 3, 1–6. [Google Scholar] [CrossRef]
- Yi, F. Study on forest carbon density and spatial distribution parttern of Taiyue Mountain in Shanxi Province. J. Shanxi Agric. Sci. 2017, 45, 1814–1817. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, L.D.; Wang, L.; Jia, Z.; Ma, L. Stock volume and productivity of Larix principis-rupprechtii in northern and northwestern China. J. Beijing For. Univ. 2015, 37, 24–31. [Google Scholar] [CrossRef]
- Hu, J.; Yang, B.; Xu, S. Enhancing carbon sink capacity and promoting green development—Carbon sink change of Saihanba mechanized forest farm based on FORECAST model. For. Sci. Technol. 2023, 48, 48–51. [Google Scholar] [CrossRef]
- Tao, B.; Li, K.; Shao, X.; Cao, M. Temporal and spatial pattern of net primary production of terrestrial ecosystems in China. Acta Geogr. Sin. 2003, 58, 372–380. [Google Scholar] [CrossRef]
- Liu, M. Land-Use/Land-Cover Change and Terrestrial Ecosystem Phytomass Carbon Pool and Production in China. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, 2001. [Google Scholar]
- Zhu, W.; Pan, Y.; Zhang, J. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing. Acta Plytoecol. Sin. 2007, 31, 413–424. [Google Scholar] [CrossRef]
- Mao, F.; Du, H.; Zhou, G.; Li, X.; Xu, X.; Li, P.; Sun, S. Coupled LAI assimilation and BEPS model for analyzing the spatiotemporal pattern and heterogeneity of carbon fluxes of the bamboo forest in Zhejiang Province, China. Agric. For. Meteorol. 2017, 242, 96–108. [Google Scholar] [CrossRef]
- Ge, Z.; Guo, H.; Zhao, B.; Zhang, C.; Peltola, H.; Zhang, L. Spatiotemporal patterns of the gross primary production in the salt marshes with rapid community change: A coupled modeling approach. Ecol. Model. 2016, 321, 110–120. [Google Scholar] [CrossRef]




| Level | Value of S | Meaning |
|---|---|---|
| I | 0 ≤ S ≤ 0.1 | Insensitive |
| II | 0.1 < S ≤ 0.25 | Slight Sensitive |
| III | 0.25 < S ≤ 0.5 | Medium Sensitive |
| IV | 0.5 < S ≤ 1 | Highly Sensitive |
| Influencing Factor | Sensitivity | Level |
|---|---|---|
| LAI | 0.722 | IV |
| Radiation | 0.233 | II |
| Precipitation | 0.0004 | I |
| Stand Type | Annual NPP (g C m−2 a−1) | Total NPP (g C a−1) |
|---|---|---|
| Northern Chinese Larch | 518.05 | 1.73 × 1011 |
| Camphor Pine | 576.95 | 7.81 × 1010 |
| Spruce | 565.48 | 1.95 × 1010 |
| Silver Birch | 647.84 | 1.22 × 1011 |
| Coniferous and Broad-leaved Mixed Forest | 661.35 | 2.52 × 1010 |
| Evergreen and Deciduous Coniferous Forest | 558.05 | 2.46 × 109 |
| Sparse Forest and Shrub Forest | 292.60 | 5.11 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Huang, X.; Qing, Y.; Li, H.; Hong, L.; Lu, W. Net Primary Production Simulation and Influencing Factors Analysis of Forest Ecosystem Based on a Process-Based Model. Appl. Sci. 2024, 14, 10912. https://doi.org/10.3390/app142310912
Yang Z, Huang X, Qing Y, Li H, Hong L, Lu W. Net Primary Production Simulation and Influencing Factors Analysis of Forest Ecosystem Based on a Process-Based Model. Applied Sciences. 2024; 14(23):10912. https://doi.org/10.3390/app142310912
Chicago/Turabian StyleYang, Zhu, Xuanrui Huang, Yunxian Qing, Hongqian Li, Libin Hong, and Wei Lu. 2024. "Net Primary Production Simulation and Influencing Factors Analysis of Forest Ecosystem Based on a Process-Based Model" Applied Sciences 14, no. 23: 10912. https://doi.org/10.3390/app142310912
APA StyleYang, Z., Huang, X., Qing, Y., Li, H., Hong, L., & Lu, W. (2024). Net Primary Production Simulation and Influencing Factors Analysis of Forest Ecosystem Based on a Process-Based Model. Applied Sciences, 14(23), 10912. https://doi.org/10.3390/app142310912





