Artificial Intelligence for Earthquake Prediction: A Preliminary System Based on Periodically Trained Neural Networks Using Ionospheric Anomalies
Abstract
1. Introduction
- Anomalous TEC values are observed from around one week to some hours before a large earthquake with particular signatures that seem to start to be observable above a magnitude of Mw = 6 (even for Mw = 5 in some cases), and much more clearly for magnitudes above Mw = 7 [4,5,6,7,8,13,14,17,18,21,26,27,28].
- The area of the ionosphere in which the anomaly is perceived is usually approximately centered in the vertical of the epicenter [3,7,17,18,21] due to the injection of ions into the atmosphere subsequent to the tectonic stresses produced beneath, and its extension depends on the magnitude of the earthquake Mw so that its radius is approximately given by the following [3,26]:where e is the base of the natural logarithm, or by the equivalent (as demonstrated in [26]) Dobrovolsky formula [14,17,18,21,29]:
2. Materials and Methods
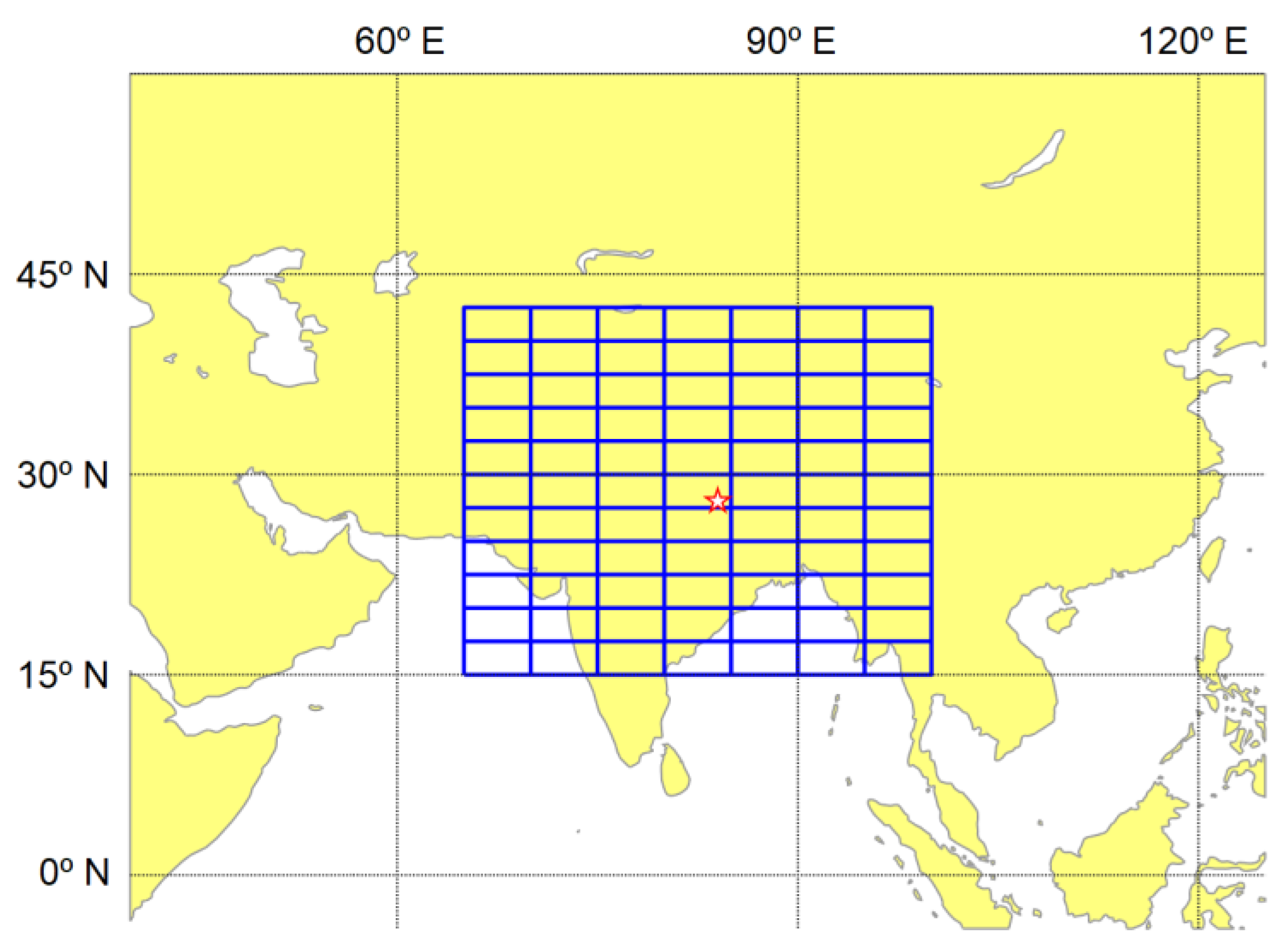
2.1. TEC Values
2.2. Earthquake Catalog
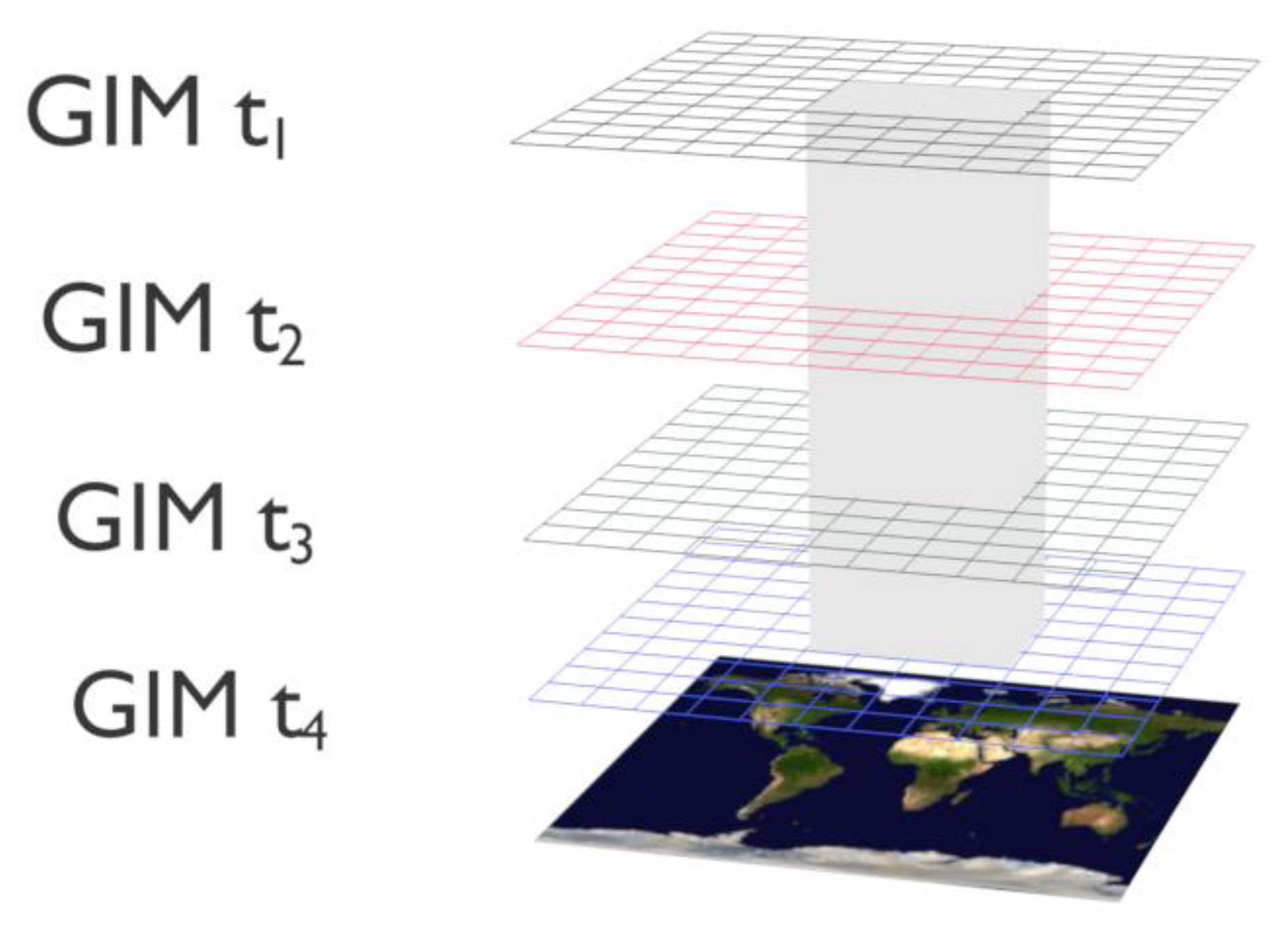
2.3. Training and Validation Data
- A predictor variable, denoted as the X variable, from the use of the GIM files of the previous few days (excluding the file of the day of the earthquake)—that is, from 7 days before to 1 day before to predict the maximum earthquake. This X variable turns out to be a 3D matrix with the following features:
- -
- 60 rows, corresponding to the latitude range explained before;
- -
- 73 columns. Since the length of the parallel arc depends on its latitude different numbers of columns were obtained for the different latitudes, with high latitudes needing the whole column range in the GIM, 73. Completing with zeros the other column ranges was necessary to have a consistent size;
- -
- 84 values in the third dimension, corresponding to the 7 days with data every 2 h in the GIM files;
- A predicted variable, denoted as the Y variable, which is obtained from the earthquake list as the highest magnitude of the earthquake occurring in the area from 7 days before to 4 days after the earthquake under analysis. This is because there could be aftershocks even larger than the selected earthquake, or previous events of greater magnitude, and the predictor should capture them. The earthquake magnitude is categorized in one of eight categories named as group number in Table 1 and this category is stored as the Y variable.
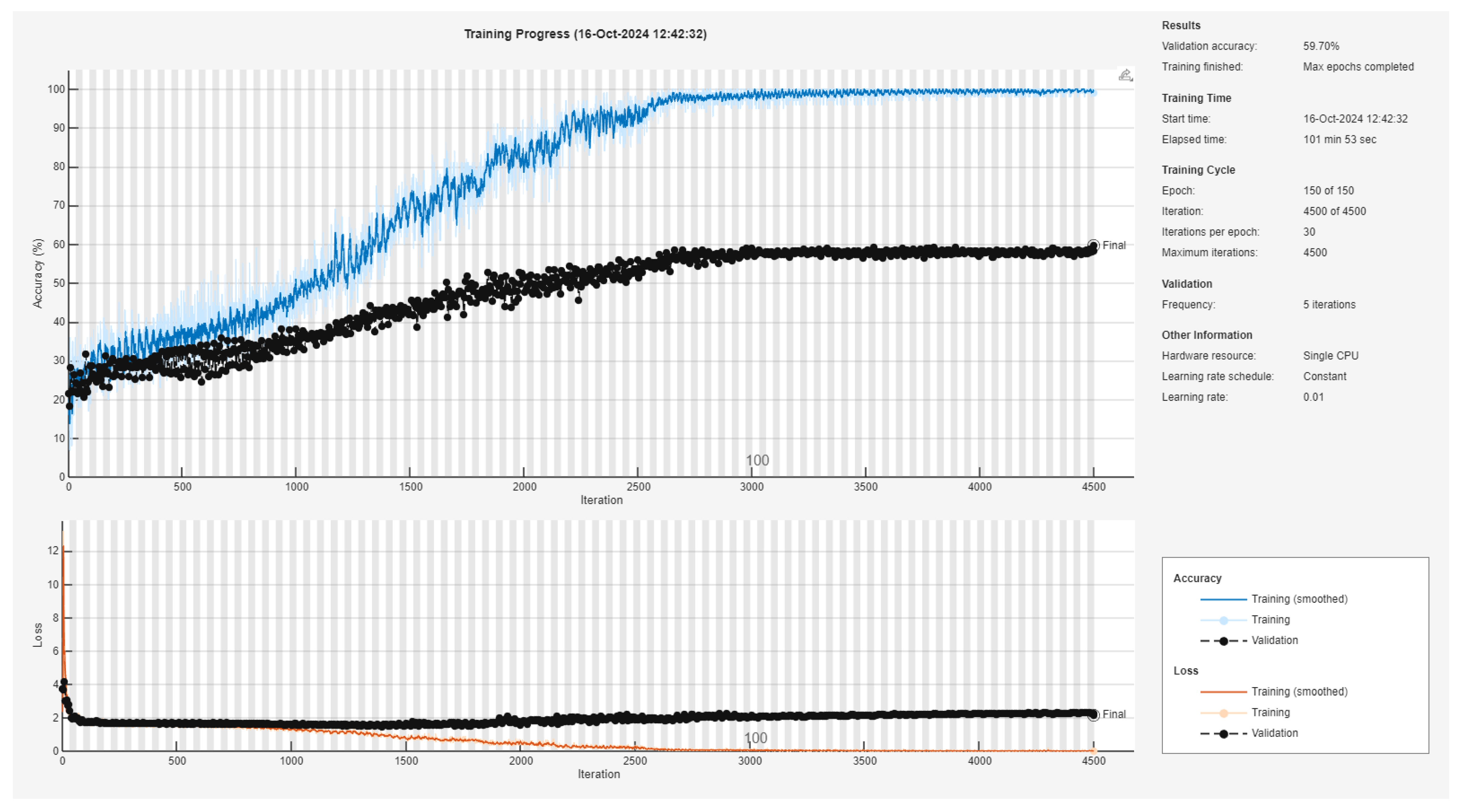
2.4. Convolutional Neural Networks
3. Results and Discussion
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buskirk, R.E.; Frohlich, C.L.; Latham, G.V. Unusual animal behavior before earthquakes: A review of possible sensory mechanisms. Rev. Geophys. 1981, 19, 247–270. [Google Scholar] [CrossRef]
- Grant, R.A.; Halliday, T. Predicting the unpredictable; evidence of pre-seismic anticipatory behaviour in the common toad. J. Zool. 2010, 281, 263–271. [Google Scholar] [CrossRef]
- Zakharenkova, I.E.; Shagimuratov, I.I.; Krankowski, A. Features of the ionosphere behavior before the Kythira 2006 earthquake. Acta Geophys. 2007, 55, 524–534. [Google Scholar] [CrossRef]
- Zakharenkova, I.E.; Shagimuratov, I.I.; Krankowski, A.; Lagovsky, A.F. Precursory phenomena observed in the total electron content measurements before great Hokkaido earthquake of September 25, 2003 (M = 8.3). Stud. Geophys. Geod. 2007, 51, 267–278. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Chen, C.H.; Liu, C.Y.; Chen, C.Y.; Nishihashi, M.; Li, J.Z.; Xia, Y.Q.; Oyama, K.I.; Hattori, K.; et al. Seismoionospheric GPS total electron content anomalies observed before the 12 May 2008 Mw7.9 Wenchuan earthquake. J. Geophys. Res. 2009, 114, A04320. [Google Scholar] [CrossRef]
- Lin, J.W. Latitude-Time Total Electron Content Anomalies as Precursors to Japan’s Large Earthquakes Associated with Principal Component Analysis. Int. J. Geophys. 2011, 2011, 763527. [Google Scholar] [CrossRef]
- Guo, J.; Yu, H.; Li, W.; Liu, X.; Kong, Q.; Zhao, C. Total Electron Content Anomalies Before Mw 6.0+ Earthquakes in the Seismic Zone of Southwest China between 2001 and 2013. J. Test. Eval. 2017, 45, 131–139. [Google Scholar] [CrossRef]
- Jia, D.; Yu, H.; Zhao, B.; Ma, Y. Geothermal Anomalies and Coupling with the Ionosphere before the 2020 Jiashi Ms6.4 Earthquake. Appl. Sci. 2023, 13, 3019. [Google Scholar] [CrossRef]
- Pura, T.; Güneş, P.; Güneş, A.; Hameed, A.A. Earthquake Prediction for the Düzce Province in the Marmara Region Using Artificial Intelligence. Appl. Sci. 2023, 13, 8642. [Google Scholar] [CrossRef]
- Fuso, F.; Crocetti, L.; Ravanelli, M.; Soja, B. Machine learning-based detection of TEC signatures related to earthquakes and tsunamis: The 2015 Illapel case study. GPS Solut. 2024, 28, 106. [Google Scholar] [CrossRef]
- Pizza, M.; Ferrario, F.; Michetti, A.M.; Velázquez-Bucio, M.M.; Lacan, P.; Porfido, S. Intensity Prediction Equations Based on the Environmental Seismic Intensity (ESI-07) Scale: Application to Normal Fault Earthquakes. Appl. Sci. 2024, 14, 8048. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, P.; Li, S. Feasibility Study on Earthquake Prediction Based on Impending Geomagnetic Anomalies. Appl. Sci. 2024, 14, 263. [Google Scholar] [CrossRef]
- Tronin, A.A.; Hayakawa, M.; Molchanov, O.A. Thermal IR Satellite Data Application for Earthquake Research in Japan and China. J. Geodyn. 2002, 33, 519–534. [Google Scholar] [CrossRef]
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer: Berlin, Germany, 2004; pp. 1–315. [Google Scholar]
- Nemec, F.; Santolík, O.; Parrot, M.; Berthelier, J.J. Spacecraft observations of electromagnetic perturbations connected with seismic activity. Geophys. Res. Lett. 2008, 35, L05109. [Google Scholar] [CrossRef]
- Grant, R.A.; Halliday, T.; Balderer, W.P.; Leuenberger, F.; Newcomer, M.; Cyr, G.; Freund, F.T. Ground Water Chemistry Changes before Major Earthquakes and Possible Effects on Animals. Int. J. Environ. Res. Public Health 2011, 8, 1936–1956. [Google Scholar] [CrossRef]
- Picozza, P.; Conti, L.; Sotgiu, A. Looking for Earthquake Precursors from Space: A Critical Review. Front. Earth Sci. 2021, 9, 676775. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient Effects in Atmosphere and Ionosphere Preceding the 2015 M7.8 and M7.3 Gorkha–Nepal Earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- Freund, F. Charge generation and propagation in rocks. J. Geodyn. 2002, 33, 545–572. [Google Scholar] [CrossRef]
- Freund, F.T.; Takeuchi, A.; Lau, B.W. Electric currents streaming out of stressed igneous rocks—A step towards understanding pre-earthquake low frequency EM emissions. Phys. Chem. Earth 2006, 31, 389–396. [Google Scholar] [CrossRef]
- Freund, F.T.; Kulahci, I.G.; Cyr, G.; Ling, J.; Winnick, M.; Tregloan-Reed, J.; Freund, M.M. Air ionization at rock surfaces and pre-earthquake signals. J. Atmos. Sol. Terr. Phys. 2009, 71, 1824–1834. [Google Scholar] [CrossRef]
- Freund, F.T. Toward a unified solid state theory for pre-earthquake signals. Acta Geophys. 2010, 58, 719–766. [Google Scholar] [CrossRef]
- Warwick, J.W.; Stoker, C.; Meyer, T.R. Radio emission associated with rock fracture: Possible application to the Great Chilean Earthquake of May 22, 1960. J. Geophys. Res. Solid Earth 1982, 87, 2851–2859. [Google Scholar] [CrossRef]
- King, B.V.; Freund, F. Surface charges and subsurface space charge distribution in magnesium oxide containing dissolved traces of water. Phys. Rev. B 1984, 29, 5814–5824. [Google Scholar] [CrossRef]
- Philippetis, A.L. Electromagnetic signals before rupture and their possible interconnection with bioeffects. Modern Phys. Lett. B 2009, 23, 1431–1436. [Google Scholar] [CrossRef]
- Baselga, S. A combined estimator using TEC and b-value for large earthquake prediction. Acta Geod. Geophys. 2020, 55, 63–82. [Google Scholar] [CrossRef]
- Şentürk, E.; Çepni, M.S. A statistical analysis of seismo ionospheric TEC anomalies before 63 Mw ≥ 5.0 earthquakes in Turkey during 2003–2016. Acta Geophys. 2018, 66, 1495–1507. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, P.; Wu, H.; Zhang, S.; Peng, W. Analysis of ionospheric anomalies before the 2011 Mw 9.0 Japan earthquake. Chin. Sci. Bull. 2012, 57, 500–510. [Google Scholar] [CrossRef][Green Version]
- Dobrovolsky, I.R.; Zubkov, S.I.; Myachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Ionosphere. International GNSS Service. Available online: https://igs.org/wg/ionosphere (accessed on 17 October 2024).
- Maurício, J.; Domingues, I.; Bernardino, J. Comparing Vision Transformers and Convolutional Neural Networks for Image Classification: A Literature Review. Appl. Sci. 2023, 13, 5521. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Legen’ka, A.D.; Gaivoronskaya, T.V.; Depuev, V.K. Main phenomenological features of ionospheric precursors of strong earthquakes. J. Atmos. Sol. Terr. Phys. 2003, 65, 1337–1347. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; Saradjian, M.R. TEC variations analysis concerning Haiti (January 12, 2010) and Samoa (September 29, 2009) earthquakes. Adv. Space Res. 2011, 47, 94–104. [Google Scholar] [CrossRef]
- Gopinath, S.; Prince, P.R. Nonextensive and distance-based entropy analysis on the influence of sunspot variability in magnetospheric dynamics. Acta Geod. Geophys. 2018, 53, 639–659. [Google Scholar] [CrossRef]
- Paul, B.; De, B.K.; Guha, A. Latitudinal variation of F-region ionospheric response during three strongest geomagnetic storms of 2015. Acta Geod. Geophys. 2018, 53, 579–606. [Google Scholar] [CrossRef]
- Earthquake Catalog. U.S. Geological Survey. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 17 October 2024).
- Deep Learning Toolbox—MATLAB—MathWorks. Available online: https://www.mathworks.com/products/deep-learning.html (accessed on 17 October 2024).

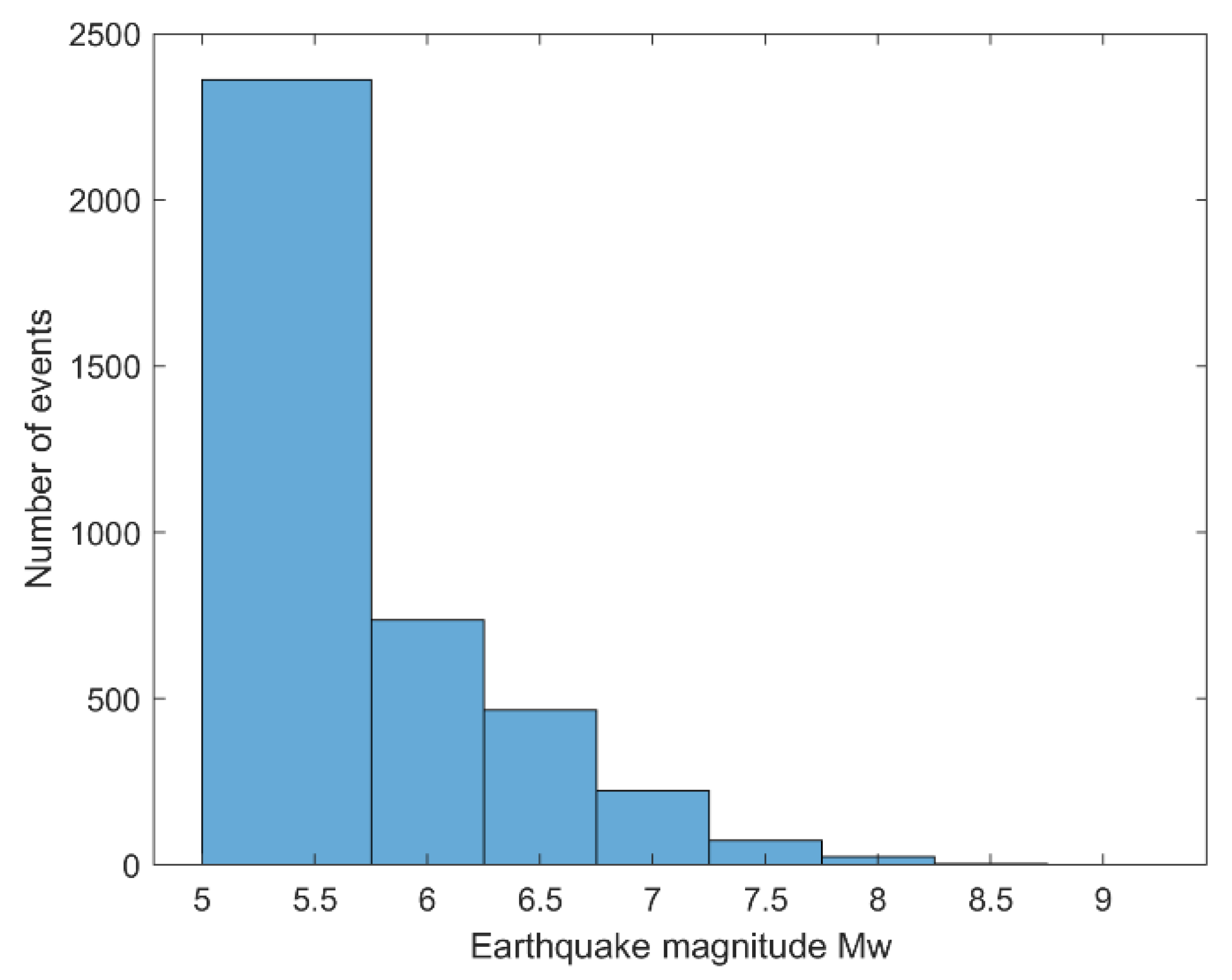


| Group Number | Approximate Magnitude Mw | Magnitude Mw Limits | Number of Events |
|---|---|---|---|
| 1 | 5.5 or less | <5.75 | 2362 |
| 2 | 6.0 | [5.75, 6.25) | 736 |
| 3 | 6.5 | [6.25, 6.75) | 466 |
| 4 | 7.0 | [6.75, 7.25) | 224 |
| 5 | 7.5 | [7.25, 7.75) | 74 |
| 6 | 8.0 | [7.75, 8.25) | 24 |
| 7 | 8.5 | [8.25, 8.75) | 3 |
| 8 | 9.0 | ≥8.75 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baselga, S. Artificial Intelligence for Earthquake Prediction: A Preliminary System Based on Periodically Trained Neural Networks Using Ionospheric Anomalies. Appl. Sci. 2024, 14, 10859. https://doi.org/10.3390/app142310859
Baselga S. Artificial Intelligence for Earthquake Prediction: A Preliminary System Based on Periodically Trained Neural Networks Using Ionospheric Anomalies. Applied Sciences. 2024; 14(23):10859. https://doi.org/10.3390/app142310859
Chicago/Turabian StyleBaselga, Sergio. 2024. "Artificial Intelligence for Earthquake Prediction: A Preliminary System Based on Periodically Trained Neural Networks Using Ionospheric Anomalies" Applied Sciences 14, no. 23: 10859. https://doi.org/10.3390/app142310859
APA StyleBaselga, S. (2024). Artificial Intelligence for Earthquake Prediction: A Preliminary System Based on Periodically Trained Neural Networks Using Ionospheric Anomalies. Applied Sciences, 14(23), 10859. https://doi.org/10.3390/app142310859






