Abstract
In this paper, we introduce a novel approach to model bending phenomena on holographic volume gratings based on Rigorous Coupled Wave Analysis (RCWA), in which the bending as a phase in the dielectric permittivity expansion is introduced, and the Shooting Method (SM) is employed to solve the resulting system of equations. Further validation of our model is conducted by comparing its predictions to those obtained from reference Finite-Difference Time-Domain (FDTD) simulations and Coupled Wave Theory (CWT, referring to Kubota’s model that includes the bending phenomenon). Furthermore, we propose a methodology for estimating the bending from the diffraction efficiency curves in transmission volume gratings based on deep learning models, with a subsequent study of their accuracy and applicability.
1. Introduction
Holographic gratings have emerged as versatile and indispensable tools in optics and photonics, finding applications in fields as diverse as spectroscopy, telecommunications, and laser technology. They occupy a central position in various scientific, industrial, and technological domains because they can disperse, reflect, or diffract light in precise and controlled ways [,,,].
Often, imperfections in the recording or fabrication process may lead to an unwanted bending of the structure of diffraction gratings, which inevitably impacts its optical properties in uncontrolled ways. A non-uniform deformation of its fringes characterises this phenomenon, and it is mainly associated with a pre-stress in the recording material. On the other hand, many researchers have focused on bending as a crucial element for holographic sensors [,]. Zhou et al. [] considered the bending deformation of a hydrogel actuator to be an essential deformation parameter, and Yetisen et al. have corroborated the application of holographic sensors as versatile optical sensing platform to characterise the deformation of the polymer due to its narrow diffraction spectrum, high visualisation, and stability [,]
The phenomenon of bending within holographic gratings has been understudied despite its frequent occurrence. The leading theory previously developed on the subject has been carried out by T. Kubota, which is based on Kogelnik’s coupled wave theory with an attenuated grating model [,]. This method focuses solely on the substrate itself and fails to account for air–medium discontinuities, thereby presenting limitations in its applicability. Indeed, over the years, Rigorous Coupled Wave Theory (RCWT) has been proven to be a powerful and versatile numerical method in the context of diffractive optics and photonics. This technique, initially developed by Moharam and Gaylord [,,,], has significantly advanced our understanding of light diffraction and its interaction with periodic structures. RCWT is founded on the rigorous solution of Maxwell’s equations and has been widely adopted in the study of diffraction gratings, photonic crystals, and other periodic optical structures []. Over the years, RCWT has evolved and been extended to address complex and practical problems, including incorporating anisotropic and inhomogeneous materials []. Its continued development and application have cemented RCWT as a reference of numerical techniques for diffractive optical analysis and design.
Accurately determining the bending of holographic grating fringes measured in laboratory settings implies using cost-consuming advanced techniques such as Scanning Electron Microscopy, Ellipsometry, or Interferometry. Due to the complex nature and the non-derivability of the formalism developed for the analysis of bending, an analytical approach to characterise these deformations from diffraction efficiency patterns is not feasible. Therefore, this research aims to set up a novel scheme based on deep learning solutions for estimating the parameters that define the bending in holographic gratings from the diffraction efficiency curves obtained numerically, addressing these limitations and providing a more accessible solution. Neural network-based solutions, particularly due to their nonlinear activation functions, are widely known precisely at regression problems in cases where analytical, linear solutions are not feasible. Thus, the most straightforward and viable solution is developing a computational regression model based on these technologies [,,]. For feeding the deep learning engine, we proposed a novel RCWA-SM scheme that considers bending as a phase in dielectric permittivity expansion and uses the shooting method to solve the system of equations. A numerical SF-FDTD scheme was also considered for validating the RCWA-SM implementation. It is worth noting that RCWA-SM was found to be the best candidate for use in the deep learning engine due to its performance compared to the SF-FDTD scheme.
In the present work, we propose a novel method for predicting bending parameters from theoretical data using deep learning tools. This study continues our previous work on the estimation of characteristic parameters of holographic volume gratings based on machine learning, as presented in [], where we first demonstrated the feasibility of using deep learning models to estimate grating parameters. Here, we extend that foundation by investigating optimal architectures for predicting bending parameters and comparing the performance of a Feedforward Neural Network (FNN) and a hybrid Convolutional Neural Network (CNN)–FNN model. Slight improvements in accuracy and robustness were observed in the hybrid model, even when a smaller number of weights was applied.
FNNs and CNNs have played pivotal roles in advancing machine learning capabilities, offering robust solutions to vast real-world problems [,,,]. FNNs, also known as dense networks, consist of layers where each neuron is connected to every neuron in the subsequent layer, with intertwined nonlinear activation functions. This architecture enables FNNs to learn intricate relationships within data, making them suitable for various tasks such as classification, regression, and pattern recognition [,,]. On the other hand, CNNs leverage convolutional layers to extract spatial features from input data. Although CNNs are not as commonly used for regression as for classification due to their design being intrinsically well suited for pattern extraction and hierarchical feature learning, they have proven effective for regression tasks like image super-resolution [,], depth estimation [], Image Reconstruction [], and others.
Regarding the structure of this paper, in the first section, we will set the theoretical basis for developing our RCWA-Shooting method approach and the theoretic basis for the implemented deep learning solutions. The results of our RCWA-SM study on the standard RCWA and FDTD models will be presented. Then, the application and results of the deep learning solutions will be discussed. Finally, and serving as the conclusion, a discussion on the validity and suitability of both approaches will be conducted.
2. Theory
In this section, we present the theoretical models and methodologies applied in this work. These include the development of a framework that incorporates bending into the RCWA for accurately modelling nonplanar grating structures. Furthermore, we outline the theoretical basis for the deep learning approach employed to predict bending behavior based on the RCWA-SM model.
2.1. Rigorous Coupled Wave Analysis—Shooting Method Approach
The exposure of a material to an interference pattern results in a modulation of the medium’s dielectric permittivity that can be expressed as
where K is the grating vector, and is the grating slant angle.
We can parametrize a bending in this dielectric modulation pattern as a characteristic polynomial as follows:
where d is the optical depth.
Introducing it as an expansion factor in the dielectric permittivity expression embedded in , we have the following:
and then, the more specific formula for the permittivity can be written as
Figure 1 shows the model of the thick hologram used for the analysis where the bending in the interference fringes can be identified. The terms and are related to the amplitudes of the electromagnetic field, which is detailed next.
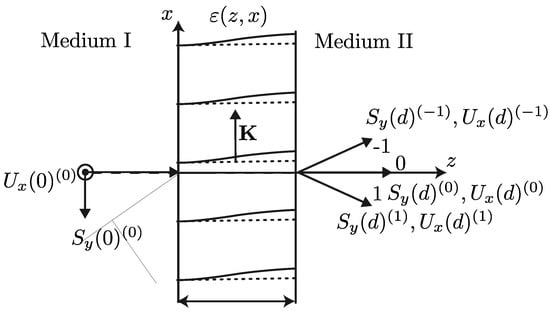
Figure 1.
Model of the thick hologram used for the analysis.
Following a similar formalism to [], we can describe the electromagnetic interaction as follows:
where and represent the amplitudes of the ith space harmonic components of the electric and magnetic fields, respectively, is the identity matrix, and are diagonal matrices, and the wave vector is ; the z-component of the grating wave vector is defined as follows:
where is the free-space wave number, n and are the refractive index values of the recording medium and the angle of incidence in the recording medium, respectively, and is the grating slant angle.
and is a Toeplitz matrix, wherein we then have the following:
with respect to the boundary conditions and letting be the normalised electric-field amplitude of the ith reflected wave in region I and be the normalised electric-field amplitude of the transmitted wave in region II:
Indeed, with being the diagonal matrices of the z-components of the wave vectors in the outer media, we can rewrite the last two in terms of the first ones:
Similarly, following [], if we now define the reflectance and transmittance vectors, and , we can express the boundary conditions in an alternative manner:
We will modify the problem, transforming it to an Initial Value Problem (IVP), with the initial conditions given by
which, in turn, define those of and its derivative through Equation (8):
The general solution will then be a linear combination of the particular solutions, with some constants to be determined:
By construction, Equation (11) at becomes
This helps us to rewrite the boundary conditions by considering .
In the previous relationships, there is a total of equations for the four sets of N unknowns: , , , and .
Proceeding as we did for the previous formalism, we only need to choose the boundary condition at with :
This is done to construct a system of equations for the constants in the form , where
are known.
In this way, we can compute the field value at the first surface using Equation (15), thus obtaining the reflection and transmission coefficients.
Figure 2 summarises the sequence of the implementation of the RCWA-SM method detailed in this section. The flowchart shows how an initial boundary value problem (BVP) is transformed into an initial value problem (IVP) and finally to a linear system of equations to solve the reflection and transmission coefficients.
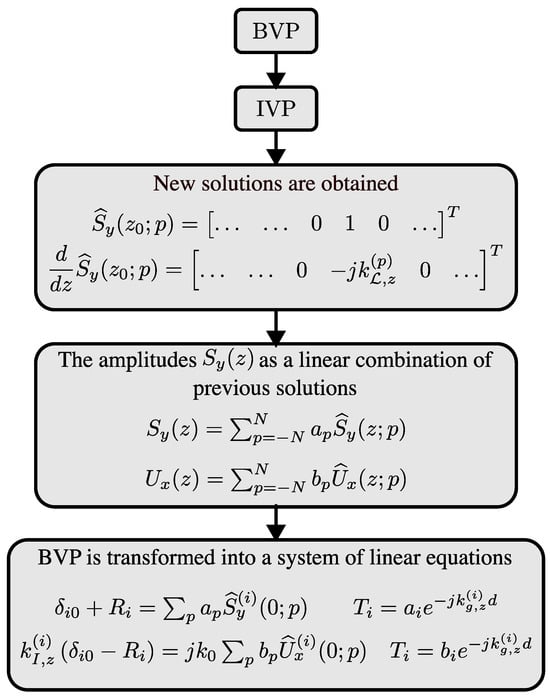
Figure 2.
Flow chart of the RCWA-SM method proposed.
2.2. FNNs and CNNs Theory Foundations
Deep learning (DL), a subset of machine learning encompassing all neural network architectures, has proven to be a revolutionary field with applications that impact a wide range of scientific and technological areas [,,]. These algorithms mimic the structure and function of the human brain and are used to recognize patterns for supervised, semi-supervised, or unsupervised purposes. The most significant distinction of DL algorithms compared to traditional machine learning algorithms is that DL algorithms autonomously learn hierarchical representations of data, eliminating the need for hand-crafted feature engineering to transform the data into a more suitable form.
All artificial neural networks are composed of interconnected nodes, or neurons, organized into layers. FNNs are the simplest form of neural networks, consisting of an input layer, an output layer, and one or more hidden layers in between, as illustrated in Figure 3a. Each hidden layer is essentially a matrix and an activation function that introduces nonlinearity to the system, which is a fundamental trait of neural networks. The components of these matrices are called weights, and they are updated iteratively to minimize the loss function between the model and the target outputs, typically using a gradient descent-based optimization algorithm [,,,].
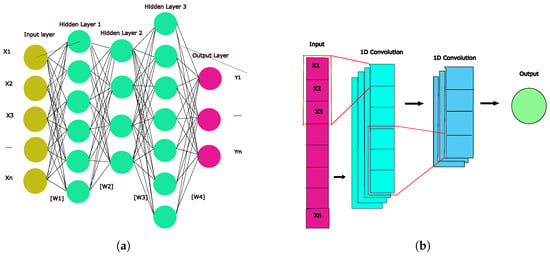
Figure 3.
Schematic of FNN and 1D CNN architectures. (a) FNN’s schematic, with weight matrices represented by the network between neurons (circles). (b) A 1D CNN’s schematic, with a kernel of 3 units represented in both convolution layers shown.
On the other hand, a one-dimensional CNN hidden layer consists of several filters or kernels that slide along the input or preceding layers sequence, as shown in Figure 3b, with its subsequent activation function [,]. The input data are typically a one-dimensional array featuring some spatial auto-correlation, such as a time series, a sequence of words in natural language processing or, in our case, a diffraction pattern. This allows kernels to extract the underlying patterns derived from that spatial auto-correlation of the input. In this case, the weights consist of the components of the convolutional kernels, which are updated in a completely analogous fashion to the FNNs mentioned above.
FNNs and CNNs differ fundamentally in how they handle data. FNNs treat individual data points as separate, fixed units, while CNNs are designed to capture local correlations, spatial hierarchies, and patterns within data through their sliding convolutional kernels. This makes CNNs ideal for image and signal processing, in which the spatial and temporal dependencies are present and critical. By optimising their kernel weights through backpropagation and gradient descent, CNNs can improve their ability to generalise spatial or temporal auto-correlated data predictions.
Given our objective of predicting the bending polynomial coefficients and other fringe parameters from spatially auto-correlated experimental diffraction efficiency patterns, it is essential to consider the inclusion of CNN layers in our deep learning solution. This study thoroughly evaluates their suitability, as discussed in the present work.
3. Results
This section presents the results of our study on modelling and predicting bending phenomena in holographic volume gratings. We begin by evaluating RCWA-SM for modelling diffraction efficiency in gratings with varying degrees of bending, comparing with Kubota’s method and Split-Field Finite-Difference Time-Domain (SF-FDTD) simulations. Following this, we explore deep learning approaches to estimate bending parameters. Specifically, we compare two architectures: an FNN and a CNN–FNN hybrid designed to predict bending polynomial coefficients, optical depth, and index modulation based on diffraction patterns.
3.1. Suitability of the RCWA-Shooting Method
This section covers the results of different gratings with different bending degrees. The bending scheme considered is the one defined by Equation (2). The term is not taken into account, since it only implies a displacement in the fringes of the grating, not influencing the diffraction efficiency of the gratings. The results here compare the diffraction efficiency obtained through Kubota’s formalism, RCWA-SM (introduced in Section 2.1), and the results from SF-FDTD method. The diffraction grating simulated is a transmission grating with . These angles produce a grating with a spatial frequency of m. The average refractive index was = 1.63, and the modulation index was = 0.025. The thickness of the grating wa m. This setup defines a volume grating where only one diffracted order will be relevant in efficiency since the parameter . Regarding FDTD simulations, the grid density was , and the illumination wavelength wa nm. The time resolution was varied as a function of the incidence angle , ensuring in all cases the Courant–Friederich–Lewy condition defined in Equation (14) in [], and the number of time steps in the simulation was chosen as 5000, ensuring the steady state of the electromagnetic waves inside the diffractive element. Due to the spatial symmetry, a 2D simulation with 1238 × 52 grid cells was considered.
Firstly, simulations for a specific value of the , and were considered. More specifically, Figure 4 shows the results for the grating matching the cases summarised in Table 1. For Figure 4a, the different methods show accurate results when no bending was present in the diffraction grating. The results in Figure 4b–d show how the bending induced a displacement on the curves for the SM-RCWA and Kubota compared to the FDTD. This displacement when bending is present is mainly because both RCWA-SM and Kubota consider a constant grating vector modulus along z and introduce the bending as a phase term. In contrast, the FDTD computes the diffraction efficiency directly using the interaction of light inside the periodic structure with the bending as they travel along the z direction. This approach is more accurate, and it translated in the results as a slight displacement of the diffraction efficiency curves compared to the RCWA-SM and Kubota. For the cases where and were the only parameters inducing the bending, SM-RCWA and Kubota’s implementations maintained the deviation to some degree (compared to the FDTD). As the modulus of the bending roe () and the amplitude of and were prominent, the SM-RCWA and Kubota significantly reduced its performance compared to the FDTD. The influence of the bending can be summarised as an angular displacement of the diffraction curve; the angular diffraction response was not symmetric around Bragg’s angle, and a rise in the curves induced a disappearance of the null diffraction efficiency values.
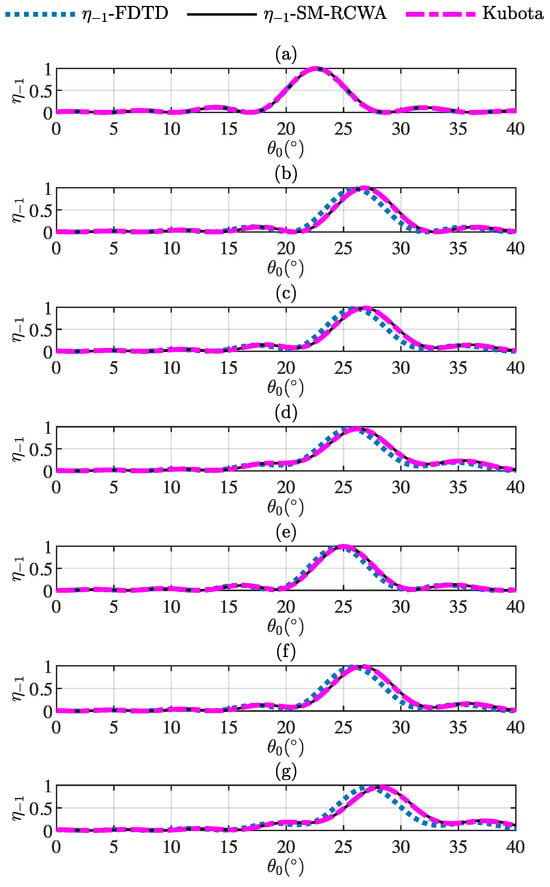
Figure 4.
Diffraction efficiency of the −1st-order as a function of the angle of incidence for different bending parameters . (a) . (b) . (c) . (d) . (e) . (f) . (g) .

Table 1.
Parameter values considered for in Figure 4.
For analysing more precisely the performance of the different methods, Figure 5 shows the error between the SM-RCWA and Kubota’s against the FDTD for the various scenarios here considered (summarised in Table 1). From Figure 5a, it can be seen that the SM-RCWA showed quite good results under the ones obtained by the traditional Kubota implementation.
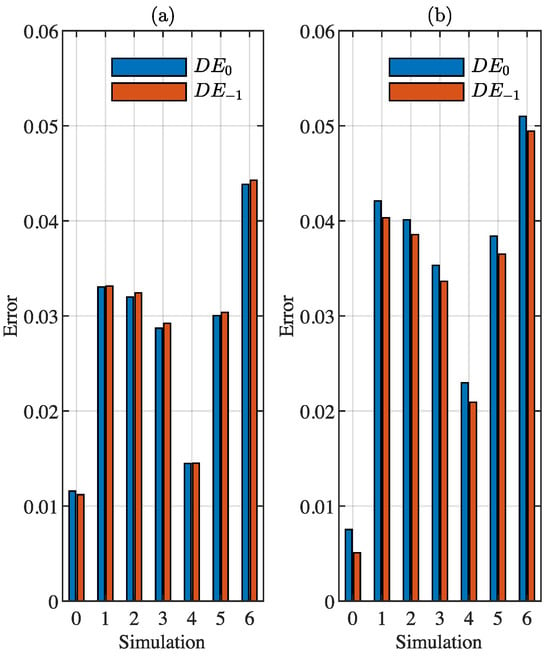
Figure 5.
(a) Absolute error between FDTD values and SM-RCWA, as well as FDTD vs. Kubota’s implementation (b) for the different simulations covered in Table 1. Blue bars represent the error for the transmitted order, and blue bar represents the error for the −1st-order.
Figure 6 shows the results for a more profound analysis when only varying from −0.5 up to 0.5. Figure 6a represents the variation in the amplitude of the maximum of the diffraction efficiency. Figure 6b shows the angle where the maximum value of the diffraction efficiency was located. Figure 6c,d represent the amplitude of the first lobes around the Bragg’s angle. Following the same procedure, Figure 6d,f show the position of these lateral lobes as a function of the parameter. The bottom graphs in Figure 6g,h represent the correlation coefficient of the diffraction efficiency compared to the response of the grating without bending and the deviation of the Bragg’s angle compared to the ideal case (no bending), respectively. The analysis of Figure 6 implies that the amplitudes analysed remained constant for different values of .
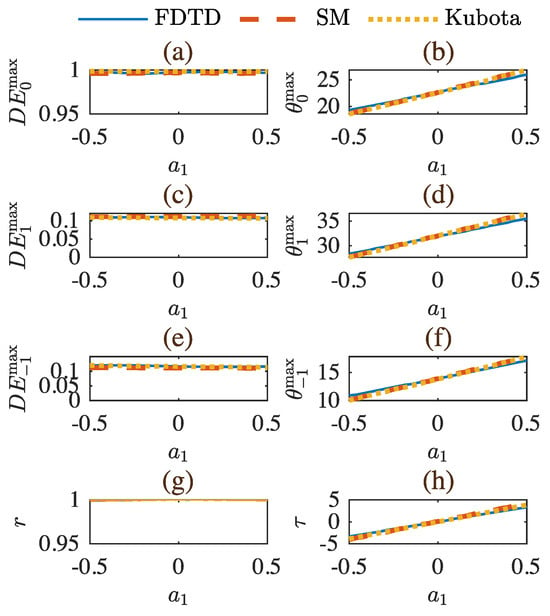
Figure 6.
Parametric analysis of the different methods as a function of the bending parameter . Here, . (a) Variation in the amplitude of the maximum of the diffraction efficiency of the −1st-order at the Bragg angle. (b) Position in degrees of the maximum of the diffraction efficiency. (c) Amplitude of the maximum of the right lobe of the −1st-order. (d) Position in degrees of the maximum of the right lobe of the −1st-order. (e) Amplitude of the maximum of the left lobe of the −1st-order. (f) Position in degrees of the maximum of the left lobe of the −1st-order. (g) Correlation parameter between the bending analysis and the response without bending. (h) Displacement of the position of the maximum correlation.
Figure 7 and Figure 8 show the same analysis for and , respectively. The linear dependence of the angular variations for seems to be not as linear as the case shown in Figure 6. The variations in amplitude also became more significant. The performance of the SM-RCWA and Kubota seems to be consistent with the previous results.
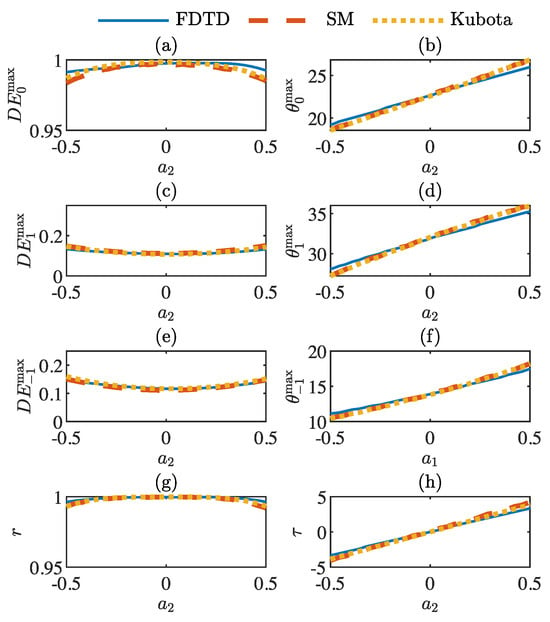
Figure 7.
Parametric analysis of the different methods as a function of the bending parameter . Here, . (a) Variation in the amplitude of the maximum of the diffraction efficiency of the −1st-order at the Bragg angle. (b) Position in degrees of the maximum of the diffraction efficiency. (c) Amplitude of the maximum of the right lobe of the −1st-order. (d) Position in degrees of the maximum of the right lobe of the −1st-order. (e) Amplitude of the maximum of the left lobe of the −1st-order. (f) Position in degrees of the maximum of the left lobe of the −1st-order. (g) Correlation parameter between the bending analysis and the response without bending. (h) Displacement of the position of the maximum correlation.
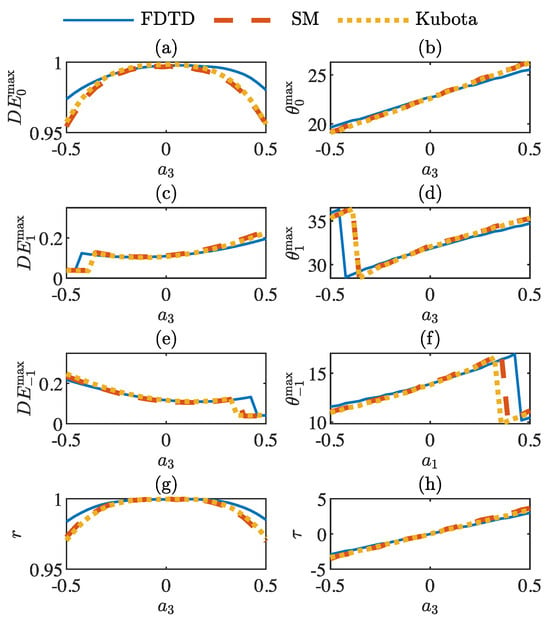
Figure 8.
Parametric analysis of the different methods as a function of the bending parameter . Here, . (a) Variation in the amplitude of the maximum of the diffraction efficiency of the −1st-order at the Bragg angle. (b) Position in degrees of the maximum of the diffraction efficiency. (c) Amplitude of the maximum of the right lobe of the −1st-order. (d) Position in degrees of the maximum of the right lobe of the −1st-order. (e) Amplitude of the maximum of the left lobe of the −1st-order. (f) Position in degrees of the maximum of the left lobe of the −1st-order. (g) Correlation parameter between the bending analysis and the response without bending. (h) Displacement of the position of the maximum correlation.
Figure 8 shows the more extreme results due to the variation in . Regarding amplitude, it can be seen that as rises, the diffraction efficiency significantly reduces. Figure 8g shows that the diffraction efficiency curve is progressively less correlated to the ideal response dealing with the disappearance of the lateral lobes of the curve, as it can be seen in the abrupt discontinuities on the tracking of the lateral lobes in Figure 8c–f. These discontinuities in the curves are produced by the severe degradation of the diffraction efficiency curve that induces the vanishing of lateral lobes.
3.2. Deep Learning-Based Bending Estimator
In this section, we present and show the results of the two deep learning models developed: one strictly based on FNNs architecture and the other one being a hybrid of CNNs and FNNs for the estimation of bending parameters as three-order polynomial coefficients alongside optical depth and index modulation. The models were trained using simulated data generated across a range of standardised index modulations, optical depths, and the three coefficients (, , ) characterising the third-degree bending polynomial ( leaves the grating’s diffraction efficiency pattern invariant). To ensure a fair comparison between the two models and to investigate the impact of CNN layers on the training process, both architectures were constructed to possess a comparable number of weights.
A five feedforward layer model, with interleaved Rectified Linear Unit (ReLU) activation functions and 20% dropouts (to prevent overfitting), was employed as our first simpler FNN model, with a total 1,459,120 weights, as the code image shows in Appendix A.1. For our hybrid model instead, we used 1- to 64- and 64- to 128-channel seven-sized kernel CNN layers with interleaved ReLU activation functions [] and a maximum pooling of two kernels before three more straightforward feedforward layers interleaved again with ReLU activation functions and 20% dropouts, with a total number of weights of 1,247,808, as shown in Appendix A.2.
We opted for an L1 mean absolute error loss function and a batch size of 100. For the optimisation algorithm, we chose Root Mean Square Propagation (RMSProp) after we tried various optimisation algorithms and observed that it yielded faster convergence and improved stability compared to others such as Adam, Adagrad, or Stochastic Gradient Descent (SGD). RMSProp is designed to address some of the limitations of traditional gradient descent methods, such as the sensitivity to learning rates and the scaling of gradients, by adjusting the learning rates for each parameter in the neural network based on the magnitudes of their gradients. It also scales down the gradients of parameters with more significant updates and those with more minor updates. This helps prevent gradients from exploding or vanishing [,]. A learning rate of with a momentum of 0.8 was chosen for the training.
FNN Only Versus Hybrid Model Comparison
In this section, the FNNs architecture and the hybrid of CNNs and FNNs are compared in terms of their accuracy, robustness, and generalisation. A dataset of 18, 000 (17,000 for training and 1000 for testing) Shooting method solved RCWA bending simulations of diffraction patterns with , , and bending parameters ranging from −0.5 to 0.5, optical depths of 10–20 m, and index modulations of 0.01–0.03. The reason behind keeping an amount of 17,000 of data for the training and 1000 of data for the test is that while the test set mades up only 5.6% of the total dataset, it was indeed large enough to validate the model itself by allowing us to employ a larger amount of data for the training. We present both the bending-only (BO) estimation and bending and n1, d estimation versions of the models. The recording theta and the object theta were symmetrically set to 15 and −15 degrees, respectively, and the recording lambda was set to 633 nm. The simulations were conducted for an air medium air, with a medium average refraction index of 1.63. Both trainings were conducted with 8000 epochs. This choice was empirically founded, as, after approximately this number of epochs, the training and validation losses stabilised, offering no significant improvement with further epochs.
Regarding the simulation time and computational performance, both the RCWA-SM simulations and the deep learning models were developed fully in Python and executed in a computer with the following main specs: Intel® Core™ i7 13700, 16 GB RAM DDR4-3200 MHz, and 512 GB PCIe NVMe. A total of 8000 epoch trainings took approximately 1 h and 32 min for the FNN model and 2 h and 21 min for the hybrid one—due to its convolutional layers being more computationally costly.
In Table 2 are shown the results for the Mean Absolute Errors for both models and for , , and for the optical depth and index modulation. While both methods achieved good results for the prediction of the aforementioned parameters, slight differences in the overall error were observed between the proposed methods, although the hybrid model achieved slightly better accuracy for the overall bending coefficient parameters, while the FNN achieved better optical depth and index modulation prediction performance. A further standard deviation analysis of the difference between the model and target values was made, shown in Table 3, showcasing that the hybrid model featured lower standard deviations for the prediction of the and coefficients, suggesting a more robust behaviour with less predictions falling outside a normal range. An outlier count analysis (Table 4) was also conducted, which confirmed our previous observations.

Table 2.
Mean absolute error comparison between hybrid and FNN models (standardised values).

Table 3.
Standard deviation comparison between hybrid and FNN models.

Table 4.
Outliers comparison between hybrid and FNN models. The threshold for the outlier criteria was set to ±0.3 for and , ±0.08 for , and ±0.05 for d and standarised values.
When we compare the bending phase polynomials that the FNN (BO) model predicted and that the hybrid (BO) model predicted with the base true data in the test subset, an excellent concordance can be observed, as shown in Figure 9a,b. When we did the proper RCWA-SM reconstruction of the diffraction patterns out of the aforementioned predicted and base bending parameters, we observe that the results are consistently closely to being identical, as shown in Figure 9c,d, proving the excellent efficiency of our bending prediction despite the non-negligible (0.04) bending coefficient losses. It can be noted that, unlike variations in optical depth and index modulation, variations of this magnitude (0.04) in bending did not significantly impact the diffraction patterns. This points out that the limit of accuracy in our prediction models are primarily constrained by such variations not translating into noticeable changes in optical properties.
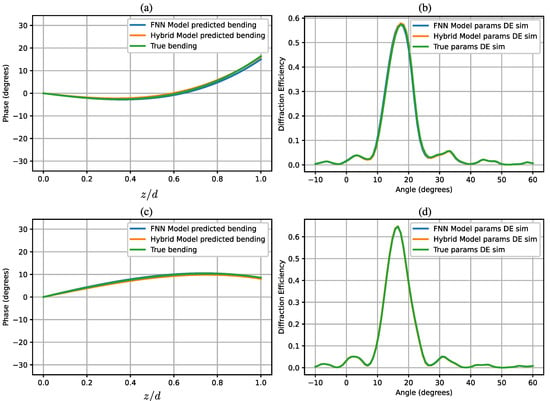
Figure 9.
Comparison of bending polynomials (a,c) and diffraction efficiency reconstructed patterns (b,d) for FNN (BO) model and hybrid (BO) model. The diffraction efficiencies for the two estimated models and the real parameters were computed by RCWA-SM. The parameters are identified as . Parameters used for (a,b) are = [−0.2170, −0.1976, −0.2144], = [0.0888, 0.1178, 0.1033], = [0.3905, 0.3609, 0.3975], d = 11.1389 m, and = 0.0174. For (b,d), the parameters are = 0.0174309 for the first set and = [0.4044, 0.3456, 0.3785], = [−0.0863, −0.0076, −0.0493], = [−0.1695, −0.1973, −0.1800], d = 11.2441 m, and = 0.0183.
4. Conclusions
This work presents the results of a novel RCWA approach for transmission holographic gratings with bending. These results were compared with those obtained from a set of rigorous SF-FDTD and Kubota’s simulations, providing a benchmark for the performance of our approach. The analysis covers a range of different bendings and a parametric analysis of the various parameters that define the bending. The results show that our method is consistent and quite accurate for low and moderate amplitudes of the bending of the fringes (). However, as the amplitude of the bending increased, our approach began to deviate from the numerical results, leading to differences in the angles at which the maximum diffraction efficiency could be found, as well as in the amplitudes of this parameter.
A deep learning optimum model for the estimation of bending polynomial coefficients was developed, as we compared the performance of two different architecture-based models. The results indicate that while both models achieved good predictive performance, the hybrid model slightly outperformed the FNN-only model in predicting bending coefficients, featuring lower standard deviations and fewer outliers, while the former model excelled in predicting optical depth and index modulation. Despite small bending coefficient losses (0.04), the predicted and true bending phase polynomials revealed high concordance, with the RCWA-SM reconstructions of diffraction patterns being nearly identical. This indicates that the limits of the accuracy of the estimators are due to the insensitivity of the optical system to small variations in bending.
In future works, the authors plan to extend the current formalism for considering different type of gratings, e.g., slanted and reflection gratings, and to compare the performance of the scheme with experimental results.
Author Contributions
Conceptualisation, J.C.-M., J.J.S.-V. and C.N.; methodology, C.N. and J.F.; software, J.C.-M., C.N., J.J.S.-V., J.C.B. and J.F.; validation, J.F., J.C.B., A.M.-A. and J.C.-M.; formal analysis, J.C.-M. and A.M.-A.; investigation, J.C.-M. and J.J.S.-V.; resources, A.B.; writing—original draft preparation, J.C.-M. and J.J.S.-V.; writing—review and editing, J.F. and C.N.; visualisation, J.C.-M. and J.F.; supervision, C.N.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the “Generalitat Valenciana” of Spain (projects PROMETEO/2021/006) and the “Ministerio de Ciencia, Innovación y Universidades” of Spain (project PID2021-123124OB-I00). J.J.S.-V. thanks the “Ministerio de Ciencia, Innovación y Universidades” for the grant FPU22/04316.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RCWA | Rigorous Coupled Wave Analysis |
| FDTD | Finite Difference Time Domain |
| CWT | Coupled Wave Theory |
| FNN | Feedforward Neural Network |
| CNN | Convolutional Neural Network |
| BO | Bending Only |
| RMSProp | Root Mean Square Propagation |
| SGD | Stochastic Gradient Descent |
| RCWA-SM | Rigorous Coupled Wave Analysis—Shooting Method |
| SF-FDTD | Split Field Finite Difference Time Domain |
Appendix A. Deep Neural Network Models Pytorch Sequential Architectures Codes
Appendix A.1. FNN’s Architecture
Deep neural network model Pytorch Sequential archtecture code for the FNN’s architecture. Total number of weights is 1,459,120.
# Model 1model = torch.nn.Sequential(
torch.nn.Linear(70, 1176),
torch.nn.ReLU(),
torch.nn.Linear(1176, 712),
torch.nn.ReLU(),
torch.nn.Dropout(0.2),
torch.nn.Linear(712, 556),
torch.nn.ReLU(),
torch.nn.Linear(556, 256),
torch.nn.ReLU(),
torch.nn.Dropout(0.2),
torch.nn.Linear(256, 5)
)
Appendix A.2. CNN-FNN Hybrid Neural Network’s Architecture
Deep neural network models Pytorch sequential archtecture codes for the CNN–FNN hybrid neural network’s architecture. Total number of weights is 1,247,808.
# Model 2model = torch.nn.Sequential(
Reshape(−1, 1, 70),
torch.nn.Conv1d(in_channels = 1,
out_channels = 64,
kernel_size = 7,
padding = ‘same’),
torch.nn.ReLU(),
torch.nn.MaxPool1d(2),
torch.nn.Conv1d(in_channels = 64,
out_channels = 128,
kernel_size = 7,
padding = ‘same’),
torch.nn.ReLU(),
torch.nn.MaxPool1d(2),
Reshape(−1, 2176),
torch.nn.Linear(2176, 512),
torch.nn.ReLU(),
torch.nn.Dropout(0.2),
torch.nn.Linear(512, 256),
torch.nn.ReLU(),
torch.nn.Dropout(0.2),
torch.nn.Linear(256, 5)
)
References
- Fink, U.; Rostalski, H.J.; Hirsch, H. Applications of holographic gratings to two-dimensional spectroscopy. Appl. Opt. 1996, 35, 1047. [Google Scholar] [CrossRef]
- Haleem, A.; Javaid, M.; Singh, R.P.; Suman, R.; Rab, S. Holography and its applications for industry 4.0: An overview. Internet Things -Cyber-Phys. Syst. 2022, 2, 42–48. [Google Scholar] [CrossRef]
- Mikulchyk, T.; Stoeva, P.; Kaworek, A.; Oubaha, M.; Rogers, B.; Martin, S.; Cody, D.; Naydenova, I. Characterisation of Holographic Recording in Environmentally Stable Photopolymerisable Glass. Appl. Sci. 2022, 12, 5969. [Google Scholar] [CrossRef]
- Weng, M.; Wang, Y.; Ren, X.; Lu, Q. Study on Two-Dimensional Exit Pupil Expansion for Diffractive Waveguide Based on Holographic Volume Grating. Appl. Sci. 2023, 13, 11858. [Google Scholar] [CrossRef]
- Yu, D.; He, Y.; Liu, H.; Wang, B.; Li, L.; Wang, R.; Luo, S. Characterizing the bending deformation of polymer utilizing the diffraction spectrum of a holographic grating on a flexible substrate. Opt. Lett. 2020, 45, 579–582. [Google Scholar] [CrossRef]
- Naydenova, I.; Jallapuram, R.; Toal, V.; Martin, S. A visual indication of environmental humidity using a color changing hologram recorded in a self-developing photopolymer. Appl. Phys. Lett. 2008, 92, 031109. [Google Scholar] [CrossRef]
- Zhou, Y.; Hauser, A.W.; Bende, N.P.; Kuzyk, M.G.; Hayward, R.C. Waveguiding Microactuators Based on a Photothermally Responsive Nanocomposite Hydrogel. Adv. Funct. Mater. 2016, 26, 5447–5452. [Google Scholar] [CrossRef]
- Yetisen, A.K.; Naydenova, I.; da Cruz Vasconcellos, F.; Blyth, J.; Lowe, C.R. Holographic Sensors: Three-Dimensional Analyte-Sensitive Nanostructures and Their Applications. Chem. Rev. 2014, 114, 10654–10696. [Google Scholar] [CrossRef] [PubMed]
- Yetisen, A.K.; Montelongo, Y.; da Cruz Vasconcellos, F.; Martinez-Hurtado, J.; Neupane, S.; Butt, H.; Qasim, M.M.; Blyth, J.; Burling, K.; Carmody, J.B.; et al. Reusable, Robust, and Accurate Laser-Generated Photonic Nanosensor. Nano Lett. 2014, 14, 3587–3593. [Google Scholar] [CrossRef] [PubMed]
- Kubota, T. Characteristics of Thick Hologram Grating Recorded in Absorptive Medium. Opt. Acta Int. J. Opt. 1978, 25, 1035–1053. [Google Scholar] [CrossRef]
- Kubota, T. The Bending of Interference Fringes inside a Hologram. Opt. Acta Int. J. Opt. 1979, 26, 731–743. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Diffraction analysis of dielectric surface-relief gratings. J. Opt. Soc. Am. 1982, 72, 1385. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Three-dimensional vector coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1983, 73, 1105. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K.; Grann, E.B.; Pommet, D.A. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K.; Pommet, D.A.; Grann, E.B. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: Enhanced transmittance matrix approach. J. Opt. Soc. Am. A 1995, 12, 1077. [Google Scholar] [CrossRef]
- Li, L. Use of Fourier series in the analysis of discontinuous periodic structures. J. Opt. Soc. Am. A 1996, 13, 1870. [Google Scholar] [CrossRef]
- Sun, W.; Fu, Q. Finite-difference time-domain solution of light scattering by dielectric particles with large complex refractive indices. Appl. Opt. 2000, 39, 5569. [Google Scholar] [CrossRef]
- Heaton, J. Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep learning. In Genetic Programming and Evolvable Machines; The MIT Press: Cambridge, MA, USA, 2016; 800p, ISBN 0262035618. [Google Scholar] [CrossRef]
- Zhang, G. Neural networks for classification: A survey. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2000, 30, 451–462. [Google Scholar] [CrossRef]
- Panda, S.S.; Hegde, R.S. A learning based approach for designing extended unit cell metagratings. Nanophotonics 2022, 11, 345–358. [Google Scholar] [CrossRef]
- Martínez, J.C.; Sirvent-Verdú, J.J.; Bravo, J.C.; Pérez-Bernabeu, A.; Álvarez, M.L.; Francés, J.; Neipp, C. Estimation of characteristic parameters of holographic volume gratings based on machine learning. In Proceedings of the Photosensitive Materials and Their Applications III; International Society for Optics and Photonics; McLeod, R.R., Villalobos, I.P., Tomita, Y., Eds.; SPIE: Bellingham, WA, USA, 2024; Volume 13015, p. 1301516. [Google Scholar] [CrossRef]
- Kim, S.B.; Lee, S.H. Application of Deep Learning Techniques for the State of Charge Prediction of Lithium-Ion Batteries. Appl. Sci. 2024, 14, 8077. [Google Scholar] [CrossRef]
- Allani, H.; Santos, A.T.; Ribeiro-Vidal, H. Multidisciplinary Applications of AI in Dentistry: Bibliometric Review. Appl. Sci. 2024, 14, 7624. [Google Scholar] [CrossRef]
- Lee, K.H.; Choi, J.W.; Park, C.O.; Han, D.H.; Kang, M.S. A Development and Validation of an AI Model for Cardiomegaly Detection in Chest X-rays. Appl. Sci. 2024, 14, 7465. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, Y.; Wu, R.; Li, J.; Cai, Z. Sustainable Maritime Transport: A Review of Intelligent Shipping Technology and Green Port Construction Applications. J. Mar. Sci. Eng. 2024, 12, 1728. [Google Scholar] [CrossRef]
- Scarselli, F.; Chung Tsoi, A. Universal Approximation Using Feedforward Neural Networks: A Survey of Some Existing Methods, and Some New Results. Neural Netw. 1998, 11, 15–37. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Feng, F.; Huang, T. FNNS: An Effective Feedforward Neural Network Scheme with Random Weights for Processing Large-Scale Datasets. Appl. Sci. 2022, 12, 12478. [Google Scholar] [CrossRef]
- Touvron, H.; Bojanowski, P.; Caron, M.; Cord, M.; El-Nouby, A.; Grave, E.; Izacard, G.; Joulin, A.; Synnaeve, G.; Verbeek, J.; et al. ResMLP: Feedforward Networks for Image Classification with Data-Efficient Training. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5314–5321. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, C. Hyperspectral image super-resolution using cluster-based deep convolutional networks. Signal Processing Image Commun. 2023, 110, 116884. [Google Scholar] [CrossRef]
- Feng, X.; Su, X.; Shen, J.; Jin, H. Single Space Object Image Denoising and Super-Resolution Reconstructing Using Deep Convolutional Networks. Remote Sens. 2019, 11, 1910. [Google Scholar] [CrossRef]
- Paul, S.; Mishra, D.; Marimuthu, S.K. Nested DWT–Based CNN Architecture for Monocular Depth Estimation. Sensors 2023, 23, 3066. [Google Scholar] [CrossRef]
- Yao, B.; Li, W.; Pan, W.; Yang, Z.; Chen, D.; Li, J.; Qu, J. Image reconstruction with a deep convolutional neural network in high-density super-resolution microscopy. Opt. Express 2020, 28, 15432. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811. [Google Scholar] [CrossRef]
- Chateau, N.; Hugonin, J.P. Algorithm for the rigorous coupled-wave analysis of grating diffraction. J. Opt. Soc. Am. A 1994, 11, 1321. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D Convolutional Neural Networks for Signal Processing Applications. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar] [CrossRef]
- Oh, C.; Escuti, M.J. Time-domain analysis of periodic anisotropic media at oblique incidence: An efficient FDTD implementation. Opt. Express 2006, 14, 11870. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; ICML’10. pp. 807–814. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).