Abstract
Evaluating the brittleness of rocks or rock masses is a fundamental problem in geotechnical engineering. This study proposed a new index that expresses brittleness as the rate of damage development in rock. The brittleness index was derived from statistical damage theory. It depends on the four material parameters, i.e., the peak strain, peak strength, Poisson’s ratio and elastic modulus. The validity of the proposed brittleness index was confirmed through two case studies, including triaxial compression test results for coals subjected to varying confining pressures and for sandstones at various temperatures. Uniaxial compression experiments were then performed on rock-like materials to examine the effects of model size and joint dip angle on rock brittleness using the proposed brittleness index. Results show that the brittleness of the jointed specimens varies in a complex pattern with the model size and joint dip angle. Generally, the brittleness index initially reduces and then grows with the increasing joint dip angle, and larger specimens tend to be more brittle. Furthermore, large specimens containing horizontal or vertical joints are particularly susceptible to brittle damage. The proposed brittleness index has merits such as a clear physical meaning and simple expression, making it a valuable tool for evaluating rock brittleness.
1. Introduction
The characterization of the brittleness of rocks or rock masses is a fundamental topic in rock mechanics and engineering, and it can be affected by a variety of factors, e.g., the in situ stress environment and the physical properties of the rock itself [1,2,3]. To ensure the safe building and operation of rock-related engineering structures, it is crucial to propose a straightforward and reasonable brittleness index.
Rock brittleness is considered an indirect test parameter as it cannot be obtained directly from tests but needs to be acquired via substituting test data into a series of formulas derived from different definitions [4]. Due to the complexity of rock stress vs. strain curve characteristics and the effects of different coupled factors on the rock damage characteristics [5], it is challenging to establish a uniform standard for quantifying the brittleness characteristics of rocks. Numerous brittleness definitions for rock-like materials have been proposed, including mineral composition-based, mechanical parameter-based, stress–strain curve-based and strain energy-based definitions [6,7,8,9]. Recently, there has been a growing recognition that the deformation process of rocks can be considered as the evolution of various strain energies (including elastic energy, dissipation energy, etc.) [10], and this concept has gained attention in the establishment of rock-like material brittleness evaluation indexes based on strain energy. For example, Liu et al. [11] put forward an energy-based brittleness index applicable to coal that can avoid the subjectivity of human experience. Zhang et al. [12] proposed a new index applicable to the evaluation of the brittleness of rock-like materials subjected to a true triaxial stress state and used the index to accurately identify the brittleness strength of basalt, granite and marble. Gong and Wang [13] proposed a new brittleness index for rock-like materials via the peak elastic energy consumption proportion and tested the validity of the index with multiple rocks.
The deformation and destabilization process of rocks involves both strain energy and damage evolution [14,15]. The degree of damage in rock-like materials is typically described by a dimensionless damage variable ranging from 0 to 1. Statistical damage models based on phenomenological models, particularly statistical damage theory, have attracted attention for modelling rock deformation due to their simplicity and small number of parameters [16,17,18]. Li et al. [19] and Li et al. [20] used the exponential function, Weibull function and Gaussian function distributions to develop statistical damage models and correlated brittleness with damage parameters. Their approaches demonstrated the relationship between the damage and brittleness of rocks. Nevertheless, these brittleness indexes are still based on strain energy and their calculation processes are complicated. Furthermore, existing studies on brittleness evaluation mainly focus on intact rocks and there are few studies related to jointed rock masses.
Given the significant need and existing deficiencies, a novel brittleness index for rock-like materials is put forward via the statistical damage theory and rock damage mechanics. The proposed brittleness index represents the rate of damage development and is expressed concisely. It can identify brittleness responses to changes in confining pressure and temperature. Uniaxial compression tests of rock-like materials are performed using the proposed index to investigate the impact of model size and joint dip angle on rock brittleness.
2. The Proposed Rock Brittleness Index
According to the theory of elasticity, the axial strain of a lossless material under the pseudo-triaxial condition can be expressed as follows:
where σ and ε represent stress and strain, respectively, and the subscripts denote the stress direction; ν and E symbolize the Poisson’s ratio and elastic modulus, respectively.
Similarly, the axial strain of a damaged material is obtained from Equation (1) using Lemaitre’s strain equivalence assumption [21], i.e.,
where the superscript denotes the effective stress. Let the damage variable be D; Equation (2) is rephrased as
Transforming Equation (3) yields
According to the statistical damage theory [22], the damage variable can be determined by the following:
where m and F denote two fitting parameters. Substituting Equation (5) into Equation (4) leads to
It is clear that the following relationship is satisfied when the stress reaches the peak point:
where and denote the peak stress and peak strain, respectively.
Substituting Equation (6) into Equations (7) and (8) yields the display expressions for the fitting parameters m and F as follows:
where Dp represents the damage value at the peak point. It can be obtained by transforming Equation (4).
According to the damage mechanics, it is found that the faster the damage develops, the more brittle the rock [23]. Changes in damage variables can be used to represent the rock’s brittleness. Therefore, we can define a brittleness index as follows:
Generally, the damage variable (D) ranges from 0 to 1, but it cannot reach 1 due to residual strength and other factors. Previous studies have shown that the damage variable reaches approximately 0.9 when the rock is destroyed [24]. D is taken as 0.9 in this paper. At a damage variable of 0.9, the physical interpretation of Equation (12) is shown in Figure 1. This indicates that the faster damage development corresponds to a more brittle rock. Incorporating Equations (9) and (10) into Equation (12), the following formula is derived:
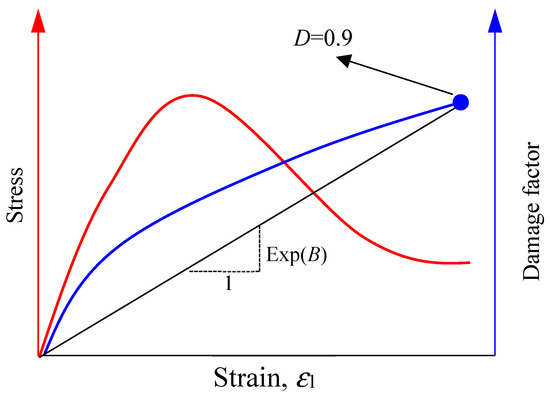
Figure 1.
A schematic diagram for the definition of the proposed brittleness index.
Additionally, substituting Equation (11) into Equation (13), the brittleness index, which depends on the peak strain, peak strength, Poisson’s ratio and elastic modulus, can be expressed as
By making , the brittleness index (B) can be abbreviated as follows:
The brittleness index B characterizes the brittleness of the rock or rock mass. Specifically, the greater the brittleness index B, the more brittle the rock or rock mass. The proposed brittleness index is dependent on four material parameters (as shown in Table 1), which can be obtained through conventional tests. It should be noted that the statistical damage theory used in this study does not account for the impact of the initial damage (or so-called initiation stress [25]) but assumes that damage is present and gradually increases during rock mass deformation. To maintain reasonableness while minimizing material parameters, this paper simplifies the rock deformation process, as suggested in previous studies [6,7].

Table 1.
Mechanical parameters of coal in Case 1.
3. Verification
3.1. Case 1: Verification of Rock Brittleness Under Different Confining Pressures Using Proposed Index
The triaxial compression test is an essential approach to investigate the mechanical behaviour of rocks. Over the years, numerous triaxial compression tests have been conducted [27,28,29], revealing that rock brittleness is significantly affected by confining pressure. The deformation behaviour of rocks changes from brittleness to ductility with the increment of confining pressure. We utilized triaxial compression test data of coal obtained by Zhang et al. [30] to verify Equation (15). Table 1 shows the calculated parameters (peak strain, peak strength, Poisson’s ratio and elastic modulus) for various circumferential pressures (0, 6, 12, 18, 24 and 30 MPa). Note that the selection of Poisson’s ratio refers to Gao, Stead and Kang [26]. Based on Table 1, Figure 2 displays the brittleness index of coal obtained by Equation (15). As the confining pressure rises from a zero-stress level to 30 MPa, the brittleness index declines from 4.75 to 2.60, which indicates that the defined brittleness index validly identifies the influence of confining pressure on brittleness characteristics. The results acquired from our proposed index are consistent with an energy-based indicator proposed by Zhang et al. [30].
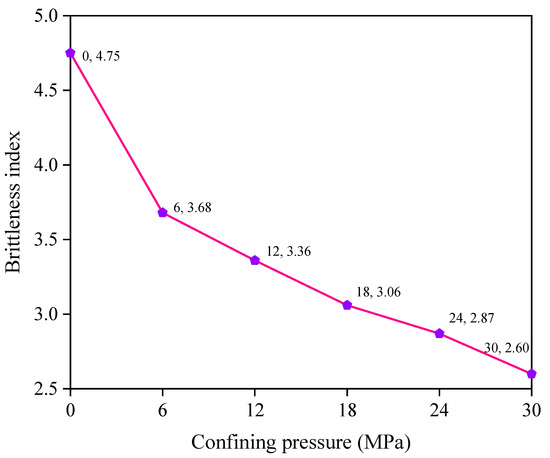
Figure 2.
Brittleness indexes under different confining pressures.
3.2. Case 2: Verification of Rock Brittleness Under Varying Temperatures Using Proposed Index
Triaxial compression tests have shown that temperature poses an obvious effect on rock brittleness. The properties of rocks shift from brittleness to ductility with the increasing temperature. To further validate Equation (15), we referred to triaxial compression test data conducted by Wei et al. [31] on sandstone under a constant confining pressure of 10 MPa. For different temperature conditions (25, 400, 600, 800 and 1000 °C), the mechanical parameters were calculated, including peak strain, peak strength, Poisson’s ratio and elastic modulus, as listed in Table 2. Using Equation (15), the sandstone brittleness index is shown in Figure 3, which decreases from 3.70 to 2.95 as the temperature grows from 25 to 1000 °C. This result confirms that the proposed index accurately captures the impact of temperature on rock brittleness characteristics. Our findings are consistent with an index proposed by Wang et al. [4].

Table 2.
Mechanical parameters of sandstone in Case 2.
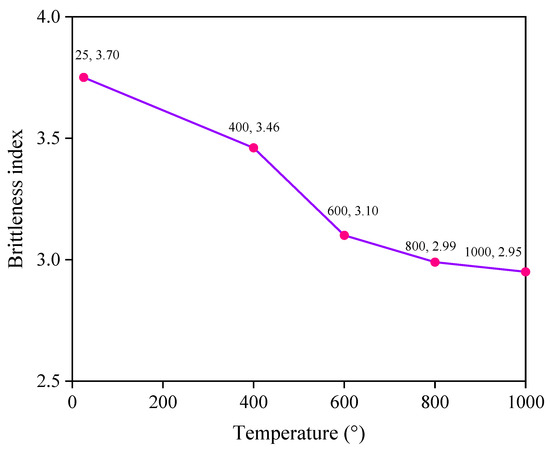
Figure 3.
Brittleness indexes under different temperatures.
It should be noted that some composite indicators based on combinatorial approaches have been proposed as a means of evaluating rock brittleness [32]. Although these composite indicators can effectively characterize the brittle properties of rock-like materials, they often contain complex expressions. In contrast, the proposed index has an explicit physical background and can accurately identify the brittleness of rock-like materials.
4. Investigation of Influence of Model Size and Joint Dip Angle on Rock Brittleness
4.1. Experimental Scheme and Design
Previous research has emphasized the significance of model sizes and joint dip angles in determining the strength and deformation properties of rocks. Nonetheless, there are very few studies on how the brittleness of rock masses is influenced by model size and joint dip angle. To address this gap, we conducted uniaxial compression tests on rocks that considered both size effects and joint dip angle in our previous work [33]. Specifically, we examined the impact of these two factors on the brittle characteristics of rock masses using the proposed brittleness index (Equation (15).
Figure 4 displays the test specimens. Note that L, H and W symbolize the length, height and width of the specimens, respectively, and α denotes the dip angle of the joints. We prepared the specimens using comparable materials (silicate cement, pure water and fine sand in a ratio of 2:1:2). Given the practical constraints of laboratory tests, we neglected the boundary effects of the joints. To simulate the intermittent joints typically encountered in real-world conditions, we combined the smallest specimens of the test design in equal ratios to create larger specimens for assessing the influence of size on rock properties.
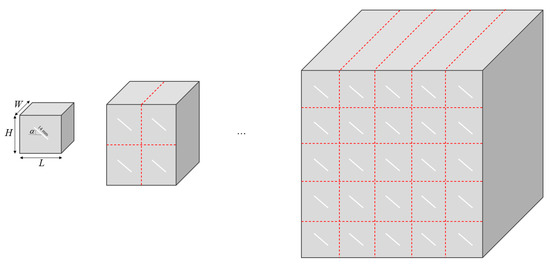
Figure 4.
Schematic diagram of jointed specimens.
For the test, we examined a total of 20 groups, with three specimens in each group, using four joint dip angles (α = 0°, 30°, 60° and 90°) and five model sizes (L = 40, 80, 120, 160 and 200 mm). Table 3 illustrates the testing protocol. We employed a rock mechanics rigid servo testing machine (model: RMT-150C) manufactured by the Chinese Academy of Sciences (Beijing, China), to conduct the laboratory experiments. The tests were performed using a constant displacement-controlled loading of 0.005 mm/s. The test equipment and loading diagram are shown in Figure 5.

Table 3.
Experimental scheme of jointed specimens.

Figure 5.
Experimental equipment and loading conditions.
4.2. Experimental Results
A representative relationship between stress and strain is illustrated in Figure 6. The deformation process of the jointed specimens under all conditions is similar to intact rock specimens and it includes the crack closure phase, elastic deformation phase, crack growth phase and post-peak phase. Unlike intact rock, the jointed specimens may exhibit “multi-peak” characteristics in their deformation curves due to the presence of joints.
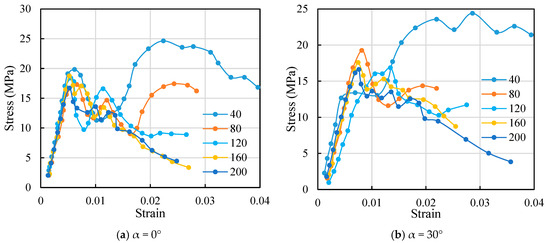
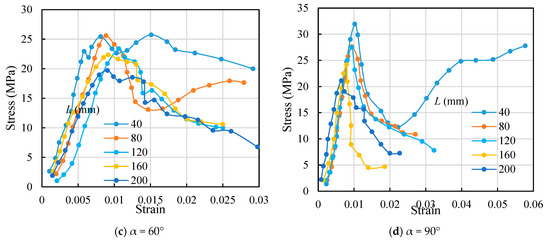
Figure 6.
Stress–strain curves of jointed specimens.
The uniaxial compression strength (UCS) is an indispensable strength indicator of the rock mass. The UCS values of jointed specimens present an overall V-shaped distribution with the increasing joint dip angle (Figure 7). Specifically, the UCS value originally declines and then grows as the dip angle of joints increases. This conclusion agrees with the law obtained from the existing compression experiments of joints [34,35]. Generally, the UCS values of the rock mass decline with the growth in the model size, which indicates an obvious size effect.
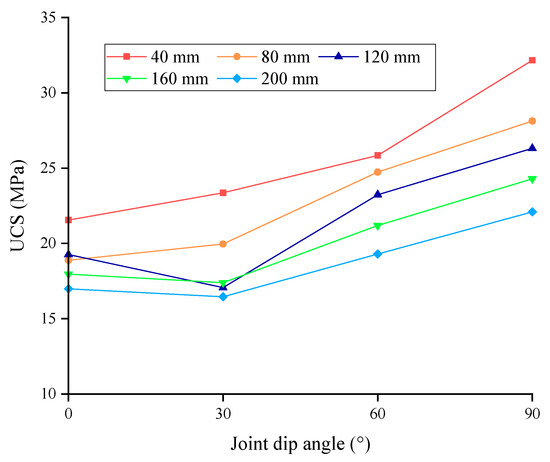
Figure 7.
Variation in UCS of jointed specimens with joint dip angle.
Elastic modulus is an important deformation index of the rock mass. Similarly to the uniaxial compression strength, the elastic modulus generally falls down and then grows with the increasing joint dip angle. Elastic modulus presents an overall downward trend as the model size grows. It is worth emphasizing that the above experimental results reveal the model size effect of rock mass, which indicates it is necessary to obtain the equivalent mechanical parameters of rock mass through a representative element volume (REV) [36] in practical engineering design.
4.3. Analysis of Brittleness Characteristics
This study quantitatively analyzed the influence of joint dip angle and model size on the brittleness features of the specimens using Equation (15). Figure 8a shows changes in the brittleness index of the specimens concerning the model size. The brittleness index displays a monotonic increasing pattern as the model size increases when the joint dip angle is constant at 0°. As the dip angle of the joints increases to 30°, the specimen gradually shifts from plasticity to brittleness with the growth in model size. Similarly, as for the joint dip angle of 60°, the brittleness of the specimen maintains an upward tendency with the model size. When the joint dip angle reaches 90°, the brittleness index rises from 3.74 to 4.45 with the increasing model size. Among these four joint dip angles, the least significant impact of model size on the specimen brittleness is found in the case where the joint dip angle is 60°.
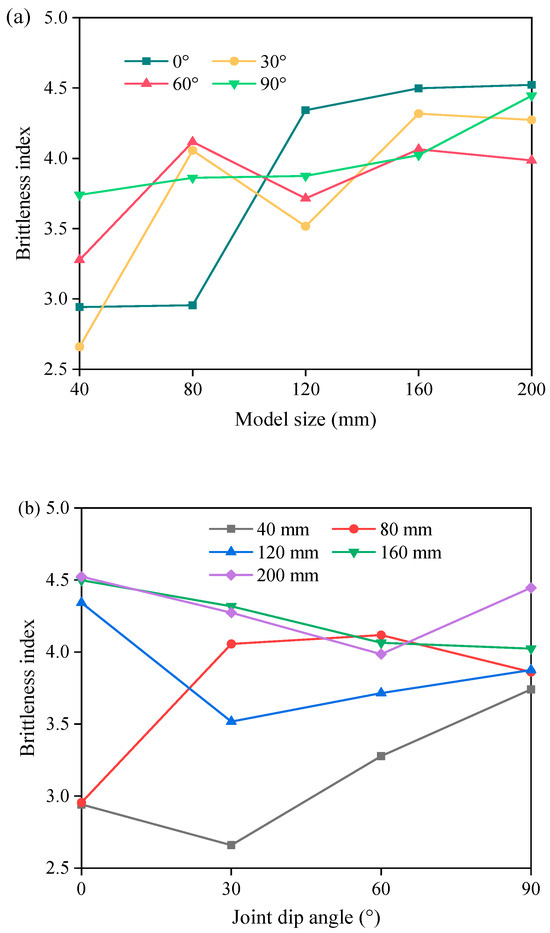
Figure 8.
Effects of model size (a) and joint dip angle (b) on brittleness characteristics of jointed specimens.
The impact of joint dip angle on the rock brittleness properties was quantitatively discussed using Equation (15), as illustrated in Figure 8b. For a model size of 40 mm, the brittleness index initially drops and then increases with the increasing joint dip angle. For a model size of 80 mm, there is no clear correlation between the specimen brittleness and the joint dip angle, which could result from the inherent discreteness of the specimen material. The brittleness of the jointed specimen with a model size of 120 mm initially declines and then grows with the increasing joint dip angle, while it decreases for a model size of 160 mm. For a model size of 200 mm, the brittleness index initially decreases and then increases as the joint dip angle grows. Among the mentioned sizes, the effect of the joint dip angle on the brittleness of the specimens is relatively insignificant for a model size of 160 mm. Furthermore, the brittleness index of the specimens has been observed to decrease at joint dip angles of 30° or 60°, which may be attributed to the impact of the initial damage on the jointed rock mass at these angles, as demonstrated by Liu et al. [23].
Figure 9 and Figure 10 illustrate the relationships between the two fitting parameters (m and F) and the model size (L) and joint dip angle (α). The parameter m generally increases with the model size, while it shows a trend of first increasing and then declining as the joint dip angle grows. Previous research has demonstrated that the parameter m refers to a shape parameter related to the shape of the post-peak stress–strain curve [15]. The larger the value of m, the more brittle the material. This result aligns with the overall results of the proposed index and offers further confirmation supporting the proposed index’s soundness. In contrast, the parameter F tends to decrease as the model size increases and there is no clear relationship with the joint dip angle.
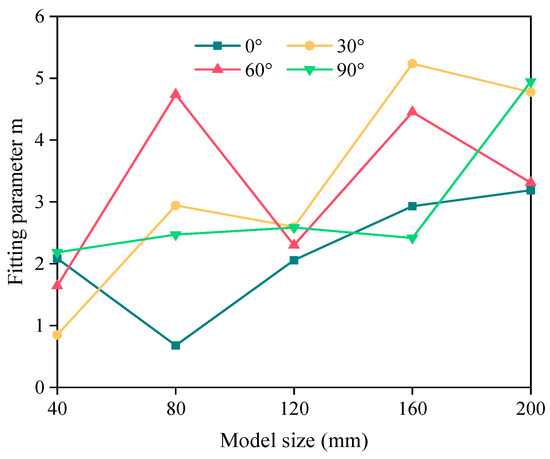
Figure 9.
The relationship between the fitting parameter (m) and model size of the jointed specimens.
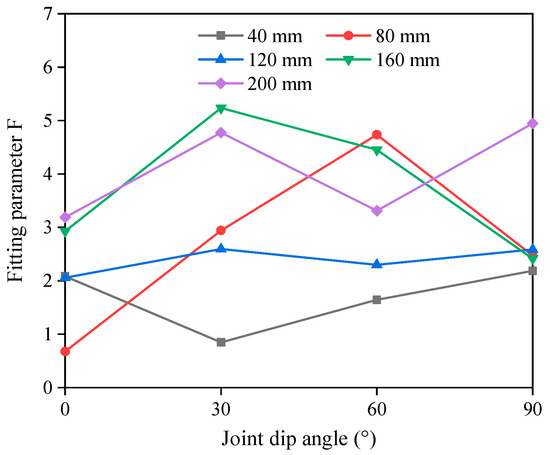
Figure 10.
The relationship between the fitting parameter (F) and joint dip angle of the jointed specimens.
As depicted in Figure 11, the brittleness distribution of jointed rock masses was plotted using an interpolation method for various combinations of model sizes (ranging from 40 mm to 200 mm) and joint dip angles (ranging from 0° to 90°). It can be observed that the rock brittleness index increases with the increase in model size, and the brittleness index shows an approximate V-shaped variation with the increase in joint dip angle. In fact, the brittleness index of rock mass is very complex, which is not only related to the mechanical properties of the rock itself, but also to the geometric distribution of joints in the rock mass and the size of the model. Additionally, the results show that large-sized specimens with horizontal or vertical joints are more prone to brittle damage.
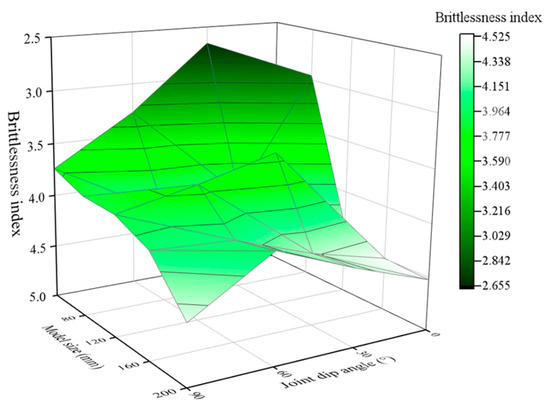
Figure 11.
Brittleness distribution of jointed specimens under different combinations of model sizes and joint dip angles.
5. Conclusions
This study put forward a novel statistical damage theory-based index to evaluate rock brittleness, which is defined as the rate of damage development. The proposed brittleness index was calculated by the four material parameters, i.e., peak strain, peak strength, Poisson’s ratio and elastic modulus. It can accurately identify the effects of temperature and confining pressure on rock brittleness. The results indicate that the properties of rocks shift from brittleness to ductility with the increment of confining pressure and temperature. Moreover, uniaxial compression tests on rock-like materials were conducted to analyze the influence of model size and joint dip angle on rock brittleness. The results show a complex pattern of rock brittleness with the model size and joint dip angle. Generally, the brittleness index increases with the increasing model size and there is an approximate V-shaped change in the brittleness index with the increasing joint dip angle. The impact of model size on the brittleness of jointed specimens is least obvious with a joint angle of 60°, while the influence of joint dip angle on the brittleness of jointed specimens is least significant when the model size is equal to 160 mm. The results can provide a reference for the evaluation of the brittleness index of fractured rock masses.
Author Contributions
Conceptualization, Z.L.; methodology, N.W.; software, Z.L.; formal analysis, N.W.; investigation, B.J.; resources, N.W.; data curation, N.W.; writing—original draft preparation, N.W.; writing—review and editing, Z.L.; supervision, Z.L.; project administration, T.A.; funding acquisition N.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Foundation of China (Grant No. 52209123), the State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining & Technology /China University of Mining & Technology, Beijing (SKLGDUEK2219) and the Open Fund of the Key Laboratory of Deep Earth Science and Engineering (Sichuan University).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors thank the anonymous reviewers, who provided valuable suggestions that improved the manuscript.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
| Stress | |
| Effective stress | |
| εi | Strain |
| Peak stress | |
| Peak strain | |
| D | Damage variable |
| ν | Poisson’s ratio |
| E | Elastic modulus |
| B | Brittleness index |
| i | Stress/strain direction |
| m | Fitting parameter of damage variable |
| F | Fitting parameter of damage variable |
| Dp | Damage value at the peak stress |
| L | Length of specimen |
| H | Height of specimen |
| W | Width of specimen |
| α | Dip angle of the joint |
| UCS | Uniaxial compressive strength |
References
- Munoz, H.; Taheri, A.; Chanda, E.K. Fracture Energy-Based Brittleness Index Development and Brittleness Quantification by Pre-peak Strength Parameters in Rock Uniaxial Compression. Rock Mech. Rock Eng. 2016, 49, 4587–4606. [Google Scholar] [CrossRef]
- Zou, C.J.; Cheng, Y.; Li, J.C. Strain rate and size effects on the brittleness indexes of Carrara marble. Int. J. Rock Mech. Min. Sci. 2021, 146, 104860. [Google Scholar] [CrossRef]
- Peng, J.; Xu, C.H.; Dai, B.B.; Sun, L.J.; Feng, J.J.; Huang, Q.S. Numerical Investigation of Brittleness Effect on Strength and Microcracking Behavior of Crystalline Rock. Int. J. Geomech. 2022, 22, 04022178. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Chai, B.; Du, J.; Xing, L.X.; Xia, Z.H. An Energy-Based Method to Determine Rock Brittleness by Considering Rock Damage. Rock Mech. Rock Eng. 2022, 55, 1585–1597. [Google Scholar] [CrossRef]
- Meng, F.Z.; Zhou, H.; Zhang, C.Q.; Xu, R.C.; Lu, J.J. Evaluation Methodology of Brittleness of Rock Based on Post-Peak Stress-Strain Curves. Rock Mech. Rock Eng. 2015, 48, 1787–1805. [Google Scholar] [CrossRef]
- Meng, F.Z.; Wong, L.N.Y.; Zhou, H. Rock brittleness indices and their applications to different fields of rock engineering: A review. J. Rock Mech. Geotech. Eng. 2021, 13, 221–247. [Google Scholar] [CrossRef]
- Kuang, Z.H.; Qiu, S.L.; Li, S.J.; Du, S.H.; Huang, Y.; Chen, X.Q. A New Rock Brittleness Index Based on the Characteristics of Complete Stress-Strain Behaviors. Rock Mech. Rock Eng. 2021, 54, 1109–1128. [Google Scholar] [CrossRef]
- Xu, R.C.; Li, Z.; Jin, Y.D. Brittleness Effect on Acoustic Emission Characteristics of Rocks Based on a New Brittleness Evaluation Index. Int. J. Geomech. 2022, 22, 04022185. [Google Scholar] [CrossRef]
- Xie, J.Y.; Zhang, J.J.; Fang, Y.P.; Cao, J.X.; Deng, J.X. Quantitative Evaluation of Shale Brittleness Based on Brittle-Sensitive Index and Energy Evolution-Based Fuzzy Analytic Hierarchy Process. Rock Mech. Rock Eng. 2023, 56, 3003–3021. [Google Scholar] [CrossRef]
- Tarasov, B.G.; Stacey, T.R. Features of the Energy Balance and Fragmentation Mechanisms at Spontaneous Failure of Class I and Class II Rocks. Rock Mech. Rock Eng. 2017, 50, 2563–2584. [Google Scholar] [CrossRef]
- Liu, X.B.; Zhang, Z.Y.; Ge, Z.L.; Zhong, C.L.; Liu, L. Brittleness Evaluation of Saturated Coal Based on Energy Method from Stress-Strain Curves of Uniaxial Compression. Rock Mech. Rock Eng. 2021, 54, 3193–3207. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.T.; Yang, C.X.; Han, Q.; Wang, Z.F.; Kong, R. Evaluation Method of Rock Brittleness under True Triaxial Stress States Based on Pre-peak Deformation Characteristic and Post-peak Energy Evolution. Rock Mech. Rock Eng. 2021, 54, 1277–1291. [Google Scholar] [CrossRef]
- Gong, F.Q.; Wang, Y.L. A New Rock Brittleness Index Based on the Peak Elastic Strain Energy Consumption Ratio. Rock Mech. Rock Eng. 2022, 55, 1571–1582. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Luo, S.; Li, J.C.; Huang, D. Theoretical damage characterisation and damage evolution process of intact rocks based on linear energy dissipation law under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2021, 146, 104858. [Google Scholar] [CrossRef]
- Ren, C.H.; Yu, J.; Liu, S.Y.; Yao, W.; Zhu, Y.L.; Liu, X.Y. A Plastic Strain-Induced Damage Model of Porous Rock Suitable for Different Stress Paths. Rock Mech. Rock Eng. 2022, 55, 1887–1906. [Google Scholar] [CrossRef]
- Li, X.; Cao, W.G.; Su, Y.H. A statistical damage constitutive model for softening behavior of rocks. Eng. Geol. 2012, 143, 1–17. [Google Scholar] [CrossRef]
- Huang, S.B.; Liu, Q.S.; Cheng, A.P.; Liu, Y.Z. A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application. Cold Reg. Sci. Tech. 2018, 145, 142–150. [Google Scholar] [CrossRef]
- Xie, S.J.; Han, Z.Y.; Hu, H.H.; Lin, H. Application of a novel constitutive model to evaluate the shear deformation of discontinuity. Eng. Geol. 2022, 304, 106693. [Google Scholar] [CrossRef]
- Li, Y.W.; Jia, D.; Rui, Z.H.; Peng, J.Y.; Fu, C.K.; Zhang, J. Evaluation method of rock brittleness based on statistical constitutive relations for rock damage. J. Petrol. Sci. Eng. 2017, 153, 123–132. [Google Scholar] [CrossRef]
- Li, Y.W.; Long, M.; Zuo, L.H.; Li, W.; Zhao, W.C. Brittleness evaluation of coal based on statistical damage and energy evolution theory. J. Petrol. Sci. Eng. 2019, 172, 753–763. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: London, UK, 1994. [Google Scholar]
- Deng, J.A.; Cu, D.S. On a statistical damage constitutive model for rock materials. Comput. Geosci. 2011, 37, 122–128. [Google Scholar] [CrossRef]
- Liu, H.Y.; Lv, S.R.; Zhang, L.M.; Yuan, X.P. A dynamic damage constitutive model for a rock mass with persistent joints. Int. J. Rock Mech. Min. Sci. 2015, 75, 132–139. [Google Scholar] [CrossRef]
- Cao, W.; Zhao, H.; Zhang, L.; Zhang, Y. Damage statistical softening constitutive model for rock considering effect of damage threshold and its parameters determination method. Chinese J. Rock Mech. Eng. 2008, 27, 1148–1154. [Google Scholar]
- Nicksiar, M.; Martin, C.D. Crack initiation stress in low porosity crystalline and sedimentary rocks. Eng. Geol. 2013, 154, 64–76. [Google Scholar] [CrossRef]
- Gao, F.Q.; Stead, D.; Kang, H.P. Numerical Simulation of Squeezing Failure in a Coal Mine Roadway due to Mining-Induced Stresses. Rock Mech. Rock Eng. 2015, 48, 1635–1645. [Google Scholar] [CrossRef]
- Khan, J.A.; Padmanabhan, E.; Ul Haq, I.; Franchek, M.A. Hydraulic fracturing with low and high viscous injection mediums to investigate net fracture pressure and fracture network in shale of different brittleness index. Geomech. Energy Environ. 2023, 33, 100416. [Google Scholar] [CrossRef]
- Liu, S.F.; Ma, P.; Meng, F.F.; Dintwe, T.K.M.; Mao, P.; Moses, D. Strain softening and brittleness characteristics of gangue-containing coal samples. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 28. [Google Scholar] [CrossRef]
- Wang, X.K.; Wei, W.S.; Niu, Y.; Xia, C.C.; Song, L.B.; Han, G.S.; Zhu, Z.M. Triaxial Creep Mechanical Behaviors and Creep Damage Model of Dolomitic Limestone Material under Multi-Stage Incremental Loading. Materials 2023, 16, 1918. [Google Scholar] [CrossRef]
- Zhang, J.; Ai, C.; Li, Y.W.; Che, M.G.; Gao, R.; Zeng, J. Energy-Based Brittleness Index and Acoustic Emission Characteristics of Anisotropic Coal Under Triaxial Stress Condition. Rock Mech. Rock Eng. 2018, 51, 3343–3360. [Google Scholar] [CrossRef]
- Wei, S.J.; Yang, Y.S.; Su, C.D.; Cardosh, S.R.; Wang, H. Experimental Study of the Effect of High Temperature on the Mechanical Properties of Coarse Sandstone. Appl. Sci. 2019, 9, 2424. [Google Scholar] [CrossRef]
- Zhang, D.C.; Ranjith, P.G.; Perera, M.S.A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: A review. J. Petrol. Sci. Eng. 2016, 143, 158–170. [Google Scholar] [CrossRef]
- Wu, N. Study on the Scale Effect and Anisotropy of Mechanical Properties of Jointed Rock Masses. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Chen, X.; Liao, Z.; Li, D. Experimental study of effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression. Chinese J. Rock Mech. Eng. 2011, 30, 781–789. [Google Scholar]
- Ghazvinian, A.; Hadei, M.R. Effect of discontinuity orientation and confinement on the strength of jointed anisotropic rocks. Int. J. Rock Mech. Min. Sci. 2012, 55, 117–124. [Google Scholar] [CrossRef]
- Wu, N.; Liang, Z.Z.; Zhang, Z.H.; Li, S.H.; Lang, Y.X. Development and verification of three-dimensional equivalent discrete fracture network modelling based on the finite element method. Eng. Geol. 2022, 306, 106759. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).