Evaluating the Current Situation of River and Lake Shoreline Planning and Utilization Using an Improved Matter-Element Extension Model
Abstract
:1. Introduction
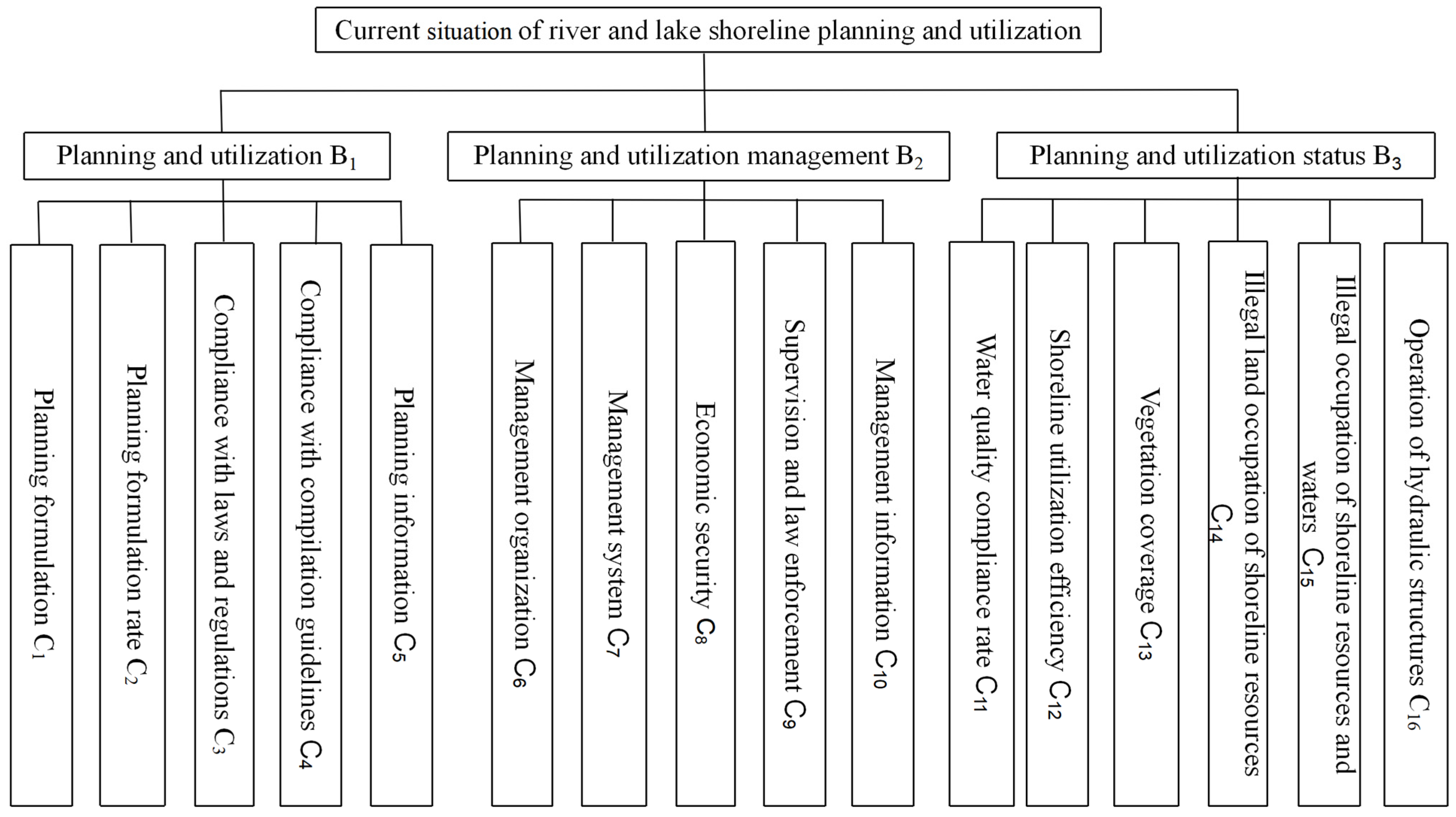
2. Evaluation Index System of Current Situation of River and Lake Shoreline Planning and Utilization
2.1. Planning and Utilization Preparation
2.2. Planning and Utilization Management
2.3. Current Status of Planning and Utilization
3. Evaluation Model of Current Situation of River and Lake Shoreline Planning and Utilization
3.1. Combined Weighting Method to Calculate Weights
3.1.1. Determining Weight Based on Triangular Fuzzy Number Method
3.1.2. Calculation of Weights Based on the Improved CRITIC Method
3.1.3. Minimum Discriminative Information Principle to Determine Portfolio Weights
3.2. Improved Matter-Element Extension Evaluation Model
3.2.1. The Principle of the Matter-Element Extension Model
3.2.2. Improved Matter-Element Extension Model
4. Evaluation of the Current Situation of River and Lake Shoreline Planning and Utilization in a Typical Region
4.1. Calculation of Indicator Weights
4.2. Evaluation of the Current Situation of Shoreline Planning and Utilization Based on Different Models
4.2.1. Current Situation Evaluation of Shoreline Planning and Utilization Based on Improved Matter-Element Extension Model
4.2.2. Evaluation of the Current Situation of Shoreline Planning and Utilization Based on the TOPSIS Method
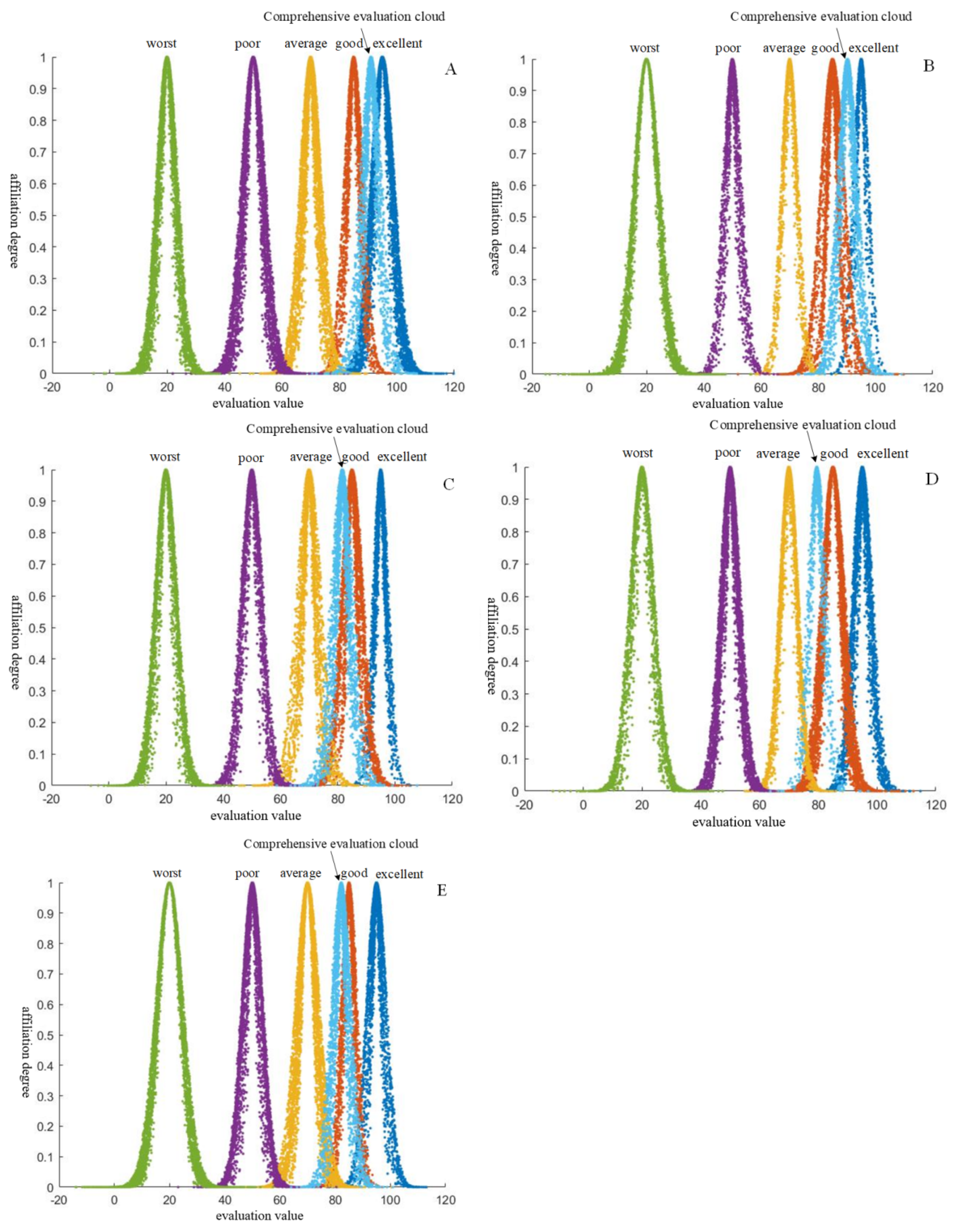
4.2.3. Evaluation of the Current Situation of River and Lake Shoreline Planning and Utilization Based on Cloud Model
4.2.4. Comparative Analysis of Evaluation Methods
4.3. Analysis of Evaluation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chu, V.C.; Michael, R.; Sharon, B. Using shoreline video Assessment for coastal planning and restoration in the context of climate change in Kien Giang, Vietnam. Ocean. Sci. J. 2015, 50, 413–432. [Google Scholar]
- David, G.; Chris, H.; Rangel-Buritago, N. An assessment of areal and transect-based historic shoreline changes in the context of coastal planning. J. Coast. Conserv. 2019, 23, 315–330. [Google Scholar]
- Zhang, X.; Shen, K. Reflections on the protection and utilization of the Yangtze River shoreline under the new situation. Water Resour. Hydropower Express 2018, 39, 8–11. [Google Scholar]
- Wang, C.; Li, J.; Sun, X. Evaluation and development and utilization of coastline resources in the Jiujiang-Xinjizhou section of the main stream of the Yangtze River. Resour. Sci. 2002, 3, 71–78. [Google Scholar]
- Yang, Y.; Han, Z. Comprehensive evaluation of coastal port site resources in Liaoning Province and its geographical combination. Geogr. Res. 2000, 1, 65–72. [Google Scholar]
- Cao, W.; Cao, Y.; Wu, W.; Liang, S. Study on shoreline resource evaluation and port development in Chaohu section of Yangtze River. Hum. Geogr. 2008, 3, 64–68. [Google Scholar]
- Duan, X.; Zou, H. Spatial functions, development problems and management countermeasures of the Yangtze River shoreline. Geoscience 2016, 36, 1822–1833. [Google Scholar]
- Tian, H.; Liu, X.; Wang, H.; Shi, Y.; Li, Q.; Wang, Y. Characterization of the spatial and temporal evolution of the Caofeidian shoreline island over the past three decades. Mar. Sci. 2015, 39, 68–74. [Google Scholar]
- Bin, G.; Li, X.; Dhillon, B.S.; Chu, W. A new method for quantitative evaluation of equipment condition system based on fuzzy hierarchical analysis. Syst. Eng. Theory Pract. 2010, 30, 744–750. [Google Scholar]
- Propana, O.A.; Kyung, N.K. Analysis of Indonesia’s priority selection: Energy transition, energy-related measures, mining governance, and resource transition using the analytic hierarchy process (AHP). Energy Sustain. Dev. 2024, 83, 101559. [Google Scholar]
- Yang, W.; Li, J. Safety Risk Analysis of Assembly Building Lifting Construction Based on Dynamic Bayesian Network. J. Saf. Environ. 2024, 24, 1329–1331. [Google Scholar]
- Chen, X.; Lin, W.; Huang, X.; Yang, F. Firne Risk Assessment of Ultra-High-Rise Buildings Based on Fuzzy Bayesian Network. Saf. Environ. Eng. 2023, 30, 44–45. [Google Scholar]
- Chen, Y.; Wu, G.; Zhang, Y.; Li, G. Operation and maintenance risk analysis of urban underground comprehensive pipeline corridor based on fuzzy Bayesian network. Saf. Environ. Eng. 2021, 28, 65–69. [Google Scholar]
- Zhang, J.; Huang, D.; You, Q.; Kang, J.; Liu, M.; Guo, Y. Dynamic risk evaluation of gas leakage in urban integrated pipeline corridors based on dynamic Bayesian network. J. Saf. Environ. 2023, 23, 2456–2458. [Google Scholar]
- Landuyt, D.; Broekx, S.; Goethals, P.L. Bayesian belief networks to analyse trade-offs among ecosystem services at the regional scale. Ecol. Indic. 2016, 71, 327–335. [Google Scholar] [CrossRef]
- Hu, M.; Fu., C.; Deng., J.; Luo, Y.; Han, H. Analysis of shoreline resource utilization of Yangtze River based on fuzzy comprehensive evaluation method. People’s Yangtze River 2021, 52, 42–48. [Google Scholar]
- Wan, T.; Cheng, F.; Cheng, Y.; Liao, C.; Bai, Y. Investigation into effect of non-uniform thermal environment on thermal sensation under stratum ventilation for heating by using interpolation-based multi-level fuzzy comprehensive evaluation. J. Build. Eng. 2023, 64, 105592. [Google Scholar] [CrossRef]
- Qu, Z.; Tian, X.; Xie, G.; Wu, Y.; Wang, H. Fuzzy comprehensive evaluation of high parameter waste power station corrosion prevention system based on hierarchical analysis method. Corros. Prot. 2024, 45, 91–96. [Google Scholar]
- Ye, Y.; Liang, L.; Cao, Y.; Zhou, Z.; Gong, J.; Zhao, H.; Jiang, Y. Preferential selection and ranking method for planning layout scheme of river-lake water system connectivity project based on Vague set and cloud model. Syst. Eng. Theory Pract. 2017, 37, 1926–1936. [Google Scholar]
- Mu, R.; Zhang, J. Hierarchical comprehensive evaluation based on grey correlation analysis. Syst. Eng. Theory Pract. 2008, 10, 125–130. [Google Scholar]
- Yang, W.; Yang, D.; Xie, Q. A cloud model-based slope risk assessment method and its application. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 46, 30–34. [Google Scholar]
- Zhu, J.; Zhang, J.; Qin, C. Multi-objective optimization of group decision-making based on matter-element extension set. Can. Soc. Sci. 2009, 5, 90–103. [Google Scholar]
- Lu, R.; Chen, Z. Matter-element modeling of parallel structure and application about extension PID control system. J. Syst. Sci. Complex. 2006, 19, 227–235. [Google Scholar] [CrossRef]
- Yu, W.; Jia, C.; Di, S.; Li, K.; Yuan, H. Groundwater quality evaluation based on comprehensive weight and improved material element topologizable evaluation model. J. Jilin Univ. (Earth Sci. Ed.) 2019, 49, 539–547. [Google Scholar]
- Wang, R.; Liao, P.; Han, X. Comprehensive benefit evaluation of watershed management based on the material element topologizable model. Water Resour. Hydropower Technol. 2018, 49, 29–35. [Google Scholar]
- Yi, X.; Zhang, L.; Zhang, J.; Li, B.; Jiao, A. Topologically scalable evaluation of material elements for green manufacturing process optimization. Manuf. Autom. 2019, 41, 118–121. [Google Scholar]
- Huang, C.; Wu, X.; Lin, M.; Xu, Z. Reliability assessment of multi-stage task systems based on triangular intuitionistic fuzzy numbers, Operations. Res. Manag. 2024, 33, 3–4. [Google Scholar]
- Zhang, L.; Shi, Y.; Liu, H.; Li, F. Research on the initial water right allocation of reservoirs based on the theory of material elemental topology. China Popul. -Resour. Environ. 2019, 29, 110–117. [Google Scholar]
- Wang, S.; Cen, Y. A triangular fuzzy number method for sequencing decision. Ind. Eng. Manag. 2009, 14, 44–47. [Google Scholar]
- Razmi, J.; Seifoory, M.; Pishvaee, M.S. A fuzzy multi-attribute decision making model for selecting the best supply Chain strategy lean, agile or leagile. J. Ind. Eng. 2011, 45, 127–142. [Google Scholar]
- Chen, C. Extensions of the TOPSIS for group decision making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Wang, T.; Chang, T. Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Syst. Appl. 2007, 33, 870–880. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, C.; Huang, K. Fuzzy hierarchical TOPSIS for supplier selection. Appl. Soft Comput. 2009, 9, 377–386. [Google Scholar] [CrossRef]
- Wang, J. Multi-objective decision ideal point method for comprehensive evaluation of groundwater environmental quality in Huabei. Environ. Sci. Manag. 2005, 4, 111–112. [Google Scholar]
- Xu, X.; Liu, J.; Wang, Z. Enterprise evaluation model and empirical research based on entropy TOPSIS method. J. Intell. 2011, 4, 78–82. [Google Scholar]
- Zhang, M.; Wang, S.; Sun, Z.; Xu, Z.; Wang, H. Comprehensive evaluation of oil and gas pipeline landslide hazard based on cloud theory. J. Eng. Sci. 2018, 40, 427–437. [Google Scholar]
| Evaluation Level | Excellent | Good | Medium | Little Poor | Poor |
|---|---|---|---|---|---|
| Score | (90, 100) | (80, 90) | (60, 80) | (40, 60) | (0, 40) |
| Expert/Mandarin | Expert 1 | Expert 2 | Expert 3 | ||||
|---|---|---|---|---|---|---|---|
| Index | |||||||
| C1 | [69, 75, 91] | [75, 80, 93] | [67, 85, 92] | 0.0648 | 0.1029 | 0.0839 | |
| C2 | [61, 72, 85] | [73, 80, 89] | [69, 81, 90] | 0.0624 | 0.0838 | 0.0743 | |
| C3 | [63, 71, 84] | [65, 75, 85] | [71, 80, 91] | 0.0616 | 0.0451 | 0.0542 | |
| C4 | [69, 75, 91] | [75, 80, 93] | [67, 85, 92] | 0.0648 | 0.0973 | 0.0816 | |
| C5 | [70, 82, 92] | [68, 79, 89] | [70, 85, 95] | 0.0648 | 0.1131 | 0.088 | |
| C6 | [62, 71, 80] | [65, 75, 85] | [70, 79, 89] | 0.0600 | 0.0328 | 0.0456 | |
| C7 | [63, 75, 80] | [65, 75, 87] | [70, 85, 95] | 0.0624 | 0.0621 | 0.064 | |
| C8 | [63, 70, 85] | [70, 82, 92] | [68, 79, 95] | 0.0624 | 0.0883 | 0.0763 | |
| C9 | [61, 72, 88] | [73, 80, 89] | [69, 81, 93] | 0.0632 | 0.0282 | 0.0434 | |
| C10 | [70, 82, 92] | [68, 79, 89] | [70, 85, 95] | 0.0648 | 0.0421 | 0.0537 | |
| C11 | [63, 70, 85] | [65, 76, 90] | [68, 79, 93] | 0.0608 | 0.0823 | 0.0727 | |
| C12 | [70, 82, 92] | [68, 79, 89] | [70, 85, 95] | 0.0648 | 0.0390 | 0.0517 | |
| C13 | [61, 75, 83] | [65, 72, 88] | [64, 78, 86] | 0.0600 | 0.0152 | 0.031 | |
| C14 | [65, 75, 85] | [62, 77, 89] | [66, 79, 93] | 0.0616 | 0.0654 | 0.0653 | |
| C15 | [65, 75, 85] | [62, 77, 91] | [66, 79, 93] | 0.0616 | 0.0600 | 0.0625 | |
| C16 | [61, 75, 83] | [65, 72, 88] | [64, 78, 86] | 0.0600 | 0.0424 | 0.0518 | |
| Index | Excellent (S1) | Good (S2) | Medium (S3) | Little Poor (S4) | Poor (S5) | Section Field |
|---|---|---|---|---|---|---|
| C1 | (90, 100) | (80, 90) | (60, 80) | (40, 60) | (0, 40) | (0, 100) |
| C2 | (90, 100) | (80, 90) | (60, 80) | (40, 60) | (0, 40) | (0, 100) |
| (90, 100) | (80, 90) | (60, 80) | (40, 60) | (0, 40) | (0, 100) | |
| C15 | (90, 100) | (80, 90) | (60, 80) | (40, 60) | (0, 40) | (0, 100) |
| C16 | (90, 100) | (80, 90) | (60, 80) | (40, 60) | (0, 40) | (0, 100) |
| Typical Area | H1 | H2 | H3 | H4 | H5 |
|---|---|---|---|---|---|
| A | 1.000 | 0.996 | 0.962 | 0.888 | 0.815 |
| B | 0.999 | 0.997 | 0.964 | 0.890 | 0.817 |
| C | 0.970 | 1.002 | 0.992 | 0.919 | 0.845 |
| D | 0.965 | 0.999 | 0.998 | 0.925 | 0.852 |
| E | 0.971 | 1.001 | 0.993 | 0.934 | 0.876 |
| Typical Area | s′ | Judgment Results | S** |
|---|---|---|---|
| A | 0.991 | Excellent | 1 |
| B | 0.997 | Excellent | 2 |
| C | 0.998 | Good | 3 |
| D | 0.999 | Good | 5 |
| E | 0.997 | Good | 4 |
| Typical Area | Optimal Ideal Solution Distance | Worst Ideal Solution Distance | Relative Closeness | Sort Results |
|---|---|---|---|---|
| A | 0.0777 | 0.2272 | 0.7451 | 1 |
| B | 0.0823 | 0.2151 | 0.7232 | 2 |
| C | 0.1999 | 0.0950 | 0.3223 | 4 |
| D | 0.2355 | 0.0451 | 0.1609 | 5 |
| E | 0.1949 | 0.1206 | 0.3823 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Li, S.; Yang, K.; Zhu, X.; Luo, F. Evaluating the Current Situation of River and Lake Shoreline Planning and Utilization Using an Improved Matter-Element Extension Model. Appl. Sci. 2024, 14, 9857. https://doi.org/10.3390/app14219857
Wang B, Li S, Yang K, Zhu X, Luo F. Evaluating the Current Situation of River and Lake Shoreline Planning and Utilization Using an Improved Matter-Element Extension Model. Applied Sciences. 2024; 14(21):9857. https://doi.org/10.3390/app14219857
Chicago/Turabian StyleWang, Bo, Shihua Li, Kang Yang, Xinyu Zhu, and Fan Luo. 2024. "Evaluating the Current Situation of River and Lake Shoreline Planning and Utilization Using an Improved Matter-Element Extension Model" Applied Sciences 14, no. 21: 9857. https://doi.org/10.3390/app14219857
APA StyleWang, B., Li, S., Yang, K., Zhu, X., & Luo, F. (2024). Evaluating the Current Situation of River and Lake Shoreline Planning and Utilization Using an Improved Matter-Element Extension Model. Applied Sciences, 14(21), 9857. https://doi.org/10.3390/app14219857






