Impact of Various High Intensity Earthquake Characteristics on the Inelastic Seismic Response of Irregular Medium-Rise Buildings
Abstract
1. Introduction
1.1. Review of Chosen Former Intense Earthquakes
1.2. Metodologhy of Seismic Analysis
2. Ground Motion Parameters
3. Nonlinear Dynamic Analysis
3.1. FEA Model
3.2. Results of the Dynamic Response and Discussion
4. Conclusions
- The first model consists of RC and masonry walls and the second model consists of just RC walls. The building’s dynamic characteristics were examined before the calculations. The calculations focused on the base shear, displacement, and evaluation of the damage caused by the earthquakes.
- The study highlights that changes in seismic characteristics can significantly affect a building’s dynamic response.
- The main contribution of this study is its attempt to consider the effect of different earthquakes with varying magnitudes, PGA and PGV values, and durations of the intense shock phase on the behavior of medium-rise structures. The level of ground velocity (PGV) has the most significant impact on structural damage. The horizontal velocity earthquakes analyzed ranged from 67 to 487.9 mm/s.
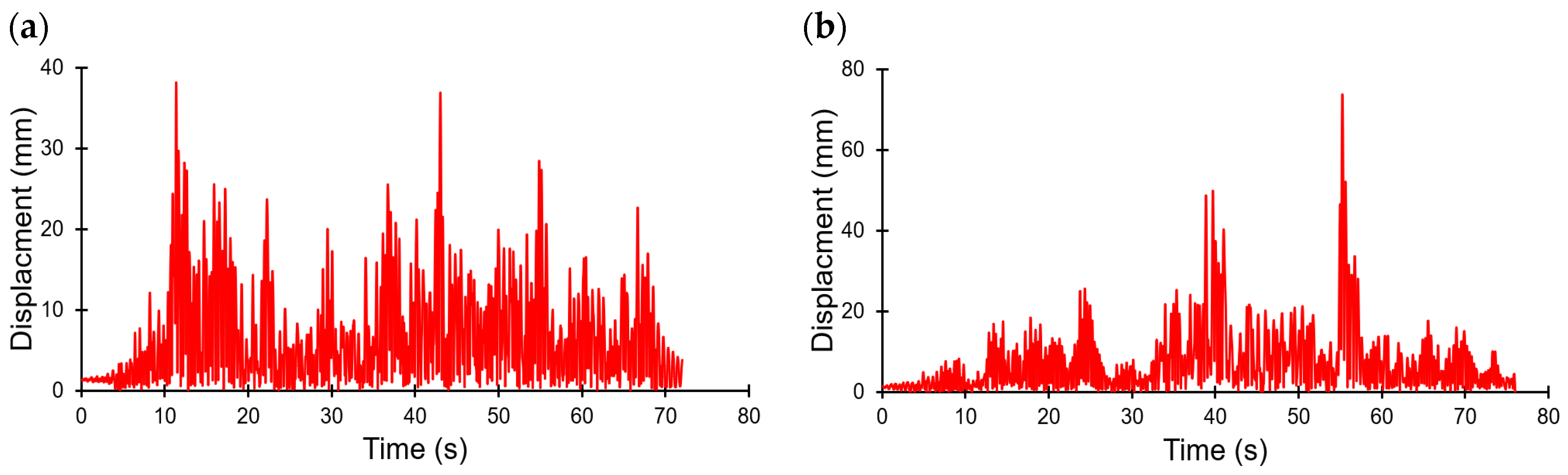
- The locations of structural damage were identified, and the dynamic resistance of the structure was assessed. It was observed that there is a significant displacement between the highest point of the building’s roof and the level of the 6th floor ceiling. This displacement is caused by the design of that section of the building, which functions as a cantilever. However, the displacement between the ceiling on the top floor and the foundation is smaller, due to the stiffer bearing wall throughout the height of the building. Based on these observations, it is recommended that such floors are not constructed in areas prone to earthquakes.
- The results of the calculations have led to significant conclusions. These findings should be taken into account when constructing new buildings or demolishing old ones. It is essential to avoid several design flaws, such as fragile columns, insufficient steel reinforcement, the improper tying of transverse reinforcement bars, the absence of beams and shear walls (even in tall buildings), improperly sized top floors, and incorrect joints.
- The presented analysis results are a supplement to research on the impact of seismic shocks on buildings with irregular structures. The results were presented for a specific building with a mixed irregular structure (column-wall) structure. The results obtained are consistent with the results obtained by other authors [20,24,25].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Menke, W.; Abend, H.; Bach, D.; Newman, K.; Levin, V. Review of the source characteristics of the Great Sumatra–Andaman Islands earthquake of 2004. Surv. Geophys. 2006, 27, 603–613. [Google Scholar] [CrossRef][Green Version]
- Papazachos, V.; Papazachou, K. The Earthquakes of Greece; Editions Ziti; University of Michigan: Ann Arbor, MI, USA, 1997. [Google Scholar]
- Giacomelli, L.; Perrotta, A.; Scandone, R.; Scarpati, C. The eruption of Vesuvius of 79 AD and its impact on human environment in Pompeii. Episodes 2003, 26, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Satake, K.; Shimazaki, K.; Tsuji, Y.; Ueda, K. Time and size of a giant earthquake in Cascadia inferred from Japanese tsunami records of January 1700. Nature 1996, 379, 246–249. [Google Scholar] [CrossRef]
- Rafferty, J.P. “New Madrid Earthquakes of 1811–1812”. Encyclopedia Britannica. 9 December 2023. Available online: https://www.britannica.com/event/New-Madrid-earthquakes-of-1811-1812 (accessed on 12 January 2024).
- Gutscher, M.-A. What Caused the Great Lisbon Earthquake? Science 2004, 305, 1247–1248. [Google Scholar] [CrossRef] [PubMed]
- Wald, D.J.; Kanamori, H.; Helmberger, D.V.; Heaton, T.H. Source study of the 1906 San Francisco earthquake. Bull. Seism. Soc. Am. 1993, 83, 981–1019. [Google Scholar] [CrossRef]
- Satake, K.; Atwater, B.F. Long-Term Perspectives on Giant Earthquakes and Tsunamis at Subduction Zones. Annu. Rev. Earth Planet. Sci. 2007, 35, 349–374. [Google Scholar] [CrossRef]
- Plafker, G. Tectonics of the March 27, 1964, Alaska Earthquake; U.S. Geological Survey Professional Paper 543-I, 74 p. 2 sheets, scales 1:2,000,000 and 1:500,000; US Government Printing Office: Washington, DC, USA, 1969. Available online: https://pubs.usgs.gov/pp/0543i/ (accessed on 19 August 2024).
- Kanaori, Y.; Kawakami, S.-I. The 1995 7.2 magnitude Kobe earthquake and the Arima-Takatsuki tectonic line: Implications of the seismic risk for central Japan. Eng. Geol. 1996, 43, 135–150. [Google Scholar] [CrossRef]
- Norio, O.; Ye, T.; Kajitani, Y.; Shi, P.; Tatano, H. The 2011 eastern Japan great earthquake disaster: Overview and comments. Int. J. Disaster Risk Sci. 2011, 2, 34–42. [Google Scholar] [CrossRef]
- Rafferty, J.P.; Pletcher, K. “Japan Earthquake and Tsunami of 2011”. Encyclopedia Britannica. 10 January 2024. Available online: https://www.britannica.com/event/Japan-earthquake-and-tsunami-of-2011 (accessed on 12 January 2024).
- Ichiyanagi, M.; Takai, N.; Shigefuji, M.; Bijukchhen, S.; Sasatani, T.; Rajaure, S.; Dhital, M.R.; Takahashi, H. Aftershock activity of the 2015 Gorkha, Nepal, earthquake determined using the Kathmandu strong motion seismographic array. Earth Planets Space 2016, 68, 1–6. [Google Scholar] [CrossRef]
- Garini, E.; Gazetas, G. The 2 Earthquakes of February 6th 2023 in Turkey—Preliminary Report; NTUA: Athens, Greece, 2023. [Google Scholar]
- EN 1998-1:2004; Eurocode 8 Design of structures for earthquake resistance—Part 1: General rules, seismic actions and rules for buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- FEMA 356; NEHRP Prestandard and Commentary for Seismic Rehabilitation of Buildings. American Society of Civil Engineering Reston, Virginia, Federal Emergency Management Agency: Washington, DC, USA, 2000.
- FEMA 440; NEHRP Improvement of Nonlinear Static Seismic Analysis Procedures. Applied Technology Council (ATC-55 Project): Washington, DC, USA, 2005.
- ATC-40; Seismic Evaluation and Retrofit of Concrete Buildings. Applied Technology Council: Redwood City, CA, USA, 1996; p. 94065.
- Fajfar, P. The Story of the N2 Method; International Association for Earthquake Engineering (IAEE): Tokyo, Japan, 2021. [Google Scholar]
- Zembaty, Z. Rockburst induced ground motion—A comparative study. Soil Dyn. Earthq. Eng. 2004, 24, 11–23. [Google Scholar] [CrossRef]
- Habib, A.; Houri, A.A.; Habib, M.; Elzokra, A.; Yildirim, U. Structural Performance and Finite Element Modeling of Roller Compacted Concrete Dams: A Review. Lat. Am. J. Solids Struct. 2021, 18, e376. [Google Scholar] [CrossRef]
- Habib, M.; Bashir, B.; Alsalman, A.; Bachir, H. Evaluating the accuracy and effectiveness of machine learning methods for rapidly determining the safety factor of road embankments. Multidiscip. Model. Mater. Struct. 2023, 19, 966–983. [Google Scholar] [CrossRef]
- Pachla, F.; Kowalska-Koczwara, A.; Tatara, T.; Stypuła, K. The influence of vibration duration on the structure of irregular RC buildings. Bull. Earthq. Eng. 2019, 17, 3119–3138. [Google Scholar] [CrossRef]
- Lavan, O.; De Stefano, M. Seismic Behaviour and Design of Irregular and Complex Civil Structures; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Zembaty, Z.; Stefano, M. Seismic Behaviour and Design of Irregular and Complex Civil Structures II; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Köber, D.; Stefano, M.; Zembaty, Z. Seismic Behaviour and Design of Irregular and Complex Civil Structures III; Springer: Dordrecht, The Netherlands, 2020. [Google Scholar]
- Bento, R.; Stefano, M.; Köber, D.; Zembaty, Z. Seismic Behaviour and Design of Irregular and Complex Civil Structures IV; Springer: Dordrecht, The Netherlands, 2024. [Google Scholar]
- Habib, A.; Yildirim, U. Distribution of strong input energy in base-isolated structures with complex nonlinearity: A parametric assessment. Multidiscip. Model. Mater. Struct. 2023, 19, 324–340. [Google Scholar] [CrossRef]
- Habib, A.; Yildirim, U. Proposing unsupervised clustering-based earthquake records selection framework for computationally efficient nonlinear response history analysis of structures equipped with multi-stage friction pendulum bearings. Soil Dyn. Earthq. Eng. 2024, 182, 108732. [Google Scholar] [CrossRef]
- Habib, A.; Alnaemi, A.; Habib, M. Developing a framework for integrating blockchain technology into earthquake risk mitigation and disaster management strategies of smart cities. Smart Sustain. Built Environ. 2024. ahead-of-print. [Google Scholar] [CrossRef]
- Habib, A.; Youssefi, I.; Kunt, M.M. Identification of pulse-like ground motions using artificial neural network. Earthq. Eng. Eng. Vib. 2022, 21, 899–912. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Brady, A.G. A study on the duration of strong earthquake ground motion. Bull. Seismol. Soc. Am. 1975, 65, 581–626. [Google Scholar]
- Koehler, R. Active Faults and Seismic Hazards in Alaska; Alaska Division of Geological & Geophysical Surveys: Fairbanks, Alaska, 2018; p. 160. [Google Scholar] [CrossRef]
- Wyss, M. A search for precursors to the Sitka, 1972, earthquake: Sea level, magnetic field, and P-residuals. Pure Appl. Geophys. 1975, 113, 297–309. [Google Scholar] [CrossRef]
- Schell, M.M.; Ruff, L.J. Rupture of a seismic gap in southeastern Alaska: The 1972 Sitka earthquake (Ms 7.6). Phys. Earth Planet. Inter. 1989, 54, 241–257. [Google Scholar] [CrossRef]
- Sykes, L.R. Aftershock zones of great earthquakes, seismicity gaps, and earthquake prediction for Alaska and the Aleutians. J. Geophys. Res. 1971, 76, 8021–8041. [Google Scholar] [CrossRef]
- Tocher, D. The Alaska earthquake of July 10, 1958: Movement on the Fairweather fault and field investigation of southern epicentral region. Bull. Seism. Soc. Am. 1960, 50, 267–292. [Google Scholar] [CrossRef]
- Ulrich, F.P. The Imperial Valley earthquakes of 1940*. Bull. Seism. Soc. Am. 1941, 31, 13–31. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Brune, J.N. Complexity of energy release during the Imperial Valley, California, earthquake of 1940. Bull. Seismol. Soc. Am. 1970, 60, 137–160. [Google Scholar]
- Akinci, A.; Malagnini, L.; Sabetta, F. Characteristics of the strong ground motions from the 6 April 2009 L’Aquila earthquake, Italy. Soil Dyn. Earthq. Eng. 2010, 30, 320–335. [Google Scholar] [CrossRef]
- Chioccarelli, E.; Iervolino, I. Near-source seismic demand and pulse-like records: A discussion for L’Aquila earthquake. Earthq. Eng. Struct. Dyn. 2010, 39, 1039–1062. [Google Scholar] [CrossRef]
- DIANA. Finite Element Analysis User’s Manual Release 10.2—Bing. [Online]. Available online: https://manuals.dianafea.com/d102/Analys/Analys.html (accessed on 19 May 2022).
- Broyden, C.G. The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A Family of Variable-Metric Methods Derived by Variational Means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- De Domenico, D.; Gandelli, E.; Gioitta, A. Displacement-based design procedure for the seismic retrofit of existing buildings with self-centering dissipative braces. Structures 2024, 62, 106174. [Google Scholar] [CrossRef]
- Yan, X.; Shu, G.; Rahgozar, N.; Alam, M.S. Seismic design and performance evaluation of hybrid braced frames having buckling-restrained braces and self-centering viscous energy-dissipative braces. J. Constr. Steel Res. 2024, 213, 108359. [Google Scholar] [CrossRef]
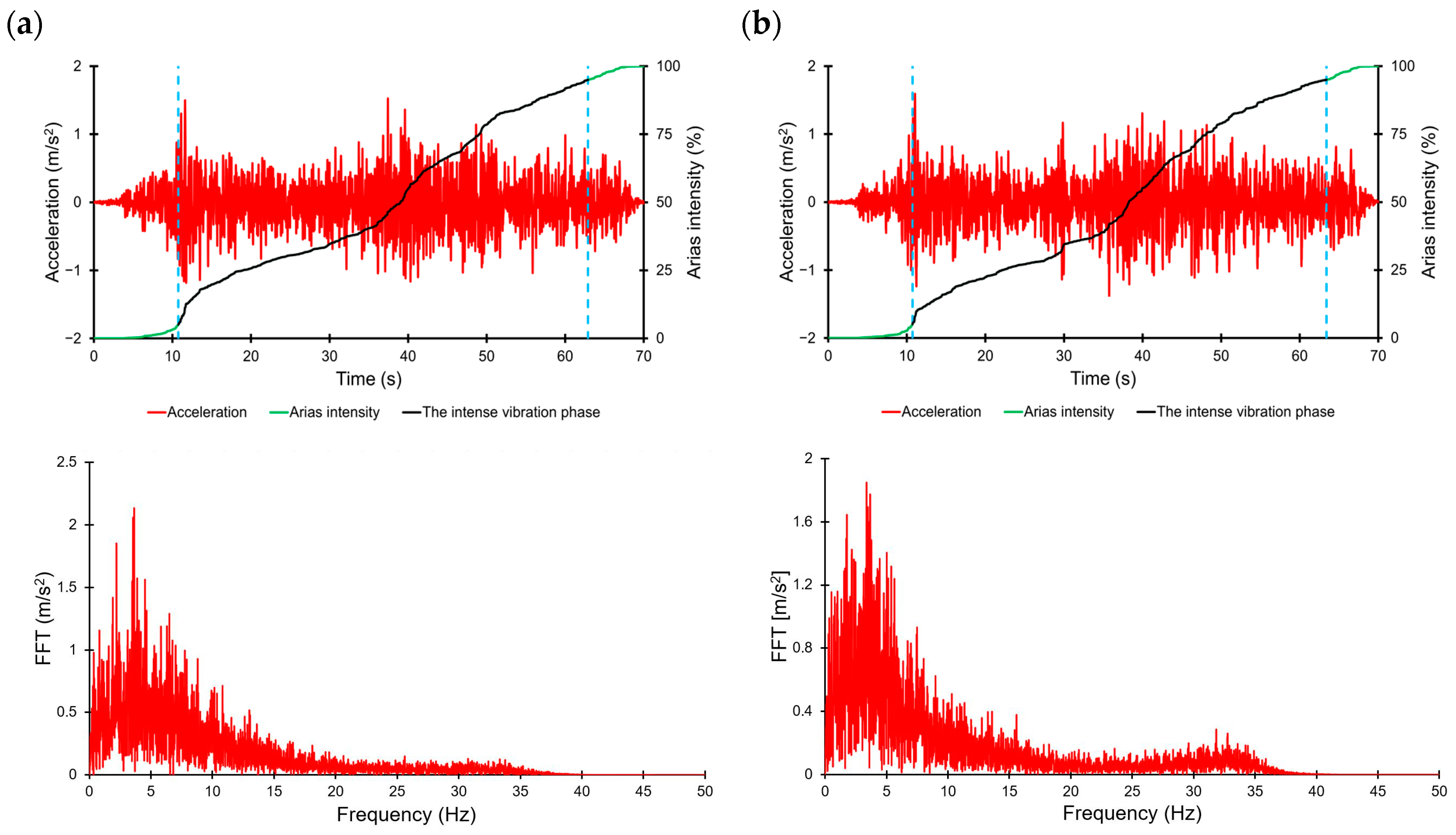
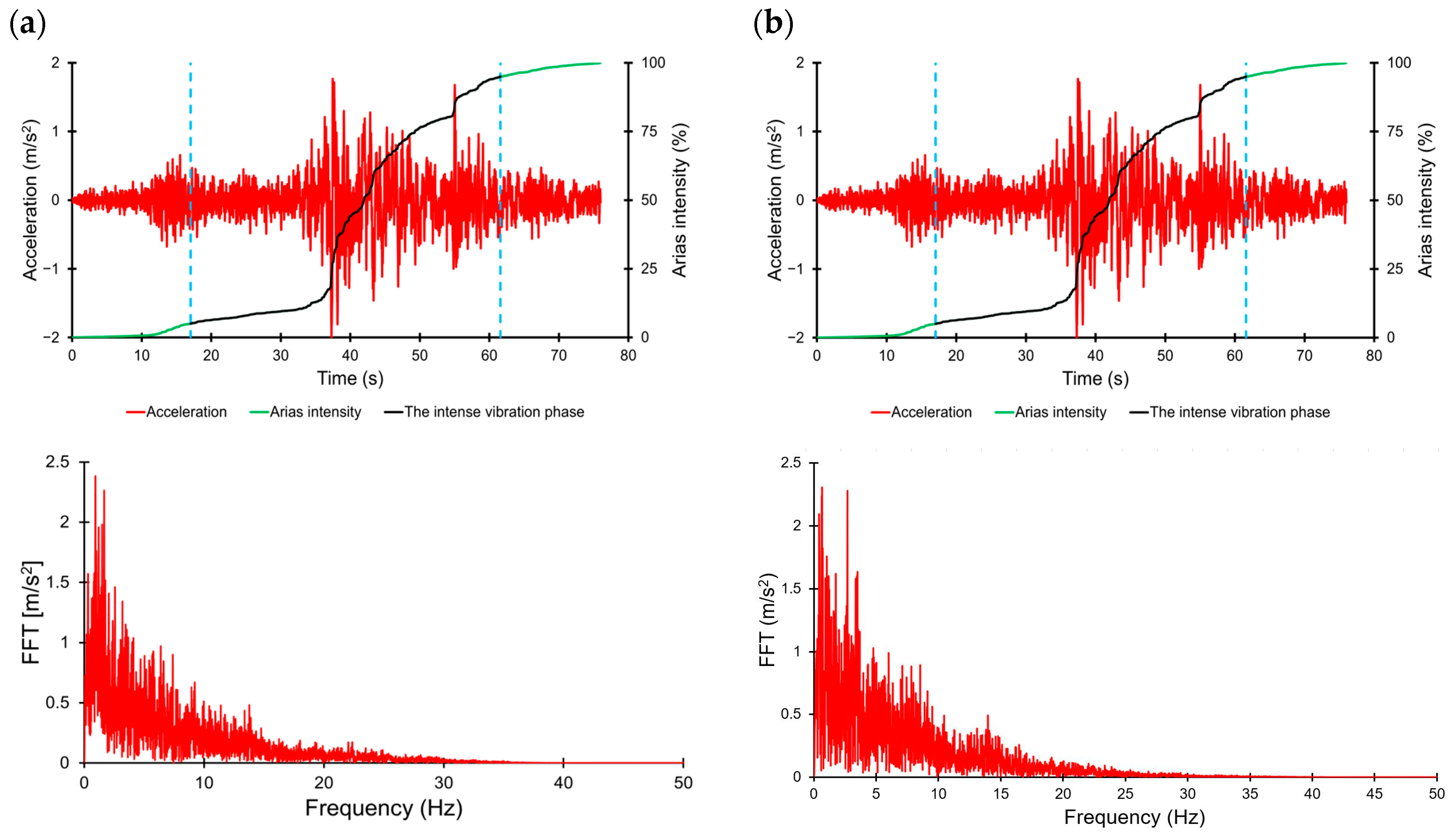
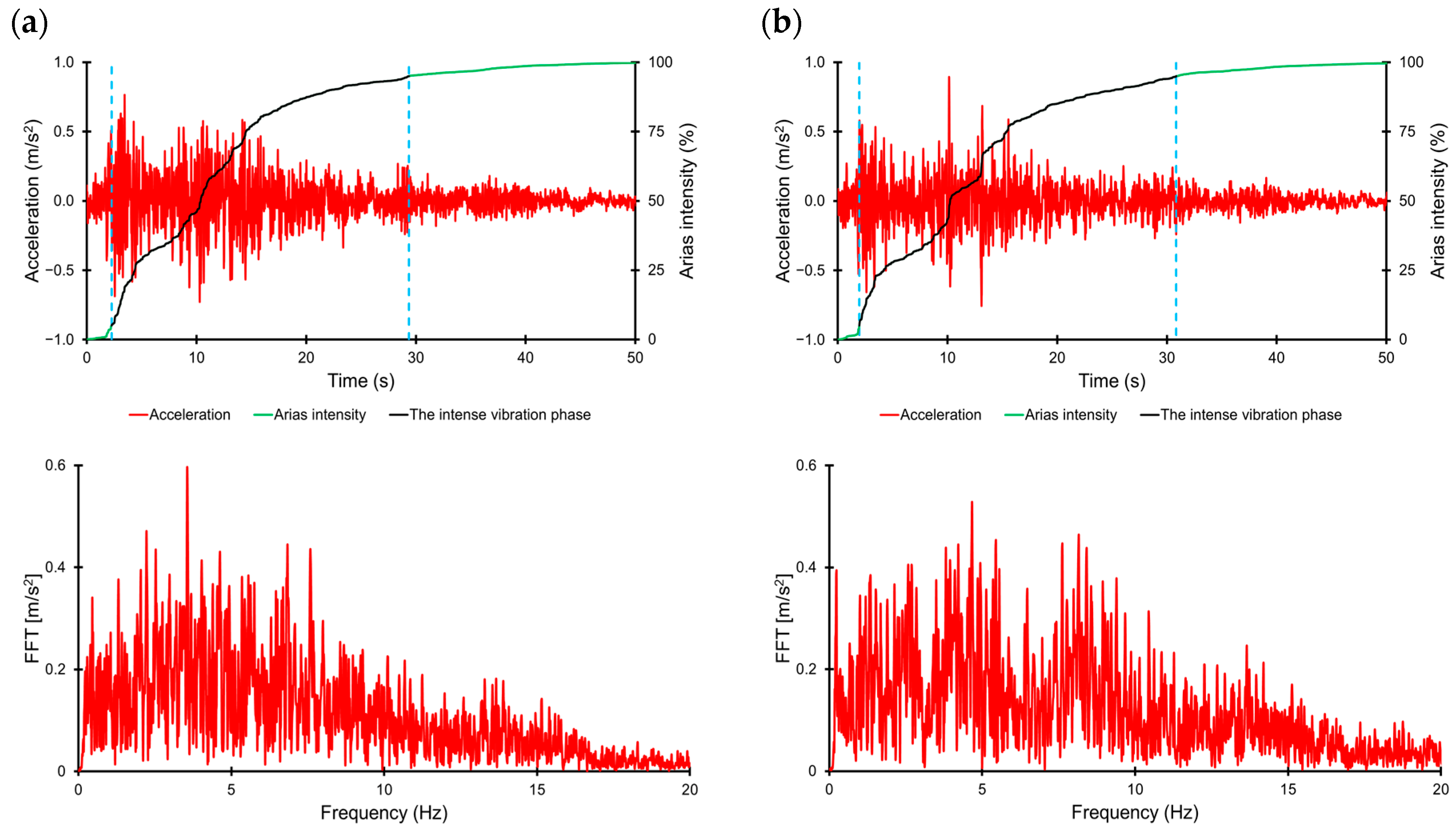
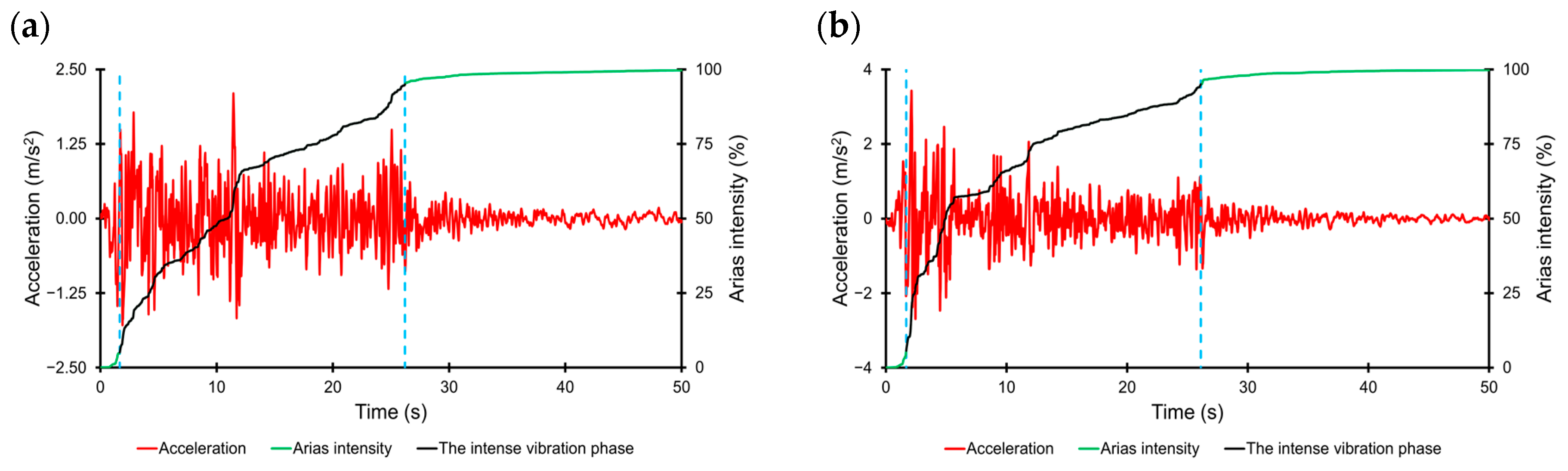
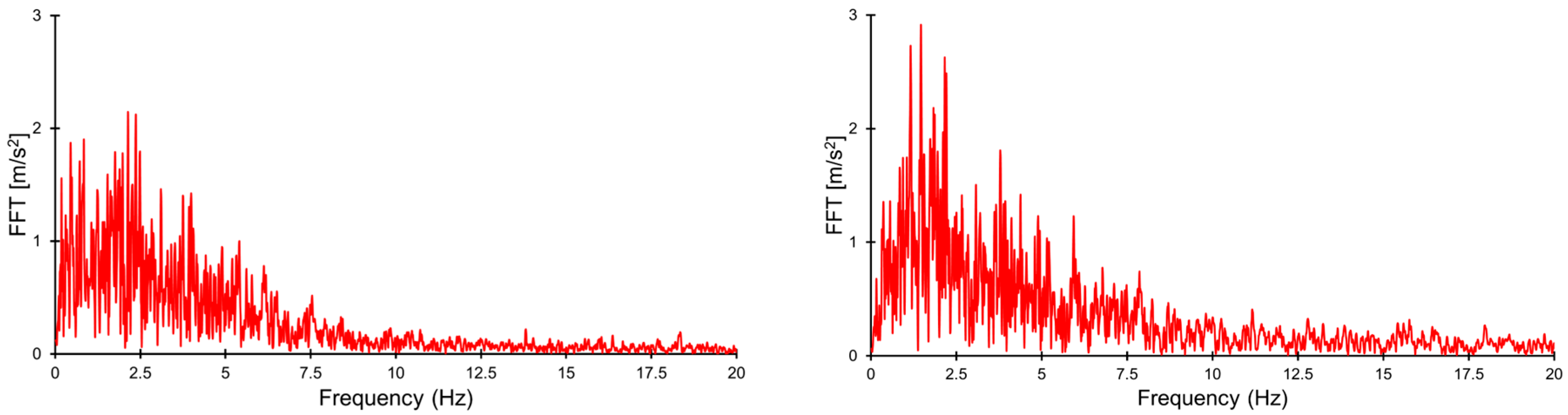
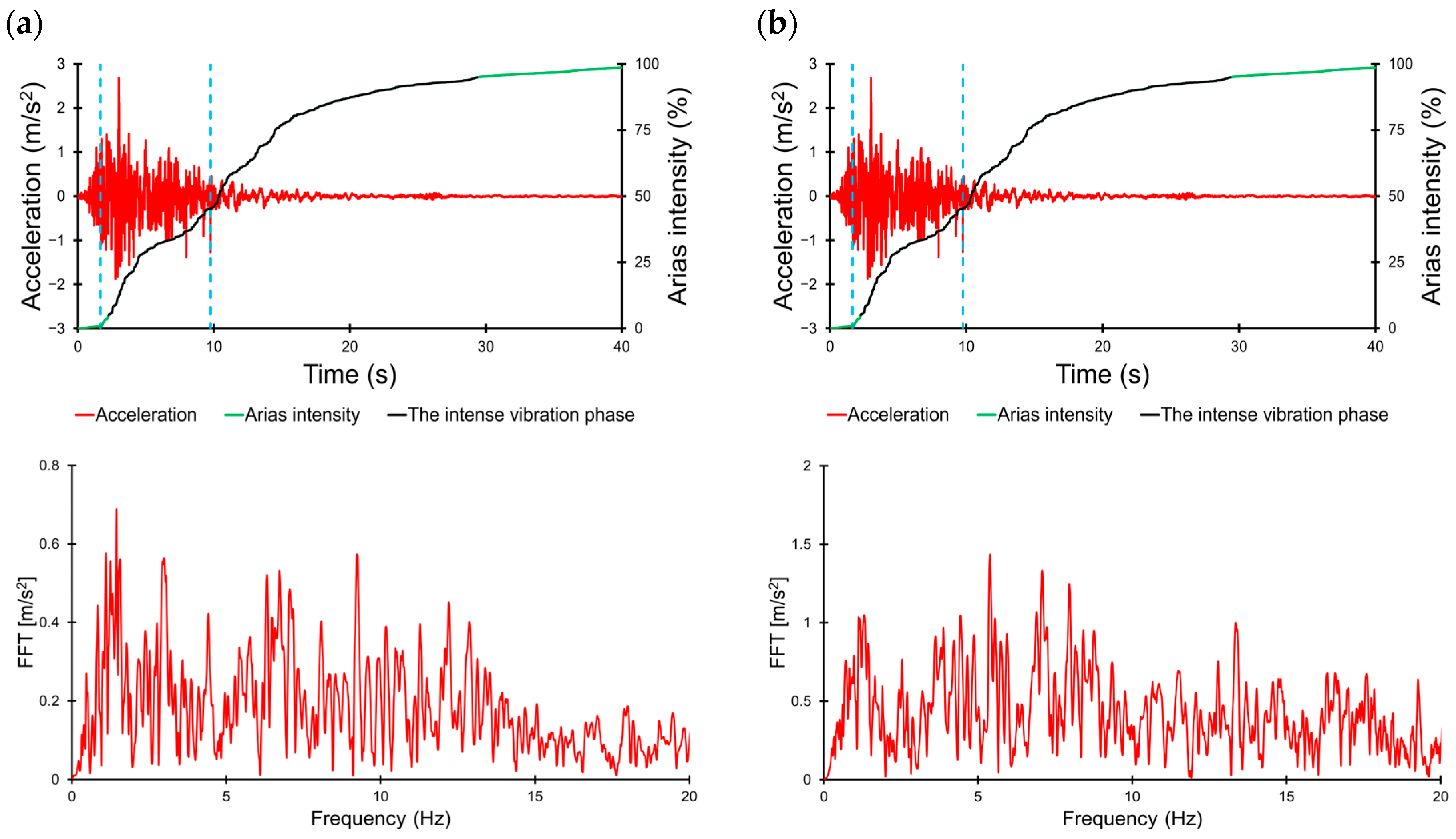

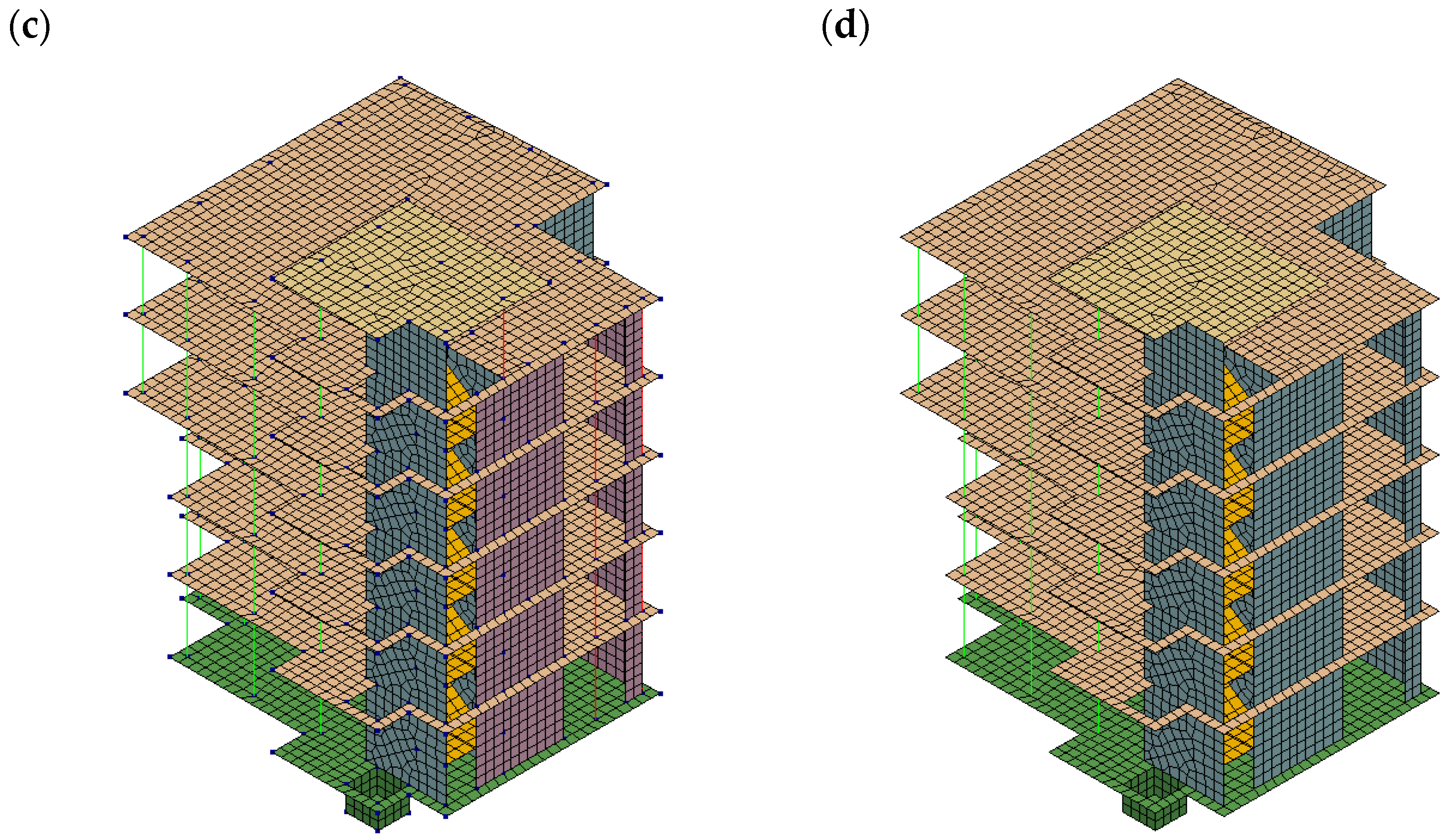
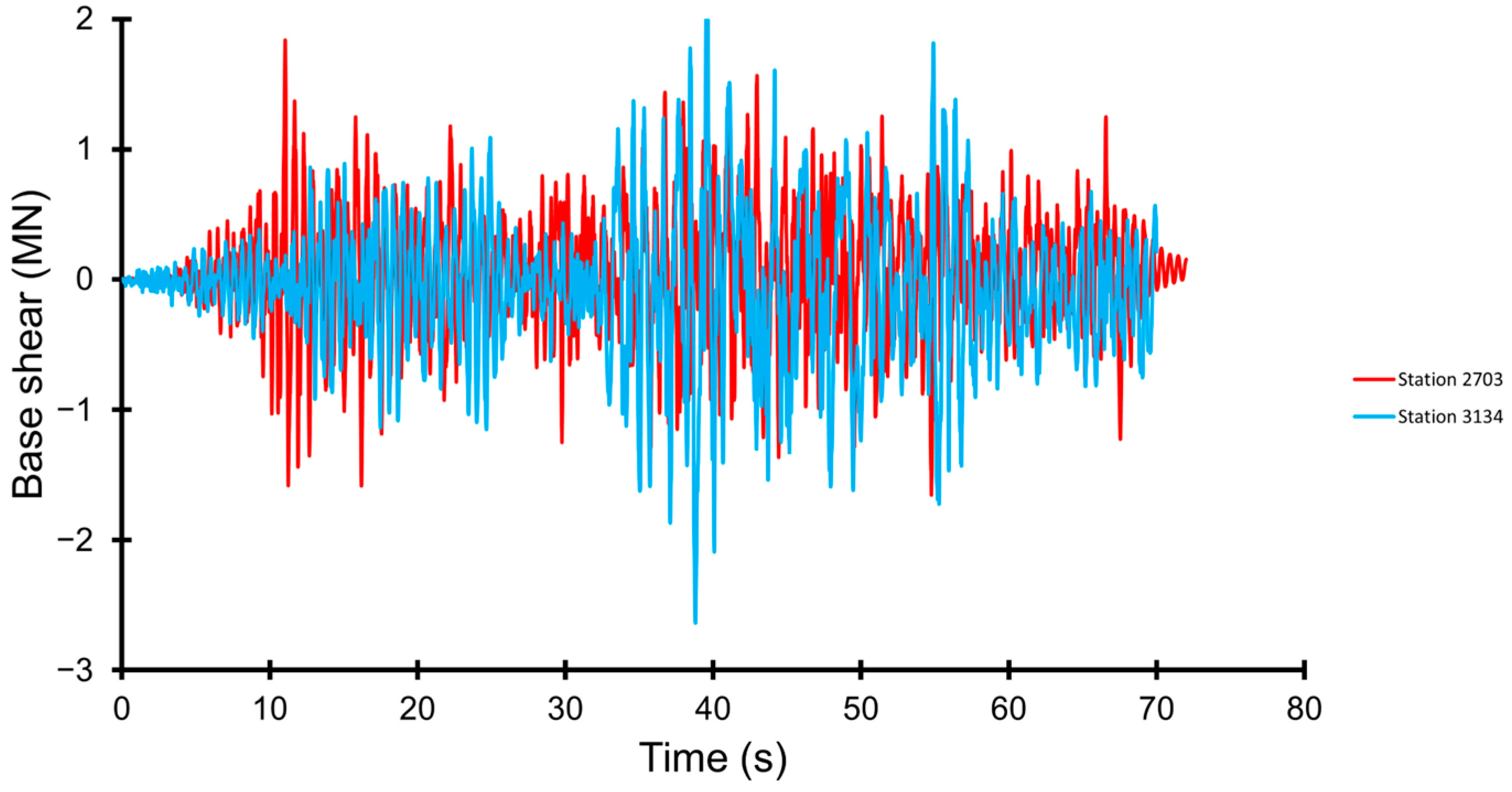

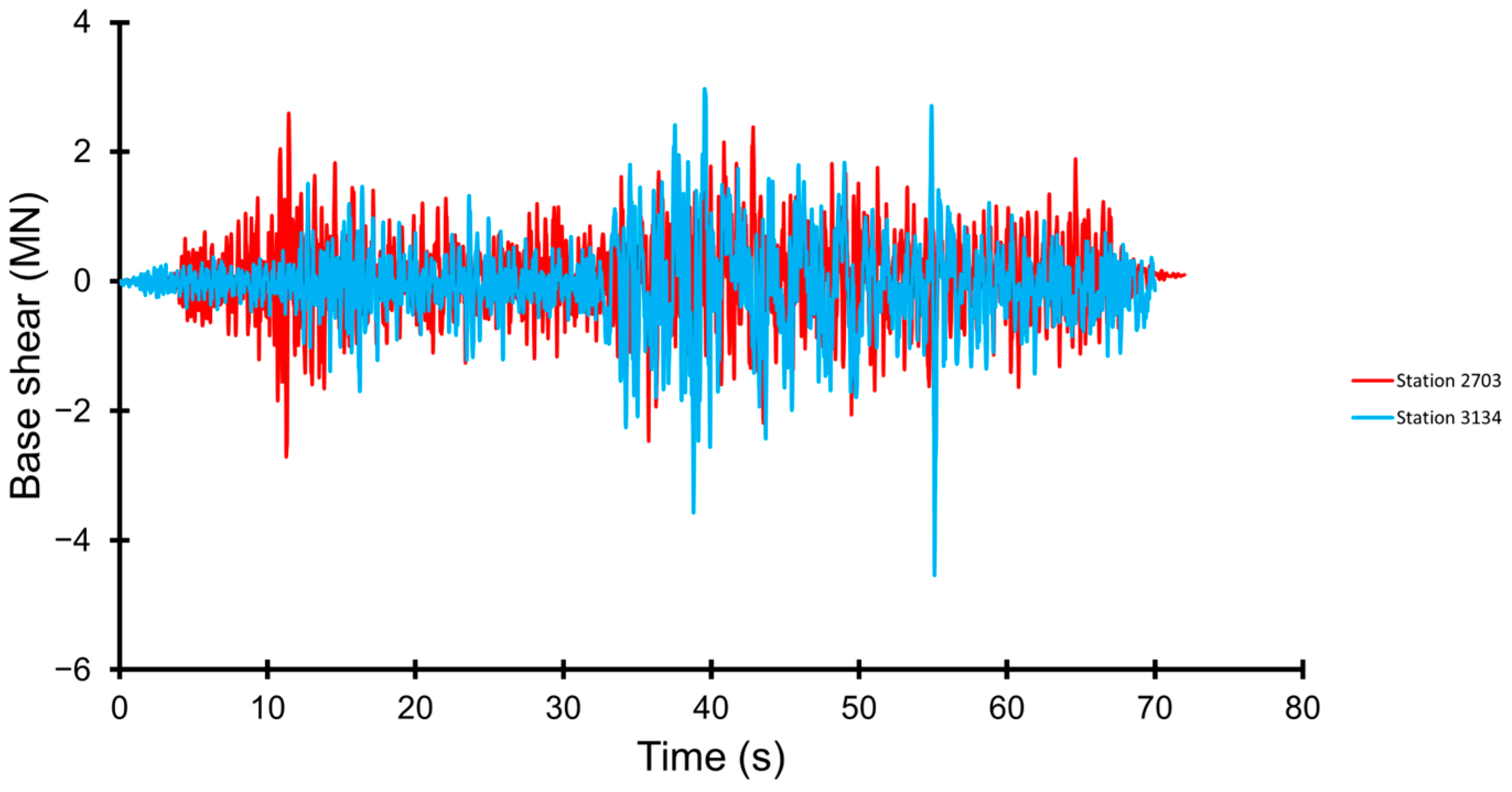

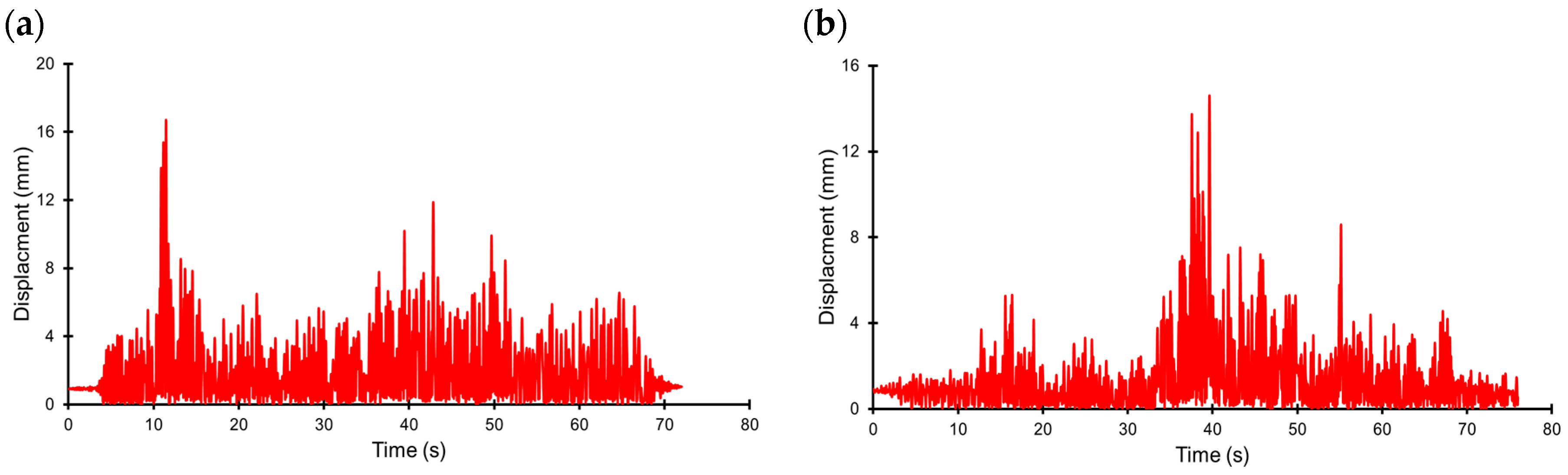

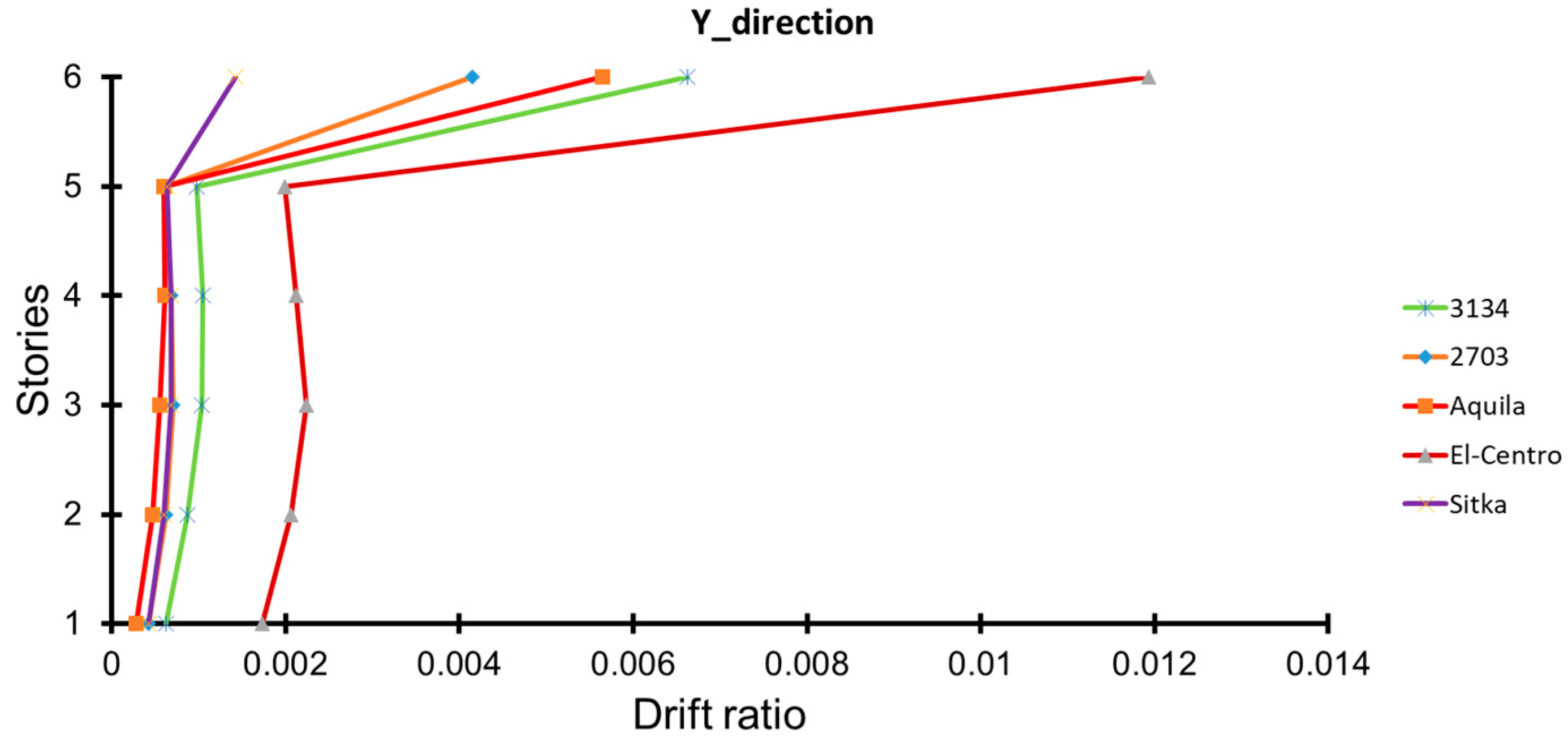


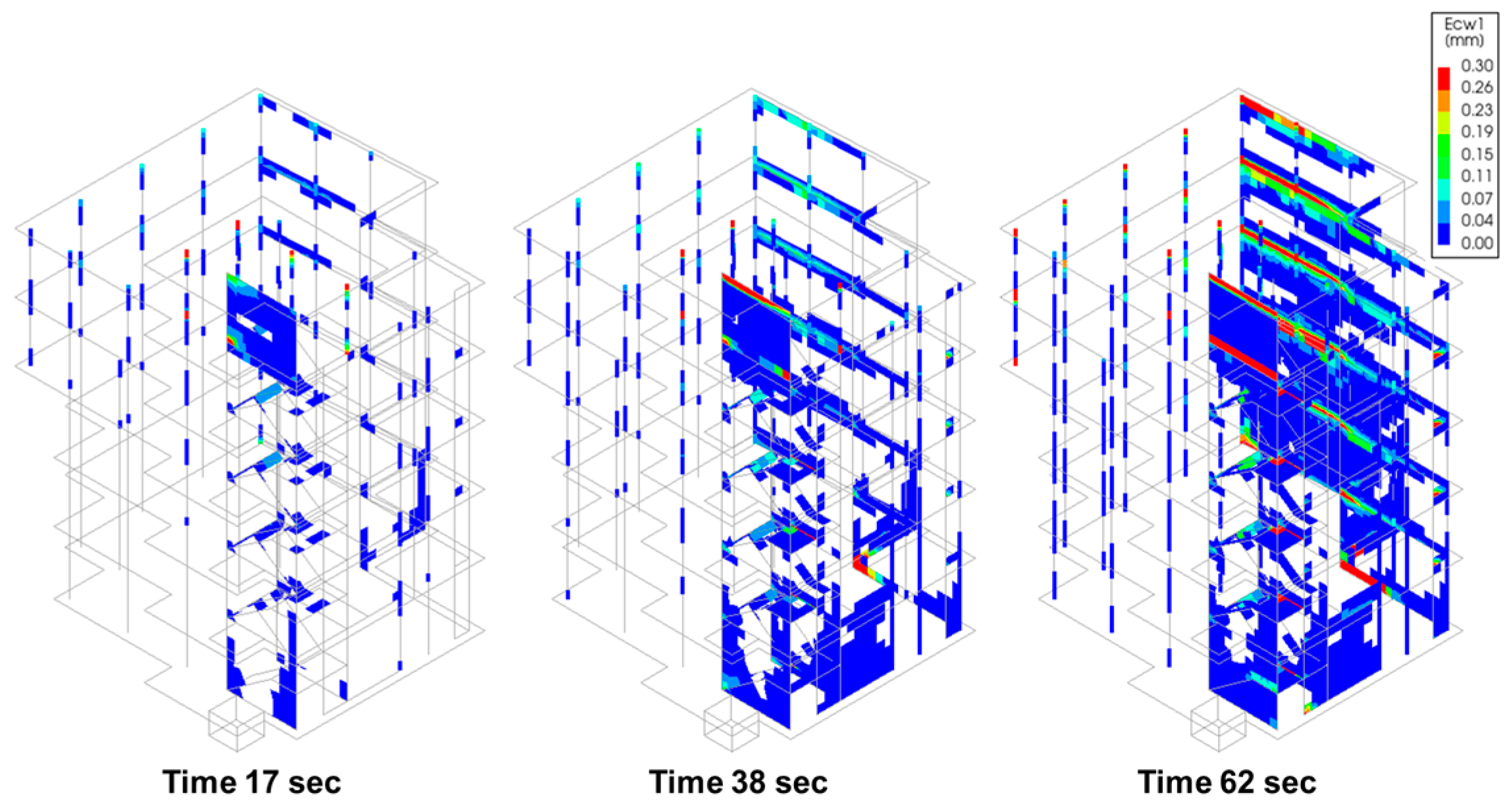
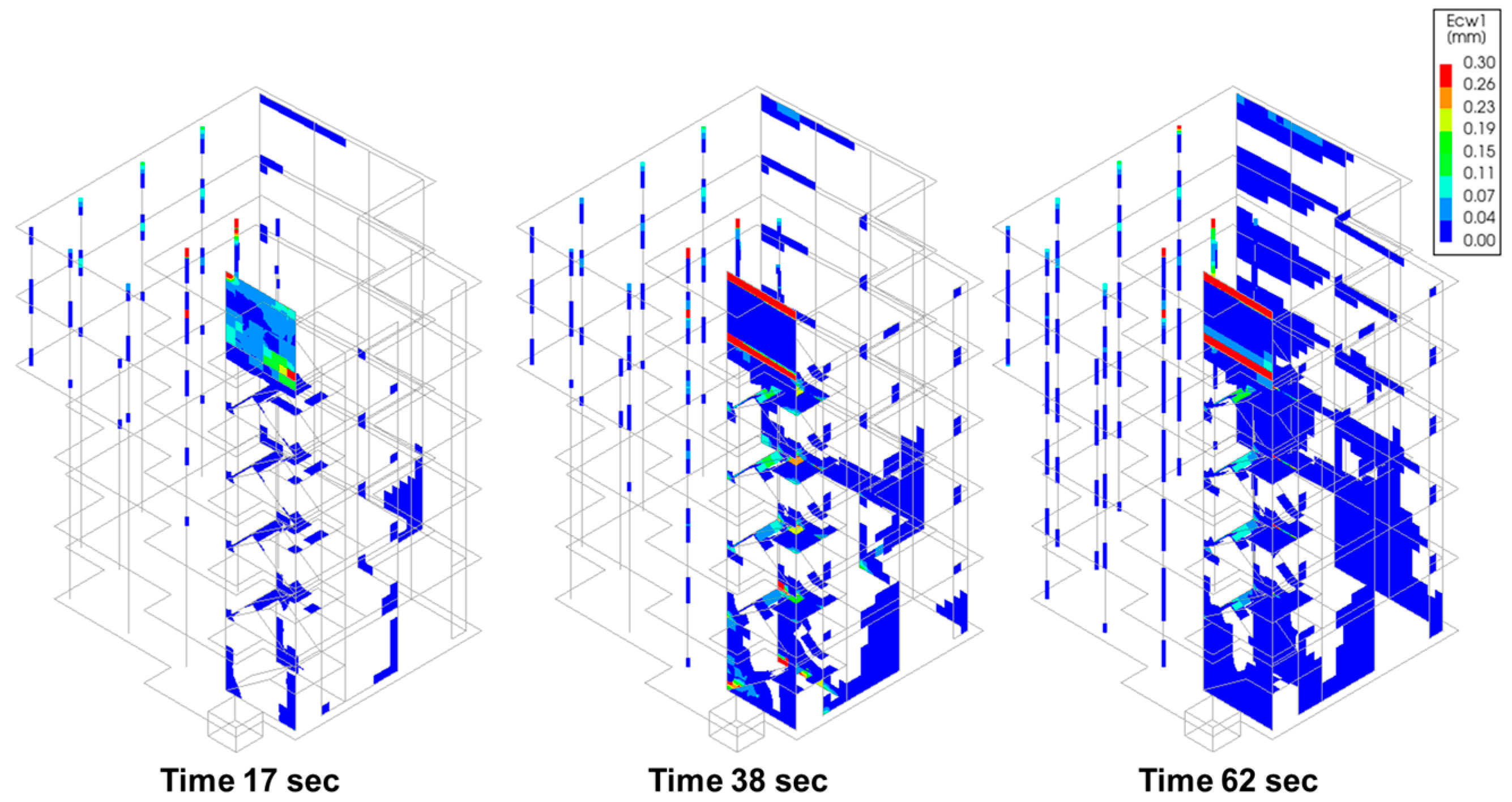
| Parameter | Direction | Station No. 2703 | Station No. 3134 | Sitka | El Centro | L’Aquila |
|---|---|---|---|---|---|---|
| Magnitude [-] | 7.8 | 7.8 | 7.3–8.1 | 6.9 | 6.3 | |
| PGA (mm/s2) | X | 1650.64 | 2039.09 | 765 | 2099.3 | 2677 |
| Y | 1566.34 | 2461.07 | 894 | 3423 | 3975 | |
| PGV (mm/s) | X | 165.29 | 396.42 | 74.2 | 487.9 | 109 |
| Y | 130.67 | 391.53 | 67 | 380.9 | 318 | |
| PGA/PGV (s−1) | X | 9.986 | 5.144 | 10.3 | 4.3 | 24.5 |
| Y | 11.987 | 6.286 | 13.3 | 9.0 | 12.5 | |
| t * (s) | X | 52.68 | 44.56 | 28.88 | 24.42 | 7.4 |
| Y | 52.16 | 44.83 | 27.1 | 24.54 | 8.1 |
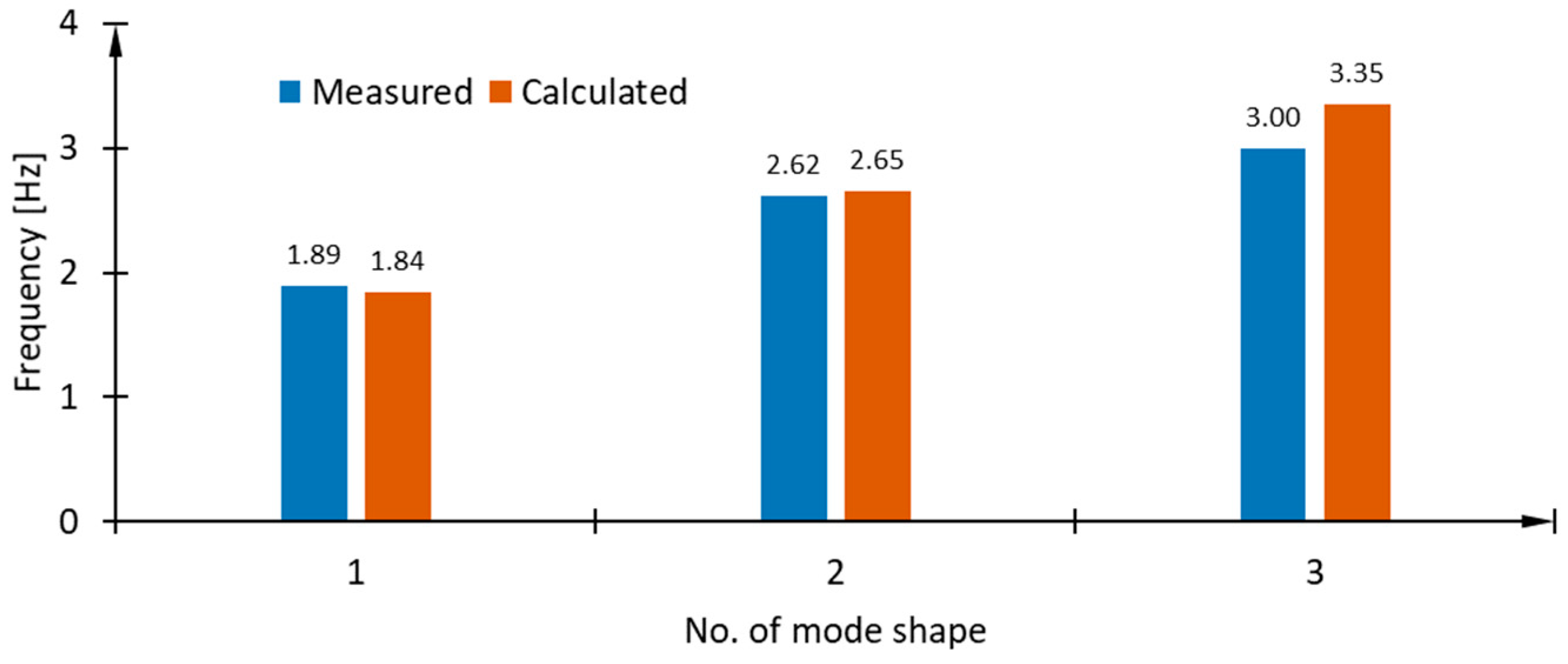
| Mode Shape | Measured Values of Frequency [Hz] | Calculated Values of Frequency [Hz] |
|---|---|---|
| Flexural in ‘y’ direction | 1.89 | 1.84 |
| Flexural in ‘x’ direction | 2.62 | 2.65 |
| Torsional | (2.5–3.5) | 3.35 |
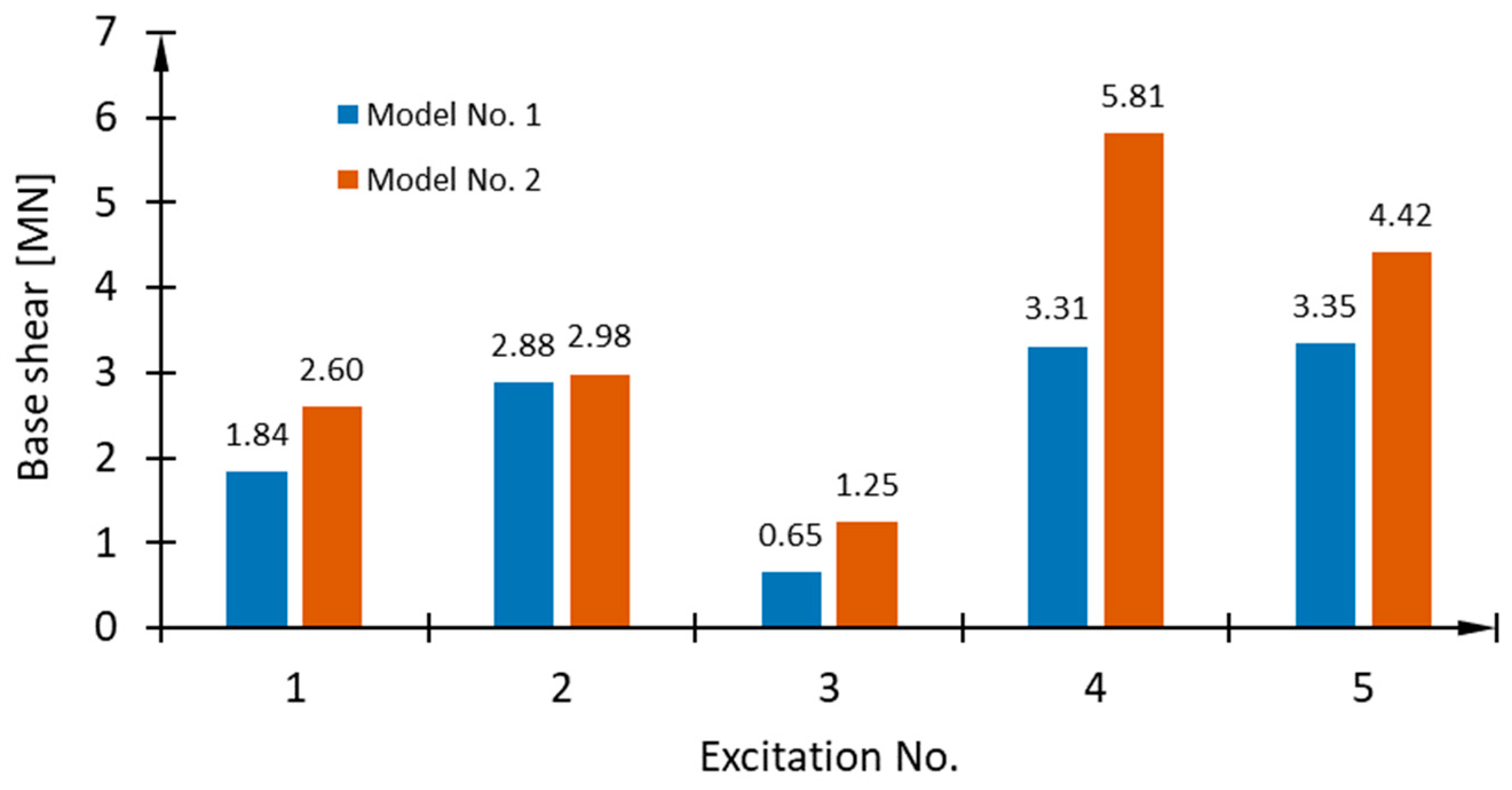
| Selected Results | Excitations from the Station | ||||
|---|---|---|---|---|---|
| Station No. 2703 | Station No. 3131 | Sitka | El Centro | L’Aquila | |
| No. | 1 | 2 | 3 | 4 | 5 |
| Base Shear, MN for model No. 1 | 1.84 | 2.88 | 0.65 | 3.31 | 3.35 |
| Base Shear, MN for model No. 2 | 2.60 | 2.98 | 1.25 | 5.81 | 4.42 |
| Selected Results | Excitations from the Station | ||||
|---|---|---|---|---|---|
| Station No. 2703 | Station No. 3134 | Sitka | El Centro | L’Aquila | |
| Maximum relative displacement between the roof and 6th floor in Model No. 1 | 20.22 | 32.00 | 20.67 | 57.60 | 21.49 |
| Maximum relative displacement between 6th floor and foundation in Model No. 1 | 16.68 | 31.74 | 8.26 | 60.02 | 36.72 |
| Resultant maximum displacement in Model No. 1 | 26.15 | 54.03 | 26.40 | 96.14 | 49.52 |
| Maximum relative displacement between roof and 6th floor in Model No. 2 | 33.26 | 42.62 | 23.85 | 62.41 | 27.67 |
| Maximum relative displacement between 6th floor and foundation in Model No. 2 | 15.91 | 24.44 | 7.55 | 58.38 | 18.59 |
| Resultant maximum displacement in Model No. 2 | 33.33 | 44.38 | 23.06 | 62.41 | 28.04 |
| Type of Excitation | Type of Damage | Degree of Damage |
|---|---|---|
| Turkey earthquake No. 2703—very high PGA values, long duration | Damages in structural elements | High |
| Turkey earthquake No. 3134—very high PGA values, long duration | Damages in structural elements | High |
| Sitka earthquake—small PGA values, long duration | Cracks in structural elements | Slight |
| El Centro earthquake—very high PGA values, long duration | Damages in structural elements | High |
| L’Aquila—very high PGA values, short duration | Damages in structural elements | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pachla, F.; Tatara, T.; Aldabbik, W. Impact of Various High Intensity Earthquake Characteristics on the Inelastic Seismic Response of Irregular Medium-Rise Buildings. Appl. Sci. 2024, 14, 9740. https://doi.org/10.3390/app14219740
Pachla F, Tatara T, Aldabbik W. Impact of Various High Intensity Earthquake Characteristics on the Inelastic Seismic Response of Irregular Medium-Rise Buildings. Applied Sciences. 2024; 14(21):9740. https://doi.org/10.3390/app14219740
Chicago/Turabian StylePachla, Filip, Tadeusz Tatara, and Waseem Aldabbik. 2024. "Impact of Various High Intensity Earthquake Characteristics on the Inelastic Seismic Response of Irregular Medium-Rise Buildings" Applied Sciences 14, no. 21: 9740. https://doi.org/10.3390/app14219740
APA StylePachla, F., Tatara, T., & Aldabbik, W. (2024). Impact of Various High Intensity Earthquake Characteristics on the Inelastic Seismic Response of Irregular Medium-Rise Buildings. Applied Sciences, 14(21), 9740. https://doi.org/10.3390/app14219740






