Abstract
We numerically demonstrate the dispersion map configured by random-based residual dispersion per span (RDPS) applied into the mid-span spectral inversion (MSSI) system to mitigate the impact of chromatic dispersion and the fiber nonlinearity in wavelength division multiplexed (WDM) signals. The dispersion map proposed was a scheme in which the RDPS of all optical fiber spans in the front section of the midway optical phase conjugator (OPC) are randomly selected, and the arrangement order of the RDPS in the rear section is inverted from that of the front section. Numerical simulations were performed by evaluating the compensation of the distorted 960 Gb/s WDM signal as a function of the variation of the DCF length and the SMF length, which are involved in determining RDPS. It was confirmed that the compensation effect of the proposed dispersion maps has improved compared to the conventional dispersion map since the dispersion maps examined in this paper have antipodal symmetry around the midway OPC. In particular, it was confirmed that the method of randomly determining the RDPSs by varying the DCF length slightly improved system performance compared to the variation of SMF lengths. We also found that the feature of the RDPS random distribution patterns can achieve excellent compensation for the distorted WDM signal through 50 iterations.
1. Introduction
The capacity of optical communication links has increased exponentially since their introduction in the late 1970s [1]. This trend is expected to continue in the coming years, driven by new applications requiring high bandwidth, such as cloud computing, 5G/6G wireless, high-definition video streaming, and virtual reality [2]. In addition to these high-capacity issues, network services are becoming more dynamic and heterogeneous. However, there is growing recognition that this continued bandwidth demand will drive the required capacity closer to the maximum capacity theoretically predicted for that fiber [1].
Regarding the channel capacity of a transmission line, C. E. Shannon derived a specific closed-form expression for the capacity of an additive white Gaussian noise (AWGN) channel [3] that increases logarithmically with the signal-to-noise ratio. That is, for such a channel, the ultimate theoretical limit on transmission rate is determined only by the available signal power. Optical fiber behaves essentially like an AWGN channel at low signal powers. However, contrary to the case with AWGN, when the signal power is increased, the resulting nonlinearity damages existing systems to the point that they cease to operate at higher powers [3]. This naturally increases the impact of nonlinearity on the capacity of the optical fiber channel, and as signal power increases, the possibility that a finite limit on the capacity of the optical fiber channel actually exists increases, which is defined as the nonlinear Shannon limit (NSL) [3,4].
Experiments based on various analytical expressions and simulation technologies have been attempted to overcome NSL, but no one has been able to show a system that overcomes it. These attempts were based on a variety of individual technologies, including third-window distributed feedback lasers (DFB), erbium-doped fiber amplifiers (EDFA), wavelength division multiplexing (WDM), forward error correction (FEC), and Raman amplification [1]. What is important to note here is that these individual technologies were generally accomplished in single-mode fiber (SMF)-based systems. To increase transmission capacity to approach NSL in an SMF-based transmission system, the link design technology that basically eliminates or reduces chromatic dispersion (CD) and nonlinearity is required.
Two general approaches to compensating for CD are inline dispersion compensation (DC) and electronic DC [5]. Electronic DC uses digital signal processing (DSP) to compensate for signal distortion caused by CD. Inline DC, on the other hand, mitigates the effects of CD by adding passive optical components to each fiber span. Using a fiber Bragg grating (FBG) as the passive optical component eliminates the effects of CD locally within each wavelength division multiplexing (WDM) channel [6]. By inserting a dispersion-compensating fiber (DCF) into each fiber span, WDM can be compensated across the entire spectrum [5]. We call these two systems per-channel dispersion-managed (CDM) link and dispersion-managed (DM) link, respectively.
Optical phase conjugation (OPC) is an optical signal processing technique to mitigate dispersion and Kerr effect-based nonlinear effects in SMF. By placing the OPC in the middle of a symmetrical link, the signal phase is conjugated, thereby inverting both the uniform dispersion and nonlinear effects due to Kerr in the second half of the link and providing the possibility of compensation [7]. A symmetrical link refers to a case where the dispersion-power profile is symmetrical with respect to the OPC location, and a system with the OPC located at the center of the symmetrical link is called mid-span spectral inversion (MSSI). There are some approaches to maximize symmetry in MSSI systems. One way is to use short span lengths that monotonically increase symmetry as spacing decreases. However, this increases the number of amplifiers required and initially reduces energy consumption [8], but the optimal spacing is a trade-off between energy consumption and symmetry. Another approach is to use distributed Raman amplification using primary or secondary pumping or short-interval Raman amplification [9,10,11]. In this context, Minzioni et al. proposed the introduction of dispersion elements co-located with OPC to improve symmetry by aligning regions where fiber nonlinearity has a significant influence on the same cumulative dispersion [12].
The authors of this paper also proposed and verified the various MSSI-based DM links as the link technology for CD and nonlinear distortion compensation of 960 Gb/s WDM signals [13,14,15]. In applying the DM link to the MSSI system, the most important thing to prioritize to satisfy the dispersion-power symmetry condition is to ensure that the cumulative dispersion profile versus the transmission distance, i.e., the dispersion map, is symmetrical around the midway-OPC. We have confirmed that antipodal symmetry is more effective in compensating for distortion in the WDM channel than bilateral symmetry with respect to midway-OPC [13]. However, to form an antipodal-symmetric dispersion map, the lengths and dispersion coefficients of SMF and DCF consisting of the optical fiber span must be selected and distributed artificially and regularly. The amount of dispersion accumulated for each optical fiber span constructing the dispersion map is defined as residual dispersion per span (RDPS). The RDPS is determined by the length and dispersion coefficient of SMF and DCF in the corresponding optical fiber span. In other words, the application of an antipodal symmetrical dispersion map to the DM link means that the RDPS of all optical fiber spans is artificially allocated under special rules. Consequently, the method of artificially selecting and allocating RDPS improves the performance of WDM channels but also limits the diversity of link designs.
The design rule in which the RDPS of each optical fiber span is randomly determined is most desirable in terms of flexibility in DM link design. However, due to the random distribution of RDPS, it is difficult to symmetrize the dispersion profile with respect to the midway OPC, so it is predicted that less than excellent compensation will be obtained.
In a previous study, the authors proposed the MSSI-based DM link with the dispersion map composed of random-based RDPS [15]. As a result of numerical analysis of those dispersion maps, it was confirmed that among the three proposed methods of arranging the random RDPSs, the ‘random-inverse’ configuration provides the most effective compensation. The ‘random-inverse’ scheme is a method in which the RDPS of the optical fiber spans constituting the front section of the midway-OPC are randomly selected, and at the same time, the arrangement order of the RDPS of the optical fiber spans in the rear section is artificially reversed. This scheme is based on the random distributed RDPSs and makes the dispersion map antipodal–symmetric because the RDPS arrangement before and after midway-OPC is opposite to each other. In other words, we have confirmed that this scheme can satisfy both the improvement of link flexibility and the system performance to some extent.
The sign and magnitude of the randomly selected RDPS were determined only by the length of the DCF in [15]. However, as mentioned earlier, the RDPS is determined by the correlation between the length and dispersion coefficient of the SMF and DCF in each optical fiber span. In other words, if the method of determining the sign and magnitude of the RDPS in the dispersion map of the ‘random-inverse’ scheme discussed in [15] is different, the degree of distortion compensation for the WDM signal may be different.
In this paper, we numerically demonstrate the compensation characteristics of the WDM channels using different methods of determining the sign and magnitude of the RDPS in a ‘random-inverse’ dispersion map. The factors that change the sign and magnitude of the RDPS of the optical fiber span considered in this study are the DCF length and SMF length, respectively. That is, in a situation where the dispersion coefficients of SMF and DCF are each fixed to one value in all optical fiber spans, to determine the sign and magnitude of the RDPS, we consider the following two cases: first, the sign and magnitude of the RDPS are determined by only the length of the DCFs under the condition of the length of SMFs is fixed at 80 km, and second, only the SMF length change is involved in determining the sign and magnitude of the RDPS when the DCFs is fixed at 16 km. All other matters considered in this study, such as the WDM transmission/reception method, WDM channel specifications, the deployment of optical fibers, midway-OPC configuration, etc., are the same as in reference [15].
2. Dispersion-Managed Link and WDM System Modelling
2.1. Dispersion-Managed Link with Random-Based RDPS
Figure 1 shows the dispersion-managed link combined with the midway-OPC, transmitters, and receivers of WDM 24 channels of 40 Gb/s. Each half link comprises 15 optical fiber spans; thus, the total link consists of 30 fiber spans. All fiber spans include SMF and DCF for inline DM. The arrangement of the two types of optical fiber before and after the midway OPC is also important in making power-distribution symmetry in the MSSI system. As verified in the previous study of [15], this study also follows the scheme of inserting DCF before SMF in all optical fiber spans in the first half before the midway-OPC and arranging them in the opposite order in the second half.
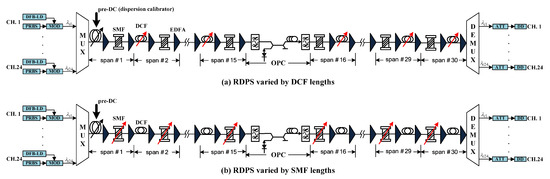
Figure 1.
The 960 Gbps WDM transmission system through the dispersion-managed link and the midway-OPC.
In this study, the RDPS of the optical fiber span is randomly determined to be one of 15 values from −560 ps/nm to 560 ps/nm, separated by 80 ps/nm intervals. These 15 RDPS values are determined solely by the length of the SMF or the length of the DCF in every span. We assume SMF parameters as follows: the dispersion coefficient is 16 ps/nm/km, the attenuation coefficient is 0.2 dB/km, and the nonlinear coefficient is 1.41 W−1 km−1. DCF is characterized as follows: the dispersion coefficient is −80 ps/nm/km, the attenuation coefficient is 0.6 dB/km, and the nonlinear coefficient is 5.06 W−1 km−1. These parameter values are assumed for wavelengths of 1550 nm.
Each optical fiber length involved in determining the sign and magnitude of RDPS is changed by the selected RDPS based on the length that makes RDPS = 0 ps/nm. For RDPS = 0 ps/nm, the SMF length and the DCF length must be 80 km and 16 km, respectively. If the SMF length of each optical fiber span is fixed at 80 km and the RDPS is changed from −560 ps/nm to 560 ps/nm at 80 ps/nm intervals, the DCF length must be changed from 23 km to 9 km at −1 km intervals. From now on, we will call this method ‘varied DCF length’, as shown in Figure 1a. On the other hand, with the DCF length of each optical fiber span fixed at 16 km, the SMF length from 45 km to 115 km (5 km interval) corresponds to the RDPS from −560 ps/nm to 560 ps/nm. We call this method ‘varied SMF length’, which is plotted in Figure 1b.
The random array scheme of RDPS considered in this paper is called ‘random-inverse.’ In this scheme, the RDPSs of each fiber span in the first half section are randomly selected as one of 15 values; the RDPS arrangement order of the second half section reverses the RDPS order assigned to the first half section to construct a dispersion map with antipodal symmetry. In summary, the purpose of this study is to evaluate the distortion compensation of 960 Gb/s WDM signals in cases where the factors that determine the random-based RDPS are the DCF length (Figure 1a) or the SMF length (Figure 1b) in the dispersion-managed link configured with the ‘random-inverse’ scheme.
As the number of random cases increases, the resulting value can converge to a general value. Since the RDPS that are randomly determined in each optical fiber span of the first half section are independent of each other, if the RDPS are randomly selected for all 15 spans at the same time, the RDPS arrangement order also becomes independent. In other words, the overall arrangement order of the RDPS changes whenever the RDPS in each of the 15 spans of the first half section are selected simultaneously and randomly. We repeat 50 times to obtain 50 mutually independent RDPS array patterns under the conditions mentioned above and analyze compensation performance for all cases.
Whatever the factor that determines the RDPS, the sum of the 15 RDPSs selected at random once becomes 0 ps/nm. Therefore, the accumulated dispersion of each half section shown in Figure 1 becomes 0 ps/nm. If the accumulated dispersion across all optical links is defined as net residual dispersion (NRD), the value in both Figure 1a,b is 0 ps/nm. However, according to Killey, in a pseudo-linear system, the best NRD should have a value near 0 ps/nm rather than 0 ps/nm to increase the compensation effect [16]. Setting NRD to a value near 0 ps/nm means that some fiber span must play a role in adjusting NRD. In this study, the DCF of the first fiber span plays that role, as indicated by ‘pre-DC’ in Figure 1, where ‘DC’ stands for dispersion calibrator.
2.2. WDM Transmitters, Receivers, and Midway-OPC
The configuration and specification of 24 transmitters/receivers for the WDM channel and midway OPC shown in Figure 1 are the same as in the previous study by [15]. The WDM transmitter and receiver modeled in this study are based on intensity modulation/direct detection (IM/DD). First, we assume that the center wavelengths of the 24 WDM channels are 1550 nm to 1568.4 nm, spaced at 100 GHz (0.8 nm), according to ITU-T recommendation G.694.1. An independently generated 127 (=27 − 1) PRBS (pseudo-random bit sequence) intensity-modulates the optical continuous wave emitted from each distributed feedback laser diode (DFB-LD). The output of the modulator is assumed to be return-to-zero (RZ) pulses. The output electric field of the RZ format is assumed to be a second-order super-Gaussian pulse with a 10-dB extinction ratio (ER), duty cycle of 0.5, and chirp-free.
The specific type of midway-OPC required to build the MSSI system uses highly nonlinear dispersion shifted fiber (HNL-DSF) OPC, as in the previous study by [15]. The characteristics of HNL-DSF are assumed as follows: the attenuation coefficient of 0.61 dB/km, the nonlinear coefficient of 20.4 W−1 km−1, the zero-dispersion wavelength of 1550.0 nm, the dispersion slope of 0.032 ps/nm2/km, and the length of 0.75 km. The 24 optical signals incident to the midway-OPC are phase conjugated through a four-wavelength mixing (FWM) process with the pump light. The power and wavelength of the pump light in the midway-OPC are assumed to be 18.5 dBm and 1549.75 nm, respectively. Consequently, each wavelength of the conjugated 24 channels in the midway-OPC is then arranged from 1549.5 nm to 1528.5 nm (−0.8 nm interval).
The receiving part of each WDM channel consists of a fiber amplifier, optical filter, photodetector, pulse-shaping filter, and decision circuit. The assumptions for simulation are as follows: receiver bandwidth of 0.65 times 40 Gb/s, erbium-doped fiber amplifier (EDFA) with 5 dB noise figure, PIN diode as photodetector, and Butterworth filter as pulse shaping filter.
3. Numerical Analysis and Performance Evaluation
The nonlinear SchrÖdinger equation (NLSE) of Equation (1) is only known as the expression for the propagation of the optical signal in the silica fiber such as SMF and DCF [17].
In Equation (1), j, k = 1, 2, …, 24 (j ≠ k), Aj represents the complex amplitude of the optical signal of the j-th channel, z is the propagation distance, β2j is the group velocity dispersion (GVD), β3j is dispersion slope, γj is nonlinear coefficient, and T = t − z/vj is the time measured in a retarded frame. The last two terms of (1) express the effect of nonlinearity, including self-phase modulation (SPM) and cross-phase modulation (XPM). It has been reported that the effect of XPM on WDM signals decreases as the dispersion of optical fiber increases [18]. The WDM signal may be affected by XPM due to the relatively high power of WDM signals, but since SMF with a large dispersion coefficient was used as the basic fiber constituting the optical link, we excluded the effect of XPM based on the inference that the effect of XPM would be lower than that of SPM.
The most common approach for solving (1) is the split-step Fourier method [17]. The split-step Fourier method divides the transmission medium dominated by NLSE into small steps and processes linear calculations in the frequency domain and nonlinear calculations in the time domain separately and continuously through the Fourier transform and inverse Fourier transform for each step [17].
The performance evaluation in this study is based on an an eye diagram. An eye diagram can simultaneously determine the level (amplitude) characteristics and timing characteristics of the signal. We use the eye-opening penalty (EOP) and timing jitter (TJ) to assess the compensated optical signals as the level characteristics and the timing characteristics, respectively.
The EOP is quantified (in dB) as Equation (2), where EOrec and EObtb are the eye opening of receiving optical signals and the back-to-back optical signals (i.e., the reference signals), respectively. The eye opening is defined as twice the average power of all of the received signals divided by the smallest power level of the ‘one’ optical signal minus the largest power level of the ‘zero’ optical signal.
The compensation performance criterion is 1-dB EOP, which is equivalent to the pulse broadening (the ratio of root mean square (RMS) width of the received pulse to RMS width of the initial pulse) of 1.25 and corresponds to a bit error rate (BER) of 10−12 [19]. We also use 2 ps, which is 8% of the duration of 40 Gb/s, as a performance criterion for timing jitter.
In the ‘random-inverse’ schemed dispersion map examined in this paper, the RDPS of each optical fiber span has different values, but their total sum is 0 ps/nm, i.e., NRD is 0 ps/nm. The simplest general way to form the DM link with NRD of 0 ps/nm is to fix the SMF length at 80 km and the DCF length at 16 km. We call this method a ‘non-random fixed’ scheme. For the DM link with the ‘random-inverse’ dispersion map to be used for distortion compensation of WDM signals, the compensation performance must at least be better than the ‘non-random fixed’ scheme. For this reason, we also analyze the compensation characteristics of the WDM signal in the DM link designed with a ‘non-random fixed’ scheme, and the EOP and TJ of the worst channel obtained from this link will be used for comparison.
4. Simulation Results and Discussion
Figure 2 shows the eye diagrams of the worst channel launched with 9 dBm power into the ‘random-inverse’ schemed dispersion-managed link configured by the specific random distribution (random pattern numbers 24 and 39). Among the 50 random pattern numbers, the 24th and 39th random patterns of RDPS are selected because they clearly showed the difference in compensation for changes in DCF length and SMF length, which are ultimately factors that determine RDPS.
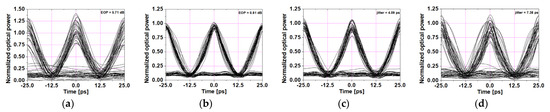
Figure 2.
The eye diagrams. (a) random pattern number 24; varied DCF length, (b) random pattern number 24; varied SMF length, (c) random pattern number 39; varied DCF length and (d) random pattern number 39; varied SMF length.
The results in Figure 2 are all obtained from the DM link with NRD set to 8 ps/nm. The EOP in Figure 2a,b are obtained as 5.71 dB and 0.81 dB, respectively, and the TJ in Figure 2c,d are obtained as 4.09 ps and 7.48 ps, respectively. When comparing the compensation of the distorted WDM channel depending on the length of the DCF or SMF length that determines the RDPS, it is reasonable to apply the same arrangement of RDPS in each case. Thus, the eye diagrams in Figure 2a,b and Figure 2c,d are results obtained from the dispersion-managed link with the same RDPS random arrangement applied, respectively.
The reason the authors show Figure 2 is to inform that even for the same RDPS random arrangement, EOP and TJ should vary depending on the factors contributing to each RDPS. In other words, we confirmed from Figure 2 that the amplitude and phase component compensation for the distorted WDM signal depends on the RDPS random array and the specific method of creating it. From now on, the evaluation and analysis of the compensated WDM will be based on the comparison of each method of creating the RDPS random array.
Figure 3a,b show the maximum launch power values corresponding to 1-dB EOP and 2 ps TJ, respectively. In Figure 3, “descending order number” means that the resulting maximum launch power is sorted from the largest value to the smallest value to facilitate comparative analysis. The values of 5.33 dB and 2.5 dB shown in Figure 3a,b represent the maximum launch power at which the worst channel received through the ‘non-random fixed’ DM would result in 1-dB EOP and 2 ps TJ, respectively.
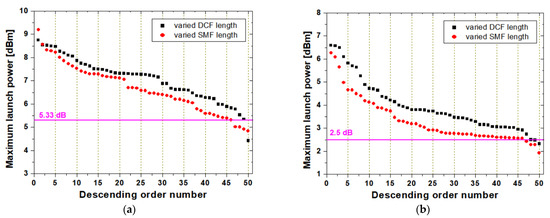
Figure 3.
The maximum launch power of the worst channel. (a) resulting 1-dB EOP and (b) resulting 2 ps TJ.
It can be confirmed from Figure 3a,b that the EOP and TJ characteristics through compensation in more than 45 RDPS array patterns out of 50 randomly generated in this study are superior to ‘non-random fixed’ scheme. In particular, the results in Figure 3 show that even if the same RDPS random arrangement is applied, the method of determining the RDPS by the DCF length can achieve improved performance in more random cases than the method of determining the RDPS by the SMF length.
Figure 3a,b show the results when the NRD of individual DM link is set to 8 ps/nm, but as mentioned in previous research [15], there are several NRDs other than this value of the DM link that can obtain EOP of 1 dB or TJ of 2 ps. As in the previous study [15], the minimum and maximum NRD can be obtained for the launch powers of the WDM channel in the considered 102 types of DM links, which are classified according to the random pattern of RDPS and the method for determining it. Of course, the minimum and maximum NRD are the lower and upper limits that meet EOP of 1 dB or TJ of 2 ps. The width from this minimum NRD to the maximum NRD is defined as the effective NRD range, and the trajectory of the effective NRD range for the launch power becomes a closed curve. The effectiveness of applying the ‘random-inverse’ schemed dispersion map into the DM link increases as the area of the corresponding closed curve increases. We have defined the area of this closed surface in reference [15] as the product of the effective NRD and the launch power.
Figure 4 shows the product of the effective NRD and launch power for all ‘random-inverse’ schemed dispersion maps. It can be confirmed that the product characteristics of most random-based RDPS distribution patterns examined are also better than those of ‘non-random fixed’ DM, as shown in the results in Figure 3. More strictly speaking, the proposed ‘random-inverse’ schemed dispersion maps are judged to be superior in terms of flexibility as the DM link because the number of random patterns outperforms the results in the ‘non-random fixed’ DM is greater than in the maximum launch power characteristic of Figure 3. An additional fact that can be known from the results in Figure 4 is that the proposed ‘random-inverse’ schemed dispersion map is more advantageous for amplitude component compensation than for phase component compensation of distorted WDM channel signals.
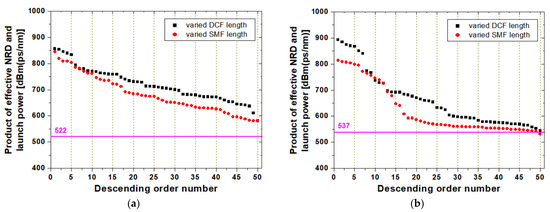
Figure 4.
The product of the effective NRD and launch power. (a) resulting 1-dB EOP, and (b) resulting 2 ps TJ.
So far, through numerical analysis based on eye diagram evaluation of the received WDM signal, we confirmed that the proposed ‘random-inverse’ schemed dispersion map can improve the distortion compensation and increase the allowable launch power and residual dispersion compared to the ‘non-random fixed’ dispersion map, which is the most common DM link configuration method. As analyzed in a previous study [15], the reason why the ‘random-inverse’ dispersion map is superior to the ‘non-random fixed’ dispersion map for compensating for the distorted WDM channels is the large symmetry of power-dispersion with respect to the midway-OPC. That is, the random-inverse distribution can make the dispersion-power profile almost symmetrical with respect to the midway OPC; thus, it is possible to satisfy the conditions necessary for compensation of the signal distortion in the MSSI system. However, these results do not say that the ‘random-inverse’ schemed dispersion map is the best DM link configuration method. This is because the compensation characteristics vary depending on the arrangement of the randomly selected RDPS, and consequently, this limits the application of random arrays of RDPS in DM link design.
In order to increase the usability of the ‘random-inverse’ dispersion map as the DM link for compensating for distorted WDM channels, it is necessary to derive general and reasonable features that can improve compensation performance without specific limitations from 50 random-based RDPS array patterns. Figure 5a,b show the top five dispersion maps, which are formed with random numbers that allow good performance for both maximum launch power and product characteristics. On the other hand, Figure 5c,d shows the bottom five dispersion maps created with random numbers that allow poor performance. The results in Figure 5 were all obtained through EOP evaluation and analysis. Meanwhile, Figure 6a–d shows dispersion maps shown through TJ evaluation and analysis.
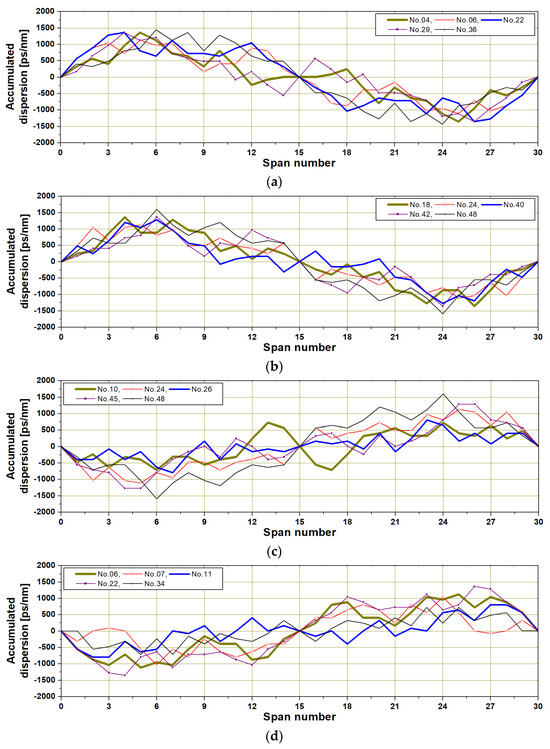
Figure 5.
Five dispersion maps with the best/worst compensation based on EOP evaluation. (a) the best compensation cases for varying DCF length, (b) the best compensation cases for varying SMF length, (c) the worst compensation cases for varying DCF length, and (d) the worst compensation cases for varying SMF length.
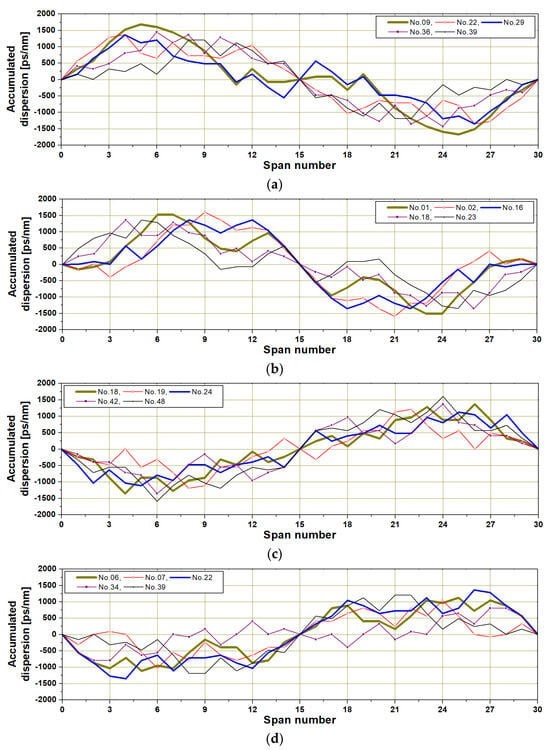
Figure 6.
Five dispersion maps with the best/worst compensation based on TJ evaluation. (a) the best compensation cases for varying DCF length, (b) the best compensation cases for varying SMF length, (c) the worst compensation cases for varying DCF length, and (d) the worst compensation cases for varying SMF length.
What can be intuitively seen from Figure 5a,b and Figure 6a,b is that even if the RDPS sign and magnitude of each optical fiber span are selected randomly, the compensation performance can be improved only when the shape of the cumulative dispersion profile over the entire link is close to antipodal symmetry. Furthermore, the cumulative dispersion profile of the antipodal symmetric configuration for good compensation should gradually increase and then decrease in the section before the midway OPC and have a positive value overall. However, it can also be seen that the compensation effect deteriorates when the shape of the cumulative dispersion profile of the antipodal symmetric configuration changes with respect to the midway OPC; that is, the overall profile gradually decreases and then increases and takes on an overall negative value, as can be seen in Figure 5c,d and Figure 6c,d.
When the optical pulse propagates in the section with the positive cumulative dispersion amount, its width becomes wider (expansion), while it narrows (compression) in the section with the negative sign. Expansion and compression increase as the cumulative amount of dispersion increases. As the width of the optical pulse increases, the intensity of the optical pulse becomes weaker, and as a result, it is less affected by the nonlinear Kerr effect. However, if the positive cumulative dispersion amount continues to increase, inter-symbol interference (ISI) occurs due to overlap with adjacent pulses due to the large broadening of the optical pulse width.
Looking at the dispersion map configurations that greatly enhance the compensation effect, it is desirable to gradually increase the amount of positive cumulative dispersion to reduce the distortion of optical pulses due to nonlinear effects in the front part of the transmission link (approximately 1/4 of the entire link) and then to gradually decrease the amount of cumulative dispersion for minimizing the occurrence of ISI in the remaining sections up to the midway OPC. To take advantage of the impact of the MSSI system, the cumulative dispersion profile of the second half can be inverted from the first half.
5. Conclusions
Up to now, we have numerically investigated the effect of the factor of determining RDPS on the compensation for the distorted WDM signals in the ‘random-inverse’ schemed DM link. The factors that determine the randomly selected RDPS sign and magnitude are the SMF length and DCF length, which make up the optical fiber span. In other words, we analyze the distortion compensation of 960 Gb/s WDM signals in the case where the DCF length (or SMF length) of all optical fiber spans varies randomly in the front section before the midway OPC.
It was confirmed that the method of determining the random-based RDPS by varying the DCF length generally improved the compensation effect of the distorted WDM channel compared to the case of varying the SMF length. This result is to inform that DCF has a slightly greater impact than SMF in determining RDPS, which is an important element of inline DM link configuration. The length of DCF, which plays a role in controlling RDPS in inline DM links, is usually shorter than the SMF length due to its large dispersion coefficient. The degree of variation of each fiber length to make the same RDPS is the same for the reference lengths of 80 km for SMF and 16 km for DCF. However, the variation ranges of optical fiber length corresponding to the same RDPS change between adjacent optical fiber spans is larger in SMF than in DCF, and in particular, as the RDPS change becomes more severe, the variation degree of SMF length becomes larger. The authors believe that because of this feature, the random-based RDPS determination by DCF length variation enables somewhat improved compensation than by SMF length variation. It is thought that the dramatic difference in optical fiber length in consecutive fiber spans may ultimately have a negative effect on the compensation.
Our current study was conducted following the results of previous research by [15]. In other words, the biggest reason why the compensation performance in most of the 50 random patterns considered was superior to the ‘non-random fixed’ dispersion map is because the ‘random-inverse’ schemed DM link, which can obtain the best compensation among the methods for randomly selecting RDPS in the previous research [15], was used. Here, the ‘random-inverse’ schemed DM link is meaningful in terms of compensation efficiency for distorted WDM channels because it is based on the MSSI system. What the authors want to emphasize is not that good compensation is achieved in most of the random patterns considered. Instead, among the dispersion maps that form ‘random-inverse’ schemed DM links through random-based RDPS, there are characteristics of random patterns that can achieve excellent compensation, and these characteristics should be utilized when designing the exact DM links. We believe that this is one of the implications of this paper. If the parameters that consist of the DM link have random values, it is very difficult to evaluate performance through analytical methods. This means that finding the random arrangement that results in the best and worst performance is only possible through numerical simulation. Accordingly, we derived the performance of all 50 random patterns through numerical simulation and compared and analyzed each result to find a specific pattern that could improve WDM compensation performance.
Strictly speaking, this paper does not have high academic originality because it is based on the ‘random-inverse’ schemed DM link with random-based RDPS evaluated in previous research. However, through this paper, there was a meaningful performance comparison as a function of the method for determining the random-based RDPS, and the characteristics of the RDPS random pattern that forms the dispersion map that may be more advantageous for improving compensation performance were derived. We hope that the random-based dispersion maps proposed in this paper, its analysis method, and the induced results from performance evaluation will be helpful in designing the DM links combined with the MSSI system.
Author Contributions
Conceptualization, J.-P.C. and S.-R.L.; methodology, S.-R.L.; software, S.-R.L.; analysis, J.-P.C. and S.-R.L.; resources, S.-R.L.; data curation, S.-R.L.; writing—original draft preparation, J.-P.C. and S.-R.L.; writing—review and editing, J.-P.C. and S.-R.L.; visualization, S.-R.L.; super-vision, J.-P.C. and S.-R.L.; project administration, S.-R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to Institutional regulations.
Conflicts of Interest
The authors declare no conflict of interest regarding the publication of this paper.
References
- Ellis, A.D.; Zhao, J.; Cotter, D. Approaching the non-linear Shannon limit. J. Light. Technol. 2009, 28, 423–433. [Google Scholar] [CrossRef]
- Roberts, K.; Zhuge, Q.; Monga, I.; Gareau, S.; Charles, L. Beyond 100 Gb/s: Capacity, flexibility, and network optimization. J. Opt. Commun. Netw. 2017, 9, C12–C23. [Google Scholar] [CrossRef]
- Secondini, M.; Forestieri, E. Scope and limitations of the nonlinear Shannon limit. J. Light. Technol. 2016, 35, 893–902. [Google Scholar] [CrossRef]
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J. Roadmap of optical communications. J. Opt. 2016, 18, 063002. [Google Scholar] [CrossRef]
- Keykhosravi, K.; Secondini, M.; Durisi, G.; Agrell, E. How to increase the achievable information rate by per-channel dispersion compensation. J. Light. Technol. 2019, 37, 2443–2451. [Google Scholar] [CrossRef]
- Brochu, G.; Morin, M.; Trépanier, F.; Maheux-Lacroix, B.; Paquet, C.; Patel, A.; Filer, M.; Meyer, C.; Tibuleac, S. Channelized fiber Bragg gratings for inline chromatic dispersion compensation of 40 Gb s links on ITU-50 grid. In Proceedings of the 37th European Conference and Exposition on Optical Communications, Geneva, Switzerland, 18–22 September 2011. paper Th-12.B.3. [Google Scholar] [CrossRef]
- Ali, A.A.I.; Costa, C.S.; Al-Khateeb, M.A.Z.; Ferreira, F.M.; Ellis, A.D. An expression for nonlinear noise in optical phase conjugation systems with lumped amplifiers. IEEE Photonics Technol. Lett. 2018, 30, 2056–2059. [Google Scholar] [CrossRef]
- Doran, D.; Ellis, A. Optical link design for minimum power consumption and maximum capacity. In Proceedings of the 39th European Conference and Exhibition on Optical Communication (ECOC 2013), London, UK, 22–26 September 2013. [Google Scholar] [CrossRef][Green Version]
- Jansen, S.; van den Borne, D.; Krummrich, P.M.; Spalter, S.; Khoe, G.-D.; de Waardt, H. Long-haul DWDM transmission systems employing optical phase conjugation. IEEE J. Sel. Topics Quantum Electron. 2006, 12, 505–520. [Google Scholar] [CrossRef]
- Ellis, A.D.; Tan, M.; Iqbal, M.A.; Al-Khateeb, M.A.Z.; Gordienko, V.; Mondaca, G.S.; Fabbri, S.; Stephens, M.F.C.; McCarthy, M.E.; Perentos, A.; et al. 4 Tb/s transmission reach enhancement using 10400 Gb/s super-channels and polarization insensitive dual band optical phase conjugation. J. Light. Technol. 2016, 34, 1717–1723. [Google Scholar] [CrossRef]
- Solis-Trapala, K.; Inoue, T.; Namiki, S. Nearly-ideal optical phase conjugation based nonlinear compensation system. In Proceedings of the Optical Fiber Communication Conference 2014, San Francisco, CA, USA, 9–14 March 2014. paper W3F.8. [Google Scholar] [CrossRef]
- Minzioni, P.; Schiffini, A. Unifying theory of compensation techniques for intrachannel nonlinear effects. Opt. Express 2005, 13, 8460–8468. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.-P.; Lee, S.-R. Symmetric-type dispersion maps in dispersion-managed optical link with mid-span spectral inversion. Indones. J. Electri. Eng. Comput. Sci. 2020, 20, 222–230. [Google Scholar] [CrossRef]
- Chung, J.-P.; Lee, S.-R. Dispersion-managed link configured with repetitively shaped dispersion maps and embedded with mid-span spectral inversion. J. Inf. Commun. Converg. Eng. 2022, 20, 235–241. [Google Scholar] [CrossRef]
- Chung, J.-P.; Lee, S.-R. MSSI-based dispersion-managed link configured by randomly-distributed RDPS only in former half section. Appl. Sci. 2022, 12, 8970. [Google Scholar] [CrossRef]
- Killey, R.I.; Thiele, H.J.; Mikhailov, V.; Bayvel, P. Reduction of intrachannel nonlinear distortion in 40-Gb/s-based WDM transmission over standard fiber. IEEE Photonics Technol. Lett. 2000, 12, 1624–1626. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 3rd ed.; Academic Press: San Francisco, CA, USA, 2001; pp. 44–55. [Google Scholar]
- Talukder, M.A.; Islam, M.N. Performance of bi-end compensation in a wavelength-division multiplexed system considering the effect of self phase modulation. Opt. Eng. 2005, 44, 115005. [Google Scholar] [CrossRef]
- Kikuchi, N.; Sasaki, S. Analytical evaluation technique of self-phase modulation effect on the performance of cascaded optical amplifier systems. J. Light. Technol. 1995, 13, 868–878. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).