Intelligent Diagnosis of Bearing Failures Based on Recurrence Quantification and Energy Difference
Abstract
1. Introduction
2. Methodology
2.1. Characteristic Frequencies of Rolling Bearing
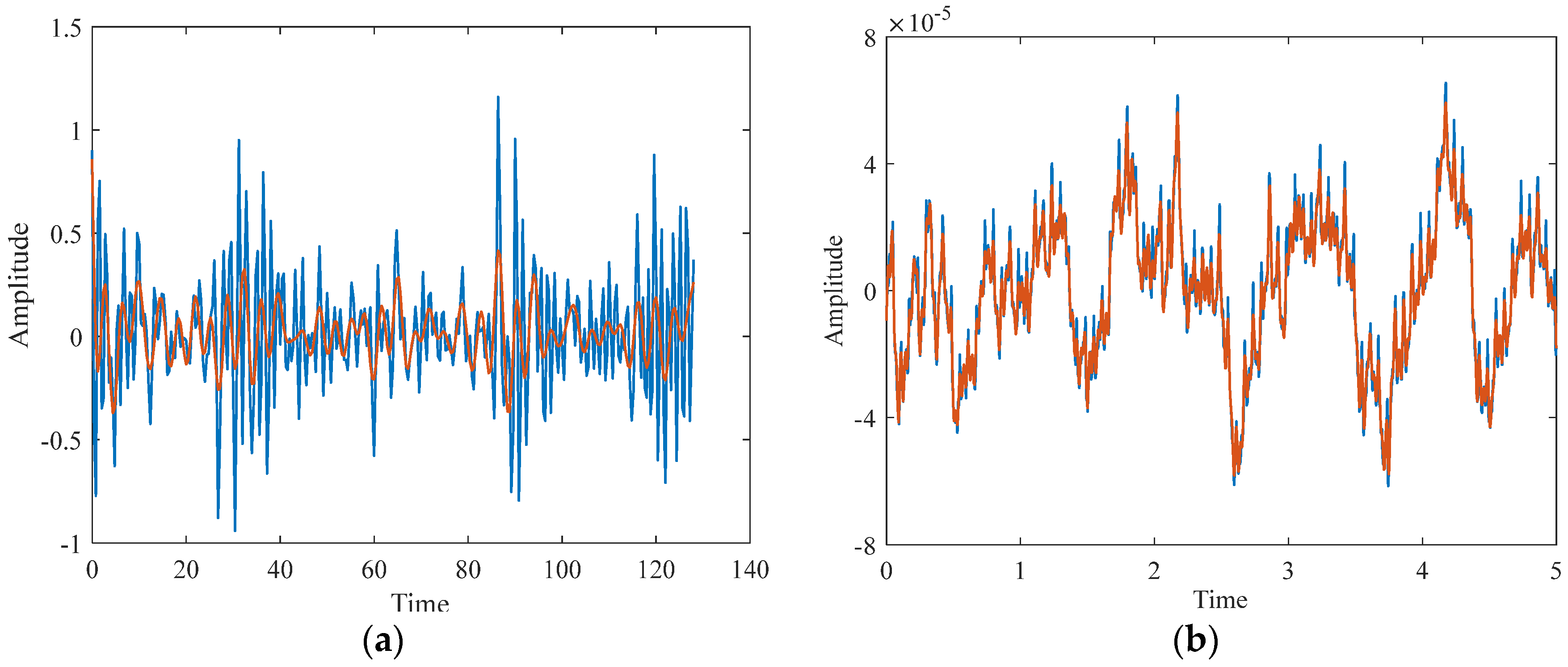
2.2. Hilbert Transformation
2.3. Low-Pass Filtering and Band-Stop Filtering
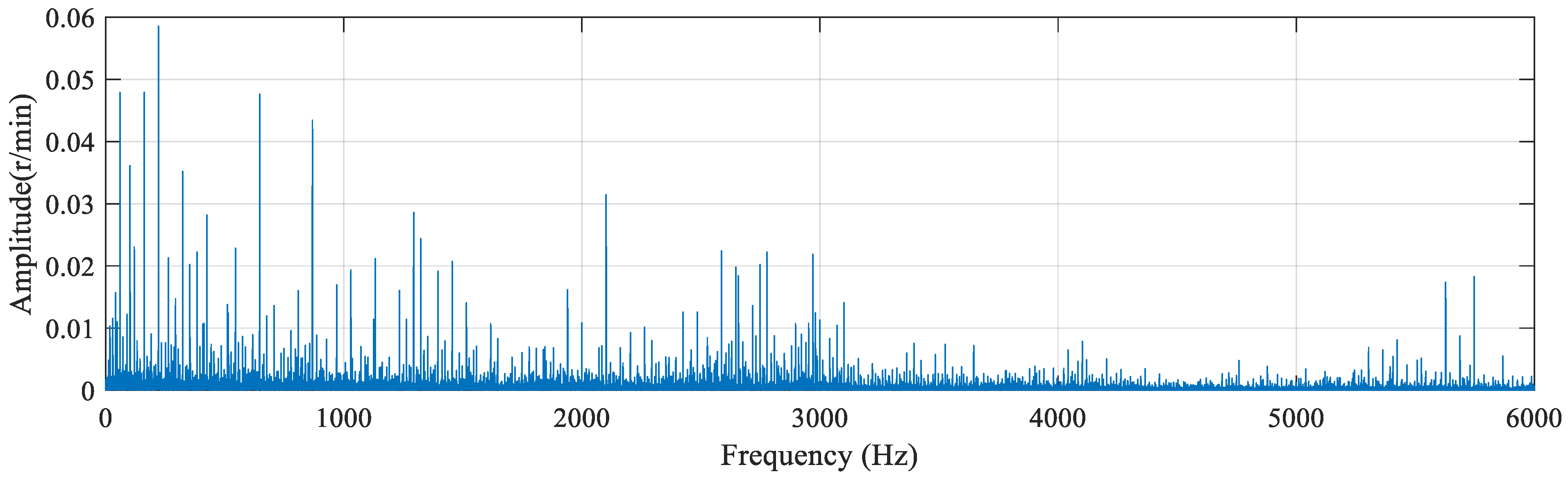
2.4. Power Spectral Density Analysis
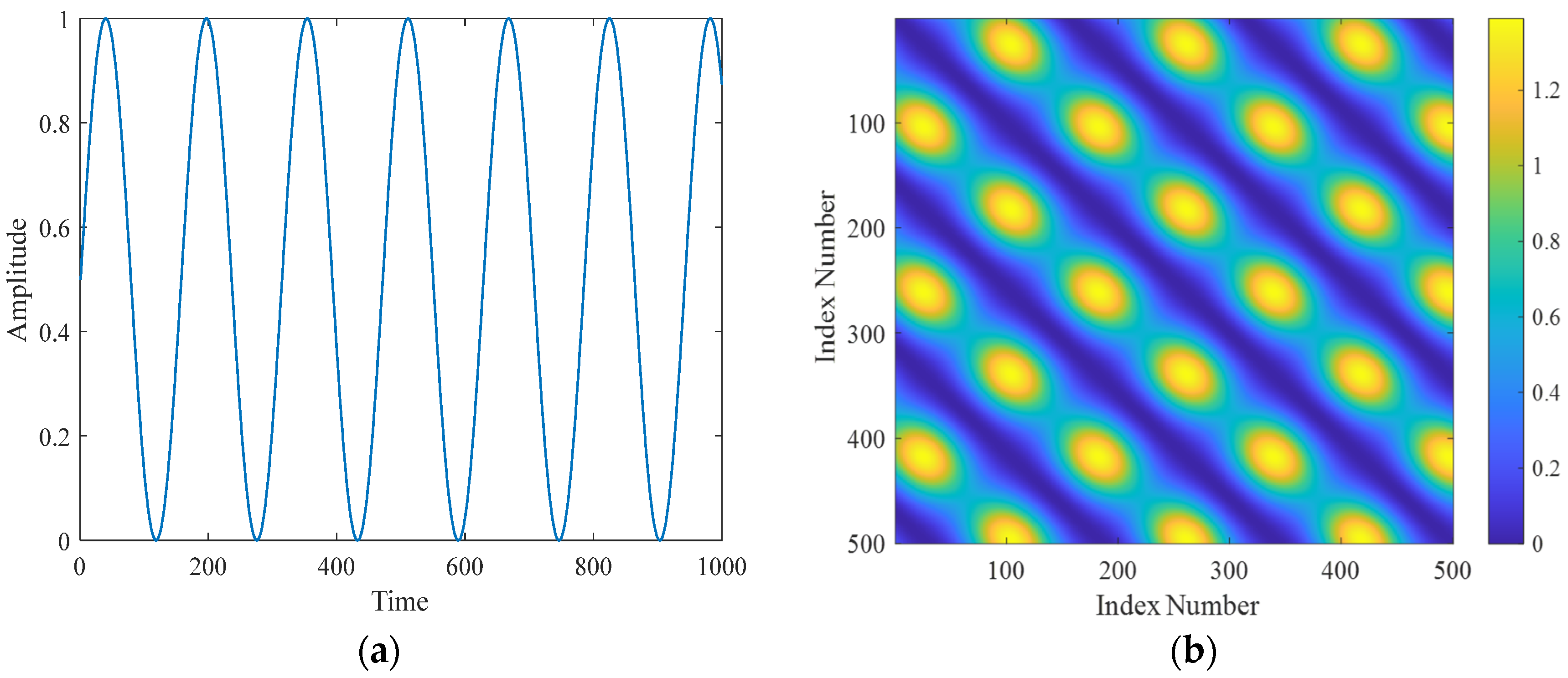
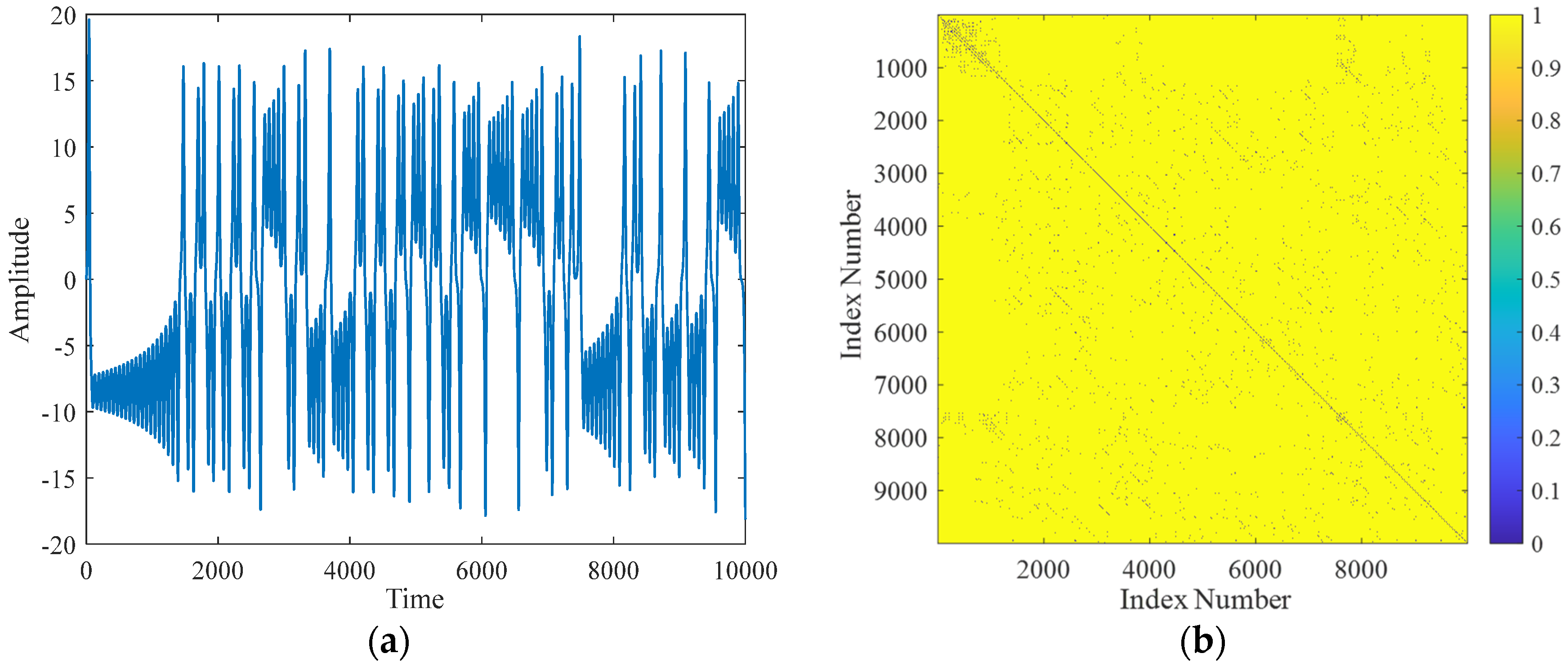
2.5. Recurrence Plots with the RQA Method
- (1)
- Assuming the initial signal is , it is reconstructed as .
- (2)
- A suitable recurrence threshold and critical distance are determined to facilitate the subsequent matrix calculations.
- (3)
- The recurrence matrix is computed according to the specified equations.
- (4)
- Based on the principles of recurrence plot construction, each point in the recurrence matrix is plotted along two axes to obtain the recurrence plot of the studied signal. Recurrence plots for the sine and Lorenz signals were generated using programming methods [16], as depicted in Figure 2 and Figure 3.
3. Experimental Implementation
3.1. Datasets
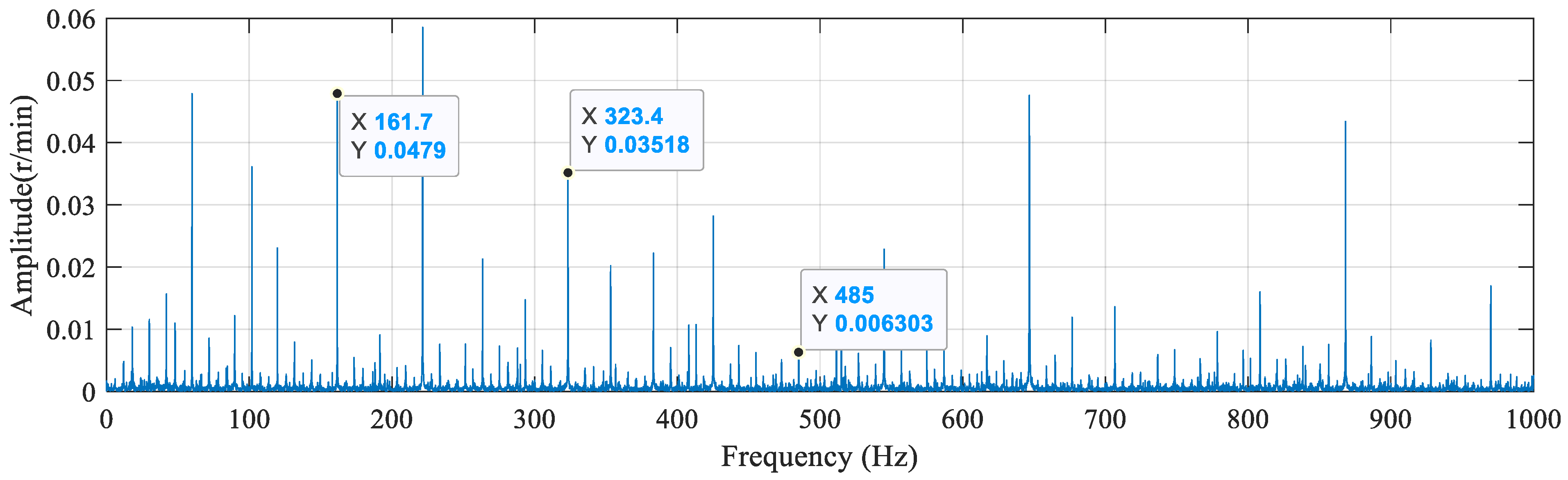
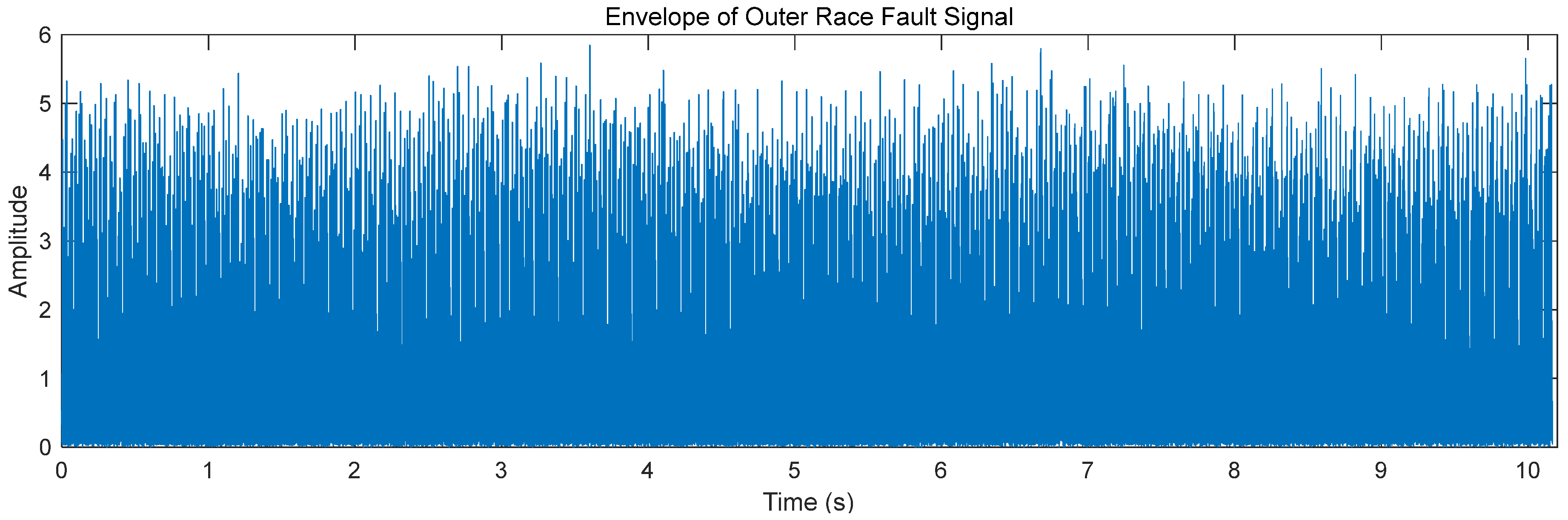
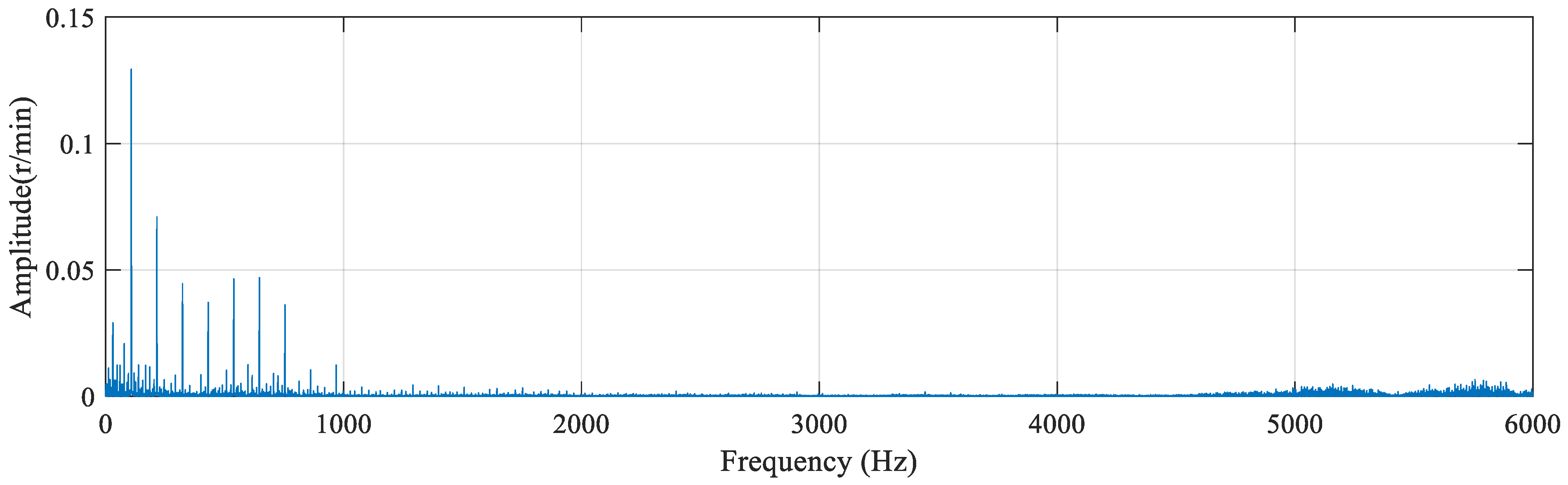
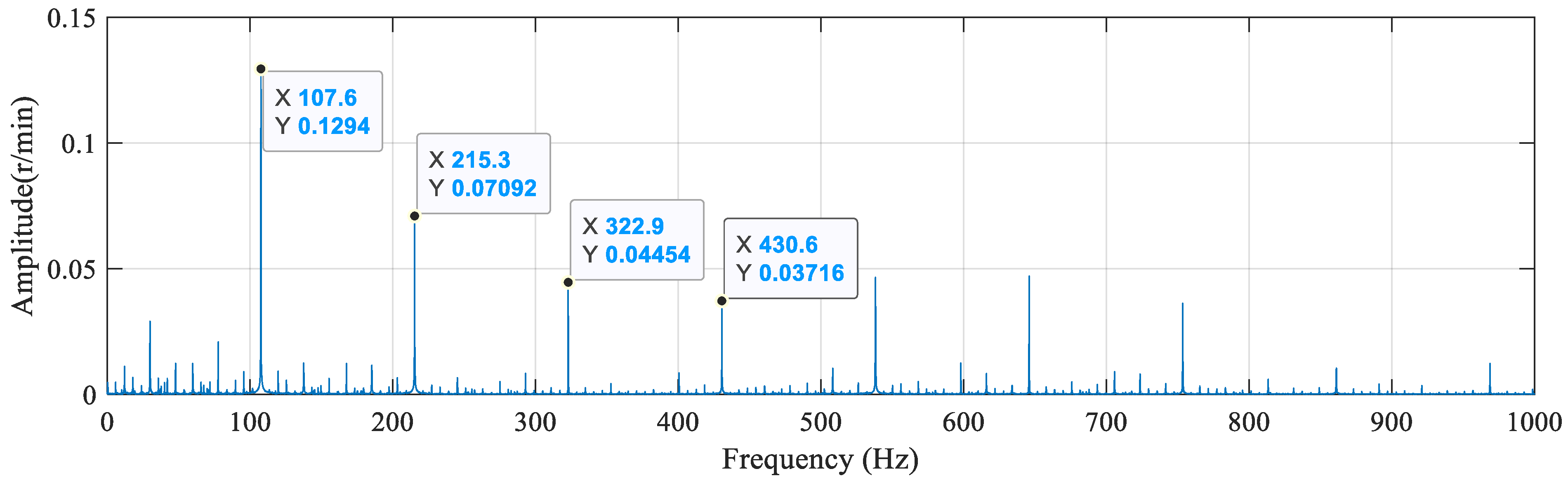
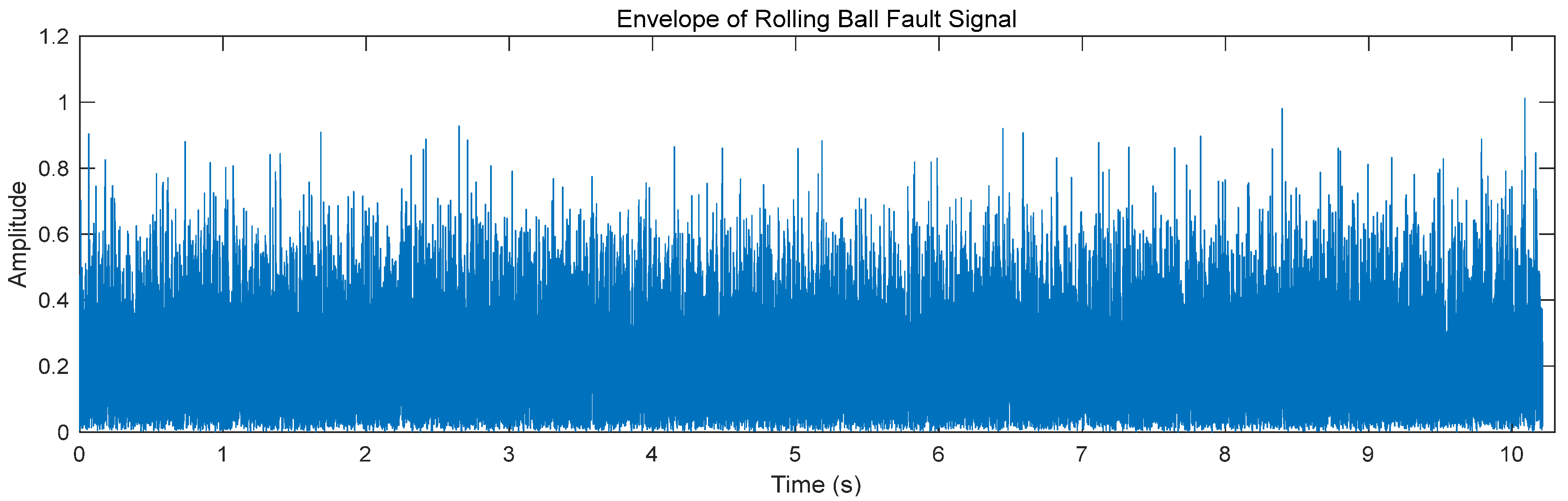
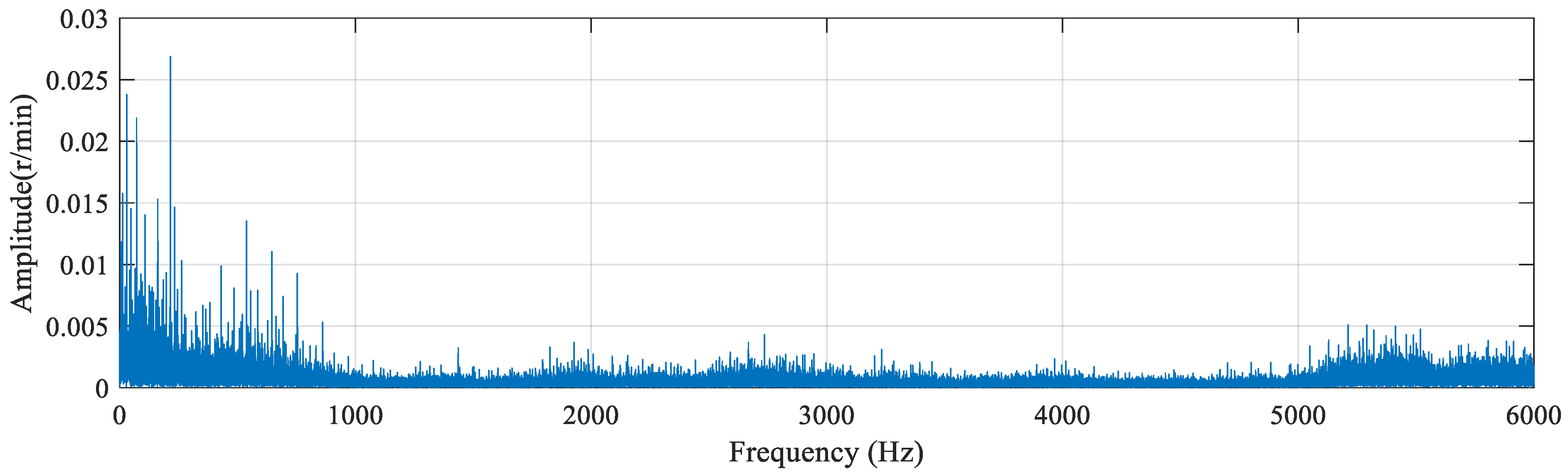
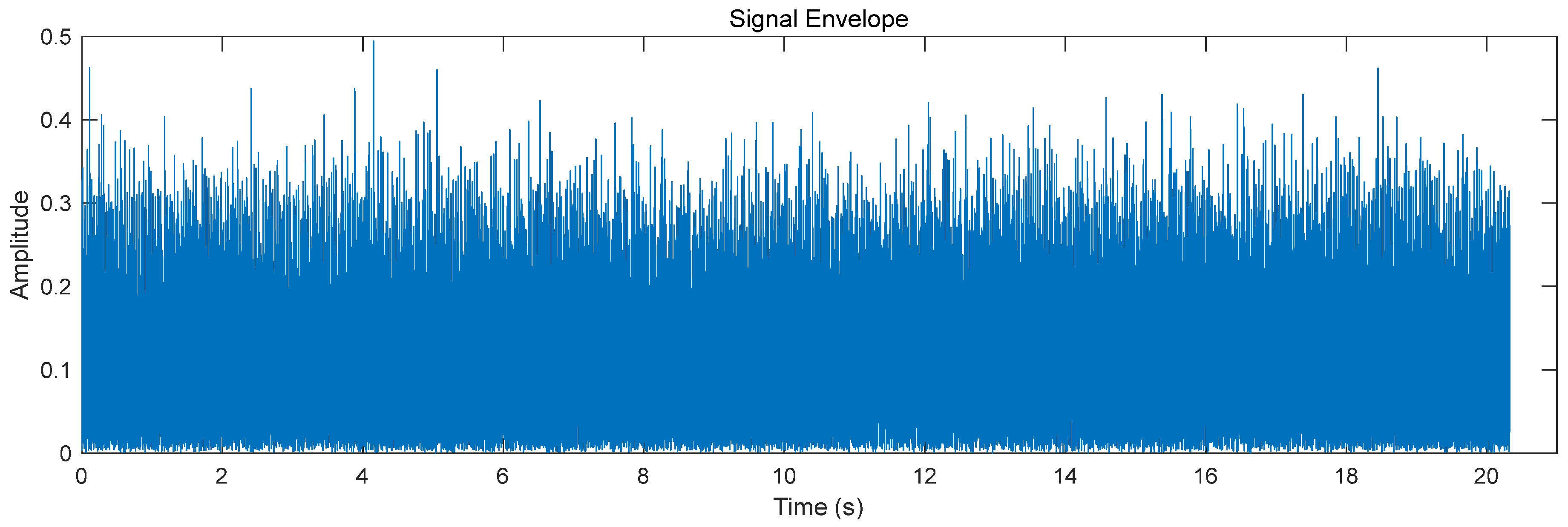
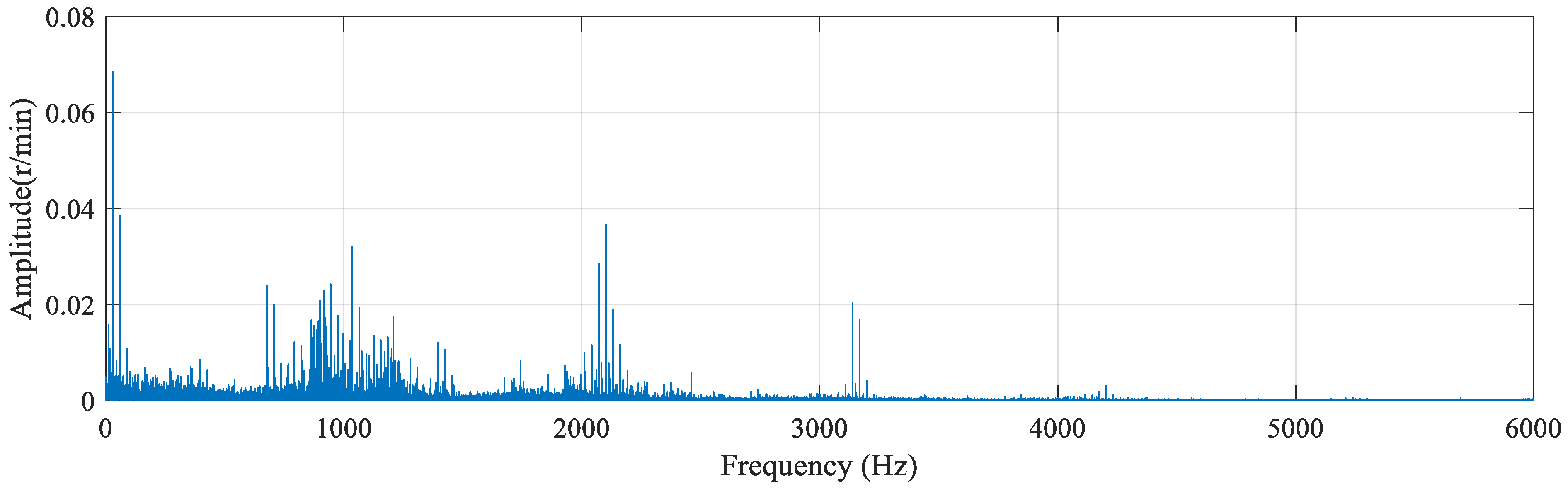
3.2. Hilbert Envelope Analysis
3.3. Extraction of Data Energy Features
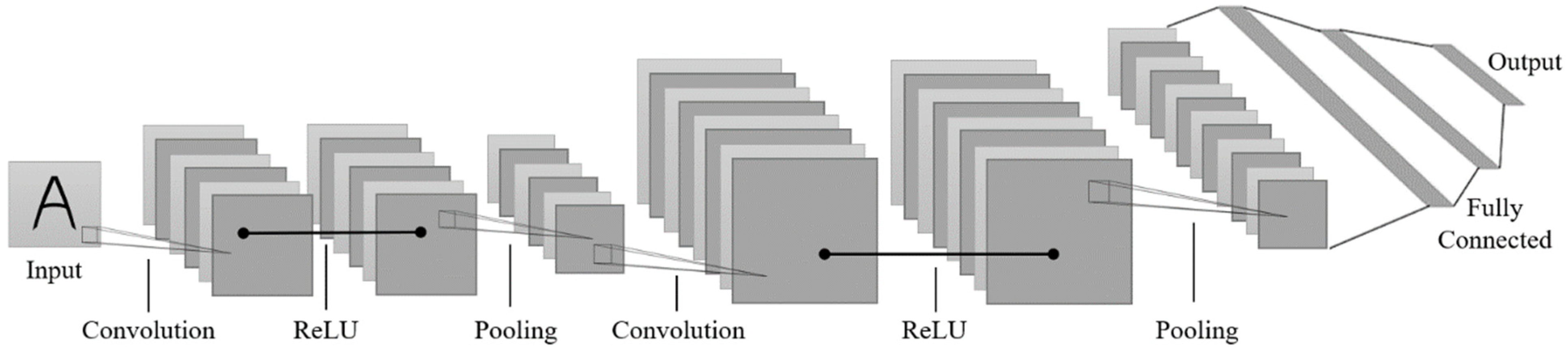
3.4. Convolutional Neural Network Architecture
3.4.1. Convolutional Layer
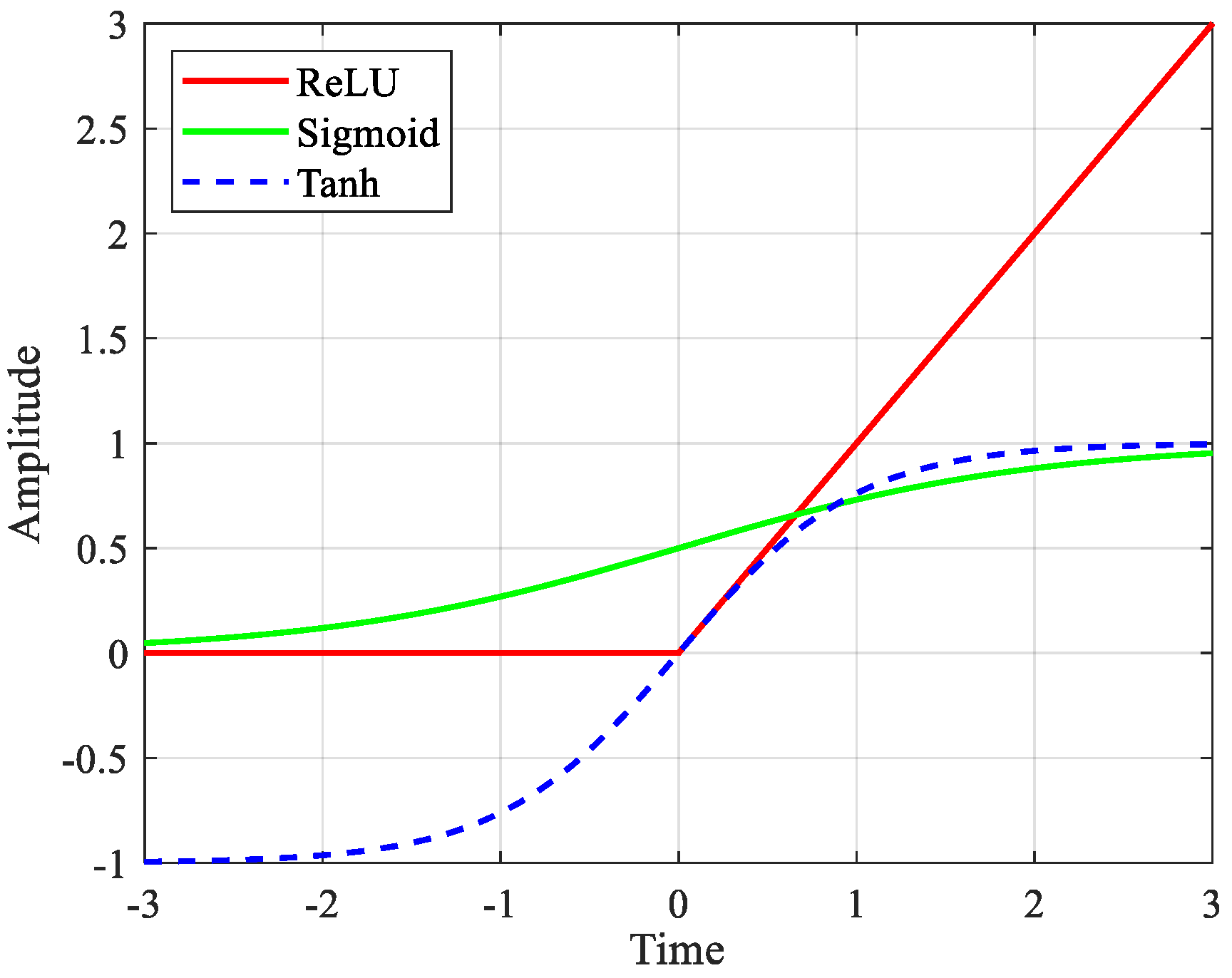
3.4.2. Activation Layer
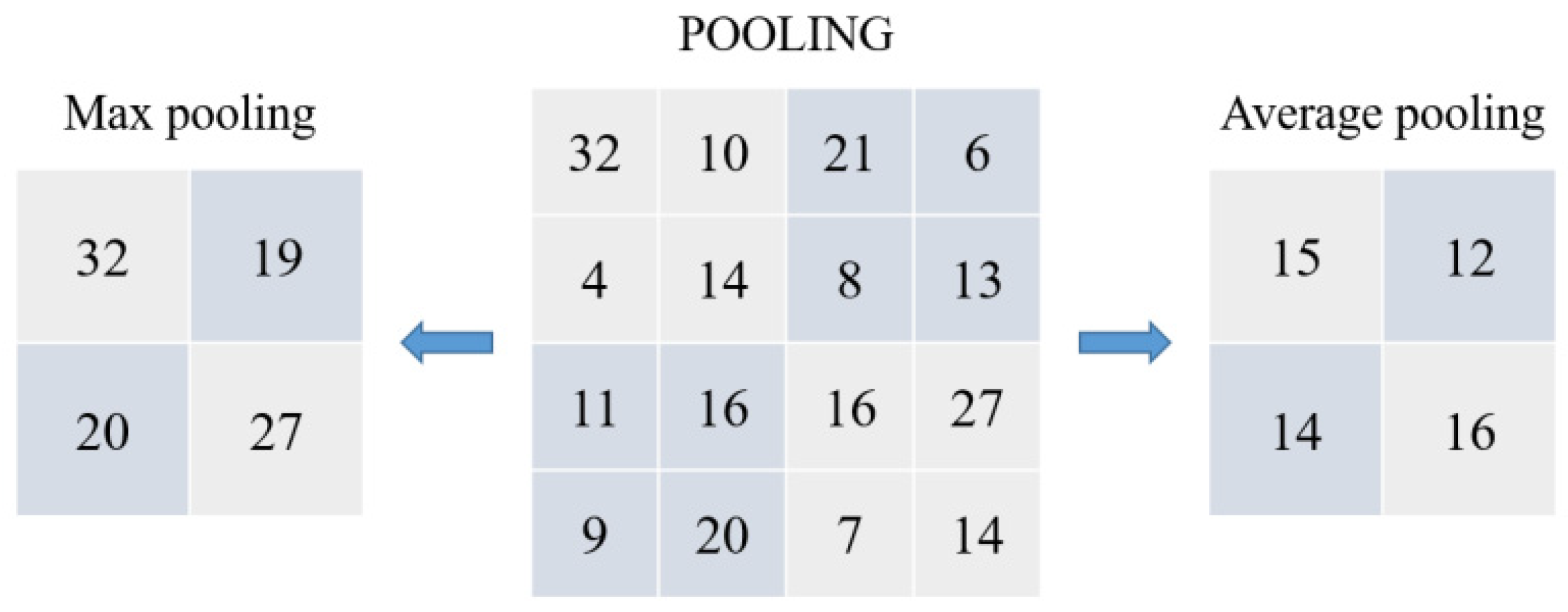
3.4.3. Pooling Layer
3.4.4. Full Connectivity Layer
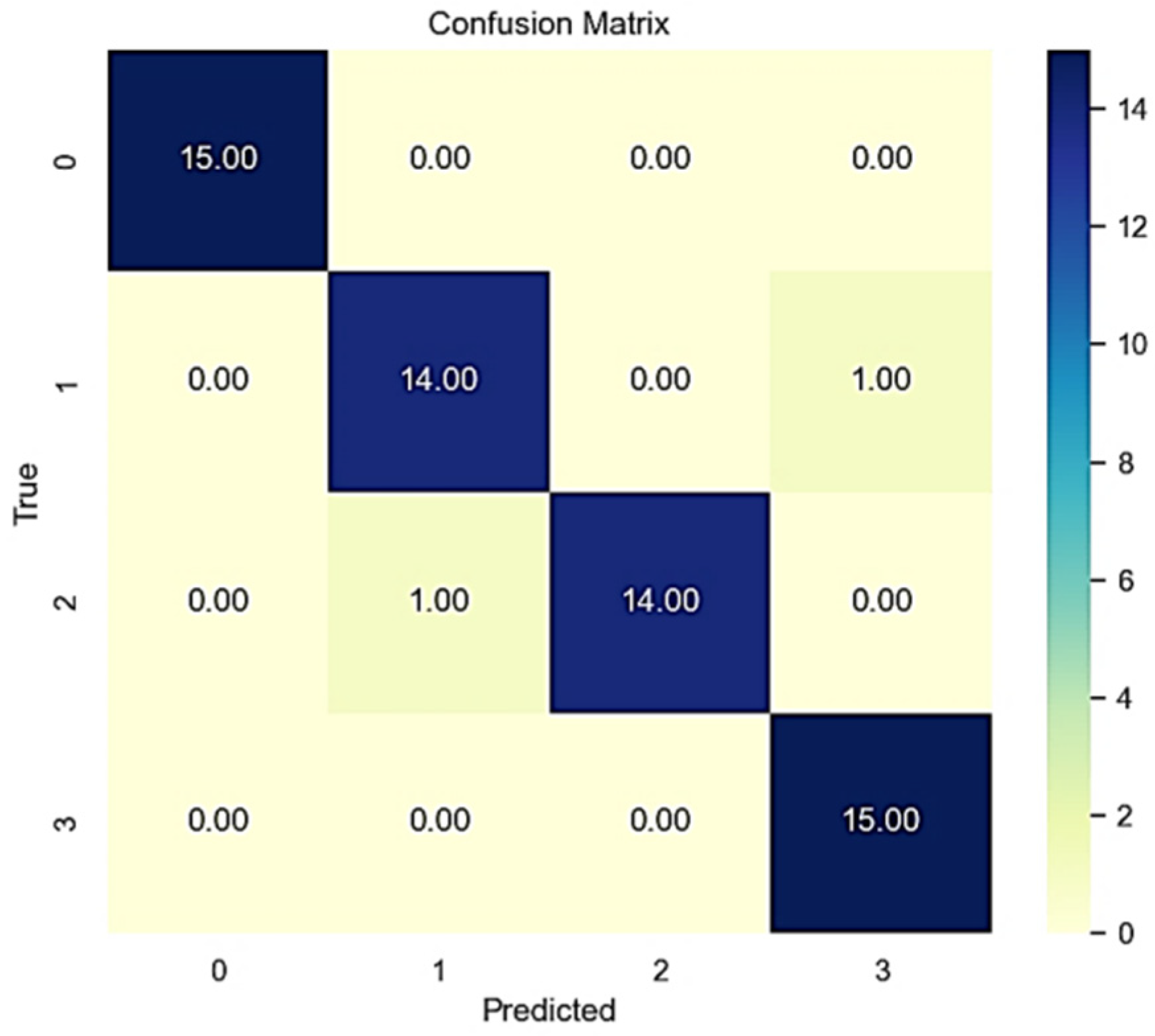
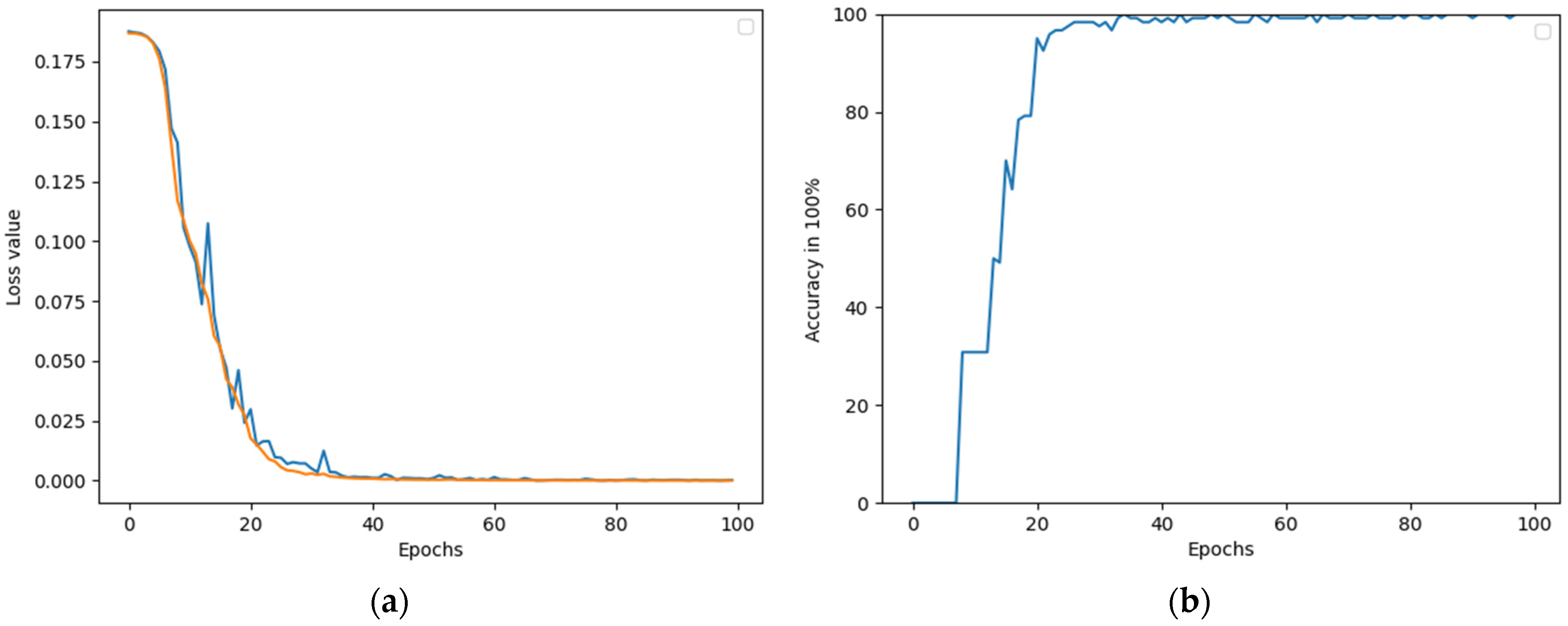
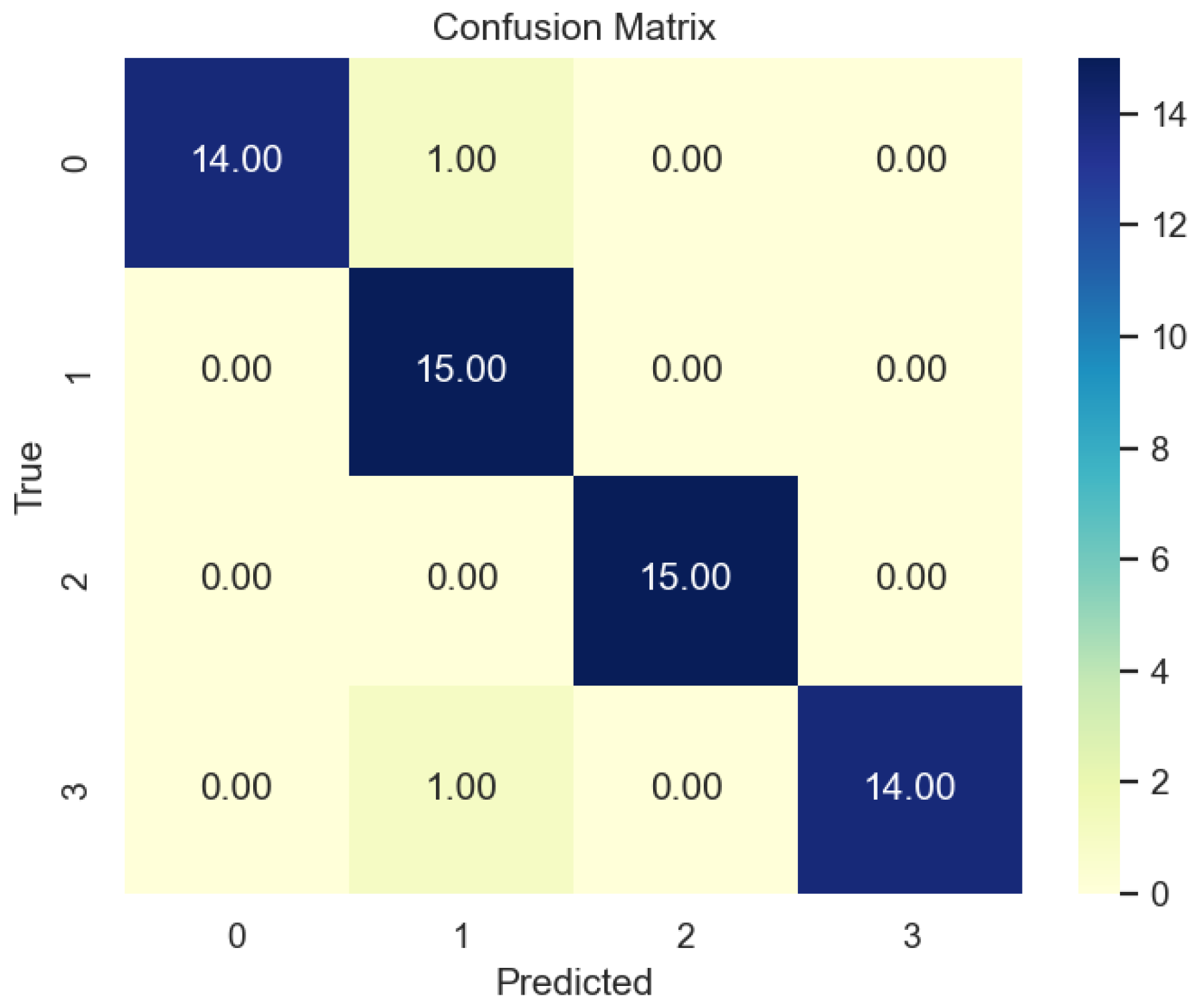
3.5. Analysis of the Results of Data Energy Features
3.6. Analysis of the Results of Data Recurrence Features
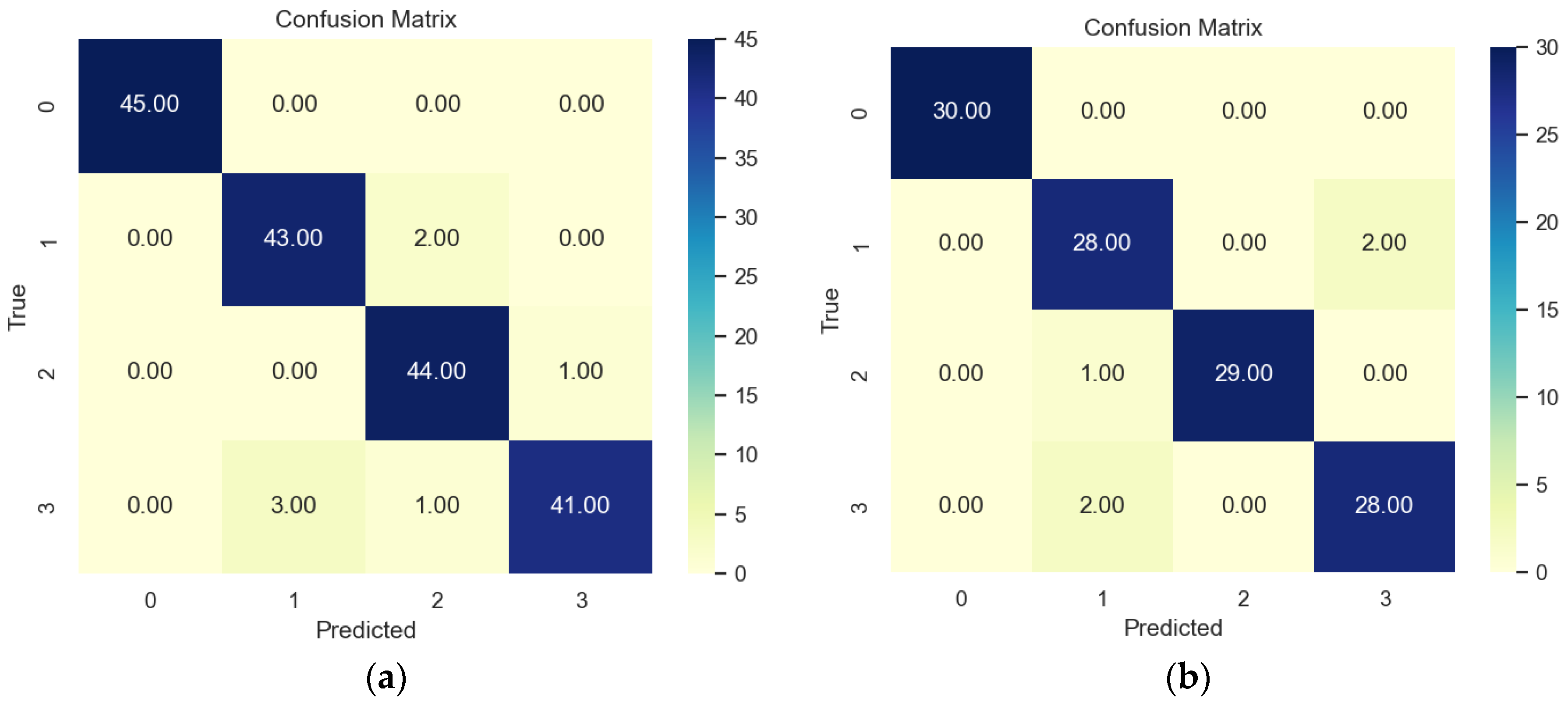
4. Model Comparison
5. Conclusions
- (1)
- Recurrence quantity spectrums were defined to obtain a comprehensive dataset with enhanced features.
- (2)
- A machine learning framework based on a convolutional neural network (CNN) was constructed. The activation functions in the activation layer were optimized for better fault diagnosis. The feature matrices were specifically defined to identify the subtlest defects of bearings accurately.
- (3)
- Comparisons of energies, recurrence quantification, and amplitude–frequency characteristics for bearing fault detection were conducted to assess the accuracy, computational efficiency, and robustness.
- (4)
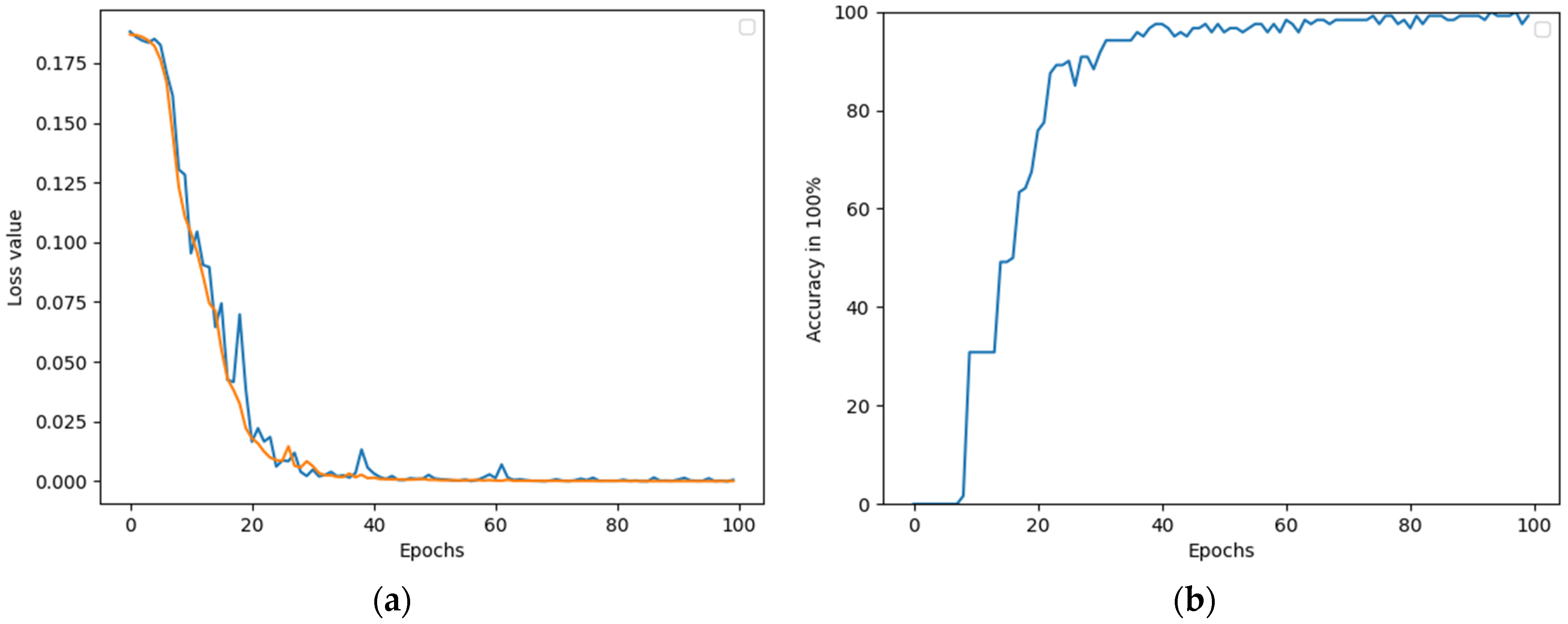
- Through the delineation of training and testing sets, an accuracy over 98% was obtained, accompanied by improved generalization ability and robustness.
- (5)
- This research developed a more efficient fault detection procedure and algorithms, which can serve as a universal model for practical bearing fault diagnosis in engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| n | Rotational speed of the rolling bearing |
| Z | Number of rolling elements in the bearing |
| d | Diameter of each individual rolling element, mm |
| D | Diameter of the pitch circle on which the centers of the rolling elements lie, mm |
| α | Contact angle between the rolling elements and the raceway |
| Ri,j | An N × N square matrix used in recurrence analysis |
| N | Dimension of the state space or the number of elements in the state vector |
| ε | A predefined threshold value used to determine the closeness of two states in phase space |
| H (·) | Heaviside step function |
| ||·|| | A norm, a function that assigns a strictly positive length or size to each vector in a vector space |
| Lout | Input size, the size of the convolution kernel |
| Lin | Length of the input feature map |
| K | Size of the convolution kernel |
| S | Stride |
| xk+1 | Current neuron output result |
| Wk | Connection weight |
| bk | Size of the bias value |
References
- Yang, C. Research on Intelligent Diagnosis Methods of Mechanical Faults Based on Uncertainty Theory; University of Science and Technology of China: Hefei, China, 2009; pp. 65–75, (In Chinese with English Abstract). [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Zhang, W. Research on Bearing Fault Diagnosis Algorithm Based on Convolutional Neural Network; Harbin Institute of Technology: Harbin, China, 2017; pp. 30–55, (In Chinese with English Abstract). [Google Scholar]
- Li, S.; Liu, G.; Tang, X.; Lu, J.; Hu, J. An Ensemble Deep Convolutional Neural Network Model with Improved D-S Evidence Fusion for Bearing Fault Diagnosis. Sensors 2017, 17, 1729. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.H.; Han, T.; Tang, J.; An, L.Z. Intelligent fault diagnosis method for rolling bearings based on wavelet time-frequency map and CNN. J. Mach. Des. Res. 2017, 33, 93–97, (In Chinese with English Abstract). [Google Scholar]
- Qu, J.; Yu, L.; Yuan, T.; Tian, Y.; Gao, F. Adaptive fault diagnosis algorithm for rolling bearings based on one-dimensional convolutional neural network. Chin. J. Sci. Instrum. 2018, 39, 134–143, (In Chinese with English Abstract). [Google Scholar]
- Xiao, X.; Wang, J.; Zhang, Y.; Guo, Q.; Zong, S. An optimized two-dimensional convolutional neural network method for bearing fault diagnosis. Proc. CSEE 2019, 39, 4558–4568, (In Chinese with English Abstract). [Google Scholar]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, Y. A fault diagnosis method for rotating machinery based on CNN with mixed information. IEEE Trans. Ind. Inform. 2023, 19, 9091–9101. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, Y.; Zhang, X. A fault diagnosis method of rotor system based on parallel convolutional neural network architecture with attention mechanism. J. Signal Process. Syst. 2023, 95, 965–977. [Google Scholar] [CrossRef]
- Firouzi, N.; Dohnal, F. Dynamic stability of the Mindlin-Reissner plate using a time-modulated axial force. Mech. Based Des. Struct. Mach. 2024, 1–18. [Google Scholar] [CrossRef]
- Li, M.; Ma, W.; Liu, X. Investigation of Rolling Bearing Fault Diagnosis Based on Multi-Fractal and General Fractal Dimension. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Andrade, M.A.; Messina, A.R.; Rivera, C.A.; Olguin, D. Identification of Instantaneous Attributes of Torsional Shaft Signals Using the Hilbert Transform. IEEE Trans. Power Syst. 2004, 19, 1422–1429. [Google Scholar] [CrossRef]
- Freeman, W.J.; Zhai, J. Simulated power spectral density (PSD) of background electrocorticogram (ECoG). Cogn. Neurodynamics 2009, 3, 97–103. [Google Scholar] [CrossRef] [PubMed]
- Peluso, E.; Craciunescu, T.; Murari, A. A Refinement of Recurrence Analysis to Determine the Time Delay of Causality in Presence of External Perturbations. Entropy 2020, 22, 865. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Xu, Y.; Wang, T. Intelligent classification of the abnormal features through time-delayed reconstruction of phase states. J. Appl. Nonlinear Dyn. 2024, 6–10. [Google Scholar]
- Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 25 August 2024).
- Zhu, Z. Research on Domain Adaptive Algorithms for Mechanical Fault Diagnosis Based on Convolutional Neural Networks; Harbin Institute of Technology: Harbin, China, 2020; pp. 10–20, (In Chinese with English Abstract). [Google Scholar]
- Zhang, H.; Zhang, Q.; Yu, J. Review of the development of activation functions and analysis of their properties. J. Xihua Univ. 2021, 40, 1–10. [Google Scholar]




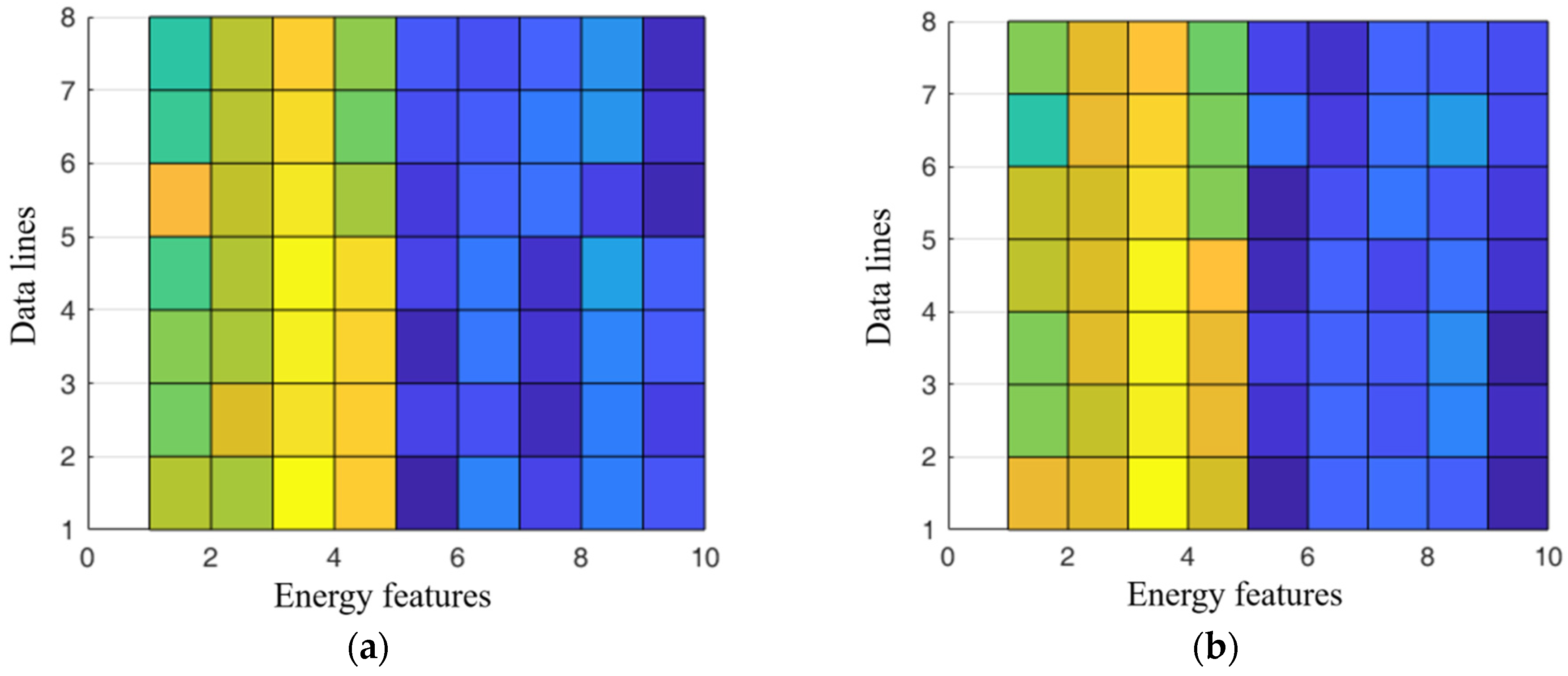
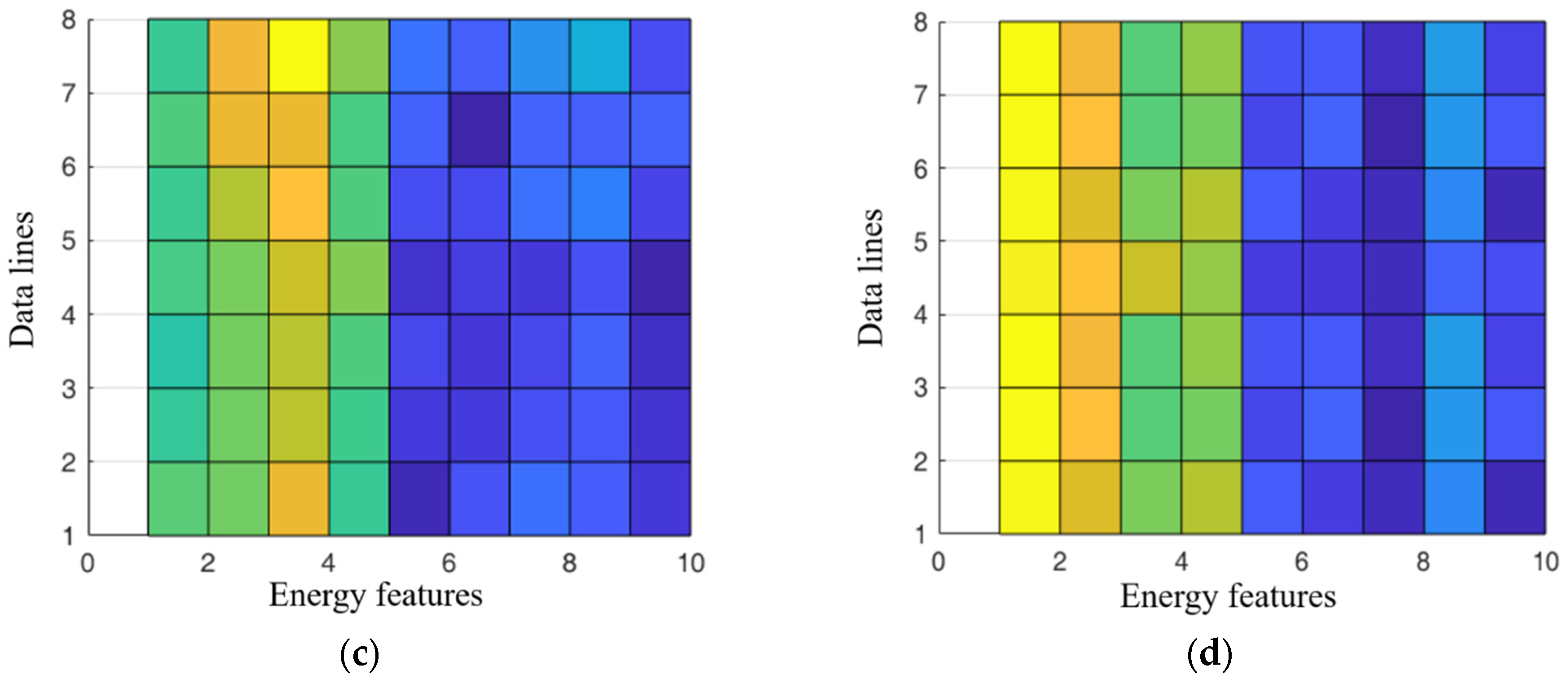


| Mechanical Motions | Frequencies |
|---|---|
| Rotation frequency of inner race | |
| Slewing frequency of outer race | |
| Relative rotation frequency of inner and outer races | |
| Inner race fault | |
| Outer race fault | |
| Rolling element failure frequency | |
| Cage failure frequency |
| PSD | PSD1 | PSD2 | PSD3 | PSD4 | Difference1 | Difference2 | Difference3 | Difference4 | Difference5 | Difference6 |
|---|---|---|---|---|---|---|---|---|---|---|
| Channel1 | 0.46797891 | 0.43254647 | 0.57853334 | 0.53355775 | 0.03543243 | 0.14598686 | 0.04497558 | 0.11055443 | 0.10101128 | 0.06557885 |
| Channel2 | 0.37865839 | 0.44737680 | 0.57607983 | 0.52894089 | 0.06871841 | 0.12870303 | 0.04713894 | 0.19742144 | 0.08156409 | 0.15028250 |
| Channel3 | 0.41025924 | 0.46283475 | 0.57174661 | 0.52734527 | 0.05257551 | 0.10891185 | 0.04440133 | 0.16148736 | 0.06451052 | 0.11708603 |
| Channel4 | 0.43215609 | 0.43742075 | 0.60494556 | 0.54830006 | 0.00526466 | 0.16752481 | 0.05664550 | 0.17278947 | 0.11087931 | 0.11614397 |
| Channel5 | 0.49463017 | 0.49092525 | 0.56641170 | 0.43228196 | 0.00370492 | 0.07548644 | 0.13412974 | 0.07178152 | 0.05864329 | 0.06234821 |
| Channel6 | 0.34663556 | 0.43162422 | 0.53340069 | 0.38812957 | 0.08498866 | 0.10177648 | 0.14527113 | 0.18676514 | 0.04349465 | 0.04149401 |
| Channel7 | 0.39908428 | 0.45614893 | 0.52513471 | 0.42520456 | 0.05706465 | 0.06898578 | 0.09993014 | 0.12605043 | 0.03094436 | 0.02612028 |
| Channel8 | 0.33629645 | 0.41131140 | 0.54140532 | 0.44243298 | 0.07501495 | 0.13009392 | 0.09897234 | 0.20510887 | 0.03112158 | 0.10613653 |
| Function Name | Equations |
|---|---|
| Sigmoid function | |
| Tanh function | |
| ReLU function |
| Layer Name | Type | Input Size | Kernel Size | Stride | Padding | Output Channels | Output Size | Activation Function |
|---|---|---|---|---|---|---|---|---|
| input | Input | 8 × 11 × 1 | - | - | - | - | 8 × 11 × 1 | - |
| conv1 | Convolutional | 8 × 11 × 1 | 3 × 3 | 1 | 1 | 6 | 6 × 9 × 10 | ReLU |
| pool1 | Pooling | 6 × 9 × 10 | 2 × 2 | 2 | 0 | - | 3 × 5 × 6 | - |
| conv2 | Convolutional | 3 × 5 × 6 | 3 × 3 | 1 | 1 | 12 | 3 × 3 × 12 | ReLU |
| pool2 | Pooling | 3 × 3 × 12 | 2 × 2 | 2 | 0 | - | 1 × 2 × 12 | - |
| conv3 | Convolutional | 1 × 2 × 12 | 3 × 3 | 1 | 1 | 24 | 1 × 1 × 24 | ReLU |
| flatten | Flatten | 1 × 1 × 24 | - | - | - | - | 96 | - |
| fc1 | Fully Connected | 96 | - | - | - | 4 | 4 | Softmax |
| Accuracy | Energy Model | Recurrence Rate Model |
|---|---|---|
| Group 1 | 96.667% | 96.667% |
| Group 2 | 96.111% | 97.778% |
| Group 3 | 95.833% | 97.500% |
| Group 4 | 97.619% | 99.048% |
| Average | 96.557% | 97.748% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Wang, T.; Lu, D.; Cui, S. Intelligent Diagnosis of Bearing Failures Based on Recurrence Quantification and Energy Difference. Appl. Sci. 2024, 14, 9643. https://doi.org/10.3390/app14219643
Wang M, Wang T, Lu D, Cui S. Intelligent Diagnosis of Bearing Failures Based on Recurrence Quantification and Energy Difference. Applied Sciences. 2024; 14(21):9643. https://doi.org/10.3390/app14219643
Chicago/Turabian StyleWang, Mukai, Tianfeng Wang, Duhui Lu, and Shuhui Cui. 2024. "Intelligent Diagnosis of Bearing Failures Based on Recurrence Quantification and Energy Difference" Applied Sciences 14, no. 21: 9643. https://doi.org/10.3390/app14219643
APA StyleWang, M., Wang, T., Lu, D., & Cui, S. (2024). Intelligent Diagnosis of Bearing Failures Based on Recurrence Quantification and Energy Difference. Applied Sciences, 14(21), 9643. https://doi.org/10.3390/app14219643





