Advancements in Technologies and Methodologies of Machine Learning in Landslide Susceptibility Research: Current Trends and Future Directions

Abstract

Landslides are pervasive geological hazards that pose significant risks to human life, property, and the environment. Understanding landslide susceptibility is crucial for predicting and mitigating these disasters. This article advocates for a comprehensive review by systematically compiling and analyzing 146 relevant studies up to 2024. It assesses current progress and limitations and offers guidance for future research. This paper provides a comprehensive overview of the diverse challenges encountered by machine learning models in landslide susceptibility assessment, encompassing aspects such as model selection, the formulation of evaluation index systems, model interpretability, and spatial heterogeneity. The construction of an evaluation index system, which serves as the foundational data for the model, profoundly influences its accuracy. This study extensively investigates the selection of evaluation factors and the identification of positive and negative samples, proposing valuable methodologies. Furthermore, this paper briefly deliberates and compares classical machine learning models, offering valuable insights for model selection. Additionally, it delves into discussions concerning model interpretability and spatial heterogeneity issues. These research findings promise to enhance the precision of landslide susceptibility assessments and furnish effective strategies for risk management.

1. Introduction

Landslides are one of the most common geological disasters and are characterized by their diverse types, large scale, frequent occurrences, and widespread distribution. These disasters significantly impact human production, livelihoods, and economic development [1]. With the development of the economy and increasing human activities disturbing the natural environment, geological disasters are occurring more frequently. According to data from the World Bank, approximately 3.7 million square kilometers of inland areas on Earth are prone to landslides. This poses a significant threat to the lives and property security of people in disaster-prone areas. People are also becoming increasingly aware of the importance of disaster assessment and prevention [2]. Therefore, there is an urgent need for an effective means of reducing the disasters caused by landslides. Currently, the most effective method believed to reduce landslide risk is through the reliable detection, assessment, and identification of landslide-prone areas [3]. In this context, landslide susceptibility assessment has become a necessary means to reduce disasters [4]. Significant progress has been made in landslide susceptibility research, both domestically and internationally. Researchers employ a diverse range of data sources, such as remote sensing images, geological survey data, meteorological data, and topographical data, to create multi-dimensional assessment models for evaluating landslide susceptibility. These frameworks typically consider factors such as terrain slope, geological structure, soil type, vegetation cover, rainfall, and human activities. By comprehensively analyzing these factors, researchers can assess the potential risk of landslides, providing a scientific basis for disaster prevention. Landslide susceptibility assessment can provide valuable insights regarding various aspects such as regional landslide disaster management, community-based monitoring, and prevention, as well as urban planning and construction. Therefore, such assessments demonstrate significant value [5].

Landslide susceptibility assessment aims to evaluate the spatial probability of landslide occurrence in a given area, with the goal of predicting high-risk zones where landslides may occur under specified environmental conditions [6]. Landslide susceptibility assessment focuses on identifying potential locations where landslides may occur in the future in a target area, without considering when or how frequently they may occur. Data-driven methods, including machine learning algorithms, are often used to calculate landslide susceptibility, which refers to the “likelihood of landslides occurring in a given area”. Research on landslide susceptibility assessment began in the early 1970s. In 1972, Brabb et al. [7] produced a landslide susceptibility map of San Mateo County, California, USA. During this period, landslide susceptibility assessment primarily relied on expert experience and subjective judgment for qualitative evaluation. Following this initial research, the concept of landslide susceptibility assessment emerged and gained widespread attention [8]. Since the 1980s, with the deepening of evaluation theories and the improvement of technical methods, geological hazard assessment has evolved from its initial qualitative analysis to today’s quantitative analysis [9]. After the 1990s, with the development of GIS (geographic information systems) technology, the unique spatial data storage, spatial analysis capabilities, and visualization capabilities of GIS have provided novel means for landslide susceptibility assessment [10]. With the development of computer technology and statistics, machine learning methods have been applied to landslide susceptibility assessment. Due to the powerful nonlinear processing capabilities of machine learning, its application has become a current research hotspot. Recently, various machine learning methods have been applied to landslide susceptibility assessment, using techniques such as logistic regression, support vector machine (SVM), random forest (RF), artificial neural networks (ANN), and deep neural networks (DNN), to improve the accuracy of predictions [11,12]. Huang et al. [13] compared the performance of heuristic models, mathematical statistical models, and machine learning models in landslide susceptibility assessment. The results showed that machine learning models have higher accuracy. According to the “2020 Research Fronts” report, using machine learning methods to study landslide susceptibility has been listed as one of the top ten research hotspots in the field of Earth Sciences [14].

Previous research has extensively reviewed landslide susceptibility assessments. Reichenbach et al. [15], through a statistical analysis of 565 papers from 1985 to 2016, found a growing inclination toward machine learning methods in landslide susceptibility assessments. The authors provided recommendations for study preparation, evaluation, and model usage based on the literature and existing experience. Pacheco et al. [16], by examining 536 papers from 2001 to 2020, recognized the impact of land use and land use changes on landslide susceptibility assessments. Merghadi et al. [17] summarized the machine learning models used for landslide susceptibility assessment and identified the latest trends. Their comprehensive study of the performance of machine learning models revealed that tree-based ensemble algorithms, particularly the random forest model, achieved superior results in accurate landslide susceptibility assessments. Chen et al. [18] reviewed common methods for landslide inventory, evaluation indices, evaluation units, models, and verification techniques, detailing their advantages and disadvantages, and identified the current shortcomings in each area. They also discussed the research challenges in terms of spatial scale, qualitative and quantitative issues, and the spatial representation of landslide information. Compared to existing studies, this paper delves deeper into uncertainties in the machine learning model selection process for landslide susceptibility assessment. Specifically, we focus on how to choose appropriate machine learning models and evaluation factors to enhance prediction accuracy. We also propose improved methods for selecting non-landslide points to address the reliability issues caused by random selection. Additionally, our research pays special attention to the interpretability and transferability of machine learning models, aspects that have been less fully explored in other studies. By thoroughly examining the construction of evaluation indicator systems and addressing spatial heterogeneity, we provide new perspectives and directions for future research, aiming to tackle key challenges in applying machine learning to landslide susceptibility assessment. Overall, our study not only enriches the theoretical foundation of landslide susceptibility evaluation but also suggests a series of specific improvements and strategies to better address complex issues in practical applications, thereby offering more reliable and effective tools for landslide risk management.

The researchers employed “machine learning” and “landslide susceptibility assessment” as key search terms, leading to a comprehensive review of 146 related papers published up to 2024. These articles were meticulously gathered from reputable databases, specifically, the Web of Science (WOS) and the China National Knowledge Infrastructure (CNKI). Through a manual selection process, each paper was evaluated for its relevance and contribution to the field, ensuring a robust representation of recent advancements in the application of machine learning techniques for assessing landslide susceptibility. This method not only highlights the current trends in research but also facilitates a deeper understanding of the intersection between machine learning methodologies and geological assessments. Among these articles, 93 are from the period between 2020 and 2024, reflecting a concentrated effort to incorporate the latest advancements and innovations in the field of machine learning. This ensures that the research findings are based on the most current methodologies, technologies, and theoretical frameworks, which is crucial in the rapidly evolving area of machine learning. This time frame captures the latest trends, including new algorithms, data sources, and interdisciplinary approaches, thereby enhancing the relevance and applicability of the research. Furthermore, by analyzing the recent literature, this study can identify emerging challenges and opportunities in landslide susceptibility assessment, ensuring that the conclusions drawn herein are aligned with the current state of knowledge and practice in the field. This approach not only strengthens the validity of the research but also positions it so as to contribute meaningfully to ongoing discussions and future developments in the discipline.

This paper summarizes previous research findings to discuss the challenges and opportunities of applying machine learning to landslide susceptibility assessment, providing theoretical, technical, and methodological support for further studies. In Section 2, we discuss the construction of an evaluation indicator system, including the selection of mapping units and evaluation factors. Section 3 introduces typical machine learning models. Section 4 provides an in-depth analysis of the uncertainties when applying machine learning to landslide susceptibility assessment. Section 5 addresses the challenges encountered in the landslide susceptibility evaluation process and proposes solutions. Finally, Section 6 presents a comprehensive summary of the study.

2. Constructing the Evaluation Index System

A scientific and rational indicator system is a necessary prerequisite to ensure the accuracy and quality of landslide susceptibility assessment [19]. Constructing a landslide susceptibility indicator system primarily involves selecting mapping units, evaluation factors, and positive and negative samples. Since landslides result from the interplay of various factors, such as meteorological and hydrological conditions, geological conditions, human activities, and topography, it is crucial to choose appropriate mapping units and evaluation factors that are based on the characteristics of the study area.

2.1. Selection of Mapping Units

According to the summary by the Italian scholar Guzzetti, landslide susceptibility assessment units comprise five types [20]: raster units, slope units, terrain units, unique condition units, and sub-basin units. Among these five types, raster units and slope units are the most widely applied.

Raster units are regularly partitioned, ensuring that the area of each computational unit is the same. For regional landslide susceptibility assessment, the number of computational units is often large, making it suitable for evaluation models requiring large datasets. The advantages of raster units include regular shapes and simple and clear calculations, making them suitable for large-area landslide susceptibility assessment. The determination of raster size is based on the empirical formula proposed by scholars such as Li et al. [21]:

$${\mathrm{G}}_{\mathrm{s}}=7.49+0.0006\times \mathrm{S}-2.0\times {10}^{-9}{\mathrm{S}}^2+2.9\times {10}^{-15}\times {\mathrm{S}}^3$$

In the formula, ${\mathrm{G}}_{\mathrm{s}}$ represents the suggested size of raster units, and S represents the denominator of the scale of the study area.

The division of slope units is primarily based on the delineation of mapping units formed by ridgelines and valley lines in the study area. This enables the terrain undulations and hydrological characteristics of the study area to be represented effectively. Compared to raster units, slope units are much fewer in number, resulting in higher computational efficiency. Additionally, compared to raster units, slope units can reflect the physical relationship between landslides and basic terrain features a priori [22]. However, obtaining slope units is indeed a time-consuming and labor-intensive task, requiring collaboration between computers and manual efforts. Therefore, slope units are suitable for detailed landslide susceptibility assessments of small areas [19]. Slope units can effectively reflect the relationship between landslides and terrain features, greatly enhancing the efficiency of landslide susceptibility assessment. Common methods for extracting slope units include hydrological methods, r.slopeunits, and MSS (multi-scale slope selection) methods. These methods have significantly promoted the application of slope units in landslide susceptibility assessment [23,24,25].

Table 1. Literature on the selection and acquisition of mapping units.

Year	Author	Method
2022	Peng [19]	raster units
2003	Li et al. [21]	raster units
2023	Chang et al. [22]	slope units + MSS
2017	Alvioli [23]	slope units + r.slopeunits
2021	Huang et al. [24]	slope units + MSS
2015	Mergili et al. [25]	slope units + r.slopeunits

lists the mapping unit types and acquisition methods used in the relevant literature.

2.2. Selection of Evaluation Factors

Selecting appropriate evaluation factors is a critical step in landslide susceptibility assessment, which requires a detailed evaluation of the factors related to landslides in the study area through field surveys and remote sensing observations [3]. According to Reichenbach et al. [15], there are 596 factors influencing landslide occurrence. However, considering all of them in practical work projects would be time-consuming and labor-intensive. In landslide susceptibility assessment, selecting more evaluation factors does not necessarily lead to higher accuracy [26]. The selection of evaluation factors needs to consider factors such as dependency, measurability, non-redundancy, and relevance to geological features. Currently, there is no unified standard for selecting evaluation factors. It is mainly performed by analyzing the relevant factors that trigger landslides, calculating the correlation coefficients between factors, and then removing highly correlated factors to reduce the influence of data redundancy. Some scholars [15,27,28,29,30] have indicated that terrain, meteorological and hydrological factors, geology, human activities, and vegetation cover have significant impacts on landslide occurrence (

Table 2. Relationship between each evaluation factor and landslides.

Data Type	Evaluation Factor	Effects on Landslides
topography	altitude	Increasing elevation significantly impacts slope stability, leading to higher potential energy and increased landslide risk [31].
	slope	Steep slopes are more prone to destabilization and landslides, usually happening between 10° and 45°.
	exposure	Different slope orientations receive varying levels of solar radiation and weathering, affecting slope stability accordingly.
	terrain relief	The greater the terrain’s undulations, the more concentrated the stress is at the base and valley floor of slopes in that area. This leads to lower safety coefficients for slopes, making landslides more likely to occur [31].
	surface curvature	Research shows that landslides are more likely to occur when the curvature is greater than 0, indicating a convex slope shape [31].
meteorology and hydrology	rainfall	Rainfall catalyzes the occurrence of landslide geological disasters, leading to slope instability and landslide formation [32].
	distance to water bodies	Increased soil moisture in areas traversed by water bodies leads to the softening of rock formations, reducing the stability of both the soil and rock. This greatly increases the likelihood of landslides.
geology	distance to faults	The formation of faults disrupts the original shapes of rock and soil formations. Structural effects directly control the occurrence of geological disasters at both individual and regional levels.
	lithology	Different types of rock and soil formations have varying degrees of influence on landslide development. They not only affect the extent of landslide development but also determine the type and scale of landslides.
human activities	distance to roads	Existing research indicates that landslides are more concentrated along the sides of roads, and the density of landslide distribution decreases as the distance from the road increases [8].
vegetation cover	Normalized Difference Vegetation Index (NDVI)	Vegetation cover has complex effects on slope stability.

).

Table 2 lists the most commonly applied evaluation factors that have significant impacts on landslides. Here, further explanations are provided for several evaluation factors. Slope angle: Landslides are more likely to occur when the slope angle ranges from 10° to 45° [33]. Dahalet et al. [34] found that the geological units of different lithologies exhibit varying sensitivities to landslide susceptibility. Landslides often occur in loose geological formations, especially in relatively fragmented and hard ancient strata. The study found that in formations with alternating soft and hard layers, such as sandstone, mudstone, shale, and coal-bearing strata, slope deformation and failure are more intense, often leading to large or medium-sized landslides. In contrast, in formations composed of carbonate rocks, slope deformation is weaker, and landslides are less likely to develop. Regarding ground curvature, previous studies have shown that when the curvature is greater than 0, indicating a convex slope, landslide occurrences are more common. This is because convex slopes experience distortion and deformation, leading to stress concentrations within the slope body, resulting in slope instability phenomena [31]. Research has indicated that shallow movements are less likely to occur on slopes with dense vegetation and deep root systems [35]. Vegetation coverage is commonly represented by the normalized difference vegetation index (NDVI), which ranges from −1 to 1. Values of less than 0 represent water bodies or snow-covered areas, a value equal to 0 indicates bare rock or soil, and values greater than 0 represent vegetated areas, with higher values indicating denser vegetation. The impact of vegetation coverage on landslides varies in different regions. More vegetation does not necessarily mean fewer landslide disasters. Just as observed by Zhan [36] in Baiyun District, Guangzhou City, the current study found a positive correlation between the number of collapse landslides and the NDVI (Figure 1). Regions with higher NDVI values are associated with more human activities, which tend to create steeper slopes, thereby leading to collapse or landslides.

2.3. Screening of Evaluation Factors

Due to the complex interrelationships among evaluation factors and their varying degrees of correlation, directly inputting selected factors into a model may introduce noise. Redundant factors can increase model instability and decrease predictive accuracy. Common methods for screening evaluation factors include correlation analysis, collinearity analysis, Relief-F, recursive feature elimination, the information gain ratio (IGR), and the geographic detector (GD) [37].

Table 3. The relevant literature discussed in Section 2.3 on evaluation factor selection.

Year	Author	Title
2024	Chen et al. [37]	A study on the landslide susceptibility of LightGBM-SHAP, based on different factor screening methods.
2023	Sun Deliang et al. [38]	Evaluation of landslide susceptibility in gentle hill-valley areas, based on an interpretable random forest-recursive feature elimination model
2023	Zhang Kai [39]	Landslide susceptibility assessment, based on an optimal computing cell and ulti-model coupling

lists the relevant studies. Chen et al. [37] employed the Pearson correlation coefficient and a geographic detector to screen the evaluation factors in the study area. The results showed that compared to using all factors, the AUC values increased by 0.023 and 0.034, respectively. Sun Deliang et al. [38] utilized the recursive feature elimination algorithm to remove factors such as the water flow dynamics index and aspect. Afterward, the model’s AUC value had increased by 0.019. Zhang Kai [39] employed entropy theory and correlation analysis to screen the evaluation factors. Before and after screening, the accuracy of the deterministic coefficient model, frequency ratio model, information content model, and evidence weight model increased from 0.881, 0.911, 0.895, and 0.886 to 0.910, 0.913, 0.920, and 0.906, respectively. This indicates that entropy theory and correlation analysis are advantageous for constructing susceptibility evaluation systems.

3. Methodology Research

Broadly speaking, landslide susceptibility assessment methods can be classified into four main types: physics-based models, heuristic models, statistical models, and machine-learning models [40,41,42,43]. These methods have been proven to have both advantages and limitations [44]. The users of physical-based models need to understand how landslide forces and resistances interact, which requires detailed information on rock types, soil properties, slope shapes, and water conditions. While they can provide the highest evaluation accuracy, these models are only suitable for individual landslides or small-scale studies and cannot be extrapolated to fit larger scales [45]. Heuristic models include geological and geomorphological analysis, factor index analysis, fuzzy comprehensive evaluation, and analytic hierarchy processes. These methods require experts to score them based on their professional knowledge, thus exhibiting a high degree of subjectivity [46,47,48,49]. Statistical models assume that there is no correlation among influencing factors; hence, they use bivariate or multivariate algorithms to assess landslide susceptibility. These mainly include the information value method, evidence weight method, logistic regression method, certainty factor method, entropy index method, and multiple linear regression method. Compared to heuristic models, these methods avoid the subjectivity of experts. However, they overlook the complexity of landslide causes, and the correlation among factors is not adequately described [50,51,52,53,54]. Machine learning models can estimate the relationship between landslide distribution and influencing factors by learning from training data. They do this without needing specific functions or extensive prior knowledge, which helps them produce more accurate evaluations. The application process of machine learning in landslide susceptibility assessment is shown in Figure 2 [55]. Commonly applied machine learning models in research include logistic regression, random forests, support vector machines, artificial neural networks, various ensemble models, and deep learning models [56,57,58,59].

This section mainly analyzes the machine learning models. Compared to traditional statistical models, machine learning models demonstrate strong nonlinear fitting capabilities in landslide susceptibility assessment. Their predictive accuracy and precision are higher than traditional statistical models [17]. They are capable of more accurately reflecting the nonlinear relationship between various evaluation factors and landslide susceptibility, thus finding broader applications in landslide susceptibility assessment [60,61]. A brief introduction to the typical machine learning models used is provided below.

3.1. Logistic Regression (LR)

The logistic regression model is a multivariate statistical model used to describe the regression relationship between a dependent variable and independent variables. This model is well-suited for fitting binary classification problems with independent variables and can reveal multivariate regression relationships between a dependent variable and multiple unrelated independent variables. It can handle both continuous and categorical variables, and the independent variable data do not need to follow a normal distribution pattern [39]. The expression for the logistic regression function is as follows:

$$\mathrm{P}={\displaystyle \frac{1}{1+{\mathrm{e}}^{-\mathrm{y}}}}$$

$$\mathrm{y}={\mathrm{w}}_0+{\mathrm{w}}_1{\mathrm{x}}_1+\cdots +{\mathrm{w}}_{\mathrm{n}}{\mathrm{x}}_{\mathrm{n}}.$$

In the equation, P represents the probability of landslide occurrence; e is the natural constant; ${\mathrm{w}}_0$ is a constant representing the logarithm of the odds ratio of landslide occurrence to non-occurrence, given all influencing factors; ${\mathrm{w}}_{\mathrm{n}}\left(\mathrm{n}=1,2,3,\dots \mathrm{n}\right)$ are the logistic regression coefficients; ${\mathrm{x}}_{\mathrm{n}}(\mathrm{n}=1,2,3,\dots \mathrm{n})$ represent the independent features of the sample.

LR requires an ample amount of sample data and entails high computational complexity. When using this model for susceptibility assessment, it is crucial to address multicollinearity issues among the variables, reducing the degree of interrelation among them. Failure to do so may lead to excessively sensitive predictions and significant biases in estimation [26]. The logistic regression model boasts high accuracy, a low memory footprint, and a fast training speed. It can establish regression relationships between landslides and various evaluation factors, identify optimal fitting functions, and, consequently, determine landslide occurrence probabilities [33]. Through feature weights, it elucidates the impact of each feature on the final outcome, providing strong interpretability. Chowdhury et al. [62] utilized three machine learning algorithms—logistic regression (LR), random forest (RF), and the decision regression tree (DRT)—to develop and evaluate landslide susceptibility maps for the Chattogram District in Bangladesh. The ROC values for the three models were 0.943, 0.917, and 0.947. The results indicate that the logistic regression model achieved the highest prediction accuracy. In eastern Tennessee, USA, researchers [63] conducted statistical tests to identify the significant factors driving landslides, using logistic regression to model these factors, and successfully created a regional landslide susceptibility map with high predictive accuracy (AUC score of 0.94), offering insights for infrastructure protection and development.

3.2. Support Vector Machine (SVM)

The SVM is a novel supervised machine learning algorithm based on statistical learning theory. It is commonly used to address binary classification problems that are characterized by small sample sizes, non-linearity, and high-dimensional data [64]. The SVM exhibits high classification accuracy and strong generalization ability and is less prone to overfitting. It demonstrates significant advantages when handling limited sample sizes and high-dimensional feature data [65]. The model aims to separate point clusters that are inseparable in low-dimensional feature space by constructing a set of hyperplanes using kernel functions. The further a data point is from the hyperplane, the more confidently it can be assigned to one class [66]; SVM minimizes empirical errors and uncertainties to enhance generalization performance. It effectively addresses issues such as multiple factors, high dimensionality, and non-linearity in data, while also boasting a fast training speed and good performance [67].

The SVM model was first applied to landslide susceptibility assessment in 2000 [15]. This model is computationally simple and cost-effective. By employing kernel functions, the model overcomes the curse of dimensionality and non-linear separability issues, avoiding the complexity of calculations associated with high-dimensional data. It has shown excellent performance on many landslide datasets [68]. The primary objective of the SVM model is not only to partition the dataset into different categories but actually to maximize the margin separating them. Such robust classification capability enables it to perform exceptionally well in landslide susceptibility assessment [69].

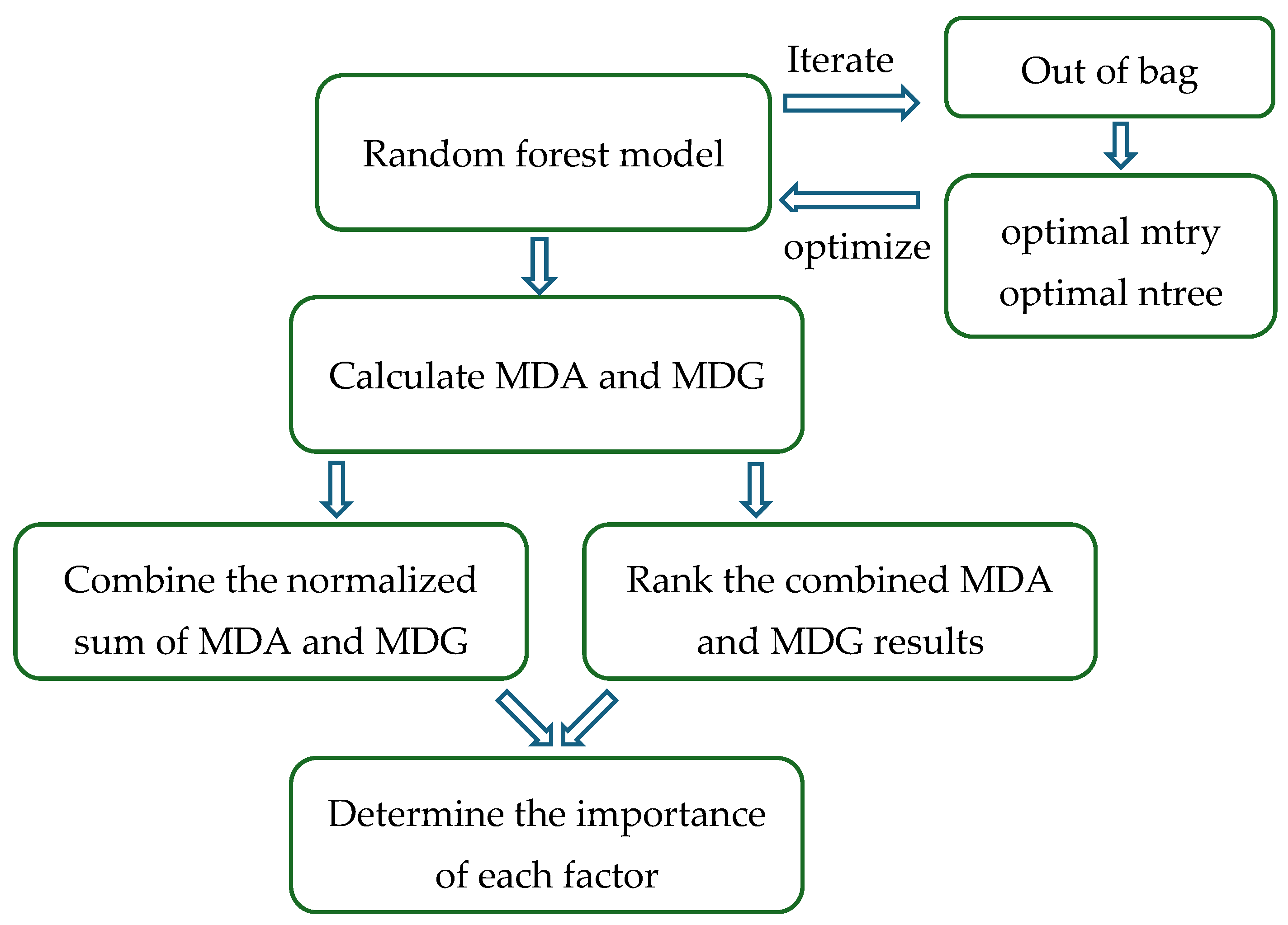
3.3. Random Forest (RF)

RF is an ensemble learning algorithm proposed by Breiman [70] in 2001, based on decision trees and bagging. It addresses the weak generalization capability of decision trees and significantly improves their accuracy [71]. A large body of research indicates that the RF model exhibits good tolerance to outliers and noise in datasets, making it widely regarded as one of the best machine-learning models currently available [31,72,73]. RF is a type of ensemble classification model composed of multiple decision trees. In the RF model, each decision tree votes to select the optimal classification result, given the independent variable X [74]. In the RF model, both the training samples for each tree and the attributes used for node splitting are randomly selected. This dual randomness helps to some extent in preventing the overfitting of the model. The RF algorithm is capable of handling high-dimensional data without the need for dimensionality reduction or feature selection. It exhibits a fast training speed, is less prone to overfitting, and is insensitive to missing values. Even when a significant portion of the features is missing, it can maintain accuracy. However, for some classification or regression problems with considerable noise, overfitting may still occur [75].

The generalization error of a random forest model typically decreases as the number of decision trees increases. This also implies that increasing the number of decision trees in a random forest model can enhance the accuracy of model predictions. This is because, with the increase in the number of decision trees, a random forest model can better utilize training data information and reduce the occurrence of model overfitting [32]. Taalab et al. [76] utilized a random forest model for landslide susceptibility assessment in the Piedmont region of Italy. The results showed that the random forest model exhibits good applicability for landslide susceptibility assessment in large, heterogeneous areas. One advantage of the random forest model is that it produces fewer errors when dealing with large sample sizes and multiple evaluation factors, and it is less prone to overfitting [77]. It can handle large datasets with high accuracy without the need to reduce high-dimensional feature input samples. Additionally, this model can be used to assess the importance of individual features in classification problems [78]. Its principle is based on the Gini index, whereby the random forest algorithm calculates the Gini index for each evaluation factor and compares it by taking the average of the Gini indices for all evaluation factors to determine their importance.

3.4. Artificial Neural Network (ANN)

Artificial neural networks (ANNs), also known as neural networks, are predictive models built on simulating the functionality of the human brain and nervous system. They consist of input layers, hidden layers, and output layers [79]. ANNs have strong nonlinear processing capabilities, with landslide-influencing factors being the input neurons. Different neurons are interconnected through weights, and their weight calculation formula is as follows [80]:

$${\mathrm{y}}_{\mathrm{i}}=\mathrm{f}\left({\sum }_{\mathrm{i}}{\mathrm{W}}_{\mathrm{i}\mathrm{j}}+{\mathrm{b}}_{\mathrm{j}}\right)$$

In the equation, ${\mathrm{W}}_{\mathrm{i}\mathrm{j}}$ represents the weight value linking neuron i and neuron j; ${\mathrm{b}}_{\mathrm{j}}$ is the bias term; f is the activation function. ANN models are applied to landslide susceptibility assessment, where the input layer consists of landslide evaluation factors, and the output layer represents the landslide susceptibility assessment results. Feature transformation is achieved by adding hidden layers [45].

ANNs are nonlinear statistical models that are commonly used for regression and classification problems. Research has shown that applying artificial neural networks to landslide susceptibility assessment can effectively enhance the automatic identification capability of other geological hazards in different regions, achieving a correct identification rate of approximately 80% [81,82,83]. The backpropagation neural network (BPNN), which employs error backpropagation, is known for its excellent nonlinear mapping capability and has been introduced into landslide susceptibility assessment [64,84].

The BPNN algorithm is the most common and representative algorithm in artificial neural networks. It is a type of supervised learning method and utilizes the gradient descent algorithm to minimize the error function. Its objective is to minimize the difference between the target output values and the inferred output values of the output units. The specific process involves initializing the model’s connection weights and biases with random values after constructing the model. Through adjusting the error function, the weights and biases are continuously updated in a backward manner, ultimately resulting in a model within the desired error range [85]. When conducting a landslide susceptibility assessment, the first step is to construct a BPNN model and obtain the final connection weight values. Then, the triggering factors are used as input data for the input layer. After the triggering factors are linearly combined and passed through the activation function, the output data of the hidden layer neurons are obtained. Subsequently, the output data of the hidden layer are linearly combined and passed through the activation function again to obtain the probability of landslide occurrence [39].

The ANN [86] model exhibits strong nonlinear adaptive capabilities. It continuously updates itself when processing information and does not rely on external rules when handling variable relationships. Therefore, the ANN model has become an effective tool for landslide susceptibility assessment.

4. Uncertainty Analysis

The use of machine learning algorithms has certainly improved the accuracy and precision of landslide susceptibility assessments to a certain extent. However, there are still several uncertain factors, such as the selection of positive and negative samples [87,88], the choice of evaluation models [89], model interpretability, and model transferability issues. All these factors can influence the accuracy of susceptibility assessments [79]. In this section, we will delve into the nature and sources of these uncertain factors and discuss their potential impacts on research/projects. By systematically analyzing these factors, our aim is to provide readers with a deeper understanding of the challenges that may arise in research.

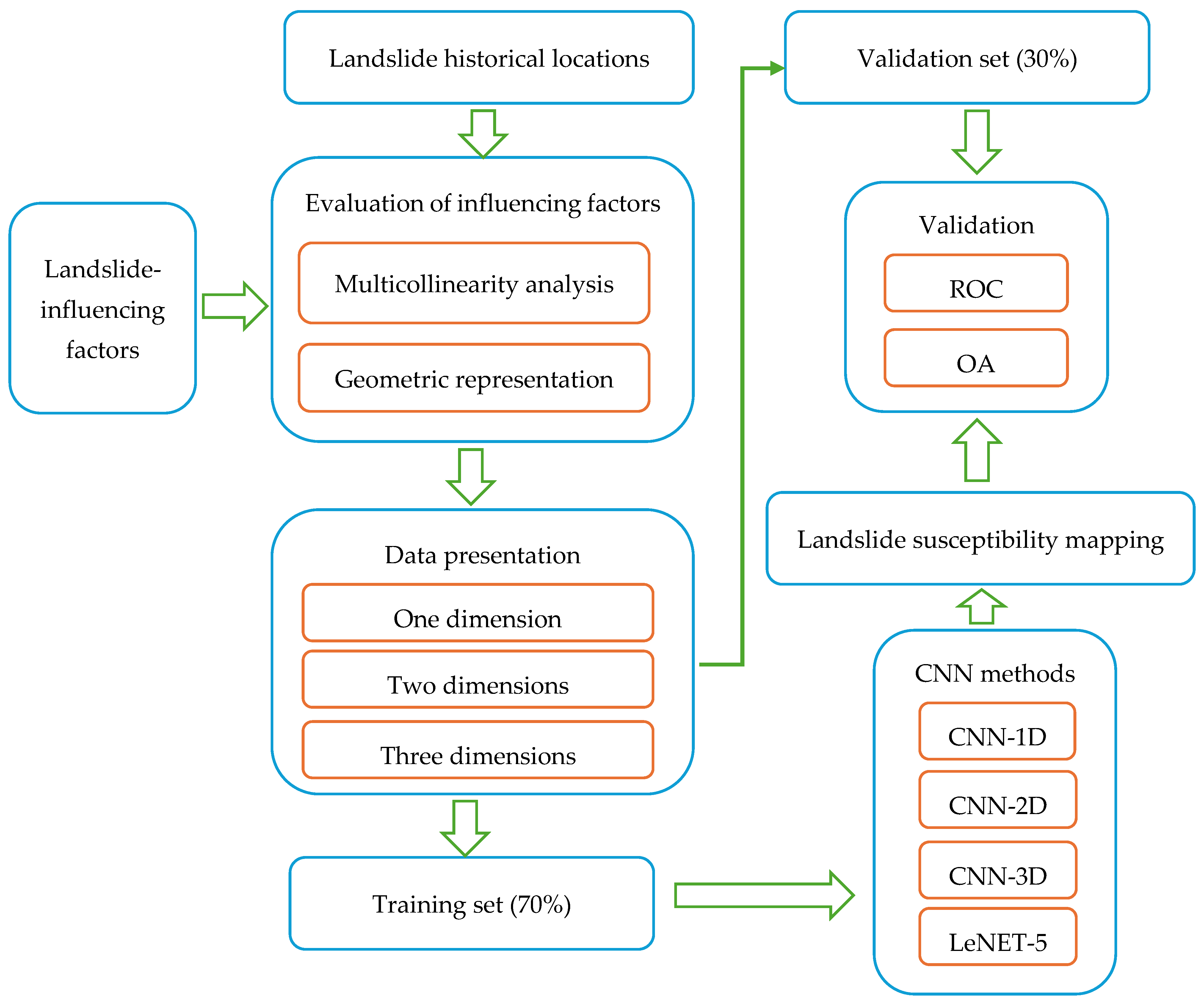
4.1. Selecting Positive and Negative Samples

In machine learning, the selection of positive samples (landslide points) and negative samples (non-landslide points) has a significant impact on the evaluation results. Positive sample compilation is typically achieved through synthetic aperture radar (SAR) interferometry [90], Google Earth imagery interpretation [91], and field surveys. Google Earth imagery is commonly used to collect landslide data for assessing landslide risk [92]. Additional information can also be found on government websites. To investigate the influence of different landslide boundaries on landslide susceptibility assessment, researchers [93] in Ruijin City constructed three models based on points, circles, and polygons for landslides. The results showed that modeling landslide boundaries more accurately led to better precision, less uncertainty, and susceptibility indices that closely matched the real-world probability distribution observed in the field. Zhang [39] compared evaluation models that used area units versus point units. The results showed that the model based on area units had a higher evaluation accuracy. Furthermore, after removing the landslide front edge, the accuracy of the models further improved. When selecting point units, points in the middle of the slope were found to best represent landslides compared to those behind or in front of the slope, and their evaluation accuracy was higher than the other two (Figure 3).

The optimized selection of negative samples can overcome any overfitting phenomenon in the model. The rational selection of negative samples has a significant impact on improving the accuracy of susceptibility evaluation [14,94]. The random selection of samples from landslide mapping by manual interpretation may result in negative samples being chosen as landslide points, due to missed or misinterpreted landslides during the interpretation process. Kalantar et al. [95] studied the impact of different training datasets on landslide susceptibility assessment. They prepared five sets of randomly generated datasets, and the results showed variations in landslide susceptibility assessments based on these different datasets. This indicates that the selection of randomly generated data significantly affects the assessment outcomes. Furthermore, it demonstrates that landslide susceptibility assessments based on randomly generated non-landslide points are not accurate.

Previous studies have attempted various approaches for selecting negative samples. Choi et al. [96] chose areas with zero slope as negative samples, but the evaluation results showed that the contribution of the slope factor was much greater than other factors. In contrast, Kavzoglu et al. [97] used high-resolution Google Earth imagery to interpret low-slope areas such as river channels and valleys in the study area and selected negative samples from them. Although this method ensured the stability of the negative samples, it either exaggerated or underestimated the contribution of the slope factor to the susceptibility model [98]. Liu et al. [99] used the frequency ratio method to select negative samples, and the comparative results showed that the improved model achieved an increase in evaluation accuracy. Guo et al. [14] employed the frequency ratio method (FR) to select negative samples from areas with extremely low and low susceptibility. They coupled this strategy with random forest (RF) and gradient-boosting decision tree (GBDT) models (FR-GDBT and FR-RF). The results demonstrated that utilizing the frequency ratio method to select negative samples from low-susceptibility areas can significantly enhance the accuracy of the predictive model. Deng et al. [100] selected non-landslide points from areas with relatively lower and low susceptibility formed by the information value model. They combined this approach with a random forest model. Compared to the random forest model using randomly selected non-landslide points, their susceptibility zoning results exhibited higher predictive accuracy. Chen et al. [101] aimed to overcome the limitation of low accuracy in non-landslide samples. They utilized the information value model for zoning and selected non-landslide samples from areas with low susceptibility. These samples were then combined with landslide samples and fed into a neural network model for training. As a result, the model’s accuracy improved by 5.1%. Rabby et al. [102] proposed an objective method based on the Mahalanobis distance (MD), chi-square distribution, and user-specified confidence levels to determine non-landslide points independent of the landslide-influencing factors. In comparison to the commonly used methods based on slope angle for selecting non-landslide points, this approach is more objective and exhibits better consistency. Especially in areas with incomplete landslide inventories, where the existing landslide points lack representativeness, the MD method can identify a safe sampling area for non-landslide points, enhancing the robustness and effectiveness of the evaluation results. The methods used in the relevant literature and the publication years of the papers referred to in the above discussion are shown in

Table 4. Studies in the literature on different negative sample selection strategies.

Year	Author	Recommendation Strategy
2018	Kalantar et al. [95]	randomly generated
2012	Choi et al. [96]	zero slope
2014	Kavzoglu et al. [97]	low-slope areas
2022	Liu et al. [99]	frequency ratio method
2023	Guo et al. [14]	frequency ratio method
2021	Deng et al. [100]	information value method
2020	Chen et al. [101]	information value method
2023	Rabby et al. [102]	Mahalanobis distance method

.

The topic of whether the ratio of positive to negative samples affects prediction accuracy has also been studied by some researchers. Based on the comprehensive grid management mechanism used in Dengfeng City, Li et al. [103] conducted a landslide susceptibility assessment in the study area using a random forest model. They utilized landslide data obtained through field surveys and heterogeneous data acquired from aerospace technology. During the evaluation process, the authors set up two control groups. One group used all the evaluation factors in the model, with a landslide point to non-landslide point ratio of 1:1. The second group employed a random forest weighting analysis method to calculate the Gini coefficient, thereby determining the contribution rates of each factor. They removed evaluation factors with lower contribution rates and adjusted the landslide point to non-landslide point ratio to 1:2. Through the optimization of evaluation factors and the increase in the number of non-landslide points, the model’s accuracy, precision, recall, and FI score improved from 0.77, 0.78, 0.94, and 0.85 to 0.84, 0.87, 0.93, and 0.90, respectively. The accuracy of landslide risk exceeded 0.8, indicating the effective application of the random forest model. Moreover, the optimization of evaluation factors and the increase in the number of non-landslide points significantly enhanced the accuracy and comprehensiveness of the model’s predictions. The increase in non-landslide points allowed the model to better learn non-landslide characteristics, thus improving its representativeness and generalization ability. Finally, the authors emphasized the importance of enriching the landslide evaluation factor library, which is crucial for improving assessment frameworks and enhancing the accuracy and applicability of future disaster predictions.

4.2. Model Selection and Application

There is currently no consensus on which machine learning model is best suited for landslide susceptibility assessment [17]. Our study demonstrates the effectiveness of machine learning models in analyzing landslide susceptibility and provides valuable insights for informed decision-making and disaster risk reduction initiatives.

4.2.1. Traditional Machine Learning Models

Aditian et al. [11] evaluated three models, namely, the frequency ratio (FR), LR, and ANN, for landslide susceptibility assessment. They demonstrated that ANNs outperformed traditional statistical models in terms of accuracy. The ANN model aims to simulate how the human brain processes information, enabling the model to learn the complex relationships between input and output variables. This model is considered an appropriate machine learning method for predicting nonlinear and complex phenomena. Consequently, artificial neural network (ANN) models are among the best techniques for accurately predicting landslides. Selamat et al. [80] used the ANN approach to create a landslide susceptibility map for the Langat River Basin in Selangor, Malaysia. The study employed a landslide inventory map containing 140 landslide locations, which were randomly divided into training and testing sets in a 70:30 ratio. The authors selected nine landslide-influencing factors as model inputs: altitude, elevation, slope, aspect, curvature, topographic wetness index (TWI), distance to roads, distance to rivers, lithology, and rainfall. To validate the effectiveness of the landslide prediction model, the authors used the area under the curve (AUC) and several statistical metrics (sensitivity, specificity, accuracy, positive predictive value, and negative predictive value). The results showed that the ANN prediction model achieved excellent performance in validation, with AUC values of 0.940 for both the training and testing sets.

Zhao et al. [104] conducted a landslide susceptibility mapping (LSM) study in Zanjan, Iran, using geographic information system (GIS) technology to identify the most critical factors contributing to landslides. The study compared convolutional neural networks (CNNs) with four machine learning (ML) algorithms, including random forest (RF), an artificial neural network (ANN), a support vector machine (SVM), and logistic regression (LR). The authors extracted 16 causative factors for landslides and prepared the corresponding spatial layers, then used these algorithms to train on landslide and non-landslide points. The results indicated that all five machine learning algorithms performed well, with accuracies ranging from 82.43% to 85.6% and AUC values from 0.934 to 0.967. Among these, the random forest algorithm achieved the best results, followed by CNN, SVM, ANN, and LR. The variable importance analysis revealed that slope and terrain curvature contributed the most to landslide prediction. These findings are significant for developing landslide risk management strategies.

Wang et al. [105] combined geographic information system (GIS) technology with five machine learning algorithms—logistic regression (LR), the support vector machine (SVM), random forest (RF), a gradient boosting machine (GBM), and multilayer perceptron (MLP)—to assess landslide susceptibility in Shexian County, China. The landslide susceptibility results of the five methods were compared using an area under the curve (AUC) analysis and grid maps. The results showed that the proportions of high or very high landslide points for LR, SVM, RF, GBM, and MLP were 1.52, 1.77, 1.95, 1.83, and 1.64, respectively. The ratios of very high landslide points to graded areas were 1.92, 2.20, 2.98, 2.62, and 2.14, respectively. The success rates of the training samples for the five methods were 0.781, 0.824, 0.853, 0.828, and 0.811, with prediction accuracies of 0.772, 0.803, 0.821, 0.815, and 0.803, respectively. The accuracy ranking of the five algorithms was RF > SVM > MLP > GBM > LR. The study results indicate that all five machine learning algorithms performed well in assessing landslide susceptibility in Shexian County, with the random forest algorithm achieving the best results.

Most studies have shown that RF exhibits higher predictive accuracy compared to other models such as LR, SVM, and ANN, making it more suitable for landslide susceptibility mapping [17,106]. The random forest model is popular among researchers due to its ease of implementation, high prediction accuracy, and lower tendency to overfit. Additionally, the random forest model can rank the importance of influencing factors, allowing for the removal of irrelevant factors from the ranking list to achieve better prediction accuracy [107].

4.2.2. Coupled Model

A coupled model combines two or more models, integrating the strengths of each model to effectively enhance the predictive accuracy of the overall model [108]. Li et al. [109] combined the deterministic coefficient method with the SVM model, while Luo et al. [110] integrated the deterministic coefficient method with the logistic regression model. Both studies confirmed that the evaluation results of the coupled model were more accurate than those of single models. In previous examples in the literature, coupled models are mainly classified into two categories: coupling between data statistical models and machine learning models, and coupling between machine-learning models.

The coupling of data-driven models with machine-learning models is illustrated in Figure 4. The main principle involves using the data-driven model (Model 1) to calculate the influence values of various evaluation factors, which are then used as inputs for the machine learning model (Model 2), ultimately yielding the prediction results.

Yuan et al. [108] utilized 1081 historical landslide data points from the Wenchuan region, along with 13 evaluation factors including terrain, geological structure, meteorology, hydrology, etc. They established three individual models of LR, SVM, and RF, as well as three coupled models integrating the certainty factor (CF). Comparative analysis of the predictive results from these six models revealed that the CF-RF model exhibited the highest prediction accuracy. Furthermore, the predictive accuracy of the coupled models surpassed that of the corresponding individual models, suggesting that coupling models can enhance the predictive accuracy of individual models to a certain extent. Sun et al. [111] and Liu et al. [112] both employed a combination of geographic detectors and machine learning models. By optimizing the evaluation factors, they improved the accuracy of the assessment results. This demonstrates that coupled models have certain advantages over individual models.

He et al. [79] conducted a landslide susceptibility assessment in Xining City using GF-2 remote sensing imagery data and field survey results to delineate landslide locations. They selected factors including slope, aspect, curvature, the topographic wetness index (TWI), relative slope position (RSP), lithology, distance to faults, distance to rivers, and distance to roads, based on the actual conditions of the study area, to construct a landslide susceptibility evaluation index system. Subsequently, they employed three coupled models: frequency ratio–random forest (FR-RF), frequency ratio–support vector machine (FR-SVM), and frequency ratio–artificial neural network (FR-ANN) for landslide susceptibility assessment in the study area. The results (Figure 5) indicated that the distribution of landslide susceptibility levels among the three models was largely consistent, with high susceptibility areas mainly being concentrated in the northeast part of the study area, and with over 87% of landslides occurring in moderate to high-susceptibility zones. This suggests that the predictive results of the three machine learning models are generally consistent with the actual situation. The AUC values of the three models were: 0.863 (FR-RF), 0.839 (FR-ANN), and 0.825 (FR-SVM), all exceeding 0.8, indicating good predictive accuracy for all models. Among them, the FR-RF model had the highest AUC value, indicating better predictive capability, making it more suitable for landslide susceptibility assessment in regions with similar geographic environments.

Research has shown [113] that using statistical models as input variables for machine learning models can assign the numerical expression of landslide susceptibility as the quantified weight values for evaluation indicator sub-intervals. This approach helps to standardize all variables to similar scales, thereby simplifying the machine learning model. Additionally, it can reduce the risk of model overfitting. Zheng et al. [114] conducted a study in Mangshi City, Yunnan Province, utilizing the certainty factor (CF) method to calculate the sensitivity values of various factors. These sensitivity values were used as classification data for RF. Appropriate training data and optimized model parameters were selected for model prediction. Additionally, the CF prior model was used to select negative samples in the study area. Subsequently, a binary logistic regression model was established. This allowed for the evaluation of landslide susceptibility zoning in the study area using the ROC curve to evaluate the model. The results showed an accuracy of 91%.

Coupling machine learning models with other machine learning models, also known as ensemble algorithms, is commonly employed in geological hazard susceptibility assessment. Currently, ensemble algorithms based on bagging and boosting are widely used. However, as they utilize homogeneous classifiers, their drawbacks may be amplified, leading to potential overfitting issues [115]. In contrast, heterogeneous ensemble methods can integrate different types of classifiers, leveraging the strengths of each type to compensate for weaknesses, thereby enhancing the robustness and generalization of the ensemble classifier [116]. This further improves the prediction accuracy of ensemble algorithms. The typical heterogeneous ensemble models mainly consist of three types: stacking, blending [117], and weighted averaging [118]. A generic ensemble learning model framework is illustrated in Figure 6. In landslide susceptibility assessment, heterogeneous ensemble models improve prediction accuracy by combining various machine learning algorithms, such as decision trees, support vector machines, and random forests. The process typically involves first training the multiple distinct base learners, then using their outputs as inputs for an ensemble strategy (such as weighted averaging or stacking) to generate the final prediction results.

Jiang et al. [119] conducted a comparative study on landslide susceptibility assessment in the border areas between Tianshui City, Gansu Province, and Baoji City, Shaanxi Province. They employed three heterogeneous ensemble learning models: stacking, blending, and weighted averaging. RF, SVM, and BPNN were used as the base learners. The results (see

Table 5. Model prediction performance results [119].

Model	Accuracy	Kappa Coefficient	Specificity	Sensitivity	AUC
RF	0.948	0.887	0.956	0.927	0.985
SVM	0.942	0.871	0.983	0.868	0.984
BPNN	0.930	0.846	0.939	0.907	0.973
Stacking ensemble	0.958	0.908	0.982	0.932	0.988
Blending ensemble	0.947	0.878	0.956	0.910	0.980
Weighted average	0.955	0.901	0.971	0.924	0.987

) indicated that the stacking ensemble model achieved greater accuracy in landslide susceptibility assessment. Wang et al. [92] combined three machine learning methods, SVM, ANN, and gradient-boosting decision trees (GDBT), to create a high-performance model. Comparing the results with three individual models, the simulation results showed that the AUC (area under the curve) value of the ensemble model was higher by 0.11–0.135 compared to the AUC value of traditional machine learning models.

4.2.3. Deep Learning Model

In recent years, an increasing number of scholars have also started exploring the application of deep learning in landslide susceptibility assessment [120,121,122]. Deep learning has the capability to automatically learn landslide features and then model and assess the data. Compared to traditional machine learning models, deep learning possesses stronger expressive power and evaluation accuracy. Currently, typical deep learning methods include convolutional neural networks (CNN) [92,123,124], recurrent neural networks (RNN) [125], and long short-term memory networks (LSTM) [126], among others. These methods have different advantages and applicability in various aspects such as data processing, feature extraction, model construction, and evaluation [127].

Wang et al. [92] were the first to introduce convolutional neural networks (CNN) for landslide susceptibility assessment. The authors developed three different data representation algorithms (1D, 2D, and 3D) to construct three distinct CNN architectures and compared these with traditional machine-learning models (Figure 7). Using OA, MCC, ROC, and AUC metrics for evaluation, the results showed that the CNN-2D model had the highest assessment accuracy. The authors concluded that CNNs are more suitable for landslide prevention and management than traditional machine-learning models. Liu et al. [52] also compared CNN models with traditional machine-learning models. The results indicated that the landslide susceptibility maps generated using CNN models had better consistency and exhibited superior predictive capabilities. However, a limitation that was noted was the relatively small scale of the study.

Deep learning does offer greater advantages in terms of evaluation accuracy, but it also sacrifices transparency and interpretability, and there is a risk of overfitting in the models. Currently, most applications of deep learning in landslide susceptibility assessment are based on small scales, such as cities or counties with simple geological conditions. How to apply deep learning on a larger scale will be a direction for future research. Compared to traditional machine learning models, deep learning models are more complex, making them harder to understand, and learning the models presents a significant challenge for researchers.

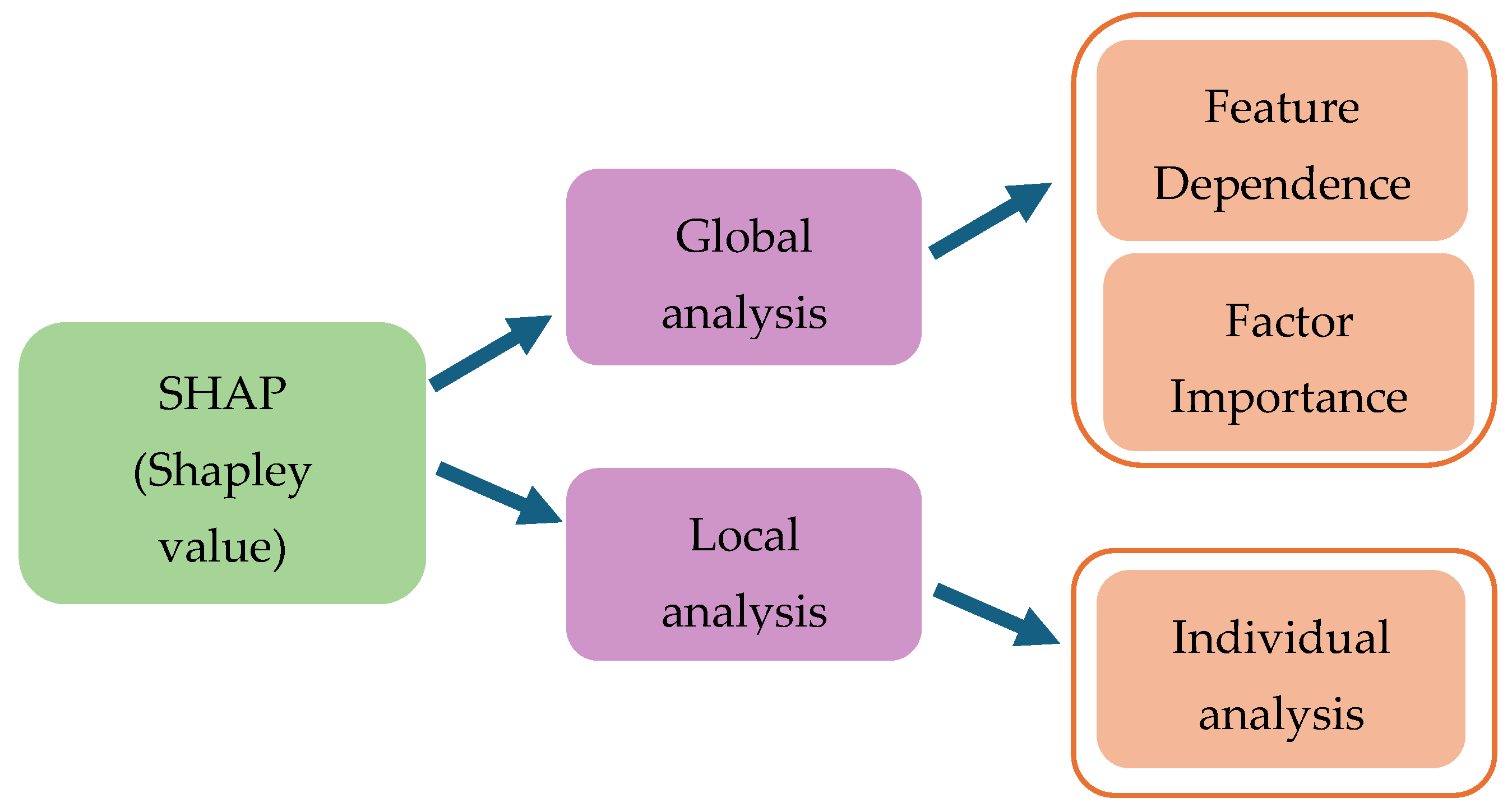
4.3. The Interpretability of “Black-Box” Models

Some scholars argue that the high accuracy of machine learning models is not sufficient to guarantee their credibility. Therefore, it is necessary to increase their interpretability so that people can understand the reasons behind their predictions [128,129,130]. Dong et al. [131] point out that white-box models like logistic regression and decision trees can provide insight into their prediction mechanisms through their weights or decision nodes. However, models like random forests and artificial neural networks lack this transparency, as the internal complexities hinder understanding of the decision mechanisms. Therefore, interpretable artificial intelligence represents a future research direction.

Lundberg and Lee [132] introduced SHAP (Shapley additive explanations), a method designed to explain the predictions of various models to non-users, particularly when the reasons behind the predictions in black-box models are difficult to understand. SHAP quantifies the contribution of each evaluation factor in the model and explains the model’s predictions as the sum of the Shapley values of each input feature, as follows:

$$\mathrm{g}\left({\mathrm{x}}^{\prime }\right)={\mathsf{\phi }}_0+\sum _{\mathrm{j}=1}^{\mathrm{M}}{\mathsf{\phi }}_{\mathrm{j}}{{\mathrm{x}}_{\mathrm{j}}}^{\prime }$$

In the equation, $\mathrm{g}\left({\mathrm{x}}^{\prime }\right)$ represents the model’s predicted value; ${\mathrm{x}}^{\prime }\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{M}}$, where ${\mathrm{x}}^{\prime }=1$ if the sample contains factor j, otherwise ${\mathrm{x}}^{\prime }=0$; ${\mathsf{\phi }}_0$ is the constant for explaining the model (i.e., the mean prediction of all training samples); ${\mathsf{\phi }}_{\mathrm{j}}$ is the estimated value (Shapley value) for each feature.

The SHAP interpretability analysis process is shown in Figure 8. The SHAP method can calculate the Shapley value of each feature in an individual sample for local explanations, demonstrating the contribution of each feature to the predicted value [133]. Additionally, it can combine individual local explanations for global explanations, ensuring a high level of consistency between local and global explanations [134]. Zhou [135] utilized SHAP models to provide explanations at both global and local levels for landslide susceptibility in the study area, using summary plots, dependency plots, and waterfall plots. The results indicated that factors such as the water dynamic index, rainfall conditions, and elevation were the primary influencers of landslides, which finding was consistent with the findings from field surveys. Sun et al. [136] utilized the SHAP algorithm to explain the landslide event on the Shangshan Highway in Baitaping, Hechuan District. They found that factors such as slope, terrain ruggedness, the NDVI (normalized difference vegetation index), and POI (point of interest) density promoted landslide occurrences, while factors such as lithology and elevation inhibited them. This effectively explained the intrinsic causal mechanisms of individual landslides, providing reference for future research into landslide susceptibility. Zhang et al. [129] proposed a comprehensive explanation framework based on the SHAP-XGBoost model, which quantifies the importance and contribution of factors at both global and local levels. This framework provides a reference for research on machine learning interpretability.

In addition, landslide evaluation factors can also be ranked through ROC-AUC analysis. Tyler Rohan et al. [136] excluded one factor at a time from the random forest analysis and calculated the relative difference in AUC between the model that excluded the factor and the model that included all factors. The difference in importance is expected to be related to larger differences.

The random forest model can utilize the out-of-bag (OOB) sorting function to assess the importance of each factor in landslide events (Figure 9). The principle behind this is that the more important the evaluation factor, the faster the OOB accuracy decreases when adding random noise to the specified evaluation factor. The calculation formula is as follows [77]:

$$\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}={\displaystyle \frac{1}{\mathrm{n}}}\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{O}\mathrm{O}{\mathrm{B}}_2-\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{O}\mathrm{O}{\mathrm{B}}_1\right|$$

$\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{O}\mathrm{O}{\mathrm{B}}_1$: For each decision tree, we select the corresponding OOB to calculate the error. $\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{O}\mathrm{O}{\mathrm{B}}_2$: Random noise interference is added randomly to all samples of feature X’s OOB, and the OOB error is recalculated.

Wu et al. [77] conducted a landslide susceptibility assessment in Muli County, Sichuan Province, using a random forest model. The model performed well, with an ACC of 99.43%, precision of 99.3%, recall of 99.48%, and an F1 score of 99.39%. By computing the out-of-bag (OOB) error, the results showed that the three most important factors were elevation, distance to roads, and annual average rainfall.

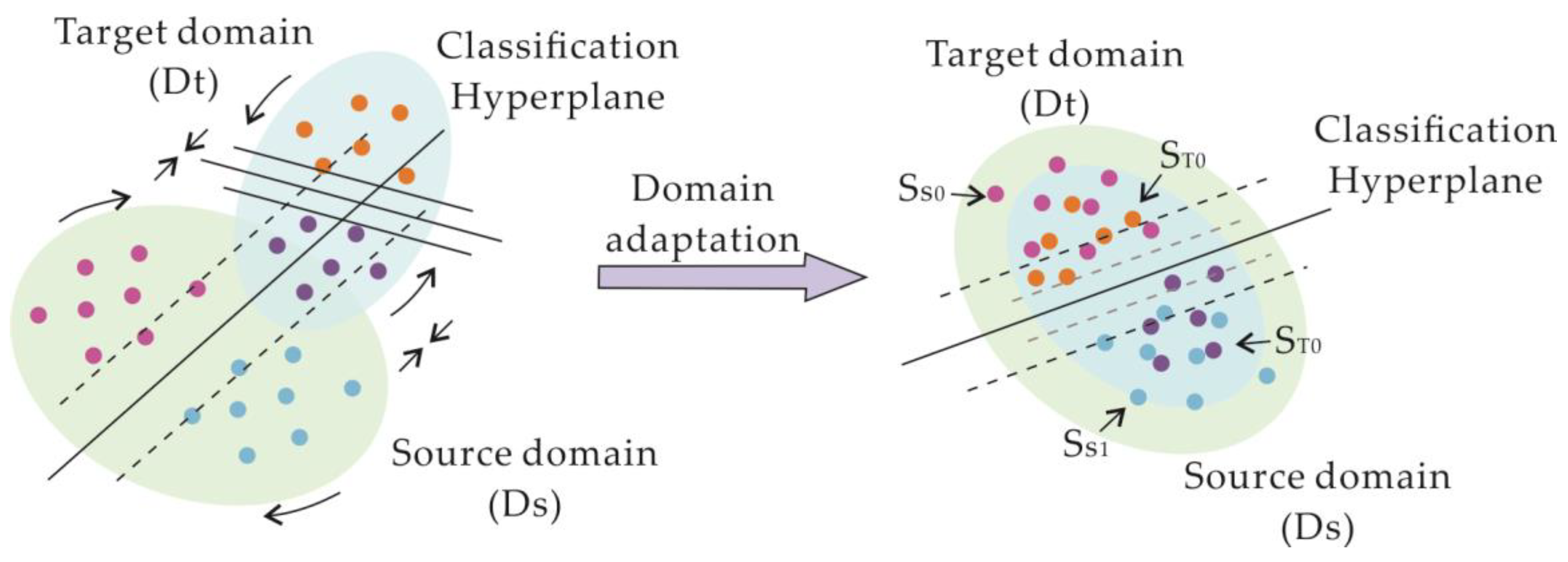
4.4. Transferability

In some regions, the scarcity of landslide samples makes it difficult to use models for landslide susceptibility assessment. Scholars have attempted to directly extend the models from one region with landslides to areas lacking landslide samples but found the results to be ineffective. For instance, Hu et al. [137] found that machine learning-based landslide susceptibility assessment models, when applied outside the study area, exhibited significantly reduced accuracy and lacked good transferability. This can be attributed to spatial heterogeneity.

In cases of spatial heterogeneity, the relationship between disaster-driving factors (dependent variables) and disaster variables (independent variables) may vary in adjacent spatial regions. Therefore, it is necessary to consider the heterogeneity of driving factors when analyzing landslide susceptibility [138]. In large-scale study areas, considering spatial heterogeneity is necessary for achieving higher accuracy in landslide susceptibility assessment. However, for regional studies, this may be disregarded [139]. Sun et al. [135] confirm the high spatial heterogeneity in landslide susceptibility and internal driving factors on the southern and northern slopes of the Himalayan region.

The spatial heterogeneity of landslide evaluation factors is the main reason for the poor generalization ability of evaluation models. However, these models demonstrate better generalization ability in regions with similar regional characteristics [2]. Therefore, for regions with lower research levels, it may be considered appropriate to search for areas with similar terrain, geology, meteorology, vegetation, and other characteristics in places where in-depth research has already been conducted and apply the model to evaluate those areas. Rolain et al. [140] created a landslide inventory for the Da Bac region in Vietnam covering the period from 2013 to 2020, which included significant landslide events in 2018 and 2019. The authors conducted a landslide susceptibility assessment using logistic regression and support vector machine models under two different data application modes. The first data mode involved using landslide data spanning the entire period (2013–2020), while the second data mode involved training the model using landslide data from 2018 and validating it using data from 2019. The results showed that: (1) under both data modes, the support vector machine model outperformed the logistic regression model in terms of evaluation accuracy; (2) the choice of different datasets had little impact on the evaluation results, indicating that landslide susceptibility assessment using limited datasets is feasible; (3) landslide susceptibility assessment models trained on representative terrain conditions can be applied to regions with similar terrain features. Zhang et al. [141] divided Yunyang County into four zones, based on their geological properties, and constructed five models for the entire region and its four subzones. The results showed that the models for the subzones exhibited better performance. Therefore, training models in locations with similar geological properties can yield predictions with higher accuracy. How to establish an accurate, interpretable, and generalizable machine learning model under conditions of small sample sizes is a question worth researching in the future [2]. Wang et al. [142] proposed a landslide susceptibility assessment method called the deep autoencoder with multi-scale residual convolutional neural network (DAE-MRCNN) to address issues such as insufficient landslide samples and the inadequate representation of nonlinear relationships among the evaluation factors. The authors applied this method to assess landslide susceptibility in Hanzhong City, Shaanxi Province, and compared it with three other methods (SVM, CPCNN, and 2D-CNN). The results showed that the DAE-MRCNN model achieved the highest accuracy, with an AUC value of 0.891, while the AUC values of the other three models were 0.842, 0.869, and 0.873, respectively. Therefore, the DAE-MRCNN model adequately captures the complex nonlinear relationships among evaluation factors, mitigates the issue of insufficient landslide samples, and significantly improves prediction accuracy. Additionally, compared to shallow machine learning methods, deep learning demonstrates greater advantages in terms of evaluation accuracy.

In order to address the issue of transferability, Su et al. [143] proposed a feature-based domain adaptation method (Figure 10) to enhance the transferability of landslide susceptibility models in two typical landslide-prone areas in the southeastern part of Fujian Province. They utilized five traditional machine learning algorithms to model the areas with samples and evaluated them in areas without samples. The results showed that the feature transfer method effectively improved the cross-regional prediction capabilities of different models, with an overall indicator improvement of 8.49%. Among them, the SVM and LOG models showed the most significant improvement, reaching 13.68% and 10.19%, respectively, thereby providing a new solution for landslide susceptibility assessment in areas without any samples.

5. Discussion and Future Opportunities

5.1. The Selection of Models

Currently, there is no consensus on which type of machine learning model yields superior evaluation results. In landslide susceptibility assessment, the selection of machine learning models plays a pivotal role in enhancing prediction accuracy and efficiency. Looking ahead, as technology continues to advance and data accumulate, we anticipate progress in the following areas:

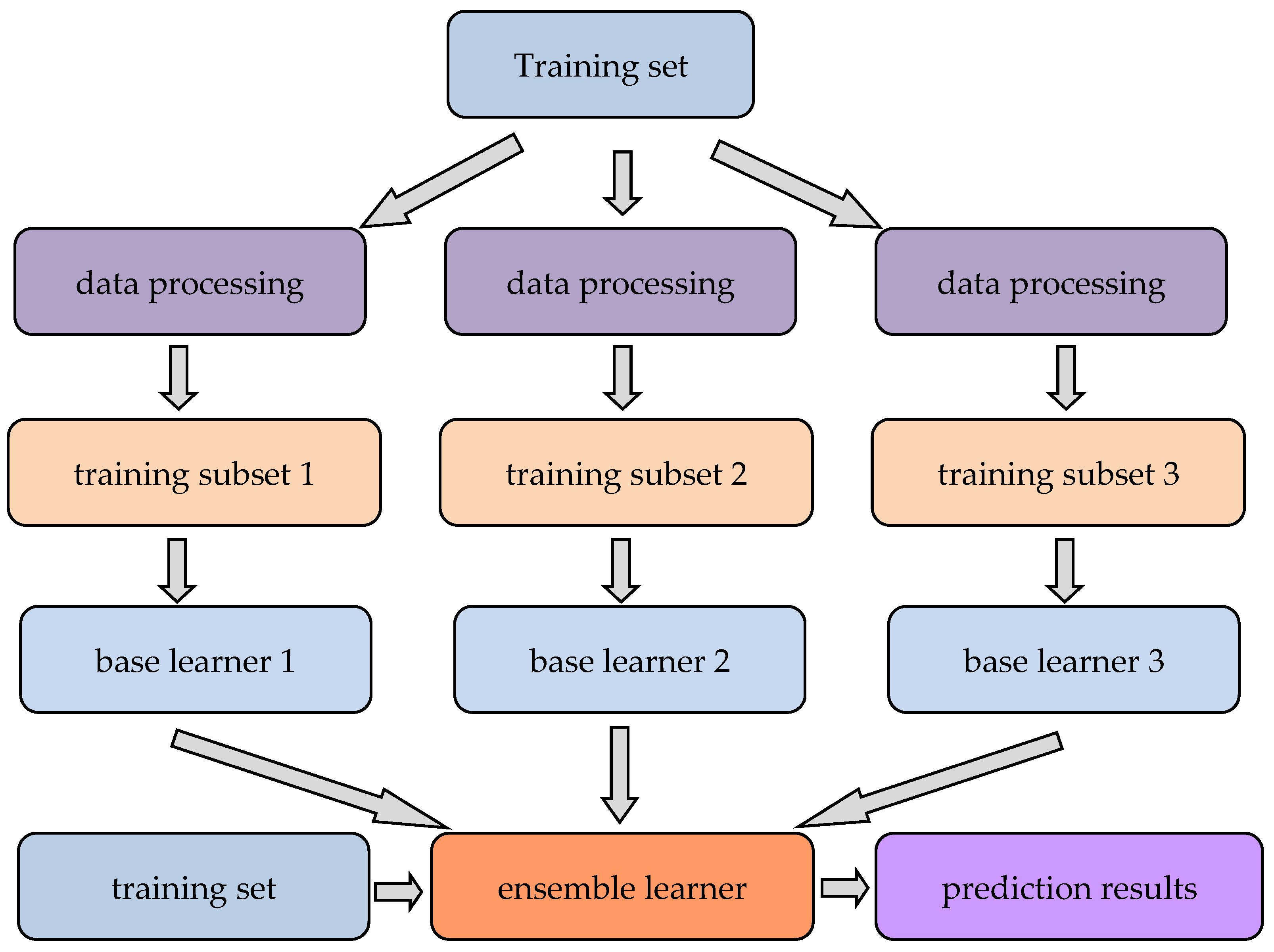
• Utilization of Coupled Models: Ensemble learning, through the integration of predictions from multiple models, has the potential to enhance overall predictive performance [108]. Section 4.2.2 details the benefits of coupled models. Figure 4 and Figure 6 illustrate two approaches to model coupling: Figure 4 shows the results of Model 1 being fed into Model 2 for further prediction, while Figure 6 depicts the evaluating factors being the input into different models, with the results of these models then being aggregated using methods such as weighted averaging or voting. Future research could delve into combining various types of machine learning models (such as decision trees, neural networks, support vector machines, etc.) to develop a more robust and reliable landslide susceptibility assessment model.
• Integration of Multi-Source Data and Interdisciplinary Collaboration: Future studies can harness diverse data sources, including satellite remote sensing data, terrain data, meteorological data, etc., and collaborate with experts in geology, geography, meteorology, and related fields. By amalgamating data and expertise from various sources, more comprehensive and precise landslide susceptibility assessment models can be developed.
• Advancement of Deep Learning Methods: With the enhancement of computing capabilities and the progression of deep learning technology, the utilization of complex models such as deep neural networks in landslide susceptibility assessment is poised for further expansion [3,144]. Future research can explore strategies to leverage deep learning methods to unearth the latent patterns and features in data, thereby enhancing the accuracy and reliability of landslide prediction. Deep learning models possess strong feature extraction capabilities, enabling them to handle multi-source data and exhibit efficient pattern recognition abilities. Therefore, future research can explore the coupling between various deep learning models as well as the coupling between traditional machine learning models and deep learning models. Such an exploration can address weaknesses in the transparency, interpretability, and susceptibility to overfitting of these models, ultimately enhancing the accuracy and reliability of landslide prediction.

5.2. The Construction of Evaluation Index Systems

The construction of evaluation index systems for landslide susceptibility assessment is directly related to the accurate evaluation and effective management of landslide risk. The evaluation index system mainly includes the selection of mapping units, the selection of evaluation factors, and the selection of positive and negative samples. Regarding the selection of mapping units, raster units and slope units are currently widely studied, each with its own advantages and disadvantages [131]. The choice of suitable mapping units depends on the specific requirements and practical circumstances of the research. Raster units are suitable for situations requiring high spatial resolution and the use of GIS data for model establishment, while slope units are more suitable for capturing terrain continuity features and terrain interpretation. Landslide susceptibility is influenced by various factors, including terrain, geology, climate, and land use. Selecting key factors from numerous factors and making reasonable trade-offs is a challenge. The future selection of evaluation factors needs to overcome the complexity, data availability, dynamics, and uncertainty of multiple factors [14]. The selection of positive and negative samples is the foundation of model training and validation. Positive samples come from historical landslide locations, but there is currently a lack of standards for selecting negative samples. In Section 4.1 of the preceding text, we discussed using the frequency ratio method and information gain method as prior models for landslide susceptibility assessment in the study area. Subsequently, we selected non-landslide points from low-susceptibility areas at random to serve as negative samples for the machine learning models. This approach significantly improved the model’s evaluation accuracy. Future research needs to establish a set of standards for selecting negative samples to adapt to different geographical environments. Additionally, the spatial distribution of positive and negative samples may be uneven, exhibiting clustering phenomena. How to select samples reasonably to cover different regions and terrain features is a challenge.

5.3. The Interpretability of the Model

While machine learning models can be highly accurate in terms of landslide susceptibility assessment, their black-box nature makes it difficult for non-users to understand how decisions are reached. This lack of transparency can make it hard to explain the decision process and outcomes, which may reduce trust in the results [129]. In landslide susceptibility assessment, comprehending the impact of evaluation factors on landslide susceptibility is paramount. However, machine learning models often automatically select features or struggle to explain the importance of features, complicating the comprehension of how the model predicts outcomes based on input features. Moreover, machine learning models frequently struggle to capture the uncertainty of assessment results, which is crucial for quantifying uncertainty in landslide susceptibility assessment [136]. In the future, developing interpretable machine learning models to enhance understandability and explanation will pose a significant challenge, such as utilizing models with stronger interpretability or devising novel methods to explain the model’s decision process. Additionally, augmenting the analysis of the importance of input features (evaluation factors) and conducting an uncertainty analysis of the model to elucidate prediction results is also a pivotal research direction. The interpretability of machine learning models in landslide susceptibility assessment presents a significant challenge, yet this can be addressed through the design of interpretable models, bolstering feature importance analysis, uncertainty estimation, and other methodologies. These endeavors will bolster an evaluator’s trust in the assessment results and deepen their understanding of the factors influencing landslide susceptibility.

5.4. Transferability

In landslide susceptibility assessment, the portability of models refers to their applicability and effectiveness across different regions or geographical conditions. Investigating model portability ensures their reliability and utility in various environments. Factors influencing model portability include geographical variations, data quality, and features, as well as the complexity of the models. Future research can focus on the following areas to enhance model portability:

• Building Cross-Regional Datasets: Creating datasets that cover multiple regions can train more generalized models, thus improving their applicability across different areas.
• Transfer Learning: Applying transfer learning techniques allows models to quickly adapt to new regions, thereby enhancing their stability and robustness.
• Ensemble Learning: Combining multiple models through ensemble learning can leverage the strengths of each model, boosting overall performance.
• Factor Importance Analysis: Analyzing the importance of various factors in the models can help identify and understand the key elements affecting landslides in different regions, thus improving model applicability.
• Model Interpretability Research: Enhancing model interpretability helps in understanding the decision-making processes and making necessary adjustments when applying models to new regions.

Despite these strategies, challenges such as data availability, regional variations, model complexity, and validation issues still persist. Future research needs to delve deeper into these areas to promote the widespread application and continuous improvement of landslide susceptibility assessment models, providing strong support for landslide prevention and disaster mitigation efforts.

6. Conclusions

Scientists have explored various technologies to mitigate landslide impacts, and this paper offers a thorough review of machine learning applications in landslide susceptibility assessment. Based on our findings, we propose the following key recommendations for future research:

(1)

Model Selection and Future Directions: There is currently no consensus on the most effective machine learning model for landslide susceptibility assessment. Selecting the right model is essential for improving prediction accuracy and efficiency. Future research should focus on combining models, integrating multi-source data, fostering interdisciplinary collaboration, and developing advanced deep learning techniques.

(2)

Indicator System and Sample Selection: An effective indicator system is vital for accurate landslide risk assessment and management. The choice of mapping units should align with research objectives, using grid units for high spatial resolution and GIS data, and slope units for terrain continuity. Challenges include the complexity of multiple factors and data uncertainties. Establishing standards for selecting positive and negative samples is crucial. Positive samples should be derived from historical landslide data, while there is a need for standardized methods to select negative samples, especially in low-susceptibility areas. Future work should focus on developing standards and ensuring a diverse sample distribution to enhance model accuracy and applicability.

(3)

Interpretability of Models: The black-box nature of machine learning models hampers non-experts’ understanding of their decision-making processes, making interpretability a significant challenge. Future research should aim at creating interpretable models, improving feature importance analysis, and estimating uncertainty to build trust in the assessment results.

(4)

Portability and Adaptability: The effectiveness of landslide susceptibility models can vary due to geographical and data quality differences. Enhancing model stability and applicability through cross-regional datasets, transfer learning, and ensemble models is crucial. Addressing the challenges related to data availability and regional variations remains a priority for future research.

By addressing these key areas, future research can significantly advance the accuracy, interpretability, and applicability of machine learning models in landslide susceptibility assessment.