Next Article in Journal
Influence of Connecting Cables on Stator Winding Overvoltage Distribution under High-Frequency Pulse Width Modulation
Previous Article in Journal
Effectiveness of Laser-Assisted Teeth Bleaching: A Systematic Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 14
Issue 20
10.3390/app14209221
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Application of Different Image Processing Methods for Measuring Rock Fracture Structures under Various Confining Stresses

by
Chenlu Song
1,
Tao Li
1,
He Li
2 and
Xiao Huang
1,*
1
School of Marine Engineering Equipment, Zhejiang Ocean University, Lincheng Street, Zhoushan 316022, China
2
School of Naval Architecture and Maritime, Zhejiang Ocean University, Lincheng Street, Zhoushan 316022, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2024, 14(20), 9221; https://doi.org/10.3390/app14209221
Submission received: 7 August 2024 / Revised: 21 September 2024 / Accepted: 7 October 2024 / Published: 11 October 2024
Browse Figures
Versions Notes

Abstract

:
Fractures within granite may become channels for fluid flow and have a significant impact on the safety of waste storage. However, internal aperture variation under coupled conditions are usually difficult to grasp, and the inevitable differences between the measured data and the real fracture structure will lead to erroneous permeability predictions. In this study, two different CT (Computed Tomography) image processing methods are adopted to grasp internal fractures. Several CT images are extracted from different positions of a rock sample under different confining stresses. Two critical factors, i.e., aperture and the contact area ratio value within a single granite fracture sample, are investigated. Results show that aperture difference occurs under these two image processing methods. The contact area ratio value under two image processing methods has less than 1% difference without confining stress. However, there is larger than ten times difference when the confining stress increases to 3.0 MPa. Moreover, the edge detection method has the capability to obtain a relatively accurate internal fracture structure when confining pressure is applied to the rock sample. The analysis results provide a better approach to understanding practical rock fracture variations under various conditions.

1. Introduction

Estimating fluid behavior within fractured rocks in the deep subsurface is essential in rock engineering fields, such as for underground nuclear waste repositories and enhanced geothermal systems. Nuclear waste storage repositories are usually placed in low-permeability rocks, such as granite. Granite has very low permeability due to its high density, low porosity, and dense texture. Moreover, fluid flow along with the fractures of granite will affect the stability of the repositories [1,2,3]. Flow behavior within the fractured rock is controlled by fracture evolution [4,5]. Fracture aperture change within the rocks under complex conditions may alter the flow direction and may result in the leakage of radioactive waste. Then, the radionuclide transports within the fractured rocks in the long term will further destroy the environment [6]. Some laboratory works focus on hydraulic aperture variations under various conditions. Experiment results clarify that fracture aperture is altered by the interactions between various conditions (i.e., THMC process, thermal–hydraulic–mechanical–chemical coupled process) [7,8,9,10,11]. Moreover, fracture geometry is changed in the long term under coupled conditions [12,13,14], which is a fundamental problem influencing underground water flow within the fractured rock mass.
Microfocus X-ray CT scanning has been widely applied in the medical field [15,16,17,18]. It has the capability to detect the internal structures of materials and to measure the rock aperture, length, void, contact area, and orientation immediately [19,20,21,22,23]. Previous studies show that the rock fracture geometry can be observed using X-ray CT. Internal rock pore structures pre- and post-experiments are compared [10,24]. Moreover, mineral dissolution and precipitation reactions within the internal fracture are also observed [21,25]. Therefore, fracture aperture reduction and tortuosity of the flow path within the fractured rock can be verified using CT observations.
In general, a 2D fractured rock sample CT image is composed by three primary regions, i.e., the void phase of the fracture position, the rock phase, and the mineral composition on the rock surface [26,27]. Those components are quantified and distinguished by several image processing technologies such as the threshold method [28,29,30], which has been used to detect rock fractures. In recent years, several studies applied the threshold method to segment the fracture from the rock region in a CT image [31,32,33]. A certain CT value is chosen at each component; then, the neighboring voxels, which have a similar CT number around this value, may be considered as the same region. Therefore, this specific value, which is used to distinguish different regions, is a decisive factor in the threshold method. However, it also has some limitations, such as the fact that it will result in the misidentification of neighboring voxels. Lai et al. [34] used the CT threshold method to identify rock fractures in a CT image (as shown in Figure 1). The study shows that the extracted fracture position has several misidentifications, i.e., the marked red area in original CT image was misidentified as the white part, i.e., the rock phase after the CT image segmentation. It is noted that the threshold method is not suitable for a relatively low-resolution CT image.
The misidentification results have a great effect on grasping the rock fracture information accurately. Some previous researchers verified the rock fracture permeability evolution and established the numerical model through CT image analyses [35,36,37,38]. Therefore, efficient image processing technology and an image analysis method for analyzing rock fracture CT images are critical. Edge detection is a common method for identifying medical CT images, such as human tissues and bone structures [16,39,40]. The characteristic of this method is that it focuses on the discontinuity and similarity region in a CT image with high efficiency [41]. The common process of edge detection includes three steps: the differentiation of the different regions, enhancing the boundary, and removing the unwanted voxels [42]. The overlapping line, which is located around the perimeter, can be removed subtly. Canny [43] deduced the best Canny edge detection algorithm in 1986, which was widely utilized [44,45]. A high-quality method for edge detection and sifting through an image’s noise are the advantage of Canny. Particularly, a relatively low-resolution CT image can also be better detected.
Not many researchers have aimed at the image processing of rock fracture structures. Therefore, in order to further explore the granite fracture structure variation under the confining conditions, this study uses the granite sample as the research object. Moreover, none of the previous studies clarified that different image processing methods have an influence on the rock aperture and fracture contact area value changes. Therefore, in this study, two different image processing methods (i.e., the region growing technique and edge detection, respectively) are applied in the identification of a single granite fracture. Several CT images under various stress conditions (i.e., at 0 MPa and at 3.0 MPa, respectively) are extracted from different granite rock positions. The critical factors (i.e., aperture value and contact area ratio, respectively) are analyzed and compared under two different methods. Then, the characteristics of the different image processing methods for rock fracture are discussed from several comparative results. Aperture and fracture contact area variation are further verified.

2. Materials and Methods

2.1. Experimental Material

A cylindrical granite rock sample with diameter and length 15.2 mm × 33.3 mm is split by the Brazilian tensile test, and it is made a single fracture along the cylindrical axis, as depicted in Figure 2. Then, the fractured rock sample is set into a triaxial cell, and it is mounted on the rotation table and faced to the X-ray source, as shown in Figure 3a. The triaxial cell has heating capability, and the sample is enclosed with jacket in order to avoid excessive temperature directly functioned to the sample, as presented in Figure 3b. The microfocus X-ray CT scanner in this study is the KYOTOGEO-XCT (TOSCANER-32250 hdk, which is made by TOSHIBA IT and Control Systems Corporation, Kyoto, Japan). This CT scanner has an X-ray focal spot size of 4 μm and resolution of 5 μm. The maximum current and voltage are 1 mA and 225 kV, respectively. The scan condition is listed in Table 1. The granite sample is scanned with two steps through using X-ray CT. Firstly, it is scanned as received (i.e., dry condition) without confining stress. The sample is scanned into 1788 CT images slices with the pixel size and the slice thickness of 15.1 μm × 15.1 μm× 17.0 μm in each direction. Secondly, the sample is fixed into the water-saturated triaxial cell, and it is scanned with confining stress of 3.0 MPa. In this step, the sample is scanned into 1736 slices with the pixel size and the slice thickness of 18.4 μm× 18.4 μm× 21.0 μm. The cross-section CT image matrix is 1024 × 1024 at each x- and y-direction. The CT images are output as 16-bit grayscale.
The total length of the granite rock sample is 33.3 mm. In order to compare RG and ED image processing methods difference, several 2-D cross-section CT images (i.e., set CT image number as Slice A to E) are picked up from different length of the rock sample at each confining stress condition, as depicted in Figure 4. Although the CT image slices are chosen randomly and those CT slices are extracted from different length of the granite rock sample, the comparative results only focus on the image processing difference. The extracted CT image slices represent fracture variation in different positions. Table 2 lists the extracted CT image conditions under each confining stress condition.

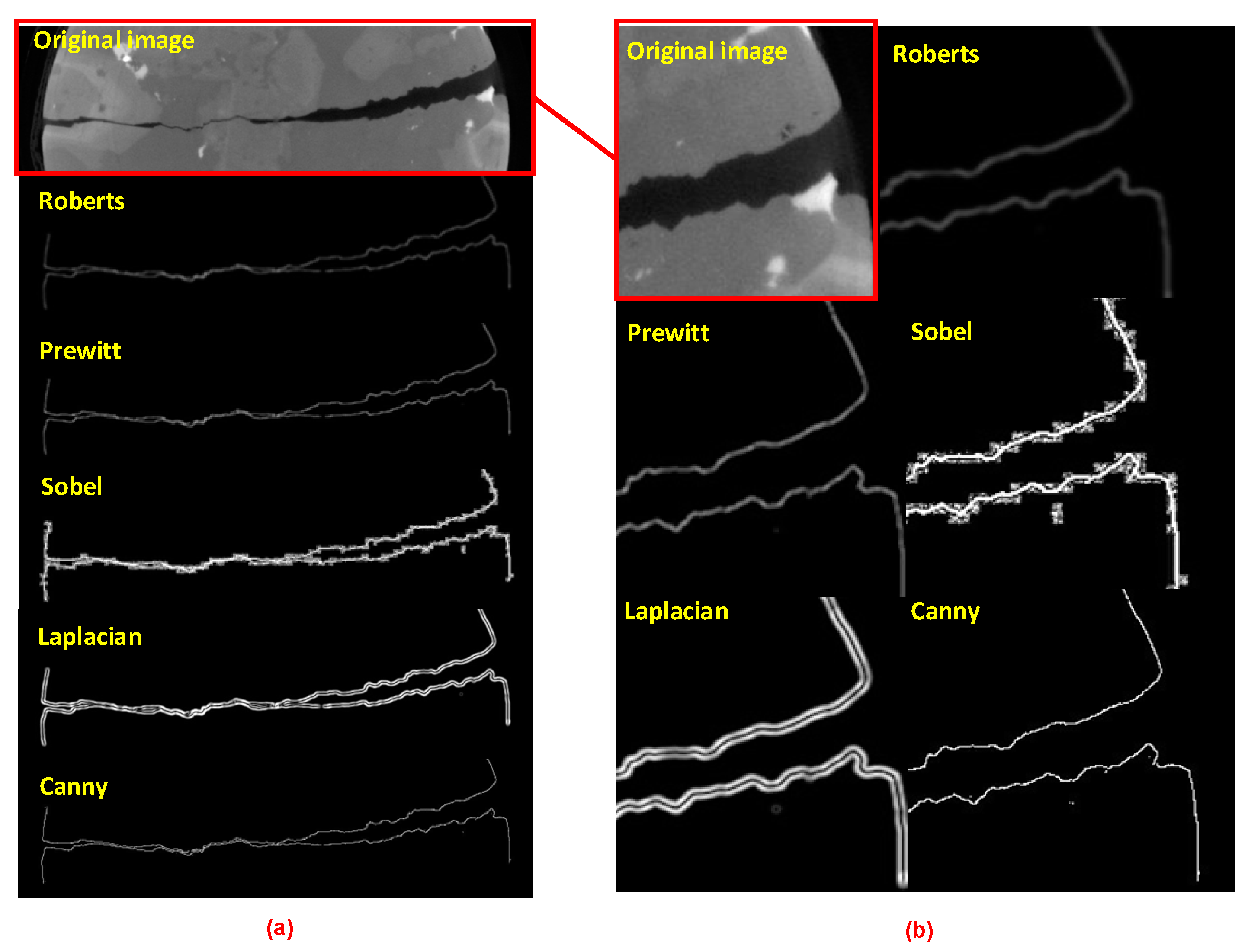
2.2. Image Processing Method

Two different image processing methods (i.e., region growing and edge detection) are applied to identify the fracture variation using measured CT images. Moreover, fracture structure variation factors, such as aperture and contact area ratio value in each cross-section, are calculated under these two image processing methods.

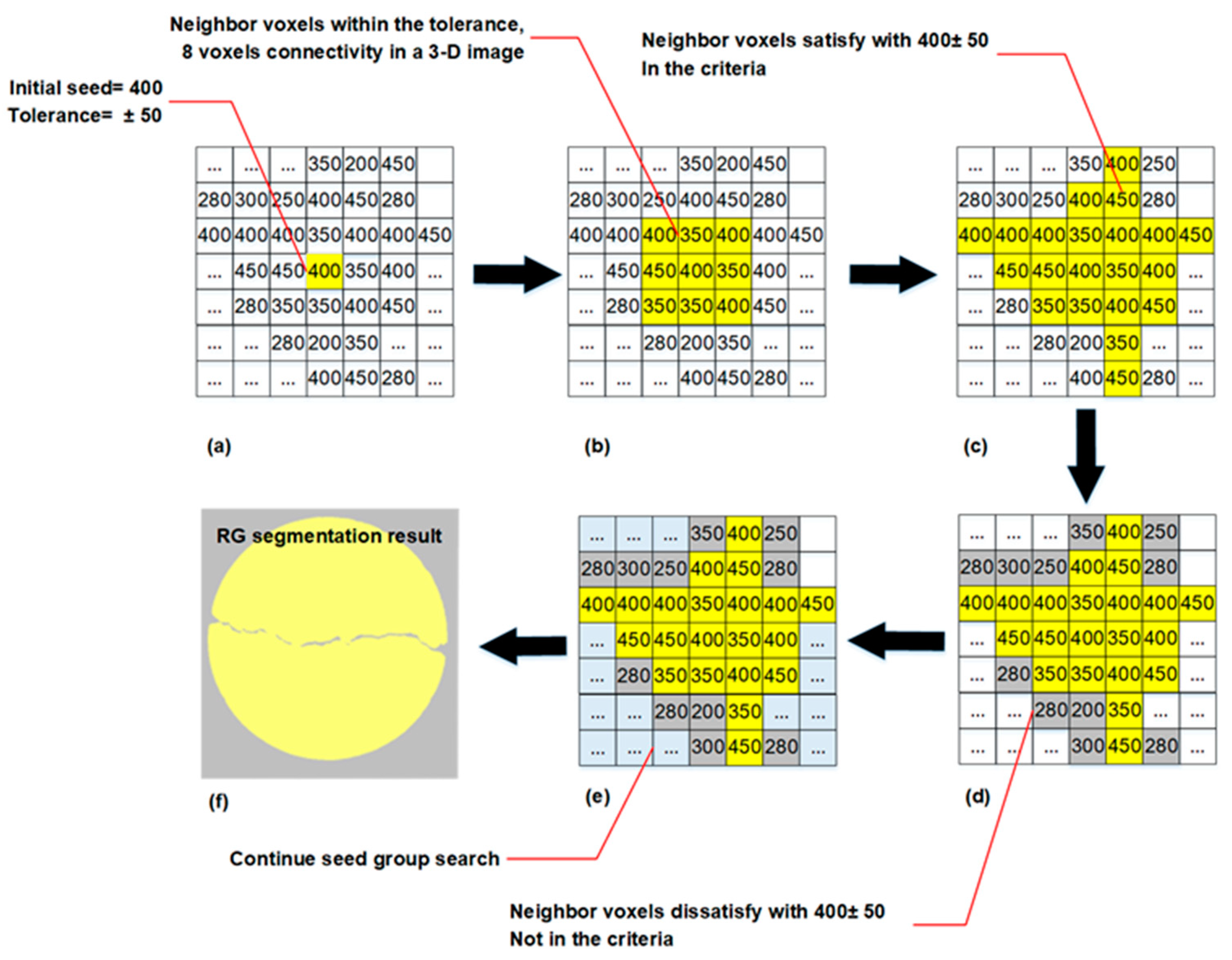
2.2.1. Region Growing Method (RG)

Original CT images are segmented by the region growing method [46,47,48]. An image analysis software VGstudioMax3.1 (Volume Graphics GmbH, Kyoto, Japan) is used to conduct the region growing process. An effective voxel selection in a region growing process is essential [49,50,51,52]. The process of region growing method is schematically illustrated in Figure 5. The final segmentation image can be obtained until the total number of seed voxels stops increasing, then the segmented CT image slice can be achieved.
The voxel connectivity (i.e., in this study 26-connected neighborhood) will assimilate the same voxel number in x-, y-, and z-direction into the representative value, and the voxel connectivity in 3-D can be ensured. In contrast, if the CT voxel membership probability is over the threshold, those voxel values can be distinguished. The value of different region in a CT image is listed in Table 3. It includes the mean value of each phase (i.e., σ1 and σ2); the standard of the mean value (i.e., μ1 and μ2); and a threshold value of 85 that is decided through the Gaussian distribution. The representative voxel value 118.6 is chosen to represent the rock initial value. The neighboring voxels are assimilated through the distance (i.e., the tolerance T = 33) between the threshold value and the mean value of the rock region. If the adjacent voxels around the initial value are larger than the threshold value of 85, these voxels will also be assimilated into the rock-phase seed groups with this region growing. Then, the rock aperture is extracted from the rock region by this segmentation process.
The CT value of rock and void region in the 2-D CT image is measured by counting CT voxel number of each region. The mean values of void and rock region are equal to 4.5 and 118.6, and the standard deviation of them are 8.6 and 29.5, respectively. The mean value and the standard deviation are used to determine the threshold parameter of region growing. The normal distribution of void and rock are calculated from the CT value, as the dashed line presented in Figure 6. Therefore, the threshold value is decided from this normal distribution, which is equal to 33. From Figure 6, it is noted that the RG segmentation image value corresponds well with the original CT image value.

2.2.2. Edge Detection Method (ED)

Edge detection method is an efficient operation for object recognition and boundary extraction in image processing. Canny edge detection deduces best approximation of the optimal edge detection operation through the algorithm of the first derivative of the Gaussian function, and it shows better edge detection performance than the other operators such as Sobel, Roberts, and Prewitt [53,54]. The Robert and Prewitt operators have a relatively accurate positioning. But they are sensitive to noise because they do not include smoothing. Moreover, those two methods always show the detail loss of the image and lower accuracy of the edge. The Sobel operator has poor processing performance for images with mixed multiple complex noises. The Laplacian operator always processes edge lines too smoothly and lacks the authenticity of edge detection. However, the detection performance of Canny operator is better than that of gradient operator, and it can detect finer edge parts of an image [53]. Figure 7a shows a comparative result of those different image processing methods on a fractured rock CT image. Figure 7b represents a comparative result of the expanded CT fracture boundary. It can be clearly seen that Canny operator has an advantage in capturing the aperture edges.
Moreover, this study focuses on grasping the fracture aperture variation under different confining stresses, and the Canny edge detection method is a new attempt in grasping the fracture aperture boundary, and it is important to know the microscopic changes in the aperture boundary and the contact area variation in fractured rock. Then, the accurate data in a rock fracture structure can reduce underground engineering disasters.
Using the Canny edge detection method, a smooth image is successfully achieved through deducing the 2-dimensional Gaussian function:
G ( x , y ) = e _ x 2 + y 2 2 σ 2 2 π σ 2 ,
In Equation (1), σ represents the scale of smoothing. However, superfluous noise suppression may produce an image lacking fidelity. A comparative figure is shown in Figure 8. In this study, the value of σ is set as σ = 0. It can keep the aperture boundary accuracy, i.e., as the same shape with the original CT image. If an unsuitable σ is chosen equal to 4, the aperture boundary will become more smooth. It is not the same shape with the original CT image.
In a CT image, an edge gradient is the vector which depends on the magnitude and the direction. The edge strength (magnitude) is calculated through the first-order derivative expression in x- and y-direction; then, the second-order derivatives is written in Equation (2):
L = ∂ f ∂ x 2 + ∂ f ∂ y 2 ,
where L is the first-order image derivative (the gradient magnitude) and f is the CT value at coordinates (x, y) in a CT image. ∂f/∂x and ∂f/∂y are the vectors in the maximum rate change of f in x- and y-direction. Then, the vectors in x- and y-direction are calculated by the Sobel operator equation, as illustrated in Equation (3):
− 1 − 2 − 1 0 0 0 1 2 1                       − 1 0 1 − 2 0 2 − 1 0 1 ,
Then, gradient direction ϕ is computed as in Equation (4):
φ = tan − 1 ∂ f ∂ y / ∂ f ∂ x ,

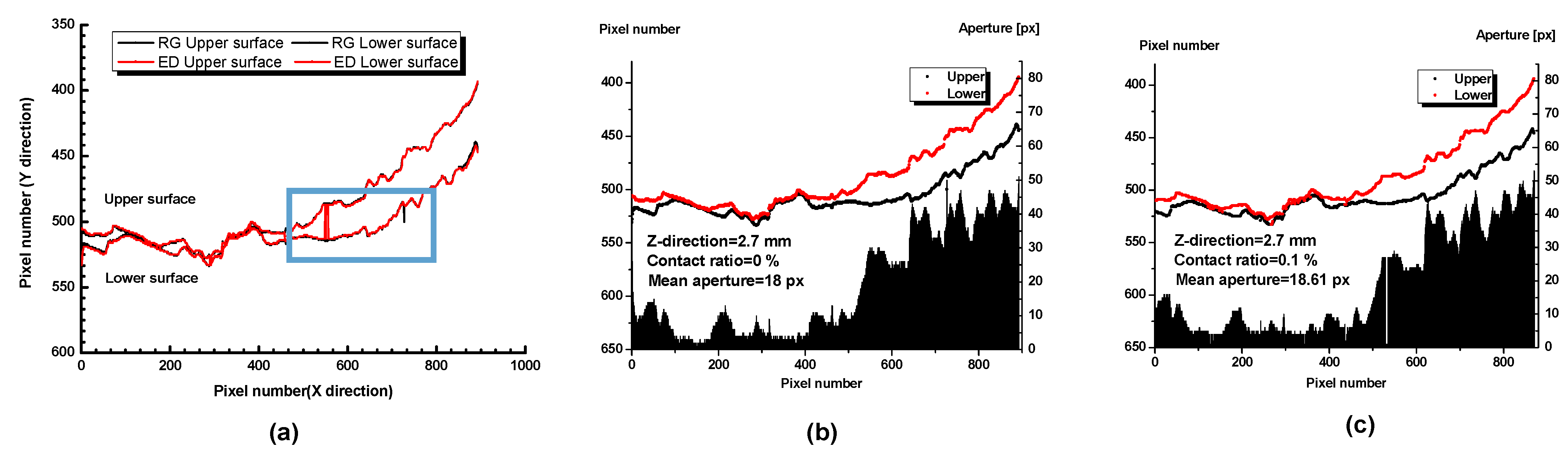
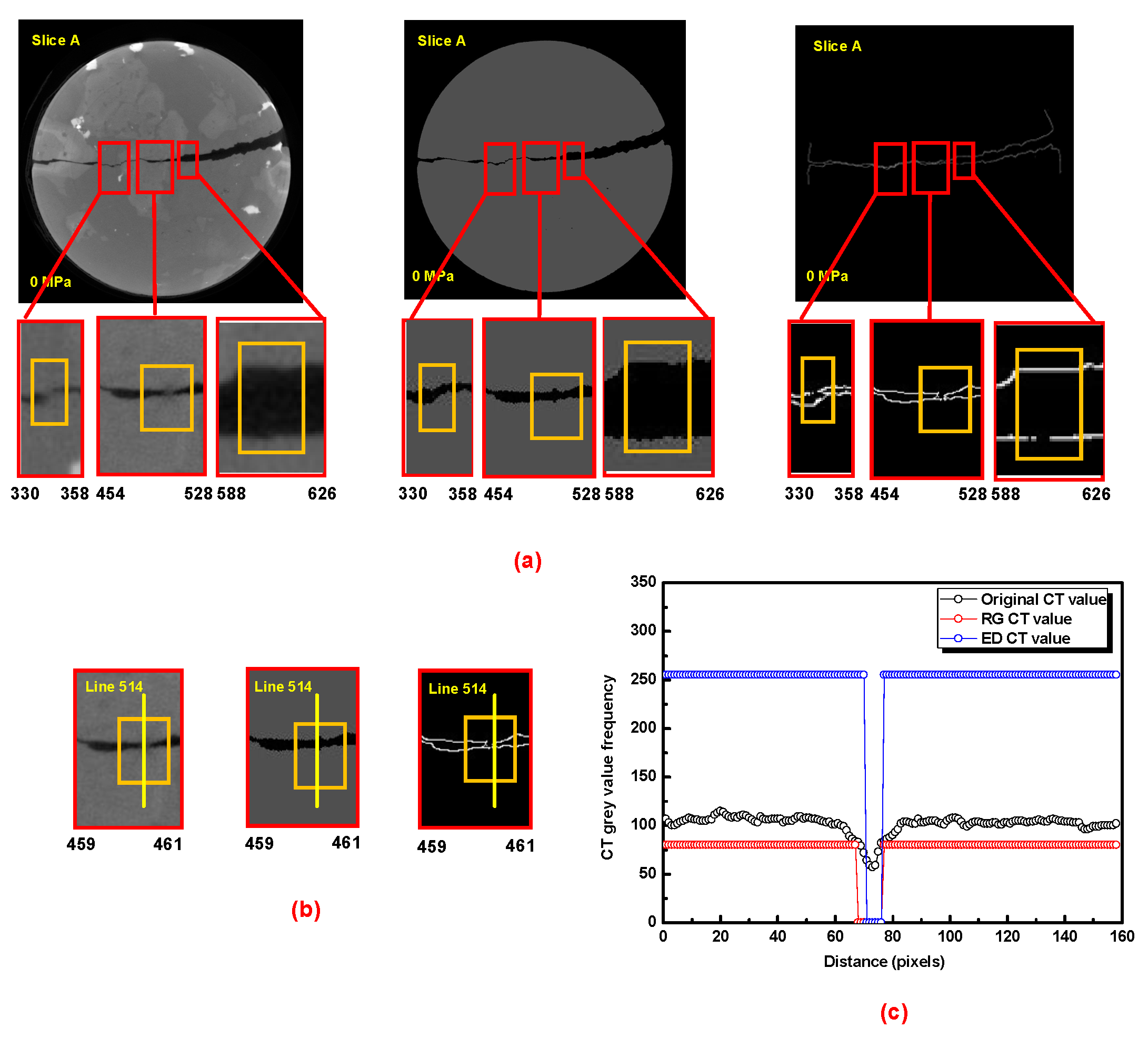
2.2.3. A Representative Image Processing Comparative Result under Region Growing and Edge Detection Method

The region growing method (RG) and the edge detection method (EG) are applied to grasp the rock fracture in a CT image. Figure 9 shows two image processing results. From Figure 9a, Slice A is one of the CT images chosen from the whole CT image slices of rock sample without confining stress. It is confirmed that the boundaries of upper and lower fracture are successfully identified with these two methods. Region growing method successfully distinguishes the rock region and the fracture aperture region using this segmentation process, as depicted in Figure 9b. Edge detection method has filtered the nonsignificant regions and only concentrates on the fracture aperture boundary, as presented in Figure 9c.

3. Results

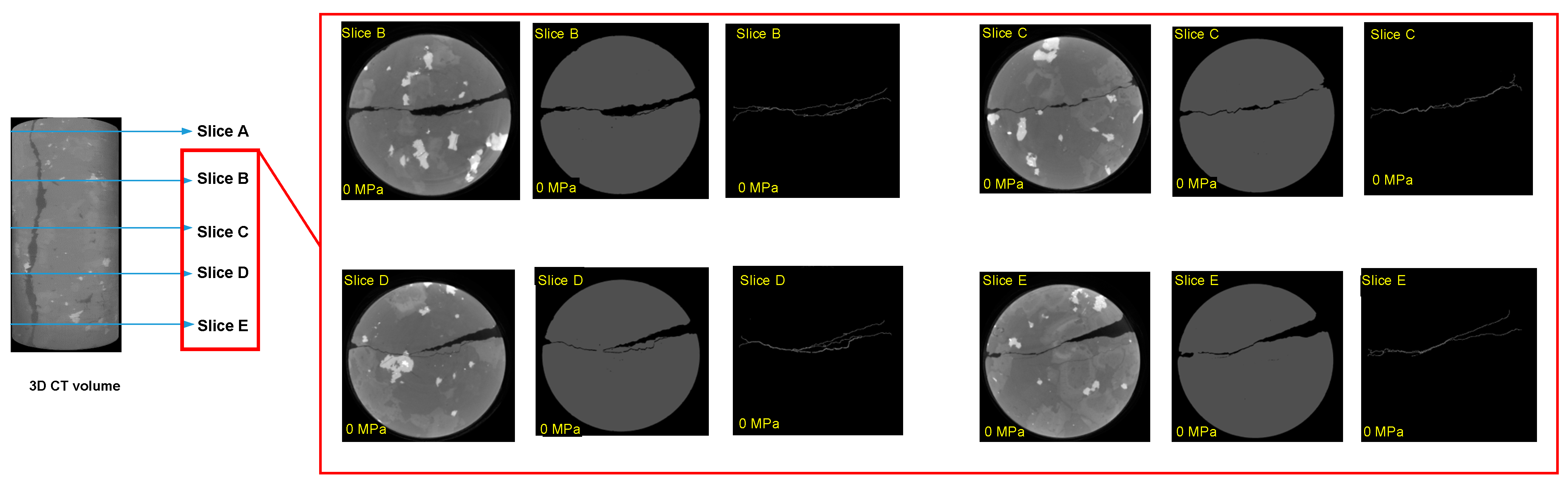
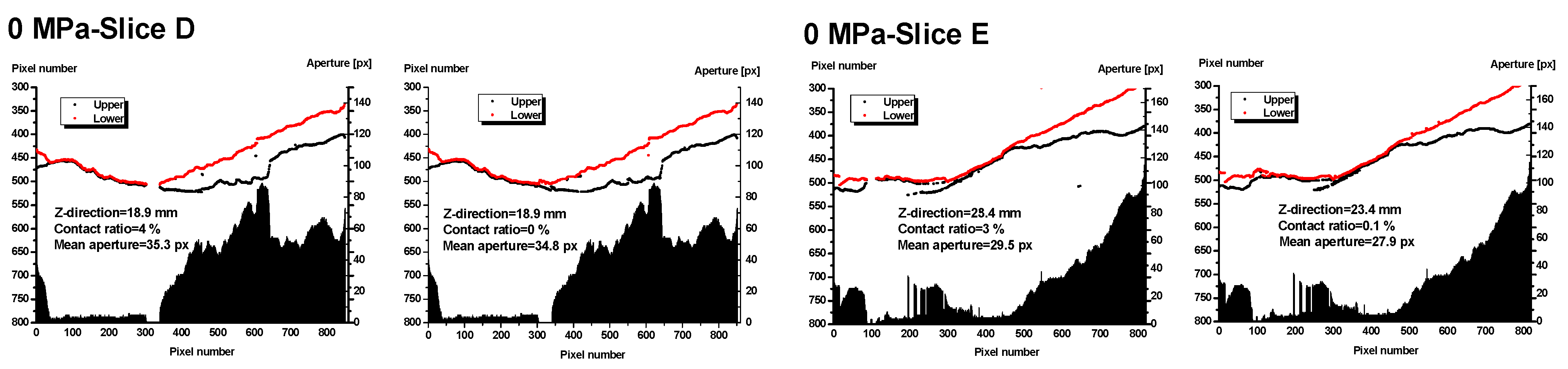
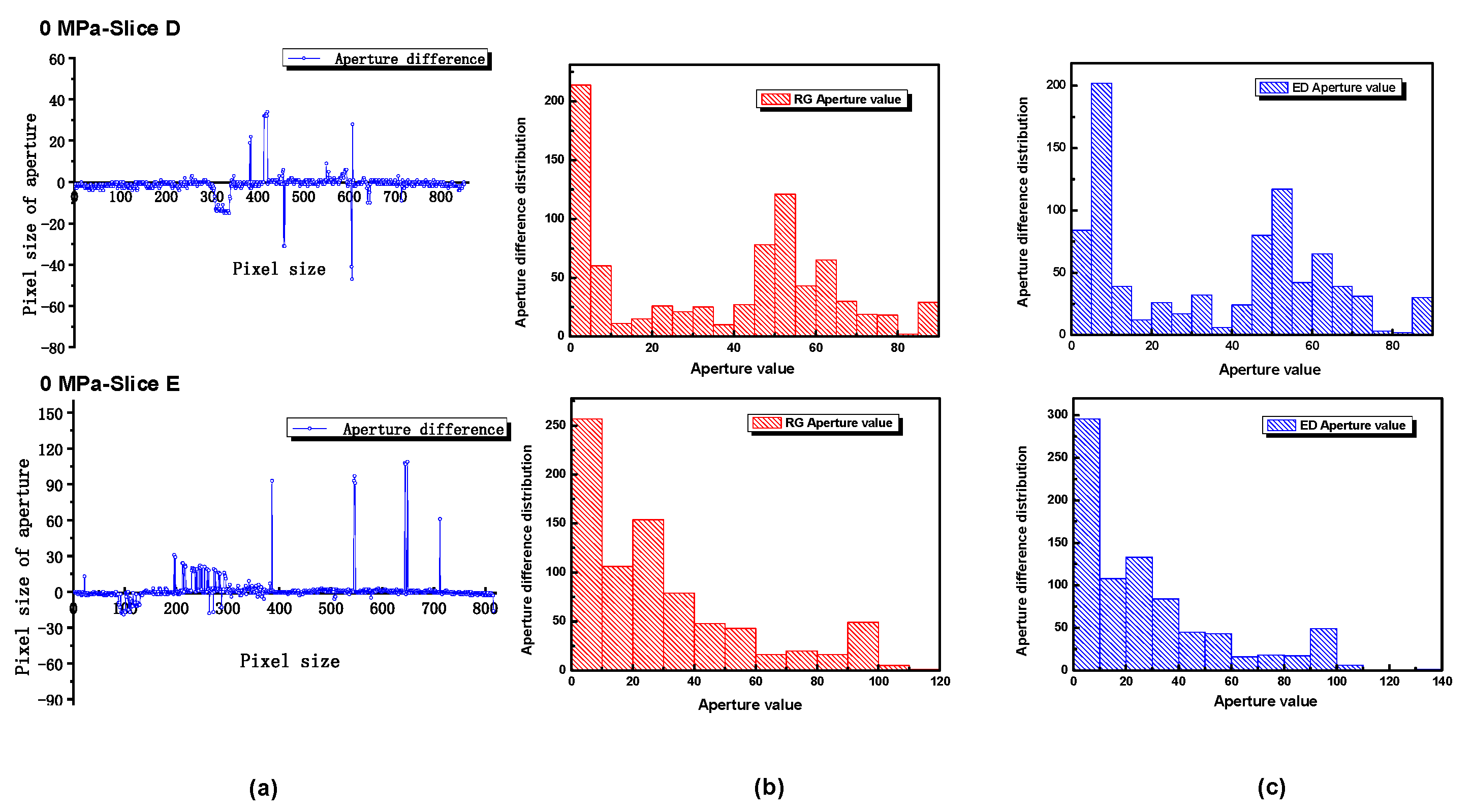
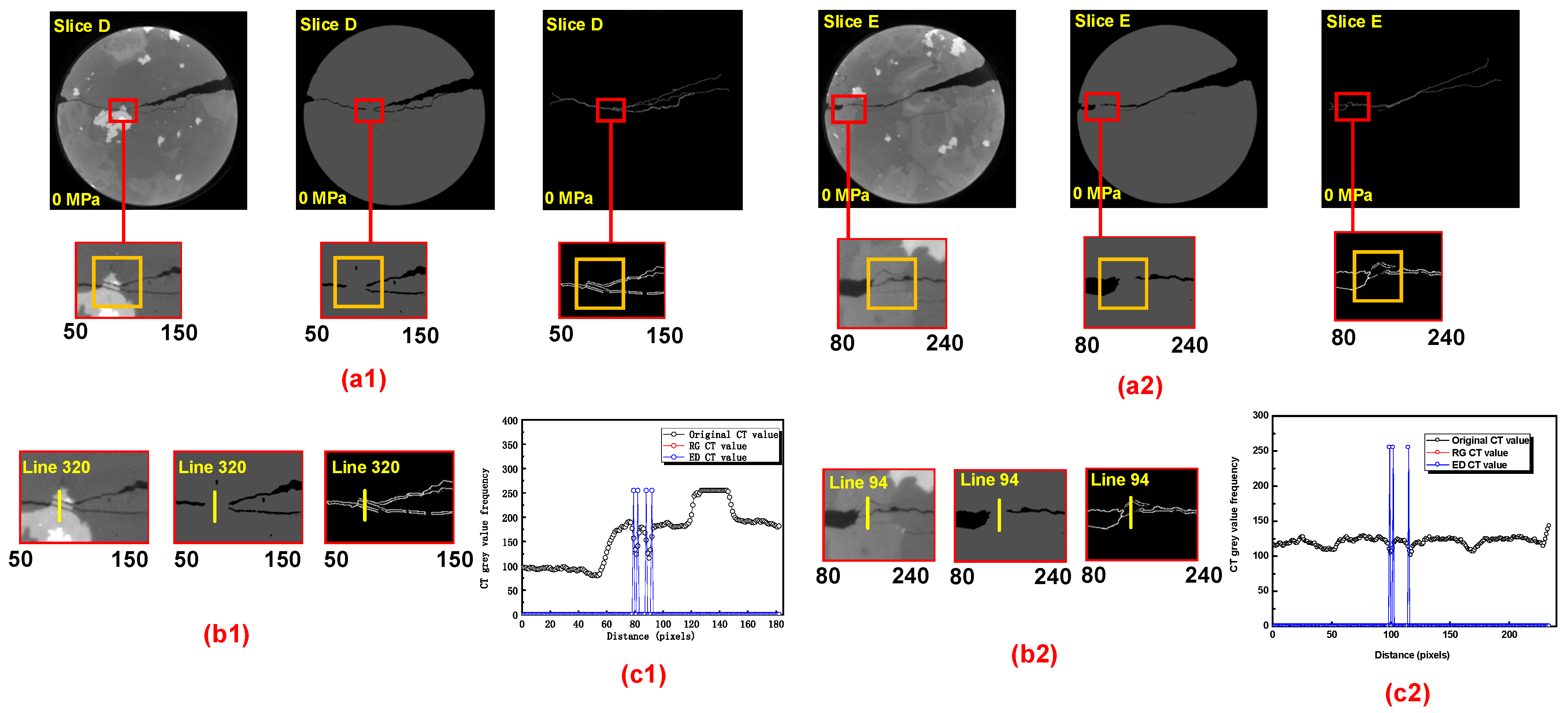
3.1. Image Processing of CT Images without Confining Stress

Figure 10a shows the comparative results of the profile line of aperture boundaries. (i.e., upper and lower fracture surfaces) under the RG and ED method. The black profile represents the fracture surface measured from the region growing method, and the red profile is from the edge detection method. Figure 10b,c represent the fracture apertures and contact area ratios under these two methods. Although the profile line and calculation results are almost the same, the mean aperture value of RG and ED has 0.61 px difference. The values of them are 18 px and 18.61 px, respectively. Meanwhile, the contact area ratio value has 0.1% difference. A slight image identification difference between RG and ED is illustrated in the blue rectangle in Figure 10a. Results show that there is no obvious image identification difference under different image processing methods at 0 MPa. However, a slight calculation difference is generated under these two methods.
From Figure 11, it is noted that an image processing difference may easily generate on the aperture boundary, and an aperture value difference under the RG and ED methods are compared at each pixel number in the x-direction, as shown in Figure 11a. It is obvious that several aperture differences existed, as depicted at the pixel number positions of 300, 450, 550, and 750. The aperture value has a 1.52-pixel size difference after calculation. The aperture differences histogram under the RG and ED methods are illustrated in Figure 11b,c. The result shows that the aperture value has an apparent difference from 0 to 20. It can be guessed that the aperture closure position may result in this slight difference. The RG result shows that the aperture value of 0~5 is larger than the value under the ED method. Although the RG method has an advantage in identifying the aperture closure position, the ED method has a dominant position in grasping the low density of a rock region in the CT image. The low density of a rock region is estimated as the continuous voxel of the rock region under the RG method. Therefore, the aperture value of 0~5 under the ED method is relatively lower than the RG result.
In order to verify the image processing difference, a relatively large aperture value difference (i.e., at the pixel number positions of 300, 450, 550, and 750) is further analyzed. Those pixel positions can be directly identified from the original CT image and the segmentation CT images. Therefore, the intercepted CT images are picked up and magnified, as illustrated in the red rectangular frame in Figure 12a. It clearly shows that the image processing difference existed in these positions. The difference between the original CT image and the CT segmentation images under RG and ED can be ensured. In order to further certify the image processing difference, a profile line is portrayed at the same position (i.e., a position located on the pixel number of 459–461 in x-direction in different CT images, as shown in Figure 12b). Moreover, a yellow profile line comparative result with the number of 514 is depicted. In addition, a value comparison of profile line 514 is shown in three colors, namely, blue-, black-, and red-color dot lines that represent the value of 514 in CT original, RG, and ED segmentation images in Figure 12c.
From Figure 11, the fact of different image processing methods resulting in different CT image identification results is confirmed. Those intercepted CT images are located on the pixel number positions that range from 330~358, 454~528, to 588~626 in each CT image in the x-direction (i.e., original CT image, RG segmentation image, ED segmentation image), as presented in Figure 12a. Especially, the CT image difference is primely presented in the pixel number range from 454 to 528, and the original CT image shows that the low-density position exists in the range of 454–528. It is further illustrated through the difference of yellow profile line 514 in Figure 12b. The continuity of the rock voxel and the aperture closure in this position are supposed. This low-density position is segmented as an aperture open under the RG method. In contrast, the boundary of this low-density position is identified as a rock continuity using the ED method. Moreover, from the comparative result of line 514, it can be seen that in the distance of 70 to 80 in the original CT image in Figure 12c, the result shows that the CT gray value is relatively lower. It may correspond to the aperture open position. Compared with the gray value of the original CT image, both of the RG and ED images show that the gray values in the distance of 70 to 80 are equal to 0. Therefore, the aperture open position is verified. The RG method shows that the gray value position is relatively larger. However, the gray value under the ED method corresponds well with that in the original CT image. From observing 0 MPa Slice A, it is noted that different image processing methods are a main reason for influencing the calculation result, and the aperture value difference may easily occur on the aperture closed position. To further verify the image processing and the aperture difference, CT image analysis is separated with two steps: Firstly, several CT image slices are extracted and checked from different positions in rock sample CT images without confining stress. Secondly, the aperture closure influence under confining stress is also studied.
In order to further demonstrate the image processing difference, the CT images of Slice B~E at 0 MPa are extracted and analyzed. The image segmentation results of each CT image are shown in Figure 13. The aperture boundary is successfully identified under these two methods. Compared with Slice A, fractures of Slice B~E at 0 MPa show that the plural aperture boundaries are recognized in the original CT image, which may result in an obvious image processing difference occurring on the segmented CT images. Moreover, the CT image shows that the fracture aperture boundary at different positions often has complicated shapes. The purpose of image processing is to auto-trace the aperture boundary, and the most difficult target is the aperture boundary extraction. The CT image segmentation algorithms generally depend on the CT gray values, and different gray values are used to judge the discontinuity and the similarity in a region. The image processing goal is to partition different regions in the CT image depending on the gray value abrupt variation.
Results show that a bit difference occurs on each CT slice. Although the profile continuity under two methods is confirmed at each slice, several image identification differences also appear. The complicated shape of the aperture boundary leads to different image identification, especially on a relative aperture closed position, as presented in the comparative result of Slice D and Slice E in Figure 13. A relative aperture closed position is a difficult target on the boundary extraction.
To further check the aperture boundary difference under the RG and ED methods, relative aperture closure CT slices are chosen for comparison. After calculating the fracture aperture and contact area ratio values, the result shows that a large image processing difference occurred on Slice D~E at 0 MPa, as shown in Figure 14. Several aperture boundary positions are identified as the aperture closed under RG. Moreover, the contact area ratio value of RG is revealed to be a bit higher, and the values of Slice D and Slice E are equal to 4% and 3%, respectively. In contrast, the contact area ratio values of Slice D and E are equal to 0% and 0.1%, respectively. It is confirmed that a bit of difference happens. The RG method has a characteristic of assuring the spatial continuity of the same region after the image segmentation, which may lead to the relative low-density areas assimilating into the rock region. Therefore, the aperture boundary is neglected after RG segmentation.
The aperture value difference of Slice D~E at 0 MPa is depicted in Figure 15. Figure 15a shows the aperture value difference under the RG and ED methods. The result of Slice D illustrates that the aperture value difference occurred in the x-direction with the pixel number of 400~600, and the result of Slice E shows that a relatively large aperture value difference occurs in the x-direction with the pixel number range from 400 to 700. Moreover, the aperture difference distribution of Slice D is more significant in the value of 0~5, as shown in Figure 15b,c. However, the aperture value difference of Slice E is more diverse in the value of 0–10. In general, it can be confirmed that there is a significant difference happening in the aperture value calculation under different image processing methods, and the aperture closed position under each condition should be clarified further.
The original CT images and the CT segmentation images of Slice D and Slice E under the RG and ED methods are shown in Figure 16. From Figure 16(a1,a2), it is shown that the aperture difference occurs on each CT image slice. The aperture closed position is chosen as an analytical object from each CT image slice. (i.e., the position of Slice D which is located in the pixel number range from 50 to 150 in Figure 16(a1), and Slice E is located in 80–240 in Figure 16(a2) in the x-direction). A significant difference between RG and ED segmentation images is observed. RG identifies different density of the rock as the same density from the original CT images, and they are recognized as the aperture closure; meanwhile, the ED method can grasp the aperture boundary of the high- or the low-density areas from the original CT images.
The image segmentation result indicates that the aperture value difference easily happens on the different density areas of rocks, or on the aperture closed positions. Therefore, the profile line (i.e., line 320 of 0 MPa Slice D, and line 94 of 0 MPa Slice E) are chosen and compared, as shown in Figure 16(b1,b2). From the comparative results, it is shown that the ED method successfully identifies the aperture boundary, and the range of the profile line is quite similar to the original CT image. In contrast, several image misidentifications occur after RG segmentation. From observing 0 MPa Slice D~E, several aperture open positions are misidentified as the aperture closed, and the profile line value is equal to 0, i.e., with the aperture closed, as presented in Figure 16(c1,c2). Those misidentifications may also result in a great difference in the contact area ratio value in Figure 13. The contact area ratio value has a big difference in those misidentifications.
At 0 MPa, different image processing methods have the capability of distinguishing the bits and pieces of the fracture surface properly, and the aperture difference is confirmed after image segmentation. The discontinuity and the similarity in a CT image determine the partition of a CT image. The RG method has a characteristic of partitioning the similar voxel into the same region according to a set of an initial value. The ED method is one method for searching intensity discontinuities (i.e., the aperture boundary) in a CT image. Based on these features, the image processing result shows that the aperture value has an obvious difference, especially on a relative aperture closed position. Compared with the image segmentation results at 0 MPa, different density areas of the rock and the aperture closure may result in the aperture difference. However, the aperture closure influence should be further verified when the external confining stress is applied on the rock fractures. The confining stress influence may also have a big effect on the image processing result. Therefore, the image processing of the rock fracture under confining stress needs to be focused. The aperture becomes much narrower, and it becomes more difficult for image identification from the original CT images.

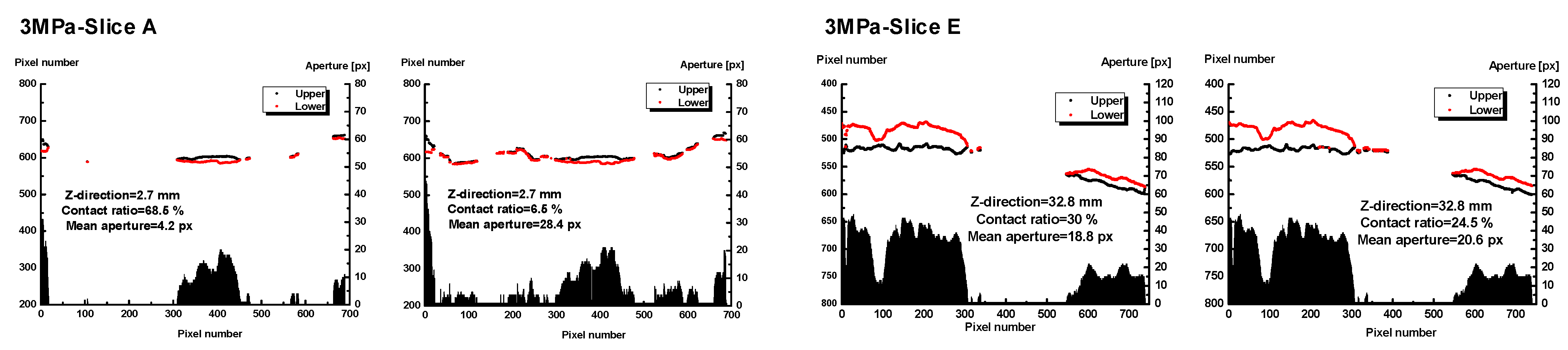
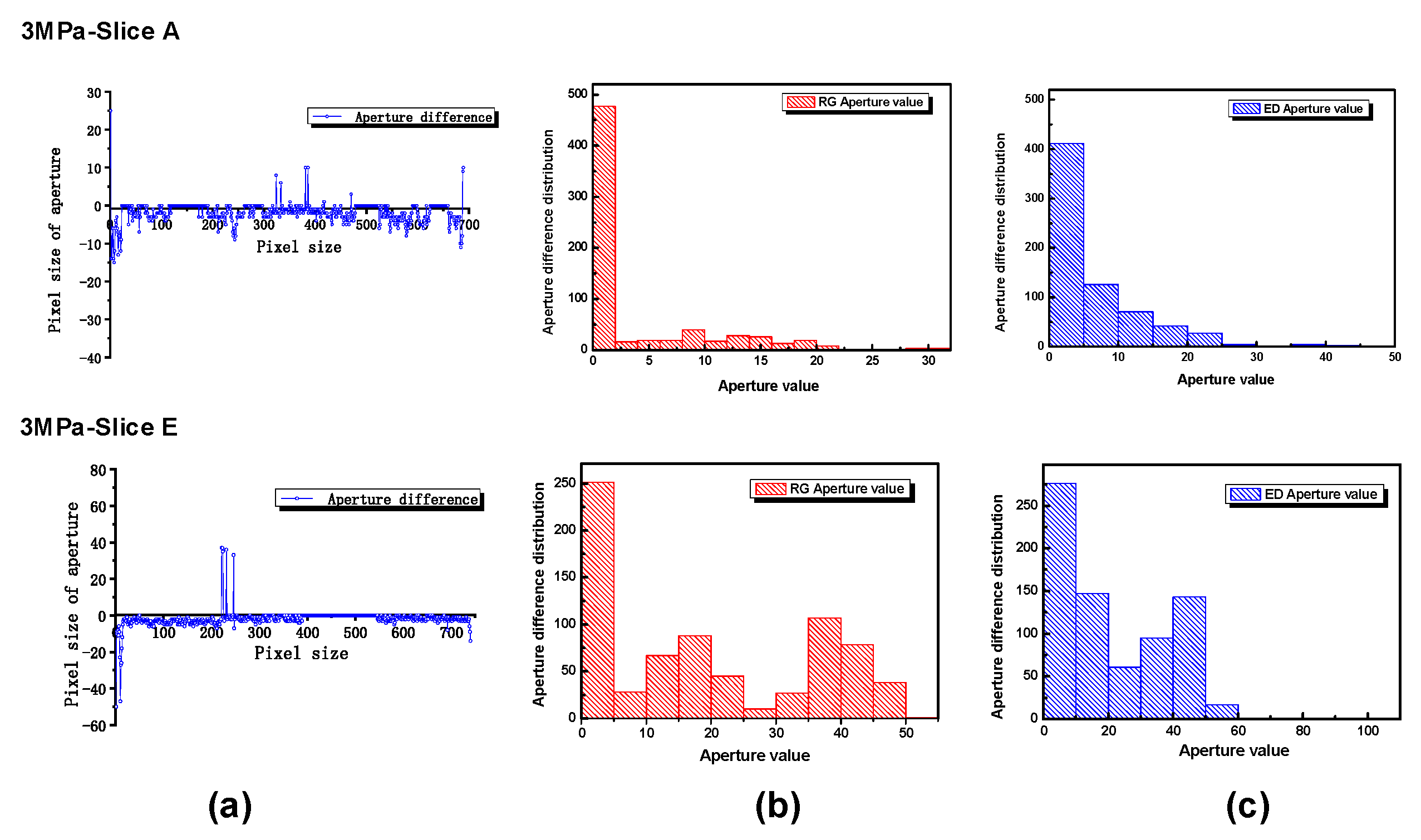
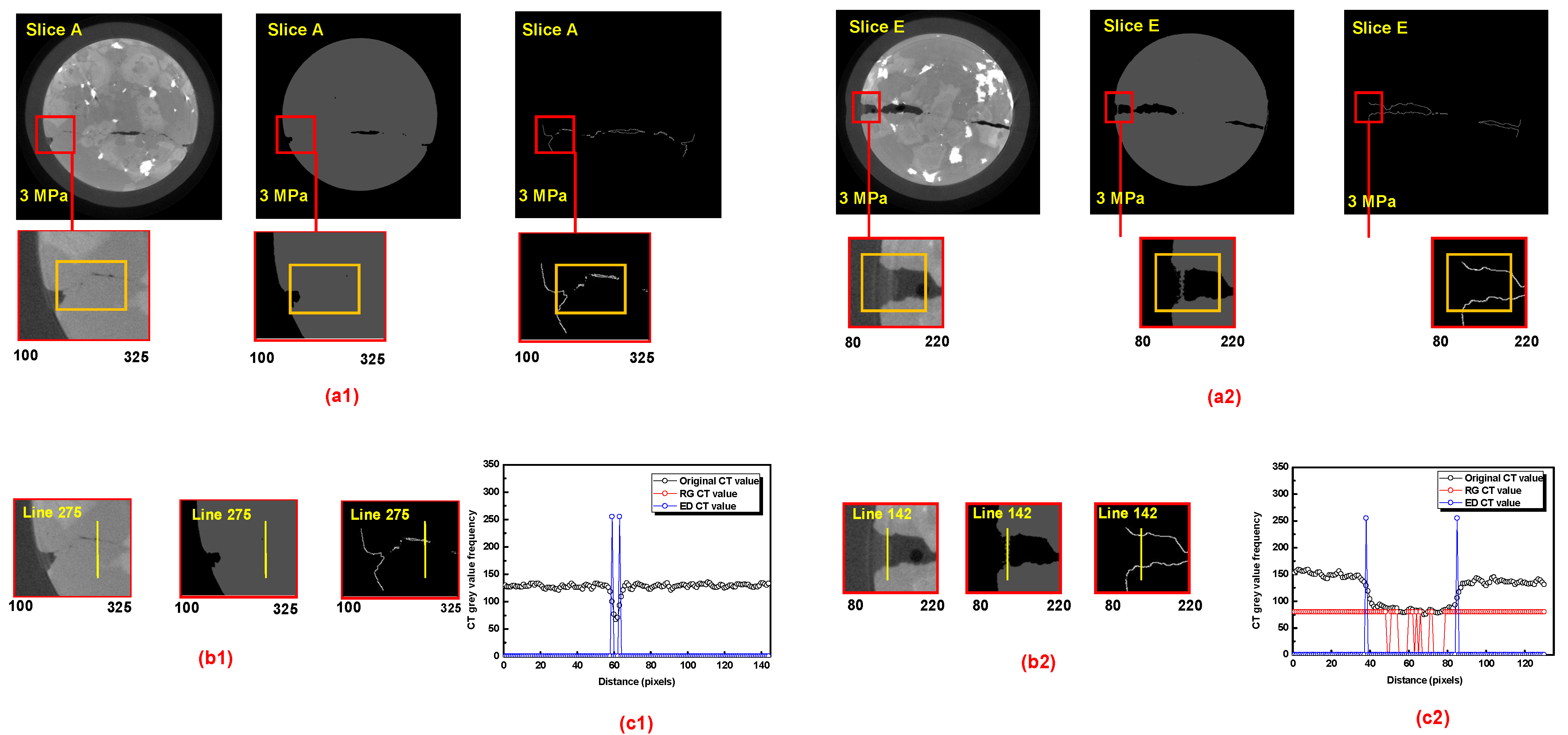
3.2. Image Processing of CT Images under Confining Stress

From observing the image processing results of CT images at 0 MPa, it can be noted that some image identification differences are easily generated on the aperture closed positions. In this section, CT images at 3.0 MPa are extracted from the rock sample and checked under the RG and ED methods.
The segmented CT images at 3.0 MPa (i.e., Slice A~E under RG and ED methods) are depicted in Figure 17. At 3.0 MPa, a membrane is set outside of the rock sample and used to avoid external thermal influence. Therefore, an external membrane region occurs around the rock and it may affect the image partition. The shape of the aperture boundary is shown to be more complicated to identify under confining stress. Compared with the original CT images, several RG segmentation images illustrate that the aperture becomes more contacted. On the one hand, it poses a great challenge in identifying the aperture closed positions due to the voxel connectivity. The similarity voxel value which is located in the different region partition into a set of predefined values. On the other hand, an abrupt variation in intensity value is difficult to occur in an aperture closed area, which will result in the discontinuity region being impossible to distinguish.
The CT image segmentation results show that the aperture boundary of Slice A~C become much narrower at 3.0 MPa. It is noted that the ED segmentation is more obvious than the RG one at 3.0 MPa. Contrarily, 3 MPa Slice D and E have a bit of a difference because the aperture becomes open at the lower part of the rock sample. The result demonstrates that the ED method has preferable ability to grasp the intensity discontinuity positions from the original CT image. It concentrates a lot on the immediate change around the object. Therefore, the boundary profile of the aperture is better distinguished although the aperture becomes much narrower under an external stress. However, several aperture boundary profiles after RG segmentation are omitted under higher confining stress, especially in observing the aperture closed CT image such as Slice A at 3.0 MPa. In order to clarify this difference, the relative aperture closed CT image slice (i.e., 3 MPa Slice A) and the relative aperture open CT image slice (i.e., 3 MPa Slice E) are selected as a comparative object. Then, the aperture and the contact area ratio value at 3 MPa are calculated.
The aperture and the contact area ratio value results are shown in Figure 18. A significant difference in this result is illustrated. Particularly, the calculation difference of Slice A is much larger. Several aperture boundary profiles are omitted after RG segmentation. In contrast, the aperture boundary profile of ED is shown more clearly. The result of Slice A shows that the contact area ratio value of RG is higher than that of ED. They are 68.5% and 6.5% after RG and the ED segmentation, respectively. This is almost 10 times different when the confining stress becomes higher. Moreover, the result of 3 MPa Slice E shows that the contact area ratio values are 30% and 24.6% after RG and ED segmentation, respectively. It also generates a calculation difference although it does not present a big difference in the aperture boundary identification. Therefore, the inaccurate image segmentation result may easily occur under a higher confining stress, and it is difficult to correctly achieve the internal rock fracture information.
The aperture boundary is a linear curved object, and some image misidentifications may appear due to the image noise generated around the aperture boundary or on the rough profile. The aperture value difference and the histogram at 3.0 MPa are illustrated in Figure 19. The aperture difference of Slice A generates a pixel number of around 300 to 400 at 3 MPa, and a big aperture difference of Slice E occurs in the pixel size of around 200 to 300, as shown in Figure 19a. A membrane region located around the rock may also result in image segmentation noise, which will also produce an aperture value difference. Moreover, the aperture becomes narrower, and this will result in a more rough boundary profile. Therefore, the boundary profile of Slice A is influenced by a relatively low-density value around the rock.
From observing the histogram results of 3 MPa Slice A and Slice E, it can be seen that the aperture value is completely different under RG and ED segmentation. A large aperture value difference is observed through a comparison with Slice A and E, as shown in Figure 19b,c. Several rough boundary profiles and image noise are admitted under different image processing methods. This great difference also corresponds to the image calculation results in Figure 18. It is also illustrated that the low-density area exists within the aperture, and it becomes much harder to distinguish. Moreover, at 3.0 MPa, a much narrower aperture will result in a change of grayscales. Therefore, the image processing becomes much more difficult when analyzing all of these characteristics that occurred on the fractured rock CT image.
Several aperture positions of Slice A and Slice E at 3.0 MPa are picked up and employed to make a comparison in Figure 20. After RG segmentation, results show that some void positions are difficult to be distinguished. Some void regions are misrecognized and assimilated into the rock region, and this results in image misidentification, as presented in Figure 20(a1,a2). Moreover, this will also result in the inaccurate calculation of the contact area ratio.
Image misidentification positions are also selected and presented as follows: In the x-direction, the aperture position of Slice A with the pixel number of 100~335 in Figure 20(a1) and the aperture position of Slice E with the pixel number of 80~220 in Figure 20(a2) are presented with several misidentifications. These positions on the original CT images and the CT segmentation images under RG and ED are compared. Results shows that the Slice A has a large difference in RG and ED at 3.0 MPa. The RG segmentation misrecognizes some different regions around the void region as the rock voxel continuity, and the aperture boundary is neglected. In contrast, ED only concentrates on the boundary, and the segmentation result is quite similar to that of the original CT image. Moreover, the yellow profile line is picked up and compared, i.e., profile line 275 of Slice A in the x-direction, and profile line 142 of Slice E in the x-direction, as depicted in Figure 20(b1,b2). From observing the 3 MPa Slice A, it is presented that the ED profile line is well reflected from the original CT image. However, the RG profile line value is equal to 0, as shown in Figure 20(c1), which is corresponds to the RG segmentation results. The relative aperture narrow position is misrecognized as the connectivity of the rock region. However, the 3 MPa Slice E also shows a significant difference in the profile line comparison. The profile line under the RG method shows an oscillation variation in Figure 20(c2). However, the profile line value under ED is equal to 0, which means this position is the aperture open position. The value of this position ranges from the pixel number of 40~85, which also corresponds to the aperture position in the original CT image.

3.3. Summary

From observing the analysis results, it is confirmed that two different image processing methods have a significant difference on the aperture boundary identification. Two kinds of experimental CT images are used, i.e., the CT images at 0 MPa and at 3.0 MPa. The aperture value generates a bit difference at 0 MPa. In contrast, the aperture difference presents itself as more significant at 3.0 MPa when the aperture becomes much narrower under an external confining stress. Moreover, the RG method concentrates on the voxel connectivity of the same region. However, this will result in several misidentifications of the fracture aperture, and the voxel that existed around the discontinuity positions cannot be well recognized. The aperture boundary is omitted especially when applying the confining pressure. However, the ED segmentation method has a good property of recognizing the fracture aperture boundary at fine scales. The fracture undulation trend under a high stress and the aperture closure also can be extracted successfully from the original CT images. It is successful in avoiding the noise of the neighboring voxels and achieving more accurate image processing results than those of the RG segmentation method.

4. Conclusions

In this study, there is a new attempt in identifying the rock fracture aperture boundary under virous conditions using different image processing methods. Two image processing methods (region growing method and edge detection method) are applied to estimate the fracture aperture and the contact area ratio. The internal structural information of the fractures is calculated, and results show that different image processing methods have an impact on fracture recognition. The fracture aperture and the contact area ratio are two representation parameters for estimating internal fracture structure information, and this calculation result shows that both the RG and ED method can grasp the aperture condition well from the original CT image. Both of the two methods illustrate that the fracture contact area ratio becomes larger, and the aperture becomes closed from 0 MPa to 3.0 MPa, which corresponds to the original CT experimental results. Namely, the aperture becomes more closed at a relatively high confining condition. This also reflects the accuracy of image processing results under these two methods. Moreover, the contact area ratio has less than 1% difference under the RG and ED methods at 0 MPa, but it has a larger than 10 times difference at 3.0 MPa. It is confirmed that the confining stress has a significant influence on grasping the fracture aperture boundary. However, there is still a limitation in the present study because the edge detection method was only applied on low-permeability granite rock. Therefore, future research should verify this method applied on some other rock types such as sedimentary or metamorphic rocks with/without confining conditions. In addition, the fracture aperture becomes more closed under a higher confining condition, and the other accurate image processing methods should be further studied and widely applied in identifying rock fracture structures and fracture positions in the rock engineering field. This is also a better channel for preventing underground engineering disasters in the future.

Author Contributions

Conceptualization, C.S. and T.L.; methodology, T.L.; software, H.L.; validation, C.S. and X.H.; formal analysis, H.L.; investigation, T.L.; resources, C.S.; data curation, C.S. and X.H.; writing—original draft preparation, C.S.; writing—review, C.S. and X.H.; editing, C.S. and X.H.; visualization, C.S., T.L. and X.H. All authors have read and agreed to the published version of the manuscript.

Funding

This work was gratefully supported by the Fundamental Research Funds for Zhejiang Provincial Universities and Research Institutes (Grants Nos. JX6311040523).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Tsang, C.F.; Bernier, F.; Davies, C. Geo-hydromechanical processes in the excavation damaged zone in crystalline rock, rock salt, and indurated and plastic clays—In the context of radioactive waste disposal. Int. J. Rock Mech. Min. Sci. 2005, 42, 109–125. [Google Scholar] [CrossRef]
  2. Ellis, B.R.; Fitts, J.P.; Bromhal, G.S.; McIntyre, D.L.; Rappero, R.; Peters, C.A. Dissolution-driven permeability reduction of fractured carbonate caprock. Environ. Eng. Sci. 2013, 30, 187–193. [Google Scholar] [CrossRef] [PubMed]
  3. Lei, Z.H.; Zhang, Y.L.; Lin, X.J.; Shi, Y.; Zhang, Y.H.; Zhou, L.; Shen, Y.P. A thermo-hydro-mechanical simulation on the impact of fracture net-work connectivity on the production performance of a multi-fracture enhanced geothermal system. Geothermics 2024, 122, 103070. [Google Scholar] [CrossRef]
  4. McGuire, T.P.; Elsworth, D.; Karcz, Z. Experimental measurements of stress and chemical controls on the evolution of fracture permeability. Transp. Porous Med. 2013, 98, 15–34. [Google Scholar] [CrossRef]
  5. Xie, Y.C.; Liao, J.X.; Zhao, P.F.; Xia, K.W.; Li, C.B. Effects of fracture evolution and non-Darcy flow on the thermal performance of enhanced geothermal system in 3D complex fractured rock. Int. J. Min. Sci. Technol. 2024, 34, 443–459. [Google Scholar] [CrossRef]
  6. Silveira, C.S.d.; Alvim, A.C.M.; Oliva, J.d.J.R. Radionuclide Transport in Fractured Rock: Numerical Assessment for High Level Waste Repository. Sci. Technol. Nucl. Install. 2013, 2013, 827961. [Google Scholar] [CrossRef]
  7. Elsworth, D.; Yasuhara, H. Short-Timescale Chemo-Mechanical Effects and their Influence on the Transport Properties of Fractured Rock. Pure Appl. Geophys. 2006, 163, 2051–2070. [Google Scholar]
  8. Danko, G.; Bahrami, D. A new T-H-M-C model development for discrete-fracture EGS studies. GRC Trans. 2012, 36, 383–392. [Google Scholar]
  9. Ghassemi, A. A review of some rock mechanics issues in geothermal reservoir development. Geotech. Geol. Eng. 2012, 30, 647–664. [Google Scholar] [CrossRef]
  10. Abdullah, S.; Wang, K.; Chen, X.H.; Khan, M. The impact of thermal transport on reactive THMC model for carbon capture and storage. Geomech. Energy Environ. 2023, 36, 100511. [Google Scholar] [CrossRef]
  11. Xu, H.R.; Liu, G.H.; Zhao, Z.H.; Ma, F.; Wang, G.L.; Chen, Y.D. Coupled THMC modeling on chemical stimulation in fractured geothermal reservoirs. Geothermics 2024, 116, 102854. [Google Scholar] [CrossRef]
  12. Polak, A.; Elsworth, D.; Yasuhara, H.; Grader, A.; Halleck, P. Permeability reduction of a natural fracture under net dissolution by hydrothermal fluids. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
  13. Yasuhara, H.; Polak, A.; Mitani, Y.; Grader, A.S.; Halleck, P.M.H.; Elsworth, D. Evolution of fracture permeability through fluid–rock reaction under hydrothermal conditions. Earth Planet. Sci. Lett. 2006, 244, 186–200. [Google Scholar] [CrossRef]
  14. Yasuhara, H.; Elsworth, D. Compaction of a Rock Fracture Moderated by Competing Roles of Stress Corrosion and Pressure Solution. Pure Appl. Geophys. 2008, 165, 1289–1306. [Google Scholar] [CrossRef]
  15. Joseph, P.M.; Spital, R.D. A method for correcting bone induced artifacts in computed tomography scanners. J. Comput. Assist. Tomogr. 1978, 2, 100–108. [Google Scholar] [CrossRef]
  16. Vig, R.; Agrawal, S.; Kaur, J. A Comparative Analysis of Thresholding and Edge Detection Segmentation Techniques. Int. J. Comput. Appl. 2012, 39, 29–34. [Google Scholar]
  17. Hata, A.; Yanagawa, M.; Honda, O.; Kikuchi, N.; Miyata, T.; Tsukagoshi, S.; Uranishi, A.; Tomiyama, N. Effect of Matrix Size on the Image Quality of Ultra-high-resolution CT of the Lung: Comparison of 512 × 512, 1024 × 1024, and 2048 × 2048. Acad Radiol. 2018, 25, 869–876. [Google Scholar] [CrossRef]
  18. Jumanazarov, D.; Alimova, A.; Ismoilov, S.K.; Atamurotov, F.; Abdikarimov, A.; Olsen, U.L. Method for the determination of electron density from multi-energy X-ray CT. NDT E Int. 2024, 145, 103105. [Google Scholar] [CrossRef]
  19. Van, G.M.; Swennen, R.; David, P. Quantitative coal characterisation by means of microfocus X-ray computer tomography, colour image analysis and back-scattered scanning electron microscopy. Int. J. Coal Geol. 2001, 46, 11–25. [Google Scholar]
  20. Ketcham, R.A.; Slottke, D.T.; Sharp, J.M. Three-dimensional measurement of fractures in heterogeneous materials using high-resolution X-ray computed tomography. Geosphere 2010, 6, 499–514. [Google Scholar] [CrossRef]
  21. Farough, A.; Moore, D.E.; Lockner, D.A.; Lowell, R.P. Evolution of fracture permeability of ultramafic rocks undergoing serpentinization at hydrothermal conditions: An experimental study. Geochem. Geophys. Geosyst. 2016, 17, 44–55. [Google Scholar] [CrossRef]
  22. Okamoto, A.; Tanaka, H.; Watanabe, N.; Saishu, H.; Tsuchiya, N. Fluid Pocket Generation in Response to Heterogeneous Reactivity of a Rock Fracture Under Hydrothermal Conditions. Geophys. Res. Lett. 2017, 44, 10,306–10,315. [Google Scholar] [CrossRef]
  23. Kumaria, W.G.P.; Ranjith, P.G.; Pererab, M.S.A.; Li, X. Hydraulic fracturing under high temperature and pressure conditions with micro CT applications: Geothermal energy from hot dry rocks. Fuel 2018, 230, 138–154. [Google Scholar] [CrossRef]
  24. Polak, A.; Elsworth, D.; Liu, J.H.; Grader, A.S. Spontaneous switching of permeability changes in a limestone fracture with net dissolution. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
  25. Yasuhara, H.; Kinoshita, N.; Lee, D.S.; Choi, J.H.; Kishida, K. Long-term observation of permeability in sedimentary rocks under high-temperature and stress conditions and its interpretation mediated by microstructural investigations. Water Resour. Res. 2015, 51, 5425–5449. [Google Scholar] [CrossRef]
  26. Bertels, S.P.; Dicarlo, D.A.; Blunt, M.J. Measurement of aperture distribution, capillary pressure, relative permeability, and in situ saturation in a rock fracture using computed tomography scanning. Water Resour. Res. 2001, 37, 649–662. [Google Scholar] [CrossRef]
  27. Gouze, P.; Noiriel, C.; Bruderer, C.; Loggia, D.; Leprovost, R. X-ray tomography characterization of fracture surfaces during dissolution. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
  28. Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
  29. Niu, Y.S.; Song, J.F.; Zou, L.L.; Yan, Z.X.; Lin, X.L. Cloud detection method using ground-based sky images based on clear sky library and superpixel local threshold. Renew. Energy 2024, 226, 120452. [Google Scholar] [CrossRef]
  30. Elen, A.; Dönmez, E. Histogram-based global thresholding method for image binarization. Optik 2024, 306, 171814. [Google Scholar] [CrossRef]
  31. Karpyn, Z.T.; Alajmi, A.; Radaelli, F.; Halleck, P.M.; Grader, A.S. X-ray CT and hydraulic evidence for a relationship between fracture conductivity and adjacent matrix porosity. Eng. Geol. 2009, 103, 139–145. [Google Scholar] [CrossRef]
  32. Deng, H.; Fitts, J.P.; Peters, C.A. Quantifying fracture geometry with X-ray tomography: Technique of Iterative Local Thresholding (TILT) for 3D image segmentation. Comput. Geosci. 2016, 20, 231–244. [Google Scholar] [CrossRef]
  33. Tachi, Y.; Ito, T.; Akagi, Y.; Satoh, H.; Martin, A.J. Effects of Fine-Scale Surface Alterations on Tracer Retention in a Fractured Crystalline Rock From the Grimsel Test Site. Water Resour. Res. 2018, 54, 9287–9305. [Google Scholar] [CrossRef]
  34. Lai, J.; Wang, G.W.; Fan, Z.; Chen, J.; Qin, Z.Q.; Xiao, C.W.; Wang, S.C.; Fan, X.Q. Three-dimensional quantitative fracture analysis of tight gas sandstones using industrial computed tomography. Sci. Rep. 2017, 7, 1825. [Google Scholar] [CrossRef]
  35. Li, M.Y. Creep characteristics analysis of asphalt mixture in meso-scale based on Drucker-Prager model. J. North China Inst. Sci. Technol. 2017, 14, 96–100. [Google Scholar]
  36. Fathani, T.F.; Legono, D.; Karnawati, D. A Numerical Model for the Analysis of Rapid Landslide Motion. Geotech. Geol. Eng. 2017, 35, 1–16. [Google Scholar] [CrossRef]
  37. Yehuda, N.G.; Nachshon, U.; Assouline, S.; Mau, Y. The effect of mechanical compaction on the soil water retention curve: Insights from a rapid image analysis of micro-CT scanning. CATENA 2024, 242, 108068. [Google Scholar] [CrossRef]
  38. Kong, M.Y.; Wang, F. Comparative analysis of computer-aided imaging col-laboration: MRI versus CT for detection of knee joint injuries in athletes. J. Radiat. Res. Appl. Sci. 2024, 17, 100960. [Google Scholar]
  39. Shubhangi, D.C.; Chinchansoor, R.S.; Hiremath, P. Edge Detection of Femur Bones in X-ray images—A comparative study of Edge Detectors. Int. J. Comput. Appl. 2012, 42, 13–16. [Google Scholar]
  40. Mahendran, S.K. A Comparative Study on Edge Detection Algorithms for Computer Aided Fracture Detection Systems. Int. J. Eng. Innov. Technol. 2012, 2, 191–193. [Google Scholar]
  41. Jiang, X.Y.; Binke, H. Edge Detection in Range Images Based on Scan Line Approximation. Comput Vis Image Und. 1999, 73, 183–199. [Google Scholar] [CrossRef]
  42. Rong, W.B.; Li, Z.J.; Zhang, W. An Improved Canny Edge Detection Algorithm. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014. [Google Scholar]
  43. Canny, J. A computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679698. [Google Scholar] [CrossRef]
  44. Monicka, S.G.; Manimegalai, D.; Karthikeyan, M. Detection of microcracks in silicon solar cells using Otsu-Canny edge detection algorithm. Renew. Energy 2022, 43, 183–190. [Google Scholar]
  45. Huang, M.L.; Liu, Y.L.; Yang, Y.M. Edge detection of ore and rock on the sur-face of explosion pile based on improved Canny operator. Alex. Eng. J. 2022, 61, 10769–10777. [Google Scholar] [CrossRef]
  46. Rosenfeld, A.; Kak, A.C. Digital Picture Processing; Academic Press: San Diego, CA, USA, 1982. [Google Scholar]
  47. Xia, Y.J.; Hu, B.X.; Wang, J.G.; Brown, G. An object-based region-growing phase unwrapping method for mapping vertical displacement in permafrost landscapes. Int. J. Appl. Earth Obs. 2024, 131, 103975. [Google Scholar] [CrossRef]
  48. Firouznia, M.; Koupaei, J.A.; Faez, K.; Jabdaragh, S.A.; Gunduz-Demir, C. Advanced fractal region growing using Gaussian mixture models for left atrium segmentation. Digit. Signal Process. 2024, 147, 104411. [Google Scholar] [CrossRef]
  49. Zucker, S.W. Region growing: Childhood and adolescence. Comput. Graph. Image Process. 1976, 5, 382–399. [Google Scholar] [CrossRef]
  50. Fan, J.P.; Zeng, G.H.; Mathurin, B.; Mohand, S.H. Seeded region growing: An extensive and comparative study. Pattern Recogn. Lett. 2005, 26, 1139–1156. [Google Scholar] [CrossRef]
  51. Nahar, M.; Ali, M.S.; Rahman, M.M. Improvement of single seeded region growing algorithm on image segmentation. Glob. J. Comput. Sci. Technol. 2018, 18, 15–22. [Google Scholar]
  52. Reddy, D.A.; Roy, S.; Kumar, S.; Tripathi, R. A scheme for effective skin disease detection using optimized region growing segmentation and au-toencoder based classification. Procedia Comput. Sci. 2023, 218, 274–282. [Google Scholar] [CrossRef]
  53. Liao, D.; Yang, J.F.; Liao, X.Q.; Fang, C.F.; Zheng, Q.; Wang, W. A detection method of Si3N4 bearing rollers point microcrack defects based on adap-tive region growing segmentation. Measurement 2024, 235, 114958. [Google Scholar] [CrossRef]
  54. Katiyar, S.k.; Arun, P.V. Comparative analysis of common edge detection techniques in context of object extraction. Comput. Vis. Pattern Recognit. 2014, 50, 68–78. [Google Scholar]
Applsci 14 09221 g001
Figure 1. Fracture position in an original CT image has several misidentifications (red areas) by threshold method [27]. (A) Original CT image. (B) Image segmentation after threshold method.
Figure 1. Fracture position in an original CT image has several misidentifications (red areas) by threshold method [27]. (A) Original CT image. (B) Image segmentation after threshold method.
Applsci 14 09221 g001
Applsci 14 09221 g002
Figure 2. Granite sample used in this study.
Figure 2. Granite sample used in this study.
Applsci 14 09221 g002
Applsci 14 09221 g003
Figure 3. Triaxial cell coupled with microfocus X-CT (granite sample is fixed into the triaxial cell and faced to X-ray).
Figure 3. Triaxial cell coupled with microfocus X-CT (granite sample is fixed into the triaxial cell and faced to X-ray).
Applsci 14 09221 g003
Applsci 14 09221 g004
Figure 4. The extracted CT images (Slice A to Slice E) from the granite rock sample.
Figure 4. The extracted CT images (Slice A to Slice E) from the granite rock sample.
Applsci 14 09221 g004
Applsci 14 09221 g005
Figure 5. The principle of region growing method in separating a CT image (yellow color represents the rock phase, and gray color is the void phase). (a) Initial seed voxel of rock. (b) Neighbor voxels within the tolerance of rock. (c) Neighbor voxels in the rock criteria. (d) Neighbor voxels not in the rock criteria. (e) Rock seed group search. (f) RG segmentation result.
Figure 5. The principle of region growing method in separating a CT image (yellow color represents the rock phase, and gray color is the void phase). (a) Initial seed voxel of rock. (b) Neighbor voxels within the tolerance of rock. (c) Neighbor voxels in the rock criteria. (d) Neighbor voxels not in the rock criteria. (e) Rock seed group search. (f) RG segmentation result.
Applsci 14 09221 g005
Applsci 14 09221 g006
Figure 6. Histogram comparison between original CT image and RG segmentation. (Black dot chart line is the original CT value of void phase, black dashed line is the normal distribution of void phase, red dot chart line is the original CT value of rock phase, and red dashed line is the normal distribution of rock phase.)
Figure 6. Histogram comparison between original CT image and RG segmentation. (Black dot chart line is the original CT value of void phase, black dashed line is the normal distribution of void phase, red dot chart line is the original CT value of rock phase, and red dashed line is the normal distribution of rock phase.)
Applsci 14 09221 g006
Applsci 14 09221 g007
Figure 7. Comparative result of different image processing methods for grasping the aperture boundary of an original CT image (0 MPa Slice A). (a) Different image processing methods for grasping the rock fracture in a CT image. (b) Expanded CT fracture boundaries under those methods.
Figure 7. Comparative result of different image processing methods for grasping the aperture boundary of an original CT image (0 MPa Slice A). (a) Different image processing methods for grasping the rock fracture in a CT image. (b) Expanded CT fracture boundaries under those methods.
Applsci 14 09221 g007
Applsci 14 09221 g008
Figure 8. σ value difference in grasping the rock aperture boundary. (Red frames are the comparative parts of original CT image, edge detection result when σ = 0, and edge detection result when σ= 4).
Figure 8. σ value difference in grasping the rock aperture boundary. (Red frames are the comparative parts of original CT image, edge detection result when σ = 0, and edge detection result when σ= 4).
Applsci 14 09221 g008
Applsci 14 09221 g009
Figure 9. Comparison of different CT images. (a) Original CT image, (b) region growing method (RG) result, (c) edge detection method (ED) result.
Figure 9. Comparison of different CT images. (a) Original CT image, (b) region growing method (RG) result, (c) edge detection method (ED) result.
Applsci 14 09221 g009
Applsci 14 09221 g010
Figure 10. Aperture boundary profiles and calculation results under RG and ED methods. (a) Comparison of aperture boundary profiles; blue frame shows the aperture boundary profile difference under RG and ED methods. (b) Aperture and contact area ratio results (RG). (c) Aperture and contact area ratio results (ED).
Figure 10. Aperture boundary profiles and calculation results under RG and ED methods. (a) Comparison of aperture boundary profiles; blue frame shows the aperture boundary profile difference under RG and ED methods. (b) Aperture and contact area ratio results (RG). (c) Aperture and contact area ratio results (ED).
Applsci 14 09221 g010
Applsci 14 09221 g011
Figure 11. Aperture value difference at 0 MPa. (a) Aperture value difference of Slice A under RG and ED methods. (b) Aperture value histogram (RG). (c) Aperture value histogram (ED).
Figure 11. Aperture value difference at 0 MPa. (a) Aperture value difference of Slice A under RG and ED methods. (b) Aperture value histogram (RG). (c) Aperture value histogram (ED).
Applsci 14 09221 g011
Applsci 14 09221 g012
Figure 12. Comparison of different CT images in different positions. (a) Comparison of different positions in x-direction (i.e., positions at the pixel number of 330~358, 454~528, 588~626, respectively.) (b) Comparison of the profile line in different CT images (i.e., the profile line is picked up from the pixel number equal to 514). (c) Comparison of the value of 514.
Figure 12. Comparison of different CT images in different positions. (a) Comparison of different positions in x-direction (i.e., positions at the pixel number of 330~358, 454~528, 588~626, respectively.) (b) Comparison of the profile line in different CT images (i.e., the profile line is picked up from the pixel number equal to 514). (c) Comparison of the value of 514.
Applsci 14 09221 g012
Applsci 14 09221 g013
Figure 13. CT image comparison under RG and ED methods at 0 MPa (Slice B~E).
Figure 13. CT image comparison under RG and ED methods at 0 MPa (Slice B~E).
Applsci 14 09221 g013
Applsci 14 09221 g014
Figure 14. Comparative result of the aperture boundary profiles under RG and ED methods (0 MPa Slice D~E).
Figure 14. Comparative result of the aperture boundary profiles under RG and ED methods (0 MPa Slice D~E).
Applsci 14 09221 g014
Applsci 14 09221 g015
Figure 15. Aperture value difference of Slice D and Slice E at 0 MPa. (a) Aperture difference under RG and ED methods. (b) Aperture value histogram (RG). (c) Aperture value histogram (ED).
Figure 15. Aperture value difference of Slice D and Slice E at 0 MPa. (a) Aperture difference under RG and ED methods. (b) Aperture value histogram (RG). (c) Aperture value histogram (ED).
Applsci 14 09221 g015
Applsci 14 09221 g016
Figure 16. CT image comparison in different positions of Slice D and Slice E at 0 MPa. (a1,a2) as the comparative results of different positions in x-direction (i.e., positions of Slice D with the pixel number of 80~150, and Slice E is 80~240, respectively.). (b1,b2) are the profile line comparative results of different CT images (i.e., the profile line of Slice D is picked up from the pixel number equal to 320 in Slice D and Slice E is 94, respectively). (c1,c2) Comparative result of the 320 and 94 profile line value.
Figure 16. CT image comparison in different positions of Slice D and Slice E at 0 MPa. (a1,a2) as the comparative results of different positions in x-direction (i.e., positions of Slice D with the pixel number of 80~150, and Slice E is 80~240, respectively.). (b1,b2) are the profile line comparative results of different CT images (i.e., the profile line of Slice D is picked up from the pixel number equal to 320 in Slice D and Slice E is 94, respectively). (c1,c2) Comparative result of the 320 and 94 profile line value.
Applsci 14 09221 g016
Applsci 14 09221 g017
Figure 17. CT image comparison under RG and ED methods at 3.0 MPa (Slice A to E).
Figure 17. CT image comparison under RG and ED methods at 3.0 MPa (Slice A to E).
Applsci 14 09221 g017
Applsci 14 09221 g018
Figure 18. Comparative result of the aperture boundary profiles under RG and ED methods (3 MPa Slice A~E).
Figure 18. Comparative result of the aperture boundary profiles under RG and ED methods (3 MPa Slice A~E).
Applsci 14 09221 g018
Applsci 14 09221 g019
Figure 19. Aperture value difference of Slice A and Slice E at 3.0 MPa. (a) Aperture difference under RG and ED methods. (b) Aperture value histogram (RG). (c) Aperture value histogram (ED).
Figure 19. Aperture value difference of Slice A and Slice E at 3.0 MPa. (a) Aperture difference under RG and ED methods. (b) Aperture value histogram (RG). (c) Aperture value histogram (ED).
Applsci 14 09221 g019
Applsci 14 09221 g020
Figure 20. CT image comparison in different positions of Slice A and Slice E at 3.0 MPa. (a1,a2) are the comparative results of different positions in x-direction (i.e., positions of Slice A with the pixel number of 100~325 and Slice E is 80~220, respectively.). (b1,b2) are the profile line comparative results of different CT images (i.e., the profile line of Slice A is picked up from the pixel number equal to 275 and Slice E is 142, respectively). (c1,c2) Comparative results of the 275 and 142 profile line value.
Figure 20. CT image comparison in different positions of Slice A and Slice E at 3.0 MPa. (a1,a2) are the comparative results of different positions in x-direction (i.e., positions of Slice A with the pixel number of 100~325 and Slice E is 80~220, respectively.). (b1,b2) are the profile line comparative results of different CT images (i.e., the profile line of Slice A is picked up from the pixel number equal to 275 and Slice E is 142, respectively). (c1,c2) Comparative results of the 275 and 142 profile line value.
Applsci 14 09221 g020
Table 1. CT scan conditions.
Table 1. CT scan conditions.
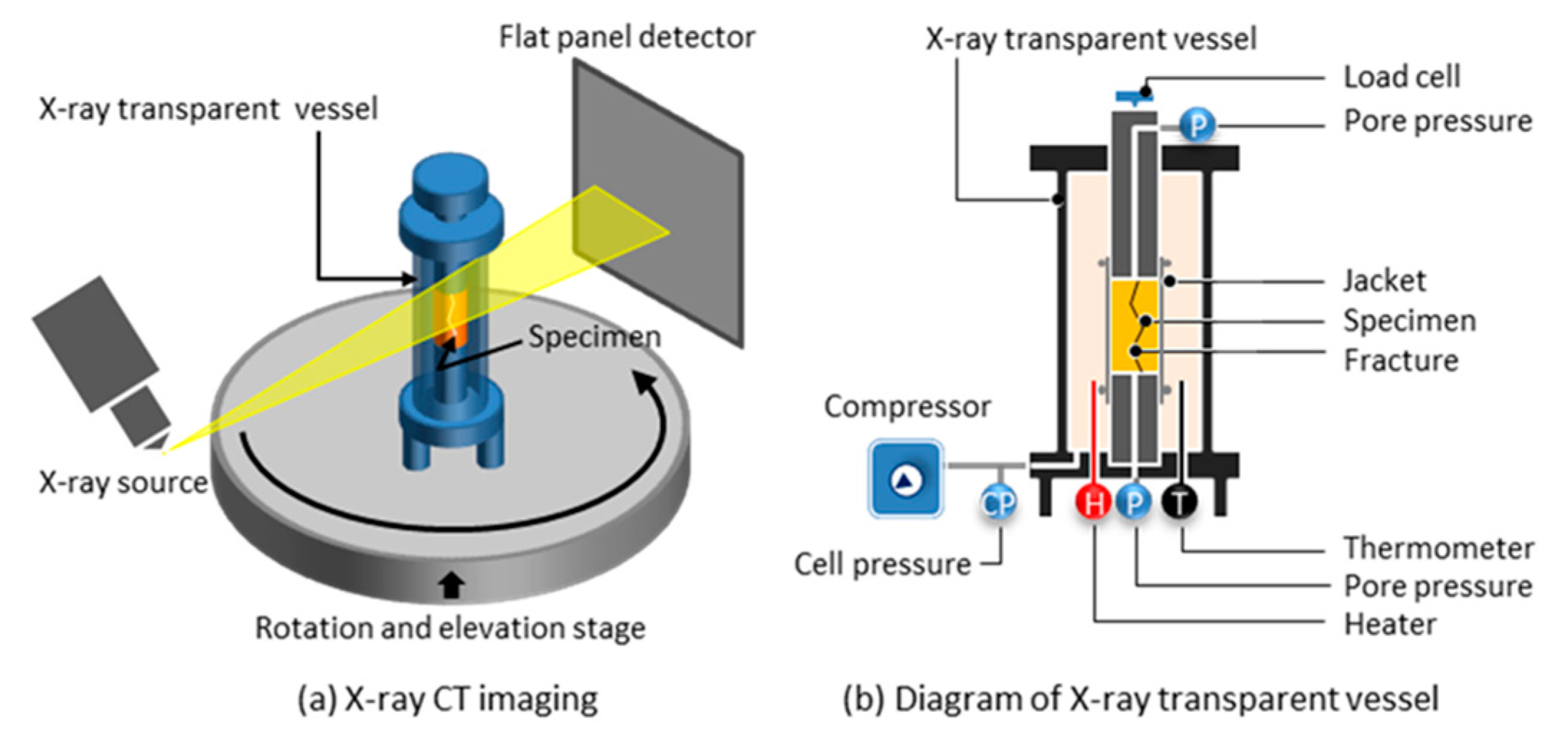
Confining Stress (MPa)Voltage (kV)Current
(μA)		Voxel Size
(μm3)		Projection ViewScan Area
(mm)		Integrated Images for One Projection
01506515.12 × 17.0450615.46210
31609018.42 × 21.0225318.82415
Table 2. Different conditions of CT images.
Table 2. Different conditions of CT images.
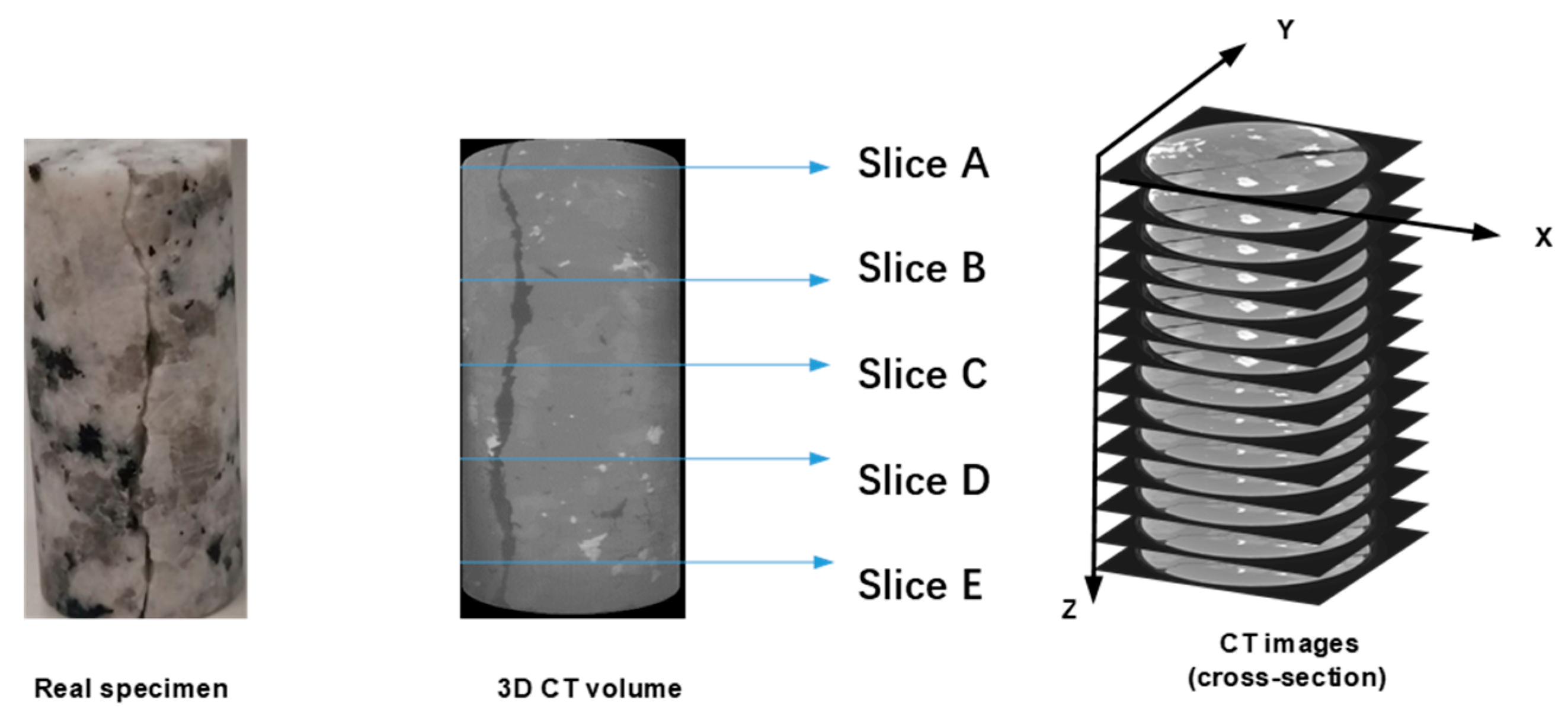
0 MPa3.0 MPa
Analysis ConditionCT Image Slice NumberZ-Direction
(mm)		CT Image Slice NumberZ-Direction
(mm)
Slice A1612.71612.7
Slice B3616.13617.6
Slice C6619.966113.9
Slice D126118.9126126.5
Slice E156123.4156132.8
Table 3. Histogram values of CT images.
Table 3. Histogram values of CT images.
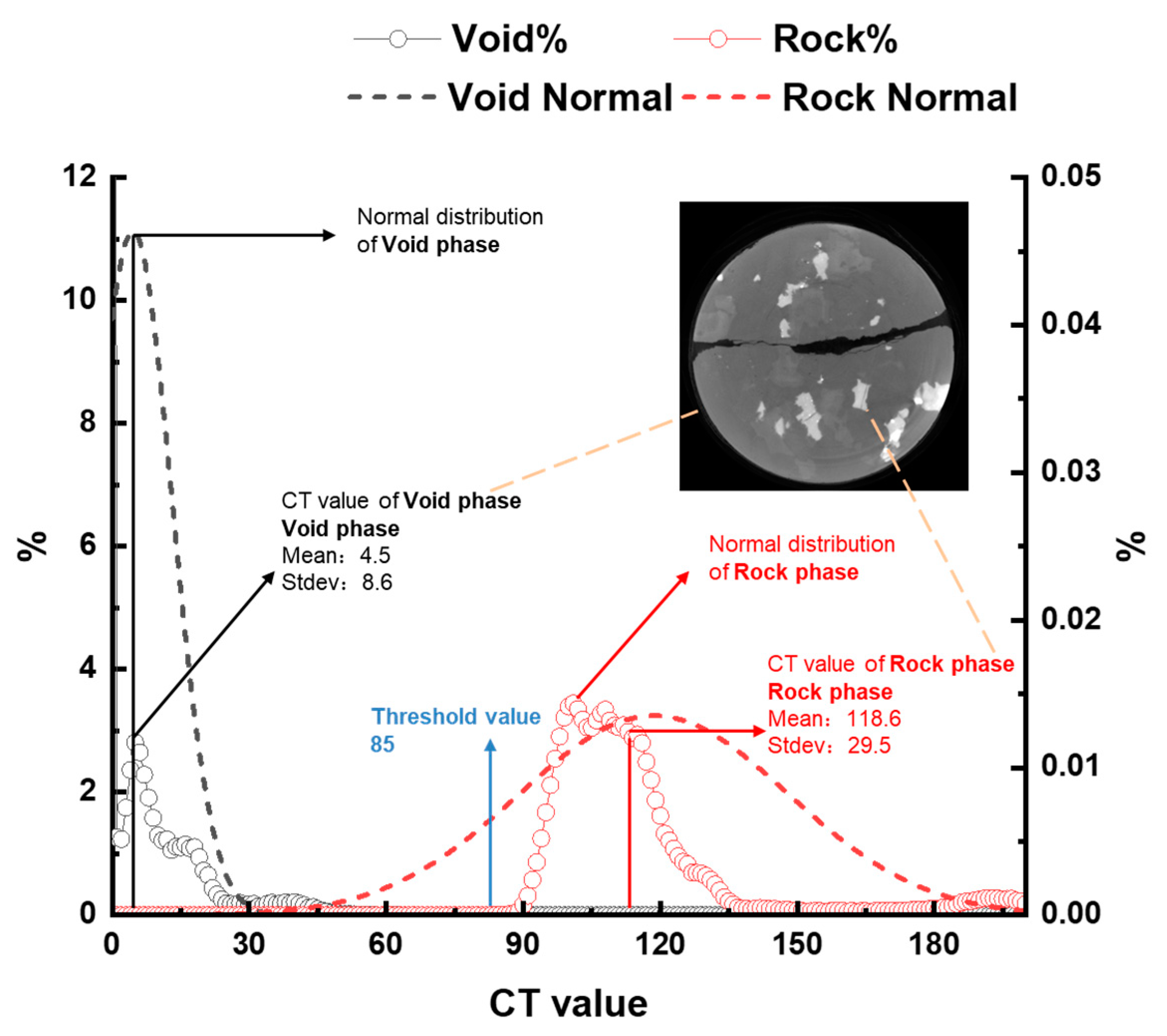
Mean Value of Rock σ1Mean Value of Void σ2Standard Distribution of Rock μ1Standard Distribution of Void μ2Tolerance
T		Threshold
118.64.529.58.63385
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Song, C.; Li, T.; Li, H.; Huang, X. Application of Different Image Processing Methods for Measuring Rock Fracture Structures under Various Confining Stresses. Appl. Sci. 2024, 14, 9221. https://doi.org/10.3390/app14209221

AMA Style

Song C, Li T, Li H, Huang X. Application of Different Image Processing Methods for Measuring Rock Fracture Structures under Various Confining Stresses. Applied Sciences. 2024; 14(20):9221. https://doi.org/10.3390/app14209221

Chicago/Turabian Style

Song, Chenlu, Tao Li, He Li, and Xiao Huang. 2024. "Application of Different Image Processing Methods for Measuring Rock Fracture Structures under Various Confining Stresses" Applied Sciences 14, no. 20: 9221. https://doi.org/10.3390/app14209221

APA Style

Song, C., Li, T., Li, H., & Huang, X. (2024). Application of Different Image Processing Methods for Measuring Rock Fracture Structures under Various Confining Stresses. Applied Sciences, 14(20), 9221. https://doi.org/10.3390/app14209221

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop