Secure Proxy Re-Encryption Protocol for FANETs Resistant to Chosen-Ciphertext Attacks

Abstract

In emergency situations, ensuring the secure transmission of medical information is critical. While existing schemes address on-road emergencies, off-road scenarios present unique challenges due to hazardous locations inaccessible to conventional vehicles. This research introduces a protocol for off-road emergencies, leveraging flying ad hoc networks (FANETs) formed by drones. The protocol, designed for users receiving emergency treatment, employs cryptographic techniques to protect sensitive information. To overcome the challenge of decrypting user medical records at emergency centers without the healthcare provider’s key, proxy re-encryption is employed. The control center (CC) securely generates encryption and decryption keys, facilitating the re-encryption process by the cloud server (CS) and transmission to the emergency center (E). The proposed protocol, free from pairing functions, underwent security and efficiency analyses, demonstrating resilience against chosen-ciphertext attacks (CCA) and collusion resistance (CR). Execution times of approximately 0.02 and 0.0 s for re-encryption and decryption processes, respectively, for a message size of 2000 bytes highlighted the efficiency of the protocol. The research contributes a secure and efficient proxy re-encryption protocol for off-road emergency medical information transmission within FANETs.

1. Introduction

In emergency situations, the secure transmission of medical information requires significant security technologies. Ref. [1] proposed a scheme for safe medical information transmission in on-road emergency situations. However, emergencies can occur not only on-road, but also off-road, presenting the challenge that off-road emergency locations are often inaccessible to conventional vehicles due to their hazardous nature. This became my motivation and expanded into the following research. To address hazardous emergency locations, drones are commonly employed for initial situational assessment, forming a communication network known as FANET (flying ad hoc network) with other participants.

In this paper, we establish off-road emergency scenarios and design an information transmission protocol for users who are receiving emergency treatment at a hospital with a smartphone. The protocol utilizes cryptographic techniques to prevent the exposure of sensitive user information. For a patient arriving at the emergency room of a nearby hospital due to an accident, accurate and effective treatment requires healthcare providers to have detailed knowledge of the patient’s medical history. Typically, user medical records are encrypted with the secret key of the healthcare provider and stored on a cloud server. Notably, the challenge arises as to whether the medical staff of the emergency center, without knowledge of the healthcare provider’s key, can decrypt the user’s medical records stored in encrypted form. To solve this issue, we employed proxy re-encryption.

The trusted third party, the control center (CC), generates encryption and decryption keys for re-encryption and securely transmits them to the cloud server (CS) and emergency center (E). The semi-trusted entity CS then uses these keys to re-encrypt the user’s medical records, sending them to the emergency center. The emergency center can subsequently decrypt the re-encrypted medical records using the received key from CC.

The proposed proxy re-encryption protocol does not use pairing functions and is secure against chosen-ciphertext attacks (CCA) and is collusion-resistant (CR). The re-encryption keys are also transmitted in encrypted form, ensuring the confidentiality of the original encryption keys. Security analysis is conducted in Section 5, where we formally prove unidirectional proxy re-encryption CCA security, prove unidirectional proxy re-encryption collusion-resistant (CR) security, and explain the defense mechanism against proxy forgery attacks. In Section 6, an efficiency analysis is conducted. The complexity of the proposed scheme is analyzed, and based on that, a comparative analysis is performed with relevant studies. When compared with the best efficient paper [2], it was found to exhibit the same complexity. The implementation of the re-encryption and decryption processes, for time measurements for a message size of 2000 bytes, resulted in execution times of approximately 0.02 and 0.0 s, respectively. Consequently, the paper proposes that the proxy re-encryption protocol demonstrates a secure and efficient performance, free from the use of pairing functions, and resilient against CCA and collusion attacks.

Our paper is structured as follows: Section 1 is an introduction, providing an overview of the research’s significance, methodology, and overall results. In Section 2, we delve into related studies and establish the application scenarios to be employed in this paper. Section 3 constitutes the security building blocks of this paper, introducing seven algorithms. Utilizing these algorithms, Section 4 constructs a protocol for the application scenarios. Section 5 conducts a security analysis, while Section 6 performs an efficiency analysis. Finally, Section 7 concludes the paper.

2. Related Works and Applications

2.1. Related Works

The suggested scheme focuses on the proxy re-encryption protocol for medical information within FANET (flying ad hoc network) environments. Considering a scenario involving off-road accidents, real-time video recording by drones becomes essential, necessitating a security protocol for transmission in the FANET environment.

FANETs are a system in which unmanned aerial vehicles (UAV) or drones exchange information by forming a network. It is primarily a collection of communication technologies that allows drones or unmanned aerial devices to work together and share information. In particular, FANETs can be used to implement autonomous flight systems. Drones or UAVs can communicate with each other to monitor and control the situation while performing a given mission. This allows them to be applied to a variety of missions and applications: exploration and surveillance, rescue operations in disaster situations, crop surveillance in agriculture, and building communications infrastructure. FANETs implement various technologies related to security and safety through efficient communication and cooperation, and this is an area where more research and development is expected as the use of unmanned aerial devices increases.

Consequently, this section will explore existing drone security protocols and research on securing medical information during emergency situations as related works. Subsequently, a specific focus will be given to proxy re-encryption, particularly unidirectional proxy re-encryption.

First, we looked at drone-security-related protocols. Ref. [3] introduced a key management and delegation system to enhance multi-drone control system security. It minimizes the storage of sensitive data like group keys and flight information, employing a “saveless” property. Future work aims to adapt the system for small IoT devices and determine an optimal key renewal period balancing low computation cost and high security. Ref. [4] focused on a group authentication-based solution for drone swarm security, ensuring rapid and secure verification of new drones. The novel authentication scheme is faster than 3GPP Release 17, with credentials not transmitted to the core network. Group authentication by guard drones and new parties facilitates swarm integration with reduced complexity. Ref. [5] discussed a lightweight authentication and key agreement (AKA) scheme for the internet of drones, addressing security challenges and privacy issues in a cost-effective manner. The scheme ensures secure data transmission using a lightweight encryption algorithm and a secure key exchange protocol. Ref. [6] introduced an anonymous mutual and batch authentication scheme with location privacy for UAVs (unmanned aerial vehicles) in FANETs. It ensures mutual authentication, batch authentication, and location privacy using group and ring signature schemes. The proposed scheme has potential applications in various fields, including military surveillance, emergency management, and environmental monitoring.

The following is a study on medical information transmission security protocols. Ref. [1] proposed a secure medical record access scheme for on-road emergencies using a patient’s smartphone and a cloud server. It ensures user privacy through pseudonyms and password-based authentication, improving the efficiency of accessing medical records during emergencies. The scheme enables timely healthcare in life-threatening situations. However, because this paper dealt with on-road emergency situations, drones were not involved. Ref. [7] is a review paper to discuss the security protocols for medical information using UAVs. It aimed to analyze the applicability of UAVs to support emergency medical systems in the areas of delivery and emergency urgent care.

Next, we address proxy re-encryption. In emergency situations, having access to the previous medical records of the injured patient is crucially necessary. Therefore, a proxy re-encryption process is required, where the STP (semi-trusted party) transmits the previously encrypted sensitive medical information to emergency medical institutions without decrypting it. The information is re-encrypted by the STP before transmission, delegating the decryption process to emergency institutions.

Ref. [8] is known as the first method introduced for delegating decryption rights, which marked an improvement over the traditional decrypt-and-then-encrypt approaches. In [9], Blaze et al. suggested an application called atomic proxy re-encryption, where a semi-trusted proxy converts a ciphertext for Alice into a ciphertext for Bob without seeing the underlying plaintext. Ref. [10] proposed a distributed-based authentication mechanism for drones in a swarm compatible with 5G D2D ProSe standard [11] mechanisms. It relies on a delegation-based proxy signature authentication scheme, reducing drones’ communication overhead to the core network. The authentication scheme is lightweight, efficient, and scalable, suitable for resource-constrained drone networks. Ref. [12] presented a privacy-preserving sharing scheme for drone videos in public safety scenarios, using proxy re-encryption. It allows secure access for third parties, like first responders, without compromising video content privacy. The original encryption key remains confidential, and the scheme minimizes overhead, making it feasible for live streaming. Ref. [13] suggested a proxy re-encryption (PRE) scheme for decentralized storage networks using permissionless blockchains. It allows data owners to delegate access rights without revealing content. The PRE scheme is efficient, scalable, and resistant to collusion attacks, providing secure data access control in decentralized storage networks. Ref. [14] covered improved proxy re-encryption schemes for secure distributed storage, including their design, implementation, and performance measurements. It also discussed the benefits of using proxy re-encryption for access control in a secure file system. The pairing-based schemes introduced significant advancements, including the protection of the delegator’s master secret key from collusion between the proxy and delegate.

We now address proxy re-encryption papers that are secure against CCAs (chosen-ciphertext attacks). Ref. [15] presented a new definition of security against chosen-ciphertext attacks for PRE schemes and proposed a scheme that satisfies the definition. The construction is efficient and based only on the decisional bilinear Diffie–Hellman assumption in the standard model.

The main contribution of Ref. [16] was the first construction of a unidirectional proxy re-encryption scheme with chosen-ciphertext security in the standard model. The construction is efficient and requires a reasonable complexity assumption in bilinear map groups. Ref. [2] proposed a new scheme for more efficient unidirectional proxy re-encryption and analyzed its security in detail, demonstrating its robustness against various attacks. The scheme has potential applications in various real-world scenarios and can contribute to the advancement of cryptography and data protection. Ref. [17] proposed a new scheme for proxy re-encryption that is secure against chosen-ciphertext attacks and collusion attacks, and does not require pairings. The scheme is unidirectional and the first of its kind with CCA security and collusion resistance. Ref. [18] proposed a unidirectional proxy re-encryption and proved its chosen-ciphertext security in the adaptive corruption model without random oracles, addressing an important question in the field. Overall, the paper’s contribution laid in advancing the state of the art in secure proxy re-encryption schemes.

2.2. Participants

• Smartphone (S): It is the user’s smartphone, to which various sensors (wearable devices) are connected to monitor the patient’s health condition. The smartphone periodically transmits encrypted records to the healthcare provider and stores them in the cloud server.
• Healthcare provider (H): It refers to an institution that provides and records medical practice. H manages the user’s health status monitored through the S, and performs medical treatment when users visit.
• Emergency center (E): An institution that carries out medical practice in case of emergency.
• Vehicle (including ambulances, V): V means vehicles or helicopters that transport users. It may or may not have medical equipment installed.
• Cloud server (CS): CS is a storage space. It stores the user’s medical records (medical practices performed by H, the patient’s conditions measured by S’s sensors, etc.) and video files taken by drones. This is assumed to be a semi-trusted party.
• First responders (F): F stands for police, fire engines, rescue helicopters, etc.
• Drone (D): The drone is registered in the CC in advance.
• Control center (CC): This is a kind of trusted third party (TTP), which controls security-related matters such as the generation and management of encryption keys and the registration of participants. Hence, CC knows all the security keys for every participant.

2.3. Application Scenario

Ref. [1] covered secure medical records in on-road emergencies. However, emergencies often occur not only on-road but also off-road. In other words, numerous incidents, such as a vehicles rolling down a cliff or a natural disaster on a beach, often occur in places where vehicles cannot approach. In preparation for this situation, we propose a security system in which drones participate by assuming the following specific accident scenarios:

• CC receives and checks reports from a citizen or a drone monitoring an accident situation in the air.
• CC orders D to take a detailed shot, and F to respond first.
• According to CC’s orders, the drone takes some actions, encrypts and transmits the video taken in detail to the CC in real time. F also notifies the CC of the processing status.
• CC analyzes it and transmits the information about nearby E to the available F or vehicle, which transfers the patient to E.
  ** The patient’s condition is measured with the sensor device of the smartphone and vehicle, and the record is encrypted and transmitted to the arriving E.
• In the meantime, CC generates secret key values for re-encryption/decryption and transmits them to CS and E.
• CS re-encrypts the user’s medical records encrypted by H and transmits them to E.
• E decrypts the record that has been re-encrypted by CS using the decryption key sent by CC.
• After decrypting the records, E proceeds to treat the patient. Following the treatment, the results are encrypted and sent to H, where they are subsequently stored in CS.

Figure 1 shows the communication between each participant according to the application scenario.

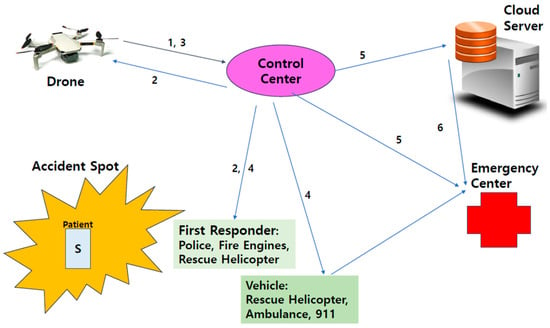
Figure 1. Participants and scenario flow.

3. Preliminaries

3.1. Notations

·

$f$: pseudorandom function.

·

$f^{-1}$: reverse function of $f$, in other words, decryption function of $f$.

·

i or j: each participant such as H or E.

·

$k_i$: secret key between participant i and CC.

·

$f_{k_i}$: encryption using pseudorandom function $f$ with a secret key $k_i$.

·

$x_i$: private key of participant I.

·

$y_i=g^{x_i}$: public key of participant I.

·

$m$: a message.

·

$C=(C_1,C_2)$: ElGamal-style ciphertext of $m$.

·

$D$: decryption of $m$.

·

$RE=(R_1,R_2)$: re-encryption of $m$.

·

$r,\alpha ,\gamma$: randomly generated numbers every time.

·

$O_i$: an order from CC to participant i.

·

$R_i$: report of participant i.

·

$S_1,S_2/S_3,S_4$: re-encryption/decryption keys.

·

$\mathfrak{O}$: oracle.

3.2. Security Building Blocks

Definition 1.

Discrete Logarithm Problem (DLP): It is a hard problem that involves finding the integer x $(0\le x\le p-2$) such that ${\alpha }^x\equiv \beta$ (mod p), given a prime p, a generator α of $Z_p^{*}$, and an element $\beta \in Z_p^{*}$ [19].

Definition 2.

Decisional Diffie–Hellman Problem (DDH): Let G be a group with prime order q, and let g be a generator of G. The decisional Diffie–Hellman (DDH) problem involves distinguishing between two types of triplets: $(g^a,g^b,g^{ab}$) and ($g^a,g^b,g^c$), where random elements $a,b,c\in \{1,\dots ,q-1\}$.

The experiment with a polynomial-time adversary A is as follows: flip a coin δ to obtain either 0 or 1, if $\delta =1,setc=ab;otherwise,choosecatrandom.$ It is said that the DDH problem is hard if, for any polynomial-time adversary A, the absolute value of the difference between the probability $\left|Pr(A\left(G,g^a,g^b,g^c\right)=\delta )-\frac{1}{2}\right|$ is negligible [19].

Definition 3.

Group Decisional Diffie–Hellman (GDDH): The ${GDDH}_{\Gamma }$ problem is ($T,\epsilon$)–intractable if there is no ($T,\epsilon$)–${GDDH}_{\Gamma }$-distinguisher in G for all polynomial $T$ and non-negligible $\epsilon$. (Refer to [20]):

The ($T,\epsilon$)–${GDDH}_{\Gamma }$-distinguisher in G is a probabilistic Turing machine $\Delta$ running in time $T$ such that ${Adv}_G^{{GDDH}_{\Gamma }}\left(\Delta \right)=\left|{[Pr}_{x_i}\Delta \left({GDH}_{\Gamma }^{*}\right)=1]-{[Pr}_{x_i,r}\Delta \left({GDH}_{\Gamma }^S\right)=1]\right|\ge \epsilon$.

Remark 1.

The Decisional Diffie–Hellman Assumption: Let us define two additional distributions from the GDH-Distribution:

$${GDH}_{\Gamma }^{*}=\{\left.{(J,g^{{\Pi }_{j\in j^{x_j}}})}_{J\in \Gamma },(I_n,g^{x_1\cdots x_n})\right|x_1,\dots ,x_n{\in }_R{Z}_q\}$$

$${GDH}_{\Gamma }^S=\{\left.{(J,g^{{\Pi }_{j\in j^{x_j}}})}_{J\in \Gamma },(I_n,g^r)\right|x_1,\dots ,x_n,r{\in }_R{Z}_q\}$$

Definition 4.

Pseudorandom Function (PRF): It is said that $F:K_f\times X⟶Yis(t,q,ϵ)$-secure pseudorandom function if any oracle algorithm, which makes a maximum of q oracle queries and has a running time of at most t, exhibits an advantage ${Adv}_A<ϵ$. The advantage ${Adv}_A$, representing the probability of adversary A succeeding in an attack, is defined as follows: ${Adv}_A=\left|\mathit{Pr}\left[A^{F_k}=1\right]-Pr[A^R=1]\right|$. Here, R denotes a randomly chosen function uniformly selected from the set of all mappings from X to $Y$. The probabilities are considered with respect to the selection of k and R [21].

Definition 5.

Pseudorandom Generator (PRG): It is said that $G_r:K_{G_r}⟶S$ is a $(t,ϵ)$-secure pseudorandom generator if any algorithm A, operating within a time limit of t, demonstrates an advantage ${Adv}_A<ϵ$. The advantage ${Adv}_A$ is defined as follows: ${Adv}_A=\left|\mathit{Pr}\left[A(G_r\left(U_{K_{G_r}}\right))=1\right]-Pr[A(U_S)=1]\right|$. The random variables $U_{K_{G_r}}$ and $U_S$ are uniformly distributed over the sets $K_{G_r}$ and S, respectively [21].

Definition 6.

Public Key Encryption (PKE). The PKE system consists of three probabilistic polynomial-time (PPT) algorithms (KGen, EnC, DeC):

-

KGen($1^k$) → (pk, sk). Given the security parameter $1^k$, the key generation algorithm KGen produces a public key pk and a secret key sk.

-

EnC(pk, m) → C. Given a public key pk and a message m in the message space, the encryption algorithm EnC produces a ciphertext C.

-

DeC(sk, C) → m. With the input of a secret key sk and a ciphertext C, the decryption algorithm DeC robustly generates a message m within the message space or ⊥ [17].

ElGamal: ElGamal cryptography provides security based on the difficult mathematical problem of finding the private key x from the public key y.

·

Key generation:

·

Select a mathematically secure large prime p and a primitive root g modulo p.

·

Choose a random private key x. Compute the public key $y=g^x$ mod  p.

·

Encryption:

·

Choose a random k such that 0 < r < p − 1.

·

Compute: $C_1=g^r$ mod p and $C_2={(y}^r·m)$ mod p to generate the ciphertext $C=(C_1,C_2)$.

·

Decryption:

·

Compute: $D=C_2·C_1^{-x}=m$ [19].

Definition 7.

Unidirectional Proxy Re-Encryption. The UniPRE(unidirectional proxy re-encryption) scheme is comprised of a set of PPT algorithms (KGen, RKeyGen, EnC, PrxyRE, DeC):

-

KGen, EnC, DeC: Similar to those found in public key encryption.

-

RKeyGen(${sk}_i$, ${pk}_j$) → ${rk}_{i\to j}$. Given a secret key ${sk}_i$, a public key ${pk}_j$, the re-encryption key generation algorithm, RKeyGen, produces a unidirectional re-encryption key ${rk}_{i\to j}$.

-

PrxyRE (${rk}_{i\to j}$, $C_1$) → $C_2$. Given a re-encryption key ${rk}_{i\to j}$ and a ciphertext $C_1$, the re-encryption algorithm PrxyRE produces a re-encrypted ciphertext $C_2$ or ⊥ [17].

Definition 8.

Uni-PRE-CCA game. This security game based on [17] is too long and will be explained later in the proof. So, here, we will omit it for now and refer to [17] for details.

Definition 9.

Uni-PRE-CR(collusion resistance) security. It is said that a UniPRE scheme is collusion-resistant if, for any polynomially bounded adversary $\mathcal{A}$, the probability described below is negligible:

Pr[(${sk}_1$, ${pk}_1$) ← KGen($1^k$), {(${sk}_i$, ${pk}_i$) ← KGen($1^k$)},

{${rk}_{i\to 1}$← ReKeyGen(${sk}_i$, ${pk}_1$)},

{${rk}_{1\to i}$ ← ReKeyGen(${sk}_1$, ${pk}_i$)},

i = 2, ⋯,

α ← A(${pk}_1$, {${pk}_i$, ${sk}_i$}, {${rk}_{1\to i}$}, {${rk}_{i\to 1}$}):

α = ${sk}_1$]

[17].

3.3. Algorithms

Our scheme consists of the following algorithm, which is based on [17] and that we modified:

·

SysParm($1^s$) → λ: The parameter generating algorithm SysParm takes a security parameter s as input and generates a set of system parameters λ.

·

KGen($\lambda$) → pk, sk, k: Given λ as input, the key generating algorithm KGen generates a public key pk, a private key sk and a secret key k with a control center CC for a symmetric cryptographic system(pseudorandom function).

·

EnC(pk,m) → C: Given a public key pk and a message m as input, the encryption algorithm EnC produces a ciphertext C.

·

Ord_$P(R)$ → $O_p$: CC analyses the report R, produces an Order $O_p$ and transmits it to a participant P.

·

Rpt_CC($O_p)$ → Act: According to the received order $O_p$, P reacts the Act and reports it to CC.

·

RKeyGen(${sk}_1,{sk}_2$) → ${rk}_{1\to 2}^1,{rk}_{1\to 2}^2$: Given secret keys ${sk}_1$ and ${sk}_2$ as input, the re-encryption key generation algorithm RKeyGen generates unidirectional re-encryption keys ${rk}_{1\to 2}^1,{rk}_{1\to 2}^2$.

·

PrxyRE($f_{k_{STP}}\left({rk}_{1\to 2}^1\right),C)$ → RE: STP (semi-trusted party) decrypts the encryption of the re-encryption key $f_{k_{STP}}({rk}_{1\to 2}^1)$. With this, STP re-encrypts C, then produces the re-encryption RE.

·

DeC$(f_{k_E}\left({rk}_{1\to 2}^2\right),$ $RE$) → m: Given a re-encryption key $f_{k_E}\left({rk}_{1\to 2}^2\right)$ and $RE$ as input, the decryption algorithm DeC outputs the original message m.

·

Trt_Str$(m_P)$ → $C_P$: Upon input of a treatment $m_P$ by the participant P, this treatment and storage algorithm outputs the encryption $C_P$ for $m_P$. Then, $C_P$ is stored in CS.

4. Construction of UPF Model

In this section, we construct a security model UPF (unidirectional proxy re-encryption in FANETs) which is composed of ten algorithms.

4.1. System Setup

SysParm(1^s) Construction

• Input: s: security parameter.
• Output: λ = {$f,G_r, g, G,C,D,RE, i$}: system parameters’ set.

The basis of the unidirectional proxy re-encryption system is established. $f:{\{0,1\}}^k\times {\{0,1\}}^{*}$ → ${\{0,1\}}^k$ is a pseudorandom function and $G_r$ is a pseudorandom generator. G is a group of order p which is a large prime and g is a generator of a group G. i is each participant of group G. C and D are encryption and decryption functions, and RE is a re-encryption function.

4.2. Registration and Encryption

4.2.1. KGen($\lambda$) Construction

• Input: $\lambda$.
• Output: pk, sk, k.

Key materials are generated. pk and sk are the public key and private key for ElGamal encryption and k is the secret key shared with CC in advance for pseudorandom function f.

4.2.2. EnC Construction

• Input: pk,m.
• Output: $C=(C_1,C_2)$.

The first encryption for message m is processed, where an ElGamal algorithm is used as an encryption function. When we assume that the healthcare provider (H) encrypts their information m, the public key is $g^{x_H}(=y)$ and the ciphertext is $C_1=g^r,C_2=\left(y^r·m\right).$

4.3. Accident Occurrence

4.3.1. Ord_P(R) Construction

• Input: R(reporting).
• Output: $O_D$.

CC checks R (reporting) for an accident, then gives orders $O_p$ to each participant P (D and F). CC orders D to take a detailed shot, and F to make an initial response. The communications in this step are made in plaintext.

4.3.2. Rpt_CC($O_p$) Construction

• Input: $O_D$.
• Output: $f_{k_D}(R_D)$, $f_{k_F}(R_F)$.

According to the order $O_D$, the drone takes some actions. Then, it encrypts and transmits the detailed video file report $R_D$ to the CC in real time, and F also reports the processing status $R_F$ to the CC. All communications from this step are encrypted.

4.3.3. Ord_F Construction

• Input: $f_{k_D}(R_D)$.
• Output: $f_{k_F}(O_{F_2})$.

CC checks and analyzes $R_D$ after decrypting $f_{k_D}\left(R_D\right)$ with security key $k_D$. Then, CC sends F the encrypted order $f_{k_F}(O_{F_2})$, which includes information about emergency medical agencies nearby.

4.4. Proxy Re-Encryption

4.4.1. RKeyGen(${sk}_1,{sk}_2$) Construction

• Input: $x_H$, $x_E$.
• Output: $f_{k_{CS}}(S_1,S_2)$, $f_{k_E}(S_3,S_4)$.

This algorithm is for the setting of re-encryption keys. CC generates random numbers $\alpha ,\gamma$ and then computes $S_1=x_H\alpha$, $S_2=x_E\alpha \gamma ,$ $S_3=x_E\alpha ,$ $S_4=x_E\gamma$. We put ${rk}_{1\to 2}^1=(S_1,S_2)$ as re-encryption key and ${rk}_{1\to 2}^2=(S_3,S_4)$ as decryption key for the re-encrypted message. With this, CC encrypts $S_1,S_2$ with the secret key $k_{CS}$, and $S_3,S_4$ with $k_E$. Then, CC transfers the generated re-encryption/decryption keys to CS and E.

4.4.2. PrxyRE ($f_{k_{CS}}\left({rk}_{1\to 2}^1\right),C)$ Construction

• Input: $f_{k_{CS}}\left({rk}_{1\to 2}^1\right),C$.
• Output: ${R=(R}_1,R_2)$.

CS decrypts the received encryption of ${rk}_{1\to 2}^1;{f^{-1}(f}_{k_{CS}}({rk}_{1\to 2}^1))={rk}_{1\to 2}^1=(S_1,S_2)$, where CS is a STP(semi-trusted party). With them, CS re-encrypts the stored user cipher text C =$(C_1,C_2$) as follows:

$RE=\left({C_1}^{S_1},{C_2}^{S_2}\right)=\left({{(g}^r)}^{x_H\alpha },{{(y}^{r}m)}^{x_E\alpha \gamma }\right)=(R_1,R_2)$. Here, $y=g^{x_H}$.

Then, CS transmits the re-encryption $\left(R_1,R_2\right)$ to E.

4.5. Treatment

4.5.1. DeC($f_{k_E}\left({rk}_{1\to 2}^2\right),$ $RE$) Construction

• Input: $f_{k_E}\left({rk}_{1\to 2}^2\right),$ $RE=\left(R_1,R_2\right)$.
• Output: $m$.

E decrypts the cipher text received from CC to obtain the decryption keys ${rk}_{1\to 2}^2=$ $(S_3,S_4)$. Then, it decrypts $RE=\left(R_1,R_2\right)$ with $S_3,S_4$.

$$\begin{array}{cc}\hfill D& ={(R_2·{{(R}_1)}^{{-S}_4})}^{\frac{x_E}{S_3,S_4}}\hfill \\ & {=({{(y}^{r}m)}^{x_E\mathsf{\alpha }\mathsf{\gamma }})·{{{((g}^r)}^{x_H\mathsf{\alpha }})}^{{-x}_E\mathsf{\gamma }})}^{\frac{x_E}{x_E\mathsf{\alpha }·x_E\mathsf{\gamma }}}\hfill \\ & {=({g^{x_H{x}_{E}r\mathsf{\alpha }\mathsf{\gamma }}·m}^{x_E\mathsf{\alpha }\mathsf{\gamma }}·{(g}^{r{x}_H\mathsf{\alpha }}{)}^{{-x}_E\mathsf{\gamma }})}^{\frac{x_E}{x_E\mathsf{\alpha }·x_E\mathsf{\gamma }}}\hfill \\ & {=(m^{x_E\mathsf{\alpha }\mathsf{\gamma }})}^{\frac{1}{x_E\mathsf{\alpha }\mathsf{\gamma }}}=m\hfill \end{array}$$

4.5.2. Trt_Str Construction

• Input: $m_E$.
• Output: $C_E$.

E treats the patient. Thereafter, E encrypts the resulting $m_E$ of treating the patient with H’s public key and sends it to H. H checks the received $C_E$ and stores it in CS.

4.6. Whole Protocol Flow

1. System Setup  •SysParm

2. Registration and Encryption  2.1. KGen → pk, sk, k  2.2. EnC → $C=\left(C_1,C_2\right)=(g^r,y^r·m)$

3. Accident Occurrences  3.1. Ord_P  •$\mathrm{CC}\stackrel{O_D}{\to }\mathrm{D},$ $\mathrm{CC}\stackrel{O_F}{\to }\mathrm{F}$  3.2. Rpt_CC  •$\mathrm{D}\stackrel{f_{k_D}(R_D)}{\to }\mathrm{CC},$ $\mathrm{F}\stackrel{f_{k_F}(R_F)\mathrm{CC}}{\to }$  3.3. Ord_F  •$\mathrm{CC}\stackrel{f_{k_F}(O_{F_2})}{\to }\mathrm{F}$

4. Proxy Re-Encryption  4.1. RKeyGen  •$\mathrm{CC}\mathrm{computes}:S_1=x_H\alpha$$,S_2=x_E\alpha \gamma ,$$S_3=x_E\alpha ,$ $S_4=x_E\gamma$  •$\mathrm{CC}\stackrel{f_{k_{CS}}(S_1,S_2)}{\to }\mathrm{CS}$  $\stackrel{f_{k_E}\left(S_3,S_4\right)}{\to }\mathrm{E}$  4.2. PrxyRE  •$\mathrm{CS}\mathrm{re}$-$\mathrm{encrypts}:RE=(R_1,R_2)=\left({C_1}^{S_1},{C_2}^{S_2}\right)$  •$\mathrm{CS}\stackrel{(R_1,R_2)=\left({C_1}^{S_1},{C_2}^{S_2}\right)}{\to }\mathrm{E}$

5. Treatment  5.1. DeC  •$\mathrm{E}\mathrm{decrypts}:D={(R_2·{{(R}_1)}^{{-S}_4})}^{\frac{x_E}{S_3,S_4}}=m$   5.2. Trt_Str  •$\mathrm{E}\mathrm{encrypts}:C_E=\left(C_1,C_2\right)=\left(g^{r\prime },y^{r\prime }·m_E\right),wherey=g^{x_H}$  •$\mathrm{E}\stackrel{C_E}{\to }\mathrm{H}$ $\stackrel{C_E}{\to }\mathrm{CS}$

5. Security Analysis

5.1. Proof of Security

Theorem 1.

(Unidirectional Proxy Re-Encryption CCA Security) UPF(unidirectional proxy re-encryption in FANETs) is secure according to Uni-PRE-CCA game, if GDDH is hard.

Proof. 

We use contraposition. A is assumed as an adversary that wins the Uni-PRE-CCA game with advantage ε. We construct the adversary $\mathsf{\Delta },$ which uses A as a subroutine and breaks the GDDH with non-negligible advantage. □

Phase 1. The adversary A initiates queries $q_1,\dots ,q_n$, with each $q_i$ being one of the following:

The oracle ${\mathfrak{O}}_{pk}$(public key generation): When provided with an index i, $\mathsf{\Delta }$ conclusively determines whether ${pk}_i$ is the attacked public key ${pk}^{\star }$.

·

If affirmative, Δ initializes $(g,g^r,g^x,g^{xr}$) and records this information in table $T_k$.

·

Otherwise, $\mathsf{\Delta }$ executes KGen → $({pk}_i$, ${sk}_i$) and provides ${pk}_i({=g}^x)$ to A, and records $(g,g^r,g^x,g^{xr},x(=sk)$) in $T_k$.

${\mathfrak{O}}_{sk}$(secret key generation): Given the input ${pk}_X=(g,g^r,g^x,g^{xr})$, $\mathsf{\Delta }$ verifies the existence of ${pk}_X$ in $T_k$.

·

If ${pk}_X$ is not found, $\mathsf{\Delta }$ terminates.

·

In case ${pk}_X$ is the attacked public key, $\mathsf{\Delta }$ reports failure and aborts.

·

Otherwise, $\mathsf{\Delta }$ replies to A with $(p_x\prime ,q_x\prime$) and records ${pk}_X$ into $T_{sk}$.

${\mathfrak{O}}_{rk}$(re-encryption key generation): Given the input ${(pk}_X,{pk}_Y$), $\mathsf{\Delta }$ verifies the existence of both ${pk}_X, {pk}_Y$ in $T_k$.

·

If either is missing, $\mathsf{\Delta }$ terminates.

·

Subsequently, $\mathsf{\Delta }$ checks whether $({pk}_X,{pk}_Y$, ${rk}_{X\to Y}^1,{rk}_{X\to Y}^2$) is present in $T_{rk}$. If it is, $\mathsf{\Delta }$ returns $({rk}_{X\to Y}^1,{rk}_{X\to Y}^2$) to A. If not:

-

If ${pk}_X$ is in $T_{sk}$, or not the guessed attacked public key, $\mathsf{\Delta }$ responds with $(f_{\mathrm{X}}\left({rk}_{X\to Y}^1\right)$, $f_{\mathrm{Y}}\left({rk}_{X\to Y}^2\right)$) = $(f_{\mathrm{X}}\left(S_1,S_2\right)$, $f_{\mathrm{Y}}\left(S_3,S_4\right)$)$\leftarrow \mathrm{R}\mathrm{K}\mathrm{e}\mathrm{y}\mathrm{G}\mathrm{e}\mathrm{n}\left({sk}_X,{sk}_Y\right)$, recording $({pk}_X,{pk}_Y,{rk}_{X\to Y}^1,{rk}_{X\to Y}^2,f_{\mathrm{X}}\left({rk}_{X\to Y}^1\right)$, $f_{\mathrm{Y}}\left({rk}_{X\to Y}^2\right)$) in $T_{rk}$.

-

If ${pk}_X$ is the guessed attacked public key and ${pk}_Y$ is not in $T_{sk}$, $\mathsf{\Delta }$ selects random numbers $x_X,x_Y,\alpha ,\gamma$, computes $S_1,S_2,S_3,S_4$, sets ${rk}_{X\to Y}$ = $({rk}_{X\to Y}^1,{rk}_{X\to Y}^2)=(\left(S_1,S_2\right),\left(S_3,S_4\right))$, and records $({pk}_X,{pk}_Y,{rk}_{X\to Y}^1,{rk}_{X\to Y}^2,f_{\mathrm{X}}\left({rk}_{X\to Y}^1\right)$, $f_{\mathrm{Y}}\left({rk}_{X\to Y}^2\right)$) in $T_{urk}$.

-

If ${pk}_X$ is the guessed attacked public key and ${pk}_Y$ is in $T_{sk}$, $\mathsf{\Delta }$ reports failure.

${\mathfrak{O}}_{re}$(re-encryption): Upon receiving input $({pk}_X,{pk}_Y,C$), $\mathsf{\Delta }$ verifies the existence of both ${pk}_X$ and ${pk}_Y$ in $T_k$. If either is absent, $\mathsf{\Delta }$ terminates. Subsequently, $\mathsf{\Delta }$ parses $C=(C_1,C_2)$.

·

If ${pk}_X$ is the guessed attacked public key and ${pk}_Y$ is in $T_{sk}$, $\mathsf{\Delta }$ selects random numbers $x_X,x_Y,\alpha ,\gamma$, puts ${rk}_{X\to Y}$ = $({rk}_{X\to Y}^1,{rk}_{X\to Y}^2)=(\left(S_1,S_2\right),\left(S_3,S_4\right))$, and returns $({rk}_{X\to Y}^1,{\mathrm{R}}_1,{\mathrm{R}}_2$) to A, stores it in $T_{ure}.$

·

Otherwise, $\mathsf{\Delta }$ calls ${\mathfrak{O}}_{rk}$ to obtain ${rk}_{X\to Y}$, and returns PrxyRE(${rk}_{X\to Y}^1,C)$ and stores it in $T_{re}.$

${\mathfrak{O}}_{dec}(\mathrm{d}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n})$: When receiving input $({pk}_X,{rk}_{X\to Y}^1,R_1,R_2$), $\mathsf{\Delta }$ checks whether ${rk}_{X\to Y}^1$ is present in either $T_{rk}$ or $T_{urk}$. If it is absent in both, $\mathsf{\Delta }$ terminates. However:

·

If ${rk}_{X\to Y}^1$ is not the guessed attacked re-encryption key, $\mathsf{\Delta }$ knows ${rk}_{X\to Y}^2$ = $\left(S_3,S_4\right)$ from $T_{rk}$. $\mathsf{\Delta }$ responds A with $m\leftarrow Dec\left({rk}_{X\to Y}^2,{\mathrm{R}}_1,{\mathrm{R}}_2\right).$

·

If ${rk}_{X\to Y}^1$ is the guessed attacked re-encryption key and $RE=({rk}_{X\to Y}^1,R_1,R_2)$, $\mathsf{\Delta }$ searches $({pk}_X,{pk}_Y,a^{*},b^{*},c^{*},d^{*}$) in $T_{urk}$ or $(a^{*},R_1,R_2)$ in $T_{ure}$, for $a^{*}=$ ${rk}_{X\to Y}^1$.

-

If it does exist, $m\leftarrow \mathrm{D}\mathrm{e}\mathrm{c}\left(b^{*},R_1,R_2\right).$

-

If it does not exist, $\mathsf{\Delta }$ aborts.

Challenge. At a certain stage, A issues a challenge tuple $({pk}^{\#},m_0,m_1)$. If ${pk}^{\#}$ is not the public key $\mathsf{\Delta }$ guessed in oracle ${\mathfrak{O}}_{pk}$, $\mathsf{\Delta }$ declares failure and terminates. On the contrary, if ${pk}^{\#}$ aligns with the guessed public key, $\mathsf{\Delta }$ responds by randomly selecting $b\in \left\{0,1\right\}$ and choosing random numbers $x_1,x_2,\alpha ,\gamma .$ $\mathsf{\Delta }$ then sets: $(g^r,R_1={(g^r)}^{x_1\alpha },R_2={(g^r)}^{x_1·x_2\alpha ·\gamma }·m_b^{x_2\alpha ·\gamma }$).

Phase 2.

${\mathfrak{O}}_{pk}$: $\mathsf{\Delta }$ follows the Phase 1 response protocol.

${\mathfrak{O}}_{sk}$: When provided with ${pk}_i$, if ${pk}_i$ = ${pk}^{\#}$, or $({pk}^{\#}$, ${pk}_i$) is found in the table $T_{rk}$, $\mathsf{\Delta }$ immediately terminates. Otherwise, $\mathsf{\Delta }$ follows the Phase 1 response protocol.

${\mathfrak{O}}_{rk}$: When receiving input $({pk}_i$, ${pk}_j$), if ${pk}_i$ = ${pk}^{\#}$, and ${pk}_j$ is in table $T_{sk}$, $\mathsf{\Delta }$ terminates. Otherwise, $\mathsf{\Delta }$ responds in line with the Phase 1 protocol.

${\mathfrak{O}}_{re}$: On input $({pk}_i$, ${pk}_j,C$), if $({pk}_i$, C) = $({pk}^{*}$,$C^{*})$ and ${pk}_j$ is present in the table $T_{sk}$, $\mathsf{\Delta }$ terminates. Otherwise, $\mathsf{\Delta }$ responds as in Phase 1, except when ${pk}_i$ = ${pk}^{\#}$ and $\left(C_1,C_2\right)$=$(C_1^{*},C_2^{\#})$. $\mathsf{\Delta }$ should record the result ${(pk}_j,g^r,R_1,R_2)$ in $T_{der}.$

${\mathfrak{O}}_{dec}$: On input $({pk}_i,{rk}_{i\to j}^1,R_1,R_2$), if $({pk}_i,{rk}_{i\to j}^1,R_1,R_2$) = $({pk}^{\#}$, $({{rk}^1)}^{\#},R_1^{\#},R_2^{\#})$ or is in $T_{der}$, or ${(R}_1,R_2)=\mathrm{P}\mathrm{r}\mathrm{x}\mathrm{y}\mathrm{R}\mathrm{E}(O_{rk}\left({pk}^{\#},{pk}_i\right),C^{\#})$, $\mathsf{\Delta }$ terminates. Otherwise, $\mathsf{\Delta }$ responds as in Phase 1.

Guess. A outputs a guess b’. If b = b’, $\mathsf{\Delta }$ outputs 0 (GDDH instance). Otherwise, it outputs 1 (not a GDDH instance), because the encryption will be random for RE if and only if the challenge is not a GDDH tuple, $\mathsf{\Delta }$ solves the GDDH challenge with the same advantage as A. In more detail, in the case of b = 0, ${RE=(R}_1,R_2)=\left({\left(g_0\right)}^{\alpha x_1},{\left(g_0\right)}^{\alpha x_{1·}{x}_2·\gamma }·m^{x_2\alpha ·\gamma }\right)=\left({\left(g_0\right)}^{\beta },{\left(g_0\right)}^{\beta \delta \tau }·\mathrm{m}\right)=({\left(g_0\right)}^{\beta },{\left(g_0\right)}^{\rho }·m)$. If b = 1, $\mathsf{\Delta }$ returns a random value in reply to the GDDH challenge. If $\rho =\beta \delta \tau$, it is the encryption of RE. Otherwise, it is not an encryption.

It is shown that $\mathsf{\Delta }$ can solve the GDDH problem $(\rho =\beta \delta \tau$) with non-negligible probability.

$$\begin{array}{cc}\hfill {Adv}_{\mathsf{\Delta }}& =\mathrm{Pr}\left[{Exp}_{\mathsf{\Delta }}^{GDDH}=1\right]=\mathrm{Pr}\left[b=b^{\prime }\right]\hfill \\ & =\mathrm{P}\mathrm{r}[b^{\prime }=b\left|b=1]·\mathrm{Pr}\left[b=1\right]+\mathrm{P}\mathrm{r}[b^{\prime }=b\left|b=0]·\mathrm{Pr}\left[b=0\right]\right.\right.\hfill \\ & =\mathrm{P}\mathrm{r}[b^{\prime }=1\left|b=1]·\frac{1}{2}+\mathrm{P}\mathrm{r}[b^{\prime }=0\left|b=0]·\frac{1}{2}\right.\right.\hfill \\ & =\mathrm{P}\mathrm{r}[b^{\prime }=1\left|b=1]·\frac{1}{2}+(1-\mathrm{P}\mathrm{r}[b^{\prime }=1\left|b=0])·\frac{1}{2}\right.\right.\hfill \\ & =\frac{1}{2}+\frac{1}{2}(\mathrm{P}\mathrm{r}[b^{\prime }=1\left|b=1]-\mathrm{P}\mathrm{r}[b^{\prime }=1\left|b=0]\right.\right.)\hfill \\ & =\frac{1}{2}+\frac{1}{2}(\mathrm{Pr}\left[{Exp}_{\mathrm{A}}^{UPF-1}=1\right]-\mathrm{Pr}\left[{Exp}_{\mathrm{A}}^{UPF-0}=1\right])\hfill \\ & =\frac{1}{2}+\frac{1}{2}{Adv}_{\mathrm{A}}^{UPF}=\frac{1}{2}+\frac{1}{2}\epsilon \hfill \end{array}$$

Theorem 2.

(Unidirectional Proxy Re-Encryption Collusion-Resistant(CR) Security) If f is a secure pseudorandom function and random numbers are generated from a secure pseudorandom generator, then scheme UPF is collusion-resistant.

Remark 2.

The cryptographic elements for the whole protocol are PRF (pseudorandom function, e.g., 128 bit-AES) and PRG (pseudorandom generator, e.g., middle-square method, Naor–Reingold pseudorandom function, etc.).

Proof. 

We assume C as an adversary against the Uni-PRE-CR with advantage ε and $\beta$ as a distinguisher between random and pseudorandom. Here, we also use contraposition, so all we have to do is to construct $\beta$ using C as a subroutine. C can collude and know the secret key (k) values of other pre-registered members. Since the encrypted and transmitted $f_{k_{CS}}(S_1,S_2)$, $f_{k_E}(S_3,S_4)$ can be decrypted to $\left(S_1,S_2\right),(S_3,S_4)$ using the secret key, the re-encrypted message $(R_1,R_2)$ can be decrypted to the original message m. Then, $\beta$ will also be able to distinguish whether the challenged message is the result of an encrypted value or a random value. □

5.2. Proxy Forgery Attack

A proxy forgery attack is a type of security breach in which an attacker uses a forged proxy server to intercept or manipulate data on a specific network. Proxies are responsible for relaying or filtering communications between clients and servers, and attackers can forge such proxies to intercept and manipulate communications in the middle. The main characteristics and process of proxy forgery attacks are as follows:

(1)

Proxy server forgery: Attackers either build proxy servers under their control or exploit and use proxy servers that already exist.

(2)

Man-in-the-middle attack: An attacker intercepts communications between the victim (client) and the target server. We assume that the proxy server is controlled by an attacker.

(3)

Data manipulation or interception: An attacker can intercept communications in the middle and view or manipulate data. This can lead to attacks such as leaking confidential information, stealing session tokens, or injecting malicious code.

Defense mechanism:

(1)

To successfully carry out a forgery attack, instead of CC (Control Center), the CS (Cloud Server) needs to compute $S_1=x_H\alpha$,$S_2=x_E\alpha \gamma ,$ $S_3=x_E\alpha ,$ $S_4=x_E\gamma$, then transmit RE=$(R_1,R_2)=\left({C_1}^{S_1},{C_2}^{S_2}\right)$ and $f_{k_E}\left(S_3,S_4\right)$ to E. CS can calculate $S_1$,$S_2,S_3,S_4$ by generating random values for private keys $x_H$, $x_E$ and random numbers α, γ. The re-encryption values $\left(R_1,R_2\right)=\left({C_1}^{S_1},{C_2}^{S_2}\right)$ are computed as $\left({{(g}^r)}^{x_H\alpha },{{(y}^{r}m)}^{x_E\alpha \gamma }\right)$. CS then sends $f_{k_E}\left(S_3,S_4\right)$ and $\left(R_1,R_2\right)$ to E for decryption. However, a challenge arises in transmitting $f_{k_E}\left(S_3,S_4\right)$ to allow E to decrypt $S_3,S_4$, the value of $k_E$ must be known. Since $k_E$ is a secret key pre-registered for secure communication between E and CC, an attacker cannot determine its value, preventing the creation of a valid $f_{k_E}\left(S_3,S_4\right)$. Consequently, E cannot decrypt it, rendering RE undecryptable.

(2)

In order for the CS to intercept and succeed in MitMs (man-in-the-middle attacks) and data manipulation, the attacker must first intercept and decrypt $f_{k_{CS}}\left(S_1,S_2\right)$ and $f_{k_E}\left(S_3,S_4\right)$ transmitted by CC to CS and E. However, as the attacker cannot know the secret keys $k_{CS}$ and $k_E$ of CS and E, respectively, eavesdropping becomes impossible, and as a result, MitMs and data manipulation also become impossible.

6. Efficiency Analysis

6.1. Complexity Analysis

When L represents the number of bits in the prime used in the ElGamal scheme, efficiency is analyzed by representing the time and space complexity for each construction as a Big-O notation.

System Setup

• SysPrm Construction:

  ·

  Time Complexity: O(g(s)), where g is the complexity of the parameter generation algorithm.

  ·

  Space Complexity: O(L).

  Registration and Encryption
• KeyGen Construction:

  ·

  Time Complexity: O(L) for selecting random values.

  ·

  Space Complexity: O(L).

• Enc Construction:

  ·

  Time Complexity: O($L^2$) for modular exponentiation.

  ·

  Space Complexity: O(L).

  Accident Occurrence
• Ord_P(R) Construction:

  ·

  Time Complexity: O(1).

  ·

  Space Complexity: O(L).

• Rpt_CC Construction:

  ·

  Time Complexity: O(1).

  ·

  Space Complexity: O(L).

• Ord_F Construction:

  ·

  Time Complexity: O(1).

  ·

  Space Complexity: O(L).

  Proxy Re-Encryption
• RKeyGen Construction:

  ·

  Time Complexity: O(L).

  ·

  Space Complexity: O(L).

• PrxyRE Construction:

  ·

  Time Complexity: O($L^2$) (involving exponentiation and multiplication of keys and messages).

  ·

  Space Complexity: O(L).

  Treatment
• Dec Construction:

  ·

  Time Complexity: O($L^2$) (involving exponentiation and decryption).

  ·

  Space Complexity: O(L).

• Trt_Str Construction:

  ·

  Time Complexity: O(1) (assuming treatment and storage are basic operations).

  ·

  Space Complexity: O(L).

  Simplifying, we can approximate the overall complexity as:
  O_total(L)$\approx O(L^2)$.

6.2. Complexity Comparison with Other Methods

Ref. [16] was the first paper to present unidirectional chosen-ciphertext secure proxy re-encryption published in 2008. Ref. [17], published by Shao et al. in 2009, was the first study to consider not only CCA but also CR. Ref. [2] was the most efficient unidirectional proxy re-encryption published in 2010. Ref. [13] was a scheme announced in 2022 that is not unidirectional, but is secure for CCA and CR.

We compared and analyzed the computational complexity of the four papers above to evaluate the proposed scheme. Here, L represents the number of bits in the modulus used in the scheme, k is the length of the generated key.

As shown in Table 1, the paper focusing on efficiency published in 2010 had the best performance out of the papers published before our study was proposed. So, it is necessary to compare our paper with the paper published in 2010. The computational complexity of the 2010 paper was $O(k{L}^2)$, and our paper was $O(L^2+kL)$. In complexity notation, $O(k{L}^2)$ and $\mathrm{O}(L^2+\mathrm{k}\mathrm{L})$ can be said to have the same complexity.

Table 1. Comparison with previous schemes.

Schemes	2008	2009	2010	2022	Ours
Enc	$O(k{L}^3)$	$O(k{L}^2+kL)$	$O(kL)$	$O(k{L}^2)$	$O(L^2+kL)$
ReKeyGen	$O(k{L}^3)$	$O(k{L}^2+kL)$	$O(k{L}^2)$	$O(k^2{L}^3)$	$O(L^2+kL)$
ReEnc:	$O(k{L}^6)$	$O(k{L}^2+kL)$	$O(k{L}^2)$	N/A	$O(L^2+kL)$
Dec	$O(k{L}^6)$	$O(k{L}^2+kL)$	$O(kL)$	$O(k{L}^2)$	$O(L^2)$
Security	CCA, RCCA (Replayable CCA)	CCA, CR	CCA	CCA, CR	CCA, CR
Assumption	3-QDBDH	DDH	CDH	CDH	GDDH
Pairing Free	X	O	O	O	O

All schemes are based on the assumption that the ‘Diffie Hellman problem is difficult’, and papers did not use pairing functions, apart from (2008).

6.3. Performance Analysis for Re-Encryption/Decryption

To evaluate the actual performance of the proposed proxy re-encryption protocol, we not only conducted a complexity analysis but also implemented the re-encryption and decryption processes to measure the time. Because the whole protocol heavily depends on network conditions and event situations, we only measured the core components of the proposed protocol, which are the re-encryption and decryption processes. The experimental environment is shown in Table 2.

Table 2. Experimental environments.

Hardware	CPU	11th Gen Intel(R) Core™ i5-1155G7 @ 2.50GHz
	Memory	16G
	Disk	1TB
System type	64-bit operating system, ×64-based processor
OS	Windows 11 Home
Language	Python 3.12

Cryptographic parameters and libraries are addressed in the following Table 3.

Table 3. Cryptographic parameters and libraries.

Pseudorandom Function f	AES 128 bits
Group parameter	cyclic group
Modulus p	2048 bits
Order q	256 bits
Generator g	2048 bits
Crypto library	PyCryptodome
Time measurement function	time.time()

The experiment involved measuring the time for the re-encryption and decryption processes with message sizes set to 10 bytes, 100 bytes, 500 bytes, and 1000 bytes. The result is as follows in the Table 4.

Table 4. Processing time for each message size.

Message Size (Bytes)	Re-Encryption Process (Seconds)	Decryption (Seconds)
100	0.015946626663208008	0.0
500	0.016944408416748047	0.0
1000	0.01795029640197754	0.0
2000	0.020200729370117188	0.0

For the re-encryption process, it was observed that as the message size increased, the process time gradually increased. For a message size of 2000 bytes, an exceptionally fast performance of approximately 0.02 s was demonstrated. For the decryption process, all recorded times showed as 0.0 s. This was likely due to the elapsed time being extremely small and showing as 0 s.

7. Conclusions

This paper presents a secure proxy re-encryption protocol for FANETs that can be used to securely transmit medical information in off-road emergency situations. The proposed protocol utilizes cryptographic techniques, including proxy re-encryption, to protect sensitive user information and enables authorized participants to access the encrypted medical records without revealing the original encryption key. The use of proxy re-encryption allows for secure transmission of medical information even when the original encryption key is not known by the recipient.

The use of drones and smartphones in emergency communication networks can significantly improve the response time and accuracy of emergency medical services. The analysis results show that the proposed protocol is resistant to CCA, collusion attacks, and forgery attacks and effective in protecting user privacy and ensuring the secure transmission of medical information.

Our proposed protocol did not use a pairing function with severe computational overhead, but because it used an exponential operation, it required a time complexity of $O(L^2+kL)$. The proposed protocol can be further improved by incorporating more advanced cryptographic techniques such as lightweight encryption or hybrid encryption technologies and optimizing the communication network.