Natural Frequency Response of FG-CNT Coupled Curved Beams in Thermal Conditions

Abstract

This study investigates the sensitivity of dynamic properties in coupled curved beams reinforced with carbon nanotubes (CNTs) to thermal variations. Temperature-dependent (TD) mechanical properties are considered for poly methyl methacrylate (PMMA) to be strengthened with single-walled CNTs (SWCNTs), employing the basic rule of mixture to define the equivalent mechanical properties of nanocomposites. The governing equations of motion are derived using a first-order shear deformation theory (FSDT) and Hamilton’s principle, accounting for elastic interfaces modeled using elastic springs. A meshfree solution method based on a generalized differential quadrature (GDQ) approach is employed to discretize the eigenvalue problem and to obtain the frequency response of the structure. The proposed numerical procedure’s accuracy is verified against predictions in the literature for homogeneous structural cases under a fixed environmental temperature. The systematic investigation assesses the impact of various geometric and material properties, including curvature, boundary conditions, interfacial stiffness, and CNT distribution patterns, on the vibrational behavior.

1. Introduction

Among novel structural systems in civil engineering, coupled beams have increasingly been used in the last decades for highways, subgrades, and other facilities. This kind of system consists of beams with a straight or curved geometry, connected by an elastic layer, with a linear, non-linear, and plastic behavior. Despite the large amount of studies from the literature focusing on the structural behavior of single beams [1,2,3,4], some static and dynamic aspects for coupled beam systems have already been explored in the pioneering works by Seelig and Hoppmann [5] and Dublin and Friedrich [6], drawing increased attention from researchers in the recent years. These studies focused on static and dynamic behavior [7,8,9], transverse vibration [10], and forced vibration [11], using viscously damped interlayer [8,12] among others. Among the most recent works, we can find studies focusing on the dynamic response of coupled curved beams, including both singly curved [13,14,15,16] and doubly curved systems [17,18,19].

The earliest research on the vibrational behavior of beams resting on an elastic foundation was performed by Mathews [20,21] and Eisenberger [22], involving one or two foundation parameters. Several researchers have recently been concerned with obtaining the natural frequencies of a curved beam with different geometries, loading, boundary conditions, and elastic foundations [23,24,25,26,27,28,29,30]. Although few studies have assessed the vibration of homogeneous coupled beams [31,32,33,34,35,36], research has focused on the effect of nanomaterials on the frequency behavior of these systems. Recently, Han et al. [37] have presented an exact solution to define the dynamic characteristics of double-beam systems using an improved Wittrick–Williams algorithm. The vibrational behavior of a double-beam system connected to a viscoelastic layer was also studied [38]. Additionally, numerical studies have been performed to determine the damping properties of a system using two beams [39].

Advanced nanomaterials and their application have also motivated many studies to investigate their possible application in civil (structural and geotechnical) engineering, to create more efficient and sustainable materials [40,41]. Among them, single-layered hollow tubes are largely used as single-walled carbon nanotubes with diameter 0.4 to 2 mm [42]. Functionally graded materials (FGMs) have been also proposed for their high performance, capacity, and low weight with an overall improvement of the mechanical behavior of the structure due to a non-uniform distribution of the material along different directions. Among them, functionally graded carbon nanotubes (FG-CNTs) represent the most common type of nanocomposite used in many structural members, such as beams, plates, and shells [43,44,45,46,47,48,49,50,51]. Ong et al. [52] investigated the dynamic response of double-beam systems in which CNTs were used as the reinforcing phase in the structure with different distribution patterns. In the further work [53], the authors focused on the natural frequency of FG-CNT reinforced double beam systems in a thermal environment, where FG-CNTs stand for the reinforcing phase. The dynamic behavior of nanocomposite coupled beam systems is still being considered by different researchers. In such a context, many scientists have continued to investigate the dynamic responses of structures over the past few decades, accounting for different analytical solutions such as GDQ and DSC [54,55,56,57,58]. The GDQ approach is a semi-analytical solution method with a fast convergence rate, as largely demonstrated in many applications of beams, plates, and shells [59,60,61,62,63,64,65,66,67,68,69,70,71,72] for different curved geometries, both in a static and dynamic sense. It is crucial to satisfy the boundary conditions accurately in order to obtain reliable and accurate solutions. It is worth mentioning that there is only one boundary condition that must be satisfied at each boundary point of a second-order differential equation describing a Timoshenko beam. For this reason, in a GDQ method, the discrete boundary conditions can be placed at the boundary points.

Starting with the literature overview, the vibrational behavior of curve coupled beams seems to be an interesting and relevant topic of structural engineering, possibly introducing a beneficial and efficient procedure for investigating their dynamic behavior, especially for nanomaterial reinforcements. This corresponds to the main purpose of the present work, which considers the effect of temperature on the frequency response of the selected systems, involving thermal-dependent mechanical properties for each phase. Notably, our novelty lies in the exploration of temperature-dependent (TD) mechanical properties, specifically focusing on poly methyl methacrylate (PMMA) strengthened with single-walled CNTs (SWCNTs). The unique aspect is the application of the basic rule of mixture to define equivalent mechanical properties for nanocomposites with TD characteristics. The equivalent mechanical properties of the composite material reinforced with CNTs are determined using a simple rule of mixture, where the governing equation of the beam is obtained by means of the Hamiltonian principle, which is then solved in discrete form based on the GDQ method. A validation study is performed against the reference literature to show the correctness and accuracy of the proposed procedure, where a systematic investigation examines the sensitivity of the frequency response to different input parameters, for both thermal-dependent and independent mechanical parameters of the composite material. Our analysis extends beyond the existing literature by comprehensively assessing the vibrational behavior of the structure under these varied conditions.

2. CNT Beams Material Properties

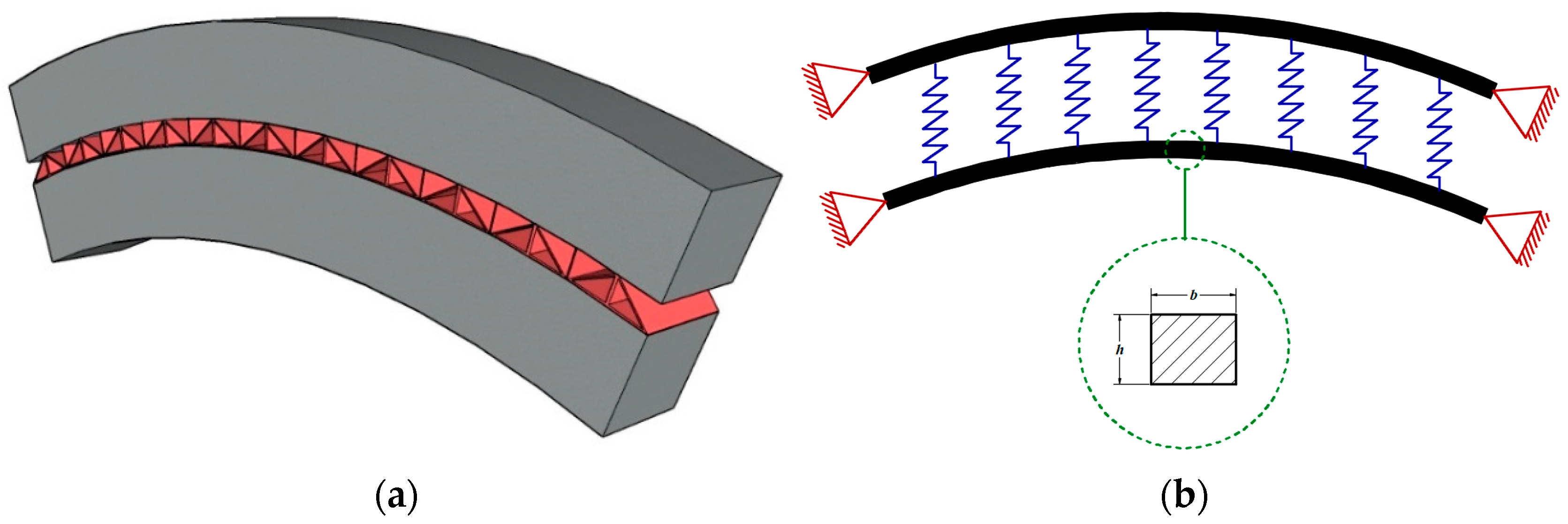
Let us consider a coupled curved CNT beam, with two curved beams connected with a layer of linear springs. The geometry of beams is described by a radius R, length L, central angle θ, and transverse width and height, b and h, respectively, of the beam section. Different combinations of boundary conditions can be considered per beam, namely, clamped–clamped (C-C), clamped–simply supported (C-S), clamped–free (C-F) or simply–simply supported (S-S). Figure 1 shows a simply supported (S-S/S-S) curved system with $\theta =45°$ made of a composite material reinforced with CNTs.

More specifically, the selected example considers a PMMA matrix and SWCNTs (10,10) as the reinforcement phase. Five types of reinforcement patterns are used here, including a uniform distribution of CNTs (UD-CNTs), as well as FG distributions of CNTs of type V, Λ, O, and X, as depicted in Figure 2.

From an analytical standpoint, for example, a Λ−type variation of a function in the z direction can be defined as [29]

$$F(z)={\left(\frac{1}{2}-\frac{z}{h}\right)}^n -\frac{h}{2}\le z\le \frac{h}{2}$$

(1)

In the particular case of CNTs volume fraction varying with a Λ distribution, it is

$$V_{CNT}(z)=\left(n+1\right)\hspace{0.17em}{\left(\frac{1}{2}-\frac{z}{h}\right)}^n\hspace{0.17em}{V}_{CNT}^{\ast }$$

(2)

which reverts to a linear distribution throughout the thickness for n = 1, namely

$$V_{CNT}(z)=\hspace{0.17em}{\left(1-2\frac{z}{h}\right)}^{}\hspace{0.17em}{V}_{CNT}^{\ast }$$

(3)

Based on the assumption of linear distribution, the mathematical definitions of all the selected CNT patterns along the z direction are summarized in

Table 1. Mathematical definition of different CNTs patterns throughout the thickness.

Pattern Type	Distribution Factor
UD	$V^{\ast }{}_{CNT}$
FG-V	($1+2\frac{z}{h}$) $V^{\ast }{}_{CNT}$
FG-Λ	($1-2\frac{z}{h}$) $V^{\ast }{}_{CNT}$
FG-O	$2\hspace{0.17em}(1-2\frac{\left|z\right|}{h})$ $V^{\ast }{}_{CNT}$
FG-X	($4\frac{\left|z\right|}{h}$) $V^{\ast }{}_{CNT}$

.

Based on the role of mixture, we determine the equivalent mechanical properties of the reinforced beam as follows [29]:

$$V_{CNT}+V_{Matrix}=1$$

(4)

$$E_{11}={\eta }_1\hspace{0.17em}{V}_{CNT}\hspace{0.17em}{E}_{11}^{CNT}+V_{Matrix}\hspace{0.17em}{E}^{Matrix}$$

(5)

$$E_{22}=\frac{{\eta }_2}{\frac{V_{CNT}}{E_{22}^{CNT}}+\frac{V_{Matrix}}{E^{Matrix}}}$$

(6)

$$G_{12}=\frac{{\eta }_3}{\frac{V_{CNT}}{G_{12}^{CNT}}+\frac{V_{Matrix}}{G^{Matrix}}}$$

(7)

$${\upsilon }_{CNT}={\upsilon }_{CNT}\hspace{0.17em}{V}_{CNT}+{\upsilon }_{Matrix}\hspace{0.17em}{V}_{Matrix}$$

(8)

$${\rho }_{CNT}={\rho }_{CNT}\hspace{0.17em}{V}_{CNT}+{\rho }_{Matrix}\hspace{0.17em}{V}_{Matrix}$$

(9)

where $V_{CNT}$ and $V_{Matrix}$ refer to the CNTs and matrix volume fraction, respectively; $E_{11}^{CNT}$, $E_{22}^{CNT}$ and $G_{12}^{CNT}$ indicate the normal and shear elasticity moduli of SWCNTs; $E^{Matrix}$ and $G^{Matrix}$ stand for the elasticity moduli of the matrix, respectively; ${\eta }_i\hspace{0.17em}(i=1,\hspace{0.17em}2,\hspace{0.17em}3)$ is a factor that considers the size-dependent material properties.

3. Theory and Formulation

The theoretical background of the selected in-plane vibration problem stems from the FSDT curved beam assumptions, while neglecting the deflections and rotations, and assuming a distribution of linear elastic normal springs at the interfaces. Thus, the kinematic field of the reference layer for each curved beam is defined as

$$\begin{array}{l}{D}_1^i\hspace{0.17em}(x_i,z,t)\hspace{0.17em}=\hspace{0.17em}{d}_1^i\hspace{0.17em}(x_i,t)+z\hspace{0.17em}{\Phi }_i\hspace{0.17em}(x_i,t)\\ D_2^i\hspace{0.17em}(x_i,z,t)\hspace{0.17em}=\hspace{0.17em}{d}_2^i\hspace{0.17em}(x_i,t)\end{array}$$

(10)

where $D_1^i$ and $D_2^i$ define the displacement components of an arbitrary point in the longitudinal $\left(x_i\right)$ and thickness $\left(z\right)$ directions, respectively, whereas $d_1^i$ and $d_2^i$ refer to the displacement field of the neutral axis in the longitudinal $\left(x_i\right)$ and thickness (z) directions, respectively. For details about the geometrical definition of this system in its bottom and upper parts can be found in [1]. The relation between the strain components of an arbitrary point and the reference neutral strain field is defined as

$$\left\{\begin{array}{c}{\epsilon }_x^i\\ {\gamma }_{xz}^i\end{array}\right\}=\left[\begin{array}{ccc}{\varphi }_1^i& {\varphi }_2^i& 0\\ 0& 0& {\varphi }_3^i\end{array}\right]\hspace{0.17em}\left\{\begin{array}{c}{\epsilon }_x^{i0}\\ {\eta }_x^i\\ {\gamma }_{xz}^{i0}\end{array}\right\}$$

(11)

with

$${\varphi }_1^i=\frac{1}{1+{{\rm Y}}_i}, {\varphi }_2^i=\frac{z}{1+{{\rm Y}}_i}$$

(12)

where ${\epsilon }_x^i$ and ${\gamma }_{xz}^i$ are normal and shear strain components, ${\epsilon }_x^{i0}$ and ${\gamma }_{xz}^{i0}$ are the normal and shear neutral strain components, and ${\eta }_x^i$ represent the curvature of beams on the reference surface, with ${{\rm Y}}_i=\frac{z}{R_i}$. Based on the FDST assumptions for cylindrical panels, the kinematic relations are defined for each $i$th beam as

$$\left\{\begin{array}{c}{\epsilon }_x^{i0}\\ {\eta }_x^i\\ {\gamma }_{xz}^{i0}\end{array}\right\}=\left\{\begin{array}{ccc}\frac{\partial }{\partial x_i}& \frac{1}{R_i}& 0\\ -\frac{1}{R_i}& \frac{\partial }{\partial x_i}& 1\\ 0& 0& \frac{\partial }{\partial x_i}\end{array}\right\}\hspace{0.17em}\left\{\begin{array}{c}{d}_1^i\\ {\Phi }_i\\ d_2^i\end{array}\right\}$$

(13)

For an FG material, we consider the following constitutive relations:

$$\left\{\begin{array}{c}{\sigma }_x^i\\ {\tau }_{xz}^i\end{array}\right\}=\left[\begin{array}{cc}E\left(z\right)& 0\\ 0& \frac{E\left(z\right)}{2\hspace{0.17em}\left(1+\nu \left(z\right)\right)}\end{array}\right]\hspace{0.17em}\left\{\begin{array}{c}{\epsilon }_x^i\\ {\gamma }_{xz}^i\end{array}\right\}$$

(14)

where ${\sigma }_x^i$ is the normal stress, ${\tau }_{xz}^i$ is the shear stress, and $E$ and $\nu$ are elastic modulus and Poisson’s ratio of the beam, respectively. Therefore, forces and moments can be calculated by employing the integration of stresses in the z-direction.

$$\left[\begin{array}{c}{N}_x^i\\ Q_x^i\\ M_x^i\end{array}\right]=b_i{\displaystyle \underset{-\frac{h_i}{2}}{\overset{\frac{h_i}{2}}{\int }}\left\{\begin{array}{c}{\sigma }_x^i\\ {\tau }_{xz}^i\\ z\hspace{0.17em}{\sigma }_x^i\end{array}\right\}}\hspace{0.17em}dz$$

(15)

Forces and moments can be, thus, defined as

$$\begin{array}{l}{N}_x^i={\epsilon }_x^{i0}\hspace{0.17em}{A}_{11}^i+\hspace{0.17em}{\eta }_x^i\hspace{0.17em}{B}_{11}^i\\ Q_x^i=\hspace{0.17em}{\gamma }_{xz}^{i0}\hspace{0.17em}{A}_{55}^i\\ M_x^i=\hspace{0.17em}{\epsilon }_x^{i0}\hspace{0.17em}{B}_{11}^i+\hspace{0.17em}{\eta }_x^i\hspace{0.17em}{D}_{11}^i\end{array}$$

(16)

in which

$$\begin{gathered} A_{11}^i=\hspace{0.17em}{b}_i{\displaystyle \underset{-\frac{h_i}{2}}{\overset{\frac{h_i}{2}}{\int }}{\varphi }_1^{i}E\left(z\right)dz}, B_{11}^i=\hspace{0.17em}{b}_i{\displaystyle \underset{-\frac{h_i}{2}}{\overset{\frac{h_i}{2}}{\int }}{\varphi }_2^{i}E\left(z\right)dz} \\ {D}_{11}^i=\hspace{0.17em}{b}_i{\displaystyle \underset{-\frac{h_i}{2}}{\overset{\frac{h_i}{2}}{\int }}{\varphi }_3^i\hspace{0.17em}E\left(z\right)dz}, A_{55}^i=\hspace{0.17em}\kappa \hspace{0.17em}{b}_i{\displaystyle \underset{-\frac{h_i}{2}}{\overset{\frac{h_i}{2}}{\int }}{\varphi }_1^i\hspace{0.17em}\frac{E\left(z\right)}{2\hspace{0.17em}(1+\nu )}\hspace{0.17em}dz} \end{gathered}$$

(17)

In these equations, $N_x^i$, $Q_x^i$ and $M_x^i$ are normal and shear force and moments and $\kappa$ is the shear factor which is equal to $\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$6$}\right.$. By using the Hamilton’s law and Gauss-Green theory, we obtain the following governing equations for the arched system (see more details in [16]):

$$\begin{array}{c}{A}_{11}^{top}\left(\frac{d^2{F}_1}{d{x}^2}+\frac{1}{R_1}\hspace{0.17em}\frac{d{F}_3}{dx}\right)+B_{11}^{top}\frac{d^2{F}_2}{d{x}^2}+A_{55}^{top}\left(\frac{1}{R_1}\hspace{0.17em}\frac{d{F}_3}{dx}-\frac{F_1}{R_1^2}+F_2\right)\\ =\hspace{0.17em}{I^{\prime }}_0\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_1}{\partial t^2}+{I^{\prime }}_1\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_2}{\partial t^2}\end{array}$$

(18)

$$\begin{array}{c}{A}_{55}^{top}\left(\frac{d^2{F}_3}{d{x}^2}-\frac{1}{R_1}\hspace{0.17em}\frac{d{F}_1}{dx}+\hspace{0.17em}\frac{d{F}_2}{dx}\right)+A_{11}^{top}\left(\frac{1}{R_1}\hspace{0.17em}\frac{d{F}_1}{dx}+\frac{1}{R_1^2}\hspace{0.17em}\frac{d{F}_3}{dx}\right)+\\ B_{11}^{top}\hspace{0.17em}\frac{1}{R_1}\hspace{0.17em}\frac{d{F}_2}{dx}+K_s\left(F_3-F_6\right)={I^{\prime }}_0\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_3}{\partial t^2}\end{array}$$

(19)

$$\begin{array}{c}{B}_{11}^{top}\hspace{0.17em}\left(\frac{d^2{F}_1}{d{x}^2}+\frac{1}{R_1}\hspace{0.17em}\frac{d{F}_3}{dx}\right)+D_{11}^{top}\hspace{0.17em}\frac{d^2{F}_2}{d{x}^2}-A_{55}^{top}\left(\frac{d{F}_3}{dx}-\frac{F_1}{R_1}+F_2\right)\\ ={I^{\prime }}_1\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_1}{\partial t^2}+{I^{\prime }}_2\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_2}{\partial t^2}\end{array}$$

(20)

$$\begin{array}{c}{A}_{11}^{bottom}\left(\frac{d^2{F}_4}{d{x}^2}+\frac{1}{R_2}\hspace{0.17em}\frac{d{F}_6}{dx}\right)+B_{11}^{bottom}\hspace{0.17em}\frac{d^2{F}_5}{d{x}^2}+A_{55}^{bottom}\hspace{0.17em}\left(\frac{1}{R_2}\hspace{0.17em}\frac{d{F}_6}{dx}-\frac{F_4}{R_2^2}+F_5\right)\\ ={I^{\prime }}_0\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_4}{\partial t^2}+{I^{\prime }}_1\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_5}{\partial t^2}\end{array}$$

(21)

$$\begin{array}{c}{A}_{55}^{bottom}\left(\frac{d^2{F}_6}{d{x}^2}-\frac{1}{R_2}\hspace{0.17em}\frac{d{F}_4}{dx}+\hspace{0.17em}\frac{d{F}_5}{dx}\right)+A_{11}^{bottom}\left(\frac{1}{R_2}\hspace{0.17em}\frac{d{F}_4}{dx}+\frac{1}{R_2^2}\hspace{0.17em}\frac{d{F}_6}{dx}\right)+\\ B_{11}^{bottom}\hspace{0.17em}\frac{1}{R_2}\hspace{0.17em}\frac{d{F}_5}{dx}+K_s\left(F_6-F_3\right)={I^{\prime }}_0\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_6}{\partial t^2}\end{array}$$

(22)

$$\begin{array}{c}{B}_{11}^{bottom}\hspace{0.17em}\left(\frac{d^2{F}_4}{d{x}^2}+\frac{1}{R_2}\hspace{0.17em}\frac{d{F}_6}{dx}\right)+D_{11}^{bottom}\hspace{0.17em}\frac{d^2{F}_4}{d{x}^2}-A_{55}^{bottom}\hspace{0.17em}\left(\frac{d{F}_6}{dx}-\frac{1}{R_2}\hspace{0.17em}{F}_4+F_5\right)\\ ={I^{\prime }}_1\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_4}{\partial t^2}+{I^{\prime }}_2\hspace{0.17em}{\omega }^2\hspace{0.17em}\frac{{\partial }^2{F}_5}{\partial t^2}\end{array}$$

(23)

In these equations, $F_i\hspace{0.17em}(i=1\cdots 6)$ is used as a symbol to indicate the reference layer displacements for each beam, whereas the inertial terms $I_j$ and ${I^{\prime }}_j$ are obtained as follows:

$$\{I_0,\hspace{0.17em}{I}_1,\hspace{0.17em}{I}_2,\hspace{0.17em}{I}_3\}\hspace{0.17em}=\hspace{0.17em}{\alpha }_i\hspace{0.17em}{\displaystyle \underset{-\frac{h_i}{2}}{\overset{\frac{h_i}{2}}{\int }}\rho \hspace{0.17em}\{1,\hspace{0.17em}z,}\hspace{0.17em}{z}^2,\hspace{0.17em}{z}^3\}\hspace{0.17em}dz$$

(24)

$${I^{\prime }}_0=I_0+\frac{I_1}{R_i}, {I^{\prime }}_1=I_1+\frac{I_2}{R_i}, {I^{\prime }}_2=I_2+\frac{I_3}{R_i}$$

(25)

4. Solution Approach

It is well known from the literature that the GDQ method was introduced by Shu [73] to solve the partial equation in fluid mechanics, but is was then developed for many engineering practices [74,75,76,77,78]. To obtain a simple expression for weighting coefficients, Shu used the Lagrange interpolated polynomials. These coefficients can be calculated from the following expression:

$$W_j(x)\hspace{0.17em}=\hspace{0.17em}\frac{w(x)}{(x-x_i)\hspace{0.17em}{w}^{(1)}(x)},\hspace{1em}j=1,\hspace{0.17em}2,\hspace{0.17em}\dots ,\hspace{0.17em}N$$

(26)

in which

$$w\hspace{0.17em}(x)={\displaystyle \prod _{i=1}^N(x-x_i)}, w^{(1)}(x)={\displaystyle \prod _{i=1,\hspace{0.17em}i\ne j}^N(x_j-x_i)}$$

(27)

To determine the weighting coefficients together with their first and higher order of derivatives, the following expressions can be used:

$$c_{ji}^{(1)}=\{\begin{array}{c}\hspace{0.17em}\frac{w^{(1)}(x_j)}{(x_j-x_i)\hspace{0.17em}{w}^{(1)}(x_j)},\hspace{1em}when\hspace{0.17em}\hspace{0.17em}i\ne j\hfill \\ {\displaystyle \sum _{k=1,\hspace{0.17em}j\ne k}^N{c}_{jk}^{(1)},\hspace{1em}\hspace{1em}\hspace{0.17em}when\hspace{0.17em}\hspace{0.17em}i\ne j}\hfill \end{array}$$

(28)

for the first order derivative, where

$$w^{(1)}(x_j)\hspace{0.17em}=\hspace{0.17em}{\displaystyle \prod _{i=1,\hspace{0.17em}j\ne i}^N(x_j-x_i)}, i=j=1,\hspace{0.17em}2,\hspace{0.17em}\dots ,\hspace{0.17em}N$$

(29)

For higher order derivatives, instead, it is

$$c_{ji}^{(n)}=\{\begin{array}{c}\hspace{0.17em}n\left(c_{jj}^{(n-1)}\hspace{0.17em}{c}_{ji}^{(1)}-\frac{c_{ji}^{(n-1)}}{x_j-x_i}\right),\hspace{1em}when\hspace{0.17em}\hspace{0.17em}i\ne j\\ {\displaystyle \sum _{k=1,\hspace{0.17em}j\ne k}^N{c}_{jk}^{(n)},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{1em}when\hspace{0.17em}\hspace{0.17em}i\ne j}\end{array}$$

(30)

In this study, we use a direct way to import boundary conditions. The grid points related to the boundary conditions are removed and their effect on the other grid points (internal points) is ignored. Such boundary conditions are defined mathematically as

$$\begin{gathered} \mathrm{For} \mathrm{C}\text{-}\mathrm{C}: d_1^i=d_2^i={\Phi }_i=0 \\ \mathrm{For} \mathrm{S}\text{-}\mathrm{S}: d_1^i=d_2^i=M_x^i=0 \\ \mathrm{For} \mathrm{F}\text{-}\mathrm{F}: N_x^i=Q_{xz}^i=M_x^i=0 \end{gathered}$$

(31)

The natural frequencies of the system can be calculated by using the following equation:

$$\left|S{M}_{eff}-{\omega }^2\hspace{0.17em}{M}_{eff}\right|=0$$

(32)

Here, $S{M}_{eff}$ and $M_{eff}$ refer to the effective stiffness and mass matrices related to the internal points. These matrices can be obtained as

$$\left[S{M}_{eff}\right]=\left[S{M}_I\right]-\left[S{M}_{IB}\right]\hspace{0.17em}{\left[S{M}_B\right]}^{-1}\left[S{M}_{BI}\right]\hspace{0.17em}$$

(33)

$$\left[M_{eff}\right]=\left[M_I\right]$$

(34)

where $S{M}_I$ is the stiffness matrix related to the internal points, $S{M}_{IB}$ is the internal stiffness matrix associated with boundary conditions, and $S{M}_B$ is the boundary condition stiffness matrix.

5. Validation and Convergence Study

A numerical algorithm has been developed to compute the natural frequencies of coupled curved CNT beams, where the accuracy of results has been checked against frequency predictions in the literature [13], based on a finite element method (FEM) for different boundary conditions. The geometry of the S-S curved beam is defined as R = 0.75 m, A = 4 m², I = 0.01 m⁴, and R/h = 4, whereas the C-C example features the geometrical properties R = 0.6366 m, A = 1 m², I = 0.0016 m⁴, and R/h = 6. The mechanical properties of the structure are set as E = 70 GPa, υ = 0.4166, ρ = 2777 kg/m³, and κ = 0.85, in line with Ref. [13].

Table 2. Dimensionless frequency of the homogenous curved beam.

Mode	S-S		C-C
	This Study	Ref. [13]	This Study	Ref. [13]
1	29.2757	29.2850	36.7045	36.7160
2	33.2995	33.3210	42.2656	42.2780
3	67.1136	67.2020	82.2368	82.3610
4	79.9578	80.0490	84.4943	84.5650
5	107.835	108.169	122.311	122.722

summarizes the dimensionless frequency for the curved beam obtained in this research compared to results from Ref. [13]. Based on the results, the frequencies computed with our approach are very close to predictions from Ref. [13], thus confirming the accuracy of the proposed formulation.

At the same time, Sobhani and Masoodi [16] applied the finite element approach to the vibration of coupled arched beams, connected elastically by a layer of springs at the interface, for different boundary conditions.

Table 3. Natural frequencies of coupled homogenous curved beams.

Mode	C-C/C-C		C-S/C-S		S-S/S-S		C-F/C-F
	This Study	Ref. [16]	This Study	Ref. [16]	This Study	Ref. [16]	This Study	Ref. [16]
1	10.931	10.932	8.6624	8.6624	6.7019	6.7023	2.9378	2.9378
2	11.342	11.342	9.1684	9.1684	7.3345	7.3349	3.5271	3.5271
3	20.620	20.621	18.031	18.032	15.545	15.546	4.5757	4.5756
4	20.860	20.861	18.304	18.304	15.860	15.861	11.003	11.003
5	37.380	37.382	33.306	33.306	29.528	29.530	11.423	11.424

validates our method for coupled arched beams with the results from Ref. [16]. In this example, the geometry of the beams is defined as L_i = 10, R₁ = R₂ = 7.5, and h₁ = h₂ = b₁ = b₂ = 0.1. Material properties are E = 200 GPa, υ = 0.34, ρ = 7850 kg/m³, and κ = 0.87, and mid-layer stiffness is 16,000. Based on Table 3, it is worth observing the very good correspondence among our results and the literature [16] for all boundary conditions.

In accordance to Babaei [30], we studied the free vibration of FG-CNTRC curved beams on nonlinear elastic foundations, and a convergence study was done to obtain the optimum value of grid points (N) in GDQM. Based on results, it was found that nine grid points is sufficient to ensure the accuracy of the frequency results for CNT beams.

Table 4. Dimensionless frequency of CNT curved beam with S-S boundary condition (L/R = 0.2 and L/h = 25).

CNTs Pattern	$V_{CNT}^{\ast }$	This Study					Ref. [30]
		ω1	ω2	ω3	ω4	ω5	ω1	ω2	ω3
UD	0.12	33.0910	53.0608	95.5477	137.195	178.955	31.6373	53.6617	94.5798
	0.17	39.7517	65.6635	119.925	173.818	227.912	38.0857	66.2890	118.645
	0.28	49.3183	75.6428	133.685	189.651	245.808	47.6137	77.3944	133.310
FG-O	0.12	31.1475	43.3217	83.5019	124.939	167.510	29.8088	43.4827	79.4926
	0.17	37.3037	52.9235	103.529	156.791	211.891	35.8071	53.2657	99.2077
	0.28	46.4691	63.0713	119.963	177.582	236.519	45.0041	64.6479	117.180
FG-X	0.12	34.4999	58.4039	101.363	142.768	184.100	33.1091	59.2156	101.272
	0.17	41.5231	72.9407	128.366	182.309	236.097	39.9296	73.3581	127.006
	0.28	51.2700	83.6055	143.256	200.258	257.278	49.5523	83.0986	138.326

also indicates the first three dimensionless frequency $\left(\omega \frac{L^2}{h}\hspace{0.17em}\sqrt{\frac{{\rho }_0}{E_0}}\right)$ for the CNT curved beam, while comparing successfully them with our results, under the following assumptions for the properties of CNTs and size-dependent coefficient

$$\begin{array}{l}\hspace{0.17em}{V}_{CNT}^{\ast }=0.12\to {\eta }_1=0.137,\hspace{0.17em}{\eta }_2=1.022,\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\eta }_3=0.715\\ \hspace{0.17em}{V}_{CNT}^{\ast }=0.17\to {\eta }_1=0.142,\hspace{0.17em}{\eta }_2=1.626,\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\eta }_3=1.138\\ \hspace{0.17em}{V}_{CNT}^{\ast }=0.28\to {\eta }_1=0.141,\hspace{0.17em}{\eta }_2=1.585,\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\eta }_3=1.109\end{array}$$

(35)

$$\begin{array}{l}{E}_{11}^{CNT}=5646.6\hspace{0.17em}\hspace{0.17em}\mathrm{GPa},\hspace{0.17em}\hspace{0.17em}{E}_{22}^{CNT}=7080\hspace{0.17em}\hspace{0.17em}\mathrm{GPa},\hspace{0.17em}\mathrm{and}\hspace{0.17em}{G}_{12}^{CNT}=1944.5\hspace{0.17em}\hspace{0.17em}\mathrm{GPa}\\ {\rho }_{CNT}=1400\hspace{0.17em}\raisebox{1ex}{$\mathrm{kg}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{cm}}^2$}\right.,\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\upsilon }_{CNT}=0.175\\ E_{Matrix}=2.5\hspace{0.17em}\mathrm{GPa},\hspace{0.17em}{\rho }_{Matrix}=1150\hspace{0.17em}\raisebox{1ex}{$\mathrm{kg}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{cm}}^2$}\right.,\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\upsilon }_{Matrix}=0.34\end{array}$$

(36)

Table 5. Dimensionless frequency of CNT curved beam with S-S boundary condition on elastic foundation.

$V_{CNT}^{\ast }$	CNTs Pattern	This Study		Ref. [30]
		ω1	ω2	ω1	ω2
0.17	FG-O	20.9321	47.1825	21.4803	48.6612
	FG-X	28.2739	64.3162	27.0170	64.3032

also shows the results in terms of first two dimensionless frequency of curved beams resting on the elastic foundation. The stiffness of the springs is equal to $100\hspace{0.17em}{E}_{Matrix}{h}^3/L^4$. The geometry of the curved beam is defined as $L/R=0.1$ and $L/h=20$.

6. Parametric Investigation

In this section, several examples have been solved to investigate the vibration properties of the system. For all examples, PMMA and SWCNTs (10,10) are used as matrix and reinforcement phase, respectively. More specifically, for CNTs we assume the following properties:

$$\begin{array}{l}{E}_{11}^{CNT}=600\hspace{0.17em}\hspace{0.17em}\mathrm{GPa},\hspace{0.17em}\hspace{0.17em}{E}_{22}^{CNT}=10\hspace{0.17em}\hspace{0.17em}\mathrm{GPa},\hspace{0.17em}\mathrm{and}\hspace{0.17em}{G}_{12}^{CNT}=17.2\hspace{0.17em}\hspace{0.17em}\mathrm{GPa}\\ {\rho }_{CNT}=1400\hspace{0.17em}\raisebox{1ex}{$\mathrm{kg}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{cm}}^2$}\right.,\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\upsilon }_{CNT}=0.19\\ V_{CNT}^{\ast }=0.12,\hspace{0.17em}0.17,\hspace{0.17em}0.28\end{array}$$

(37)

The PMMA instead features the following Young’s modulus, density and Poisson’s ratio:

$$E_{Matrix}=2.5\hspace{0.17em}\mathrm{GPa},\hspace{0.17em}{\rho }_{Matrix}=1190\hspace{0.17em}\raisebox{1ex}{$\mathrm{kg}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{cm}}^2$}\right.,\hspace{0.17em}\mathrm{and}\hspace{0.17em}{\upsilon }_{Matrix}=0.30$$

(38)

The following efficiency parameters are set as

$$\begin{array}{l}\hspace{0.17em}{V}_{CNT}^{\ast }=0.12\to {\eta }_1=1.2833,\hspace{0.17em}{\eta }_2={\eta }_3=1.0556\\ \hspace{0.17em}{V}_{CNT}^{\ast }=0.17\to {\eta }_1=1.3414,\hspace{0.17em}{\eta }_2=\hspace{0.17em}{\eta }_3=1.7101\\ \hspace{0.17em}{V}_{CNT}^{\ast }=0.28\to {\eta }_1=1.3238,\hspace{0.17em}{\eta }_2=\hspace{0.17em}{\eta }_3=1.7380\end{array}$$

(39)

The stiffness of the interfacial springs is related to the mechanical and geometrical properties of the beams, as follows:

$$K=k_s\times \raisebox{1ex}{$A_{BM}$}\!\left/ \!\raisebox{-1ex}{$L^2$}\right.$$

(40)

where $K$ is the interfacial stiffness, $k_s$ refers to the stiffness factor, and $A_{BM}$ can be determined as

$$A_{BM}={\displaystyle \int \frac{E}{2\hspace{0.17em}(1-\nu )}\hspace{0.17em}dz}$$

(41)

where $E$ and v stand for the Young’s modulus and Poisson’s ratio of the pure PMMA matrix beam which was made by matrix, respectively. For such a case, the dimensionless frequency of the structure is determined as

$$\overline{\omega }=\omega \hspace{0.17em}R\hspace{0.17em}\sqrt{\frac{I_{BM}}{A_{BM}}}$$

(42)

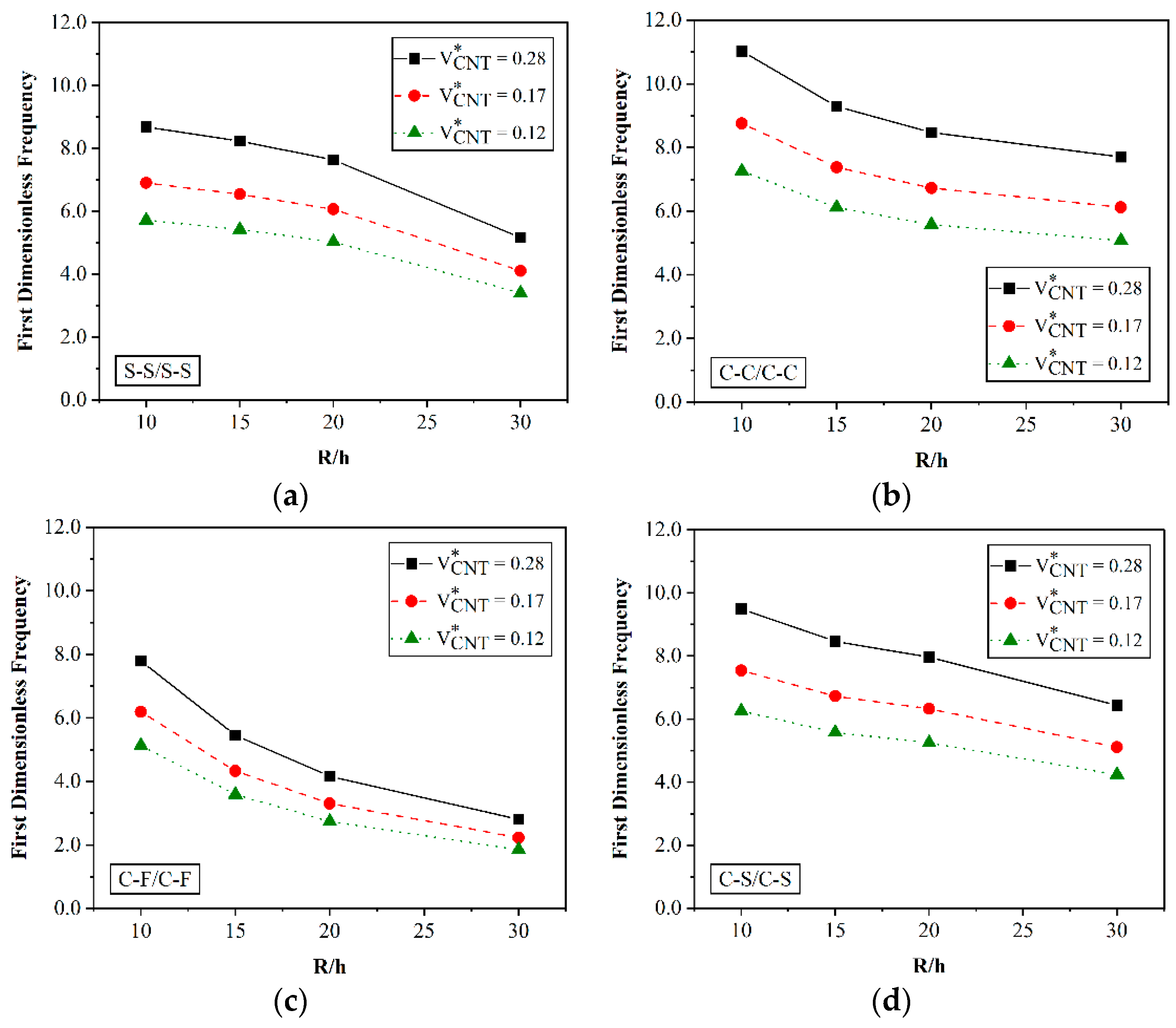
where the inertial quantity I_BM of the beam is obtained as ${\displaystyle \int \rho \hspace{0.17em}dz}$. Figure 3 shows the effect of the rational radius-to-height quantity of the beam on the first dimensionless frequency of the coupled curved beams. To this end, four values of 10, 15, 20, and 30 are considered for $R/h$, while setting the stiffness factor equal to 100. The geometrical properties of the beams are $\theta =45°$, R₁ = R₂ = 10, and $L_1=L_1=2R\sin \left(\frac{\theta }{2}\right)$. To investigate the effect of the CNT content, three different values of volume fraction are employed for CNTs, namely, $V_{CNT}^{\ast }=$ 0.12, 0.17, and 0.28. A uniform distribution of CNTs is employed throughout the beam for comparative purposes, under the same assumption of CNT volume fraction for each arm of the specimen. The frequency response is obtained for a system with S-S/S-S, C-C/C-C, C-S/C-S, and C-F/C-F boundary conditions. The results show that the frequency of the system decreases for an increased value of $R/h$. This is true for all boundary conditions and all CNT volume fractions. Also, for this example, we investigate the effect of the CNT volume on the frequency response of the system. Based on the results in Figure 3, a higher value of CNT volume fraction yields higher frequencies. For example, for a system with S-S/S-S boundary conditions and a fixed value of $R/h=10$, the first dimensionless frequency of the system increases from about six to nine by increasing $V_{CNT}^{\ast }$ from 0.12 to 0.28.

By comparing the rate of reduction of frequencies for an increased R/h, we can deduce that the CNTs volume fraction does not affect the reduction rate. In addition, the reduction rate for S-S/S-S, C-C/C-C, and C-S/C-S boundary conditions is nonlinear, whereas it becomes approximately linear for a C-F/C-F example. Such effect of BCs can be observed from a comparative evaluation of the plots in Figure 3. It can be also noticed that the frequency results associated with clamped boundary conditions are higher compared to other boundary conditions, in the following decreasing order: C-C/C-C > C-S/C-S > S-S/S-S > C-F/C-F.

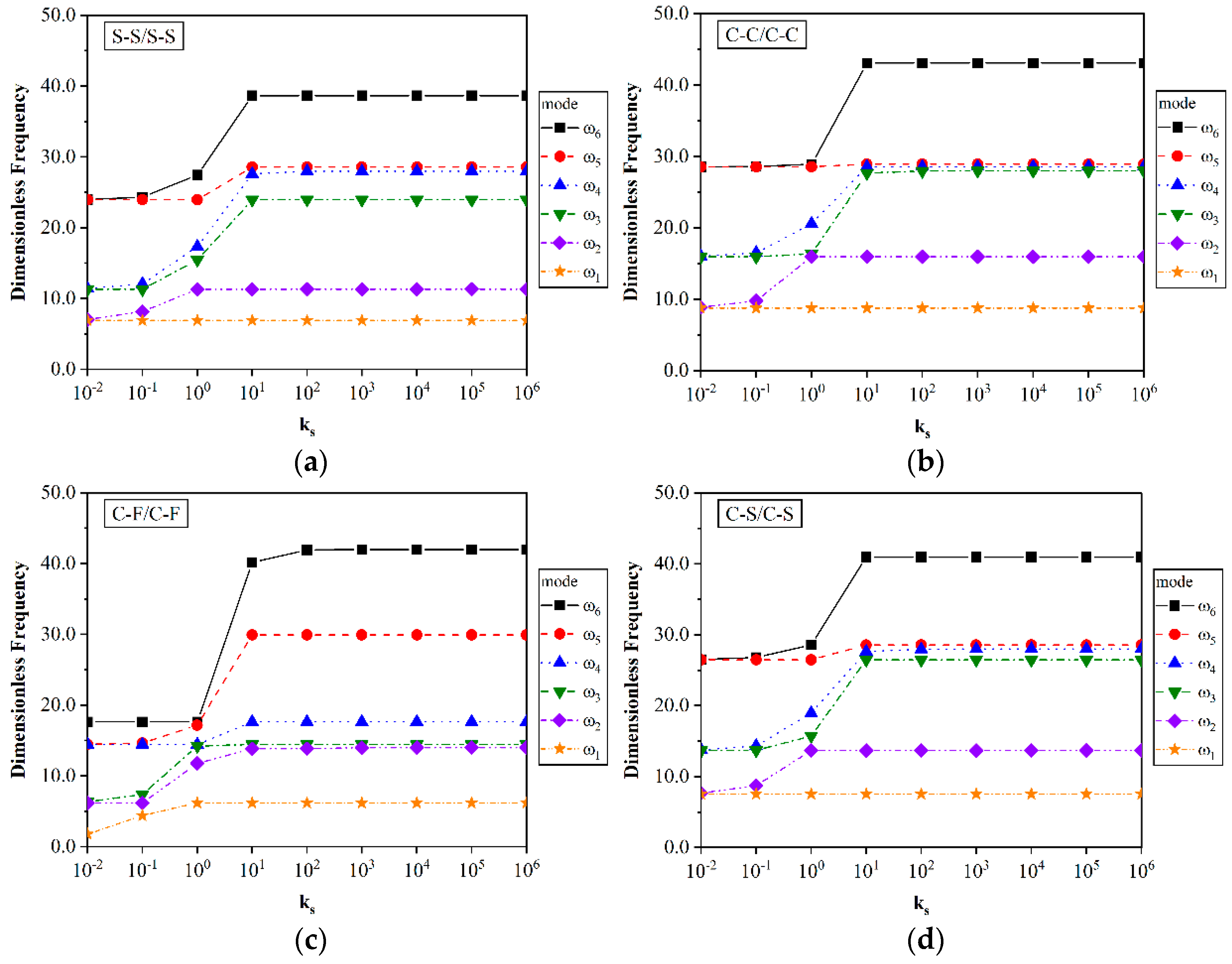
Figure 4 shows the effect of the interfacial stiffness on the first six frequencies of the system, here defined by means of the coefficient A_BM which is obtained from the matrix properties. Nine different values are here considered as the stiffness factor, from 0.01 up to 10⁶, whereas the CNTs volume fraction is assumed equal to 0.17 for a uniform distribution of CNTs. The geometry of beams is kept the same as in previous example, while assuming R/h is equal to 10. As already commented in the previous example, the higher values of frequencies are related to the system with C-C/C-C boundary conditions. For all boundary conditions, except C-F/C-F, the stiffness of the interfacial springs does not affect the first dimensionless frequency of system. Such sensitivity becomes more evident for higher modes of frequencies. The frequencies of the system increased for an increased interfacial stiffness up to a certain value of $k_s$, above which frequencies remain constant. From this figure, it seems that the effect of the interfacial stiffness on the frequency response has a direct relationship with boundary conditions and mode frequency.

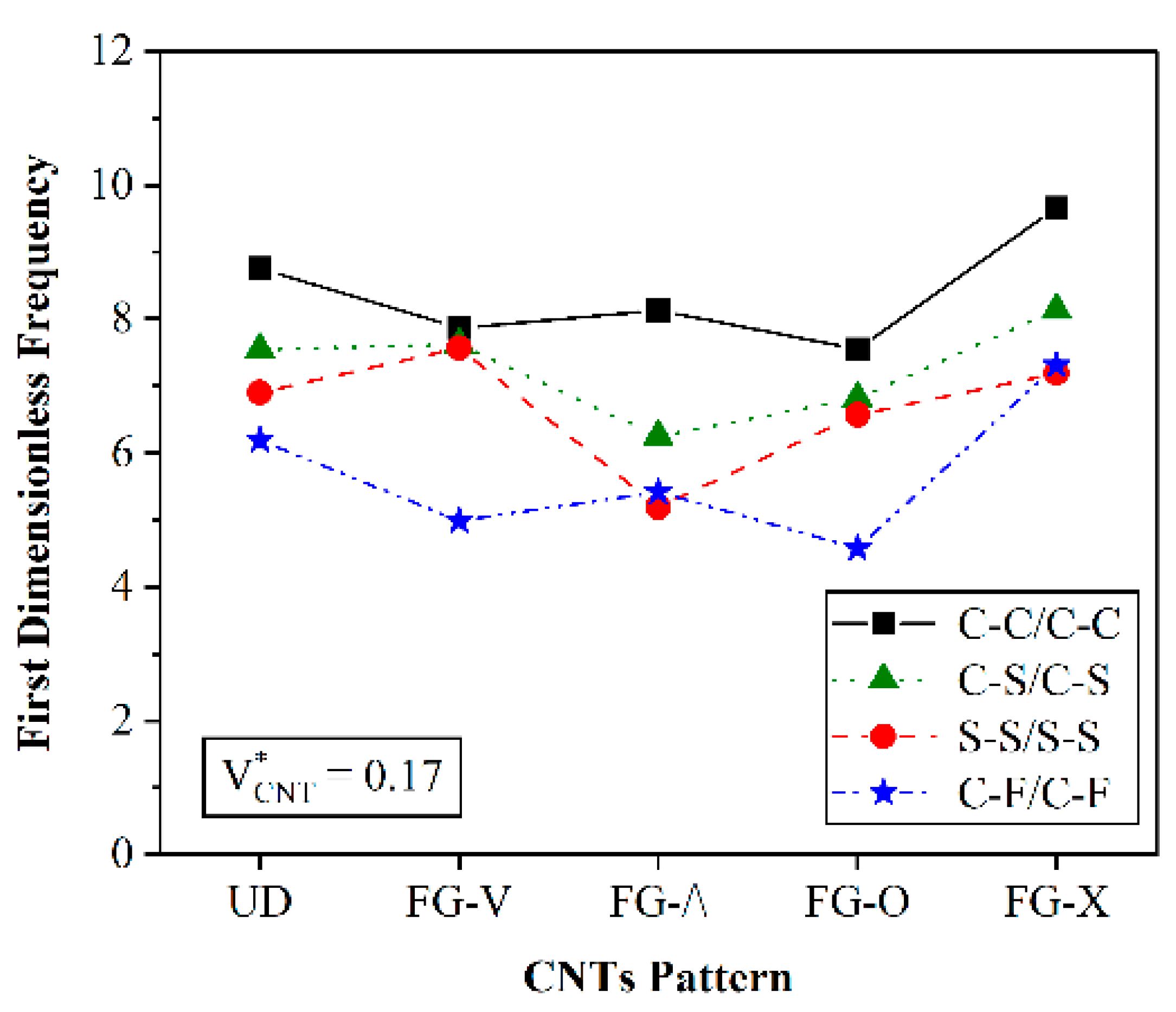
Figure 5 shows the effect of the CNTs pattern on the first mode frequency of the system, with the same geometry discussed before, and for an interfacial stiffness equal to 100. The volume of CNTs is 0.17 and CNTs are assumed to be distributed linearly in the same pattern in both beams (UD). Based on this figure, the effect of the distribution pattern is related to the boundary condition of the system. In all BCs, except for S-S/S-S, the highest value of the first dimensionless frequency is associated with the FG-X pattern. The lowest values of frequencies are associated with the Λ distribution (for S-S/S-S and C-S/C-S boundary conditions), and to circular CNTs distribution (for C-C/C-C or C-F/C-F boundary conditions). Based on a comparative evaluation of the frequencies, we get the following sequencies of frequency for each selected boundary condition and different distribution patterns of the reinforcement phase:

For a C-C/C-C system: FG-X > UD > FG-Λ > FG-V > FG-O,

For a C-S/C-S system: FG-X > UD ≈ FG-V > FG-O > FG-Λ,

For a S-S/S-S system: FG-V > UD > FG-X > FG-O > FG-Λ,

For a C-F/C-F system: FG-X > UD > FG-Λ > FG-V> FG-O.

Furthermore, for V and O distribution patterns of CNTs, the boundary conditions do not affect the first frequency of the system. This statement is true for C-C/C-C, S-S/S-S, and C-S/C-S boundary conditions.

Table 6. The first six dimensionless frequency of the system when the CNTs volume of one beam of system changed.

$\hspace{0.17em}{V}_{CNT}^{\ast }$	Modes
	1	2	3	4	5	6	7	8	9	10
$\hspace{0.17em}{V}_{CNT}^{\ast }$ in both beams is 0.12
0.12	7.2572	13.217	23.18	23.678	23.952	35.684	46.194	46.352	48.478	61.03
$\hspace{0.17em}{V}_{CNT}^{\ast }$ at the top side of both beams is 0.12 and varies at the bottom beam
0.17	8.0452	14.644	23.46	26.546	28.234	39.526	46.428	53.038	56.246	67.324
0.28	9.3562	16.973	23.574	30.798	35.456	45.702	46.478	60.972	69.564	70.608
$\hspace{0.17em}{V}_{CNT}^{\ast }$ at the bottom side of both beams is 0.12 and varies at the top beam
0.17	8.0452	14.644	23.46	26.546	28.234	39.526	46.428	53.038	56.246	67.324
0.28	9.3562	16.973	23.574	30.798	35.456	45.702	46.478	60.972	69.564	70.608

represent the frequency values for different CNTs volume fractions in the system. In this example, the CNT volume fraction at the top beam remains constant at 0.12, whereas $\hspace{0.17em}{V}_{CNT}^{\ast }$ at the bottom beam increases from 0.12 to 0.28. CNTs are uniformly distributed along the beams and the stiffness factor is equal to 100. The geometry of the beams is the same as in the previous example. Based on Table 6, the frequencies of the system slightly increase by increasing the CNT volume in the bottom beam. It also seems that there are no differences in the system frequencies for an increased number of CNTs at the top beam and bottom beam. In other words, it is not important which beam contains a higher volume of CNTs to increase the frequency response of the system.

Table 7. Dimensionless frequency for system which one of beams is made by matrix and another beam reinforced by different volumes of CNTs.

$V_{CNT}^{\ast }$	Modes
	1	2	3	4	5	6	7	8	9	10
Totally Matrix Beam
0	1.1917	2.168	3.8106	3.8894	3.9268	5.848	7.5844	7.6196	7.9462	9.996
bottom	Top Beam Made by pure Matrix
0.12	3.8044	5.2178	7.6306	9.6256	11.439	15.219	16.913	19.022	19.156	20.510
0.17	3.8066	6.2744	7.6400	11.311	11.675	15.224	19.022	19.173	19.501	21.104
0.28	3.8082	7.5500	7.9988	11.418	14.532	15.225	19.022	19.201	20.186	22.138
top	Bottom Beam Made by pure Matrix
0.12	3.8044	5.2178	7.6306	9.6256	11.439	15.219	16.913	19.022	19.156	20.510
0.17	3.8066	6.2744	7.6400	11.311	11.675	15.224	19.022	19.173	19.501	21.104
0.28	3.8082	7.5500	7.9988	11.418	14.532	15.225	19.022	19.201	20.186	22.138

shows the frequency response of the system when only the bottom beam is reinforced by CNTs, and the top beam is made totally by PMMA. The volume fraction in the bottom beam varies from zero to 0.28 with an X-type functional graduation, where the condition $\hspace{0.17em}{V}_{CNT}^{\ast }$ = 0 corresponds to a pure matrix material. The geometrical properties of the beams are $\theta =45°$, R₁ = R₂ = 10, R/h = 10, and $L_1=L_2=2\hspace{0.17em}R\hspace{0.17em}\sin \left(\frac{\theta }{2}\right)$, with a stiffness factor equal to 100. For an increased volume fraction of CNTs from zero to 0.12 in the bottom beam, the frequencies of the system increase for all boundary conditions, while keeping constant for volume fractions from 0.12 to 0.28. This means that the volume of CNTs as reinforcement at the bottom beams can affect the frequencies of the system when the top beam remains unreinforced. Based on the same table, there is no difference in the frequency system when the top or bottom beam is reinforced with CNTs.

Figure 6 shows the effect of curvature on the first dimensionless frequencies of the system. The CNTs volume fraction is 0.17 and distributed uniformly along the beams, under the same geometrical assumptions R₁ = R₂ = 10, R/h = 10, $L_1=L_2=2\hspace{0.17em}R\hspace{0.17em}\sin \left(\frac{\theta }{2}\right)$, and $k_s$ equal to 100. In this example, six values of $\theta$ are employed, where the frequencies of the system are computed for three different types of boundary condition. Note that by increasing $\theta$, the first frequency of the system decreases. For example, for C-C/C-C systems with a curvature factor of 15°, the frequency value is about thirty-nine and it tends to the unit value for $\theta$ = 180°.

In this section, we investigate the thermal-dependent vibration of the system. There are several studies in which the effect of temperature variation on the structural behavior has been investigated [79,80]. Thus far, the mechanical properties of SWCNTs (10,10) and PMMA have been represented at room temperature (300 °K). For other environmental temperatures, we consider the following expressions to define the thermal-dependent mechanical properties for SWCNTs:

$$\begin{array}{c}{E}_{CNT}^{11}=6.565376-1.76156\hspace{0.17em}\hspace{0.17em}\left(\frac{T}{T_0}\right)+1.13347\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^2-0.32260\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^3+0.03193\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^4\hspace{1em}\mathrm{TPa}\hfill \\ E_{CNT}^{22}=8.22710-2.19725\hspace{0.17em}\hspace{0.17em}\left(\frac{T}{T_0}\right)+1.41176\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^2-0.40125\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^3+0.03964\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^4\hspace{1em}\mathrm{TPa}\hfill \\ G_{CNT}^{12}=1.10442+1.88427\hspace{0.17em}\hspace{0.17em}\left(\frac{T}{T_0}\right)-1.47623\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^2+0.49029\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^3-0.05829\hspace{0.17em}{\left(\frac{T}{T_0}\right)}^4\hspace{1em}\mathrm{TPa}\hfill \\ {\rho }_{CNT}=1400\hspace{1em}\raisebox{1ex}{$kg$}\!\left/ \!\raisebox{-1ex}{$c{m}^2$}\right. \mathrm{and} {\nu }_{CNT}=0.175\hfill \end{array}$$

(43)

where T and T₀ represent the environment and room temperatures, respectively. The thermal-dependent Young’s modulus for PMMA can be obtained at any temperature by employing the following equation:

$$E_{Matrix}(T)=\{3.52-0.0034\hspace{0.17em}(300+\Delta T)\}\hspace{0.17em}\mathrm{GPa}$$

(44)

The density and Poisson’s ratio in PMMA are also 1150 kg/m³ and 0.34, respectively, in thermal environment.

Table 8. Properties of PMMA and SWCNT (10,10) at different temperatures.

T	EMatrix	E11	E22	G12
°K	GPa	TPa	TPa	TPa
300	2.50	5.6466	7.080	1.9445
400	2.16	5.5679	6.9816	1.9704
600	1.48	5.5062	6.9039	1.9578
800	0.80	5.4253	6.8026	1.9813
1000	0.12	5.2814	6.6219	1.9454

summarizes the variation of the mechanical properties for a SWCNT (10,10) and PMMA, with an overall monotonic decrease of all properties for an increased temperature.

It is worth observing that the mechanical properties of a pure PMMA matrix are more affected by temperature than the corresponding composite SWCNT (10,10). It is observed that the mechanical properties of PMMA and SWCNT decreases as the temperature increases. The following size-dependent parameters are here used in the rule of mixture to obtain the equivalent properties of beams in a thermal environment:

$$\begin{array}{l}\hspace{0.17em}{V}_{CNT}^{\ast }=0.12\to {\eta }_1=0.137,\hspace{0.17em}{\eta }_2=1.022,\hspace{0.17em}and\hspace{0.17em}{\eta }_3=0.715\\ \hspace{0.17em}{V}_{CNT}^{\ast }=0.17\to {\eta }_1=0.142,\hspace{0.17em}{\eta }_2=1.626,\hspace{0.17em}and\hspace{0.17em}{\eta }_3=1.138\\ \hspace{0.17em}{V}_{CNT}^{\ast }=0.28\to {\eta }_1=0.141,\hspace{0.17em}{\eta }_2=1.585,\hspace{0.17em}and\hspace{0.17em}{\eta }_3=1.109\end{array}$$

(45)

In this section, we ignore the possible effect of αΔT in the theoretical formulation, where we compute the dimensionless frequencies as

$$\overline{\omega }=\omega \hspace{0.17em}R\hspace{0.17em}\sqrt{\frac{I_{BM}}{A_{BM}}}$$

(46)

where I_BM and A_BM are computed at a room temperature (T = 300 °K).

Table 9. Effect of the environmental temperature on frequencies of S-S/S-S and C-C systems with beams made of pure PMMA matrix.

Mode	S-S/S-S					C-C/C-C
	Temperature (°K)					Temperature (°K)
	300	400	600	800	1000	300	400	600	800	1000
1	0.9258	0.9259	0.9258	0.9258	0.9258	1.1733	1.1733	1.1733	1.1733	1.1733
2	1.5133	1.5133	1.5133	1.5133	1.5133	2.1276	2.1276	2.1276	2.1276	2.1276
3	3.1968	3.1968	3.1968	3.197	3.1968	3.7566	3.7566	3.7566	3.7566	3.7566
4	3.7566	3.7566	3.7566	3.7566	3.7566	3.8338	3.8338	3.8338	3.8338	3.8338
5	3.8318	3.8318	3.8318	3.8316	3.8318	3.8476	3.8476	3.8476	3.8476	3.8476
6	5.1474	5.1474	5.1472	5.1472	5.1472	5.7232	5.7232	5.7232	5.7232	5.7232
7	7.1842	7.1844	7.1840	7.1840	7.1842	7.4620	7.4620	7.4620	7.4620	7.4620
8	7.5116	7.5116	7.5116	7.5114	7.5114	7.5116	7.5116	7.5116	7.5116	7.5116
9	7.5964	7.5966	7.5962	7.5962	7.5964	7.7844	7.7844	7.7844	7.7844	7.7844
10	9.4024	9.4028	9.4024	9.4024	9.4026	9.7662	9.7662	9.7662	9.7662	9.7662

presents the first ten dimensionless frequencies of the system made of a pure PMMA matrix. Results show that an increased environmental temperature does not affect the frequency response of S-S/S-S and C-C/C-C structures.

Table 10. Effect of the environment temperature on the frequency response of the S-S and C-C system.

Mode	S-S/S-S					C-C/C-C
	Temperature (°K)					Temperature (°K)
	300	400	600	800	1000	300	400	600	800	1000
1	5.6356	6.0120	7.1998	9.6892	24.602	7.1458	7.6232	9.1294	12.286	31.196
2	9.2200	9.8358	11.779	15.852	40.250	12.978	13.845	16.581	22.314	56.656
3	19.493	20.794	24.904	33.514	85.094	22.850	24.372	29.178	39.230	98.294
4	22.848	24.372	29.176	39.226	97.840	23.336	24.896	29.812	40.124	101.87
5	23.324	24.882	29.798	40.100	101.82	23.490	25.058	30.008	40.384	102.54
6	31.408	33.508	40.126	54.000	137.11	34.960	37.294	44.664	60.108	141.58
7	43.854	46.782	56.026	75.398	140.49	45.466	48.504	58.086	78.170	150.78
8	45.688	48.736	58.340	78.414	145.38	45.690	48.738	58.346	78.428	152.62
9	46.250	49.340	59.090	79.520	158.29	47.524	50.698	60.714	81.708	169.18
10	57.446	61.284	73.392	98.768	191.23	59.706	63.694	76.278	102.65	198.48

summarizes the first six frequencies of the system at different temperatures. Five values of temperature (300°, 400°, 600°, 800°, and 1000 °K) are assumed to evaluate the thermal sensitivity of the vibration response. The fraction volume of CNTs in both beams kept equal to 0.12 under the assumption of uniform distribution for the reinforcement phase. The geometry properties of the beam are still assumed as R₁ = R₂ = 10, R/h = 10, and $L_1=L_2=2\hspace{0.17em}R\hspace{0.17em}\sin \left(\theta /2\right)$. The stiffness factor and the curvature angle are assumed equal to 100 and 45°, respectively. Despite the expected decrease in frequency for an increased environment temperature, we do not observe any meaningful variation in the vibration response of the selected system, since both curved beams are subjected to the similar temperature simultaneously, therefore, the frequency of the total system does not change.

In the last example, we study the vibration response of the structural system in thermal conditions, such that the temperature of one beam maintains constant to 300° and the temperature on the other beam varies from 300° to 1000°. In both beams, the CNT volume fraction is equal to 0.12 and a uniform distribution is assumed for the reinforcement phase. All geometrical properties of the beam, together with k_s and θ, are assumed the same as in the previous example. In

Table 11. Dimensionless frequency of the system in the condition that the bottom beam temperature increased.

BCs	mode	Ttop beam= 300 °K					Tbottom beam= 300 °K
		Tbottom beam (°K)					Ttop beam (°K)
		300	400	600	800	1000	300	400	600	800	1000
S-S/S-S	1	5.6356	5.6120	5.5878	5.5590	5.5142	5.6356	6.0376	7.2624	9.8268	25.168
	2	9.2200	9.1812	9.1418	9.0944	9.0212	9.2200	9.8776	11.881	16.077	41.172
	3	19.493	19.411	19.327	19.228	19.072	19.493	20.884	25.120	33.990	87.022
	4	22.848	22.734	22.584	22.380	22.036	22.848	24.454	29.340	39.512	99.016
	5	23.324	23.244	23.194	23.160	23.132	23.324	25.006	30.144	40.928	105.02
	6	31.408	31.276	31.142	30.982	30.732	31.408	33.648	40.474	54.764	140.12
	7	43.854	43.666	43.472	43.228	42.830	43.854	46.978	56.498	76.408	140.61
	8	45.688	45.444	45.128	44.710	44.052	45.688	48.886	58.626	78.936	145.90
	9	46.250	46.110	46.040	45.998	45.96	46.25	49.606	59.832	81.262	159.43
	10	57.446	57.204	56.958	56.66	56.198	57.446	61.544	74.024	100.15	193.62
C-C/C-C	1	7.1458	7.116	7.0854	7.0486	6.992	7.1458	7.6556	9.2088	12.46	31.912
	2	12.978	12.924	12.869	12.801	12.698	12.978	13.904	16.725	22.628	57.948
	3	22.850	22.734	22.588	22.384	22.042	22.850	24.456	29.344	39.524	99.452
	4	23.336	23.256	23.206	23.168	22.982	23.336	25.02	30.158	40.944	104.84
	5	23.490	23.39	23.29	23.170	23.138	23.490	25.164	30.270	40.958	105.16
	6	34.960	34.814	34.664	34.484	34.206	34.960	37.454	45.052	60.954	141.76
	7	45.466	45.184	44.83	44.384	43.676	45.466	48.610	58.252	78.400	151.48
	8	45.690	45.584	45.532	45.470	45.348	45.690	49.038	59.158	80.308	155.92
	9	47.524	47.328	47.142	46.930	46.644	47.524	50.918	61.266	82.946	170.71
	10	59.706	59.456	59.198	58.888	58.408	59.706	63.964	76.938	104.08	200.04

, we summarize the frequency response of the system. Results show that by increasing the bottom beam temperature from 300 to 1000, the frequencies of the system slightly decrease. For example, for a S-S/S-S system, when T_bottom = 400°, the first frequency is equal to 5.6356 and reduces to 5.5142 when T_bottom = 1000°. An increased temperature at the top beam induces a variation in the structural behavior, when the temperature of the bottom beam is kept constant to 300 °K. Based on Table 11, an increased temperature at the top beam yields an increased frequency response of the system, whereas the contrary occurs for an increased temperature at the bottom beam, which decreases the frequency response.

7. Conclusions

This paper has studied the vibrational behavior of nanocomposite coupled curved beams under a temperature variation, with an elastic interface modeled as an elastic distribution of elastic springs both in the normal and tangential direction. Each arm of the coupled specimen is made of a PMMA matrix reinforced with SWCNTs with a considerable and effective improvement in the vibrational response of the system. The equivalent temperature-dependent mechanical properties of the nanocomposite material have been obtained based on the well-known rule of mixture and approximate temperature-dependent formulation. Various distribution patterns of the reinforcement phase have been considered throughout the specimen, whose natural frequencies are determined by applying the GDQ technique as useful tool to discretize the governing differential equations of the problem, here determined according to a FSDT. A comparative analysis of the results against further theoretical predictions in the literature has confirmed the correctness and accuracy of the proposed procedure, where a large parametric investigation has evaluated the sensitivity of the vibrational response to different key input parameters, both in a geometric and mechanical sense—primarily, the curvature and the boundary conditions, along with the CNT distribution patterns, the interfacial stiffness, and the thermal dependence of the mechanical properties. It was observed that there is strong agreement between the obtained results and the responses from previous research (less than 5%). Some specific results can be pointed out:

• The system frequency declines with an increased value of R/h. This holds true for all boundary conditions and various volume fractions of CNTs.
• In all boundary conditions, except C-F/C-F, variations in the stiffness of the interfacial springs do not considerably influence the first dimensionless frequency of the system.
• As the volume fraction of CNTs in the bottom beam rises from zero to 0.12, the system frequencies increase across all boundary conditions. However, they remain constant for volume fractions ranging from 0.12 to 0.28.
• Elevating the temperature at the upper beam leads to an augmented frequency response of the system. Conversely, raising the temperature at the lower beam diminishes its frequency response.

These theoretical studies on the natural frequency response of FG-CNT coupled curved beams in thermal conditions have practical implications for optimizing structural design, material selection, and performance in aerospace, automotive, and related applications. The insights gained also contribute to vibration control, energy harvesting, and structural health monitoring.