Experimental Study on Damage Constitutive Model of Rock under Thermo-Confining Pressure Coupling
Abstract
1. Introduction
2. Experimental Program
2.1. Specimen Preparation
2.2. Testing System
2.3. Test Procedure
- (1)
- The standard granite sample was securely enclosed in a specialized fluoro rubber sleeve to prevent hydraulic oil infiltration, ensuring test accuracy. After clearing debris from the steel block connections, the rock core was placed flat with end blocks at both ends. The axial strain gauge was carefully adjusted to its proper position, and the circumferential strain gauge was installed at the center of the specimen. A slight touch confirmed proper connection by displaying minimal displacement on the computer. Initial values were then set on the computer.
- (2)
- Using the GCTS high-temperature and high-pressure rock triaxial apparatus, the rock samples were subjected to an initial confining pressure state (σ2 = σ3 of 0 MPa) and maintained consistently. In this experiment, the loading was controlled by a fixed axial displacement rate. The loading rate was set to 0.03 mm/min in the computer software control system, and the stress limit was set to 70% of the standard uniaxial compressive strength of the rock samples at room temperature [37]. When the axial stress reached the preset stress limit, the system automatically stopped loading. Subsequently, the confining pressure and stress were unloaded to 0 MPa. During the loading process, the system continuously collects and records the stress and strain values of the rock sample in real-time. Peak strength, residual strength, axial strain, and circumferential strain are directly obtained from the recorded data. The real-time stress–strain curve is monitored to ensure that the test data meet the requirements of this study.
- (3)
- Repeat step (2), applying initial confining pressures of σ2 = σ3 at 5 MPa, 10 MPa, 15 MPa, 20 MPa, and 25 MPa. Complete the triaxial compression tests at 20 °C under different confining pressure conditions.
- (4)
- After unloading the confining pressure and stress to 0 MPa, the hydraulic oil in the pressure chamber was heated to the preset temperature of 40 °C using the temperature control system of the GCTS high-temperature, high-pressure rock triaxial apparatus. The temperature was maintained for a period of time to ensure uniform heating of the specimen. Once the temperature stabilized, steps (2) and (3) were repeated to conduct the triaxial compression test at 40 °C under different confining pressure conditions.
- (5)
- Repeat step (4), heating the samples to the predetermined temperatures of 60 °C, 80 °C, and 120 °C. When the experiment reaches the condition of 25 MPa confining pressure and 120 °C temperature, the loading continues until the sample fails. Complete the triaxial compression tests at 60 °C, 80 °C, and 120 °C under different confining pressure conditions.
- (6)
- After the sample failure, turn off the loading system and temperature control system of the triaxial apparatus. Once the temperature of the hydraulic oil in the pressure chamber drops to room temperature, unload the confining pressure, drain the hydraulic oil, and remove the samples. Observe and record the failure characteristics of the samples and organize and analyze the experimental data.
3. Results and Discussion
3.1. Failure Modes
3.2. Analysis of Mechanical Properties of Rocks
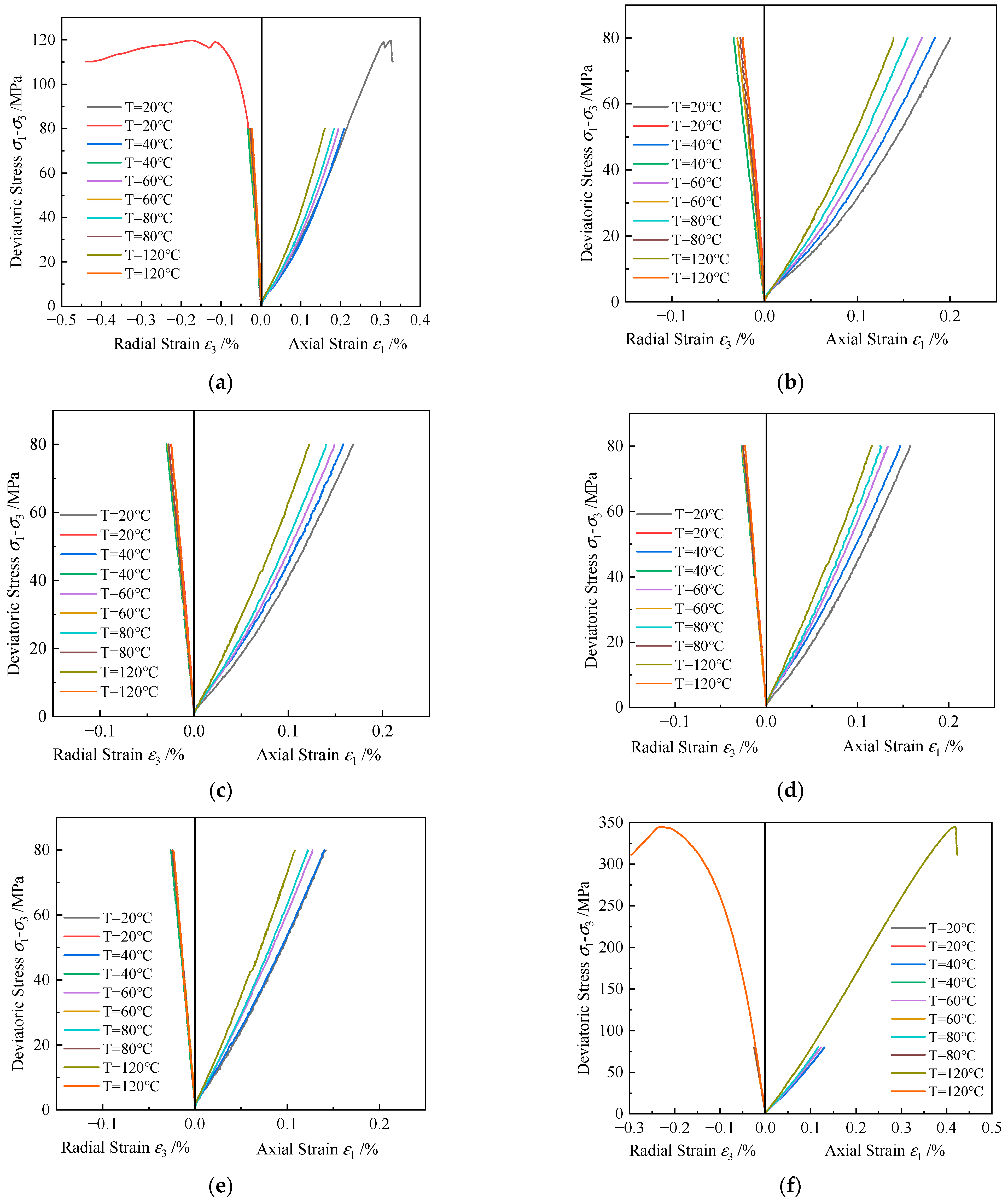
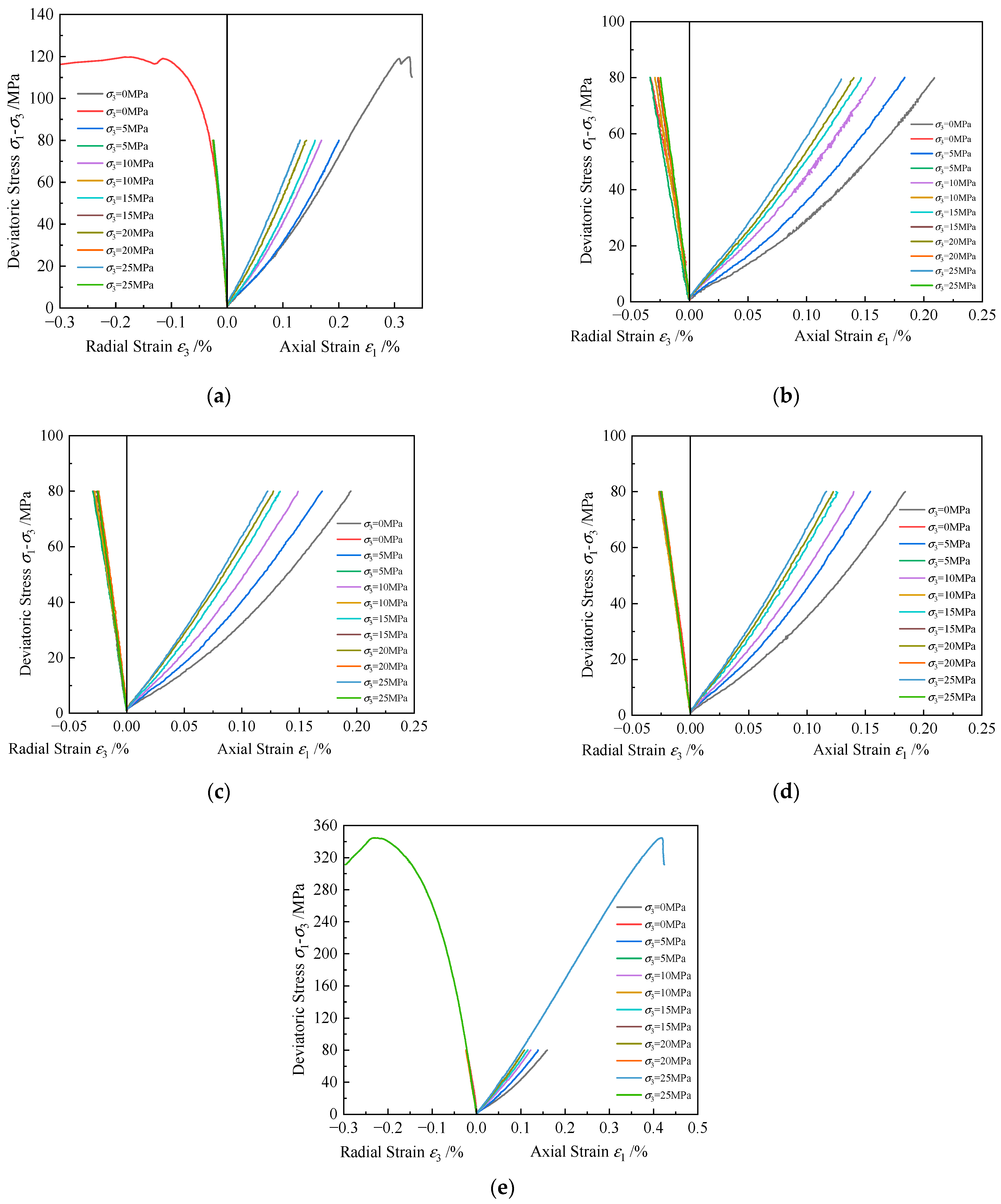
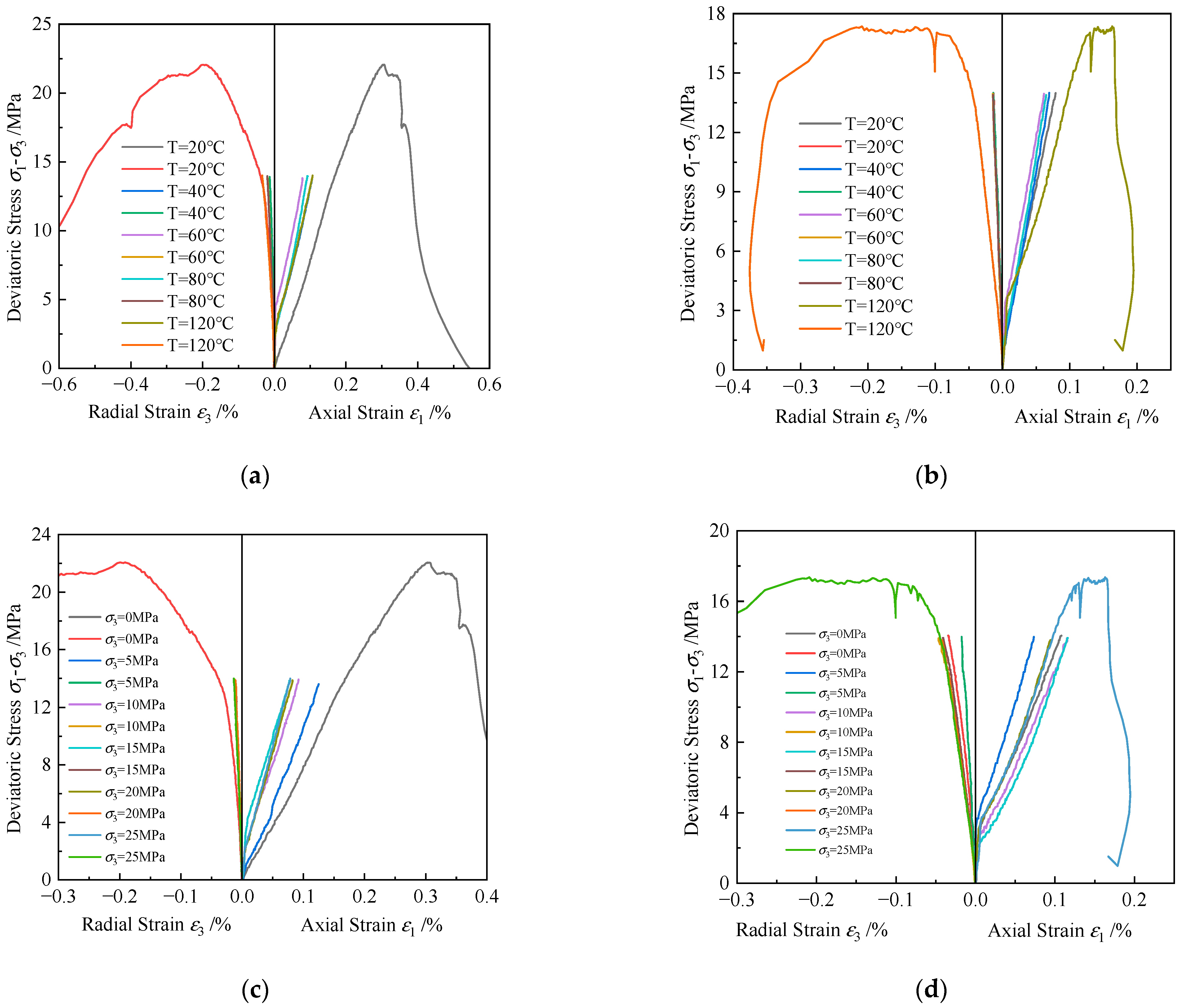
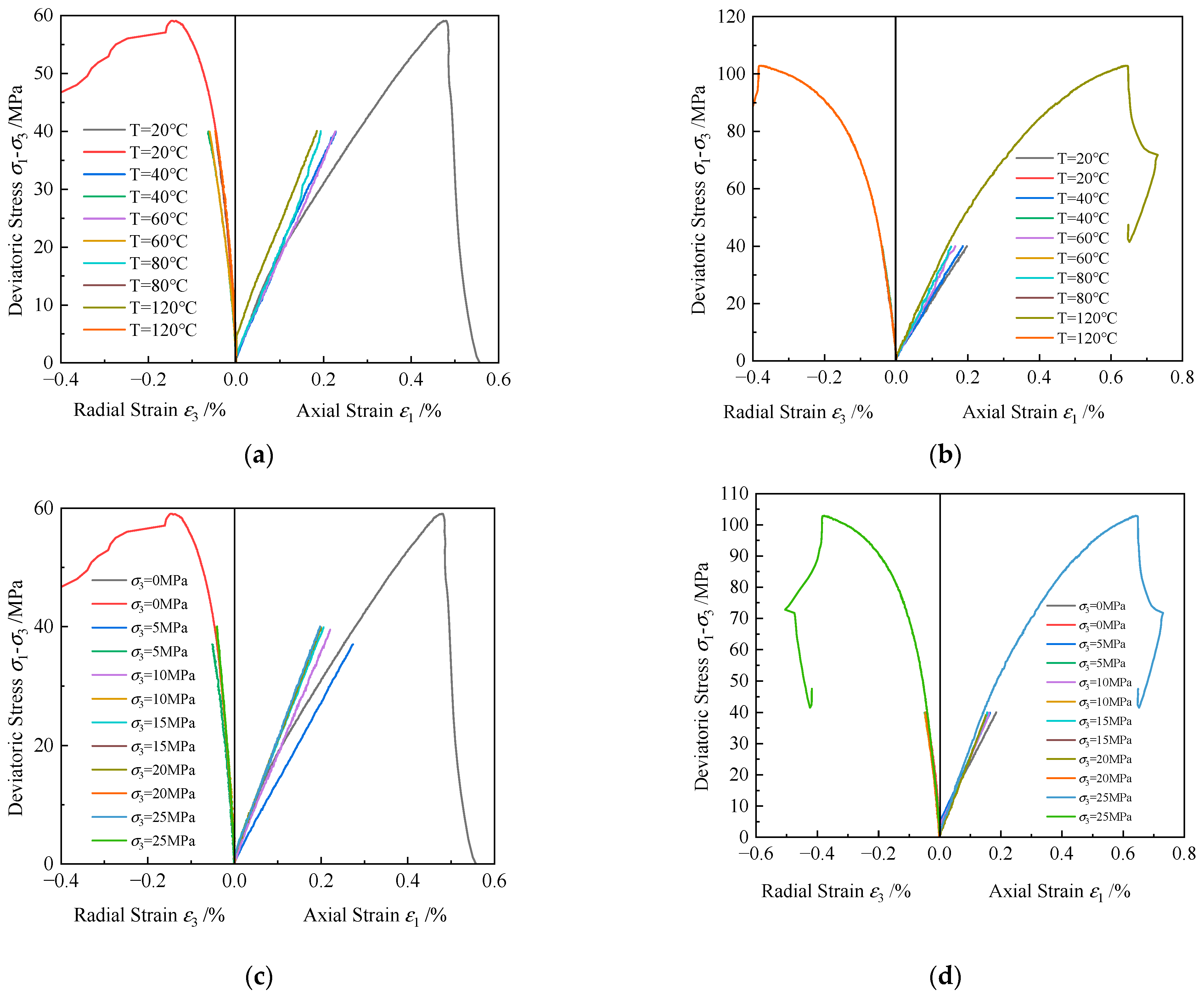
3.2.1. Analysis of Stress–Strain Curves for Different Rocks
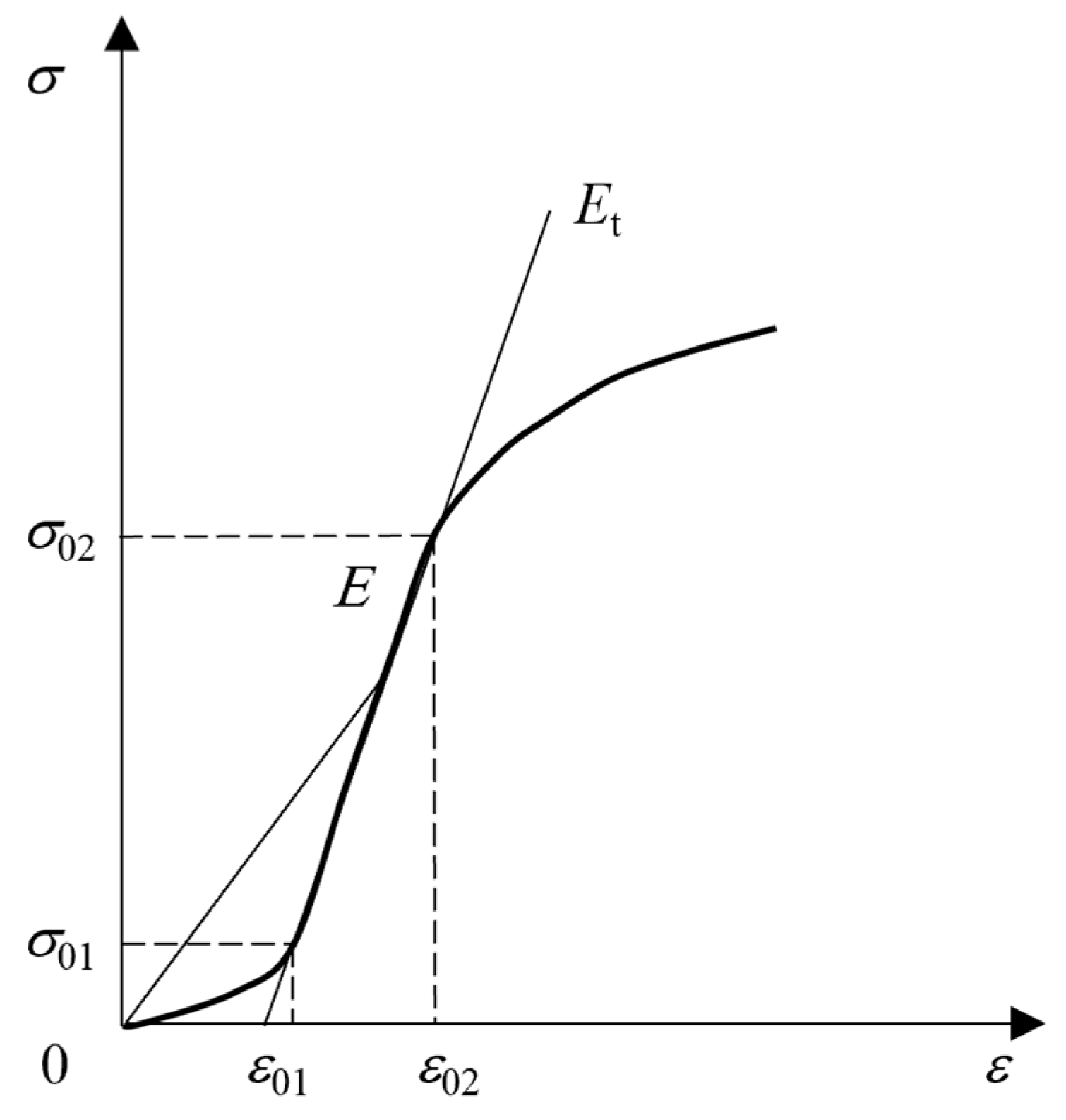
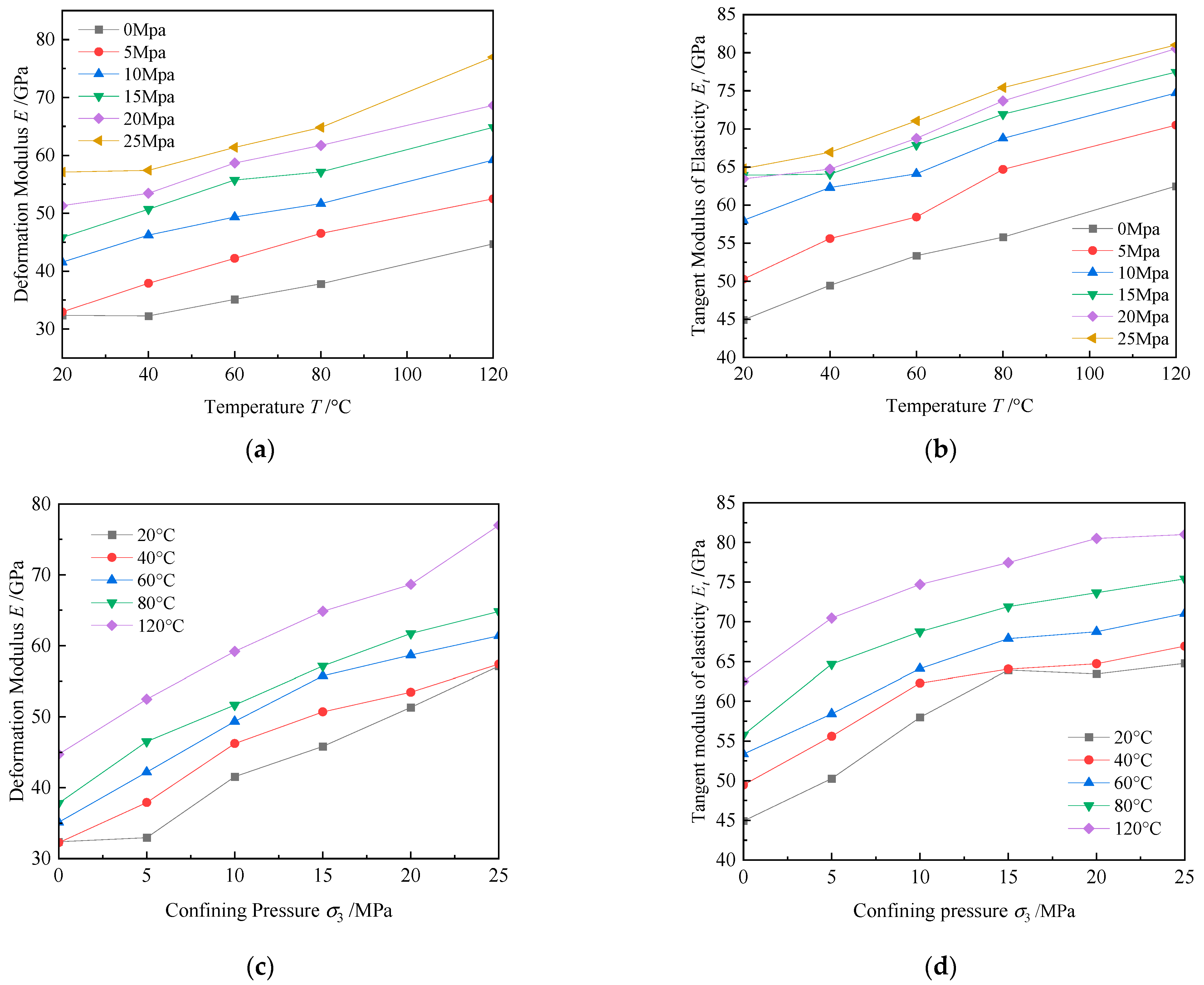
3.2.2. Analysis of Elastic Modulus for Different Rocks
3.3. Model Analysis of Elastic Modulus of Rock
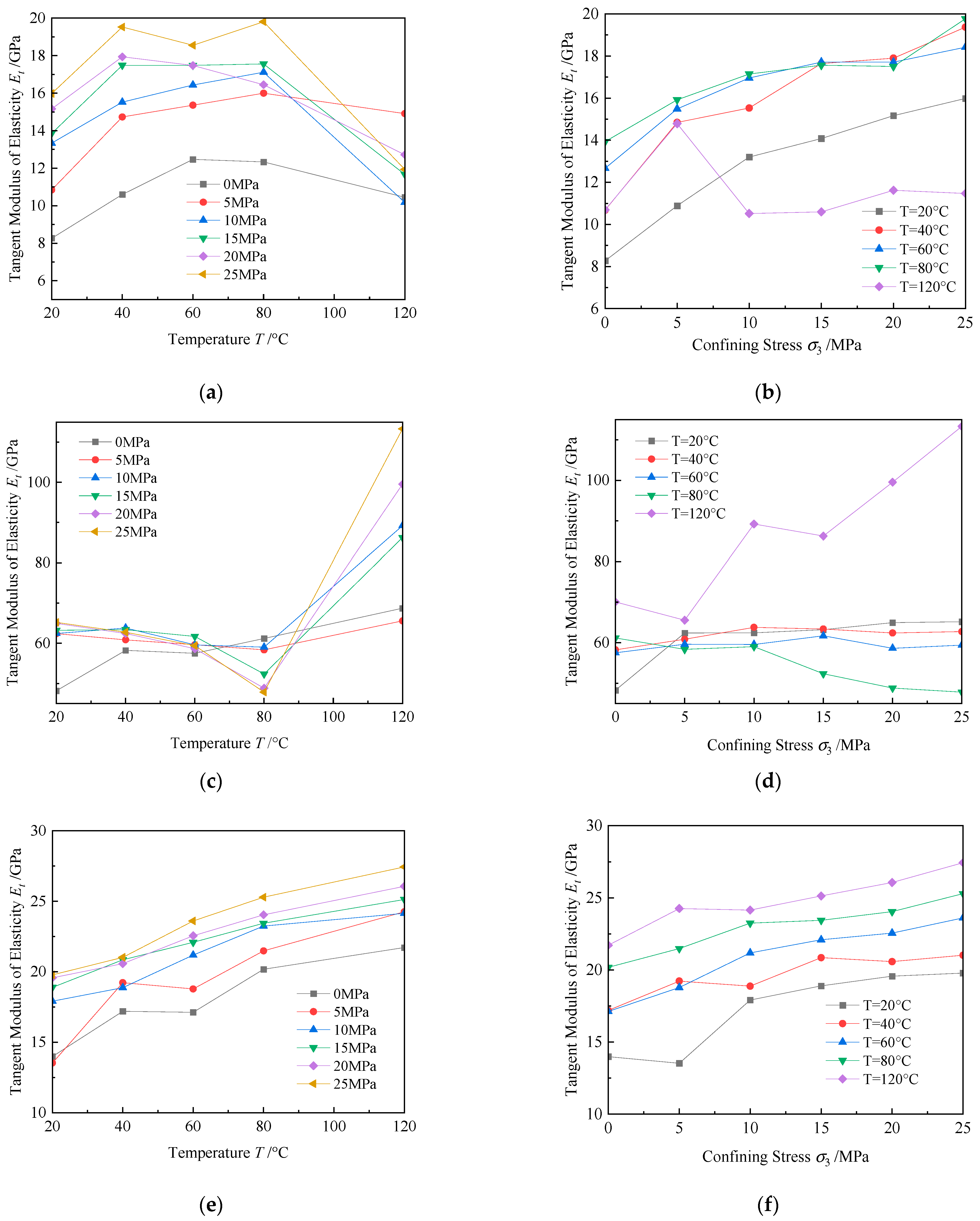
3.3.1. Modeling the Elastic Modulus of Rock under the Influence of Temperature
3.3.2. Modeling the Elastic Modulus of Rock under the Influence of Confining Pressure
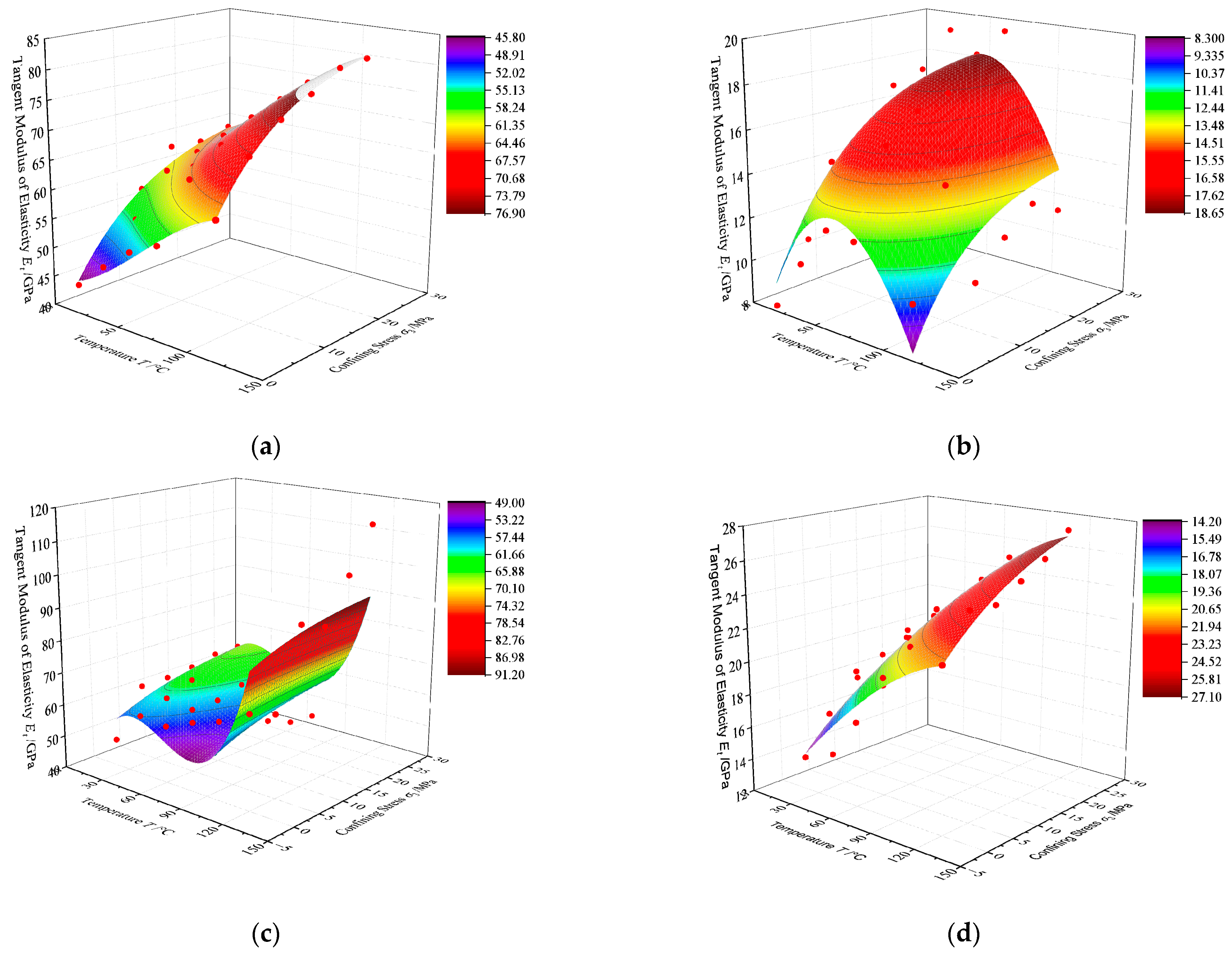
3.3.3. Modeling the Elastic Modulus of Rock under the Influence of Temperature and Confining Pressure
4. Damage Constitutive Model of Rock
4.1. Rock Damage Theory Based on the Drucker–Prager Criterion
4.1.1. Rock Damage under Confining Pressure
4.1.2. Rock Damage under Temperature
4.1.3. Total Damage of Rock under Thermo-Confining Pressure Coupling
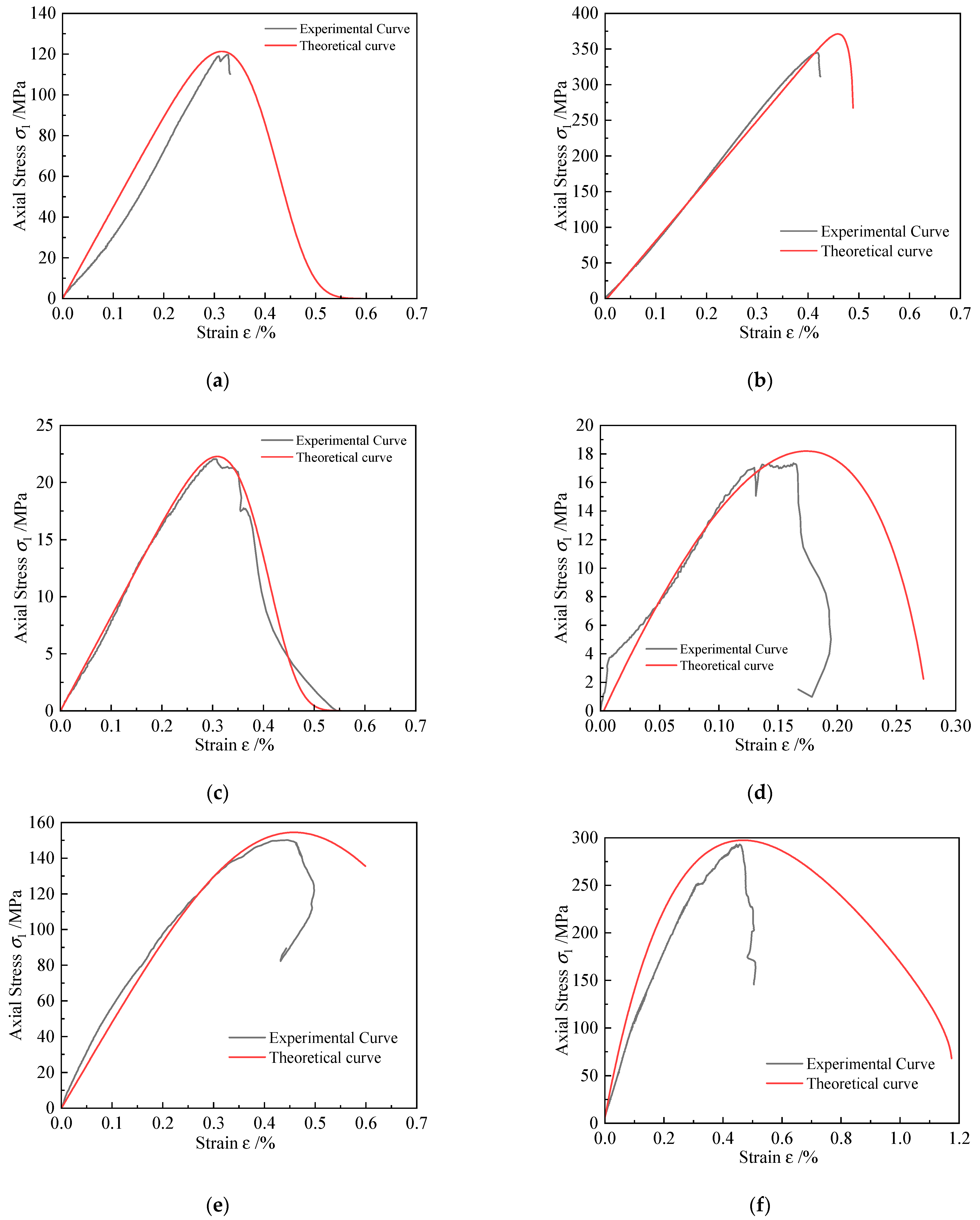
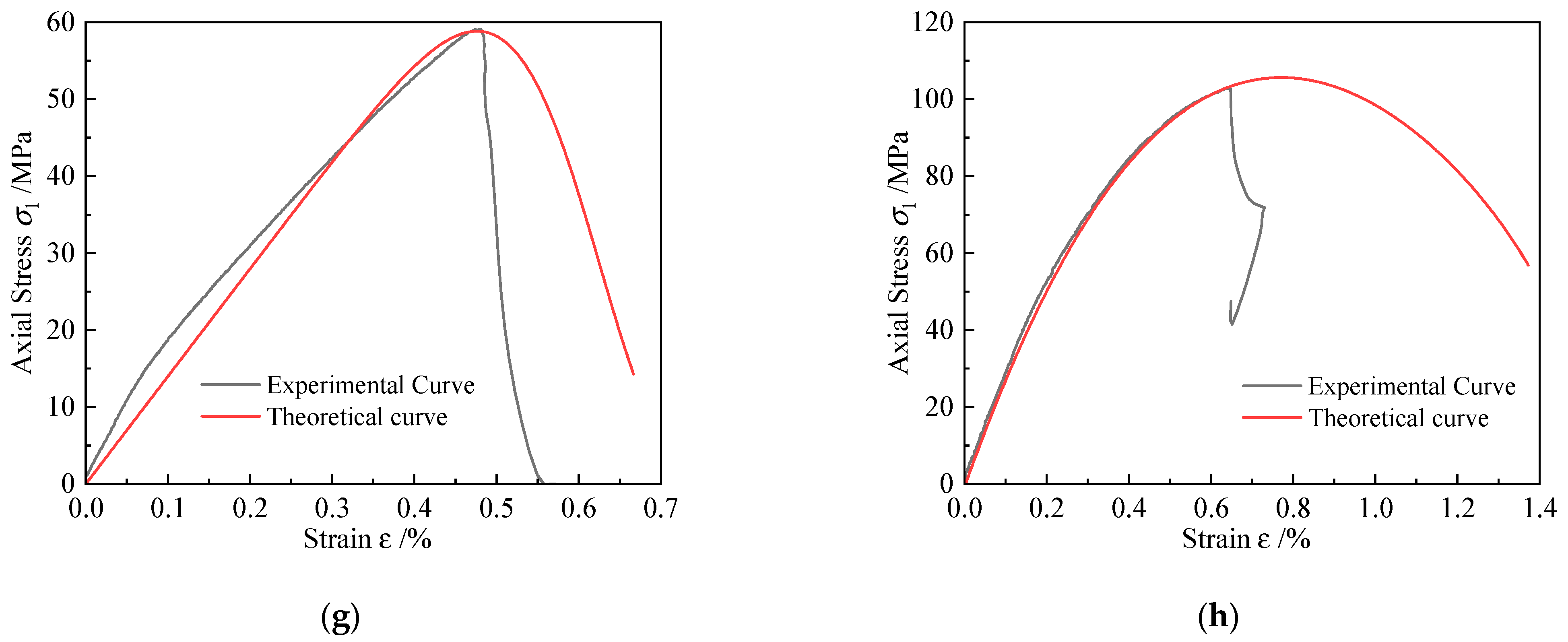
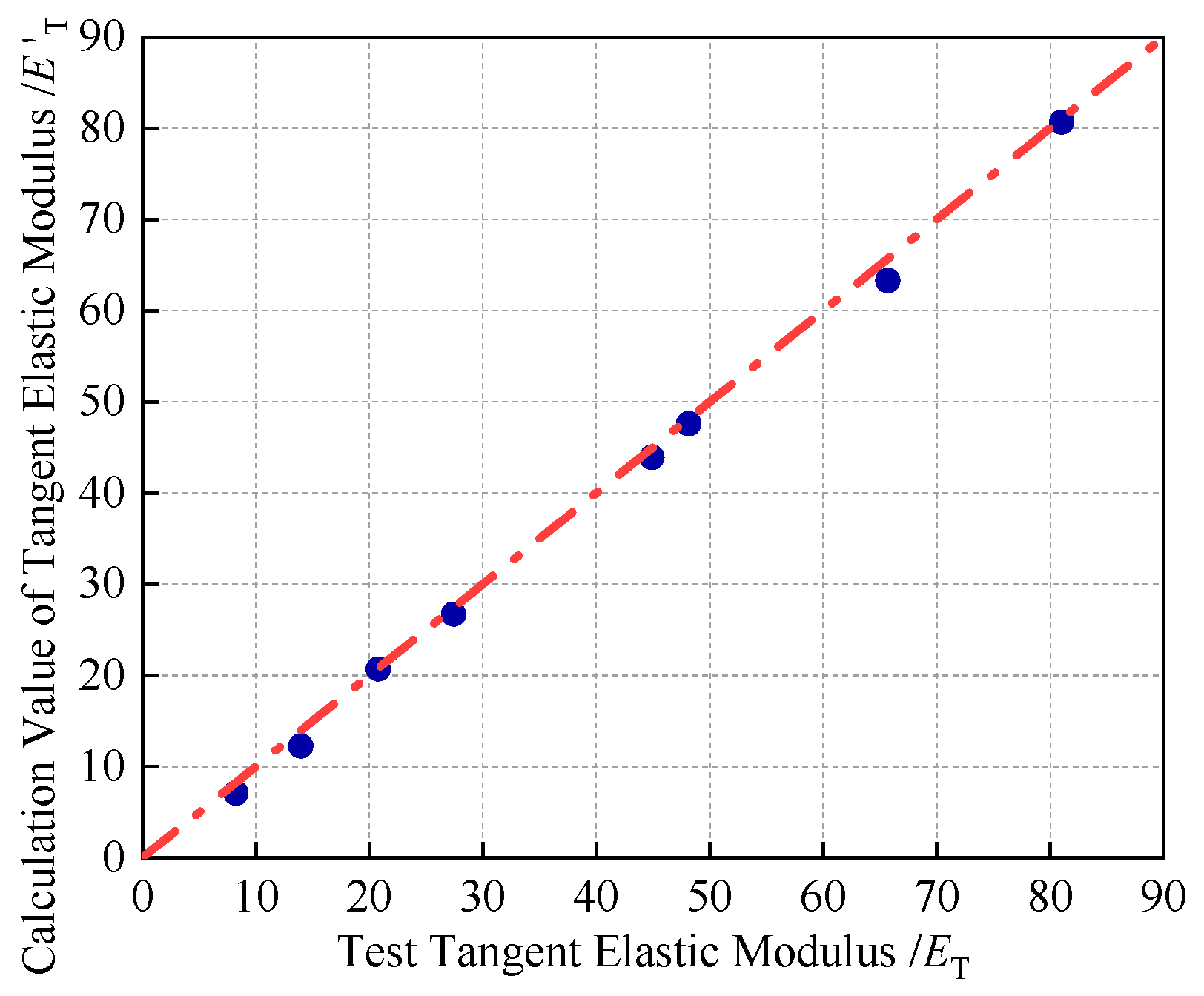
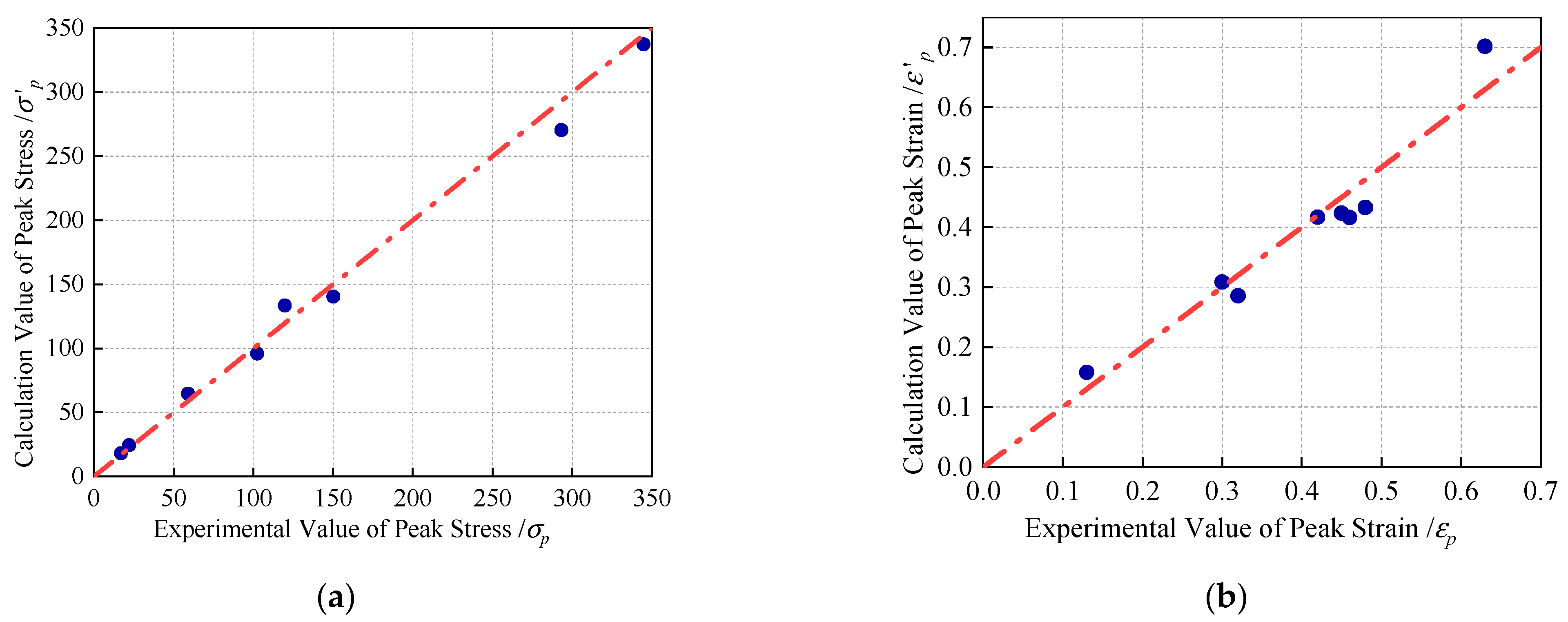
4.2. Experimental Validation of the Damage Constitutive Model of Rock under Thermo-Confining Pressure Coupling
5. Conclusions
- (1)
- Temperature influences the elastic modulus of rocks differently. Granite and shale show an increase in elastic modulus with temperature. Red sandstone’s elastic modulus increases initially, then decreases after a threshold, while gray sandstone exhibits the opposite trend. These differences are attributed to variations in internal structure, mineral composition, and the behavior of microcracks. Confining pressure significantly impacts elastic modulus and strain, with more pronounced changes under low confining pressure.
- (2)
- The combined effects of temperature and confining pressure enhance the peak strength and strain of granite, gray sandstone, and shale at 120 °C and 25 MPa, compared to 20 °C and 0 MPa, indicating increased density, load-bearing capacity, and ductility. Conversely, red sandstone shows reduced strength at higher temperatures, likely due to thermal expansion and internal crack propagation. The coupling also affects rock failure characteristics, with smoother fracture surfaces under triaxial conditions compared to uniaxial conditions.
- (3)
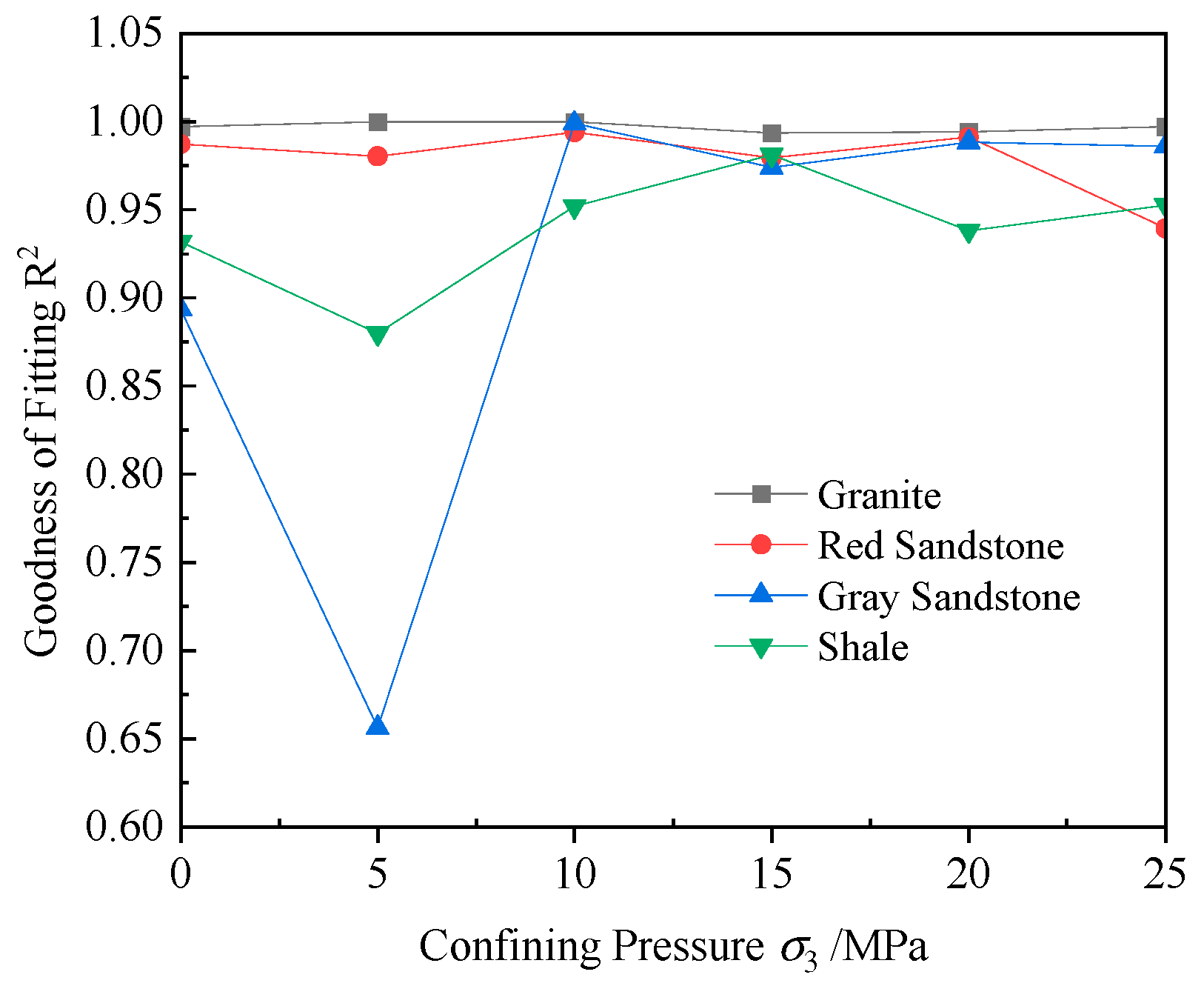
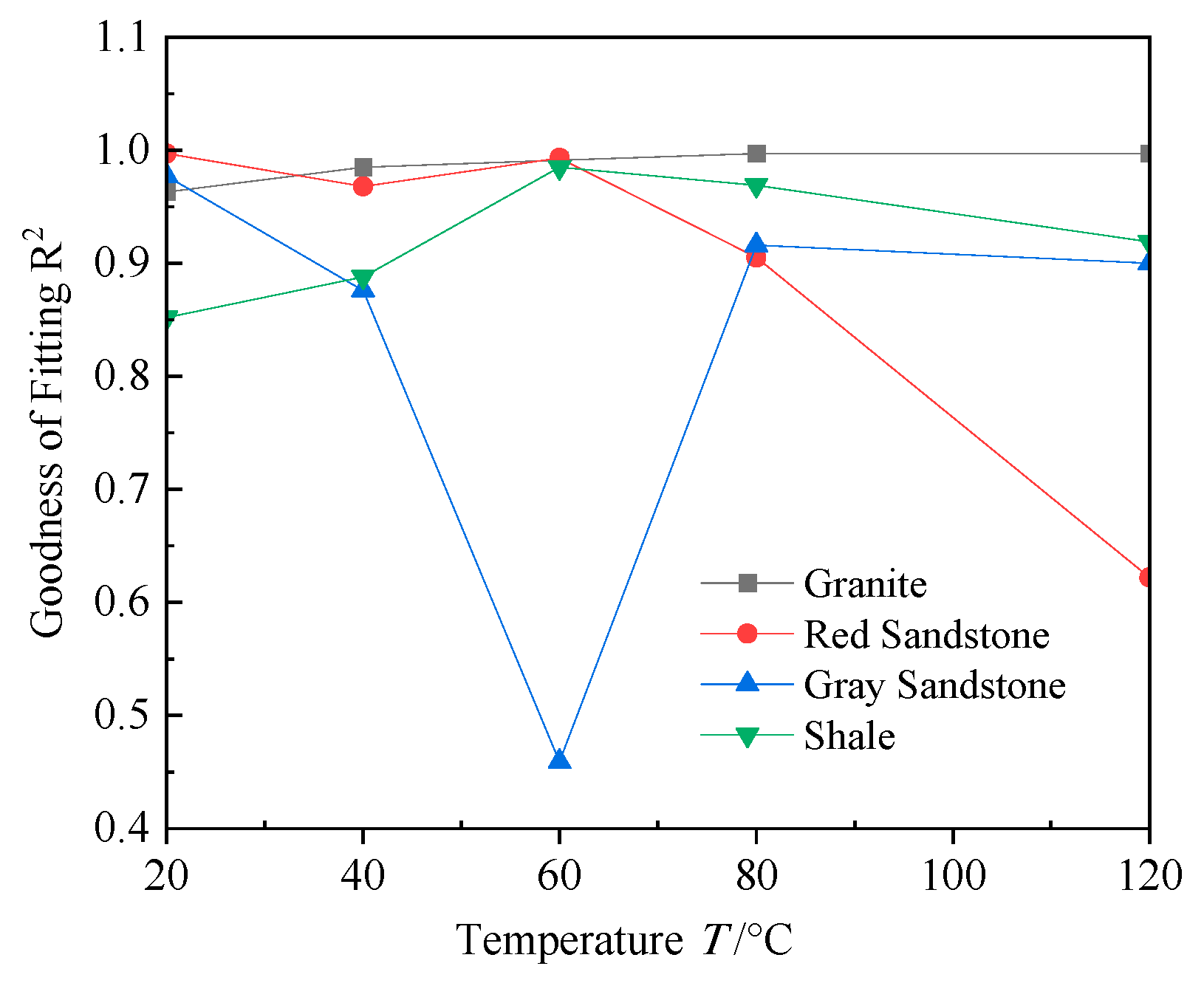
- A fitting model for the tangent elastic modulus (Et) under temperature and confining pressure was developed. A polynomial model captures temperature-induced changes, particularly the decline in Et, while a composite exponential model fits the confining pressure effects. The combined model accurately predicts Et under dual influences, with a high goodness-of-fit (R2 close to 1), offering a reliable reference for evaluating rock deformation.
- (4)
- A constitutive model accounting for temperature and confining pressure coupling was formulated based on the Drucker–Prager criterion and Weibull statistical damage theory. Empirical formulas were derived for different rocks under varying conditions, and the model was validated against experimental results, showing strong consistency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, N.; Liang, H.L.; Shen, T.; Yang, W.H. Temperature Dependence of Young’s Modulus of Red Sandstone. Therm. Sci. 2019, 23, 1599–1606. [Google Scholar] [CrossRef]
- Tian, H.; Kempka, T.; Xu, N.X.; Ziegler, M. Physical Properties of Sandstones After High Temperature Treatment. Rock Mech. Rock Eng. 2012, 45, 1113–1117. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Sun, Q.; Hao, S.Q.; Geng, J.S.; Lv, C. Experimental study on the variation of physical and mechanical properties of rock after high temperature treatment. Appl. Therm. Eng. 2016, 98, 1297–1304. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhu, H.H. Three-dimensional Hoek-Brown strength criterion for rocks. J. Geotech. Geoenviron. 2007, 133, 1128–1135. [Google Scholar] [CrossRef]
- Fan, L.F.; Gao, J.W.; Wu, Z.J.; Yang, S.Q.; Ma, G.W. An investigation of thermal effects on micro-properties of granite by X-ray CT technique. Appl. Therm. Eng. 2018, 140, 505–519. [Google Scholar] [CrossRef]
- Yin, T.B.; Chen, Y.J.; Li, X.B.; Li, Q. Effect of high temperature and strain rate on the elastic modulus of rocks: A review. Int. J. Earth Sci. 2021, 110, 2639–2660. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, L.; Luo, N. Elastic modulus evolution of rocks under heating-cooling cycles. Sci. Rep. 2020, 10, 13835. [Google Scholar] [CrossRef]
- Suknev, S.V. Determination of elastic properties of rocks under varying temperature. J. Min. Sci. 2016, 52, 378–387. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jiang, Y.Z.; Xu, W.Y.; Chen, X.Q. Experimental investigation on strength and failure behavior of pre-cracked marble under conventional triaxial compression. Int. J. Solids Struct. 2008, 45, 4796–4819. [Google Scholar] [CrossRef]
- Liu, J.-T.; Wang, J.-B.; Ge, H.-K.; Zhou, W.; Chen, B.-B.; Li, X.-D.; Xue, X.-J.; Luo, S.-L. Effect of gravel on rock failure in glutenite reservoirs under different confining pressures. Pet. Sci. 2023, 20, 3022–3036. [Google Scholar] [CrossRef]
- Arzúa, J.; Alejano, L.R.; Walton, G. Strength and dilation of jointed granite specimens in servo-controlled triaxial tests. Int. J. Rock Mech. Min. 2014, 69, 93–104. [Google Scholar] [CrossRef]
- Chen, M.; Zang, C.-W.; Ding, Z.-W.; Zhou, G.-L.; Jiang, B.-Y.; Zhang, G.-C.; Zhang, C.-P. Effects of confining pressure on deformation failure behavior of jointed rock. J. Cent. South Univ. 2022, 29, 1305–1319. [Google Scholar] [CrossRef]
- Yang, H.; Dahlhaus, N.; Renner, J. On the Effect of Lateral Confinement on Rock-Cutting Tool Interactions. Rock Mech. Rock Eng. 2024, 57, 6063–6083. [Google Scholar] [CrossRef]
- Meng, Y.; Jing, H.; Liu, X.; Yin, Q. Effects of initial unloading level on the mechanical, micro failure and energy evolution characteristics of stratified rock mass under triaxial unloading confining pressure. Theor. Appl. Fract. Mech. 2023, 128, 104161. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H.; Zhang, W.; Lou, J.; Shan, B. An analytical solution of equivalent elastic modulus considering confining stress and its variables sensitivity analysis for fractured rock masses. J. Rock Mech. Geotech. Eng. 2022, 14, 825–836. [Google Scholar] [CrossRef]
- Wang, H.W.; Wang, Y.Y.; Fu, X. Experimental Study on Coupling Influence of Temperature and Confining Pressure to Deformation and Strength Characteristics of Rock-like Material with Pre-Existing Crack. Materials 2021, 14, 7572. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Weng, L.; Ji, J.; Liu, Q. Numerical Investigation of Coupled Effects of Temperature and Confining Pressure on Rock Mechanical Properties in Fractured Rock Mass Using Thermal-Stress-Aperture Coupled Model. Int. J. Geomech. 2021, 21, 04021195. [Google Scholar] [CrossRef]
- Yang, J.; Fu, L.-Y.; Fu, B.-Y.; Wang, Z.; Hou, W. High-temperature effect on the material constants and elastic moduli for solid rocks. J. Geophys. Eng. 2021, 18, 583–593. [Google Scholar] [CrossRef]
- Demirci, A.; Görgülü, K.; Durutürk, Y.S. Thermal conductivity of rocks and its variation with uniaxial and triaxial stress. Int. J. Rock Mech. Min. 2004, 41, 1133–1138. [Google Scholar] [CrossRef]
- Kumari, W.G.P.; Ranjith, P.G.; Perera, M.S.A.; Shao, S.; Chen, B.K.; Lashin, A.; Al Arifi, N.; Rathnaweera, T.D. Mechanical behaviour of Australian Strathbogie granite under in-situ stress and temperature conditions: An application to geothermal energy extraction. Geothermics 2017, 65, 44–59. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, Y.; Yan, X.; Yang, S.; Li, C.; Peng, H. Experimental study on P-wave response characteristics of hot dry rock under high temperature and high confining pressure. Geomech. Energy Environ. 2023, 36, 100514. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhu, Z.; Liu, W.; Lu, H.; Fan, Z.; Nie, X.; Li, C.; Wang, J.; Ren, L. Hydraulic fracturing behaviors of shale under coupled stress and temperature conditions simulating different burial depths. Int. J. Min. Sci. Technol. 2024, 34, 783–797. [Google Scholar] [CrossRef]
- Yang, J.P.; Chen, W.Z.; Yang, D.S.; Tian, H.M. Estimation of Elastic Moduli of Non-persistent Fractured Rock Masses. Rock Mech. Rock Eng. 2016, 49, 1977–1983. [Google Scholar] [CrossRef]
- Wu, F.Q.; Deng, Y.; Wu, J.; Li, B.; Sha, P.; Guan, S.G.; Zhang, K.; He, K.Q.; Liu, H.D.; Qiu, S.H. Stress-strain relationship in elastic stage of fractured rock mass. Eng. Geol. 2020, 268, 105498. [Google Scholar] [CrossRef]
- Hua, D.J.; Jiang, Q.H.; Liu, R.Y.; Gao, Y.C.; Yu, M. Rock mass deformation modulus estimation models based on in situ tests. Rock Mech. Rock Eng. 2021, 54, 5683–5702. [Google Scholar] [CrossRef]
- Malkowski, P.; Ostrowski, L. The Methodology for the Young Modulus Derivation for Rocks and Its Value. Procedia Eng. 2017, 191, 134–141. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, C.; Zhao, M.; Li, X. Statistical Damage Constitutive Model for Rocks Considering Residual Strength. Int. J. Geomech. 2017, 17, 04016033. [Google Scholar] [CrossRef]
- Xu, X.L.; Gao, F.; Zhang, Z.Z. Thermo-mechanical coupling damage constitutive model of rock based on the Hoek-Brown strength criterion. Int. J. Damage Mech. 2018, 27, 1213–1230. [Google Scholar] [CrossRef]
- Chen, Y.; Xiao, P.; Du, X.; Wang, S.; Wang, Z.; Azzam, R. Study on Damage Statistical Constitutive Model of Triaxial Compression of Acid-Etched Rock under Coupling Effect of Temperature and Confining Pressure. Materials 2021, 14, 7414. [Google Scholar] [CrossRef]
- Li, X.; Yin, Z.; Falsone, G. A Time-Dependent Creep Constitutive Model of Deep Surrounding Rock under Temperature-Stress Coupling. Math. Probl. Eng. 2021, 2021, 9938869. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Zhang, Y.; Wu, Z. Rock strengthening or weakening upon heating in the mild temperature range? Eng. Geol. 2020, 272, 105619. [Google Scholar] [CrossRef]
- Zhao, G.; Guo, Y.; Chang, X.; Jin, P.; Hu, Y. Effects of temperature and increasing amplitude cyclic loading on the mechanical properties and energy characteristics of granite. Bull. Eng. Geol. Environ. 2022, 81, 155. [Google Scholar] [CrossRef]
- Rao, G.M.N.; Murthy, C.R.L. Dual role of microcracks: Toughening and degradation. Can. Geotech. J. 2001, 38, 427–440. [Google Scholar] [CrossRef]
- Taheri, A.; Royle, A.; Yang, Z.; Zhao, Y. Study on variations of peak strength of a sandstone during cyclic loading. Geomech. Geophys. Geo-Energy Geo-Resour. 2015, 2, 1–10. [Google Scholar] [CrossRef]
- Lin, H.; Liu, J.; Yang, J.; Ran, L.; Ding, G.; Wu, Z.; Lyu, C.; Bian, Y. Analysis of damage characteristics and energy evolution of salt rock under triaxial cyclic loading and unloading. J. Energy Storage 2022, 56, 106145. [Google Scholar] [CrossRef]
- Miao, S.; Liu, Z.; Zhao, X.; Ma, L.; Zheng, Y.; Xia, D. Plastic and damage energy dissipation characteristics and damage evolution of Beishan granite under triaxial cyclic loading. Int. J. Rock Mech. Min. 2024, 174, 105644. [Google Scholar] [CrossRef]
- Tiang, Y.; Chen, H.; Xiong, L.; Xu, Z. Conventional triaxial loading and unloading test and PFC numerical simulation of rock with single fracture. Arch. Civil. Eng. 2024, 70, 233–254. [Google Scholar] [CrossRef]
- Krajcinovic, D.; Fonseka, G.U. The Continuous Damage Theory of Brittle Materials, Part 1: General Theory. J. Appl. Mech. 1981, 48, 809–815. [Google Scholar] [CrossRef]
- Fonseka, G.U.; Krajcinovic, D. The Continuous Damage Theory of Brittle Materials, Part 2: Uniaxial and Plane Response Modes. J. Appl. Mech. 1981, 48, 816–824. [Google Scholar] [CrossRef]




| Rock Specimen | Peak Strength/MPa | Average Uniaxial Compressive Strength/MPa | Standard Value of Compression Strength/MPa | Upper Limit of Stress/MPa |
|---|---|---|---|---|
| G-JZ-1 | 119.96 | 133.73 | 115.49 | 80.84 |
| G-JZ-2 | 133.72 | |||
| G-JZ-3 | 147.50 | |||
| RS-JZ-1 | 25.40 | 25.04 | 21.36 | 14.95 |
| RS-JZ-2 | 21.98 | |||
| RS-JZ-3 | 27.75 | |||
| GS-JZ-1 | 148.26 | 158.17 | 138.47 | 96.93 |
| GS-JZ-2 | 151.24 | |||
| GS-JZ-3 | 175.03 | |||
| SH-JZ-1 | 60.72 | 60.29 | 59.28 | 41.49 |
| SH-JZ-2 | 60.74 | |||
| SH-JZ-3 | 59.42 |
| A | B | C | D | E | R2 | |
|---|---|---|---|---|---|---|
| G | −1.5519 × 10−5 | 0.00319 | −0.01056 | 23.53821 | 11.65526 | 0.98819 |
| RS | 3.6669 × 10−6 | −0.00245 | 0.26988 | 2.36925 | 8.99786 | 0.81258 |
| GS | 1.7180 × 10−4 | −0.02891 | 1.35263 | 35.58206 | 15.28693 | 0.71489 |
| SH | −1.5150 × 10−6 | −6.6366 × 10−5 | 0.11000 | 6.38303 | 20.27230 | 0.95229 |
| Rock Type | T/°C | σ3/MPa | σp/MPa | εp/% | φ/° | ET/GPa | υ | m | F0 |
|---|---|---|---|---|---|---|---|---|---|
| G | 20 | 0 | 119.02 | 0.31 | 45 | 44.93 | 0.15 | 6.56 | 44.42 |
| 120 | 25 | 344.60 | 0.42 | 50 | 81.02 | 0.21 | 35.59 | 93.30 | |
| RS | 20 | 0 | 22.06 | 0.29 | 45 | 8.27 | 0.23 | 14.24 | 6.92 |
| 120 | 25 | 17.04 | 0.13 | 53 | 11.93 | 0.22 | 1.00 | 32.90 | |
| GS | 20 | 0 | 150.22 | 0.45 | 45 | 48.16 | 0.07 | 2.80 | 68.49 |
| 120 | 25 | 289.53 | 0.43 | 45 | 113.34 | 0.35 | 0.94 | 124.62 | |
| SH | 20 | 0 | 59.09 | 0.48 | 45 | 13.99 | 0.30 | 8.07 | 20.98 |
| 120 | 25 | 102.63 | 0.63 | 45 | 27.43 | 0.28 | 1.24 | 80.31 |
| Rock Type | T/°C | σ3/MPa | Constitutive Model |
|---|---|---|---|
| G | 20 | 0 | |
| 120 | 25 | ||
| RS | 20 | 0 | |
| 120 | 25 | ||
| GS | 20 | 0 | |
| 120 | 25 | ||
| SH | 20 | 0 | |
| 120 | 25 |
| Rock Type | T/°C | σ3/MPa | Et/GPa | Et’/GPa | Specific Value |
|---|---|---|---|---|---|
| G | 20 | 0 | 44.93 | 43.92 | 0.98 |
| 120 | 25 | 81.02 | 80.68 | 1.00 | |
| RS | 20 | 0 | 8.27 | 7.08 | 0.86 |
| 120 | 25 | 20.81 | 20.71 | 0.99 | |
| GS | 20 | 0 | 48.16 | 47.58 | 0.99 |
| 120 | 25 | 65.71 | 63.29 | 0.96 | |
| SH | 20 | 0 | 13.99 | 12.25 | 0.88 |
| 120 | 25 | 27.43 | 26.71 | 0.98 |
| Rock Type | T/°C | σ3/MPa | σp/MPa | σ‘p/MPa | Specific Value | εp | εp’ | Specific Value |
|---|---|---|---|---|---|---|---|---|
| G | 20 | 0 | 119.73 | 121.31 | 1.01 | 0.32 | 0.32 | 1.00 |
| 120 | 25 | 344.60 | 371.13 | 1.08 | 0.42 | 0.46 | 1.10 | |
| RS | 20 | 0 | 22.07 | 22.27 | 1.01 | 0.30 | 0.31 | 1.03 |
| 120 | 25 | 17.04 | 18.20 | 1.09 | 0.13 | 0.17 | 1.31 | |
| GS | 20 | 0 | 150.22 | 154.48 | 1.03 | 0.45 | 0.46 | 1.02 |
| 120 | 25 | 293.08 | 297.46 | 1.01 | 0.46 | 0.47 | 1.02 | |
| SH | 20 | 0 | 59.09 | 58.82 | 0.99 | 0.48 | 0.48 | 1.00 |
| 120 | 25 | 102.43 | 105.59 | 1.03 | 0.63 | 0.77 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Zhang, Z.; Hou, C.; Pan, T.; Lan, X.; Ji, Y. Experimental Study on Damage Constitutive Model of Rock under Thermo-Confining Pressure Coupling. Appl. Sci. 2024, 14, 9122. https://doi.org/10.3390/app14199122
Zheng Y, Zhang Z, Hou C, Pan T, Lan X, Ji Y. Experimental Study on Damage Constitutive Model of Rock under Thermo-Confining Pressure Coupling. Applied Sciences. 2024; 14(19):9122. https://doi.org/10.3390/app14199122
Chicago/Turabian StyleZheng, Yonglai, Zhengxie Zhang, Chenyu Hou, Tanbo Pan, Xin Lan, and Yifan Ji. 2024. "Experimental Study on Damage Constitutive Model of Rock under Thermo-Confining Pressure Coupling" Applied Sciences 14, no. 19: 9122. https://doi.org/10.3390/app14199122
APA StyleZheng, Y., Zhang, Z., Hou, C., Pan, T., Lan, X., & Ji, Y. (2024). Experimental Study on Damage Constitutive Model of Rock under Thermo-Confining Pressure Coupling. Applied Sciences, 14(19), 9122. https://doi.org/10.3390/app14199122







